自动控制原理及其应用答案第二版_黄坚_课后答案

格式：ppt
大小：4.94 MB
文档页数：95

下载文档原格式

《自动控制原理》黄坚课后习题答案

4
=
-3
4
A2=
-3
4
A2=
+
-
4
3
+
f(t)=
e-t3
2
e-3t2
-t
e-t12
1
+
-
4
3
+
f(t)=
e-t3
2
e-3t2
-t
e-t12
1
= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)]
A1(s+1)2A1=(s+1)2s
(s+1)2(s+2)s=-1A1=(s+1)2s(s+1)2(s+2)s=-1A3=(s+2)
s
(s+1)2(s+2)s=-2A3=(s+2)
s
(s+1)2(s+2)s=-2
d
ds
s
s+2
][
A2= s=-1
d
R2I1(s)
Uc(s)L1L2 L1=-R2 /LsL2=-/LCs2L3=-1/sCR1Δ1=1
L1L3=R2/LCR1s2P1=R2/LCR1s2=
R1CLs2+(R1R2C+L)s+R1+R2Ur(s)
Uc(s)
R2=
R1CLs2+(R1R2C+L)s+R1+R2Ur(s)
i2Lu1 解
u1=ui-uoi2=C

《自动控制原理》黄坚课后习题答案解析

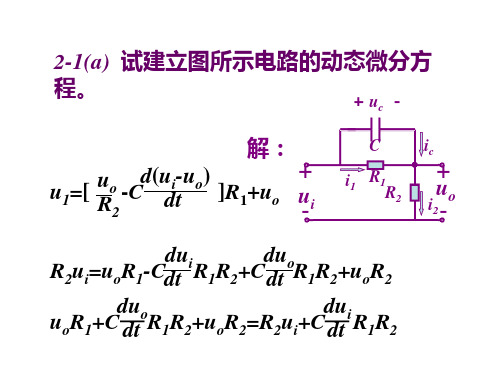
2-1试建立图所示电路的动态微分方程-u o+u o解：u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解：du )-R 2(u i -u o )=R 1u 0-CR 1R 2(idt dt du oCR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。

(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解：解：L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解：(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解：2-3求下列函数的拉氏反变换。

A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解：A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解：= A 2s+1s+2+A 3+ A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解：= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++解：=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。

自动控制原理及其应用答案第二版_黄坚课后答案_图文

2-8 设有一个初始条件为零的系统，系统的输入、输出曲线如图，求G(s)。
δ (t)
c(t)
T
解: t
δ (t)
c(t)
T
K 0
K 0
t
K K tc(t)= T T (t-T)
-TS K C(s)= Ts2 (1-e )
2-9 若系统在单位阶跃输入作用时，已知初始条件为零的条件下系统的输出响应，求系统的传递函数和脉冲响应。 1 R(s)= s 2+4s+2) (s 1 1 1 解: C(s)= s - s+2 + s+1 = s(s+1)(s+2) 2+4s+2) ( s = (s+1)(s+2) 2+4s+2) ( s 2 - 1 C(s)= (s+1)(s+2) =1+ s+ 2 s+1
2-5-b 试画出题 2-1图所示的电路的动态结构图,并求传递函数。 uo ∴ iL= R2
＋ ui －
R1 C
L
R2
＋ uo －
diL uL=L dt duc ic=C dt
UO(s) I2(s)= R2 UI(s)+UC(S) I1(s)= 即： R1
UO(s) I1(s)= R2 UC(s) IC(s)= Cs
i1 R1 R2
＋ uo i2 －
UI(s)-UO(s) 即: =I1(s) R1
UI(s)
UI(s) sC
1＋ sC )R2 (R 1 IC(s) ＋ I2(s) ＋ I1(s)
UO(s)
-
1 R1
R2
UO(s)

自动控制原理及其应用(第2版)黄坚第二章习题课

第二章习题课
(2-9)
2-9 若系统在单位阶跃输入作用时，已知初若系统在单位阶跃输入作用时，始条件为零的条件下系统的输出响应，始条件为零的条件下系统的输出响应，求系统的传递函数和脉冲响应。系统的传递函数和脉冲响应。 -t 1 -2t R(s)= s c(t)=1-e +e r(t)=I(t) 1 - 1 + 1 = (s2+4s+2) 解: C(s)= s s+2 s+1 s(s+1)(s+2) (s2+4s+2) G(s)=C(s)/R(s)= (s+1)(s+2) (s2+4s+2) =1+ 2 - 1 脉冲响应: 脉冲响应 C(s)= (s+1)(s+2) s+2 s+1 c(t)= (t)+2e-2t-e-t δ
第二章习题课
(2) dy(t) 2 dt +y(t)=t
(2-4)
y(0)=0
第二章习题课
(2-5)
2-5 试画题图所示电路的动态结构图，试画题图所示电路的动态结构图， c 并求传递函数。并求传递函数。 i1 (1) 解： + R
Ur(s)
Cs _
I1(s)
+ +
i2
1
+
I(s)
R2
Uc(s)
+ i uo -
第二章习题课
(b) 解： (ui-u1) i=i1+i2 i= R
1
(2-1)
u1 L i
R1 C
＋
ui
i1 i2
R2
+ uo -

自动控制原理黄坚第二版第三章习题答案

第三章习题课 (3-13)
3-13 已知系统结构如图，试确定系统稳定时τ值范围。 R(s) 10 C(s) １解: 10(1+ 1 ) s G(s)=s2+s+10 s τ 10(s+1) =s(s2+s+10 s) τ 10(s+1) Φ(s)= s3 +s2+10 s2+10s+10 τ 10(1+10 )-10 τ b31= 1+10 >0 τ
e
-1.8
第三章习题课 (3-6)
3-6 已知系统的单位阶跃响应: -60t -10t c(t)=1+0.2e -1.2e (1) 求系统的闭环传递函数。 (2) 求系统的阻尼比和无阻尼振荡频率。 1 + 0.2 - 1.2 = 600 解: C(s)= s s+60 s+10 s(s+60)(s+10) 1 C(s)= 600 R(s)= s R(s) s2+70s+600 ω n=24.5 ζ 2 ω n=70 ω n2 =600 ζ=1.43
第三章习题课 (3-17)
1 r(t)=I(t), t , 2 t2 (2) 求系统的稳态误差： 1 K1 τ = 1 G(s)= 2 解: s +Kτ s s( 1 Kτ s+1)
1
1 R(s)= s υ=1
Kp=∞ K =K υ
ess1=0 τ ess2= =0.24 ess3=∞
R(s)= s1 2 R(s)= s1 3
(3) 求d1(t)作用下的稳态误差． 1 K F(s)= Js G(s)=Kp + s -F(s) 1 essd= lim s1+G(s)F(s) s s→0 - 1 1 =0 Js = lim s K) 1 s s→0 1+(Kp+ s Js

自动控制原理黄坚第二版课后答案第四章

4-1 已知系统的零、极点分布如图，大解:(5)(7)(8)4-2 已知开环传递函数，试用解析法绘制出系统的根轨迹，并判断点(-2+j0),(0+j1),(-3+j2)是否在根轨迹上。

解:K r (s+1)G(s)=K rΦ(s)=s+1+Kr K r =0s=-1-K r系统的根轨迹s=-1K r =→∞s=-∞s=-2+j0s=0+j14-3 已知系统的开环传递函数，试绘制出根轨迹图。

解: 1p 1=0 p 2=-1 2p 1~p 2 z 1=-1.5 z 2z 1~p 3 3）根轨迹的渐近线 n-m= 1 θ= + 180o4）分离点和会合点A (s )B'(s )=A'(s )B (s )A(s)=s 3+6s 2+5s B(s)=s 2+7s+8.25A(s)'=3s 2+12s+5B(s)'=2s+7s 1=-0.63s 2=-2.5s 3=-3.6s 4=-7.28解得K s(s+1)(s+4)(2) G(s)=r (s+1.5)1）开环零、极点p 1=0p 2=-1p3=-42）实轴上根轨迹段p 1~p 2z 1=-1.5p 3~z 13）根轨迹的渐近线n-m= 2θ= +90o 2σ=-1-4+1.5=-1.754）分离点和会合点 A(s)=s 3+5s 2+4s B(s)=s+1.5 A(s)'=3s 2+10s+4 B(s)'=1 解得 s=-0.62 5）系统根轨迹K s(s+1)2(3) G(s)=r1）开环零、极点p 1=0p 2=-1p 3=-12）实轴上根轨迹段p 1~p 2p 3~-∞3）根轨迹的渐近线n-m=34θ= +180+60o ,闭环特征方程为s 3+2s 2+s+K r =05）分离点和会合点A(s)=s 3+2s 2+s B(s)=1A(s)'=3s 2+4s+1B(s)'=0解得s=-0.336）系统根轨迹1p 1=0p2p 1~p 2p 4=-15p 3~z 143）根轨迹的渐近线n-m=3(4) G(s)=3σ=-3-7-15+8=-5.67θ= +180o +60o , K r =0 ω1=0K r =638 ω2,3=±6.25）分离点和会合点A(s)=s 4+25s 3+171s 2+315s B(s)=s+8A(s)'=4s 3+75s 2+342s+315B(s)'=2s+7解得s=-1.44）根轨迹与虚轴的交点闭环特征方程为s 4+25s 3+171s 2+323s+8K r =04-5 已知系统的开环传递函数。

《自动控制原理》黄坚课后习题答案解析word版本

《⾃动控制原理》黄坚课后习题答案解析word版本2-1试建⽴图所⽰电路的动态微分⽅程-u o+u o解：u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解：)-R 2(u i -u o )=R 1u 0-CR 1R 2(dui dt dt duo CR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉⽒变换。

(1) f(t)=sin4t+cos4tL [sin ωt ]= ωω2+s 2=s+4s 2+16L [sin4t+cos4t ]= 4s 2+16s s 2+16+s ω2+s 2L [cos ωt ]=解：(2) f(t)=t 3+e 4t解：L [t 3+e 4t ]= 3!s 41s-4+6s+24+s 4s 4(s+4)=(3) f(t)=t n e atL [t n e at ]=n!(s-a)n+1解：(4) f(t)=(t-1)2e 2tL [(t-1)2e 2t ]=e -(s-2)2(s-2)3解：2-3求下列函数的拉⽒反变换。

A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解：A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解：= A 2s+1s+2+ A 3+A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds s s+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解：= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解：=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分⽅程。

《自动控制原理》黄坚课后习题答案

2-1试建立图所示电路的动态微分方程-u o+u o解：u 1=u i -u oi 2=C du 1dt i 1=i-i 2u o i=R 2u 1i 1=R 1=u i -u oR1dtd (u i -u o )=C(a)u C d (u i -u o )dtu o -R 2=i -u o R 1i=i 1+i 2i 2=C du 1dt u o i 1=R 2u 1-u o =L R2du odtR 1i=(u i -u 1)(b)解：)-R 2(u i -u o )=R 1u 0-CR 1R 2(dui dt dt duo CR 1R 2du o dt du idt +R 1u o +R 2u 0=CR 1R 2+R 2u iu o+C R 2du 1dt o +L R 2du odtu du o dt R 1R 2L du o dt +CL R 2d 2u o dt 2=--i R 1u o R 1u oR 2+C )u o R 1R 2L du o dt ) CL R 2d 2u o dt 2=++(u i R 11R 11R 2+(C+2-2 求下列函数的拉氏变换。

A 1=(s+2)s+1(s+2)(s+3)s=-2=-1=2f(t)=2e -3t -e -2t(1) F(s)=s+1(s+2)(s+3)解：A 2=(s+3)s+1(s+2)(s+3)s=-3F(s)= 2s+31s+2-= A 1s+2s+3+ A 2(2) F(s)=s (s+1)2(s+2)f(t)=-2e -2t -te -t +2e -t解：= A 2s+1s+2+ A 3+A 1(s+1)2A 1=(s+1)2s (s+1)2(s+2)s=-1A 3=(s+2)s (s+1)2(s+2)s=-2d ds ss+2][A 2= s=-1=-1=2=-2(3) F(s)=2s 2-5s+1s(s 2+1)F(s)(s 2+1)s=+j =A 1s+A 2s=+jA 2=-5A 3=F(s)s s=0f(t)=1+cost-5sint解：= s + A 3s 2+1A 1s+A 2=12s s 2-5s+1=A 1s+A2 s=j s=jj -2-5j+1=jA 1+A 2-5j-1=-A 1+jA 2A 1=1F(s)= 1s s 2+1s -5s 2+1++(4) F(s)=s+2s(s+1)2(s+3)解：=+s+1A 1s+3A 2(s+1)2+s A 3+A 4-12A 1= 23A 3= 112A 4= A 2= d [s=-1ds ](s+2)s(s+3) -34= -34A 2= +-43+f(t)=e -t 32e -3t 2-t e -t 121= s=-1 [s(s+3)]2[s(s+3)-(s+2)(2s+3)](2-4)求解下列微分方程。

《自动控制原理》黄坚课后习题答案解析

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章习题课
(2-8)
2-8 设有一个初始条件为零的系统，系统的输入、输出曲线如图，求G(s)。
δ (t)
c(t)
T
解: t
δ (t)
c(t)
T
K 0
K 0
t
-TS K K K c(t)= T t- T (t-T) C(s)= Ts2 (1-e ) C(s)=G(S)
第二章习题课
(2-９)
2-9 若系统在单位阶跃输入作用时，已知初始条件为零的条件下系统的输出响应，求系统的传递函数和脉冲响应。 -t 1 -2t R ( s )= c(t)=1-e +e r(t)=I(t) s 2+4s+2) (s 1 1 1 解: C(s)= s - s+2 + s+1 = s(s+1)(s+2) 2+4s+2) ( s G(S)=C(s)/R(s) = (s+1)(s+2)
G3 R(s) G1_ G1(s)+ R(s) 1+G4HG1 G4H G
G3(s)
G2 (1+HG1G4) 1+ +G1G2H +G4G1HC(s)
_ G2(s)C(s) G2 HG1 H(s) 1+G4HG1
1 G1G +G 3 (1+HG1G4) 1+G H 4 1 1+G4HG1
第二章习题课
解 : C(s) G G (G -G ) R(s) =1+G3G2G6 +G3G4G5+GG 1G 2 3 4 7 8 6
G6(s)X3(s) C(s) R(s) G G G2 G1 4 3 G G C(s) R(s) 3 4 X1(s) X3(s) G1G2 X2(s) 1+G G G 3 2 6 G5 C (s) G (s) C(s)[G7(s)-G8(s)] 5 G5 G7 G7-G8 G 8
7 G 8 (s)[G (s)-G (s)]C(s) X1(s)=R(s)G1(s)1 7G 8 7 XX G C (s)= X G (s)X6 (s) (s) X3 G (s)[ X (s)(s) G ](s)] -CG 2(s)= 2 1 4(s) 3 3(s)= 3(s)[ 2 5(s) G1G2G G X1(s)={R(s)-C(s)[ G (s)(s)]}G G 37 4 G8 1(s) 8
求下列函数的拉氏变换。 (1) f(t)=sin4t+cos4t w 解:∵L[sinwt]= 2 2 w +s s L[coswt]= 2 2 w +s
习题课一 (2-2)
4 + s ∴L[sin4t+cos4t]= s2+16 s2+16 s+4 = 2 s +G2H1 L2=-G1G2H1
Δ=1+G2H1+G1G2H2 P1=G1G2 Δ1 =1 P2=G3G2 Δ2 =1 n PkΔk G2G1+G2G3 C(s) Σ k= 1 = = R(s) 1+G2H1+G1G2H2 Δ
第二章习题课
(2-11b)
2-11(b) G3(s) G3(s) 求系统的 R(s) + C(s) C(s) + R(s) G G2+ G G +G1G2 G GG H (s) 1 2 C(s) G G (s) _ 2 1 3 3 4 1 传递函数 G (s) _ 1+G HG 2 = 4 G R(s) 1+G H + 1 1 2H+G1G4G (s) 4 H(s) 解: H(s)
s=-3 s=-2
= -1
=2
2 - 1 F(s)= s+3 s+2
f(t)=2e-3t-e-2t
2-3-2 函数的拉氏变换。 s F(s)= (s+1)2(s+2) s d [ s est] st 解:f(t)= e +lim (s+1)2 s=-2 s -1 ds s+2 st st 2 -2t st) =-2e +lim( e + e s -1 s+2 (s+2)2 =-2e-2t-te-t+2e-t =(2-t)e-t-2e-2t
第二章习题课
(2-1b)
2-1(b) 试建立图所示电路的动态微分方程。 duc CL d2uo duo du L ic= = +C o L 2 R 1 uL= dt R2 dt dt R2 dt ＋＋ 2 uo C CL d uoR2 duo uo u u + +C i1= i o i2= R ui=u1+uo 2 dt － R2 R2 dt － 2 输入量为ui，输出量为uo。 duc d(ui-uo) u1=i1R1 ic=C dt = dt diL uo u =L L dt iL=i2= i1=iL+ic R2
C(s) + C(s) + _ G1(s) _ G (s) G 2(s) 2 _ _ H1(s) H1(s) H2(s) G 1(s)H2(s)
G2 1+G2H1
第二章习题课
2-11(a)
G3(s) R(s)
(2-11a)
+ L1 C(s)
求系统的传递函数解:
_
G1(s) L2
_
G2(s) H1(s)
C C ic
＋ ui －
i1 R1 R2
＋ uo i2 －
IC(s)=CsUC(s)
[UI(s)-UO(s)]Cs=IC(s)
UI(s)
UI(s) sC
1＋ sC )R2 (R 1 IC(s) ＋ I2(s) ＋ I1(s)
UO(s)
-
1 R1
R2
UO(s)
1 ( ＋sC)R2 UO(s) R1 R2+R1R2sC = = 1 UI(s) R1+R2+R1R2sC ( sC)R ＋ 1+ R 2 1
第二章习题课
2-11(a)
求系统的传递函数 G1+G3
R(s) R(s) G1(s) G3(s) G3(s)
(2-11a)
G2 解: 3(s) 1+G2HG G2 1 =1+ R(s) C(s) +G2H1+G1G2H G 2 1+G1H21+ _ G1(s) _ G2(s) 2 G2H1 H1(s) G2G1+G2G C(s ) 3 = R(s) 1+G2H1+ HG 1G2H2 2(s)
(2-4-1) 求下列微分方程。 A3=(s+3)Y(s) A2=(s+2)Y(s) s=-2
s=-3
d2y(t) dy(t) +5 dt +6y(t)=6 ，初始条件： 2 dt · y(0)=y(0)=2 。 A1=1 , A2=5 , A3=-4 ∴ y(t)=1+5e-2t-4e-3t
′ 解:s2Y(s)-sY(0)-Y(0)+5sY(s)-5Y(0)+6Y(s)=
第二章习题课
(2-1a)
2-1(a) 试建立图所示电路的动态微分方程。 u
＋
c
－
i1=i2-ic
＋ d1(ui-uo＋ ) ＋ uo R u1u =[ -C R2 ]R1+uo ui u dt i R2 o －－－
C
解：
C C i1 R1 R2
ic
＋ uo i2 －
dui du。 o 输入量为 u ，输出量为 u i=u 1+uo i o R2ui=uoR1-Cdt R1R2+C dt R1R2u +u R o 2 duc d(ui-uo) uo u1=i1R1 duo ic=C dui dt = dt i2= R uoR1+C dt R1R2+uoR 2 2=R2ui+C dt R1R2
s+2 2 1 -3t 3 -t t -t (4) F(s)= = + e - e - e 2 s(s+1) (s+3) 3 12 4 2 s+2 s+2 st st 解:f(t)= e + e 2 2 (s+1) (s+3) s=0 s(s+1) s=-3 s+2 est ] d[ s(s+3) + lim s -1 ds st 2 st (s+2)te 2 1 -3t (-s -4s-6)e = + e +lim [ + 2 ] 2 2 s -1 3 12 (s +3) s +3s
2+4s+2) ( s 2 - 1 脉冲响应: C(s)= (s+1)(s+2) =1+ s+ 2 s+1 -t -2t c(t)=δ (t)+2e +e
第二章习题课
(2-10)
G2G6 G G G G 2-10 已知系统的微分方程组的拉氏变换 C(s) R(s) 1 2 3 4 - +G G G C(s) R(s) 1+ G G G G G 3 2 6 3 4 5 G G1 4 3 2 式，试画出系统的动态结构图并求传递 G5 函数。 G -G
6+2s2+12s ∴ Y(s)= 2 s(s +5s+6) A1=sY(s)
s=0
1 s
(2-4-2)
求下列微分方程。
d3y(t) d2y(t) dy(t) 初始条件: +4 2 +29 =29, 3 dt dt dt · · y(0)=0 , y(0)=17 , · y(0)=-122 解:

自动控制原理及其应用答案第二版_黄坚_课后答案

合集下载

《自动控制原理》黄坚课后习题答案

《自动控制原理》黄坚课后习题答案解析

自动控制原理及其应用答案第二版_黄坚课后答案_图文

自动控制原理及其应用(第2版)黄坚第二章习题课

自动控制原理黄坚第二版第三章习题答案

自动控制原理黄坚第二版课后答案第四章

《自动控制原理》黄坚课后习题答案解析word版本

《自动控制原理》黄坚课后习题答案

《自动控制原理》黄坚课后习题答案解析

《自动控制原理》黄坚课后习题答案解析

文档推荐

最新文档

自动控制原理及其应用答案第二版_黄坚_课后答案

合集下载

《自动控制原理》黄坚课后习题答案

《自动控制原理》黄坚课后习题答案解析

自动控制原理及其应用答案第二版_黄坚 课后答案_图文

自动控制原理及其应用(第2版)黄坚第二章习题课

自动控制原理黄坚 第二版 第三章习题答案

自动控制原理黄坚第二版课后答案第四章

《自动控制原理》黄坚课后习题答案解析word版本

《自动控制原理》黄坚课后习题答案

《自动控制原理》黄坚课后习题答案解析

《自动控制原理》黄坚课后习题答案解析

文档推荐

最新文档

自动控制原理及其应用答案第二版_黄坚课后答案_图文

自动控制原理黄坚第二版第三章习题答案