七年级数学上册第4章典型分析：补全统计图(青岛版)

第4章参考答案1~4.DDCD5. 问卷查阅资料实验。

6. 实地调查。

7.问卷。

8。

印刷问卷。

发放收集问卷。

9.（1）问卷。

(2)查阅资料。

（3）实地调查。

（4）查阅资料。

10.略。

11.都不正确。

我认为利用实验最好。

1~4.CBDD5. 8。

6.人数依次是：5、30、4、1、40。

百分数依次是：12.5%、75%、10%、2.5%。

7.（1）2、11、11、11、8、2.（2）在70~99分的人数最多。

60分以下的最少。

8.（1）280~300人数为5. 0~180人数为4. 百分数依次是：14%、20%、18%、16%、14%、8%。

（2）24%。

9.A．6、B．5、C．8、D.16、E5。

该班最喜欢的颜色是蓝色。

10.超速的有5辆。

占15.6%。

1~4.AADC。

5.条形、折线、扇形。

6.52、12、4/13.7. 138、272、下降。

8. 条形统计图。

9.（1）生活支出最多，占35%。

（2）在体育和教育两方面的支出相差不大。

（3）略。

（4）不知道，因为不知道各家庭的总支出。

10.（1）合计一月二月三月四月五月六月18000 2000 2500 3000 3000 3500 4000（2）六月份3000 1.5倍。

1~4.BCBD 5.85.9%。

6.30%。

7.40%、144. 8.4009.162度。

90度。

10。

岁数/岁15岁以下16~24 25~32 32岁以上人数/ 1 1 15 3百分比5% 5% 75% 15%1~4.CBDC。

5.500人。

6.32人。

7.52人。

8.90度9.（1）16人。

（2）骑自行车115.2度、步行86.4度、其它57.6度。

（3）略。

10.（1）略。

（2）60~69.（3）54度。

（4）60~69.1~5.CACBB。

6.条形、折线、扇形。

7问卷。

8.20%9.（1）9~11时。

（2）13~15时。

（3）1200。

10.10%。

11.（1）略。

章节测试题1.【答题】沃尔玛商场为了了解本商场的服务质量，随机调查了本商场的100名顾客，调查的结果如图所示，根据图中给出的信息，这100名顾客中对该商场的服务质量表示不满意的有（）A. 6名B. 11名C. 39名D. 44名【答案】A【分析】先求出表示不满意的顾客占总体的百分比，再求出这100名顾客中对该商场的服务质量表示不满意的数量即可．【解答】因为表示不满意的顾客占总体的百分比为：1-44%-39%-11%=6%，所以这100名顾客中对该商场的服务质量表示不满意的有100×6%=6名．选A.【点评】本题考查扇形统计图的意义．扇形统计图能直接反映部分占总体的百分比大小．2.【答题】如图的扇形图描述了安踏某一款运动女鞋的36号，37号，38号，39号，40号在一家专卖店的销售情况，请你为这家专卖店提出进货建议：应多进______号鞋.【答案】38【分析】直接根据各种鞋号的鞋销售情况即可得出结论.【解答】解：∵30%＞24%＞22%＞16%＞18%，∴应多进38号鞋.故答案为：应多进38号鞋.【点评】本题考查的是扇形统计图，熟知从扇形图上可以清楚地看出各部分数量和总数量之间的关系是解答此题的关键.3.【答题】某学校“你最喜爱的球类运动”调查中，随机调查了若干名学生（每个学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为______名．【答案】60【分析】设被调查的总人数是x人，根据最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，即可列方程求解．【解答】解：设被调查的总人数是x人，则40%x-30%x=6，解得：x=60．故答案是：60．【点评】本题考查的是扇形统计图的综合运用，读懂统计图，从统计图中得到必要的信息是解决问题的关键．扇形统计图直接反映部分占总体的百分比大小．4.【答题】某校对学生上学方式进行了一次抽样调查，并根据此次调查结果绘制了一个不完整的扇形统计图，其中“其他”部分所对应的圆心角是36°，则“步行”部分所占百分比是______%．【答案】40【分析】先根据“其他”部分所对应的圆心角是36°，算出“其他”所占的百分比，再计算“步行”部分所占百分比，即可解答．【解答】解：∵“其他”部分所对应的圆心角是36°，∴“其他”部分所对应的百分比为： ×100%=10%，∴“步行”部分所占百分比为：100%-10%-15%-35%=40%，故答案为：40%．【点评】本题考查的是扇形统计图，熟知从扇形图上可以清楚地看出各部分数量和总数量之间的关系是解答此题的关键．5.【答题】为了解学生课外阅读的喜好，某校从八年级1200名学生中随机抽取50名学生进行问卷调查，整理数据后绘制如图所示的统计图．由此可估计该年级喜爱“科普常识”的学生约有______人．【答案】360【分析】根据扇形图求出喜爱科普常识的学生所占的百分比，1200乘百分比得到答案．【解答】解：喜爱科普常识的学生所占的百分比为：1-40%-20%-10%=30%，1200×30%=360，故答案为：360．【点评】本题考查的是扇形统计图的知识，读懂统计图，从统计图中得到必要的信息是解决问题的关键，扇形统计图直接反映部分占总体的百分比大小．6.【答题】小明同学根据全班同学的血型绘制了如图所示的扇形统计图，已知A型血的有20人，则O型血的有______人．【答案】10【分析】根据A型血的有20人，所占的百分比是40%即可求得班级总人数，根据AB型所对应的扇形圆心角的度数求得对应的百分比，则用总人数乘以O型血所对应的百分比即可求解．【解答】解：全班的人数是：20÷40%=50（人），AB型的所占的百分比是：×100%=10%，则O型血的人数是：50（1-40%-30%-10%）=10（人）．故答案为：10．【点评】本题考查的是扇形统计图的运用，读懂统计图，从统计图中得到必要的信息是解决问题的关键．扇形统计图直接反映部分占总体的百分比大小．7.【答题】某班数学老师想了解学生对数学的喜欢程度，对全班50名学生进行调查，根据调查结果绘制了扇形统计图（如图所示），其中A表示“很喜欢”，B表示“一般”，C表示“不喜欢”，则该班“很喜欢”数学的学生有______人．【答案】18【分析】根据扇形统计图求出A占的百分比，由调查的总人数50计算即可得到结果．【解答】解：根据题意得：（1-16%-48%）×50=18（人），则该班“很喜欢”数学的学生有18人．故答案为：18【点评】此题考查了扇形统计图，弄清图形中的数据是解本题的关键．8.【答题】某校男生、女生以及教师人数的扇形统计图如图所示，若该校师生的总人数为1500人，结合图中信息，可得该校教师人数为______人．【答案】120【分析】用学校总人数乘教师所占的百分比，计算即可得解．【解答】1500×（1-48%-44%）=1500×8%=120人．故答案为：120．【点评】本题考查的是扇形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．扇形统计图直接反映部分占总体的百分比大小．9.【答题】某实验中学九年级（1）班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示，其中评价为“A”所在扇形的圆心角是______度．【答案】108【分析】首先计算出A部分所占百分比，再利用360°乘百分比可得答案．【解答】A所占百分比：100%-15%-20%-35%=30%，圆心角：360°×30%=108°，故答案为：108．【点评】此题主要考查了扇形统计图，关键是掌握圆心角度数=360°×所占百分比．10.【答题】某校根据去年初三学生参加中考的数学成绩的等级，绘制成如图的扇形统计图，则图中表示A等级的扇形的圆心角的大小为______°．【答案】108【分析】根据C等级的人数与所占的百分比计算出参加中考的总人数，再求出A等级所占的百分比，然后乘360°计算即可得解．【解答】参加中考的人数为：60÷20%=300人，A等级所占的百分比为：×100%=30%，所以，表示A等级的扇形的圆心角的大小为360°×30%=108°．故答案为：108．【点评】本题考查扇形统计图及相关计算．在扇形统计图中，每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比．11.【答题】如图，是八年级（3）班学生参加课外活动人数的扇形统计图，如果参加艺术类的人数是16人，那么参加其它活动的人数是______人．【答案】4【分析】先求出参加课外活动人数，再求出参加其它活动的人数即可．【解答】∵参加艺术类的学生占的比例为32%，∴参加课外活动人数为：16÷32%=50人，则参加其它活动的人数为：50×（1-20%-32%-40%）=4人．故答案为：4．【点评】本题主要考查了扇形统计图，扇形统计图是用整个圆表示总数，用圆内各个扇形的大小表示各部分数量占总数的百分数．通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系．12.【答题】如图，某校根据学生上学方式的一次抽样调查结果，绘制出一个未完成的扇形统计图，若该校共有学生700人，则据此估计步行的有______人．【答案】280【分析】先求出步行的学生所占的百分比，再用学生总数乘步行学生所占的百分比即可估计全校步行上学的学生人数．【解答】∵骑车的学生所占的百分比是×100%=35%，∴步行的学生所占的百分比是1-10%-15%-35%=40%，∵若该校共有学生700人，∴据此估计步行的有700×40%=280（人）．故答案为：280．【点评】本题考查了扇形统计图及用样本估计总数的知识，解题的关键是从统计图中得出步行上学学生所占的百分比．13.【答题】如图是某足球队全年比赛情况统计图：根据图中信息，该队全年胜了______场．【答案】22【分析】用平的场次除以所占的百分比求出全年比赛场次，然后乘胜场所占的百分比计算即可得解．【解答】全年比赛：10÷25%=40场，胜：40×（1-20%-25%）=40×55%=22场．故答案为：22．【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．14.【答题】某冷饮店一天售出各种口味雪糕数量的扇形统计图如图，其中售出红豆口味的雪糕200支，那么售出水果口味雪糕的数量是______支．【答案】150【分析】首先根据红豆口味的雪糕的数量和其所占的百分比确定售出雪糕的总量，然后乘水果口味的所占的百分比即可求得其数量．【解答】观察扇形统计图知：售出红豆口味的雪糕200支，占40%，∴售出雪糕总量为200÷40%=500（支），∵水果口味的占30%，∴水果口味的有500×30%=150（支），故答案为：150．【点评】本题考查了扇形统计图的知识，解题的关键是正确地从扇形统计图中整理出进一步解题的有关信息．15.【答题】期末考试后，小红将本班50名学生的数学成绩进行分类统计，得到如图所示的扇形统计图，则优生人数为______名．【答案】10【分析】用总人数乘对应的百分比即可求解．【解答】50×（1-16%-36%-28%）=50×20%=10（名）．故优生人数为10名，故答案为：10．【点评】本题考查的是扇形统计图的应用，扇形统计图直接反映部分占总体的百分比大小．16.【答题】小亮对60名同学进行节水方法选择的问卷调查（每人选择一项），人数统计如图，如果绘制成扇形统计图，那么表示“一水多用”的扇形圆心角的度数是______°．【答案】240【分析】用圆周角乘一水多用的所占的百分比即可求得其所占的圆心角的度数．【解答】解：表示“一水多用”的扇形圆心角的度数是360°×=240°，故答案为：240．【点评】本题考查了扇形统计图的知识，能够从统计图中整理出进一步解题的信息是解答本题的关键．17.【答题】某校在今年“五•四”开展了“好书伴我成长”的读书活动．为了解八年级450名学生的读书情况，随机调查了八年级50名学生本学期读书册数，并将统计数据制成了扇形统计图，则该校八年级学生读书册数等于3册的约有______名．【答案】153【分析】首先根据扇形统计图求出样本中读书册数等于3册所占的百分比，即m%的值，再利用样本估计总体的思想，用450乘m%即可求出该校八年级学生读书册数等于3册的人数．【解答】由扇形统计图可知，样本中读书册数等于3册所占的百分比为：1-6%-24%-30%-6%=34%，即m%=34%，所以该校八年级学生读书册数等于3册的约有：450×34%=153（名）．故答案为153．【点评】本题考查了扇形统计图及用样本估计总体的思想，从统计图中正确地获取信息是解题的关键．18.【答题】某校对去年毕业的350名学生的毕业去向进行跟踪调查，并绘制出扇形统计图（如图所示），则该校去年毕业生在家待业的学生数有______名．【答案】28【分析】首先求得在家待业的百分比，然后乘毕业的总人数即可．【解答】在家待业的毕业生所占百分比为：1-24%-68%=8%，故该校去年毕业生在家待业的学生数有350×8%=28名，故答案为：28．【点评】此题考查了扇形统计图的知识，解题的关键是了解扇形统计图的作用．19.【答题】某班围绕“舞蹈、乐器、声乐、其他等四个项目中，你最喜欢哪项活动（每日只限一项）”的问题，对全班50名学生进行问卷调查，调查结果如右扇形统计图，请问该班喜欢乐器的学生有______名．【答案】20【分析】根据扇形统计图得出该班喜欢乐器的学生所占比例，进而得出该班喜欢乐器的学生数．【解答】∵该班喜欢乐器的学生所占比例为：1-22%-10%-28%=40%，∴该班喜欢乐器的学生有：50×40%=20（名）．故答案为：20．【点评】此题主要考查了扇形统计图的应用，根据已知得出该班喜欢乐器的学生所占比例是解题关键．20.【答题】某学校为了做好道路交通安全教育工作，随机抽取本校100名学生就上学的交通方式进行调查，根据调查结果绘制扇形图如图所示．若该校共有1000名学生，请你估计全校步行上学的学生人数约有______名．【答案】400【分析】用学生总数乘步行学生所占的百分比即可估计全校步行上学的学生人数．【解答】∵步行上学在扇形图中所占比例为40%，∴全校步行上学的学生人数为：1000×40%=400（名），故答案为：400．【点评】本题考查了扇形统计图及用样本估计总数的知识，解题的关键是从统计图中得出步行上学学生所占的百分比．。

青岛版七年级上册数学电子课本青岛版七年级上册数学电子课本第一章：实数1.1 正实数与负实数1.2 数轴与有理数1.3 无理数第二章：代数式与方程2.1 代数式的定义和性质2.2 一元一次方程2.3 两个一元一次方程的联立2.4 解一元一次方程的应用第三章：图形的初步认识3.1 图形元素：点、直线、线段、射线、角、面3.2 基本图形：三角形、四边形、圆3.3 图形的相似第四章：解直角三角形的问题4.1 直角三角形及其判定4.2 正弦定理4.3 余弦定理第五章：数据的统计与分析5.1 统计图5.2 中心倾向度量5.3 离散程度度量5.4 相关度量第六章：平面直角坐标系6.1 平面直角坐标系及其基本性质6.2 相关线段和中点6.3 点与直线的位置关系6.4 直线的斜率6.5 点到直线的距离第七章：多边形7.1 多边形的定义和性质7.2 三角形的性质7.3 角平分线与垂线7.4 几何作图第八章：函数8.1 函数的概念8.2 一次函数8.3 反比例函数表格索引：第一章：实数1.1 正实数与负实数本章重点介绍了实数的概念以及正实数和负实数的性质。

正实数是指大于零的实数，负实数是指小于零的实数，零既不是正实数也不是负实数。

实数集包括有理数和无理数两部分。

有理数是可以表示为两个整数的比的数，无理数是不能表示为两个整数的比的数，例如，$\sqrt{2}$为无理数。

1.2 数轴与有理数本章介绍了数轴的概念和用法，以及有理数在数轴上的表示。

数轴是一条用于表示数的直线，数轴上的左侧表示负数，右侧表示正数，零位于数轴的中央。

有理数可以用分数的形式表示，也可以用小数的形式表示。

对于无限不循环小数，可以通过近似值来表示，例如，$\pi$可以近似为3.14。

1.3 无理数本章介绍了无理数的概念和性质。

无理数是不能表示为两个整数的比的数，例如，根号2、根号3等。

无理数的表示法有小数表示法和根式表示法。

在小数表示法中，无理数可以用无限不循环小数表示，例如，$\sqrt{2}$可以表示为1.41421356...；在根式表示法中，无理数可以用根式表示，例如，$\sqrt{2}$。

青岛版七年级数学上册第四章《数据的搜集、整理与描述》2020暑假预习卷学校:___________姓名：___________班级：___________得分：___________一、选择题（本大题共10小题，共30分）1.下列调查方式，你认为最合适的是（）。

A.日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式B.旅客上飞机前的安检，采用抽样调查方式C.了解南通市区居民日平均用水量，采用全面调查方式D.了解南通市区每天的平均用电量，采用抽样调查方式2.要调查某校学生学业负担是否过重，选用下列哪种方法是恰当的（）。

A.查阅文献资料B.对学生问卷调查C.上网查询D.对校领导问卷调查3.从一块稻田中抽取100穗稻穗，测量这些稻穗的质量．以下说法正确的是（）。

A.这块稻田中的每一穗稻穗是个体B.这块稻田中所有的稻穗是总体C.抽出的100穗稻穗的质量是总体的一个样本D.以上说法都是不正确的4.为了解铜陵市约160万常住人口的出行要求，以便科学规划交通，500名调查志愿者走入10000户家庭，发放了30000份问卷，进行问卷调查．这次抽样调查的样本容量是（）。

A.160万B.500C.10000D.300005.为了解一批某种型号的电风扇的使用寿命，从中随机抽出20台进行测试．在这个问题中，20台电风扇的使用寿命是（）。

A.总体B.个体C.样本D.样本容量6.在党和国家的领导下，全国人民的共同努力，全国疫情进入尾声，各行各业纷纷复工复产，经济形势也越来越好．下列调查中，不适合用抽样调查方式的是（）。

A.调查全国餐饮企业员工的复工情况B.调查全国医用口罩日生产量C.青岛市高三学生全面复学，调查和检测某校高三学生和老师的体温D.调查疫情期间北京地铁的客流量7.下列调查中,适合采用“抽样调查”方式的是（）。

A.为了了解某次考试试卷的质量,对全班所有学生的试卷进行分析B.调查某一品牌5万袋包装鲜奶是否符合卫生标准C.调查我国所有城市中哪些是第一批沿海开放城市D.了解全校学生100米短跑的成绩8.为了了解我市6000名学生参加的初中毕业会考数学考试的成绩情况，从中抽取了200名考生的成绩进行统计，在这个问题中，下列说法：（1）这6000名学生的数学会考成绩的全体是总体；（2）每个考生是个体；（3）200名考生是总体的一个样本；（4）样本容量是200，其中说法正确的有（）。

典型分析：补全统计图与图表描述数据有关的试题中重要的一类就是根据所给的不完整的统计图、根据题目信息补全统计图.下列举例说明这类问题的解法.例1 小刘对本班同学的业余兴趣爱好进行了一次调查，她根据采集到的数据，绘制了下面的图1和图2.图1 图2请你根据图中提供的信息，解答下列问题：（1）在图1中，将“书画”部分的图形补充完整；（2）在图2中，求出“球类”部分所对应的圆心角的度数，并分别写出爱好“音乐”、“书画”、“其它”的人数占本班学生数的百分数；（3）观察图1和图2，你能得出哪些结论？（只要写出一条结论）.分析：要补全统计图中的“书画”部分，则需要知道爱好书画的人数，为此，需要联合这两个统计图去获取信息.从条形统计图可知，爱好“球类”的人数为14人，从扇形统计图可知，爱好“球类”的人数占总人数的百分比为35%，由此可以计算出总人数，用总人数减去球类、音乐和其他人数，即可的爱好“书画”的人数.进而补全“书画”条形统计图.用音乐、书画和其他具体人数除以总人数，即可解决第（2）问.解：（1）如图1，由14÷35%=40，40-14-12-4=10知，补图如图3所示.图3（2）360°×35%=126°.所以“球类”部分所对应的圆心角为126°，12÷40=0.3，10÷40=0.25，4÷40=0.1，即喜欢音乐、书画、其他的人数分别占总人数的30%，25%，10%.（3）略评注：求到问题中的总人数是解决问题的关键，而确定总人数需要借助两个统计图中的已知数据信息.例2 某网站公布了某城市一项针对2006年第一季度购房消费需求的随机抽样调查结果，图4是根据调查结果制作的购房群体可接受价位情况的比例条形统计图和扇形统计图的一部分.（1）若2500～3000可接受价位所占比例是3500以上可接受价位所占比例的5倍，则这两个可接受价位所占的百分比分别为.（2）补全条形统计图和扇形统计图.图4分析：要补全条形统计图，需要计算出2500～3000，3500以上两部分所占的百分比；要补全扇形统计图，可根据各部分占总体的百分比，计算出相应圆心角的度数，根据圆心角进行补图.解：（1）因为2500～3000和3500以上这两部分占总体的百分比的和为1-15%-35%-20%=30%，根据两者之间的关系可求得2500～3000占25%，3500以上占5%.（2）所补全的统计图如图5所示.图5评注：补全统计图问题是中考中的热点,应加强此类类型题的训练.。

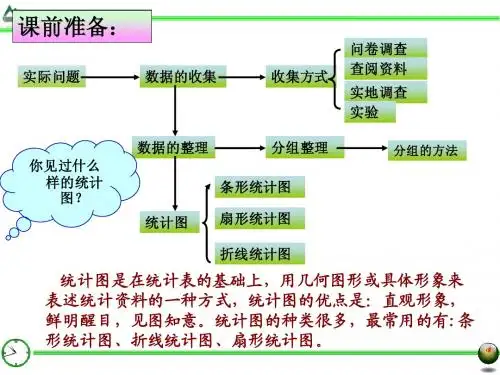
统计图的特点
（1）条形统计图：条形统计图是用一个单位长度表示一定的数量，根据数量的多少画成长短不同的直条，然后把这些直条按照一定的顺序排列起来。

作用：从条形统计图中很容易看出各种数量的多少。

（2）拆线统计图：折线统计图是用一个单位长度表示一定的数量，根据数量的多少描出各点，然后把各点用线段顺次连接起来。

作用：折线统计图不但可以表示出数量的多少，而且能够清楚地表示出数量增减变化的情况。

（3）扇形统计图：扇形统计图是用整个圆表示总数，用圆内各个扇形的大小表示各部分数量占总数的百分数。

作用：通过扇形统计图可以很清楚地表示各部分数量同总数之间的关系。

折线统计图不但能反映数据（量）的多少，更能反映某一项目在某一时间内的数据(量)增减变化情况。