大学物理填空题

大学物理填空题填空题:1.两辆车A和B,在笔直的公路上同向行驶，它们从同一起始线上同时出发,并且由出发点开始计时,行驶的距离x(m)与行驶时间t(s）的函数关系式：A为x A＝4t＋t2，B为x B＝2t2＋2t3.（1)它们刚离开出发点时，行驶在前面的一辆车是；（2）出发后，两辆车行驶距离相同的时刻是;(3）出发后，B车相对A车速度为零的时刻是.2。

当一列火车以10 m·s－1的速率向东行驶时，若相对于地面竖直下落的雨滴在列车的窗子上形成的雨迹偏离竖直方向30°,则雨滴相对于地面的速率是；相对于列车的速率是.3.质量为m的小球,用轻绳AB，BC连接，如题1。

2。

1图。

剪断绳AB的瞬间,绳BC中的张力比T∶T′＝。

4。

一质量为30 kg的物体以10 m·s－1的速率水平向东运动，另一质量为20 kg的物体以20 m·s－1的速率水平向北运动。

两物体发生完全非弹性碰撞后，它们速度大小v＝；方向为。

5。

题1.2.2图示一圆锥摆,质量为m的小球在水平面内以角速度ω匀速转动.在小球转动一周的过程中：（1）小球动量增量的大小等于；（2）小球所受重力的冲量的大小等于；(3）小球所受绳子拉力的冲量大小等于.题1。

2。

1图题1。

2.2图6。

光滑水平面上有一质量为m的物体，在恒力F作用下由静止开始运动，则在时间t 内,力F做的功为。

设一观察者B相对地面以恒定的速度v0运动，v0的方向与F方向相反，则他测出力F在同一时间t内做的功为.7.一冰块由静止开始沿与水平方向成30°倾角的光滑斜屋顶下滑10 m后到达屋檐.若屋檐高出地面10 m。

则冰块从脱离屋檐到落地过程中越过的水平距离为.(忽略空气阻力，g值取10 m·s－2)8。

在两个质点组成的系统中，若质点之间只有万有引力作用，且此系统所受外力的矢量和为零，则此系统(）(A）动量与机械能一定都守恒.(B)动量与机械能一定都不守恒.(C)动量不一定守恒，机械能一定守恒。

牛顿力学一、选择题1．（本题3分）0586一质点作直线运动，某时刻的瞬时速度s m v /2=，瞬时加速度2/2s m a =，则一秒钟后质点的速度： [ ]（A ）等于零； （B ）等于s m /2；（C ）等于s m /2 ； （D ）不能确定。

2．（本题3分）0587如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动，设该人以匀速率0v 收绳，绳不伸长、湖水静止，则小船的运动是：[ ]（A ）匀加速运动； （B ）匀减速运动；（C ）变加速运动； （D ）变减速运动；（E ）匀速直线运动；3．本题3分）0519 对于沿曲线运动的物体，以下几种说法中哪一种是正确的：（A ）切向加速度必不为零；（B ）法向加速度必不为零（拐点处除外）；（C ）由于速度沿切线方向，法向分速度必为零，因此法向加速度必为零；（D ）若物体作匀速率运动，其总加速度必为零。

（Ｅ）若物体的加速度a 为恒矢量，它一定作匀变速率运动。

[ ]4．（本题3 分）0518 以下五种运动形式中，a 保持不变的运动是：（A ）单摆的运动； （B ）匀速率圆周运动；（C ）行星的椭圆轨道运动； （D ）抛体运动；（E ）圆锥摆运动。

[ ]5．（本题3分）0001 一质点在平面上作一般曲线运动，其瞬时速度为v ，瞬时速率为v ，某一段时间内的平均速度为v ，平均速率为v ，它们之间的关系必定有： (A)v v v v ==, ； （B ）v v v v = ,≠； （C ）v v v v ≠,≠； （D ）v v v v ≠,= 。

[ ] 6．（本题3分）0604某物体的运动规律为t kv dt dv 2/-=，式中的K 为大于零的常数，当t = 0时，初速为0v，则速度v 与时间t 的函数关系是：（A ）0221v kt v += ； （B ）0221v kt v +-= ； （C ）02121v kt v += ； （D ）02121v kt v +-= 。

质 点 运 动 学一．选择题：1、质点作匀速圆周运动，其半径为R ，从A 点出发，经过半圆周到达B 点，则在下列各 表达式中，不正确的是 （A ）（A ）速度增量 0=∆v ，速率增量 0=∆v ； （B ）速度增量 j v v 2-=∆，速率增量 0=∆v ； （C ）位移大小 R r 2||=∆ ，路程 R s π=； （D ）位移 i R r 2-=∆，路程 R s π=。

2、质点在平面上运动，已知质点位置矢量的表达式为j bt i at r 22+=（其中a 、b 为常量）则该质点作 （ D ）（A ）匀速直线运动； （B ）一般曲线运动； （C ）抛物线运动； （D ）变速直线运动。

3、质点作曲线运动，r 表示位置矢量，s 表示路程，v 表示速度, a 表示加速度。

下列表达式中， 正确的表达式为 （ B ）（A ）r r ∆=∆|| ； (B) υ==dt s d dt r d ； （C ） a dtd =υ； （D ）υυd d =|| 。

4、一个质点在做圆周运动时，则有 （ B ）（A ）切向加速度一定改变，法向加速度也改变；（B ）切向加速度可能不变，法向加速度一定改变；（C ）切向加速度可能不变，法向加速度不变；（D ）切向加速度一定改变，法向加速度不变。

5、质点作匀变速圆周运动，则：（ C ）（A ）角速度不变； （B ）线速度不变； （C ）角加速度不变； （D ）总加速度大小不变。

二．填空题：1、已知质点的运动方程为x = 2 t －4 t 2（SI ），则质点在第一秒内的平均速度 =v -2 m/s ； 第一秒末的加速度大小 a = -8 m/s 2 ；第一秒内走过的路程 S = 2.5 m 。

2、xoy 平面内有一运动的质点，其运动方程为 j t i t r 5sin 105cos 10+=（SI ），则t 时刻其速度=v j t i t 5cos 505sin 50+- ；其切向加速度的大小a t = 0 ；该质点运动的轨迹是 圆 。

大学物理
第1章质点运动学
填空题
一、填空题
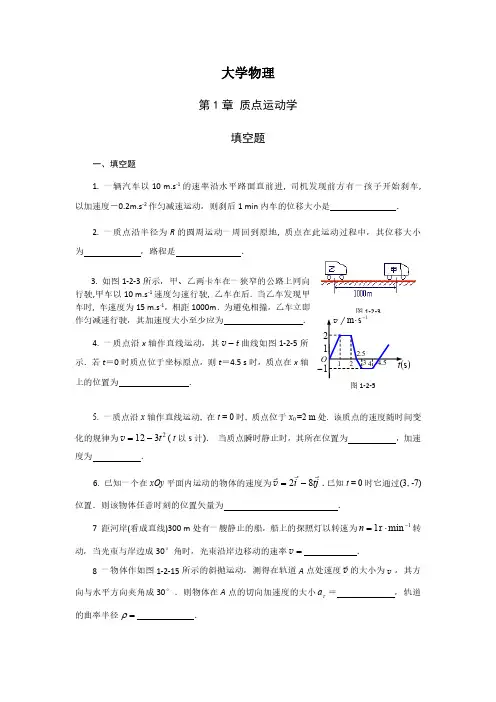
1.一辆汽车以10m.s -1的速率沿水平路面直前进,司机发现前方有一孩子开始刹车,以加速度－0.2m.s -2作匀减速运动，则刹后1min 内车的位移大小是．
2.一质点沿半径为R 的圆周运动一周回到原地,质点在此运动过程中，其位移大小为，路程是．
3.如图1-2-3所示，甲、乙两卡车在一狭窄的公路上同向
行驶,甲车以10m.s -1速度匀速行驶,乙车在后.当乙车发现甲车时,车速度为15m.s -1，相距1000m ．为避免相撞，乙车立即作匀减速行驶，其加速度大小至少应为．
4.一质点沿x 轴作直线运动，其t v -曲线如图1-2-5所
示．若t ＝0时质点位于坐标原点，则t ＝4.5s 时，质点在x 轴上的位置为．5.一质点沿x 轴作直线运动,在t =0时,质点位于x 0=2m 处.该质点的速度随时间变化的规律为2312t -=v (t 以s 计)．当质点瞬时静止时，其所在位置为，加速度为．
6.已知一个在xOy 平面内运动的物体的速度为j t i
82-=v ．已知t =0时它通过(3,-7)位置．则该物体任意时刻的位置矢量为．7距河岸(看成直线)300m 处有一艘静止的船，船上的探照灯以转速为1min r 1-⋅=n 转
动，当光束与岸边成30°角时，光束沿岸边移动的速率=v ．
8一物体作如图1-2-15所示的斜抛运动，测得在轨道A 点处速度v 的大小为v ，其方向与水平方向夹角成30°．则物体在A 点的切向加速度的大小τa ＝，轨道的曲率半径=ρ
．图1-2-3图1-2-51s m -⋅/v 1221345.25.4()s t O 1-。

1. 哈雷彗星绕太阳运动的轨道是一个椭圆。

它离太阳最近的距离是r 1 = 8.75×107 km ，此时它的速率为v 1 = 5.46×104 m/s 。

它离太阳最远时的速率为v 2 = 9.08×102 m/s ，这时它离太阳的距离r 2为5.26×109 km .2. 一质量为0m ，长为 l 的棒能绕通过o 点的水平轴自由转动。

一质量为m ，速率为0v 的子弹从水平方向飞来，击中棒的中点且留在棒内，则棒中点的速度为mm mv 34300+。

3. 一颗子弹质量为m ，速度为v ，击中一能绕通过中心的水平轴转动的轮子（看作圆盘）边缘，并嵌在轮边，轮子质量为m0 ，半径为R ，则轮的角速度为()R m m mv220+。

4. 人造地球卫星绕地球作椭圆运动，地球在椭圆的一焦点上，则卫星的动量________，动能__________，角动量__________（填守恒或不守恒）。

5. 根据天体物理学的观测和推算，宇宙正在膨胀，太空中的天体都离开我们的星球而去。

假定在地球上观察到一颗脉冲星（看来发出周期性脉冲无线电波的星）的脉冲周期为0.50s ，且这颗星正沿观察方向以运行速度0.8c （c 为真空中光速）离我们而去，那么这颗星的固有脉冲周期应是Δτ =0.3 s 。

6. 静止时边长为 50 cm 的立方体，当它沿与一边平行的方向相对观察者以速度2.4×108 m/s 运动时，观察者测得它的体积为0.075立方米.7. 一宇宙飞船以2c的速度相对于地面运动，飞船中的人又以相对飞船为2c的速度向前发射一枚 火箭，则地面上的观察者测得火箭速度为c 54。

8. 静止长度为l 0 的车厢，以速度c v 23=相对地面行驶，一 粒子以cu 23=的速度（相对于车）沿车前进方向从后壁射向前壁， 则地面上观察者测得粒子通过的距离为04l 。

9. 简述狭义相对论的二个基本假设:(1) 相对性原理：物理定律在所有惯性系中都相同的(2) 光速不变原理：在所有惯性系中，自由空间（真空中）的光速具有相同量值C10. 一宇宙飞船以0.8c 的速度离开地球。

填空题 第一章1. ()t r 与()t t r ∆+为某质点在不同时刻的位置矢量(矢径)，()t v 与()t t ∆+v 为不同时刻的速度矢量，试在两个图中分别画出 ， 以及 ， . 二2. 假设作用在一质量为10 kg 的物体上的力，在4秒内均匀地从零增加到50 N ，使物体沿力的方向由静止开始作直线运动．则物体最后的速率v ＝______________． 七3.. 以一定初速度斜向上抛出一个物体，若忽略空气阻力，当该物体的速度v与水平面的夹角为θ 时，它的切向加速度a t 的大小为______________，法向加速度a n 的大小为_______ ____________． 三4一质点沿x 轴作直线运动，它的运动学方程为 x =3+5t +6t 2-t 3 (SI)则(1) 质点在t =0时刻的速度=0v____ _____________；(2) 加速度为零时，该质点的速度=v ____________________． 七5.一质点沿直线运动其坐标x 与时间t 有如下关系: t A x tωβcos e -= (SI) (A 、β 皆为常数)(1) 任意时刻ｔ质点的加速度a = _______________________；(2) 质点通过原点的时刻t =___ ________________________．十一6 在x 轴上作变加速直线运动的质点，已知其初速度为0v ，初始位置为x 0，加速度2Ct a =（其中C 为常量），则其速度与时间的关系为=v __________，运动学方程为=x __________． 六7. 一小珠可以在半径为R 的竖直圆环上作无摩擦滑动．今使圆环以角速度ω绕圆环竖直直径转动．要使小珠离开环的底部而停在环上某一点，则角速度ω最小应大于__ __________． 三9. 一圆锥摆摆长为l 、摆锤质量为m ，在水平面上作匀速圆周运动，摆线与铅直线夹(1) 摆线的张力T ＝______ _______________； (2) 摆锤的速率v ＝________ _____________． 四10. 飞轮作加速转动时，轮边缘上一点的运动学方程为S = 0.1 t 3 (SI).飞轮半径为2 m ．当此点的速率=v 30 m/s 时，其切向加速度为___________________，法向加速度为_______ ___________． 四11. 一质点从静止出发沿半径R =1 m 的圆周运动，其角加速度随时间t 的变化规律是AB AB )(t r )(t t r ∆+)(t t ∆+v)(t v O O m=12t 2-6t (SI)， 则质点的角速ω =_________________________；切向加速度 a t =__________________． 六13. 一质点沿半径为 0.1 m 的圆周运动，其角位移θ 随时间t 的变化规律是 θ = 2 + 4t 2 (SI)．在t =2 s 时，它的法向加速度a n =____________；切向加速度a t =_______________． 七14. 一质点沿半径为R 的圆周运动，其路程S 随时间t 变化的规律为221ct bt S -= (SI) ， 式中b 、c 为大于零的常量,且b 2>Rc. 则此质点运动的切向加速度a t =____ _________；法向加速度a n ＝____ ____________． 五15. 一块水平木板上放一砝码，砝码的质量m ＝0.2 kg ，手扶木板保持水平，托着砝码使之在竖直平面内做半径R ＝0.5 m 的匀速率圆周运动，速率v =1 m/s ．当砝码与木板一起运动到图示位置时，砝码受到木板的摩擦力为____________，砝码受到木板的支持力为________________． 六16. 利用皮带传动，用电动机拖动一个真空泵．电动机上装一半径为 0.1m 的轮子，真空泵上装一半径为0.29m 的轮子，如图所示．如果电动机的转速为1450 rev/min ，则真空泵上的轮子的边缘上一点的线速度为___ _______________，真空泵的转速为___________________．十二17. 距河岸(看成直线)500 m 处有一艘静止的船，船上的探照灯以转速为n =1 r/min 转动．当光束与岸边成60°角时，光束沿岸边移动的速度v =_________． 一18.两条直路交叉成α 角，两辆汽车分别以速率1v 和2v 沿两条路行驶，一车相对另一车的速度大小为________ ___________________________. 二第二章1.质量相等的两物体A 和B ，分别固定在弹簧的两端，竖直放在光滑水平面C 上，如图所示．弹簧的质量与物体A 、B 的质量相比，可以忽略不计．若把支持面C 迅速移走，则在移开的一瞬间，A 的加速度大小a A ＝_______，B 的加速度的大小a B ＝_______． 一3. 假如地球半径缩短 1％，而它的质量保持不变，则地球表面的重力加速度g 增大的百分比是______________． 七4.如图所示，一个小物体A 靠在一辆小车的竖直前壁上，A 和车壁间静摩擦系数是μs ，若要使物体A 不致掉下来，小车的加速度的最小值应为a =_______________．. 五5. 一质量为1kg0.200.16，现对物体施一水平拉力F ＝t+0.96(SI)，则2秒 末物体的速度大小v ＝______________． 十二7. 质量为m 的小球，用轻绳AB 、BC 连接，如图，其中AB 水平．剪断绳AB 前后的瞬间，绳BC 中的张力比 T : T ′=___________________． 二第三章2. 设作用在质量为1 kg 的物体上的力F ＝6t ＋3（SI ）．如果物体在这一力的作用下，由静止开始沿直线运动，在0到2.0 s 的时间间隔内，这个力作用在物 体上的冲量大小Ｉ＝___ _______________． 十二5.一个打桩机，夯的质量为m 1，桩的质量为m 2．假设夯与桩相碰撞时为完全非弹性碰撞且碰撞时间极短，则刚刚碰撞后夯与桩的动能是碰前夯的动能的________倍． 九6.. 一个人站在平板车上掷铅球，人和车总质量为M ，铅球的质量为m ，平板车可沿水平、光滑的直轨道移动．设铅直平面为xy 平面，x 轴与轨道平行，y 轴正方向竖直向上．已知未掷球时，人、车、球皆静止．球出手时沿斜上方，它相对于车的初速度在xy 平面内，其大小为v 0，方向与x 轴正向的夹角为θ ，人在掷球过程中对车无滑动，则球被抛出之后，车对地的速度=V ______________________，球对地的速度=v______________________．三7. 如图所示，一斜面倾角为θ，用与斜面成α角的恒力F将一质量为m 的物体沿斜面拉升了高度h ，物体与斜面间的摩擦系数为μ．摩擦力在此过程中所作的功W f ＝________________________． 一8. 图中，沿着半径为R 圆周运动的质点，所受的几个力中有一个是恒力0F，方向始终沿Ax 轴正向，即i F F00=.当质点从A 点沿逆时针方向走过3 /4圆周到达B 点时，力0F 所作的功为W ＝__ ________． 三 10.某质点在力F ＝(4＋5x )i(SI)的作用下沿x 轴作直线运动，在从x ＝0移动到x ＝10 m 的过程中，力F所做的功为_________． 八11.有一劲度系数为k 的轻弹簧，竖直放置,下端悬一质量为m 的小球．先使弹簧为原长，而小球恰好与地接触．再将弹簧上端缓慢地提起，直到小球刚能脱离地面为止．在此过程中外力所作的功为______________________． 五12.已知地球质量为M ，半径为R ．一质量为m 的火箭从地面上升到距地面高度为2R 处．在此过程中，地球引力对火箭作的功为____________________． 十一14. 如图所示，质量m ＝2 kg 的物体从静止开始，沿1/4圆弧从A 滑到B ，在B 处速度的大小为v ＝6 m/s ，已知圆的半径R ＝4 m ，则物体从A 到B 的过程中摩擦力对它所作的功W ＝___________________． 二15. 光滑水平面上有一轻弹簧，劲度系数为k ，弹簧一端固定在O 点，另一端拴一个质量为m 的物体，弹簧初始时处于自由伸长状态，若此时给物体m 一个垂直于弹簧的初速度0v如图所示，则当物体速率为21v 0时弹簧对物体的拉力f =_________________．九第四章1.一长为l ，质量可以忽略的直杆，可绕通过其一端的水平光滑轴在竖直平面内作定轴转动，在杆的另一端固定着一质量为m 的小球，如图所示．现将杆由水平位置无初转速地释放．则杆刚被释放时的角加速度β0＝__ __________，杆与水平方向夹21v m角为60°时的角加速度β ＝________________． 六2.地球的质量为m ，太阳的质量为M ，地心与日心的距离为R ，引力常量为G ，则地球 绕太阳作圆周运动的轨道角动量为L ＝_________． 二3. 质量为m 的质点以速度v沿一直线运动，则它对直线外垂直距离为d 的一点的角动量大小是__ ________． 八4. 若作用于一力学系统上外力的合力为零，则外力的合力矩___ _________（填一定或不一定）为零；这种情况下力学系统的动量、角动量、机械能三个量中一定守恒的量是 ______ __________ 八7. 两个质量都为100 kg 的人，站在一质量为200 kg 、半径为3 m 的水平转台的直径两端．转台的固定竖直转轴通过其中心且垂直于台面．初始时，转台每5 s 转一圈．当这两人以相同的快慢走到转台的中心时，转台的角速度ω ＝_________________．(已知转台对转轴的转动惯量J ＝21MR 2，计算时忽略转台在转轴处的摩擦)． 五8.哈雷慧星绕太阳的轨道是以太阳为一个焦点的椭圆．它离太阳最近的距离是r 1＝8.75×1010 m ，此时它的速率是v 1＝5.46×104 m/s ．它离太阳最远时的速率是v 2＝9.08×102 m/s ，这时它离太阳的距离是r 2＝______． 十一第五章1. 电荷分别为q1和q2的两个点电荷单独在空间各点产生的静电场强分别为1E 和2E ，空间各点总场强为E ＝1E＋2E ．现在作一封闭曲面S ，如图所示，则以下两式分别给出通过S 的电场强度通量⎰⋅S Ed 1＝______________________________，⎰⋅SE d ＝________________________________． 四2. 一半径为R ，长为L 的均匀带电圆柱面，其单位长度带有电荷λ．在带电圆柱的中垂面上有一点P ，它到轴线距离为r (r >R )，则P 点的电场强度的大小：当r <<L 时，E ＝_____________________；当r >>L 时，E ＝__________________． 六5. 如图所示，A 、B 为靠得很近的两块平行的大金属平板，两板的面积均为S ，板间的距离为d ．今使A 板带电荷q A ，B 板带电荷q B ，且q A > q B ．则A 板的靠近B 的一侧所带电荷为___________；两板间电势差U =______ ________________． 二6. 把一个均匀带有电荷+Q 的球形肥皂泡由半径r 1吹胀到r 2，则半径为R (r 1＜R ＜r 2)的球面上任一点的场强大小E 由__________变为______________；电势U 由 __________________________变为____ ____________(选无穷远处为电势零点)． 一7. 一半径r 1 = 5 cm 的金属球A ，带电荷q 1 = +2.0×10-8 C ，另一内半径为r 2 = 10 cm 、 外半径为r 3 = 15 cm 的金属球壳B ， 带电荷q 2 = +4.0×10-8 C ，两球同心放置，如图所示．若以无穷远处为电势零点，则A 球电势U A = __________________，B 球电势U B = ___________________,八8.一带电荷q 、半径为R 的金属球壳，壳内充满介电常量为εr 的各向同性均匀电介质，壳外是真空，则此球壳的电势U =___ _______________． 十一第六章3. 源保持接通的情r 的各向同性均匀电介质充满其内．如忽略边缘效应，介质中的场强应为__________________． 四4. 一个半径为R 的薄金属球壳，带有电荷q ，壳内真空，壳外是无限大的相对介电常量为εr 的各向同性均匀电介质．设无穷远处为电势零点，则球壳的电势U =_____________ _______________． 一5. 一平行板电容器，两板间充满各向同性均匀电介质，已知相对介电常量为εr ．若极板上的自由电荷面密度为σ ，则介质中电位移的大小D =________，电场强度的大小E =__ _____________． 九6. 一个孤立导体，当它带有电荷q 而电势为U 时，则定义该导体的电容为 C =______________，它是表征导体的___ ____________的物理量． 四7. 一空气平行板电容器，电容为C ，两极板间距离为d ．充电后，两极板间相互作用力为F ．则两极板间的电势差为______________，极板上的电荷为______________． 七d8.一平行板电容器，充电后与电源保持联接，然后使两极板间充满相对介电常量为εr 的各向同性均匀电介质，这时两极板上的电荷是原来的___ ___倍；电场强度是原来的 _________倍；电场能量是原来的_________倍． 五第七章1. 在真空中，电流由长直导线1沿半径方向经a 点流入一由电阻均匀的导线构成的圆环，再由b 点沿切向从圆环流出，经长直导线2返回电源(如图)．已知直导线上的电流强度为I ，圆环半径为R ．a 、b 和圆心O 在同一直线上，则O 处的磁感强度B 的大小为__________________________． 三6. 一个绕有500匝导线的平均周长50 cm 的细环，载有 0.3 A 电流时，铁芯的相对磁导率为600 ．(1) 铁芯中的磁感强度B 为___ __________________．(2) 铁芯中的磁场强度H 为____ _________________． (μ0 =4π×10-7 T ·m ·A -1) 七7. 氢原子中，电子绕原子核沿半径为r 的圆周运动，它等效于一个圆形电流．如果外加一个磁感强度为B 的磁场，其磁感线与轨道平面平行，那么这个圆电流所受的磁力矩的大小M =__________________．(设电子质量为m e ，电子电荷的绝对值为e ) 九 8.（磁场中任一点放一个小的载流试验线圈可以确定该点的磁感强度，其大小等于放在该点处试验线圈所受的__________和线圈的________的比值． 十9. 将同样的几根导线焊成立方体，并在其对顶角A 、B 上接上电源，则立方体框架中的电流在其中心处所产生的磁感强度等于________________．十10. 已知三种载流导线的磁感线的方向如图，则相应的电流流向在图(1)中为由______向________； 图(2)中为由________向________；图(3)中为由________向________． 二ef图(1)图(2)图(3)12. 两根长直导线通有电流I ，图示有三种环路；在每种情况下，⎰⋅l Bd 于：___ _________________________________(对环路a )． （1分）____________________________________(对环路b )． （1分）____ ________________________________(对环路c )． （1分）六13.磁场中某点处的磁感强度为)SI (20.040.0j i B-=，一电子以速度j i 66100.11050.0⨯+⨯=v (SI)通过该点，则作用于该电子上的磁场力F 为__________________．(基本电荷e =1.6×10-19C) 十二14. 带电粒子穿过过饱和蒸汽时，在它走过的路径上，过饱和蒸汽便凝结成小液滴，从而显示出粒子的运动轨迹．这就是云室的原理．今在云室中有磁感强度大小为B = 1 T 的均匀磁场，观测到一个质子的径迹是半径r = 20 cm 的圆弧．已知质子的电荷为q = 1.6×10-19 C ，静止质量m = 1.67×10-27 kg ，则该质子的动能为_ ____________． 三17. 如图，在面电流密度为j的均匀载流无限大平板附近，有一载流为I 半径为R 的半圆形刚性线圈，线圈平面与载流大平板垂直，与j平行线圈所受磁力矩为_____________________，受力为_______________． 一18. 如图，半圆形线圈(半径为R )通有电流I ．线圈处在与线圈平面平行向右的均匀磁场B中．线圈所受磁力矩的大小为__________，方向为__ __________．把线圈绕OO ＇轴转过角度____________时，磁力恰截距为零. 三19. 铜的相对磁导率r = 0.9999912，其磁化率m =_________________它是_____磁性磁介质． 十第八章1. 由导线弯成的宽为a 高为b 的矩形线圈，以不变速率v 平b行于其宽度方向从无磁场空间垂直于边界进入一宽为3a 的均匀磁场中，线圈平面与磁场方向垂直(如图)，然后又从磁场中出来，继续在无磁场的空间运动．设线圈右边刚进入磁场时为t =0时刻，试在附图中画出感应电流I 与时间t 的函数关系曲线．线圈的电阻为R ，取线圈刚进入磁场时感应电流的方向为正向．(忽略线圈自感) 一3.如图所示，在一长直导线L 中通有电流I ，ABCD 为一矩形线圈，它与L 皆在纸面内，且AB 边与L 平行．(1)矩形线圈在纸面内向右移动时，线圈中感应电动势方向为 ． (2)矩形线圈绕AD 边旋转，当BC 边已离开纸面正向外运动时，线圈中感应动势的方向为________ ________________． 五4. 在磁感强度为B的磁场中，以速率v 垂直切割磁力线运动的一长度为L 的金属杆，相当于____________，它的电动势 ＝____________，产生此电动势的非静电力是__ ____________． 八5. 在直角坐标系中，沿z 轴有一根无限长载流直导线，另有一与其共面的短导体棒．若只使导体棒沿某坐标轴方向平动而产生动生电动势，则 (1) 导体棒平行x 轴放置时，其速度方向而沿___________ 轴．导体棒平行z 轴放置时，其速度方向而沿_____________ 轴． 十二6. 长为l 的金属直导线在垂直于均匀磁场的平面内以角速度ω转动．如果转轴在导线上的位置是在____________，整个导线上的电动势为最大，其值为____________；如果转轴位置是在___________，整个导线上的电动势为最小，其值为____________． 九10.一自感线圈中，电流强度在 0.002 s 内均匀地由10 A 增加到12 A ，此过程中线圈内自感电动势为 400 V ，则线圈的自感系数为L =____________． 十11.面积为S 的平面线圈置于磁感强度为B的均匀磁场中．若线圈以匀角速度ω绕位于线圈平面内且垂直于B 方向的固定轴旋转，在时刻t = 0B与线圈平面垂直．则任意时刻t 时通过线圈的磁通量为__________________，线圈中的感应电动势为__________________．若均匀磁场B是由通有电流I 的线圈所产生，且B =kI (k 为常量)，则旋转线圈相对于产生磁场的线圈最大互感系数为______________． 十一13.图示为一圆柱体的横截面，圆柱体内有一均匀电场E，其方向垂直纸面向内，E 的大小随时间t 线性增加，P 为柱体内与轴线相距为r 的一点则 (1)P 点的位移电流密度的方向为____________． (2) P 点感生磁场的方向为___________． 十一C。

单元一 简谐振动一、 选择、填空题1. 对一个作简谐振动的物体，下面哪种说法是正确的？ 【 C 】(A) 物体处在运动正方向的端点时，速度和加速度都达到最大值；(B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零；(D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一沿X 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，振动方程用余弦函数表示，如果该振子的初相为π34，则t=0时，质点的位置在： 【 D 】(A) 过A 21x =处，向负方向运动； (B) 过A 21x =处，向正方向运动； (C) 过A 21x -=处，向负方向运动；(D) 过A 21x -=处，向正方向运动。

3. 将单摆从平衡位置拉开，使摆线与竖直方向成一微小角度θ，然后由静止释放任其振动，从放手开始计时，若用余弦函数表示运动方程，则该单摆的初相为： 【 B 】(A) θ； (B) 0； (C)π/2； (D) -θ4. 图(a)、(b)、(c)为三个不同的谐振动系统，组成各系统的各弹簧的倔强系数及重物质量如图所示，(a)、(b)、(c)三个振动系统的ω (ω为固有圆频率)值之比为：【 B 】(A) 2：1：1； (B) 1：2：4； (C) 4：2：1； (D) 1：1：25. 一弹簧振子，当把它水平放置时，它可以作简谐振动，若把它竖直放置或放在固定的光滑斜面上如图，试判断下面哪种情况是正确的： 【 C 】(A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动；(B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动； (C) 两种情况都可作简谐振动；)4(填空选择)5(填空选择(D) 两种情况都不能作简谐振动。

6. 一谐振子作振幅为A 的谐振动，它的动能与势能相等时，它的相位和坐标分别为： 【 C 】A2332,3)D (;A 22,43or ,4)C (;A 23,65,6)B (;A 21,32or ,3)A (±±±±±±±±±±±±，ππππππππ7. 如果外力按简谐振动的规律变化，但不等于振子的固有频率。

第12章 气体动理论一、填空题：1、一打足气的自行车内胎,若在7℃时轮胎中空气压强为×510pa .则在温度变为37℃,轮胎内空气的压强是 ;设内胎容积不变2、在湖面下50.0m 深处温度为4.0℃,有一个体积为531.010m -⨯的空气泡升到水面上来,若湖面的温度为17.0℃,则气泡到达湖面的体积是 ;取大气压强为50 1.01310p pa =⨯3、一容器内储有氧气,其压强为50 1.0110p pa =⨯,温度为27.0℃,则气体分子的数密度为 ；氧气的密度为 ；分子的平均平动动能为 ；分子间的平均距离为 ;设分子均匀等距排列4、星际空间温度可达,则氢分子的平均速率为 ,方均根速率为 ,最概然速率为 ;5、在压强为51.0110pa ⨯下,氮气分子的平均自由程为66.010cm -⨯,当温度不变时,压强为 ,则其平均自由程为1.0mm;6、若氖气分子的有效直径为82.5910cm -⨯,则在温度为600k,压强为21.3310pa ⨯时,氖分子1s 内的平均碰撞次数为 ;7、如图12-1所示两条曲线1和2,分别定性的表示一定量的某种理想气体不同温度下的速率分布曲线,对应温度高的曲线 是 .若图中两条曲线定性的表示相同温度下的氢气和氧气的速率分布曲线,则表示氧气速率分布曲线的是 .8、试说明下列各量的物理物理意义： 112kT , 232kT , 32i kT , 42i RT , 532RT , 62M i RT Mmol ; 参考答案：1、54.4310pa ⨯ 2、536.1110m -⨯ 3、25332192.4410 1.30 6.2110 3.4510m kg m J m ----⨯⋅⨯⨯ 4、2121121.6910 1.8310 1.5010m sm s m s ---⨯⋅⨯⋅⨯⋅ 图12-15、6.06pa6、613.8110s -⨯ 7、2 ,28、略二、选择题：教材习题12-1,12-2,12-3,12-4. 见课本p207～208参考答案：12-1～12-4 C, C, B, B. 第十三章热力学基础一、选择题1、有两个相同的容器,容积不变,一个盛有氦气,另一个盛有氢气均可看成刚性分子它们的压强和温度都相等,现将 5 J 的热量传给氢气,使氢气温度升高,如果使氦气也升高同样的温度,则应向氦气传递的热量是A 6 JB 5 JC 3 JD 2 J2、一定量理想气体,经历某过程后,它的温度升高了,则根据热力学定理可以断定：1该理想气体系统在此过程中作了功；2在此过程中外界对该理想气体系统作了正功；3该理想气体系统的内能增加了；4在此过程中理想气体系统既从外界吸了热,又对外作了正功;以上正确的是：A 1,3B 2,3C 3D 3,43、摩尔数相等的三种理想气体H e 、N 2和CO 2,若从同一初态,经等压加热,且在加热过程中三种气体吸收的热量相等,则体积增量最大的气体是：AH e BN 2CCO 2 D 三种气体的体积增量相同4、如图所示,一定量理想气体从体积为V 1膨胀到V 2,AB,AC为等温过程AD 为绝热过程;则吸热最多的是： A AB 过程 B AC 过程 C AD 过程 D 不能确定 5、卡诺热机的循环曲线所包围的面积从图中abcda 增大为ab’c’da ,那么循环abcda 与ab’c’da 所作的净功和热机效率的变化情况是：A 净功增大,效率提高；B 净功增大,效率降低；C 净功和效率都不变；D 净功增大,效率不变;6、根据热力学第二定律判断下列哪种说法是正确的是：A 热量能从高温物体传到低温物体,但不能从低温物体传到高温物体；B 功可以全部变为热,但热不能全部变为功；C 气体能够自由膨胀,但不能自由压缩；D 有规则运动的能量能够变为无规则运动的能量,但无规则运动的能量不能够变为有规则运动的能量;7、 理想气体向真空作绝热膨胀A 膨胀后,温度不变,压强减小．VB 膨胀后,温度降低,压强减小．C 膨胀后,温度升高,压强减小．D 膨胀后,温度不变,压强不变．8、1mol 的单原子分子理想气体从状态A 变为状态B ,如果不知是什么气体,变化过程也不知道,但A 、B两态的压强、体积和温度都知道,则可求出：A 气体所作的功.B 气体内能的变化.C 气体传给外界的热量.D 气体的质量.9、 有人设计一台卡诺热机可逆的．每循环一次可从 400 K 的高温热源吸热1800 J,向 300 K 的低温热源放热 800 J ．同时对外作功1000 J,这样的设计是A 可以的,符合热力学第一定律．B 可以的,符合热力学第二定律．C 不行的,卡诺循环所作的功不能大于向低温热源放出的热量．D 不行的,这个热机的效率超过理论值．10、 一绝热容器被隔板分成两半,一半是真空,另一半是理想气体．若把隔板抽出,气体将进行自由膨胀,达到平衡后A 温度不变,熵增加．B 温度升高,熵增加．C 温度降低,熵增加．D 温度不变,熵不变．二、 填充题1、要使一热力学系统的内能变化,可以通过 或 两种方式,或者两种方式兼用来完成;热力学系统的状态发生变化时,其内能的改变量只决定于 ,而与 无关;2、将热量Q 传给一定质量的理想气体;1若体积不变,热量转化为 ；2若温度不变,热量转化为 ;3、卡诺循环是由两个 过程和两个 过程组成的循环过程;卡诺循环的效率只与 有关,卡诺循环的效率总是 大于、小于、等于1;4、一定量理想气体沿a →b →c 变化时作功abc W =615J,气体在b 、c 两状态的内能差J E E c b 500=-;那么气体循环一周,所作净功=WJ ,向外界放热为=Q J ,等温过程中气体作功=ab WJ ;5、常温常压下,一定量的某种理想气体可视为刚性双原子分子,在等压过程中吸热为Q,对外作功为W,内能增加为E ∆,则W Q =_ _,E Q∆=_________; 6、p V -图上封闭曲线所包围的面积表示 物理量,若循环过程为逆时针方向,则该物理量为 ;填正或负7、一卡诺热机低温热源的温度为27C,效率为40% ,高温热源的温度T 1 = .8、设一台电冰箱的工作循环为卡诺循环,在夏天工作,环境温度在35C,冰箱内的温度为0C,这台电冰箱的理想制冷系数为e = .9、一循环过程如图所示,该气体在循环过程中吸热和放热的情ab coVT况是a →b 过程 ,b →c 过程 ,c →a 过程 ;10、将1kg 温度为010C 的水置于020C 的恒温热源内,最后水的温度与热源的温度相同,则水的熵变为 ,热源的熵变为 ;水的比热容为34.1810ln1.03530.035J kg K ⨯⋅=，参考答案：一、1、C 2、C 3、A 4、A 5、D6、C7、A8、B9、D 10、A二、1、作功,传热,始末状态,过程 2、理想气体的内能,对外作功 3、绝热,等温, 4、115J ,500J ,615J 5、27,576、功,负7、 500K8、9、吸热,放热,吸热 10、11146.3,142.7J K J K --⋅-⋅自测题5一、选择题1、一定量某理想气体按2pV =恒量的规律膨胀,则膨胀后理想气体的温度 A 将升高 B 将降低 C 不变 D 不能确定;2、若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常量,R 为摩尔气体常量,则该理想气体的分子数为 A pV m B ()pV kT C ()pV RT D ()pV mT3、如题5.1.1图所示,两个大小不同的容器用均匀的细管相连,管中有一水银作活塞,大容器装有氧气,小容器装有氢气,当温度相同时,水银滴静止于细管中央,试问此时这两种气体的密度哪个大 A 氧气的密度大; B 氢气的密度大; C 密度一样大; D 无法判断;4、若室内生起炉子后温度从015C 升高到027C ,而室内气压不变,则此时室内的分子数减少了A 0.5%B 4%C 9%D 21%5、一定量的理想气体,在容积不变的条件下,当温度升高时,分子的平均碰撞次数Z 和平均自由程λ的变化情况是 A Z 增大,λ不变; B Z 不变,λ增大; C Z 和λ都增大; D Z 和λ都不变;6、一定量的理想气体,从a 态出发经过①或②过程到达b 态,acb 为等温线如题5.1.2图所示,则①,②两过程中外界对系统传递的热量12,Q Q 是A 120,0Q Q >> B 120,0Q Q << C 120,0Q Q >< D 120,0Q Q <>7、如题5.1.3图,一定量的理想气体经历acb 过程时吸热200J ;则经历acbda 过程时,吸热为 A 1200J - B 1000J - C 700J - D 1000J8、一定量的理想气体,分别进行如题5.1.4图所示的两个卡诺循环abcda 和a b c d a ''''';若在P V -图上这两个循环曲线所围面积相等,则可以由此得知这两个循环 A 效率相等; B 由高温热源处吸收的热量相等;C 在低温热源处放出的热量相等;D 在每次循环中对外做的净功相等;9、“理想气体和单一热源接触作等温膨胀时,吸收的热量全部用来对外做功;”对此说法,有如下几种评论,哪种是正确的A 不违反热力学第一定律,但违反热力学第二定律;B 不违反热力学第二定律,但违反热力学第一定律;C 不违反热力学第一定律,也不违反热力学第二定律;D 违反热力学第一定律,也违反热力学第二定律;10、一定量的理想气体向真空作绝热自由膨胀,体积由1V 增至2V ,在此过程中气体的A 内能不变,熵增加;B 内能不变,熵减少;C 内能不变,熵不变;D 内能增加,熵增加;二、填空题：1、在推导理想气体压强公式中,体现统计意义的两条假设是1 ；2 ;2、在定压下加热一定量的理想气体;若使其温度升高1K 时,它的体积增加了倍,则气体原来的温度是 ;3、在相同的温度和压强下,各为单位体积的氢气视为刚性双原子分子气体与氦气的内能之比为 ;4、分子物理学是研究 的学科,它应用的基本方法是 方法;①②题5.1.2图 1 41 4 题5.1.3图o 题5.1.4图5、解释名词：自由度 ;准静态过程 ;6、用总分子数N ,气体分子速率v 和速率分布函数()f v 表示下列各量：1速率大于0v 的分子数= ；2速率大于0v 的那些分子的平均速率= ；3多次观察某一分子的速率,发现其速率大于0v 的概率= ;7、常温常压下,一定量的某种理想气体可视为刚性分子、自由度为i ,在等压过程中吸热为Q ,对外做功为A ,内能增加为E ∆,则A Q = ;8、有一卡诺热机,用29kg 空气为工作物质,工作在027C 的高温热源与073C -的低温热源之间,此热机的效率η= ;若在等温膨胀过程中气缸体积增大倍,则此热机每一循环所做的功为 ;空气的摩尔质量为312910kg mol--⨯⋅ 自测题5参考答案一、选择题1、B2、B3、A4、B5、A6、A7、B8、D9、C 10、A二、填空题1、1沿空间各方向运动的分子数目相等； 2222x y z v v v ==;2、200K3、53;1034、物质热现象和热运动规律； 统计;5、确定一个物体在空间的位置所需要的独立坐标的数目；系统所经历的所有中间状态都无限接近于平衡状态的过程;6、0000()()/()()v v v v Nf v dv vf v dv f v dv f v dv ∝∝∝∝⎰⎰⎰⎰ 7、2;22i i i ++ 8、533.3%;8.3110J ⨯;另外添加的题目：一、选择题：1、双原子理想气体,做等压膨胀,若气体膨胀过程从热源吸收热量J 700,则该气体对外做功为 DA J 350B J 300C J 250D J 2002、在V P -图图1中,mol 1理想气体从状态A 沿直线到达B ,B A V V =2,则此过程系统的功能和内能变化的情况为 CA 0,0>∆>E AB 0,0<∆<E AC 0,0=∆>E AD 0,0>∆<E A3、某理想气体分别经历如图2所示的两个卡诺循环：)(abcd I 和)(d c b a ''''I I ,且两条循环曲线所围面积相等;设循环I 的效率为η,每次循环在高温热源处吸收的热量为Q ,循环II 的效率为η',每次循环在高温Q ',则BA Q Q '<'<,ηη;B Q Q '>'<,ηη;C Q Q '<'>,ηη;D Q Q '>'>,ηη4、一热机在两热源12400,300T K T K ==之间工作,一循环过程吸收1800J ,放热800J ,作功1000J ,此循环可能实现吗 BA 可能；B 不可能；C 无法判断;5、有两个相同的容器,容积不变,一个盛有氦气,另一个盛有氢气均可看成刚性分子它们的压强和温度都相等,现将5J 的热量传给氢气,使氢气温度升高,如果使氦气也升高相同的温度,则应向氦气传递的热量是CA 6JB 5JC 3JD 2J6、一定量理想气体,经历某过程后,它的温度升高了,则根据热力学定理可以断定：1该理想气体系统在此过程中作了功；2在此过程中外界对该理想气体系统作了功；3该理想气体系统的内能增加了；4在此过程中理想气体系统既从外界吸了热,又对外作了正功;以上正确的是 CA 1,3B 2,3C 3 D3,4 E47、对于理想气体系统来说,在下列过程中,哪个过程系统所吸收的热量、内能的增量和对外作的功三者均为负值： DA 等容降压过程B 等温膨胀过程C 绝热膨胀过程D 等压压缩过程8、对于室温下的双原子分子理想气体,在等压膨胀的情况下,系统对外所作的功与从外界吸收的热量之比/A Q 等于： DA 1/3B 1/4C 2/5D 2/79、摩尔数相等的三种理想气体e H 、2N 和2CO ,若从同一初态,经等压加热,且在加热过程中三种气体吸收的热量相等,则体积增量最大的气体是： AA e HB 2NC 2COD 三种气体的体积增量相同10、如图所示,一定量理想气体从体积为1V 膨胀到2V ,AB 为等压过程,AC 为等温过程,AD 为绝热过程,则吸热最多的是：AA AB 过程 B AC 过程 C AD 过程 D 不能确定11、根据热力学第二定律判断下列哪种说法是正确的是：CA 热量能从高温物体传到低温物体,但不能从低温物体传到高温物体；B 功可以全部变为热,但热不能全部变为功；C 气体能够自由膨胀,但不能自由压缩；D 有规则运动的能量能够变为无规则运动的能量,但无规则运动的能量不能够变为有规则运动的能量;12、汽缸内盛有一定的理想气体,当温度不变,压强增大一倍时,该分子的平均碰撞频率和平均自由程的变化情况是：C A Z 和λ都增大一倍； B Z 和λ都减为原来的一半； C Z 增大一倍而λ减为原来的一半；D Z 减为原来的一半而λ增大一倍;13、在恒定不变的压强下,气体分子的平均碰撞频率Z 与气体的热力学温度T 的关系为CA Z 与T 无关；B Z 与T 成正比；C Z 与T 成反比；D Z 与T 成正比;14、一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,而且都处于平衡状态,则它们： CA 温度相同、压强相同；B 温度、压强相同；C 温度相同,但氦气的压强大于氮气的压强；D 温度相同,但氦气的压强小于氮气的压强;15、已知氢气与氧气的温度相同,请判断下列说法哪个正确A 氧分子的质量比氢分子大,所以氧气的压强一定大于氢气的压强；B 氧分子的质量比氢分子大,所以氧气密度一定大于氢气的密度；C 氧分子的质量比氢分子大,所以氢分子的速率一定比氧分子的速率大；D 氧分子的质量比氢分子大,所以氢分子的方均根速率一定比氧分子的方均根速率大;16、按2PV =恒量规律膨胀的理想气体,膨胀后的温度为： CA 升高；B 不变；C 降低；D 无法确定17、下列各式中哪一种式表示气体分子的平均平动动能式中M 为气体的质量,m 为气体分子的质量,N 为气体分子总数目,n 为气体分子密度,0N 为阿伏加德罗常数,mol M 为摩尔质量;A 32m PV M ;B 32mol M PV M ;C 32nPV ;D 032mol M N PV M18、一定量的理想气体可以：DA 保持压强和温度不变同时减小体积；B 保持体积和温度不变同时增大压强；C 保持体积不变同时增大压强降低温度；D 保持温度不变同时增大体积降低压强;19、设某理想气体体积为V ,压强为P ,温度为T ,每个分子的质量为μ,玻尔兹曼常数为k ,则该气体的分子总数可以表示为：C A PV k μ B PT V μ C PV kT D PT kV19、关于温度的意义,有下列几种说法：1气体的温度是分子平均平动动能的量度；2气体的温度是大量气体分子热运动的集体表现,具有统计意义；3温度的高低反映物质内部分子运动剧烈程度的不同；4从微观上看,气体的温度表示每个气体分子的冷热程度；上述说法中正确的是：BA1,2,4 B1,2,3 C2,3,4 D1,3,420、设某种气体的分子速率分布函数为()f v ,则速率在12v v →区间内的分子平均速率为：CA 21()v v vf v dv ⎰B 21()v v v vf v dv ⎰ C 2121()()v v v v vf v dv f v dv ⎰⎰ D 210()()v v vf v dv f v dv∝⎰⎰ 21、两容积不等的容器内分别盛有可视为理想气体的氦气和氮气,如果它们温度和压强相同,则两气体：CA 单位体积内的分子数必相同；B 单位体积内的质量必相同；C 单位体积内分子的平均动能必相同：D 单位体积内气体的内能必相同;22、在标准状态下,体积比为1:2的氧气和氦气均视为理想气体相混合,混合气体中氧气和氦气的内能之比为：CA 1:2B 5:3C 5:6D 10:3填空题：1、要使一热力学系统的内能增加,可以通过传热或作功两种方式,或者两种方式兼用来完成;热力学系统的状态发生变化时,其内能的改变量只决定于初末状态,而与过程无关;2、16g 氧气在400K 温度下等温压缩,气体放出的热量为1152J ,则被压缩后的气体的体积为原体积的12倍,而压强为原来压强的2倍;3、一热机从温度为727o C 的高温热源吸热,向温度为527oC 的低温热量放热,若热机在最大效率下工作,且每一循环吸热2000J ,则此热机每一循环作功为400J ;4、一卡诺热机在每次循环中都要从温度为400K 的高温热源吸热418J ,向低温热源放热334.4J ,低温热源的温度为320K ;5、汽缸内有单原子理想气体,若绝热压缩使体积减半,问气体分子的平均速率变为原来速率的 倍若为双原子理想气体又为 倍6、下面给出理想气体状态方程的几种微分形式,指出它们各表示什么过程; 1()mol PdV M M RdT =表示等压过程； 2()mol VdP M M RdT =表示等容或者等体过程；30PdV VdP +=表示等温过程;7、容积为10升的容器中储有10克的氧气;1600m s -=⋅,则此气体的温度T =462K ；压强P = 51.210⨯ Pa ;8、在室温27o C 下,1mol 氢气和1mol 氧气的内能比为1:1；1g 氢气和1g 氧气的内能比为16:19、理想气体的内能是温度的单值函数; 2i kT 表示分子的平均动能； 2i RT 表示1mol 气体分子的内能 2m i RT M 表示m 千克气体分子的内能 10、氮气在标准状态下的分子平均碰撞次数为311.310s -⨯,分子平均自由程为6610cm -⨯,若温度不变,气压降为0.1atm ,则分子平均碰撞次数变为211.310s -⨯；分子平均自由程变为5610cm -⨯。

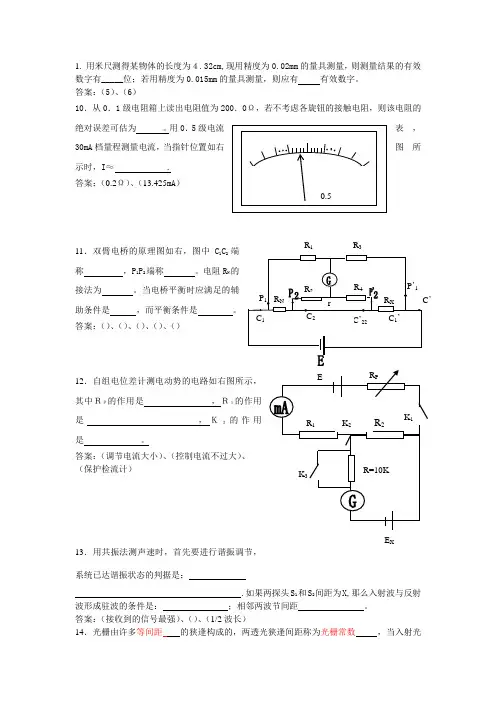
1. 用米尺测得某物体的长度为４.32cm,现用精度为0.02mm 的量具测量，则测量结果的有效数字有_____位；若用精度为0.015mm 的量具测量，则应有 有效数字。

答案：（5）、（6） 10．从0．1级电阻箱上读出电阻值为200．0Ω，若不考虑各旋钮的接触电阻，则该电阻的绝对误差可估为 。

用0．5级电流表，30mA 档量程测量电流，当指针位置如右图所示时，I ≈ . 答案：（0.2Ω）、（13.425mA ）11．双臂电桥的原理图如右，图中C 1C 2端称 ，P 1P 2端称 。

电阻R N 的接法为 。

当电桥平衡时应满足的辅助条件是 ，而平衡条件是 。

答案：（）、（）、（）、（）、（）12．自组电位差计测电动势的电路如右图所示，其中ＲＰ的作用是 ，Ｒ１的作用是 ，Ｋ３的作用是 。

答案：（调节电流大小）、（控制电流不过大）、 （保护检流计）13．用共振法测声速时，首先要进行谐振调节，系统已达谐振状态的判据是：.如果两探头S 1和S 2间距为X,那么入射波与反射波形成驻波的条件是： ；相邻两波节间距 。

答案：（接收到的信号最强）、（）、（1/2波长）14．光栅由许多等间距 的狭逢构成的，两透光狭逢间距称为光栅常数 ，当入射光0.5C ’22 C 1’R 1 R 3C 2C 1P 1 rR X R N R 4R 2P ’1C ’K 2K 2 K 3ER PR 2R 1 R=10KE XK 1K 2垂直入射到光栅上时，衍射角ϕk ，衍射级次K 满足的关系式是 ，用此式可通过实验测定 ___。

答案：（等间距）、（光栅常数）、（λϕK b a K =+sin )(）、（光的波长） 15．在光栅衍射实验中，光栅方程是 ，其中a+b 是 φK是 ，Ｋ是 ．答案：（λϕK b a K =+sin )(）、（光栅常数）、（衍射角）、（条纹级数）16．在光栅衍射实验中，光栅方程是 。

若已知入射光波长λ为理论真值，测得第一级衍射角为φK ±ΔφK ，则光栅常数的不确定度Δd = . 答案：（λϕK b a K =+sin )(）、（）17．分光计调整的任务是________能够接受平行光,使_____够发射平行光,望远镜的主光 与______的主光轴达到 ________,并与载物台的法线方向____________. 分光计用圆刻 度盘测量角度时,为了消除圆度盘的_________, 必须有相差180°的两个游标分别读数. 答案：（）、（）、（）、（）、（）、（）18.分光计读数系统设计双游标的主要作用是________________；自准直望远镜调焦到无穷 远时，分划板位于__________________________；要使平行光管出射的光是平行光，狭缝应 在会聚透镜的________________处。

填空题1．激光器谐振腔的腔镜需要极高的反射率，故常在镜表面镀一层介质膜以提高其反射率，称为增反膜. 对于输出波长为λ的激光器，在折射率为1.5的光学玻璃上镀一层厚度均匀的ZnS 薄膜（折射率为2.40）作为反射镜，则此增反膜的最小厚度为__________. (激光器内的气体折射率小于1.5)2．在单缝夫琅和费衍射实验中，波长为λ的单色光垂直入射在宽度为a = 4λ的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为____________.3．若质子的德布罗意波长为λ nm ，则它的动能为______________. (已知普朗克常量h ，质子质量m )4．电量都是Q 的四个同号点电荷，分别放在边长为a 的正方形的四个顶点上．若在正方形的正中心放一个点电荷，其受到的库仑力大小为______________.5. 在迈克耳逊干涉仪的一条光路中插入一块折射率为n ，厚度为d 的透明薄片，插入这块薄片使这条光路的光程改变了______________.6. 四条互相平行的无限长载流直导线中的电流均为I ，正方形的边长为a ，正方形中心O 点处的磁感应强度大小为（ ）． 参考答案：n 4λ 4 个 222λm h E = 0 2(n-1)d . a Iπμ201．电量都是Q 的四个同号点电荷，分别放在边长为a 的正方形的四个顶点上．若在正方形的正中心放一个点电荷，其受到的库仑力大小为 .2．一个系统由某一状态出发，经过某一过程达到另一状态，如果存在另一过程，它能使系统和外界完全复原，即系统回到原来的状态，同时消除了系统对外界引起的一切影响，则原来的过程称为 .3．能量均分定理:在热平衡态下，理想气体分子每个自由度上都具有相同的平均动能12kT ，一个分子的平均总能量为 ，i 为自由度数 .4．一卡诺热机(可逆的)，低温热源的温度为27℃，热机效率为10％，其高温热源温度为__________________ K ．今欲将该热机效率提高到20％，若低温热源保持不变，则高温热源的温度应为__________________K ．5．图中，六根无限长导线互相绝缘，通过电流均为I ，区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形，哪一个区域指向纸内的磁通量最大________________ .6．两个相同的容器，一个盛氢气，一个盛氦气(均视为刚性分子理想气体)，开始时它们的压强和温度都相等，现将6 J 热量传给氦气，使之升高到一定温度 .若使氢气也升高同样温度，则应向氢气传递热量________J . 参考答案：1．0； 2． 可逆过程 。

第一部分 选择题与填空题 （共60分）一、单项选择题（共10小题，每题3分，共30分）1．一运动质点在某瞬时位于矢径()y x r ,的端点处, 其速度大小为(A) t r d d (B) t rd d(C) t r d d (D) 22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x ［ ］2．人造地球卫星绕地球作椭圆轨道运动，卫星轨道近地点和远地点分别为A 和B ．用L 和E K 分别表示卫星对地心的角动量及其动能的瞬时值，则应有 (A) L A >L B ，E KA >E kB ． (B) L A =L B ，E KA <E KB ． (C) L A =L B ，E KA >E KB ． (D) L A <L B ，E KA <E KB ． ［ ］3．一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮，绳的两端分别悬有质量为m 1和m 2的物体(m 1＜m 2)，如图所示．绳与轮之间无相对滑动．若某时刻滑轮沿逆时针方向转动，则绳中的张力(A) 处处相等． (B) 左边大于右边． (C) 右边大于左边． (D) 哪边大无法判断．［ ］4．设图示的两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线；令()2O p v 和()2H p v 分别表示氧气和氢气的最概然速率，则(A) 图中ａ表示氧气分子的速率分布曲线； ()2O p v /()2H p v =4．(B) 图中ａ表示氧气分子的速率分布曲线； ()2O p v /()2H p v ＝1/4．(C) 图中ｂ表示氧气分子的速率分布曲线； ()2O p v /()2H p v ＝1/4．(D) 图中ｂ表示氧气分子的速率分布曲线；()2O p v /()2H p v ＝ 4．［ ］f (v )5．1 mol 理想气体从p －V 图上初态a 分别经历如图所示的(1) 或(2)过程到达末态b ．已知T a <T b ，则这两过程中气体吸收的热量Q 1和Q 2的关系是 (A) Q 1> Q 2>0． (B) Q 2> Q 1>0．(C) Q 2< Q 1<0． (D) Q 1< Q 2<0． (E) Q 1= Q 2>0．［ ］6．如图所示，在坐标(a ，0)处放置一点电荷＋q ，在坐标(－a ，0)处放置另一点电荷－q ．P 点是y 轴上的一点，坐标为(0，y )．当y >>a 时，该点场强的大小为：(A) 204y q επ． (B) 202yqεπ． (C) 302y qa επ． (D) 304y qaεπ． [ ]7. 关于静电场中某点电势值的正负，下列说法中正确的是： (A) 电势值的正负取决于置于该点的试验电荷的正负． (B) 电势值的正负取决于电场力对试验电荷作功的正负． (C) 电势值的正负取决于电势零点的选取． (D) 电势值的正负取决于产生电场的电荷的正负． ［ ］8．均匀磁场的磁感强度B垂直于半径为r 的圆面．今以该圆周为边线，作一半球面S ，则通过S 面的磁通量的大小为 (A) 2πr 2B ． (B) πr 2B ．(C) 0． (D) 无法确定的量． ［ ］9．两根无限长平行直导线载有大小相等方向相反的电流I ，并各以d I /d t 的变化率增长，一矩形线圈位于导线平面内(如图)，则：(A) 线圈中无感应电流． (B) 线圈中感应电流为顺时针方向． (C) 线圈中感应电流为逆时针方向．(D) 线圈中感应电流方向不确定． ［ ］10．在某地发生两件事，静止位于该地的甲测得时间间隔为4 s ，若相对于甲作匀速直线运动的乙测得时间间隔为5 s ，则乙相对于甲的运动速度是(c 表示真空中光速)(A) (4/5) c ． (B) (3/5) c ．(C) (2/5) c ． (D) (1/5) c ． ［ ］Vp O a b(1)(2) I IO x -a -q +q +a P (0,y ) y二、填空题（共10小题，每题3分，共30分）1．一个力F 作用在质量为 1.0 kg 的质点上，使之沿x 轴运动．已知在此力作用下质点的运动学方程为3243t t t x +-= (SI)．在0到4 s 的时间间隔内， (1) 力F 的冲量大小I =__________________．(2) 力F 对质点所作的功W =________________．2．长为l 、质量为M 的匀质杆可绕通过杆一端O 的水平光滑固定轴转动，转动惯量为231Ml ，开始时杆竖直下垂，如图所示．有一质量为m 的子弹以水平速度0v 射入杆上A点，并嵌在杆中，OA ＝2l / 3，则子弹射入后瞬间杆的角速度ω ＝__________________________．3．2 g 氢气与2 g 氦气分别装在两个容积相同的封闭容器内，温度也相同．(氢气分子视为刚性双原子分子)(1) 氢气分子与氦气分子的平均平动动能之比He H /2w w ＝__________．(2) 氢气与氦气压强之比 He H 2p p =＝ ______________________．(3) 氢气与氦气内能之比 He H /2E E ＝ ______________________．4．1 mol 的单原子理想气体，从状态I (p 1,V 1)变化至状态II(p 2,V 2)，如图所示，则此过程气体对外作的功为________________________，吸收的热量为______________________．5．热力学第二定律的开尔文表述和克劳修斯表述是等价的，表明在自然界中与热现象有关的实际宏观过程都是不可逆的，开尔文表述指出了________________ _______________的过程是不可逆的，而克劳修斯表述指出了________________的过程是不可逆的．,V 2)6．电荷分别为q 1和q 2的两个点电荷单独在空间各点产生的静电场强分别为1E和2E ，空间各点总场强为E＝1E ＋2E ．现在作一封闭曲面S ，如图所示，则以下两式分别给出通过S 的电场强度通量⎰⋅S E d 1＝______________________________，⎰⋅S Ed ＝________________________________．7．静电场中有一质子(带电荷e ＝1.6×10-19 ) 沿图示路径从a 点经c 点移动到b 点时，电场力作功8×10-15 J ．则当质子从b 点沿另一路径回到a 点过程中，电场力作功A ＝________________；若设a 点电势为零，则b 点电势U b ＝_________ .8．在如图所示的回路中，两共面半圆的半径分别为a 和b ，且有公共圆心O ，当回路中通有电流I 时，圆心O 处的磁感强度B 0 =___________________，方向___________________．9．如图，一根载流导线被弯成半径为R 的1/4圆弧，其电流方向由a →b,放在磁感强度为B 的均匀磁场中，则载流导线ab 所受磁场的作用力的大小为____________ ，方向_________________．10．狭义相对论的两条基本原理中，相对性原理说的是________________________________________________________________________________ ；光速不变原理说的是_______________________________________________________________________ ．I a b OB第二部分 计算题与证明题（共4小题，每题10分，共40分）三、（本题10分）一轴承光滑的定滑轮，质量为M ＝2.00 kg ，半径为R ＝0.100 m ，一根不能伸长的轻绳，一端固定在定滑轮上，另一端系有一质量为m ＝5.00 kg的物体，如图所示．已知定滑轮的转动惯量为J ＝221MR ，其初角速度 ω0＝10.0 rad/s ，方向垂直纸面向里．求：(1) 定滑轮的角加速度的大小和方向；(2) 定滑轮的角速度变化到ω＝0时，物体上升的高度； (3)当物体回到原来位置时，定滑轮的角速度的大小和方向．四、（本题10分）长直导线与矩形单匝线圈共面放置，导线与线圈的长边平行．矩形线圈的边长分别为a 、b ，它到直导线的距离为c (如图)．当长直导线中通有电流I = I 0sin ωt 时，求矩形线圈中的感应电动势．五、（本题10分）在实验室中测得电子的速度是0.8c ，c 为真空中的光速．假设一观察者相对实验室以0.6c 的速率运动，其方向与电子运动方向相同，试求该观察者测出的电子的动能和动量是多少？（电子的静止质量m e ＝9.11×10-31kg ）六、（本题10分）电荷Q 均匀分布在半径为R的球体内．设无穷远处为电势零点，试证明：距离球心r (r ＜R)处的电势为 ()302283Rr R Q U επ-=合肥工业大学2004-2005学年第一学期《大学物理》（Ш）参考答案及评分标准第一部分 选择题与填空题 （共60分）一、选择题（本大题共10小题，每小题3分，共30分）1、D2、C3、C4、B5、A6、C7、C8、B9、B 10、B二、填空题（本大题共10小题，每小题3分，共30分）1． 16 N ·s 1分 176 J 2分2． ()lm M /3460+v 3分3． 1 1分2 1分 10/3 1分 4．))((211221V V p p -+ 1分))((21)(2312211122V V p p V p V p -++- 2分5．功变热 2分 热传导 1分6． q 1 / ε0 1分 ( q 1+q 2) / ε0 2分7． －8×10-15 J 2分 －5×104 V 1分8． )11(40ba I +μ 2分垂直纸面向里． 1分 9． BIR 2 2分 沿y 轴正向 1分10． 一切彼此相对作匀速直线运动的惯性系对于物理学定律都是等价的 1分 一切惯性系中，真空中的光速都是相等的 2分第二部分 计算题与证明题（共4小题，每题10分，共40分）三、解： (1) ∵ mg －T ＝ma 1分 TR ＝J β 2分 a ＝R β 1分∴ β = mgR / (mR 2＋J )()R M m mgMR mR mgR +=+=222122 ＝81.7 rad/s 21分方向垂直纸面向外． 1分(2) ∵ βθωω2202-= 当ω＝0 时， rad 612.0220==βωθ物体上升的高度h = R θ = 6.12×10-2m 2分(3) ==βθω210.0 rad/s方向垂直纸面向外. 2分四、解：若长直导线中通有变化的电流t I I ωsin 01=，由安培环路定律可得空间的磁场分布为)2/(10r I B π=μ． 3分 穿过矩形线圈的磁通为⎰⎰⋅+π==a c cr b r I S B d 12d 10μΦ aac bI +π=ln 210μ 4分由法拉第电磁感应定律可得矩形回路中的感应电动势为：t aa cb I dt d ωωμεcos ln 200+-=Φ-=π 3分a五、解：设实验室为K 系，观察者在K ′系中，电子为运动物体．则K ′对K 系的速度为u = 0.6c ，电子对K 系速度为v x = 0.8c ．电子对K ′系的速度c c u u x x x 385.0)/(12=--='v v v 3分 观察者测得电子动能为J 1085.6)1)/(11(15220-⨯=-'-=c c m E x K v 4分动量为 x m p v '=2)/(1c m x xv v '-'=＝1.14×10-22 kg ·m/s 3分六、证：半径为r 处的电势应为以r 为半径的球面以内的电荷在该处产生的电势U 1和球面外电荷产生的电势U 2的叠加，即 U = U 1 + U 2球面内电荷产生的电势 3020330144/4R Qr r R Qr r q U i εεεπ=π=π= 4分 球面外电荷产生的电势. 在球面外取r '─→r '＋d r '的薄层．其上电荷r r RQ r r R Q dq ''=''ππ=d 3d 43/42323 它对该薄层内任一点产生的电势为r r RQr q U ''π='π=d 434d d 3002εε ⎰⎰''π==R r r r R Q U U d 43d 3022ε()302283Rr R Q επ-= 4分 ()()302230223022183834R r R Q R r R Q R Qr U U U εεεπ-=π-+π=+= 2分 若根据电势定义⎰⋅l Ed 直接算出，即()302220308344R r R Q dr r Q dr R Qr l d E U RRrrεπεπεπ-=+=⋅=⎰⎰⎰∞∞ 同样给分．。

大学物理填空题1-1 速度与加速度的方向之间成锐角时，质点的运动为加速运动：速度与加速度的方向成钝角时，质点的运动为减速运动。

1-2 已知质点运动的位置矢量，即运动方程。

求其速度与加速度，则采用求导数的方法；已知质点的加速度，求其速度与位置矢量，则采用求积分的方法。

1-3 若甲物体的运动速度为v1，乙物体的运动速度为v2，则甲物体相对于乙物体运动速度为 v1-v2 。

1-4质点做平抛物体运动过程中：水平速度和加速度是固定不变的；竖直速度是时刻变化的。

1-5 质点作匀速率圆周运动的过程中，切向加速度始终为零；质点做加速圆周运动过程中，切向加速度的方向始终与速度方向相同。

答案1-1 锐角，钝角1-2求导数的方法，求积分的方法1-3 v1-v21-4水平，加速度，竖直。

1-5切向，切向。

2-1 质量为0.25kg的质点，受力=t SI的作用，式中t为时间。

T=0时，该质点以v=2 m/s的速度通过坐标原点，则该质点任意时刻的位置矢量是__2-2 一质量为10kg的物体在力f=(120t+40)的作用下，沿x轴运动，t=0时其速度V0=6m/s,则t=3s时，其速度为_____.2-3 一物体质量为10kg，受到方向不变的力F=30+40t（SI）的作用，在开始的2s内，此力的冲量大小等于___;若物体的初速度大小为10m/s,方向与F同向，则在2s末物体速度的大小等于__.2-4 一长为L、质量均匀的链条，放在光滑的水平桌面上。

若使其长度的1/2悬于桌边下，由静止释放，任其自由滑动，刚刚好链条全部离开桌面时的速率为__2-5 一弹簧原长为0.5m,弹性系数为k,上端固定在天花板上，当下端悬挂一盘子时，其长度为0.6m，然后在盘中放一个物体，弹簧长度变为0.8m，则盘中放入物体后，在弹簧伸长过程中弹性力做的功为___3-1 某刚体绕定轴作匀变速转动，对刚体上距转轴为r处的任一质元的法向加速度a的大小和切向加速度a的大小来说，anrn2a。

大学物理2（上）总复习---填空题填空题（1）1．当气体的温度为300K 时，分子的平均平动动能为 。

（已知K J k /1038.123-⨯=）2．一质点作简谐振动，振幅为10cm ，频率为40Hz ，初相为2π，则其振动方程为 ，在t=0 s 时刻，质点的速度为 ，加速度为 。

3．产生机械波的必要条件是 和 。

4．一质点沿半径为m 2.0的圆周运动, 其角位置随时间的变化规律是256t +=θ（SI 制）。

在s t 2=时，它的法向加速度n a =___________；切向加速度t a =___________。

5．2mol 理想氦气的内能的理论值为 。

6．一质量为0.01 kg 的物体作简谐运动，其振幅为 0.08 m ， 周期为4 s ，起始时刻物体在 x= 0.04 m 处，向Ox 轴负方向运动，则简谐运动方程为 。

填空题（1）参考答案1. 6.21J 2110-⨯ ；2. x 0.10cos 80t m 2ππ⎛⎫=+ ⎪⎝⎭， 18m s π--， -20m s ； 3. 波源, 弹性介质 ； 4. 280/m s ， 210/m s ；5. 3RT ；6. ⎪⎭⎫ ⎝⎛+=32c o s 08.0ππt x ；填空题（2） 1．驻波中两个相邻的波节间各质点的振动振幅 ，相位 。

2．一质点沿半径为m 2.0的圆周运动, 其角位置随时间的变化规律是256t +=θ（SI 制）。

在s t 2=时，它的法向加速度n a =___________；切向加速度t a =___________。

3．2mol 理想氦气的内能的理论值为 。

4．已知平面简谐波方程为()cos y A bt cx ϕ=-+,式中A 、b 、c 、ϕ均为常量，则平面简谐波的振幅为 ，频率为 ，波速为 ，波长为 。

5． 质量为m 的小球，在合外力kx F -=作用下运动，已知t A x ωcos =，其中k 、ω、A均为正常量，在0=t 到ωπ2时间内小球动量的增量为___________。

质 点 运 动 学一．选择题：1、质点作匀速圆周运动，其半径为R ，从A 点出发，经过半圆周到达B 点，则在下列各 表达式中，不正确的是 （A ）（A ）速度增量 0=∆v ，速率增量 0=∆v ； （B ）速度增量 j v v 2-=∆，速率增量 0=∆v ； （C ）位移大小 R r 2||=∆ ，路程 R s π=； （D ）位移 i R r 2-=∆，路程 R s π=。

2、质点在平面上运动，已知质点位置矢量的表达式为j bt i at r 22+=（其中a 、b 为常量）则该质点作 （ D ）（A ）匀速直线运动； （B ）一般曲线运动； （C ）抛物线运动； （D ）变速直线运动。

3、质点作曲线运动，r 表示位置矢量，s 表示路程，v 表示速度, a 表示加速度。

下列表达式中， 正确的表达式为 （ B ）（A ）r r ∆=∆|| ； (B) υ==dt s d dt r d ； （C ） a dtd =υ； （D ）υυd d =|| 。

4、一个质点在做圆周运动时，则有 （ B ）（A ）切向加速度一定改变，法向加速度也改变；（B ）切向加速度可能不变，法向加速度一定改变；（C ）切向加速度可能不变，法向加速度不变；（D ）切向加速度一定改变，法向加速度不变。

5、质点作匀变速圆周运动，则：（ C ）（A ）角速度不变； （B ）线速度不变； （C ）角加速度不变； （D ）总加速度大小不变。

二．填空题：1、已知质点的运动方程为x = 2 t －4 t 2（SI ），则质点在第一秒内的平均速度 =v -2 m/s ； 第一秒末的加速度大小 a = -8 m/s 2 ；第一秒内走过的路程 S = 2.5 m 。

2、xoy 平面内有一运动的质点，其运动方程为 j t i t r 5sin 105cos 10+=（SI ），则t 时刻其速度=v j t i t 5cos 505sin 50+- ；其切向加速度的大小a t = 0 ；该质点运动的轨迹是 圆 。

第4章 振动与波动填空题（1）一质点在X 轴上作简谐振动，振幅A ＝4cm ，周期T ＝2s ，其平衡位置取作坐标原点。

若t ＝0时质点第一次通过x ＝－2cm 处且向x 轴负方向运动，则质点第二次通过x ＝－2cm 处的时刻为__ __s 。

[答案：23s ]（2）一水平弹簧简谐振子的振动曲线如题4.2(2)图所示。

振子在位移为零，速度为－ωA 、加速度为零和弹性力为零的状态，对应于曲线上的____________点。

振子处在位移的绝对值为A 、速度为零、加速度为－ω2A 和弹性力为－KA 的状态，则对应曲线上的____________点。

习题4.2(2) 图[答案：b 、f ； a 、e]（3）一质点沿x 轴作简谐振动，振动范围的中心点为x 轴的原点，已知周期为T ，振幅为A 。

（a ）若t=0时质点过x=0处且朝x 轴正方向运动，则振动方程为x=___________________。

（b ）若t=0时质点过x=A/2处且朝x 轴负方向运动，则振动方程为x=_________________。

[答案：cos(2//2)x A t T ππ=−； cos(2//3)x A t T ππ=+]（4）一横波的波动方程是))(4.0100(2sin 02.0SI x t y −=π，则振幅是____，波长是____，频率是____，波的传播速度是____。

[答案：0.02;2.5;100;250/m m Hz m s ]（5）产生机械波的条件是 和 。

[答案：波源；有连续的介质]（6）两列波叠加产生干涉现象必须满足的条件是 ， 和 。

[答案：频率相同，振动方向相同，在相遇点的位相差恒定。

]计算题 振动4.3 质量为kg 10103−⨯的小球与轻弹簧组成的系统，按20.1cos(8)(SI)3x t ππ=+的规律作谐振动，求：(1)振动的周期、振幅和初位相及速度与加速度的最大值；(2)最大的回复力、振动能量、平均动能和平均势能，在哪些位置上动能与势能相等? (3)s 52=t 与s 11=t 两个时刻的位相差；解：(1)设谐振动的标准方程为)cos(0φω+=t A x ，相比较则有：3/2,s 412,8,m 1.00πφωππω===∴==T A 又 πω8.0==A v m 1s m −⋅ 51.2=1s m −⋅2.632==A a m ω2s m −⋅(2) 0.63N m m F ma ==J 1016.32122−⨯==m mv E J 1058.1212−⨯===E E E k p当p k E E =时，有p E E 2=， 即)21(212122kA kx ⋅= ∴ m 20222±=±=A x (3) ππωφ32)15(8)(12=−=−=∆t t4.4 一质量为kg 10103−⨯的物体作谐振动，振幅为cm 24，周期为s 0.4，当0=t 时位移为cm 24+．求：(1)s 5.0=t 时，物体所在的位置及此时所受力的大小和方向； (2)由起始位置运动到cm 12=x 处所需的最短时间； (3)在cm 12=x 处物体的总能量． 解：由题已知 s 0.4,m 10242=⨯=−T A∴ 1s rad 5.02−⋅==ππωT又，0=t 时，0,00=∴+=φA x 故振动方程为m )5.0cos(10242t x π−⨯=(1)将s 5.0=t 代入得0.17m m )5.0cos(102425.0=⨯=−t x πN102.417.0)2(10103232−−⨯−=⨯⨯⨯−=−=−=πωxm ma F方向指向坐标原点，即沿x 轴负向． (2)由题知，0=t 时，00=φ，t t =时 3,0,20πφ=<+=t v A x 故且 ∴ s 322/3==∆=ππωφt (3)由于谐振动中能量守恒，故在任一位置处或任一时刻的系统的总能量均为J101.7)24.0()2(10102121214223222−−⨯=⨯⨯⨯===πωA m kA E4.6 题4.6图为两个谐振动的t x −曲线，试分别写出其谐振动方程．习题4.6图解：由题4.6图(a)，∵0=t 时，s 2,cm 10,,23,0,0000===∴>=T A v x 又πφ 即 1s rad 2−⋅==ππωT故 m )23cos(1.0ππ+=t x a 由题4.6图(b)∵0=t 时，35,0,2000πφ=∴>=v A x01=t 时，22,0,0111ππφ+=∴<=v x又 ππωφ253511=+⨯= ∴ πω65=故 m t x b )3565cos(1.0ππ+=波动4.11 沿绳子传播的平面简谐波的波动方程为y =0.05cos(10x t ππ4−)，式中x ,y 以米计，t 以秒计．求：(1)绳子上各质点振动时的最大速度和最大加速度；(2)求x =0.2m 处质点在t =1s 时的位相，它是原点在哪一时刻的位相?这一位相所代表的运动状态在t =1.25s 时刻到达哪一点? 解: (1)将题给方程与标准式2cos()y A t x πωλ=−相比，得振幅05.0=A m ，圆频率10ωπ=，波长5.0=λm ，波速2.52u ωλυλπ===1s m −⋅．绳上各点的最大振速，最大加速度分别为ππω5.005.010max =⨯==A v 1s m −⋅222max 505.0)10(ππω=⨯==A a 2s m −⋅(2)2.0=x m 处的振动比原点落后的时间为08.05.22.0==u x s 故2.0=x m ,1=t s 时的位相就是原点(0=x )，在92.008.010=−=t s 时的位相，即 2.9=φπ． 设这一位相所代表的运动状态在25.1=t s 时刻到达x 点，则825.0)0.125.1(5.22.0)(11=−+=−+=t t u x x m4.12 一列平面余弦波沿x 轴正向传播，波速为5m ·s -1，波长为2m ，原点处质点的振动曲线如题4.12图所示．(1)写出波动方程；(2)作出t =0时的波形图及距离波源0.5m 处质点的振动曲线． 解: (1)由题4.14(a)图知，1.0=A m ，且0=t 时，0,000>=v y ，∴230πφ=， 又5.225===λυuHz ，则ππυω52==习题4.12图(a)取 ])(cos[0φω+−=ux t A y ， 则波动方程为30.1cos[5()]52x y t ππ=−+m(2) 0=t 时的波形如题4.12(b)图习题4.12图(b) 习题4.12图(c)将5.0=x m 代入波动方程，得该点处的振动方程为50.530.1cos[5]0.1cos(5)52y t t πππππ⨯=−+=+m 如题4.12(c)图所示．第7章静电场7.2 填空题（1）在静电场中，电势不变的区域，场强必定为 。

大学物理学课程试卷（B 卷）（适应专业：用时：2小时；考试类型：闭卷；总分：100分）一、填空题（共8题，每空1分，共22分）1、一质点的运动方程为t x 2=，2219t y -=，其中y x ,以m 计，t 以s 计。

则质点的轨道方程为 ；s t 2=时的位置矢径=r；s t 2=的瞬时速度=v ；前2秒内的平均速度=v。

2、一个质点在几个力同时作用下的位移为∆r =(4i -5j +6k )米，其中一个恒力可表达成Ｆ=(-3i -5j +9k )牛顿，则这个力在这过程中做功为___ _ ___。

3、有两矢量A 和B ，则A ×A =________，若A 垂直B ，则A ·B =_______。

4、转动惯量是物体 量度，其大小与刚体的 ， ，和 有关。

5、由磁高斯定理知磁场是_ ___场，由安培环路定理知磁场是 场。

6. 质量为kg 10103-⨯的小球与轻弹簧组成的系统，按20.1cos(8)3x t ππ=+m 的规律作谐振动，则振动的周期 、振幅 、初位相 、速度的最大值 、加速度的最大值 。

7、按照产生的机理不同，电介质的极化现象可分为两种，一种是_ __，另一种是_ _ __ ___。

8、在一个带正电的大导体附近P 点处放置一点电荷q （电荷q 不是足够小）实际测得它的受力为F ，如果q>0,则F/q 与P 点场强E 关系 ,如果q<0,则F/q 与P 点场强E 关系 。

二、单项选择题（共8题，每题3分，共24分）1、船浮于静水中，船长L ，质量为m ，一个质量也为m 的人从船尾走到船头. 不计水和空气的阻力，则在此过程中船将（ ）A 、 不动 ；B 、 后退L ；C 、 后退L 21 ； D 、 后退L 31。

2、在静电场中，下列说法中正确的是 （ ）A 、带正电荷的导体其电势一定是正值；B 、等势面上各点的场强一定相等；C 、场强为零处电势也一定为零；D 、场强相等处电势不一定相等。

大学物理模拟试卷一一、填空题：（每小题3分，共10小题，30分）1. 一电量为的试验电荷放在电场中某点时，受到2010N竖直向下的力，则该点的电场强度大小为，电场强度的方向为。

2．一单匝闭合载流线圈，面积为S，通有电流I，放入匀强磁场中，载流线圈的法线方向单位矢量为，则其所受的磁力的合力为=________，磁力矩为=。

3．一面积为S的平面导线回路，置于一载流密绕长直螺线管内。

设长直螺线管单位长度上的匝数为n，通过的电流为, 其中和为常数，t为时间。

导线回路的法线方向与螺线管轴线平行且与螺线管中的电流强度的正方向呈右手螺旋关系。

则任意时刻t ，该导线回路中的感应电动势为。

4. 自感线圈中，电流强度0.002s内均匀地由10A增加到12A，此过程线圈内自感电动势大小为400V，则线圈的自感系数为L=。

5．平面电磁波的电场强度矢量与磁场强度矢量的方向互相，位相。

6. 在双缝干涉实验中，所用光波波长，双缝与屏间的距离D ，双缝间距为d ，则中央明条纹两侧的两个第三级明条纹之间的距离为。

7. 一束波长为的单色光由空气垂直入射到折射率为n的透明薄膜上，透明薄膜放在空气中，要使透射光得到干涉加强，则薄膜最小的厚度为。

8. 某单色光垂直入射到一个每毫米有800条刻线的光栅上，如果第一级谱线的衍射角为30O，则入射光的波长为。

9．一束自然光以布儒斯特角入射到平板玻璃片上，就偏振状态来说，反射光为光，反射光矢量的振动方向，透射光为。

10．狭义相对论的两条基本原理，一是相对性原理；二是_________________________原理。

二、选择题：（每小题3分，共10小题，30分）11. 在一个原来不带电的、外表面为球形、内表面形状不规则的空腔导体A内，放有一带电量为Q的带正电的导体B，则比较空腔导体A的电势和导体B的电势时，可得以下结论：【】（A）=；（B）>；（C）<；（D）因空腔形状不是球形，两者无法比较。

填空题1. 半径为R 的孤立导体球的电容＝ 4πε0R 。

2.为了提高光学仪器的分辨率,应使天文望远镜的的物镜直径 增大 显微镜摄影时波长 减小 。

3.一个半径为R 的圆形线圈，通有电流I ，放在磁感应强度为B 的均匀磁场4.则此线圈的磁矩为πR 2I ，所受的最大磁力矩为πR 2IB 。

5.螺线管的自感系数L ＝20mH ，当通过它的电流I ＝2A 时，它储存的磁场能量为 4×10-2 J 。

6.均匀磁场的磁感应强度B 垂直于半径为r 的圆面，今以该圆周为边线，作一半球面S ，则通过S 面的磁通量的大小为πR 2B 。

7.某物体辐射频率为146.010⨯赫兹的黄光，这种辐射相应光子的能量为 4×10-19 J 。

8.在一个半径为R ，带电为q 的导体球内，距球心r 处的场强大小为_0__.一个半径为R,载流为I 的圆弧,所对应的圆心角为π/4。

则它在圆心产生的9.磁场的磁感应强度大小为_u 0I/16R___.10.处于静电平衡下的导体_是_(填是或不是)等势体,导体表面是等势面,导体体内的电势_等于_(填大于,等于或小于)导体表面的电势.11.金属导体表面某处电荷面密度为σ，n 为σ处外法线方向的单位矢量，则该表面附近的电场强度为__6/ε0×n （向量Ｎ）__.12.在如图3-6所示的匀强磁场中（磁感应强度为B ），有一个长为l 的导体细棒绕过O 点的平行于磁场的轴以角速度ω在垂直于磁场的平面内转动，则导体细棒上的动生电动势大小为_1/2wbl 2___.13.用波长为λ的单色光垂直入射在缝宽a ＝4λ的单缝上，对应衍射角为30°的衍射光，单缝可以划分为__2__个半波带。

14.用波长为λ的平行单色光垂直照射折射率为n 的劈尖上形成等厚干涉条纹，若测得相邻两明条纹的间距是l ，则劈尖角为acrsin nl 2λ_.15.将一通电半导体薄片放入磁场中，测得其霍尔电压小于零，则可判断该半导体是 n 型。