18章习题详细答案

3180 (1- 1)190 304000
3.用于康普顿散射实验中的X射线波长0 0.2 1010 m。当
散射角为90°时，求：（1）X射线波长的改变量；（2） 碰撞电子所获得的动能；（3）电子所获得的动量。
解：（1）根据康普顿散射公式
（2） 碰 撞电子0 所获m 得h 0c的(1动c 能 o)s0.02A 4
速粒子的物质波公式是＿＿＿ ＿h＿m 0 ，初
速为零的电子在电势差为U的电场中加速
后，其物质波的公式是＿＿＿＿h＿2 _m _。 eU
11.电子显微镜中的电子从静止开始通过电势 差为U的静电场加速后，其德布罗电波长是 0.04nm，则U约为 940V 。
三、 计算题
1. 假设太阳和地球可看作黑体，各有其固定的表 面温度，地球的热辐射能源全部来自太阳，现取 地球表面温度TE=300K, 地球半径RE=6400km，太 阳半径Rs=6.95×105km,太阳与地球的距离 d=1.496×108km，求太阳表面温度TS。
7.康普顿效应的发现和理论解释进一步揭 示了光的 粒子 性，并且也证实了在微 观粒子相互作用过程中， 能量 守恒定 律和 动量 守恒定律依然成立。
8.在氢原子光谱中，由高能级向低能级跃 迁时发出的赖曼系谱线中，最长的波长 是＿1＿21＿.52＿nm。 ν=(E2-E1)/h λ=hc/(E2-E1)
解：太阳辐射能量分布在半径为d的球面上，其中
被地球吸收的能量为地球横截面积上的辐射能，
即 E吸4RS2TS44RdE22
E辐4RE 2TE4
E吸 E辐
TS 6.22103K
2. 利用单色光和金属钠作光电效应实验，测得当
300 n m 时，光电子的最大初动能1.85eV，当 400 n m 时，光电子的最大初动能0.82eV，由此估

不要因为长期埋头科学，而失去对生活、对美、对待诗意的感受能力。

——达尔文2019-2020学年江苏省八年级生物上册（苏科版）期末考试《生态系统的稳定》试题精选一．选择题（共32小题）1．（2019秋•吴江区期末）下列有关植物参与自然界中水循环的叙述正确的是（）A．植物通过根吸收水分和无机盐B．植物通过筛管运输水分和无机盐C．植物通过表皮细胞散失水分D．蒸腾作用散失水分对植物不利2．（2019秋•镇江期末）下列关于生态系统自我调节的说法，错误的是（）A．任何外力的影响都是可以恢复的B．生态系统结构越简单越易被破坏C．生物种类越多生态系统调节能力越强D．生态系统的自我调节能力是有限的3．（2019秋•扬中市期末）下列几个选项中，常常是食物链中最后一个环节的是（）A．绿色植物B．肉食性动物C．植食性动物D．杂食性动物4．（2019秋•扬中市期末）在“草→蚱蜢→食虫鸟→蛇”这条食物链中，能量流动的起点是（）A．草B．蚱蜢C．食虫鸟D．土壤5．（2019秋•海州区期末）下列有关生物圈中碳﹣氧平衡的叙述中，正确的是（）A．绿色植物光合作用制造的氧，低于自身呼吸作用消耗的氧B．在生物圈中，只有生物的呼吸作用才会消耗氧气C．绿色植物对于维持大气中的碳﹣氧平衡具有重要作用D．碳﹣氧平衡是指生物圈中二氧化碳和氧气各占50%6．（2019秋•海州区期末）生态系统保持自身稳定的能力被称为生态系统的自我调节能力。

与生态系统自我调节能力大小有关的主要因素是（）A．生态系统的无机环境B．生态系统的气候环境C．生态系统的生物物种和数量D．生态系统的地理位置7．（2019秋•泰兴市校级期末）在食物链“草→虫→鸡→鹰”中，属于生产者的是（）A．虫B．鸡C．鹰D．草8．（2019秋•泰兴市校级期末）2011年3月，日本东北部海域发生地震并引发海啸，地震造成核泄漏事故，最近，人们从日本近海海水中检测出放射性铯。

在硅藻→浮游动物→鲱鱼→鲟鱼这条日本近海食物链中，铯含量最高的生物是（）A．硅藻B．浮游动物C．鲱鱼D．鲟鱼9．（2019秋•泰兴市校级期末）为了保证城市市民每天都能获得新鲜的氧气应采取的措施是（）A．多植树种草B．将楼房建造得更高住在高层C．扩大每户房屋的空间D．美化环境，增加美术作品和广告10．（2019秋•泰兴市校级期末）下列各项中，能够完整地表示一条食物链的是（）A．狐吃兔子，兔子吃草B．大鱼吃小鱼，小鱼吃虾米C．人吃虎肉，老虎也吃肉D．猫头鹰捕食田鼠，狐也捕食田鼠11．（2019秋•泰兴市校级期末）在一个鱼缸内生物所形成的食物链中，数量最多的生物是（）A．浮游动物B．藻类C．小鱼D．细菌12．（2019秋•建湖县期末）下列关于生态系统说法中，正确的是（）A．物质在生态系统中是单向流动的B．生态系统中的能量可以循环使用C．可使大气中的碳进入生物体的是呼吸作用D．生态系统中的能量最终来自于太阳能13．（2019秋•清江浦区期末）生态系统的食物关系经常是复杂的网状结构（食物网）。

18章复习题及答案一、选择题1. 根据第18章内容，以下哪项不是本章讨论的主题？A. 历史事件的影响B. 社会结构的演变C. 个人心理的分析D. 经济政策的制定答案：C. 个人心理的分析2. 第18章中提到的“工业革命”主要影响了哪个领域？A. 农业B. 工业C. 文化D. 政治答案：B. 工业二、填空题1. 第18章中，______ 被描述为推动社会进步的关键因素。

答案：技术创新2. 在第18章讨论的“城市化”过程中，______ 是城市人口增长的主要原因。

答案：工业化三、简答题1. 请简述第18章中提到的“全球化”对经济的影响。

答案：第18章中提到，全球化促进了国际贸易和投资，加速了技术传播和文化交流，同时也带来了经济竞争和文化冲突。

2. 根据第18章内容，描述“环境问题”在当前社会中的重要性。

答案：第18章强调，环境问题对人类社会的可持续发展至关重要。

环境污染、资源枯竭和气候变化等问题，需要全球范围内的合作和努力来解决。

四、论述题1. 论述第18章中提到的“信息时代”对个人生活和社会结构的影响。

答案：在第18章中，信息时代被描述为一个由信息技术推动的时代，它极大地改变了人们的工作方式、沟通模式和生活习惯。

社会结构也因信息技术的发展而变得更加复杂，信息的快速流通和获取使得社会变得更加开放和互联。

结束语：通过本章的复习，我们对第18章的内容有了更深入的理解。

希望这些复习题能够帮助大家巩固知识点，并在考试中取得好成绩。

如果有任何疑问，欢迎随时提问。

祝大家学习进步！。

第18章滚动轴承(第二次作业)1. 直齿轮轴系由一对圆锥滚子轴承支承，轴承径向反力F r1>F r2，则轴承的轴向力B 。

A.F a1=F a2=0B.F a1=F a2≠0C.F a2>F a1D.F a2<F a12. 有a)7230C（旧36230）及b）7230AC（旧46230）两种滚动轴承，在同样大小的径向载荷F r作用下，它们的内部轴向力（派生轴向力）F Sa与F Sb相比较，应是 C 。

A. F Sa > F SbB. F Sa = F SbC. F Sa < F SbD.不确定3. 有一角接触球轴承数据如下：e=0.7，F a/F r>e时，X=0.41，Y=0.85，已知轴承受径向载荷F r=2100N，轴向载荷F a=1480N，则其当量动载荷P为 B N（f P=1.2）。

A. 2520B. 2542.8C. 2870.2D. 21194. 滚动轴承内部产生的附加轴向力是由于 B 而产生的。

在计算E、F 轴承所受轴向载荷时，应将该附加轴向力考虑进去。

A.受力方向不同B. 轴承结构上存在有接触角；C. 受轴向力过大；D. 能承受轴向载荷的向心轴承；E. 角接触轴承；F. 圆锥滚子轴承。

5. 一对7210B轴承如图所示，轴承分别承受径向载荷Fr1=8000N、Fr2=5200N，轴上作用轴向载荷Fa。

试求下列情况下各轴承的附加轴向力S及轴向载荷Fa1和Fa2。

(1) Fa=4000；(2) Fa=1000；(3) Fa=0由7210B，查表α＝40°C＝28200N C0＝22800计算轴承附加轴向力S由7210B S＝1.14F r轴向力S S1＝1.14F r1＝9120NS2＝1.14F r2＝5928N计算轴承的轴向载荷F a当F a=4000时S2+F a=5928+4000=9928> S11为紧端，2为松端F a1 = S2+ F a =5928+4000=9928N 紧端F a2 = S2=5928N 松端当F a=1000时S2+F a=5928+1000=6928<S1 2为紧端，1为松端Fa1=S1=9120N 松端Fa2=S1-Fa=9120-1000=8120N 紧端当F a=0时S2+F a=5928+0=5928<S1 2为紧端，1为松端Fa1=S1=9120N 松端Fa2=S1-Fa=9120N 紧端6. 蜗杆轴由一对圆锥滚子轴承支承，两轴承径向反力分别为F r1=6000N、F r2=3000N，外加轴向力F a=2500N。

大气传染统造工程课后做业习题解问之阳早格格创做第一章 概 论 解：按1mol 搞气氛预计，气氛中各组分摩我比即体积比，故n N2=0.781mol，n O2=0.209mol，n Ar =0.00934mol，n CO2=0.00033mol.品量百分数为%51.75%100197.2801.28781.0%2=⨯⨯⨯=N ，%08.23%100197.2800.32209.0%2=⨯⨯⨯=O ；%29.1%100197.2894.3900934.0%=⨯⨯⨯=Ar ，%05.0%100197.2801.4400033.0%2=⨯⨯⨯=CO .解：由我国《环境气氛品量尺度》二级尺度查得三种传染物日仄稳浓度限值如下：333.按尺度状态下1m 3搞气氛预计，其摩我数为mol 643.444.221013=⨯.故三种传染物体积百分数分别为： SO 2：ppm 052.0643.44641015.03=⨯⨯-，NO 2：ppm 058.0643.44461012.03=⨯⨯- CO ：ppm 20.3643.44281000.43=⨯⨯-. 解：1）ρ（g/m 3N ）334/031.1104.221541050.1N m g =⨯⨯⨯=-- c （mol/m3N ）3334/1070.6104.221050.1N m mol ---⨯=⨯⨯=. 2）每天流经管讲的CCl 4×10×3600×24×10－3kg=891kg 解：每小时重积量200×（500×15×60×10－6）×g μg μ解：由《大气传染统造工程》P14 （1－1），与M=2102369.0105.19102.22102422=⨯⨯⨯==--∝O p p M Hb O COHb ，COHb 鼓战度%15.192369.012369.0/1/222=+=+=+=Hb O COHb Hb O COHb Hb O COHb COHb CO ρ解：含氧总量为mL 960100204800=⨯.分歧CO 百分含量对付应CO 的量为： 2%：mL 59.19%2%98960=⨯，7%：mL 26.72%7%93960=⨯ 1）最初CO 火仄为0%时 min 0.17210102.426.7234=⨯⨯=-t ； 2）最初CO 火仄为2%时 min 4.12510102.459.1926.7234=⨯⨯-=-t . 解：由《大气传染统造工程》P18 （1－2），最大能睹度为m K d L pp v 8.115812.02.24.114006.26.2=⨯⨯⨯==ρρ.第二章 焚烧与大气传染 解：1kg 焚油含：重量（g ） 摩我数（g ） 需氧数（g ）H 2O 22.5 1.25 0 N 元素忽略.设搞气氛O 2：N 2×4.78=474.12mol/kg 重油. ×3N /kg 重油.烟气组成为CO 271.25mol ，H 2O 55.25+1.25=56.50mol ，SO 20.1325mol ，N 2×99.1875=374.93mol. ×3N /kg 重油.2）搞烟气量为502.99－56.50=446.49mol/kg 重油. SO 2百分比浓度为%07.0%10049.4463125.0=⨯，气氛焚烧时CO 2存留最大浓度%96.15%10049.44625.71=⨯.×3N /kg 重油，×10.62=12.33 m 3N /kg 重油. 解：相对付于碳元素做如下预计：%（品量） mol/100g 煤 mol/mol 碳C 65.7 5.475 1 故煤的组成为CHSO ，焚料的摩我品量（包罗灰分战火分）为molC g /26.18475.5100=.焚烧圆程式为1）表里气氛量kg m kg m /74.6/104.22100026.18)78.31(1495.1333=⨯⨯⨯+⨯-；SO 2正在干烟气中的浓度为%174.0%10018644.11495.178.3010.0292.01010.0=⨯+⨯+++2）爆收灰分的量为kg g /8.144%8010010001.18=⨯⨯ ×1.1495+1.644/18）×××10－33/kg灰分浓度为310826.68.144⨯mg/m 3×104mg/m 33）需石灰石kg 21.103%35407.100.32%7.11000=⨯⨯⨯/t 煤2.3解：按焚烧1kg 煤预计重量（g ） 摩我数（mol ） 需氧数（mol ） H 2O 52.875 2.94 0设搞气氛中N 2：O 2体积比为3.78：1， ×（66.25+7.78+0.1875）=354.76mol/kg 煤. N 2mol 54.28078.476.35478.3=⨯×354.76=436.43mol/kg 煤，SO 2浓度为%043.0%10043.4361875.0=⨯.2.4解：与1mol 煤气预计H 2CO 2 0.05mol 0H 2 CH 4共需O 2 0.003+0.143+0.063+0.014=0.223mol.设搞气氛中N 2：O 2×（3.78+1）=1.066mol.与2.1=α×1.066mol=1.279mol.气氛含干量为12g/m 3N ，即含H 23N 3N .故H 2O 体积分数为1.493%.故本量气氛量为mol 298.1%493.11279.1=-.烟气量SO 2：0.002mol ，CO 2：0.285+0.007+0.05=0.342mol ，N 2×3.78+0.524=1.367mol ，H 2× × 解：1）N 2%=1－11%－8%－2%－0.012%=78.99% 由《大气传染统造工程》P46 （2－11） 气氛过剩%5.50%100)25.08(99.78264.025.08=⨯⨯--⨯⨯-2）正在测定状态下，气体的摩我体积为mol L P T T V P V /46.39322.1337002734434.22101325221112=⨯⨯⨯⨯=⋅=； 与1m 3烟气举止预计，则SO 2120×10－6m 3，排搁浓度为63312010(18%)640.179/39.4610g m --⨯⨯-⨯=⨯. 3）322.45663.37(18%)2957/min 39.46N m ⨯⨯-=. 4）3/85.5222.439.460.03N m g =⨯.2.6解：按1kg 煤举止预计重量（g ） 摩我数（mol ） 需氧数（mol ） H 2O 83.25 4.625 0 设搞气氛中N 2：O 2××1.2=423.66mol ， ×0.0116=4.91mol.烟气中：CO 2 63.17mol ；SO 2 0.5mol ；H 2O 4.91+4.625+20.375=29.91mol ；N 2×××4.78=70.61mol.其中CO 2%25.14%10038.44317.63=⨯；SO 2 %11.0%10038.4435.0=⨯；H 2O %74.6%10038.44391.29=⨯； N 2%55.75%10038.44361.7079.019.279=⨯⨯+.O 2 %33.3%10038.443209.061.70=⨯⨯.2.7解：SO 2含量为0.11%，预计约1/60的SO 2转移为SO 3，则SO 3含量51083.1601%11.0-⨯=⨯，即P H2SO4×10－5，lg P H2SO4=-4.737.查图2－7得煤烟气酸露面约为134摄氏度. 2.8解：以1kg 油焚烧预计， C 860g 71.67mol ；H 140g 70mol ，耗氧35mol.设死成CO x mol ，耗氧0.5x mol ，则死成CO 2 （71.67－x ）mol ，耗氧（71.67－x ）mol. 烟气中O 2量610600%5.1-⨯x. 总氧量x x x x5.2467.10635)67.71(5.010600%5.16+=+-++⨯-，搞气氛中N 2：O 2体积比为3.78：1，则含N 2 ×（106.67+24.5x ）.根据搞烟气量可列出如下圆程：故CO 2%：%99.13%10010600306.0306.067.716=⨯⨯--； N 2%：%62.84%10010600306.0)67.106306.05.24(78.36=⨯⨯+⨯- 由《大气传染统造工程》P46 （2－11） 气氛过剩系数07.1)06.05.05.1(62.84264.006.05.05.11=⨯--⨯⨯-+=α第三章 大气传染局里教 3.1解：由气体静力教圆程式，大气中气压随下度的变更可用下式形貌：dP g dZρ=-⋅ （1）将气氛视为理念气体，即有m PV RT M=可写为 m PM VRTρ== （2）将（2）式戴进（1），并整治，得到以下圆程：假定正在一定范畴内温度T 的变更很小，不妨忽略.对付上式举止积分得：ln gM P Z C RT =-+ 即 2211ln ()P gMZ Z P RT =--（3） 假设山足下的气温为10.C ，戴进（3）式得： 得 5.7Z km ∆=即登山疏通员从山足进与爬了约5.7km. 3.2解：d m K z Tγγ>=---=∆∆-=-100/35.25.1102988.297105.1，没有宁静d m K z Tγγ>=---=∆∆-=-100/5.110308.2975.2973010，没有宁静d m K z Tγγ>=---=∆∆-=-100/0.130505.2973.2975030，没有宁静d m K z Tγγ>=---=∆∆-=-100/75.15.1302985.297305.1，没有宁静d m K zTγγ>=---=∆∆-=-100/44.15.1502983.297505.1，没有宁静.3.3解：288.00101)(P PT T =， 3.4解：由《大气传染统造工程》P80 （3－23），m Z Z u u )(11=，与对付数得)lg(lg 11Z Z m u u = 设y u u=1lg ，x Z Z=)lg(1，由真测数据得故m ＝0.2442. 3.5 解：0.070.07110050()2() 2.24/10Z u u m s Z ==⨯=，0.070.072200100()2() 2.35/10Z u u m s Z ==⨯= 0.070.073300200()2() 2.47/10Z u u m s Z ==⨯=，0.070.074400300()2() 2.54/10Z u u m s Z ==⨯= 0.070.075500400()2() 2.59/10Z u u m s Z ==⨯=. s m Z Z u u /55.2)1050(2)(15.015.00101=⨯==，s m Z Z u u /82.2)10100(2)(15.015.00202=⨯== s m Z Z u u /13.3)10200(2)(15.015.00303=⨯==，s m Z Z u u /33.3)10300(2)(15.015.00404=⨯== s m Z Z u u /48.3)10400(2)(15.015.00505=⨯==. s m Z Z u u /99.2)1050(2)(25.025.00101=⨯==，s m Z Z u u /56.3)10100(2)(25.025.00202=⨯== s m Z Z u u /23.4)10200(2)(25.025.00303=⨯==，s m Z Z u u /68.4)10300(2)(25.025.00404=⨯== 风速廓线图略. 3.6解：1）根据《Air Pollution Control Engineering 》可得下度与压强的闭系为dz RTgM PdP -=2、M=0.029kg 、R=8.31J/(mol.K)代进上式得T PdP dz 21.29-=.当t=.C ，气压为1023 hPa ；当t=.C ，气压为1012 hPa ，.C=283.4K ，dP=1012-1023=－11Pa.果此m m dz 894.28310181121.29=--=，z=119m.共理可预计其余测定位子下度，截止列表如下：2）图略 3）d m K z T γγ>=---=∆∆-=---100/35.1898.911212121，没有宁静；0100/22.299128.9323232<-=---=∆∆-=---m K z T γ，顺温； 0100/98.11011412434343<-=---=∆∆-=---m K z T γ，顺温； 0100/61.01631514545454<-=---=∆∆-=---m K z T γ，顺温； d m K z T γγ<=---=∆∆-=---100/37.05361315656565，宁静； d m K z T γγ<=---=∆∆-=---100/15.02716.1213878787，宁静； d m K z T γγ<=---=∆∆-=---100/85.012996.16.12989898，宁静； d m K z T γγ<=---=∆∆-=---100/28.02818.06.1109109109，宁静.3.7解：0100/22.14581.217.26111>=-=∆∆=m K z T G ，故011<-=G γ，顺温； m K z T G 100/72.07631.216.15222-=-=∆∆=，故d m K G γγ<=-=100/72.022，宁静；m K z T G 100/16.15806.159.8333-=-=∆∆=，故d m K G γγ>=-=100/16.133，没有宁静；m K z T G 100/12000.250.5444-=-=∆∆=，故d m K G γγ>=-=100/144，没有宁静；m K z T G 100/2500.300.20555-=-=∆∆=，故d m K G γγ>=-=100/255，没有宁静；0100/43.0700.250.28666>=-=∆∆=m K z T G ，故066<-=G γ顺温. 3.8解：2211ln()P gM Z Z P RT =--，代进已知数据（温度T 与二下度处的仄稳值）即458297314.8029.08.91013P ln2⨯⨯⨯＝－，由此解得P 2=961hPa.由《大气传染统造工程》P72 （3－15）可分别预计大天处位温战给定下度处位温：K P T 293)10131000(1.294)1000(288.0288.0===地面地面地面θ，K P T 16.303)9611000(7.299)1000(288.0288.0111===θ， 故位温梯度=m K 100/18.24580303293=--共理可预计得到其余数据的位温梯度，截止列表如下：3.9解：2211ln()P gM Z Z P RT =--，设大天压强为P 1，代进数据得到：458297314.8029.08.9P 970ln1⨯⨯⨯＝－，解得P 1=1023hPa.果此共理可预计得到其余数据的大天位温，截止列表如下：略.第四章 大气扩集浓度估算模式 4.1解：吹北风时以风背为x 轴，y 轴指背峭壁，本面为面源正在大天上的投影.若没有存留峭壁，则有]}2)(exp[]2)(){exp[2exp(2),,,(222222'z z y zy H z H z y u Q H z y x σσσσσπρ+-+---=现存留峭壁，可思量ρ为真源与真源正在所闭心面孝敬之战.真源]}2)(exp[]2)(){exp[2exp(22222221z z y z y H z H z y u Q σσσσσπρ+-+---= 真源]}2)(exp[]2)(]{exp[2)2(exp[22222222z z y z y H z H z y L u Q σσσσσπρ+-+----= 果此]}2)(exp[]2)(){exp[2exp(2222222z z y zy H z H z y u Q σσσσσπρ+-+---=+ =]}2)(exp[]2)(]}{exp[2)2(exp[)2{exp(222222222z z y y zy H z H z y L y u Q σσσσσσπ+-+----+- 刮冬风时，坐标系建坐没有变，则截止仍为上式. 4.2解： 霍兰德公式m D T T T uD v H s a s s 16.96)54182884187.25.1(455.13)7.25.1(=⨯-⨯+⨯=-+=∆. 布里格斯公式kW kW D v T T T Q ss a s H 210002952155.13418288418106.97.2106.97.22323>=⨯⨯-⨯⨯=-⨯⨯=--且x<=10Hs.此时3/23/213/113/23/180.2429521362.0362.0x x ux Q H H =⨯⨯==∆--.按国家尺度GB/T13201－91中公式预计， 果Q H >=2100kW ，Ts －Ta>=130K>35K.（收电厂位于都会近郊，与n=1.303，n 1=1/3，n 2=2/3） 4.3解：由《大气传染统造工程》P88（4－9）得 4.4解：阳天宁静度等第为D 级，利用《大气传染统造工程》P95表4－4查得x=500m 时m m z y 1.18,3.35==σσ.将数据代进式4－8得32222/010.0)1.18260exp()3.35250exp(1.183.35680)60,0,50,500(m mg =⨯-⨯-⨯⨯⨯=πρ. 4.5解：由霍兰德公式供得m D T T T uD v H s a s s 84.5)6.04052934057.25.1(46.020)7.25.1(=⨯-⨯+⨯=-+=∆，烟囱灵验下度为m H H H s 84.3584.530=+=∆+=.由《大气传染统造工程》P89 （4－10）、（4－11）yze H u Q σσπρ2max 2=时，m H z34.25284.352===σ.与宁静度为D 级，由表4－4查得与之相映的x=745.6m. 此时m y 1.50=σ.代进上式32max /231.01.5034.2584.354102m g e μπρ=⨯⨯⨯⨯=. 4.6解：由《大气传染统造工程》P98 （4－31）13.01121202.3)05.02()(y y q y y σσττσσ===（当h h 10012<≤τ，q=0.3）4.7解：有限少线源dP P H u Q H x P P z z L)2exp(21)2exp(22),0,0,(22221--=⎰πσσπρ.最先推断大气宁静度，决定扩集参数.中纬度天区阴朗春天下午4：00，太阳下度角30～35.安排，属于强太阳辐射；查表4-3，当风速等于3m/s 时，宁静度等第为C ，则400m 处m m zy 5.26,3.43==σσ.其次推断3分钟时传染物是可到达受体面.果为丈量时间小于0.5h ，所以没有必思量采样时间对付扩集参数的效用.3分钟时，传染物到达的距离3360540400x ut m m ==⨯⨯=>，证明已经到达受体面.有限少线源dP P H u Q H x P P z zL)2exp(21)2exp(22),0,0,(22221--=⎰πσσπρ距离线源下风背4m 处，P 1=－75/43.3=－1.732，P 2=75/43.3=1.732；)/(6.0)/(15090s m g s m g Q L⋅=⋅=.代进上式得 3732.1732.12/52.5)2exp(215.26326.02)0,0,0,400(m mg dp P =-⨯⨯⨯⨯=⎰-ππρ.端面下风背P 1=0，P 2=150/43.3=3.46，代进上式得 4.8解：设大气宁静度为C 级，m m z y 98.615.215,56.2323.4100000====σσ. 当x=1.0km ，m m z y 4.61,1.99==σσ.由《大气传染统造工程》P106 （4－49） 4.9解：设大气宁静度为C 级.m x m H D D z5.122642.7415.220036015.2=⇒=-=-=σ 当x=2km 时，x D <x<2x D ，按x= x D 战x=2x D 时浓度值内插预计.x= x D 时，m m z y 42.74,26.118==σσ，代进《大气传染统造工程》P88 （4－9）得x= 2x D 时，m m zy 10.139,41.221==σσ，代进P101 （4－36）得3222/257.041.2213605.32180)2exp(2m mg y D u Qy y=⨯⨯⨯=-=πσσπρ；通过内插供解3/181.0)5.12262000(5.1226050.0257.005.0m mg =--+=ρ 当x=6km>2x D 时，m y 474=σ，3/120.04743605.32180m mg =⨯⨯⨯=πρ预计截止标明，正在x D <=x<=2x D 范畴内，浓度随距离删大而降下. 4.10解：由所给局里条件应与宁静度为E 级.查表4－4得x=12km 处，m m z y 4.87,4277==σσ.m H y yf 25.4338504278=+=+=σσ，m H h z f 8.2244.872502=⨯+=+=σ 34/10365.125.4338.224321002)50,0,0,12000(m g h u Q yff F -⨯=⨯⨯⨯==πσπρ.解：按《大气传染统造工程》P91 （4－23） 由P80 （3－23）25.025.01010687.1)10(3)(s s mH H Z Z u u === 按都会及近郊区条件，参照表4－2，与n=1.303，n 1=1/3，n 2=2/3，代进P91（4－22）得12/54/13/23/11048.23687.128100303.121s ss n sn HH H H uH Q n H =⨯⨯==∆-.3（年均），代进P109（4－62）＝H H H s ∆-⨯-∆+⨯⨯⨯⨯⨯--625.0310)05.006.0()(687.1718.2142.35.010802解得m H H H H s s s 4.35748.2312/5≥+=∆+于是Hs>=162m.本量烟囱下度可与为170m.烟囱出心烟气流速没有该矮于该下度处仄稳风速的1.5倍，即u v ××170=9.14m/s.但是为包管烟气成功抬降，出心流速应正在20~30m/s.与u v =20m/s ，则有m u Q D v v 1.42026544=⨯⨯=≤ππ，本量直径可与为4.0m.4.12解：下架连绝面源出现浓度最大距离处，烟流核心线的浓度按 P88（4－7）z y zy u Q H H u Q σσπσσπ2018.1]2/24exp[1[222=⋅-+= （由P89（4－11）2H z =σ）而大天轴线浓度yze H u Q σσπρρ⋅==2max 22. 果此，38.12018.1)2(4018.14018.1)2/(2018.1/2222221====⋅=eH e H e H e H u Q u Q z yz z y σσσπσσπρρ 得证.第五章 颗粒传染物统造技能前提 5.1解：正在对付数概率坐标纸上做出对付数正态分集的品量乏积频次分集直线，读出d m μ、d 50m μ、d 15.9m μ.81.3501.84==d d g σ. 做图略. 解： 画图略. 5.3解：正在对付数概率坐标纸上做出对付数正态分集的品量乏积频次分集直线，读出品量中位直径d 50mμ、dmμ、d 15.9m μ.85.1501.84==d d gσ. 按《大气传染统造工程》P129（5－24）m NMD NMD MMD g μσ31.3ln 3ln ln 2=⇒+=；P129（5－26）m d NMD d L g Lμσ00.4ln 21ln ln 2=⇒+=；P129（5－29）m d NMD d sv g sv μσ53.8ln 25ln ln 2=⇒+=.5.4解：《大气传染统造工程》P135（5－39）按品量表示g cm d S Psv m /107.3623⨯==ρP135（5－38）按净体积表示323/1003.76cm cm d S svV⨯==P135（5－40）按聚集体积表示323/1011.2)1(6cm cm d S svb ⨯=-=ε.5.5解：气体流量按P141（5－43）s m Q Q Q N N N N /11000)(21321=+=； 漏风率P141（5－44）%20%100100002000%100121=⨯=⨯-=NNN Q Q Q δ；除尘效用： 思量漏风，按P142（5－47）%3.90100002.412000340.0111122=⨯⨯-=-=N N N N Q Q ρρη没有思量漏风，按P143（5－48）%9.912.4340.01112=-=-=NN ρρη 5.6解： 由气体圆程RT Mm PV =得L g RT PM V m /832.042331.829)4901001.1(5=⨯⨯-⨯===-ρ按《大气传染统造工程》P142（5－45）Pa P 13119.172832.08.92=⨯⨯=∆. 解：按《大气传染统造工程》P145（5－58） 粉尘浓度为33/10/22.22.22m g m g =3；×0.1=0.222g/s. 5.8解：按《大气传染统造工程》P144（5－52）ii i g g P121-=η（P=0.02）预计，如下表所示：据此可做出分级效用直线. 5.9解：按《大气传染统造工程》P144（5－54）∑==%86.721i i T g ηη. 解：53103.2,/912.0-⨯==μρm kg .当d p m μ时，应处正在Stokes 天区. 最先举止坎宁汉建正：s m M RT v /2.5321097.28142.35.387314.8883=⨯⨯⨯⨯==-π， m v8104.9499.0-⨯==ρμλ，47.04.0104.9222=⨯⨯==-p d Kn λ.则61.1)]10.1exp(4.0257.1[1=-++=Kn Kn C ，s m gC d u p p s /1041.11852-⨯==μρ.当d p =4000mμ时，应处于牛顿区，s m g d u p p s /34.17)(74.1=-=ρρρ.5002750103.234.17912.0104000Re 56>=⨯⨯⨯⨯==--μρud p p ，假设创造. 当d p m μ时，忽略坎宁汉建正，s m g d u pp s /088.0182==μρ.体味证Re p <1，切合Stokes 公式.思量到颗粒正在低重历程中速度正在很短时间内便格外交近u s ，果此预计重降下度时可近似按u s 预计.d p m μ×10－5××10－4m ； d p =40m μ×30=2.64m ； d p =4000m μ×30=520.5m. 5.11解：设最大石英粒径d p1，最小角闪石粒径d p2.由题意，g d g d p p p p ρρρρ221174.174.1=故35.16.25.31221===p p p p d d ρρ. 5.12解：正在所给的气氛压强战温度下，s Pa m kg ⋅⨯==-531081.1,/205.1μρ.d p =200m μ时，思量采与过度区公式，按《大气传染统造工程》P150（5－82）：85.131081.1205.103.110200Re 56=⨯⨯⨯⨯=--p ，切合过度区公式. 阻力系数按P147（5－62）82.3Re 5.186.0==pP C .阻力按P146（5－59）N u A C F p D p 822621083.703.1205.1)10200(482.32121--⨯=⨯⨯⨯⨯⨯==πρ. 5.13解：圆管里积2321085.741m d A -⨯==π.据此可供出气氛与盐酸雾滴相对付速度s m A Q u s /27.0601085.71012733=⨯⨯⨯==--.思量利用过度区公式：代进相闭参数s Pa m kg m kg p ⋅⨯=⨯==-53331082.1,/1064.1,/19.1μρρ及u s可解得d p =66m μ.117.11082.127.019.11066Re 56>=⨯⨯⨯⨯=--p ，切合过度区条件.故能被气氛夹戴的雾滴最大直径为66m μ. 5.14解：粒径为25m μ，应处于Stokes 天区，思量忽略坎宁汉建正：s m g d u pp s /1069.31822-⨯==μρ.横直目标上颗粒物疏通近似按匀速思量，则低重时间s u Ht s1221069.35.42=⨯==-×122m=171m. 5.15解：正在给定条件下s Pa m kg ⋅⨯==-53105.2,/815.0μρ. 当d p =10m μ，粉尘颗粒处于Stokes 天区：s m R u d u t p p c /768.02.016105.2182700)101(18252622=⨯⨯⨯⨯⨯=⋅=--μρ. d p =500m μ，粉尘颗粒处于牛顿区：Ru d u d t p p cp23226155.0⋅=ρππρ.果此s m R u d u t p p c /2.8003.32==ρρ.体味证，Re p =1307>500，假设创造.第六章 除尘拆置 6.1解：预计气流火仄速度sm AQ v /1087.257.414.92.120-⨯=⨯==.设粒子处于Stokes 天区，与s Pa ⋅⨯=-51082.1μ.按《大气传染统造工程》P162（6－4）即为能被100%捕集的最小雾滴直径. ：按层流思量，根据《大气传染统造工程》P163（6－5）2.229.64801812122121=⨯==⇒=ηηηηn n n n ，果此需要树坐23层.6.3解：m m m gL H v d p μμρμ10084104.8781.9105.2123.01086.118185350min<=⨯=⨯⨯⨯⨯⨯⨯⨯==--，切合层流区假设. ：设气氛温度为298K ，最先举止坎宁汉建正：s m M RT v /6.4661097.28142.3298314.8883=⨯⨯⨯⨯==-π， m v 85106.66.466185.1499.01082.1499.0--⨯=⨯⨯⨯==ρμλ，21.063.0106.622=⨯⨯=-Kn 264.1]4.0257.1[21.0121.010.1=++=-eC .故s m gC d u pp s /1058.11852-⨯==μρ525.060/1061.3202.05.01058.1)1(35=⨯⨯⨯⨯⨯=+=--Q n LW u s i ηm μ粒子的分级效用为0.864.果此总效用 695.0)864.0525.0(5.0=+=i η解：按《AirPollutionControlEngineering 》公式)]9(exp[12μρπηi pc W D NV --=.令η=50%，N=5，Vc=15m/s ，p ρ×103kg/m 3，W=0.76m ，s Pa ⋅⨯=-5102μ，代进上式得d c m μ.利用《大气传染统造工程》P170（6－18）22)/(1)/(c pi c pi id d d d +=η 预计各粒径粉尘分级效用，由此得总效用%3.55==∑i i g ηη 解：根据《大气传染统造工程》P144（5－53）ii i g Pg 32/+=ηηη（P=0.1）预计分级效用，截止如下表所示：据此可做出分级效用直线.由上表可睹，5～10m μ来除效用为49.41.果此正在工程缺面允许范畴内，d c m μ. ：据《大气传染统造工程》P169（6－13）Pa v p 144015293.19.92121221=⨯⨯⨯==∆ξρ. 解：根据《Air Pollution Control Engineering 》P258公式)]9(exp[12μρπηi pc W D NV --=.果)/(1000322m kg D D p p p pa单位取单位ρρρρ==，故p D ρ2＝1000 2pa D ；由题意，当s m V c /20%,50==η.与s Pa ⋅⨯=-51082.1μ，N=10，代进上式)]1082.191000)100.1(2010(exp[1%50526--⨯⨯⨯⨯⨯⨯⨯--=i W π，解得W i mm .根据普遍旋风除尘器的尺寸央供，D 0=4W i =2.2cm ；H ＝2 W i =1.1cm.c ×10－3m 3/s6.9解：按《大气传染统造工程》P170（6－18）22222225)5/(1)5/()/(1)/(pipipi pi c pi c pi i d d d d d d d d +=+=+=η；⎰⎰∝+==022125pi pipipi i qdd dd qdd ηη.d g =20mμ，25.1=σ，])32.020ln (exp[79.1])ln 2ln(exp[ln 2122pipi ggpi gpi d d d d d q -=-=σσπ 代进上式，利用Matlab 积分可得%3.9610==⎰pi i qdd ηη.6.10解：驱进速度按《大气传染统造工程》P187（6－33）s m d qE w p p/176.01011081.1310100103.0365315=⨯⨯⨯⨯⨯⨯⨯==---ππμ. 2885.123.0m dL A =⨯⨯==ππ3/s ，代进P188（6－34）%8.98)176.0075.0885.1exp(1)exp(1=⨯--=--=i i w Q A η.解：1）Q ’=2/3=0.667 m 322，%3.99)122.02/667.04.13exp(1=⨯--=i η.2）5.13/15.0max ==v v 故%8.9875.1%)3.991(1)1(1=--=--=Fv iηη.6.12 解：1）由题意77.0)9.0exp(15.0=⇒⨯--=k k d p m μ，%2.93)5.377.0exp(11=⨯--=η d p m μ，%8.99)0.877.0exp(12=⨯--=η d p m μ，%100)0.1377.0exp(13=⨯--=η故%98%6.9832.01%8.992.0%2.932.0>=⨯⨯+⨯+⨯=η 2）301%6.982iρ-=，则i 2ρ33.没有谦足环保确定战使用者需要.解：1）由《大气传染统造工程》P183（6－31）电场荷电为 扩集荷电按P184 （6－32）预计，与电场荷电相比很小，可忽略. ×10－16C.2）电场荷电为 ×10－19C.3）与s Pa ⋅⨯=-5105.2μd p =5m μ时，s m d qE w p p/088.0105105.23104.31004.3365516=⨯⨯⨯⨯⨯⨯⨯==---ππμ；d p m μ时，s m d qE w p p/1051.3102.0105.23104.31086.43365519----⨯=⨯⨯⨯⨯⨯⨯⨯==ππμ. 解：查图得集气板里积约1000m 3.（1000m 3/min ）－1.根据)exp(1i i w QA--=η， 0.995=1－exp （－w i ）解得w i =5.30m/min. 6.15解：%95)exp(1=--=w Q A η，故05.0)exp(=-w Q A ，0025.0)2exp(=-w QA果此%75.990025.01)2exp(1'=-=--=w QA η.6.16解：设3种粒子的分级效用分别为1η、2η、3η，则 果此%9.991=η，%0.992=η，%1.863=η. 解：1）粉尘粒径d p =10m μ 当液滴直径为50mμ时，R=0.2；碰碰数3.36618)(2=-=CD p p p I D u u d N μρ，14.19=I N .由给出预计公式可得%3.50=η共理可得液滴直径为100m μ、500m μ时捕集效用为42.6％、10.1%. 2）d p =50m μ用共样要领预计可得颗粒正在直径为50m μ、100m μ、500m μ的液滴上捕集效用分别为 0、10.2%、25.0％. 6.18解：按《大气传染统造工程》P211（6－53） 由（6－55）233.02229]101.6exp[pd gp C g l iepf d C P --=∆⨯-=μρρm μm μ，除尘效用约为1；果此故%48.981=-=P η. 6.19 解： 坎宁汉建正143.12.1172.01172.01=+=+=p C d C 6.20解：设气液比1L/m 3，d p m μ，3/8.1cm g p =ρs Pa g ⋅⨯=-51099.2μ.由O cmH v Q Q v p gl T 2323234.152100.11003.1)(1003.1=⨯⨯⨯⨯-=⨯-=∆---可解得v=121.6m/s.故喉管里积2058.06.1211.7m S ==，D T =272mm. 与喉管少度300mm ，通气管直径D 1=544mm. 241=α，62=α，则m mm ctg D D L T 64.064022111==-=α，m ctg D D L T 13.322222=-=α（与D 2=600mm ）. 解：由《Air Pollution Control Engineering 》P300 9.48式t D zc D M ηπ∆=24.t η通过P293 Figure 9.18读与.与33/102m kg p ⨯=ρ，雨滴D b =2mm ，处于牛顿区，利用《大气传染统造工程》P150（5－83）s m v /0.7]205.1/81.9)205.1100.1(100.2[74.12/133=⨯-⨯⨯=-.果此，912.01021082.1180.7)103(10218352632=⨯⨯⨯⨯⨯⨯⨯⨯==---b p p s D v d N μρt η=0.11（Cylinder ）. 故M=g μπ0083.011.080300)102(423=⨯⨯⨯⨯⨯-.而液滴自己g D M μρπ331019.461'⨯==×10－4%.6.22解：由《Air Pollution Control Engineering 》公式 t AQ D C C LD ∆-=η5.1ln 0.代进已知数据h t t A A3.12105.21.01025.11.0ln 33=∆⇒∆⨯⨯⨯⨯-=-，即需持绝半天安排的时间. 6.23解：设破裂2个布袋后气体流量调配没有变，近似供得出心浓度如下：300/0761.06002)1(600598'm g C C C =+-=η.果此%2.99%10015.90761.015.9=⨯-=η. 6.24解：设恒定速度v 1，则401=v K x ffg μ，40011=+v K x v K x ppg ffg μμ.若正在400Pa 压降下继承，则40022212=++v K x v K x v K x pp g pp g ffg μμμ解此微分圆程得Q 23. ：当T=300K 时，s Pa ⋅⨯=-51086.1μ，v=1.8m/min=0.03m/s.S x M p ρ=，1210100102.143MM S M x p =⨯⨯⨯==-ρ p K Mb p /03.01086.1125⨯⨯⨯+=∆-.利用所给数据举止线性拟战， 51.61613146+=∆x p ，即13146/03.01086.1125=⨯⨯⨯-p K M，K p ×10－12m 2.解：1）过滤气速预计为v F =1.0m/min.2）除尘效用为99%，则粉尘背荷2/94.5699.0m tg t Ct v W F =⨯=∆=. 3）除尘器压力益坏可思量为p E t P P P P ∆+∆+∆=∆t P ∆为浑净滤料益坏，思量为120Pa ；Pa v S P F E E 350=⋅=∆；)min/(50.9,43.5694.515.922m g N R tPa t Ct v R P p p p ⋅⋅=⨯⨯=∆=∆取；故)(43.56470)(43.56120350Pa t Pa t P P P P p E t +=++=∆+∆+∆=∆. 4）果除尘器压降小于1200Pa ，故min 9.12,1200)(43.56470<<+t Pa t 即最大浑灰周期.5）22402731603931000060m v Q A F =⨯⨯⨯==. 6）与滤袋d=0.8m ，l=2m.203.5m dl a ==π，7.47==aAn ，与48条布袋. 解：1）将已知数据代进所给公式即有0139.0]1082.13.0)101(1000)105.0(06.0297exp[52326=⨯⨯⨯⨯⨯⨯⨯⨯⨯-=---P ，%6.98=η2）由001.0)97exp(22≤-=εμg cpas D D Zv P 可得z>=3.23m.3）由《Air Pollution Control Engineering 》公式，脱透率)9exp(2μρπi pc W D NV P -=与Wi=0.25Dc ，而N=0.5Z/Dc ，Vc=Vs/ε，pa pa D D ρ22=，代进上式)97exp()92exp(2222εμεμπg c pas g c pas D D ZV D D ZV P -=-= （近似与72=π）解：×（1－0.3）x p =140×10－4，x p =0.01cm ；3）由（0.8－0.0006）×0.39t=140，t=449min=7.5h. 第七章 气态传染物统造技能前提 7.1解：由亨利定律P*=Ex ，500××105×10－5. ×10－5=376.×10－5很小，故C CO23.100g 与气体仄稳的火中约含44×100××10－5/18=0.013g. 解：正在1atm 下O 2×104x 解得O 2×10－6. 解：20》C 时H 2×105kPa ，分压20atm ×0.1%=2.03kPa.×10－5，故C*H2S 3.×103×10－3mol/（m 3.Pa ）=115mol/（m 3.atm ） 由185.1,542.0108121611511-==+=+=h K k k H K Al l g Al . )/(3.431.285.1)(32*2h m mol C C K N S H S H Al A ⋅=⨯=-=.解：G B =5000×0.95=4750m 3N /h.Y 1=0.053，321063.2%54750)47505000(-⨯=⨯-=Y ；4.257.26/053.000263.0053.00)(max 21min =-=--=X Y Y G L B S . 果此用火量L sB ××105m 3N /h.由图解法可解得传量单元数为5.6. 解：G B =10×3/min ，Y 1=0.124，Y 2=0.02.做出最小用火时的支配线，x max =0.068.故53.1068.002.0124.0)(min =-=Bs G L ，L s ××3/min.图解法可解得传量单元数为 3.1.mLaH y 39.2)(3.333.0=⨯=.H y ×3.1=7.4m. 7.6解：利用公式0ττ-=KL ，将已知数据代进⎩⎨⎧-=-=002.05051.0220ττK K ，解得⎩⎨⎧==min65min/28500τmK果此min 27856512850max =-⨯=τ. 7.7解：min 8.95'==KL τ，kg aSL x b 2.452301141)0129.02629.0(2=⨯⨯⨯⨯-==πρ.7.8解：依据公式nT kPX 1=，对付lgX T ~lgP 举止直线拟合：7.030P X T =，即K=30，n=1.43；依据公式mm V P BV V P +=1，对付P ~P/V 举止直线拟合：P VP005.00289.0+=， 即V m =200，B=0.173. 解：×104××3/h ，M=131.5.由理念气体圆程RT Mm PV=得果此活性冰用量kg m 4301036.541075.328100⨯=⨯⨯⨯=；体积349.925771036.5m m V =⨯==ρ.解：Y 1=0.025kg 苯/kg 搞气氛，硅胶苯kg kg YX /282.0)167.0(5.1111==，Y 2=0，X 2=0.故支配线圆程为X=11.28Y .当Y=Y b ×0.0025=0.0282kg 苯/kg 硅胶. ×=0.0008kg 苯/kg 搞气氛.08.5881*=-Y Y ，由此可供得⎰-Y Yb Y Y dY *近似值；共时， ⎰⎰---+-=-==We Wb ab a b We Wb A A b w w w w w dw w Y Y W dw Y Y W Y Q f))(1()1(000 由此供得f 的近似值，列表如下：N OG =5.948，f=0.5580；2atm ，298K 时，ρ3，果此)/(37.22s m kg v G ⋅==ρ，故H OG =m G D a p 07041.0)10835.131.21060.0(60042.1)(42.151.05251.0=⨯⨯⨯⨯=--μ； 果此吸附区下度为H 2=H OG .N OG ×5.948=0.419m.对付单位横截里积的床层，正在呵护效用时间内吸附的苯蒸汽量为（0.025－0）××60×90＝320（kg 苯/m 2） 而吸附床鼓战区吸附苯蒸汽量)0()(2--=T b x H H ρ 吸附床已鼓战区吸附苯蒸汽量)1)(0(2f x H T b --=ρ果此总吸附量320442.0282.0625419.0282.0625)419.0(=⨯⨯⨯+⨯⨯-=H 解得H=2.05m ，此即所需要的最小床下.解：反应管转移率为x A 时，反应速度为R A =－0.15（1－x A ）mol/（kg 催化剂.min ）.根据单管物料仄稳可列出如下圆程：A A Qdx Adx x =-ρ)1(15.0 其中2322101.1)108.3(4m A --⨯=⨯⨯=π，Q 单位为mol/min.数据代进并整治得AAx dx Q dx -=1098668.0，对付等式二边积分，即⎰⎰-=74.001.601098668.0AA x dx Q dx ，解得Q=0.447mol/min.反应管数目：250/0.447＝560个. 解：由T cm Q ∆=得K cm Q T 31472642.01056.45=⨯⨯==∆. 第八章 硫氧化物的传染统造 8.1解：火电厂排搁尺度700mg/m 3.3%硫含量的煤烟气中SO 2体积分数与0.3%. 则每坐圆米烟气中含SO 2mg 857110644.2233=⨯⨯； 果此脱硫效用为%8.91%10085717008571=⨯-. 8.2 解：1）↑+⋅→++22322322CO O H CaSO O H SO CaCO 2）每焚烧1t 煤爆收SO 2约kg t 7221006.3=⨯，约来除72×0.9=64.8kg.果此消耗CaCO 3 kg m 132648.641003.1=⨯⨯=.3）CaSO 4.2H 2O 死成量 kg 174172648.64=⨯；则焚烧1t 煤脱硫污泥排搁量为t 4354.0174=，共时排搁灰渣77kg.解： 1）由)1)(1(121ηηη---=T，)1%)(981(1%7.992η---=，解得%852=η.2）设总体积为100，则SO 27.8体积，O 210.8体积，N 281.4体积.经第一级催化转移后余SO 20.156体积，O 26.978体积，N 281.4体积.设有x 体积SO 2转移，则总体积为)25.88(x -.果此，5.0]2/5.882/978.6[2/5.88156.0)25.88/(300x x x x xx --⋅---=×10－3；故转移率为%99156.0106.113=⨯-- 8.4解：能源消耗W W K 07.58.0260000156.0=⨯=，即约0.51%用于克服阻力益坏. 解：1）与仄稳温度为C T 。

第18章国家审计习题参考答案1.简述财政收支审计的重点？【答】财政收支审计的重点重要包括：（1）财政部门按照本级人民代表大会批准的政府预算向各部门批复预算的情况、政府预算执行中调整情况和预算收支变化情况；（2）财政部门、税务机关、海关等预算收入征收部门，依照有关法律、行政法规和国务院财政税务部门的有关规定，及时、足额征收应征的各项税收收入、企业上缴利润、专项收入和退库拨补企业计划亏损补贴等政府预算收入情况；（3）财政部门按照批准的年度预算和用款计划、预算级次和程序、用款单位的实际用款进度，拨付政府本级预算支出资金情况；（4）财政部门依照有关法律、行政法规和财政管理体制，拨付和管理政府间财政转移支付资金情况以及办理结算、结转情况；1（5）财政部门依照有关法律、行政法规和财政部门的有关规定，国库按照国家有关规定办理预算收入的收纳、划分、留解情况和预算支出资金的拨付情况；（6）本级各部门（含直属单位）执行年度预算情况；（7）依照国家有关规定实行专项管理的预算资金收支情况；（8）法律、法规规定的其他预算执行情况。

2．分别简述事业经费、行政经费、社会保障基金审计的主要内容。

【答】事业经费审计是指审计机关依法对事业经费的筹集、管理、分配和使用等财务收支活动的真实、合法、效益进行的审计监督。

开展事业经费审计，有利于保证事业经费预算执行和决算的真实、合法、效益，促进有关事业主管部门加强事业经费管理，保障各项事业的健康、顺利发展。

其主要审计内容有：事业经费预算和财务收支计划管理的审计、事业经费收入的审计、事业经费支出的审计、事业经费资金管理的审计、事业经费往来款项的审计、用事业经费购置的财产、物资的审计。

事业经费周转金、专项基金管理和使用的审计。

行政经费审计是审计机关依法对行政经费财务收支的真实、合法和效益进行的审计监督。

其主要审计内容包括行政经费收入的审计、行政经费支出的审计、行政经费内部控制制度的审计、用行政经费购置的财产、物资的审计。

第18章第十八章浮动汇率制下的内外平衡1．浮动汇率下的政策环境和目标与固定汇率下有什么区别？答案提示：不同于固定汇率下的情况，浮动汇率可自动调节国际收支，使一国经济达到对外平衡，这样汇率调节就完成了固定汇率下政府必须考虑的内外均衡两个任务中的一个。

现在，只剩对内平衡一个目标需要考虑。

在浮动汇率制度下，政府的政策目标将只有一个，即通过宏观经济政策的实施达到充分就业和物价稳定。

2．比较固定汇率和浮动汇率下的各种宏观经济政策的效果，并对之加以解释。

答案提示：在资本具有完全流动性的情况下，如果实行固定汇率制度，财政政策有效，而货币政策完全无效；如果实行浮动汇率制度，财政政策完全无效，而货币政策是有效的，即一国货币当局在浮动汇率下可以实行独立的货币政策。

3．试解释浮动汇率下的财政政策的“挤出效用”。

答案提示：参考本章第二节。

4．假设A国和B国经济联系紧密，均实行浮动汇率制度，A国遭遇严重失业问题，遂采取放松银根政策，B国是否会受到影响？答案提示：B国会受到影响。

A国实行宽松的货币政策，将导致物价上升和货币贬值，随着A国出口的增加，B国国内市场将相对减小，不利于B国的就业和生产的增加。

5．试分析在资本完全不流动的情况下，财政政策和货币政策的作用。

答案提示：通过画图进行分析，此时BP曲线为垂直的。

6*.试讨论资本不完全流动下的财政政策和货币政策的作用，与资本完全流动下的作用效果有何差异？答案提示：在这种情况下，汇率的变化会引起BP曲线的移动。

7．在资本完全流动情况下，试分析在下列两种情形下，固定汇率与浮动汇率对国内经济的稳定作用。

（1）国内货币供给突然自发增加；（2）外国资本突然大量流入。

答案提示：（1）固定汇率下，国内货币供给突然自发增加，本国货币的利率下降，本国货币利率下降导致资本大量外流、存在国际收支逆差，这样对国内货币产生贬值压力，中央银行必须干预市场，抛出外汇，收回本币，使汇率保持固定，与此同时国内货币供给减少，直到重新达到原来的均衡点为止。

第十八章企业合并一、单项选择题1.A公司于2X19年12月3日用无形资产（专利权）换取B公司60%的股权。

另以银行存款支付评估咨询费等20万元。

无形资产原价为100万元，已摊销20万元，公允价值200万元。

假定合并前A公司与B公司不存在任何关联方关系，B 竺司当日可辨认净资产公允价值为500万元。

不考虑其他因素，A公司因该事项影响当期损益的金额为（）万元A.20B.100C.120D.1402.甲公司2X18年7月定向增发普通股80万股给丙公司，从其手中换得乙公司70%的股权，合并前甲公司与乙公司、丙公司无关联方关系。

甲公司股票每股面值为1元，每股市价为15元；合并当天乙公司可辨认净资产账面价值为 800万元，可辨认净资产公允价值为2 000万元。

甲公司支付给证券公司股票发行费用30万元，支付给中介机构审计费5万元，均以银行存款支付。

不考虑其他因素，甲公司取得该投资在个别财务报表中的入账价值为（）万元A. 1 200B. 1 230C. 1 205D. 1 2353.下列各项关于企业合并的说法不正确的是（）。

A.同一控制下的企业合并，合并方取得被合并方的资产、负债仅限于被合并方账面上原已确认的资产和负债，合并中不产生新的资产和负债B.同一控制下的企业合并投资单位应该将取得的长期股权投资以被投资方可辨认净资产的公允价值的份额入账C.同一控制下的企业合并，对于被合并方在企业合并前实现的留存收益中归属于合并方的部分，需要自合并方的资本公积转入留存收益D.非同一控制下的控股合并中，可能会产生商誉4.下列事项中，不属于企业合并准则中所界定的企业合并的是（）。

A.A公司通过发行债券自B公司原股东处取得B公司的全部股权，交易事项发生后B公司仍持续经营B.A公司支付对价取得B公司的净资产，交易事项发生后B公司失去法人资格C.A公司以其资产作为出资投入B公司，取得对B公司的控制权，交易事项发生后B公司仍维持其独立法人资格继续经营D.A公司购买B公司30%的股权，对B公司产生重大影响5.甲公司为一家规模较小的上市公司，乙公司为某大型未上市的民营企业。

人教版数学八年级下册第十八章测试题姓名：分数：一、选择题1．若顺次连接四边形ABCD各边中点所得四边形是矩形，则四边形ABCD必然是（）A．菱形B．对角线相互垂直的四边形C．正方形D．对角线相等的四边形2．下列说法中，不正确的是（）A．有三个角是直角的四边形是矩形B．对角线相等的四边形是矩形C．对角线互相垂直的矩形是正方形D．对角线互相垂直的平行四边形是菱形3．如图，矩形ABCD中，DE⊥AC于E，且∠ADE：∠EDC=3：2，则∠BDE的度数为（）A．36°B．18°C．27° D．9°4．如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）A．当AB=BC时，它是菱形 B．当AC⊥BD时，它是菱形C．当∠ABC=90°时，它是矩形D．当AC=BD时，它是正方形5．下列命题中正确的是（）A．对角线互相平分的四边形是菱形B．对角线互相平分且相等的四边形是菱C．对角线互相垂直的四边形是菱形D．对角线互相垂直平分的四边形是菱形6．如图，某花木场有一块等腰梯形ABCD的空地，其各边的中点分别是E、F、G、H，测得对角线AC=10m，现想利用篱笆围成四边形EFGH场地，则需篱笆得总长度是（）A．40 m B．30 m C．20 m D．10 m7．在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=10，BD=6，则该梯形的面积是（）A．30 B．15 C． D．608．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（）A．①②③B．①④⑤C．①②⑤D．②⑤⑥二、填空题9．平行四边形ABCD的周长为20cm，对角线AC、BD相交于点O，若△BOC的周长比△AOB的周长大2cm，则CD=cm．10．菱形的两条对角线分别是6cm，8cm，则菱形的边长为cm，面积为cm2．11．如图，△ABC中，EF是它的中位线，M、N分别是EB、CF的中点，若BC=8cm，那么EF=cm，MN=cm．12．如图，菱形ABCD中，AC=2，BD=5，P是AC上一动点（P不与A、C重合），PE∥BC交AB于E，PF∥CD交AD于F，则图中阴影部分（即多边形BCPFEB）的面积为．13．如图所示，菱形ABCD中，对角线AC，BD相交于点O，若再补充一个条件能使菱形ABCD成为正方形，则这个条件是．（只填一个条件即可，答案不唯一）14．等腰梯形两底之差为12cm，高为6cm，则其锐角底角为度．15．若矩形的对角线长为8cm，两条对角线的一个交角为60°，则该矩形的面积为 cm2．三、解答题16．如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是8cm．求：(1)两条对角线的长度；(2)菱形的面积．17．如图所示，矩形ABCD的对角线AC、BD相交于点O，AE⊥BD，垂足为E，∠1=∠2，OB=6(1)求∠BOC的度数；(2)求△DOC的周长．18．如图，在平行四边形ABCD中，E、F是AC上的两点，且AE=CF．求证：DE=BF．19．如图，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在边BC 上，且四边形AEFD是平行四边形．(1)AD与BC有何等量关系，请说明理由；(2)当AB=DC时，求证：平行四边形AEFD是矩形．20．如图，△ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE∥AB交MN于E，连接AE、CD．请判断四边形ADCE的形状，说明理由．参考答案1．若顺次连接四边形ABCD各边中点所得四边形是矩形，则四边形ABCD必然是（）A．菱形B．对角线相互垂直的四边形C．正方形D．对角线相等的四边形【考点】矩形的判定；三角形中位线定理．【专题】选择题．【分析】此题要根据矩形的性质和三角形中位线定理求解；首先根据三角形中位线定理知：所得四边形的对边都平行且相等，那么其必为平行四边形，若所得四边形是矩形，那么邻边互相垂直，故原四边形的对角线必互相垂直，由此得解．【解答】解：已知：如图，四边形EFGH是矩形，且E、F、G、H分别是AB、BC、CD、AD的中点，求证：四边形ABCD是对角线垂直的四边形．证明：由于E、F、G、H分别是AB、BC、CD、AD的中点，根据三角形中位线定理得：EH∥FG∥BD，EF∥AC∥HG；∵四边形EFGH是矩形，即EF⊥FG，∴AC⊥BD；故选B．【点评】本题主要利用了矩形的性质和三角形中位线定理来求解．2．下列说法中，不正确的是（）A．有三个角是直角的四边形是矩形B．对角线相等的四边形是矩形C．对角线互相垂直的矩形是正方形D．对角线互相垂直的平行四边形是菱形【考点】矩形的判定；菱形的判定；正方形的判定．【专题】选择题．【分析】根据各四边形的性质对各个选项进行分析从而得出最后答案．【解答】解：A、正确，有三个角是直角的四边形是矩形是矩形的判定定理；B、错误，对角线相等的四边形不一定是矩形，对角线相等的平行四边形才是矩形；C、正确，对角线互相垂直的矩形是正方形；D、正确，对角线互相垂直的平行四边形是菱形．故选B．【点评】考查了对四边形性质与判定的综合运用，特殊四边形之间的相互关系是考查重点．3．如图，矩形ABCD中，DE⊥AC于E，且∠ADE：∠EDC=3：2，则∠BDE的度数为（）A．36°B．18°C．27° D．9°【考点】矩形的性质；三角形内角和定理．【专题】选择题．【分析】本题首先根据∠ADE：∠EDC=3：2可推出∠ADE以及∠EDC的度数，然后求出△ODC各角的度数便可求出∠BDE．【解答】解：已知∠ADE：∠EDC=3：2⇒∠ADE=54°，∠EDC=36°，又因为DE⊥AC，所以∠DCE=90°﹣36°=54°，根据矩形的性质可得∠DOC=180°﹣2×54°=72°所以∠BDE=180°﹣∠DOC﹣∠DEO=18°故选B．【点评】本题考查的是三角形内角和定理以及矩形的性质，难度一般．4．如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（）A．当AB=BC时，它是菱形 B．当AC⊥BD时，它是菱形C．当∠ABC=90°时，它是矩形D．当AC=BD时，它是正方形【考点】正方形的判定；平行四边形的性质；菱形的判定；矩形的判定．【专题】选择题．【分析】根据邻边相等的平行四边形是菱形；根据所给条件可以证出邻边相等；根据有一个角是直角的平行四边形是矩形；根据对角线相等的平行四边形是矩形．【解答】解：A、根据邻边相等的平行四边形是菱形可知：四边形ABCD是平行四边形，当AB=BC时，它是菱形，故A选项正确；B、∵四边形ABCD是平行四边形，∴BO=OD，∵AC⊥BD，∴AB2=BO2+AO2，AD2=DO2+AO2，∴AB=AD，∴四边形ABCD是菱形，故B选项正确；C、有一个角是直角的平行四边形是矩形，故C选项正确；D、根据对角线相等的平行四边形是矩形可知当AC=BD时，它是矩形，不是正方形，故D选项错误；综上所述，符合题意是D选项；故选D．【点评】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握，此题涉及到的知识点较多，学生答题时容易出错．5．下列命题中正确的是（）A．对角线互相平分的四边形是菱形B．对角线互相平分且相等的四边形是菱C．对角线互相垂直的四边形是菱形D．对角线互相垂直平分的四边形是菱形【考点】菱形的判定．【专题】选择题．【分析】对角线互相垂直平分的四边形是菱形．【解答】解：根据菱形的判定，知对角线互相垂直平分的四边形是菱形，A、B、C错误，D正确．故选D．【点评】本题考查菱形的判定方法．6．如图，某花木场有一块等腰梯形ABCD的空地，其各边的中点分别是E、F、G、H，测得对角线AC=10m，现想利用篱笆围成四边形EFGH场地，则需篱笆得总长度是（）A．40 m B．30 m C．20 m D．10 m【考点】三角形中位线定理．【专题】选择题．【分析】据等腰梯形的性质和三角形的中位线定理有EF=GH=AC，EH=GF=BD，可知四边形EFGH的周长=4EF=2AC，进而可得出四边形EFGH的周长，即需篱笆得总长．【解答】解：如图，连接BD，∵E、F、G、H是等腰梯形ABCD各边中点，∴EF=GH=AC，EH=GF=BD，∵等腰梯形ABCD，∴BD=AC，∴四边形EFGH的周长=4EF=2AC=20m．故选C．【点评】此题主要考查了等腰梯形的性质和三角形中位线定理，得出四边形EFGH的周长与AC的关系是解题的关键，难度一般．7．在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC=10，BD=6，则该梯形的面积是（）A．30 B．15 C． D．60【考点】根据边的关系判定平行四边形．【专题】选择题．【分析】根据对角线互相垂直的四边形的面积公式，得该梯形的面积是10×6÷2=30．【解答】解：如图，作DE∥AC交BC延长线于E∵AD ∥BC∴四边形ADEC 为平行四边形∴CE=AD ，∠CDE=∠DCA∵AC ⊥BD ，∴AC ⊥DE ，∴△BDE 为直角三角形，∴S 梯ABCD =S △EBD ，∴S 梯ABCD =DE•BD=AC•BD=10×6÷2=30，故选A ．【点评】根据三角形的面积公式可以导出：对角线互相垂直的四边形的面积等于两条对角线乘积的一半．8．用两个全等的直角三角形拼下列图形：①矩形；②菱形；③正方形；④平行四边形；⑤等腰三角形；⑥等腰梯形．其中一定能拼成的图形是（ ）A ．①②③B ．①④⑤C ．①②⑤D ．②⑤⑥【考点】菱形的判定；等腰三角形的判定；平行四边形的判定；矩形的判定；正方形的判定；等腰梯形的判定．【专题】选择题．【分析】根据菱形、正方形、梯形、矩形、平行四边形、等腰三角形的性质判断．【解答】解：由于菱形和正方形中都四边相等的特点，而直角三角形中不一定有两边相等，故两个全等的直角三角形不能拼成菱形和正方形；由于等腰梯形有两边不等，故也不能．矩形，平行四边形，等腰三角形可以拼成．如图：故选B．【点评】本题考查了三角形的拼接图形的特点．以及特殊四边形的性质．9．平行四边形ABCD的周长为20cm，对角线AC、BD相交于点O，若△BOC的周长比△AOB的周长大2cm，则CD=cm．【考点】平行四边形的性质．【专题】填空题．【分析】根据平行四边形的性质可知，平行四边形的对角线互相平分，由于△BOC的周长比△AOB的周长大2cm，则BC比AB长7cm，所以根据周长的值可以求出AB，进而求出CD的长．【解答】解：如图∵平行四边形的周长为20cm，∴AB+BC=10cm；又△BOC的周长比△AOB的周长大2cm，∴BC﹣AB=2cm，解得：AB=4cm，BC=6cm．∵AB=CD，∴CD=4cm故答案为：4．【点评】此题主要考查平行四边的性质：平行四边形的两组对边分别相等且平行四边形的对角线互相平分．10．菱形的两条对角线分别是6cm，8cm，则菱形的边长为cm，面积为cm2．【考点】菱形的性质．【专题】填空题．【分析】根据菱形的性质利用勾股定理可求得菱形的边长，根据面积公式可求得菱形的面积．【解答】解：菱形的两条对角线分别是6cm，8cm，得到两条对角线相交所构成的直角三角形的两直角边是×6=3cm和×8=4cm，那么它的斜边即菱形的边长=5cm，面积为6×8×=24cm2．故答案为5，24．【点评】本题考查的是菱形的性质以及其面积的计算方法的运用．11．如图，△ABC中，EF是它的中位线，M、N分别是EB、CF的中点，若BC=8cm，那么EF=cm，MN=cm．【考点】三角形中位线定理；梯形中位线定理．【专题】填空题．【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出EF的长，再利用梯形的中位线等于两底和的一半求出MN的长度．【解答】解：∵EF是△ABC的中位线，BC=8cm，∴EF=BC=×8=4cm，∵M、N分别是EB、CF的中点，∴MN=（EF+BC）=（4+8）=6cm．故答案为4，6．【点评】本题主要利用三角形的中位线定理和梯形的中位线定理求解，熟练掌握定理是解题的关键．12．如图，菱形ABCD中，AC=2，BD=5，P是AC上一动点（P不与A、C重合），PE∥BC交AB于E，PF∥CD交AD于F，则图中阴影部分（即多边形BCPFEB）的面积为．【考点】菱形的性质．【专题】填空题．【分析】根据菱形性质得出AC⊥BD，求出△ABC的面积，求出△AEF的面积和△PEF的面积相等，得出阴影部分的面积等于三角形ABC的面积，即可得出答案．【解答】解：∵四边形ABCD是菱形，∴AC⊥BD，BO=OD=BD=2.5，∴△ABC的面积是×AC×BO=2.5，∵AD∥BC，AB∥DC，又∵PE∥BC，PF∥CD，∴PF∥AB，PE∥AD，∴四边形AEPF是平行四边形，∴△AEF的面积和△PEF的面积相等，∴阴影部分的面积等于△ABC的面积是2.5．故答案为：2.5．【点评】本题考查了菱形的性质，三角形的面积，平行四边形的性质和判定等知识点的应用．13．如图所示，菱形ABCD中，对角线AC，BD相交于点O，若再补充一个条件能使菱形ABCD成为正方形，则这个条件是．（只填一个条件即可，答案不唯一）【考点】正方形的判定；菱形的性质．【专题】填空题．【分析】根据菱形的性质及正方形的判定来添加合适的条件．【解答】解：要使菱形成为正方形，只要菱形满足以下条件之一即可，(1)有一个内角是直角(2)对角线相等．即∠BAD=90°或AC=BD．故答案为：∠BAD=90°或AC=BD．【点评】本题比较容易，考查特殊四边形的判定．14．等腰梯形两底之差为12cm，高为6cm，则其锐角底角为度．【考点】根据边的关系判定平行四边形．【专题】填空题．【分析】先作图，过点D作DE∥AB，四边形ABED是平行四边形，根据题意得CE=12cm，△CDE是等腰三角形，从而得出DF=CF=6cm，则锐角底角为45°．【解答】解：过点D作DE∥AB，∵AD∥BC，∴四边形ABED是平行四边形，∴AB=DE，∵AB=CD，∴DE=CD，∴△CDE是等腰三角形，又DF⊥CE，∴EF=CF=CE=（BC﹣AD）=6cm，∵高DF=6cm，∴DF=CF=6cm，而∠DFC=90°，∴∠DCF=45°．【点评】本题考查了梯形中辅助线的作法：平移一腰得出两底之差，还考查了等腰三角形的性质．15．若矩形的对角线长为8cm，两条对角线的一个交角为60°，则该矩形的面积为 cm2．【考点】矩形的性质．【专题】填空题．【分析】根据矩形的性质，画出图形求解．【解答】解：∵ABCD为矩形∴OA=OC=OB=OD∵一个角是60°∴BC=OB=cm∴根据勾股定理==∴面积=BC•CD=4×=cm2．故答案为．【点评】本题考查的知识点有：矩形的性质、勾股定理．16．如图，在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是8cm．求：(1)两条对角线的长度；(2)菱形的面积．【考点】菱形的性质．【专题】解答题．【分析】(1)由在菱形ABCD中，∠ABC与∠BAD的度数比为1：2，周长是8cm，可求得△ABO是含30°角的直角三角形，AB=2cm，继而求得AC与BD的长；(2)由菱形的面积等于其对角线积的一半，即可求得答案．【解答】解：(1)∵四边形ABCD是菱形，∴AB=BC，AC⊥BD，AD∥BC，∴∠ABC+∠BAD=180°，∵∠ABC与∠BAD的度数比为1：2，∴∠ABC=×180°=60°，∴∠ABO=∠ABC=30°，∵菱形ABCD的周长是8cm．∴AB=2cm，∴OA=AB=1cm，∴OB==，∴AC=2OA=2cm，BD=2OB=2cm；(2)S菱形ABCD=AC•BD=×2×2=2（cm2）．【点评】此题考查了菱形的性质以及含30°角的直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．17．如图所示，矩形ABCD的对角线AC、BD相交于点O，AE⊥BD，垂足为E，∠1=∠2，OB=6(1)求∠BOC的度数；(2)求△DOC的周长．【考点】矩形的性质．【专题】解答题．【分析】(1)AE⊥BD，∠1+∠ABD=∠ADB+∠ABD，得出∠ACB=∠ADB=∠2=∠1=30°，可知△AOB为等边三角形，继而求出∠BOC的度数；(2)由(1)知，△DOC≌△AOB，OD=OC=CD=OB，继而求出△DOC的周长．【解答】解：(1)∵四边形ABCD为矩形，AE⊥BD，∴∠1+∠ABD=∠ADB+∠ABD=∠2+∠ABD=90°，∴∠ACB=∠ADB=∠2=∠1=30°，又AO=BO，∴△AOB为等边三角形，∴∠BOC=120°；(2)由(1)知，△DOC≌△AOB，∴△DOC为等边三角形，∴OD=OC=CD=OB=6，∴△DOC的周长=3×6=18．【点评】本题考查矩形的性质，难度适中，解题关键是根据矩形的性质求出∠1=∠2=∠ACB=30°．18．如图，在平行四边形ABCD中，E、F是AC上的两点，且AE=CF．求证：DE=BF．【考点】平行四边形的性质．【专题】解答题．【分析】由平行四边形的性质得AD=CB，∠DAE=∠BCF，再由已知条件，可得△ADE≌△CBF，进而得出结论．【解答】证明：在平行四边形ABCD中，则AD=CB，∠DAE=∠BCF，又AE=CF，∴△ADE≌△CBF（SAS），∴DE=BF．【点评】本题主要考查平行四边形的性质及全等三角形的判定问题，应熟练掌握．19．如图，在梯形ABCD中，AD∥BC，AB∥DE，AF∥DC，E、F两点在边BC 上，且四边形AEFD是平行四边形．(1)AD与BC有何等量关系，请说明理由；(2)当AB=DC时，求证：平行四边形AEFD是矩形．【考点】平行四边形的性质；矩形的判定．【专题】解答题．【分析】(1)由题中所给平行线，不难得出四边形ABED和四边形AFCD都是平行四边形，而四边形AEFD也是平行四边形，三个平行四边形都共有一条边AD，所以可得出AD=BC的结论．(2)根据矩形的判定和定义，对角线相等的平行四边形是矩形．只要证明AF=DE 即可得出结论．【解答】(1)解：AD=BC．理由如下：∵AD∥BC，AB∥DE，AF∥DC，∴四边形ABED和四边形AFCD都是平行四边形．∴AD=BE，AD=FC，又∵四边形AEFD是平行四边形，∴AD=EF．∴AD=BE=EF=FC．∴AD=BC．(2)证明：∵四边形ABED和四边形AFCD都是平行四边形，∴DE=AB，AF=DC．∵AB=DC，∴DE=AF．又∵四边形AEFD是平行四边形，∴平行四边形AEFD是矩形．【点评】本题考查了梯形、平行四边形的性质和矩形的判定，是一道集众多四边形于一体的小综合题，难度中等稍偏上的考题．有的学生往往因为基础知识不扎实，做到一半就做不下去了，建议老师平时教学中，重视一题多变，适当地变式联系，可以触类旁通．20．如图，△ABC中，AC的垂直平分线MN交AB于点D，交AC于点O，CE∥AB交MN于E，连接AE、CD．请判断四边形ADCE的形状，说明理由．【考点】菱形的判定；线段垂直平分线的性质．【专题】解答题．【分析】根据中垂线的性质中垂线上的点线段两个端点的距离相等可得出AE=CE，AD=CD，OA=OC∠AOD=∠EOC=90°，再结合CE∥AB，可证得△ADO≌△CEO，从而根据由一组对边平行且相等知，四边形ADCE是平行四边形，结合OD=OE，OA=OC，∠AOD=90°可证得为菱形．【解答】四边形ADCE是菱形．证明：∵MN是AC的垂直平分线，∴AE=CE，AD=CD，OA=OC，∠AOD=∠EOC=90°，∵CE∥AB，∴∠DAO=∠ECO，∴△ADO≌△CEO．（ASA）∴AD=CE，OD=OE，∵OD=OE，OA=OC，∴四边形ADCE是平行四边形又∵∠AOD=90°，∴▱ADCE是菱形．【点评】本题考查了菱形的判定及线段垂直平分线的性质，利用了：中垂线的性质；全等三角形的判定和性质；平行四边形和菱形的判定．。

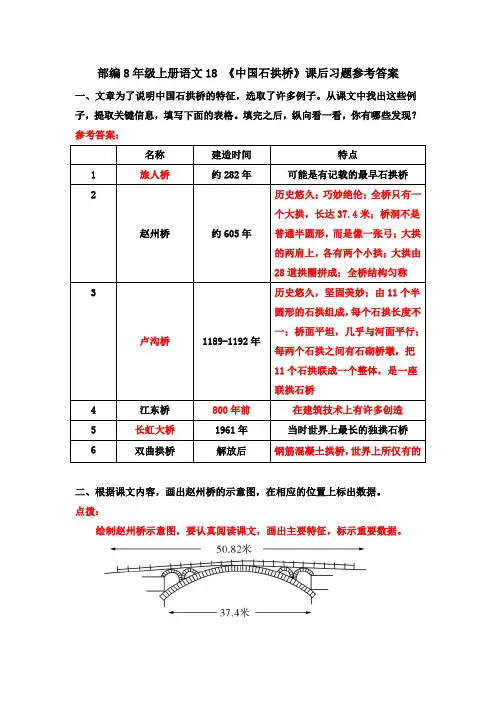
部编8年级上册语文18 《中国石拱桥》课后习题参考答案一、文章为了说明中国石拱桥的特征，选取了许多例子。

从课文中找出这些例子，提取关键信息，填写下面的表格。

填完之后，纵向看一看，你有哪些发现？参考答案：二、根据课文内容，画出赵州桥的示意图，在相应的位置上标出数据。

点拨：绘制赵州桥示意图，要认真阅读课文，画出主要特征，标示重要数据。

三、说明文中常用一些说明方法，如下定义、举例子、作比较、打比方、分类别、画图表、列数字、引用等。

看看本文中用了哪些说明方法，找出实例并说说它们的作用。

参考答案：1.打比方。

如“石拱桥的桥洞成弧形，就像虹”“桥洞不是普通半圆形，而是像一张弓”，用“虹”“弓”作比，突出了石拱桥形式上的特征，富有形象性。

2.举例子。

作者为了说明中国石拱桥的特点，列举了旅人桥、赵州桥、卢沟桥、长虹大桥这四个典型的例子。

既说明我国石拱桥历史悠久，歌颂了我国古代劳动人民的勤劳智慧；又显示了我国桥梁事业的飞跃发展，赞颂了社会主义制度的无比优越。

3.列数字。

有概数、确数之分，给人以准确鲜明的印象。

如“赵州桥非常雄伟，全长50.82米，两端宽9.6米，中部略窄，宽9米。

”4.作比较。

如“永定河发水时，来势很猛，以前两岸河堤常被冲毁，但是这座桥极少出事，足见它的坚固”，将卢沟桥和两岸河堤相比较，突出了卢沟桥的坚固。

5.引用。

如引用唐朝张嘉贞的话“制造奇特，人不知其所以为”，说明赵州桥设计施工的精巧；引用唐朝张的赞语“初月出云，长虹饮涧”，说明赵州桥形式优美……这些引用增强了文章说服力的和感染力。

6.摹状貌。

如“这些石刻狮子，有的母子相抱，有的交头接耳，有的像倾听水声，有的像注视行人，千态万状，惟妙惟肖”，描绘石刻狮子的“千态万状”，说明卢沟桥在装饰上的重要特点，突出了桥的形式美。

四、结合下列句子中加点的词语，体会说明文语言的准确、严谨。

１.《水经注》里提到的“旅人桥”，大约．．．．．．．建成于公元282年，可能是有记载的．．最早的石拱桥了。

电子测量技术基础课后习题答案 18章张永瑞第二版目录习题一 (1)习题二 (6)习题三 (16)习题四 (24)习题五 (30)习题六 (35)习题七 (37)习题八 (46)习题一1.1 解释名词：①测量；②电子测量。

答：测量是为确定被测对象的量值而进行的实验过程。

在这个过程中，人们借助专门的设备，把被测量与标准的同类单位量进行比较，从而确定被测量与单位量之间的数值关系，最后用数值和单位共同表示测量结果。

从广义上说，凡是利用电子技术进行的测量都可以说是电子测量；从狭义上说，电子测量是指在电子学中测量有关电的量值的测量。

1.2 叙述直接测量、间接测量、组合测量的特点，并各举一两个测量实例。

答：直接测量：它是指直接从测量仪表的读数获取被测量量值的方法。

如：用电压表测量电阻两端的电压，用电流表测量电阻中的电流。

间接测量：利用直接测量的量与被测量之间的函数关系，间接得到被测量量值的测量方法。

如：用伏安法测量电阻消耗的直流功率P，可以通过直接测量电压U，电流I，而后根据函数关系P＝UI，经过计算，间接获得电阻消耗的功耗P；用伏安法测量电阻。

组合测量：当某项测量结果需用多个参数表达时，可通过改变测试条件进行多次测量，根据测量量与参数间的函数关系列出方程组并求解，进而得到未知量，这种测量方法称为组合测量。

例如，电阻器电阻温度系数的测量。

1.3 解释偏差式、零位式和微差式测量法的含义，并列举测量实例。

答：偏差式测量法：在测量过程中，用仪器仪表指针的位移(偏差)表示被测量大小的测量方法，称为偏差式测量法。

例如使用万用表测量电压、电流等。

零位式测量法：测量时用被测量与标准量相比较，用零示器指示被测量与标准量相等(平衡)，从而获得被测量从而获得被测量。

如利用惠斯登电桥测量电阻。

微差式测量法：通过测量待测量与基准量之差来得到待测量量值。

如用微差法测量直流稳压源的稳定度。

1.4 叙述电子测量的主要内容。

答：电子测量内容包括：（1）电能量的测量如：电压，电流电功率等；（2）电信号的特性的测量如：信号的波形和失真度，频率，相位，调制度等；（3）元件和电路参数的测量如：电阻，电容，电感，阻抗，品质因数，电子器件的参数等：（4）电子电路性能的测量如：放大倍数，衰减量，灵敏度，噪声指数，幅频特性，相频特性曲线等。

第1节电能电功一、单选题1.下列关于电功的说法正确的是（）A.电流做功的多少跟电流的大小、电压的高低无关B.电功的单位和电能的单位是不同的C.用电器消耗电能越多，电流做功就越少D.电流做功的过程就是电能转化为其他形式能的过程2.把标有“6V3W”的小灯泡和一个阻值为10Ω的定值电阻串联后接在电压为8V的电源上，此时电路中的电流为0.4A，则（）A.小灯泡的电阻为12ΩB.定值电阻两端的电压为4VC.通电1min小灯泡消耗的电能为180JD.小灯泡两端的电压为6V3.有一块手机用的锂电池，上面标明电压为3.8V，容量为2150mA•h，则锂电池充满电后存储的电能为（）A.8170JB.8.17JC.490.2JD.29412J4.对比图中白炽灯和LED灯将电能转化为其他形式能的情况，可得（）B.白炽灯的寿命跟灯丝的温度有关，因为温度越高，灯丝就越容易凝华C.LED灯可以直接把电能全部转化为光能D.LED灯发光的效率较高5.电能表的表盘如图所示，关于电能表下列说法正确的是（）A.“50Hz”是说这个电能表在50赫的交流电路中使用B.“10（20）A”是说这个电能表的标定电流是20安C.“10（20）A”是说这个电能表的额定最大电流是10安D.“600revs/（kW•h）”是表示电能表上的转盘转过1转消耗的电能是600千瓦时6.要使某电热器在相同时间内消耗的电能变为原来的2倍，以下措施可行的是（）A.电源电压不变，阻值变为原来的二倍B.电源电压不变，阻值变为原来的一半C.电源电压和阻值均变为原来的一半D.电源电压变为原来的一半，阻值变为原来的二倍7.甲是标有“16Ω 1A”的定值电阻，乙是标有“20Ω 1.5A“的滑动变阻器。

现把它们并联起来，下列说法正确的是（）A.电路两端允许施加的最大电压是30VB.干路允许通过的最大电流是2.5AC.定值电阻工作10s产生的热量是360JD.滑动变阻器工作10s消耗的最大电能是450J8.加在某导体两端的电压为3V，1min内电流所做的功为180J，则通过这导体的电流是（）B.3AC.60AD.180A9.电能有许多优点，以下关于电能优点的叙述中，正确的是（）A.消耗少量其他形式的能，可以转化成大量的电能B.消耗少量电能，可以转化成大量其他形式的能C.其它形式的能都可以很方便地转化成电能D.电能对环境无污染，能很方便地转化成其他形式的能10.以下几种常用的用电器，1小时消耗电能最接近1度的是（）A.电饭锅B.照明用LED灯C.手机D.电视机11.两盏灯L1和L2串联在电路中，已知两灯的电阻R1＞R2，则在相同的时间内（）A.电流通过L1做功多B.电流通过L2做功多C.电流通过两灯做功一样多D.无法判断12.如下图所示，对于电能表面板上的一些参数的理解，下列说法错误的是（）A.此时电能表的读数为120.7度B.“220V”是指这个电能表应该在220伏的电路中使用C.该电能表的额定功率为4400W二、多选题1.下列关于物理概念的说法中，正确的有：（）A.磁体具有指向性和吸铁性B.在磁场中的某一点，小磁针北极所指的方向就是该点的磁场方向C.用电器的电功率越大，消耗的电能就越多D.电流功的过程就是电能转化成其他形式能的过程2.小明将家中一个标有“220V1200W”的空调单独接在家庭电路中，正常工作10min后，电能表示数如图，下列说法中正确的是（）A.，电能表能测出这段时间内空调消耗多少电能B..这段时间内空调消耗了3127.5J的电能C..小明还可以再接入一个功率是2000W的电热水器D..这段时间内电能表转盘转过120转3.小明家使用的是DDS237-1型电子式单相预付费电能表，采用专用集成电路设计，符合国际标准的先进的智能IC卡技术实现预付费方式，内置磁保持继电器。

名著阅读（8分）《海底两万里·第十八章章鱼》附答案名著阅读《海底两万里·第十八章章鱼》附答案名著阅读多么惊心动魄的场面！这个不幸的人眼看是完了。

谁能从这强大的卷抱中把他夺过来呢？可是尼摩船长跳在章鱼身上，又一斧子，他把另一只胳膊又砍下来了。

他的副手奋勇狂怒地跟那些爬在诺第留斯号两边的其他章鱼战斗。

船员们各人挥动斧头，乱砍乱杀。

加拿大人、康塞尔和我，我们也把我们的武器穿进这大团肉块中去。

一种强烈的康香味散入敌人空中。

真正是怕人。

在一瞬间，我以为那个不幸被章鱼缠住的人可能从它那强大的吸盘上救下来。

八只胳膊有七只都被砍下了。

剩下的一只把那个人像一支笔般挥动，在空中转来转去。

但当尼摩船长和他的副手扑到它身上去的时候，这个东西喷出一道黑色的液体，这是从它肚子中的一个口袋分泌出来的黑水。

我们的眼睛都被弄得昏花看不见了。

当这团浓黑雾气消散的时候，枪乌贼不见了，跟它一起，我的不幸的同胞也不见了！那时我们是何等愤怒地来跟这些章鱼拼命呀！我们一点不能自主了。

有十条或十二条章鱼侵到平台上和诺第留斯号两边来。

我们在平台上，在血泊和墨水中跳动者的一条一条的肉段中间滚来滚去，这些粘性的触须就像多头蛇的头一样，一会又生出来了。

尼德·兰的叉每一下都刺人枪鸟贼的海色眼睛中，把眼珠挖出来。

可是，我的勇敢同伴不可能躲开，突然被一条怪物的触须卷住掀倒在地。

枪乌贼的厉害可怕的嘴对着尼德·兰张开来。

这个不幸的人要被咬为两段了。

我急急跑去救他，但尼摩船长走在我的前面，先我动了手。

他的斧子砍人两排巨大齿牙里面了，加拿大人出人意料地得救了，站起来，把整条叉刺人章鱼的三个心脏中。

“我应该有这次机会报答您啊！”尼摩船长对加拿大人说。

尼德点点头，没有回答他的话。

这次战斗延长至一刻钟之久。

怪物打败了，受伤了，死了，最后给我们让出地方来，溜入水中不见了。

尼摩船长全身血红，站在探照灯附近，一动也不动，眼盯着吞噬了他的一个同伴的大海，大滴的泪珠从他的眼里淌了出来。

人教版八年级数学下册第18章《平行四边形》练习题（含答案）1．在正方形ABCD中，E是△ABD内的点，EB＝EC．（1）如图1，若EB＝BC，求∠EBD的度数；（2）如图2，EC与BD交于点F，连接AE，若S四边形ABFE＝a，试探究线段FC与BE之间的数量关系，并说明理由．2．（1）如图1，在正方形ABCD中，E是AB上一点，G是AD上一点，∠ECG＝45°，那么EG与图中两条线段的和相等？证明你的结论．（2）请用（1）中所积累的经验和知识完成此题，如图2，在四边形ABCD中，AG∥BC（BC ＞AG），∠B＝90°，AB＝BC＝12，E是AB上一点，且∠ECG＝45°，BE＝4，求EG的长？3．如图，正方形ABCD的边长为1，对角线AC、BD交于点O，E是BC延长线上一点，且AC ＝EC，连接AE交BD于点P．（1）求∠DAE的度数；（2）求BP的长．4．如图，在矩形ABCD中，点O为对角线AC的中点，过点O作EF⊥AC交BC于点E，交AD 于点F，连接AE，CF．（1）求证：四边形AECF是菱形；（2）连接OB，若AB＝8，AF＝10，求OB的长．5．如图，在平行四边形ABCD中，对角线AC，BD交于点O，E是AD上任意一点，连接EO 并延长，交BC于点F，连接AF，CE．（1）求证：四边形AFCE是平行四边形；（2）若∠DAC＝60°，∠ADB＝15°，AC＝6．求出平行四边形ABCD的边BC上的高h的值．6．如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点（不与O、C重合），作AF⊥BE，垂足为G，分别交BC、OB于F、H，连接OG、CG．（1）求证：△AOH≌△BOE；（2）求∠AGO的度数；（3）若∠OGC＝90°，BG＝，求△OGC的面积．7．如图，在矩形ABCD中，BC＝24cm，P、Q、M、N分别从A、B、C、D同时出发，分别沿边AD、BC、CB、DA移动，当有一个点先到达所在边的另一个端点时，其它各点也随之停止移动．已知移动一段时间后，若BQ＝xcm（x≠0），AP＝2xcm，CM＝3xcm，DN＝x2cm．当x为何值时，以P、Q、M、N为顶点的四边形是平行四边形？8．在正方形ABCD中，F是BC边的中点，ED⊥AF于点E，连接CE．（1）如图1，求证：CE＝CD；（2）如图2，连接BE、BD，请直接写出图2中所有与∠BEF度数相等的角．9．如图1，已知平行四边形ABCD，DE是∠ADC的角平分线，交BC于点E．（1）求证：CD＝CE．（2）如图2所示，点P是平行四边形ABCD的边BC所在直线上一点，若BE＝CE，且AE ＝3，DE＝4，求△APD的面积．10．如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC、CF为邻边作平行四边形ECFG，如图1所示．（1）证明平行四边形ECFG是菱形；（2）若∠ABC＝120°，连接BG、CG、DG，如图2所示，①求证：△DGC≌△BGE；②求∠BDG的度数；（3）若∠ABC＝90°，AB＝8，AD＝14，M是EF的中点，如图3所示，求DM的长．11．如图，已知平行四边形ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于点M、N．（1）求证：四边形CMAN是平行四边形（2）已知DE＝8，FN＝6，求BN的长．12．如图，在△ABC中，∠ACB＝90°，D是BC的中点，DE⊥BC，CE∥AD．若AC＝2，CE＝4；（1）求证：四边形ACED是平行四边形．（2）求BC的长．13．如图，长方形ABCD中，AB∥CD，∠D＝90°，AB＝CD，AD＝4cm，点P从点D出发（不含点D）以2cm/s的速度沿D→A→B的方向运动到点B停止，点P出发1s后，点Q才开始从点C出发以acm/s的速度沿C→D的方向运动到点D停止，当点P到达点B时，点Q 恰好到达点D．（1）当点P到达点A时，△CPQ的面积为3cm2，求CD的长；（2）在（1）的条件下，设点P运动时间为t（s），运动过程中△BPQ的面积为S（cm2），请用含t（s）的式子表示面积S（cm2），并直接写出t的取值范围．14．如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F．（1）求证：四边形ADCF是菱形；（2）若AC＝6，AB＝8，求菱形ADCF的面积．15．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．（1）若∠B＝30°，AC＝6，求CE的长；（2）过点F作AB的垂线，垂足为G，连接EG，试判断四边形CEGF的形状，并说明原因．参考答案1．解：（1）如图1，∵EB＝BC＝EC，∴△EBC是等边三角形，∴∠EBC＝60°，∵四边形ABCD是正方形，∴∠CBD＝45°，∴∠EBD＝∠EBC﹣∠CBD＝60°﹣45°＝15°；（2）线段FC与BE之间的等量关系是：FC•BE＝2a，理由是：如图2，连接AF交BE于G，∵四边形ABCD是正方形，∴AB＝BC，∠ABD＝∠DBC，∵BF＝BF，∴△ABF≌△CBF（SAS），∴AF＝CF，∠BAF＝∠BCF，∵EB＝EC，∴∠ECB＝∠EBC，∵∠ABC＝∠DCB＝90°，∴∠ABE＝∠DCE，∴∠ABE+∠BAF＝∠DCE+∠BCE＝90°，∴∠AGB＝90°，∴AF⊥BE，∴S四边形ABFE＝S△ABE+S△BEF，＝，＝，＝，∵S四边形ABFE＝a，∴＝a，∴FC•BE＝2a．2．解：（1）EG＝BE+DG．如图1，延长AD至F，使DF＝BE，连接CF，∵四边形ABCD为正方形，∴BC＝DC，∠ABC＝∠ADC＝∠BCD＝90°，∵∠CDF＝180﹣∠ADC，∴∠CDF＝90°，∴∠ABC＝∠CDF，∵BE＝DF，∴△EBC≌△FDC（SAS），∴∠BCE＝∠DCF，EC＝FC，∵∠ECG＝45°，∴∠BCE+∠GCD＝∠BCD﹣∠ECG＝90°﹣45°＝45°，∴∠GCD+DCF＝∠FCG＝45°，∴∠ECG＝∠FCG，∵GC＝GC，∴△ECG≌△FCG（SAS），∴EG＝GF，∵GF＝GD+DF＝GD+BE，∴EG＝GD+BE．（2）如图2，过点C作CD⊥AG，交AG的延长线于D．∵AG∥BC，∴∠A+∠B＝180°，∵∠B＝90°，∴∠A＝180°﹣∠B＝90°，∵∠CDA＝90°，AB＝BC，∴四边形ABCD是正方形，∵AB＝BC＝12，∴CD＝AD＝12，∵BE＝4，∴AE＝AB﹣BE＝8，设EG＝x，由（1）知EG＝BE+GD，∴GD＝x﹣4，∴AG＝AD﹣GD＝12﹣（x﹣4）＝16﹣x，在Rt△AEG中：GE2＝AG2+AE2，∴x2＝（16﹣x）2+82，解得x＝10，∴EG＝10．3．解：（1）∵四边形ABCD的正方形，∴∠ACB＝45°，AD∥BC，∵AC＝EC，∴∠E＝∠EAC，∵∠ACB＝∠E+∠EAC＝45°，∴∠E＝22.5°，∵AD∥BC，∴∠DAE＝∠E＝22.5°；（2）∵四边形ABCD是正方形，正方形ABCD的边长是1，∴AB＝1，∠DAB＝90°，∠DBC＝45°，∵∠DAE＝22.5°，∴∠BAP＝90°﹣22.5°＝67.5°，∠APB＝∠E+∠DBC＝22.5°+45°＝67.5°，∴∠BAP＝∠APB，∴BP＝AB＝1．4．证明：（1）∵O是AC的中点，且EF⊥AC，∴AF＝CF，AE＝CE，OA＝OC，∵四边形ABCD是矩形，∴AD∥BC，∴∠AFO＝∠CEO，在△AOF和△COE中，，∴△AOF≌△COE（AAS），∴AF＝CE，∴AF＝CF＝CE＝AE，∴四边形AECF是菱形；（2）如图，∵AB＝8，AF＝AE＝EC＝10，∴BE＝＝＝6，∴BC＝16，∴AC＝＝＝8，∵AO＝CO，∠ABC＝90°，∴BO＝AC＝4．5．证明：（1）∵四边形ABCD是平行四边形∴AD∥BC，AO＝CO∴∠AEF＝∠CFE，∠EAC＝∠FCA，且AO＝CO ∴△AOE≌△COF（AAS）∴OF＝OE，且AO＝CO∴四边形AFCE是平行四边形；（2）∵∠DAC＝60°∴，∴h＝×AC＝3．6．（1）证明：∵四边形ABCD是正方形，∴OA＝OB，∠ABC＝90°，AC⊥BD，∴∠AOB＝∠BOE＝90°，∵AF⊥BE，∴∠GAE+∠AEG＝∠OBE+∠AEG＝90°，∴∠GAE＝∠OBE，在△AOH和△BOE中，，∴△AOH≌△BOE（ASA）；（2）∠AGO＝45°；（3）S△OGC＝OG•CG＝×6＝3．7．当x为2或﹣3+时，以P、Q、M、N为顶点的四边形是平行四边形．8．（1）证明：作CH⊥DE交DE于点H，交AD于点N，∵ED⊥AF，CH⊥DE，∴AF∥CN，又AN∥CF，∴四边形AFCN为平行四边形，∴AN＝CF，∵F是BC边的中点，AD＝BC，∴N是AD边的中点，∵NH∥AE，DN＝NA，∴DH＝HE，又CH⊥DE，∴CE＝CD；（2）解：作BG⊥AF于点G，设正方形的边长为4a，则BF＝2a，由勾股定理得，AF＝＝＝2a，×AB×BF＝×AF×BG，即×4a×2a＝×2a×BG，解得，BG＝a，∵∠ABF＝90°，BG⊥AF，∴BF2＝FG•FA，即（2a）2＝FG•2a，解得，FG＝a，∵∠BAF+∠DAE＝90°，∠ADE+∠DAE＝90°，∴∠BAG＝∠ADE，在△BAG和△ADE中，∴△BAG≌△ADE（AAS）∴AE＝BG＝a，∴EG＝AF﹣AE﹣FG＝a，∴BG＝EG，∴∠BEF＝45°，则图2中所有与∠BEF度数相等的角有∠ABD、∠CBD、∠ADB、∠CDB．9．（1）证明：∵DE是∠ADC的角平分线，∴∠ADE＝∠CDE，在平行四边形ABCD中，AD∥BC，∴∠ADE＝∠CED，∴∠CDE＝∠CED，∴CD＝CE；（2）解：∵CD＝CE，BE＝CE，∴BE＝CD＝AB，∴△ABE为等腰三角形，∴设∠BAE＝∠BEA＝α，∠CED＝∠CDE＝β，∴∠ABE＝180°﹣2α，∠DCE＝180°﹣2β，又∵∠ABE+∠DCE＝180°，∴180°﹣2α+180°﹣2β＝180°，∴α+β＝90°，∴∠AED＝90°，即△AED为直角三角形，∴AD＝＝＝5，过点E作EK⊥AD，∴EK＝＝，△APD的面积＝AD•EK＝×5×＝6．10．解：（1）证明：∵AF平分∠BAD，∴∠BAF＝∠DAF，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAF＝∠CEF，∠BAF＝∠CFE，∴∠CEF＝∠CFE，∴CE＝CF，又∵四边形ECFG是平行四边形，∴四边形ECFG为菱形；（2）①∵四边形ABCD是平行四边形，∴AB∥DC，AB＝DC，AD∥BC，∵∠ABC＝120°，∴∠BCD＝60°，∠BCF＝120°由（1）知，四边形CEGF是菱形，∴CE＝GE，∠BCG＝∠BCF＝60°，∴CG＝GE＝CE，∠DCG＝120°，∵EG∥DF，∴∠BEG＝120°＝∠DCG，∵AE是∠BAD的平分线，∴∠DAE＝∠BAE，∵AD∥BC，∴∠DAE＝∠AEB，∴∠BAE＝∠AEB，∴AB＝BE，∴BE＝CD，∴△DGC≌△BGE（SAS）；②∵△DGC≌△BGE，∴BG＝DG，∠BGE＝∠DGC，∴∠BGD＝∠CGE，∵CG＝GE＝CE，∴△CEG是等边三角形，∴∠CGE＝60°，∴∠BGD＝60°，∵BG＝DG，∴△BDG是等边三角形，∴∠BDG＝60°；（3）方法一：如图3中，连接BM，MC，∵∠ABC＝90°，四边形ABCD是平行四边形，∴四边形ABCD是矩形，又由（1）可知四边形ECFG为菱形，∠ECF＝90°，∴四边形ECFG为正方形．∵∠BAF＝∠DAF，∴BE＝AB＝DC，∵M为EF中点，∴∠CEM＝∠ECM＝45°，∴∠BEM＝∠DCM＝135°，在△BME和△DMC中，∵，∴△BME≌△DMC（SAS），∴MB＝MD，∠DMC＝∠BME．∴∠BMD＝∠BME+∠EMD＝∠DMC+∠EMD＝90°，∴△BMD是等腰直角三角形．∵AB＝8，AD＝14，∴BD＝2，∴DM＝BD＝．方法二：过M作MH⊥DF于H，∵∠ABC＝90°，四边形ABCD是平行四边形，∴四边形ABCD是矩形，又由（1）可知四边形ECFG为菱形，∠ECF＝90°，∴四边形ECFG为正方形，∴∠CEF＝45°，∴∠AEB＝∠CEF＝45°，∴BE＝AB＝8，∴CE＝CF＝14﹣8＝6，∵MH∥CE，EM＝FM，∴CH＝FH＝CF＝3，∴MH＝CE＝3，∴DH＝11，∴DM＝＝．11．（1）证明：∵AE⊥BD，CF⊥BD，∴AM∥CN，∵四边形ABCD是平行四边形，∴CM∥AN∴四边形CMAN是平行四边形；（2）解：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∴∠ADE＝∠CBF，∵AE⊥BD，CF⊥BD，∴∠AED＝∠CFB＝90°，在△ADE与△CBF中，∠ADE＝∠CBF，∠AED＝∠CFB，AD＝BC，∴△ADE≌△CBF（AAS）；∴DE＝BF＝8，∵FN＝6，∴．12．解：（1）证明：∵∠ACB＝90°，DE⊥BC，∴AC∥DE又∵CE∥AD∴四边形ACED是平行四边形．（2）∵四边形ACED是平行四边形．∴DE＝AC＝2．在Rt△CDE中，由勾股定理得CD＝＝＝2．∵D是BC的中点，∴BC＝2CD＝4．13．解：（1）设点P运动时间为t（s），根据题意，得点P出发1s后，点Q才开始从点C出发以acm/s的速度沿C→D的方向运动到点D停止，当点P到达点B时，点Q恰好到达点D．∴2（t﹣2）＝a（t﹣1），当点P到达点A时，△CPQ的面积为3cm2，即a×1×4＝3，∴a＝．即2（t﹣2）＝（t﹣1），解得t＝5，所以CD＝a（t﹣1）＝6．答：CD的长为6；（2）根据题意，得BC＝AD＝4，CD＝6DP＝2t，CQ＝1.5（t﹣1），①点P的运动时间为t，0﹣1秒时点Q还在点C，△BPQ面积不变为＝12；即S＝12（0＜t≤1）②当1＜t≤2时，DQ＝6﹣1.5（t﹣1）＝7.5﹣1.5t，S＝S梯形DPBC﹣S△DPQ﹣S△BQC＝（2t+4）×6﹣×2t×（7.5﹣1.5t）﹣×1.5（t﹣1）×4 ＝1.5t2﹣4.5t+15；③当2＜t≤5时，BP＝10﹣2t，S＝BP•BC＝（10﹣2t）×4＝20﹣4t．综上所述：运动过程中△BPQ的面积为S（cm2），用含t（s）的式子表示面积S（cm2）为：S＝12 （0＜t≤1）或S＝1.5t2﹣4.5t+15（1＜t≤2）或S＝20﹣4t（2＜t≤5）．14．解：（1）证明：∵E是AD的中点∴AE＝DE∵AF∥BC∴∠AFE＝∠DBE在△AEF和△DEB中∴△AEF≌△DEB（AAS）∴AF＝DB∴四边形ADCF是平行四边形∵∠BAC＝90°，D是BC的中点∴AD＝CD＝BC∴四边形ADCF是菱形；（2）解：法一、设AF到CD的距离为h，∵AF∥BC，AF＝BD＝CD，∠BAC＝90°，∴S菱形ADCF＝CD•h＝BC•h＝S△ABC＝AB•AC＝．法二、连接DF∵AF＝DB，AF∥DB∴四边形ABDF是平行四边形∴DF＝AB＝8∴S菱形ADCF＝AC•DF＝．法三、∵三角形ABD与三角形ADC与三角形AFC的面积相等，∴菱形ADCF的面积等于三角形ABC的面积为24．答：菱形ADCF的面积为24．15．解：（1）∵∠ACB＝90°，∠B＝30°，∴∠CAB＝60°，∵CD⊥AB，∴∠ADC＝90°，∴∠ACD＝30°，∵AF平分∠CAB，∴∠CAF＝∠BAF＝30°，∴CE＝AE，过点E用EH垂直于AC于点H，∴CH＝AH∵AC＝6，∴CE＝2答：CE的长为2；（2）∵FG⊥AB，FC⊥AC，AF平分∠CAB，∴∠ACF＝∠AGF＝90°，CF＝GF，在Rt△ACF与Rt△AGF中，AF＝AF，CF＝GF，∴Rt△ACF≌Rt△AGF（HL），∴∠AFC＝∠AFG，∵CD⊥AB，FG⊥AB，∴CD∥FG，∴∠CEF＝∠EFG，∴∠CEF＝∠CFE，∴CE＝CF，∴CE＝FG，∴四边形CEGF是菱形。

第十八章：私教业务基础单选题 ( 共21题)第1题 (分值：10分)销售那些成果（如减重或备战赛事）明确的私教课程的优势是什么？A：有助于提升客户的动机，因为这些私教训练方案一般都能保证取得成功B：有助于淘汰那些不太可能长期坚持参加运动方案的客户C：允许私人教练在同一运动方案中同时训练多名客户，有助于节省时间与精力D：有助于客户坚持参加运动方案，因为客户开始运动方案时便已具备明确的运动目标第2题 (分值：10分)下列哪一项不属于企业规划中营销计划的关键内容？A：私教培训业务的需求B：提供的训练类型或训练品牌C：关于私教培训益处的宣传计划D：企业准入障碍第3题 (分值：10分)下列属于直属员工不利条件的一项是？A：私人教练必须按季度缴纳税费B：私人教练独自承担所有的营销成本C：私人教练很有可能必须按照约定至少工作几个小时D：私人教练对于健身设施可能不需要任何投入第4题 (分值：10分)私人教练在编制个人预算时，推荐第一步进行_________？A：列出每月的全部开支B：列出每月的全部收入C：确定每课堂的收费金额D：确定每周的培训次数第5题 (分值：10分)下列哪一项提问体现的是私人教练专注于客户的需求？A：“此前阻碍您实现目标的因素是什么？”B：“对于小组私教培训课产生的友情，您感兴趣吗？”C：“您觉得我们的私教服务怎么样？”D：“对于我们提供的减重训练方案，您是否感兴趣？”第6题 (分值：10分)教练因为完成季度指标而获得一笔奖金。

请问该私人教练是直接雇员还是独立合同工的可能性更大？A：直属员工B：独立合同工第7题 (分值：10分)在财务方面，小组私教培训对于教练和客户来说都有利。

A：正确B：错误第8题 (分值：10分)私人教练应在企业规划的哪个部分识别自己的营业模式，与相同领域其他健身工作室相比有何不同与独特之处？A：执行概要B：企业介绍C：经营计划D：营销计划第9题 (分值：10分)私人教练进行SWOT分析时列出下面这一条：“该健身俱乐部无法满足当前潜在私教客户的数量需求”，请问，这条分析属于？A：优势B：缺点C：机会D：风险第10题 (分值：10分)私人教练使用下列哪种策略吸引潜在新客户的效果最差？A：每周教几种团体运动课B：针对流行的健身话题每月提供一堂免费赠送的讨论课C：张贴一份充满个人运动成就的教练简历D：为当地的赛跑项目提供一堂免费的团体训练课第11题 (分值：10分)如果潜在客户不能将自己的时间调整至与教练的时间一致，最好的办法是？A：教练应调整自己的时间安排以便与客户的时间安排相符B：教练应该让客户知道自己无法提供培训C：教练应制定一份客户能够独立执行的运动方案D：教练应将此客户介绍给相同健身房的其他教练第12题 (分值：10分)让朋友或家庭成员直接向你支付私教培训服务费（而不是通过健身房收费）对于收入是一种良好的补充。

第18章 色谱法导论部分习题解答18-1、答：利用待分离的各种组分在两相间的分配系数、吸附能力等亲和能力的不同而进行分离的方法（也叫层析法或色层法）速差迁移是因为不同组分在两相间的分配系数不同而引起的。

按照)1(ms m R V V K t t +=可见，速差迁移取决于色谱热力学因素，包括固定相与流动相的性质与组成，组分性质以及固定相与流动相的体积比。

分子离散是因为分子在色谱分离过程中存在涡流扩散、纵向扩散和传质阻力造成的，按照速率方程可知，分子离散取决色谱动力学因素，包括填料颗粒大小、填充均匀程度、流动相流速、柱温、分子扩散系数、固定液膜厚度、以及色谱柱长度、形状和色谱系统死体积等因素。

18-5．解：（1）由题可知，各组分保留时间和色谱体系死时间分别为：t A = 18.0 min, t B = 25.0 min, t M = 2.0 min所以，组分A 和B 的调整保留时间分别为：t A ΄= t A – t M = 16.0 min ；t B ΄ = t B - t M =23.0 min所以，B 组分相对于A 的相对保留值为：438.11623//,===A B AB t t α （2）因为)1(k t t M R +=，所以MR M R t t t t k '1=-= 所以，A 组分的保留因子为：0.80.20.16'===M A A t t k B 组分的保留因子为：5.110.20.23'===M B B t t k （3）因为组分在流动相中的停留时间等于流动相在柱中的停留时间，分子在固定相的平均时间等于组分的调整保留时间，所以B 组分在流动相和固定相的停留时间分别为：0.2,==M m B t t min ； 0.23/,==B s B t t minB 组分在流动相的停留时间占保留时间的分数为：%0.80.250.2= B 组分在固定相的停留时间占保留时间的分数为：%0.920.250.23=18-9答：影响色谱峰区域扩张的因素包括填料颗粒大小、填充均匀程度、流动相流速、柱温、分子扩散系数、固定液膜厚度以及色谱柱长度、形状和色谱系统死体积等因素。

本章复习思考题1．试述内部审计的定义与特征。

答：一、内部审计的定义中国《审计署关于内部审计工作的规定》对内部审计的定义为：“内部审计是独立监督和评价本单位及所属单位财政收支、财务收支、经济活动的真实、合法和效益的行为，以促进加强经济管理和实现经济目标。

”国际内部审计师协会（IIA）认为，“内部审计是一种独立、客观的确认（Assurance）和咨询（Consulting）活动，旨在增加价值和改善组织运营。

它通过应用系统的、规范的方法，评价并改善风险管理、控制和治理过程的效果，帮助组织实现其目标。

”虽然对内部审计的定义部完全系统，但均包含以下要点：（一）内部审计的独立性要求独立性是审计的本质特征。

内部审计机构在实施审计过程中仍然要保持其独立性，但内部审计的独立性比外部审计要弱。

由于内部审计机构属于本部门、本单位的内部机构，与同属于本部门、本单位的被审计单位有着关联关系，因而只具有相对独立性。

（二）内部审计的职能内部审计只具有经济监督与评价职能，不具有经济鉴证职能。

这是因为内部审计机构与被审计单位同属于一个部门或单位，在外人看来，不具有形式上的独立性，因而其签发的审计报告对外就不具有经济鉴证作用。

在审计职能的侧重点方面，内部审计应当侧重于经济评价职能。

（三）内部审计的范围内部审计的范围只能局限于本部门、本单位及其所属单位内部。

（四）内部审计的对象内部审计的对象是本单位及所属单位内部受托经济责任履行情况，即本单位及所属单位为履行内部受托经济责任而发生的财务收支活动及其相关经济活动的真实性、合法性和效益性以及相关经济资料的合法性、正确性和公允性。

（五）内部审计根本目的内部审计的根本目的是促进本部门、本单位将其经济管理和实现经济目标。

2．内部审计机构应当履行哪些职责？应当赋予内部审计机构哪些职权？答：为充分发挥内部审计的职能，实现内部审计的根本目标，内部审计机构应当在本单位主要负责人或者权力机构的领导下，在本部门、本单位内部履行下列职责：1．开展财政财务审计，即对本单位及所属单位（含占控股地位或者主导地位的单位，下同）的财政收支、财务收支及其有关的经济活动进行审计；2．开展资金管理审计，即对本单位及所属单位预算内、预算外资金的管理和使用情况进行审计；3．开展经济责任审计，即对本单位内设机构及所属单位领导人员的任期经济责任进行审计；4．开展固定资产投资审计，即对本单位及所属单位固定资产投资项目进行审计；5．开展内部控制审计与风险管理审计，即对本单位及所属单位内部控制制度的健全性和有效性以及风险管理进行审计；6．开展管理审计与效益审计，即对本单位及所属单位经济管理和效益情况进行审计；7．开展其他审计，即法律、法规规定和本单位主要负责人或者权力机构要求办理的其他审计事项。