圆和曲面立体的透视画法

绘画中，圆形、圆柱体以及球体等物体的透视表现关系再绘画中，我们经常会遇到圆、圆柱体以及球体等类似的物体。

它们不像方体一样有横平竖直的边框，在圆形等物体的绘制过程中，我们通常借用方体来确定圆相关的透视，掌握其透视关系，在绘画中起到很大作品。

今天就说一下圆相关的物体的透视关系，希望能给初学者小伙伴们带来一些思路。

透视主要讲究的是近大远小。

1.正圆的透视是呈椭圆形的，当视线在视平线以下时，上半部的圆小，下半部的圆大，反之亦然。

不能画的一样大。

2.透视中的圆形最宽点你是根据视角决定的，与平面圆不同。

3.曲面物体画透视时，都借用正方形或立方体绘制。

4.距离视平线越近，圆的弧度越小，反之越大。

圆当圆面与视平线平行时，圆的形状不会变化，只有远近的透视变化。

当从不同角度观察圆面视，它的透视就成椭圆形。

孤独均匀，左右对称。

距离观察者近的距离下半部圆大，距离观察者远的距离，上半部圆小。

圆柱体在圆柱体的绘制过程中，通常借助长方形来绘制。

在长方形上下两端画出透视的正方形，作为上下两个透视圆面，注意由于透视原因，下面比上面要宽，圆柱体大小随观察角度而变化。

观察圆柱体时，距离观察点越近，圆面越扁平，反之距离越远，圆面越大。

注意多观察不同角度的圆柱体变化，和一点透视、二点透视、三点透视下不同面得关系。

球体由于球体比较特殊，所以球心到表面任何一点的距离相同。

球体的绘制主要借助正方形1.先画一个平面正方形，画上辅助线，把球体的边框先画出来，慢慢修正，直到画的圆润。

2.以横着辅助线为面画出一个有透视关系的正方形，要在圆形的最中间处。

3.根据正方形的透视画出一个椭圆，该椭圆就是球体最中心的球面。

球体的透视关系主要表现在表面的明暗关系变化上，根据光源的不同，会产生不同的倾斜角度变化，越接近轮廓线，弯曲程度越大。

今天简单说了一下圆，圆柱体以及球体相关物体的透视关系，希望初学者看到能有一定的帮助，说的不对的地方也希望高手们能多多提提意见。

曲线的透视画法1、正圆与透视圆的透视关系曲线虽然种类很多，变化很大，但可归纳为两大类：一是有规则的曲线如正圆形，圆形等：二是不规则的曲线。

在规则的曲线中我们以正圆为例，知道了正圆的画法，椭圆形等也就可依此类推。

正圆的基本画法是先把圆形纳入一个方形中，在弧上找出几个点，把方形及点先画在透视图中，然后再依照各点的位置用曲线仔细将他们连接起来，就可以画出一个透视的圆形了。

图5,在左下方有一个正圆形，如果在这个圆形的外面画上四根直线使它成为一个正方形，这时圆形就有四个点与正方形相接触，如图1,3,5,7四点，这四个点在正方形内的十字线上，如果从方形的四个角作对角交叉线，这时圆形在这交叉线上又有四个点，如2,4,6,8，透视中画圆形的方法就是利用这八个点连接成的。

步骤如下：先画一个方形的透视形状，同时作对角交叉线。

在交叉处作十字线，这十字线与方形相接触的地方就是1,3,5,7四个点的位置。

从平面图中将2，8两点用垂直线引上去与透视方形的横线相接，得2‘,8’,两点。

从2‘,8’两点对心点作直线，它与交叉线相接的地方就是2,4,6,8四点，在用曲线仔细地将这八个点连接起来，留下来地就是一个透视圆形了。

并不一定每画一个圆形都必须先画一个平面图然后再画透视图地，它还有较简便地方法，因为先画平面的目的是根据它来找2‘,8’两点的位置，如果有一个简便的方法也可以找出这两个点的位置来，就可以不必先画平面图了，这个方法如图中右方的步骤：先画透视的方形，再画对角交叉线及十字线，以方形横边的四分之一为长度，既AC的长度，在c点处画一垂直线得D点，既CD等于AC，以B点为圆心BD为半径画一半圆弧，它与横边相接得地方就是2,8两个点得位置，有了这两点，接下来就可以按照上面所说得方法来完成一个透视得圆形了。

2、认识圆在视点左，中，右不同位置的变化关于圆形的画法除了上面所讲的基本方法外，还有一些事项必须同时认识清楚，在作画时才不致于发生错误：正圆形在透视中变成一个椭圆形的形状，它的形状是上半圆较小下半圆较大，因为下半圆距离画面近而上半圆距离画面远的原因，因此，不能画成相等的大小，在描一个透视的圆形时，一定要使弧线行进的均匀自然，特别是两个尖端不能太尖，也不能太方。

圆和一般曲线的透视圆和一般曲线的透视一．圆周的透视1．圆周所在平面与画面平行见图10-35，此时圆周的透视仍位圆周，圆心的透视即为所得透视圆周的圆心，但透视圆周的直径随圆周所在平面到画面的距离变化。

求出圆周上任意一点的透视，即可定出透视圆周的半径。

当圆在画面上时，其透视与圆周本身重合。

图4-1种圆心O及圆心O1的连线与画面垂直，两圆半径相等并均与画面平行，且其中一圆在画面上。

对画面后的圆，求出其圆心O1的透视O10及水平直径上A点的妥善A0，则O10A10即为该圆的透视半径。

2．圆周所在平面与基面平行一般情况下水平圆的透视是椭圆，通常先作出圆周的外切正方形的透视，然后用八点法作图。

见图10-36所示，圆在基面上，作出该圆的外切正方形ABCD，且使AB（或CD）与基线平行，这样可用一点透视法作图。

图中，A0B0C0D0是圆周外切正方形的透视，1050和3070是圆周中一对相互垂直的直径的透视，它们的交点O0是圆心的透视，但它不是椭圆的中心。

10、30、50、70为椭圆上的四点，可如图所示的方法，以A0B0为直径作一半圆，定出对角线A0C0和B0D0上点20、40、60、80即为椭圆上四点。

光滑连接10、20、30、40、50、60、70、80即得椭圆。

图10-35 与平面平行的圆的透视图10-36 一点透视法画水平圆的透视当图形较小时，作出与圆外切的正方形的透视，徒手画出内切椭圆即可。

若将与圆周外切的正方形的对边画成与画面倾斜，则正方形的两对平行边都有灭点，如图10-37所示，可采用两点透视法作图，此时不能直接利用AB的透视，A0B0作图。

在基线OX上取B1点使A0B1等于AB实长，以A0B1为直径作一半圆，利用量点法作图，求出对角线上的四点2、4、6、8的透视20、40、60、80，光滑连接10、20…70、80即得透视椭圆。

图10-37 两点透视法画水平圆的透视图10-38 铅直圆的透视3．圆周所在平面与基面垂直一般情况下与基面垂直的圆其透视为椭圆，也可用八点法作图。

几何体的透视原理透视的基本术语:1，视平线：就是与画者眼睛平行的水平线。

2，心点：就是画者眼睛正对着视平线上的一点。

3，视点：就是画者眼睛的位置。

4，视中线：就是视点与心点相连，与视平线成直角的线。

5，消失点：就是与画面不平行的成角物体，在透视中伸远到视平线心点两旁的消失点。

6，天点：就是近高远低的倾斜物体（房子房盖的前面），消失在视平线以上的点。

7，地点：就是近高远低的倾斜物休（房子房盖的后面），消失在视平线以下的点。

8，平行透视：就是有一面与画面成平行的正方形或长方形物体的透视。

这种透视有整齐、平展、稳定、庄严的感觉。

9，成角透视：就是任何一面都不与平行的正方形成长方形的物体透视。

这种透视能使构图较有变化。

几何体透视的画法:1﹑近大远小：近大远小是视觉自然现象，正确利用这种性质有利于表现物体的纵深感和体积感，从而在二维的画面上来表现出三维的体积空间。

2﹑近实远虚：由于视觉的原因，近处的物体感觉会更清晰，而远处的物体感觉会有些模糊，这一现象在绘画中也经常用来表现物体的纵深感。

事实上，在绘画过程中，往往会对近实远虚更加以强调。

（另外应注意的是：并非在所有的绘画过程中都遵守“近实远虚”这一规则，在一幅作品中主与次的关系往往更为重要，主体物的实和次体物的虚是更好的视觉导向，这也是艺术优于现实的取舍和区别，）在素描结构中最基本的形体是立方体。

素描时，大多是以对三个面所进行的观察方法来决定立方体的表现。

另外，利用面与面的分界线所造成的角度，也能暗示出物体的深度，这就涉及到透视规律。

一点透视就是说立方体放在一个水平面上，前方的面（正面）的四边分别与画纸四边平行时，上部朝纵深的平行直线与眼睛的高度一致，消失成为一点，而正面则为正方形。

两点透视就是把立方体画到画面上，立方体的四个面相对于画面倾斜成一定角度时，往纵深平行的直线产生了两个消失点。

在这种情况下，与上下两个水平面相垂直的平行线也产生了长度的缩小，但是不带有消失点。

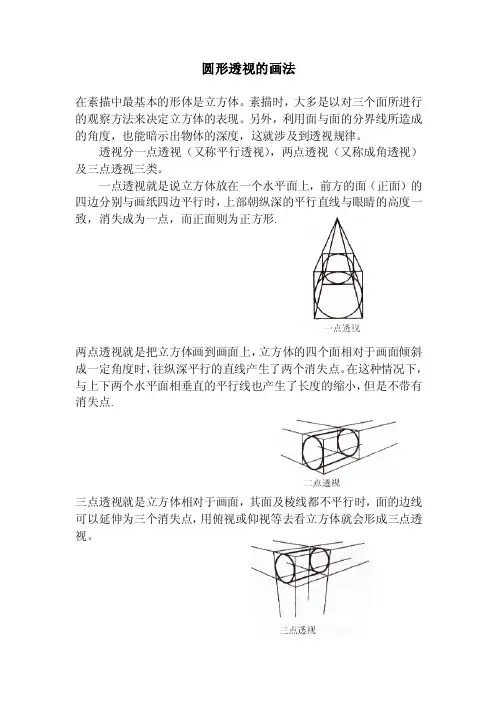
圆形透视的画法在素描中最基本的形体是立方体。

素描时，大多是以对三个面所进行的观察方法来决定立方体的表现。

另外，利用面与面的分界线所造成的角度，也能暗示出物体的深度，这就涉及到透视规律。

透视分一点透视（又称平行透视），两点透视（又称成角透视）及三点透视三类。

一点透视就是说立方体放在一个水平面上，前方的面（正面）的四边分别与画纸四边平行时，上部朝纵深的平行直线与眼睛的高度一致，消失成为一点，而正面则为正方形.两点透视就是把立方体画到画面上，立方体的四个面相对于画面倾斜成一定角度时，往纵深平行的直线产生了两个消失点。

在这种情况下，与上下两个水平面相垂直的平行线也产生了长度的缩小，但是不带有消失点.三点透视就是立方体相对于画面，其面及棱线都不平行时，面的边线可以延伸为三个消失点，用俯视或仰视等去看立方体就会形成三点透视。

透视图中凡是变动了的线称变线，不变的线称原线，要记住近大远小，近实远虚的规律。

前面所讲的立方体透视图法适用全部物体，本节就说明一下圆及圆柱体透视，分解如下：一、曲线透视的概念平行透视，成角透视，倾斜透视，我们在研究这三种透视时都是通过直线来描绘，主要是用来研究人为景观的某些空间关系，因而我们又把这三种透视统称为直线形体透视。

而在无限复杂的大自然中，在日常生活中除了直线形体以外，还存在大量的非直线形体，即曲线形体，我们把这种形体透视称为曲线透视。

曲线在一个平面内的叫做平面曲线。

曲线在空间中的叫立体曲线，如我们常见的螺旋线、螺旋楼梯等，这种曲线不常见，因而不作具体研究。

平面曲线和立体曲线又分为规则曲线和不规则曲线。

规则曲线如圆、椭圆、抛物线。

不规则曲线是指无规律的任意曲线，如山、水、云、小路、人物、图案花纹、梯田等，多表现为自然形态，也正因为其毫无规律可循，所以中国山水画的透视才选择散点透视法，这也是一个重要原因。

二、透视圆的特征1、形并非对称的椭圆（图1），AB∠BC,即透视圆.图1前后远近不对称，近的半圆较大，远的半圆较小，画透视圆时，弧线一定要均匀自然，特别是透视圆两端要弯曲光滑，不能太突或太圆。

圆面及圆形物体的透视：圆形透视的画法：先画一个立方体的透视形，正面画出两条对角线，再画两条对角线相交的四个点，共八个点，将八个点连接成圆。

圆形透视距我们近的半圆大，远的半圆小，弧线要均匀自然，两端不能画得太尖或太圆。

（如下图）画圆形物体的方法：步骤一：画出物体高和宽的比例。

步骤二：根据回旋组合体的规律，画出中轴线及对称点的平行线，画出物体外形特征。

步骤三：在每条平行线上标出近大远小的点，画出圆面透视。

步骤四：调整线条的近实远虚的关系：（如下图所示）以下是圆柱体和圆锥体的画法：正六面体的平行透视：在正六面体上下、前后、两側三个面中，只要有一个面与画面平行，同时有一面与地面平行的正方面体透视就叫“平行透视”。

（它只有一个消失点）正六面体的平行透视最少看见一个面，最多看见三个面。

正六面体作图的线段有水平线、垂直线和消失线，三组边线的透视方向是：四条边线与画面平行、有四条边线与画面垂直，有四条边线向主点消失。

如下图：正六面体的成角透视：当正六面体的一个面与地面平行，其左右各竖立饿侧面与画面成角时就叫“成角透视”（它有两个消失点）。

正六面体三组边线的透视方向是：有四条边线与画面垂直，有四条边线消失于左余点，有四条边线消失于右余点。

（如下图所示）方形景物的透视：由于我们的视觉关系，所看到的同样宽窄的道路、田野、越远越窄，同样宽窄的树木、电线竿、越远越小，最后消失不见了，最后消失不见了，我们把这种现象称之为“透视现象”。

我们画几何体、画静物、画人物、画风景等都必须掌握近大远小的透视规律，才能准确的描绘物体在空间各个位置的透视变化，使物体具有空间感、纵深感和距离感。

(如下图)。