美赛建模准备~
- 格式:ppt
- 大小:9.60 MB
- 文档页数:52

数学建模美赛题解一、题目背景在美赛中,参赛队伍通常要面对一些具有现实背景的问题,这些问题可能涉及工程、社会、经济等各个领域。
例如,某年度的美赛题目可能是关于环境保护、交通规划、金融风险等方面的问题。
二、问题分析在解题之前,参赛队伍需要先对问题进行分析。
他们需要理解问题的背景和要求,明确问题的目标和约束条件。
通过对问题的分析,可以确定问题的数学模型和求解方法。
三、建立数学模型建立数学模型是解决问题的关键步骤。
参赛队伍需要根据问题的要求,选择适当的数学工具和方法。
常用的数学模型包括线性规划模型、非线性规划模型、动态规划模型等。
建立数学模型需要将问题转化为数学表达式,并确定变量、约束条件和目标函数。
四、求解方法在建立数学模型之后,参赛队伍需要选择合适的求解方法。
常用的求解方法包括数值求解、符号求解、优化算法等。
参赛队伍需要根据问题的特点和要求,选择最合适的求解方法,并进行计算和分析。
五、结果分析在求解过程中,参赛队伍需要对结果进行分析和解释。
他们需要检查结果的合理性和可行性,并对结果进行解释。
结果分析可以帮助参赛队伍深入理解问题,并提出进一步的改进和优化方案。
六、讨论和总结在解决问题之后,参赛队伍需要进行讨论和总结。
他们可以对解题过程中遇到的困难和挑战进行讨论,并提出解决方案。
他们还可以总结解题经验和方法,为以后的问题求解提供参考。
七、实践应用数学建模在实际应用中具有广泛的应用价值。
通过数学建模,可以对现实问题进行定量分析和预测,为决策提供科学依据。
数学建模在工程、经济、医学等领域都有重要的应用。
八、结语数学建模美赛题解是一个复杂而有挑战性的过程。
参赛队伍需要通过对问题的分析、建模、求解和结果分析,最终得出合理的结论。
数学建模不仅可以提升学生的数学能力,还可以培养他们的创新思维和团队合作精神。
希望通过本文的介绍,读者对数学建模美赛有更深入的了解。


数学建模美赛队员数学建模是指运用数学工具和方法来解决实际问题,通过建立数学模型对问题进行分析和求解。
在美赛中,数学建模是一个重要的环节,需要团队成员具备一定的数学素养和建模能力。
本文将从数学建模美赛队员的角度出发,探讨数学建模的重要性、队员的要求和在比赛中的表现等方面。
一、数学建模的重要性数学建模在实际问题的解决中具有重要的作用。
它可以帮助我们理解和分析复杂的现实问题,并提供解决问题的方法和策略。
在现代科学和工程领域,数学建模已经成为一种重要的工具和方法,被广泛应用于各个领域。
无论是在经济学、物理学、生物学还是工程学等领域,数学建模都起到了不可或缺的作用。
作为一名数学建模美赛队员,首先需要具备扎实的数学基础。
数学建模涉及到多个数学分支,包括但不限于微积分、线性代数、概率论与数理统计等。
队员需要对这些数学知识有深入的理解和掌握,能够熟练运用数学工具解决实际问题。
队员需要具备良好的团队合作能力。
数学建模美赛是一个团队项目,队员之间需要紧密合作,共同解决问题。
在团队中,队员需要相互协作、相互支持,共同完成建模任务。
因此,良好的沟通能力、合作能力和团队意识是必备的素质。
队员还需要具备创新意识和问题解决能力。
数学建模涉及到实际问题的抽象和建模,需要队员具备独立思考和解决问题的能力。
队员应当能够从实际问题中找到数学模型的建立方法,提出创新的解决方案,并能够对模型进行合理的分析和求解。
三、数学建模美赛队员的表现在数学建模美赛中,队员的表现是评判成绩的重要依据。
一支优秀的数学建模队伍,应该具备以下几个方面的表现。
队员需要能够准确理解和分析问题。
在比赛中,队员面临的问题通常是复杂的、具有挑战性的。
队员需要从问题描述中准确把握问题的要求和限制条件,并能够将问题进行合理的分析和拆解。
队员需要能够建立合理的数学模型。
建模是数学建模的核心环节,队员需要能够根据问题的特点选择合适的数学模型,并能够合理地建立起模型的数学表达式。

美赛建模技巧建模前:1.多注册几个网站,便于比赛时下载论文。
2.其实没有必要去图书馆找书,因为到了比赛的时候会发现找的书基本没有用。
3.建好论文的模板。
4.对小组内各个成员按照所擅长部分进行大致的分工。
5.调整好心态,不要有太强的功利心,因为比赛中有很多客观因素,不一定付出了就会有赢得的回报,放平心态。
建模中:1.选题:(1)要按照自己擅长的部分选题。
(2)选题时间可以稍微长一点,但不要太长。
在选好题目后尽量不要更改,因为更换题目是一件很浪费时间的事情。
队员的思路要进行全面的转换。
2.思考题目:(1)由于题目是英文的,拿到题目后要把题目翻译准确,有些单词有多重含义,要考虑清楚到底是那层含义。
(2)题目要多看多分析,可以参考一些论坛或者加入建模群进行讨论,以免自己理解错题目。
(3)题目中会给出很多有用信息,要把每个方面每层意思都考虑清楚。
3.做题思路:(1)美赛中比较重视思路的创新性与严密性,队友应该大胆的讨论大胆进行创新。
越新奇的思路越好。
(2)无论思路如何,都要自圆其说,不能最后得出的结论与前面提出的假设相反。
(3)建立模型最好是用一个自己起的名字,这样会使人眼前一亮。
4.论文:(1)我们当时写论文是写出一部分中文的另一个同学进行英文翻译,由于英文水平有限,我个人认为这样还是很有用的,直接用英文写难免会因为构思语言结构而浪费时间。
(2)最好是中文论文与英文翻译一起进行,防止到最后时间不够翻译不完。
(3)摘要是很重要的部分,无论最后剩余时间还够不够,应对摘要进行细致的琢磨分析,使语言简练。
(4)论文格式一定要标准,规范。
5.其他:(1)建模期间保持适量的睡眠,美赛时间比国赛长,如果一再的熬夜脑子不清醒会降低效率。
(2)绝不要放弃,当时我们队在进行了一半卡住后曾一度想过放弃,但是最后咬咬牙坚持下来了,想想当时如果放弃真的是亏大了。
(3)不要有凑合应付的心理。

数学建模美赛(Mathematical Contest in Modeling, MCM)是一个面向大学生的国际性数学建模竞赛,旨在鼓励学生应用数学建模解决实际问题。
美赛每年一届,吸引了全球范围内的大学生参与。
以下是数学建模美赛的一般流程:### 第一阶段:报名与团队组建1. **团队组建:** 队伍通常由3名队员组成,队员之间应该具备不同的技能和专业背景,以更好地解决多方面的问题。
2. **选择题目:** 参赛团队需要选择感兴趣且有挑战性的题目。
数学建模美赛通常会提供一系列实际问题供队伍选择,这些问题跨足多个学科领域,如数学、计算机科学、经济学、生物学等。
3. **报名注册:** 参赛团队需要在规定的截止日期前完成在线报名注册。
报名通常需要提供队员信息、指导老师信息和选定的题目信息。
### 第二阶段:比赛前准备1. **学习建模技能:** 在正式比赛前,队员需要学习一些常见的数学建模技能,包括但不限于数学建模的基本流程、模型的建立与求解、报告的撰写等。
2. **准备工具和资料:** 队员需要准备好在比赛中可能用到的工具、软件和相关资料。
这可能包括数学建模软件、编程工具、参考书籍、实验数据等。
### 第三阶段:正式比赛1. **赛前说明:** 在比赛开始前,组委会通常会发布赛前说明,解释比赛规则、注意事项和评分标准。
2. **领取比赛题目:** 比赛开始后,参赛队伍将收到比赛题目。
队员需要仔细阅读并理解问题陈述,制定解决问题的计划。
3. **建模与求解:** 队员在规定的时间内进行建模与求解工作。
这一阶段包括问题分析、模型构建、数学求解、数据分析等过程。
队员需要合理地运用数学知识和建模技巧。
4. **撰写报告:** 在规定的时间内,队伍需要撰写一份完整的报告,详细阐述他们的建模过程、解决方案、结论和对问题的深刻理解。
报告要求清晰、逻辑性强、语言表达准确。
### 第四阶段:提交报告和结果公布1. **报告提交:** 比赛结束后,队伍需要按照规定的时间将他们的报告提交给组委会。

数学建模美赛比赛要求
数学建模竞赛是一个旨在培养学生解决实际问题的能力和团队合作精神的比赛。
下面是数学建模美赛的一些要求:
1. 团队组成:每个团队通常由3名或4名成员组成。
团队成员应具备各自专业领域的知识和技能,并能够有效地进行合作和交流。
2. 题目选择:参赛团队可以从官方题库中选择一个问题进行研究和建模。
问题通常会给出相关的背景信息,具体的要求和限制条件。
3. 建模过程:团队成员需要共同研究问题,收集和整理相关数据,提出问题的数学模型,并进行合理的假设和简化。
模型可以是数学方程、图表、统计分析等。
4. 数据分析:团队成员需要分析所获得的数据,运用适当的数学方法和工具进行数据处理和计算。
他们应该能够解释结果的意义,并提出合理的结论和建议。
5. 编写论文:团队需要将他们的研究成果和分析过程以论文的形式呈现。
论文应该具备清晰的逻辑结构、准确的表达和规范的格式。
6. 答辩演讲:在比赛期间,团队需要进行口头答辩演讲,向评委和其他参赛者展示他们的研究成果和思考过程。
演讲应该简洁明了、逻辑清晰,并能够回答评委的问题。
7. 时间管理:数学建模竞赛通常有严格的时间限制。
团队成员需要合理分配时间,合理安排任务,保证在规定时间内完成各个环节的工作。
数学建模美赛要求团队成员具备数学建模和分析问题的能力,能够有效合作和沟通,并在有限的时间内完成团队的研究工作。
通过这样的比赛,学生们可以提高他们的解决问题的能力,培养创新思维和团队合作精神。
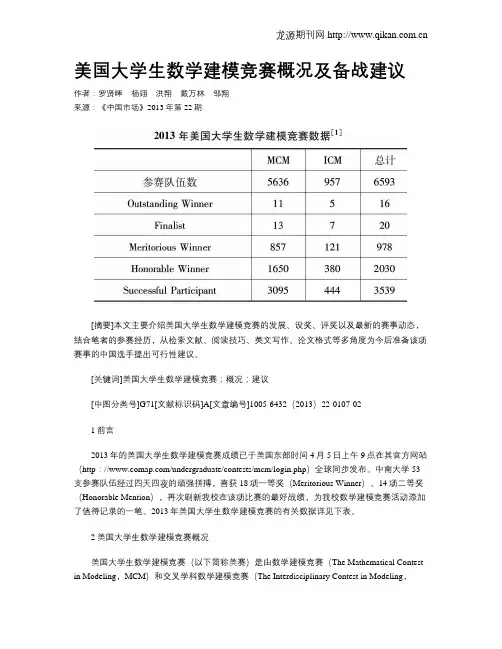
美国大学生数学建模竞赛概况及备战建议作者:罗贤晖杨翊洪翔戴万林邹翔来源:《中国市场》2013年第22期[摘要]本文主要介绍美国大学生数学建模竞赛的发展、设奖、评奖以及最新的赛事动态,结合笔者的参赛经历,从检索文献、阅读技巧、英文写作、论文格式等多角度为今后准备该项赛事的中国选手提出可行性建议。
[关键词]美国大学生数学建模竞赛;概况;建议[中图分类号]G71[文献标识码]A[文章编号]1005-6432(2013)22-0107-021前言2013年的美国大学生数学建模竞赛成绩已于美国东部时间4月5日上午9点在其官方网站(http:///undergraduate/contests/mcm/login.php)全球同步发布。
中南大学53支参赛队伍经过四天四夜的顽强拼搏,喜获18项一等奖(Meritorious Winner)、14项二等奖(Honorable Mention),再次刷新我校在该项比赛的最好战绩,为我校数学建模竞赛活动添加了值得记录的一笔。
2013年美国大学生数学建模竞赛的有关数据详见下表。
2美国大学生数学建模竞赛概况美国大学生数学建模竞赛(以下简称美赛)是由数学建模竞赛(The Mathematical Contest in Modeling,MCM)和交叉学科数学建模竞赛(The Interdisciplinary Contest in Modeling,ICM)两部分构成,由美国自然基金协会和美国数学应用协会联合成立的Consortium forMathematics and Its Applications(简称COMAP)主办,美国运筹学学会、工业与应用数学学会、数学学会等多家机构协办。
奖项设置分为:Outstanding Winner、Finalist、Meritorious Winner、Honorable Winner、Successful Participant、Unsuccessful六种,国内约定俗成地将其译为:特等奖、特等奖提名、一等奖、二等奖、成功参赛奖、未成功参赛。

美赛建模知识点总结美赛建模是指利用数学模型和算法,对美赛(Mathematical Contest in Modeling)中的实际问题进行建模和求解的过程。
美赛是全球范围内最具影响力和知名度的数学建模竞赛之一,参赛者需要在规定的时间内解决所提出的实际问题,并撰写完整的模型报告。
在美赛中,建模的过程非常重要,而建模的关键知识点也是参赛者需要掌握的重点之一。
下面将对美赛建模中的关键知识点进行总结。
1. 问题分析在美赛建模中,首先需要对所提出的实际问题进行全面的分析。
这包括了对问题的深入理解,明确问题的目标和约束条件,确定问题的关键变量和影响因素等。
同时还需要对问题的实际背景和应用领域进行了解,从而找到问题的实际意义和解决方法。
2. 数学建模数学建模是美赛中的核心环节,参赛者需要使用数学理论和方法对问题进行建模。
数学建模的关键知识点包括:微积分、线性代数、概率论与数理统计、运筹学、图论等。
参赛者需要根据实际问题的特点,选择合适的建模方法,构建数学模型,推导数学方程,进行数学分析和求解。
3. 计算机编程在美赛建模中,计算机编程是求解问题的重要手段。
参赛者需要熟练掌握一种或多种计算机编程语言,如C/C++、Python、MATLAB等。
计算机编程的知识点包括:数据结构与算法、面向对象程序设计、图形图像处理等。
通过编程实现模型的求解和仿真,对结果进行分析和展示。
4. 模型分析与评价建立数学模型后,需要对模型进行分析和评价。
这包括了对模型的合理性和可靠性进行评估,比较模型预测结果和实际数据的吻合程度,对模型的敏感性和稳定性进行分析。
同时还需要对模型的优缺点进行评价,提出改进和优化建议。
5. 模型报告撰写模型报告是美赛中的重要成果之一,参赛者需要撰写完整的模型报告,包括问题分析、数学模型构建、模型求解和分析、模型评价等内容。
模型报告的撰写需要一定的文献调研和写作技巧,能够清晰、准确地表达模型的思路和解决方法。

2024年数学建模美赛e题思路
2024年数学建模美赛E题是一个假设性的问题,因为我无法预
测未来的比赛题目。
但是,我可以向你介绍一般性的数学建模竞赛
E题的思路,希望对你有所帮助。
一般来说,数学建模竞赛E题通常是一个开放性问题,要求参
赛者结合数学模型和实际问题,提出解决方案。
在这种情况下,参
赛者需要做的第一步是理解问题,包括问题的背景、假设条件、要
解决的具体内容等。
然后,需要进行数据分析,收集相关数据并进
行整理和分析,找出数据之间的关联性和规律性。
接下来,参赛者需要选择合适的数学模型来描述问题,并进行
建模。
这可能涉及到微积分、概率统计、线性代数、差分方程等数
学知识。
建模过程中需要考虑模型的合理性、精确性和可行性。
在建立数学模型之后,参赛者需要进行模型的求解和分析。
这
可能需要借助计算机软件进行模拟和计算,得出定量的结果。
同时,也需要对结果进行合理性分析和讨论。
最后,参赛者需要总结和展示他们的建模过程和结果,包括撰
写论文、制作报告、展示PPT等形式。
在展示中需要清晰地表达问
题的解决方案、模型的建立和求解过程、结果的分析和讨论等内容。
总的来说,数学建模竞赛E题需要参赛者具备较强的数学建模
能力、问题分析能力和团队合作能力。
希望这些思路能够对你在未
来的数学建模竞赛中有所帮助。

美国大学生数学建模竞赛组队和比赛流程数学模型的组队非常重要,三个人的团队一定要有分工明确而且互有合作,三个人都有其各自的特长,这样在某方面的问题的处理上才会保持高效率。
三个人的分工可以分为这几个方面:数学员:学习过很多数模相关的方法、知识,无论是对实际问题还是数学理论都有着比较敏感的思维能力,知道一个问题该怎样一步步经过化简而变为数学问题,而在数学上又有哪些相关的方法能够求解,他可以不能熟练地编程,但是要精通算法,能够一定程度上帮助程序员想算法,总之,数学员要做到的是能够把一个问题清晰地用数学关系定义,然后给出求解的方向;程序员:负责实现数学员的想法,因为作为数学员,要完成大部分的模型建立工作,因此调试程序这类工作就必须交给程序员来分担了,一些程序细节程序员必须非常明白,需要出图,出数据的地方必须能够非常迅速地给出;ACM的参赛选手是个不错的选择,他们的程序调试能力能够节约大量的时间,提高在有限时间内工作的工作效率;写手:在全文的写作中,数学员负责搭建模型的框架结构,程序员负责计算结果并与数学员讨论,进而形成模型部分的全部内容,而写手要做的。
就是在此基础之上,将所有的图表,文字以一定的结构形式予以表达,注意写手时刻要从评委,也就是论文阅读者的角度考虑问题,在全文中形成一个完整地逻辑框架。
同时要做好排版的工作,最终能够把数学员建立的模型和程序员算出的结果以最清晰的方式体现在论文中。
一个好的写手能够清晰地分辨出模型中重要和次要的部分,这样对成文是有非常大的意义的。
因为论文是评委能够唯一看到的成果,所以写手的水平直接决定了获奖的高低,重要性也不言而喻了。
三个人至少都能够擅长一方面的工作,同时相互之间也有交叉,这样,不至于在任何一个环节卡壳而没有人能够解决。
因为每一项工作的工作量都比较庞大,因此,在准备的过程中就应该按照这个分工去准备而不要想着通吃。
这样才真正达到了团队协作的效果。
比赛流程:对于比赛流程,在三天的国赛里,我们应该用这样一种安排方式:第一天:定题+资料查找;第二天:模型框架+部分求解(数学员为主);第三天:全面求解+论文初稿(程序员+写手);第四天:摘要+反复修改全文(一起讨论);当然,很少有队伍能如此顺利地完成这些工作,所以一旦出现工作的落后或超前,都不要惊慌或者沾沾自喜,往往是经历了绝处逢生,才能迸发出积极的思想,最终完成一篇青春无悔的论文!笔者与大家共勉!。

2023美赛建模经历总结引言我参与了2023年的美赛建模比赛,并在比赛中取得了一些经验和收获。
在本文档中,我将总结我的经验,并分享我的观点和方法。
赛前准备参加美赛建模比赛需要进行一系列的准备工作。
首先,我们需要熟悉比赛的规则和要求。
这包括了解比赛的主题、时间要求、评分标准等等。
其次,我们需要组队,并明确每个队员的职责和分工。
每个队员都应该负责自己擅长的领域,这样可以充分发挥大家的优势。
最后,我们还需要制定一个详细的计划,以确保我们按时完成各个阶段的任务。
队内协作队内协作是美赛建模比赛中至关重要的一环。
在我们的队伍中,我们通过定期的会议和讨论来促进团队合作。
每个队员都有机会分享自己的想法和观点,并提出改进的建议。
我们建立了一个有效的沟通渠道,以便及时解决问题和调整计划。
此外,我们还利用在线协作工具共享文件和资源,方便队员之间的合作和交流。
数据收集和处理在比赛中,数据收集和处理是一个重要的环节。
我们需要收集相关的数据,并进行合理的处理和分析。
对于大规模的数据集,我们采用了并行计算和分布式处理的方法,以提高效率和准确性。
此外,我们还利用数据可视化工具,将数据以图表的形式展示出来,使得我们可以更直观地理解和分析数据。
模型构建和验证在美赛建模比赛中,我们需要构建一个有效的模型,并对其进行验证。
在模型构建过程中,我们采用了多种方法和技术。
我们首先对数据进行预处理,包括数据清洗、特征提取等等。
然后,我们尝试了多个模型,并比较它们的性能。
最后,我们选择了一个最好的模型,并进行了交叉验证和参数调优,以确保模型的准确性和稳定性。
结果分析和总结在比赛结束后,我们对结果进行了分析和总结。
我们回顾了我们的方法和策略,并评估了我们的模型的性能。
我们还比较了我们的结果和其他队伍的结果,以了解我们在比赛中的竞争力。
最后,我们总结了我们的经验和教训,并提出了改进的建议。
结论通过参与2023年的美赛建模比赛,我学到了很多知识和经验。
如何准备美赛数学模型:数学模型的功能大致有三种:评价、优化、预测。
几乎所有模型都是围绕这三种功能来做的。
比如,2012年美赛A题树叶分类属于评价模型,B题漂流露营安排则属于优化模型。
对于不同功能的模型有不同的方法,例如评价模型方法有层次分析、模糊综合评价、熵值法等;优化模型方法有启发式算法(模拟退火、遗传算法等)、仿真方法(蒙特卡洛、元胞自动机等);预测模型方法有灰色预测、神经网络、马尔科夫链等。
在数学中国、数学建模网站上有许多关于这些方法的相关介绍与文献。
软件与书籍:软件一般三款足够:Matlab、SPSS、Lingo,学好一个即可。
书籍方面,推荐三本,一本入门,一本进级,一本参考,这三本足够:《数学模型》姜启源谢金星叶俊高等教育出版社《数学建模方法与分析》Mark M. Meerschaert 机械工业出版社《数学建模算法与程序》司守奎国防工业出版社入门的《数学模型》看一遍即可,对数学模型有一个初步的认识与把握,国赛前看完这本再练习几篇文章就差不多了。
另外,关于入门,韩中庚的《数学建模方法及其应用》也是不错的,两本书选一本阅读即可。
如果参加美赛的话,进级的《数学建模方法与分析》要仔细研究,这本书写的非常好,可以算是所有数模书籍中最好的了,没有之一,建议大家去买一本。
这本书中开篇指出的最优化模型五步方法非常不错,后面的方法介绍的动态模型与概率模型也非常到位。
参考书目《数学建模算法与程序》详细的介绍了多种建模方法,适合用来理解模型思想,参考自学。
分工合作:数模团队三个人,一般是分别负责建模、编程、写作。
当然编程的可以建模,建模的也可以写作。
这个要视具体情况来定,但这三样必须要有人擅长,这样才能保证团队最大发挥出潜能。
这三个人中负责建模的人是核心,要起主导作用,因为建模的人决定了整篇论文的思路与结构,尤其是模型的选择直接关系到了论文的结果与质量。
对于建模的人,首先要去大量的阅读文献,要见识尽可能多的模型,这样拿到一道题就能迅速反应到是哪一方面的模型,确定题目的整体思路。
美赛准备流程
美赛准备流程包括以下步骤:
1. 组建队伍:寻找具有不同能力的队友,如构建模型、计算机编程、论文写作和英语能力。
核心是合理分工和默契程度。
2. 学习理论知识及软件使用:需要学习建模相关的知识,例如高数、线代、概率论理论知识,各类数学建模算法。
同时,要学会使用软件,如MATLAB、LINGO、Python等编程软件,Visio等绘图软件,以及LaTeX
等排版软件。
3. 阅读优秀论文,借鉴写作方法:在正式比赛前应大量阅读往年的优秀论文,将论文分为摘要、问题分析、模型建立、求解与结果分析四个部分,以五个步骤解读优秀论文:学习优秀论文中用概括性语言、流程图、计算图来表述模型求解过程的方法,思考求解的结果与绘制的图像、表格之间的联系。
4. 报名参加美赛:通过全英文的官方网址进行报名。
注意报名截止时间和比赛时间,尽量避免在春节期间参赛。
5. 提交论文:尽量提前2~3小时提交论文,避免对方邮箱拥堵。
以上信息仅供参考,具体流程和要求可能根据年份和实际情况有所不同。
一、概述1.1 美赛数学建模竞赛美国大学生数学建模竞赛(MCM/ICM)作为世界上最具影响力的大学生自然科学建模竞赛之一,吸引了来自全球各地的大学生参与。
该竞赛旨在锻炼参赛者的数学建模、计算机编程和论文撰写能力,培养他们的跨学科综合素质,具有非常广泛的参与裙体。
1.2 数学建模的适用范围数学建模是将问题抽象化并用数学语言表达,通过建立数学模型来解决实际问题的学科。
而数学建模在实际生活、科研和工程领域中有着广泛的应用。
在不同的领域和问题中,数学建模都能起到重要作用。
二、数学建模的适用范围2.1 工业工程与优化在工业生产中,通过建立数学模型和优化算法,可以使生产过程更加高效和节能。
生产调度、供应链优化、产能规划等领域都离不开数学建模的应用。
2.2 金融与风险管理在金融衍生品定价、风险管理、投资组合优化等方面,数学建模能够准确地捕捉市场变化、预测金融产品的价格波动,并提供有效的风险控制策略。
2.3 环境科学与气候变化气候变化对环境和人类社会都产生了重大影响,而数学建模可以帮助人们更好地理解气候变化的规律,并制定政策和措施应对气候变化带来的挑战。
2.4 医学与生物信息学在医学领域,数学建模能够辅助疾病的预测、诊断和治疗规划,为生物信息学的数据分析和生物医学工程提供强有力的支持。
三、数学建模的具体建模过程3.1 问题理解和问题分析在进行数学建模前,首先需要对问题有清晰的认识和理解,理解问题的背景、影响因素和要解决的具体目标。
通过对问题进行分解和分析,确定建模的方向和重点。
3.2 模型假设和参数选择在建立数学模型时,需要对问题的环境和条件进行假设,并根据实际情况选择相应的参数值。
合理的假设和参数选择对于模型的准确性具有重要影响。
3.3 模型建立和数学表达在完成问题理解和假设参数后,需要选择适当的数学方法来表达模型。
常用的数学方法包括微积分、概率统计、线性代数等,视具体问题而定。
3.4 模型求解和结果分析完成模型建立后,需要通过数学工具进行求解,并分析结果的合理性和可行性。
数学建模知识——之参考资料一、数学建模竞赛中应当掌握的十类算法1.蒙特卡罗算法该算法又称随机性模拟算法,是通过计算机仿真来解决问题的算法,同时可以通过模拟可以来检验自己模型的正确性,是比赛时必用的方法。
2.数据拟合、参数估计、插值等数据处理算法比赛中通常会遇到大量的数据需要处理,而处理数据的关键就在于这些算法,通常使用Matlab作为工具。
3.线性规划、整数规划、多元规划、二次规划等规划类问题建模竞赛大多数问题属于最优化问题,很多时候这些问题可以用数学规划算法来描述,通常使用Lindo、Lingo软件实现。
4.图论算法这类算法可以分为很多种,包括最短路、网络流、二分图等算法,涉及到图论的问题可以用这些方法解决,需要认真准备。
5.动态规划、回溯搜索、分治算法、分支定界等计算机算法这些算法是算法设计中比较常用的方法,很多场合可以用到竞赛中。
6.最优化理论的三大非经典算法:模拟退火法、神经网络、遗传算法这些问题是用来解决一些较困难的最优化问题的算法,对于有些问题非常有帮助,但是算法的实现比较困难,需慎重使用。
7.网格算法和穷举法网格算法和穷举法都是暴力搜索最优点的算法,在很多竞赛题中有应用,当重点讨论模型本身而轻视算法的时候,可以使用这种暴力方案,最好使用一些高级语言作为编程工具。
8.一些连续离散化方法很多问题都是实际来的,数据可以是连续的,而计算机只认的是离散的数据,因此将其离散化后进行差分代替微分、求和代替积分等思想是非常重要的。
9.数值分析算法如果在比赛中采用高级语言进行编程的话,那一些数值分析中常用的算法比如方程组求解、矩阵运算、函数积分等算法就需要额外编写库函数进行调用。
10.图象处理算法赛题中有一类问题与图形有关,即使与图形无关,论文中也应该要不乏图片的,这些图形如何展示以及如何处理就是需要解决的问题,通常使用Matlab进行处理。
二、数学软件的主要分类有哪些?各有什么特点?数学软件从功能上分类可以分为通用数学软件包和专业数学软件包,通用数学包功能比较完备,包括各种数学、数值计算、丰富的数学函数、特殊函数、绘图函数、用户图形届面交互功能,与其他软件和语言的接口及庞大的外挂函数库机制(工具箱)。