生活中的透视原理(精选)
- 格式:ppt
- 大小:1.58 MB
- 文档页数:37

一、透视图物体上各点与视点相连,形成的各个直线与画面的交点,为物体在画面上的透视点,将这些透视点连接,便形成透视图。
二、透视术语●面✧基面/地面(G.P)—放置物体的水平面,通常是指地面。
如下图1✧画面(P.P)—画者于被画物体之间置一假想透明平面,物体上各关键点聚向视点的视线被该平面截取(即与该平面相交),并映现出二维的物体透视图。
这一透明平面被称为画面。
如下图2✧视平面(H.P)—视点、视线和视中线所在的平面为视平面;视平面始终垂直于画面;平视的视平面平行于基面;俯视、仰视的视平面倾斜或垂直于基面。
如下图3:●线✧视平线(H.L)—视平面与画面的交线。
如图4:✧地平线/基线(G.L)—画面于基面/地面的交线。
如图5:✧视中线—视点引向正前方的视线为视中线(即从视点做画面的垂线)(视点引向物体任何一点的直线为视线,)。
平视的视中线平行于基面;俯、仰视的视中线倾斜或垂直于基面。
如图5:✧真高线—在透视图中能反映物体空间真实高度的尺寸线。
✧变线—凡是与画面不平行(包括与画面垂直的线段)的直线均为变线,此类线段在视圈内有时会消失。
✧原线—凡是与画面平行的直线均为原线,此类线段在视圈内永不消失。
原线按其对视平面(视平线)的垂直、平行、倾斜关系,分为垂直原线、平行原线和倾斜原线三种✧消失线/灭线—变线上各点与消失点连接形成的线段(物体变线的透视点是落在灭线上的)。
参考下图:●点✧视点(E)—画者眼睛的位置,视点决定视平面;视平面始终垂直于画面。
✧心点(O)—视中线与画面的交点为心点;心点是视点在画面上的正投影,位于视域的正中点,是平行透视的消失点。
如图6✧距点—在视平线上心点两边,两者和心点的距离和画者与心点的距离相等,凡是与画面呈45°角的变线一定消失于距点。
✧余点—在心点两边,与画面呈任意角度(除45°(距点)和90°(心点))的水平线段的消失点,它是成角透视的消失点。

透视原理在生活中的应用1. 什么是透视原理透视原理是一种视觉效果,通过模拟人眼的观察方式,将三维物体转化为二维平面的方法。
它基于我们的视觉系统,在处理远近关系时,会自动调整物体的大小和形状。
透视原理广泛应用于绘画、摄影、建筑设计、游戏开发等领域,为我们呈现出真实的视觉体验。
2. 透视原理在绘画中的应用•创造深度感通过使用透视原理,绘画可以呈现出三维物体的深度感。
在绘画中,远处的物体会比近处的物体更小,因为远处的物体离我们的视线更远,所以我们会认为它们更远。
同时,透视原理还可以通过处理光影、阴影和明暗等效果,使画面更加逼真。
•增强立体感透视原理可以使绘画作品更富有立体感。
通过在画面中使用透视线或消失点,可以让观者感受到深入画面的感觉。
透视原理还可用于绘制建筑、城市景观等复杂的背景,使整个画面更加有层次感。
•研究物体的形状和结构透视原理在绘画中的应用不仅仅是为了创造视觉效果,还可以帮助艺术家更好地理解物体的形状和结构。
通过观察和绘制透视,可以更好地理解物体的立体形态,从而更好地表现物体的细节和特点。
3. 透视原理在摄影中的应用•营造景深效果在摄影中,通过合理运用透视原理,可以营造出景深效果,即将画面分为前景、中景和背景。
远离摄像机的物体将显得更小,使画面更具有层次感。
这种效果可以使照片更加吸引人,增加观赏性。
•拍摄建筑物和街景透视原理在摄影中尤其适用于拍摄建筑物和街景。
通过运用透视原理,可以更好地表现建筑物立体感,展示出建筑的壮观和美感。
透视原理还可以帮助摄影师捕捉到街道的远近关系,使照片更加生动。
•细节表现透视原理可以帮助摄影师更好地捕捉物体的细节。
通过合理运用透视线和消失点,可以将物体的细节表现得更加立体和清晰。
透视原理还可以使人物在照片中更加突出,从而增强照片的视觉效果。
4. 透视原理在建筑设计中的应用•创造空间感透视原理在建筑设计中是非常重要的。
建筑师可以通过运用透视原理来创造出室内和室外的空间感。


近大远小的两点透视(成角透视)原理)两点透视,也称为成角透视,是一种常见的绘画和设计技巧,用于创造具有深度和三维感的画面。
它通过在画面中设置两个消失点来展现物体的三维形态,使得画面更加生动和有趣。
以下是两点透视的原理和运用方法的详细解析。
一、两点透视的原理1. 消失点:两点透视中的消失点是指物体在远处与画面相交的点,这些点在画面中看不到,但它们决定了物体的形状和大小。
在两点透视中,有两个消失点,分别位于画面的两侧。
2. 视平线:视平线是画面中与地面平行的线,它决定了画面的垂直方向。
在两点透视中,视平线通常位于画面的中间位置,使得画面保持平衡。
3. 斜线:在两点透视中,物体的边缘线通常是斜线,它们连接消失点与物体本身的顶点。
斜线的角度决定了物体在画面中的倾斜程度。
4. 近大远小:这是两点透视中最基本的规律,意味着物体在画面中越靠近观众,它们看起来越大;而物体在画面中越靠近消失点,它们看起来越小。
这种效果creates a sense of depth and three-dimensionality in the composition.二、两点透视的运用方法1. 构图:首先,确定画面的视平线和两个消失点的位置。
通常,消失点位于画面的两侧,视平线位于画面的中间。
然后,根据画面的需求和主题,安排物体在画面中的位置和角度。
2. 绘制线条:根据物体的形状和角度,绘制出物体的边缘线。
这些线条通常是斜线,连接消失点与物体本身的顶点。
在绘制过程中,要注意物体的近大远小关系,以及线条的透视变化。
3. 添加细节:在基本线条的基础上,添加物体的细节,如轮廓、阴影和高光等。
这些细节使得物体更加立体和真实,同时也增强了画面的视觉效果。
4. 调整和优化:最后,根据画面的整体效果进行调整和优化。
可能需要调整物体的形状、大小和位置,以达到更好的视觉效果。
同时,注意保持画面的平衡和和谐。
三、两点透视的注意事项1. 两个消失点的位置不宜过于接近,以免画面出现变形。


大远小的两点透视(成角透视)原理大远小的两点透视(成角透视)原理全文共四篇示例,供读者参考第一篇示例:两点透视,又称成角透视,是绘画中常用的一种透视方法。
它利用两个消失点来描绘物体在远近处的大小变化,使画面更加立体逼真。
在画家的作品中,大远小是常见的现象,通过两点透视原理可以更好地表现出来。
我们来了解一下两点透视的原理。
在成角透视中,画家需要确定两个消失点,它们分别代表了水平线上的两个方向,每个点都是一个远离观察者的距离。
通过连接这两个消失点和作为基准的平行线,画家可以描绘出物体在远近处的大小变化。
在两点透视中,当物体远离观察者时,它们会变得较小。
这是因为在视觉上,远处的物体会受到透视效果的影响,呈现出缩小的比例。
相反,当物体靠近观察者时,它们会显得更大。
这种大远小的效果可以通过画家灵活运用两点透视原理来表现出来。
在绘画中,运用两点透视原理可以更好地表现出物体在空间中的位置关系和大小变化。
画家可以通过透视线来确定物体的位置,通过大小的变化来体现远近距离的感觉。
这样可以使画面更加立体感和逼真,让观者感受到真实世界中物体的远近之感。
除了在绘画中,两点透视也被广泛运用在建筑设计、影视特效等领域。
通过两点透视的原理,可以更好地描绘出建筑物在不同距离下的外观,使整体布局更加合理和美观。
在影视特效中,通过透视的运用可以制造出更加逼真的特效,使画面更加震撼和引人入胜。
第二篇示例:大远小的两点透视是一种透视法,也称为成角透视。
它是在绘画中常用到的一种技巧,通过利用两个透视点创建出具有视觉深度和透视感的画面。
在这种透视法中,远处的物体看起来较小,离观察者近的物体看起来较大,给人以距离感和立体感。
下面我们来详细介绍大远小的两点透视的原理。
了解两点透视的基本原理是十分重要的。
在画面中有两个透视点,分别是视线上的两个无穷远点,它们确定了画面中的透视关系。
通过这两个透视点,我们可以确定物体在画面中的位置和大小,从而准确地表现出远近和大小的关系。

大远小的两点透视(成角透视)原理全文共四篇示例,供读者参考第一篇示例:大远小的两点透视,也称为成角透视,是一种常见的透视法之一,在绘画和建筑设计中有着广泛的应用。
这种透视法通过两个消失点来创造出远近大小的效果,使画面更具有立体感和空间感。
下面就让我们来深入探讨一下大远小的两点透视原理。
我们需要了解什么是消失点。
在透视法中,消失点是一个虚拟的点,用来表示平行线在远处汇聚的位置。
而在大远小的两点透视中,有两个消失点,分别位于画面的两侧。
这两个消失点决定了画面中物体的远近大小关系。
在大远小的两点透视中,一个消失点用来表示物体在横向上的远近关系,另一个消失点用来表示物体在纵向上的远近关系。
通过这两个消失点的配合,画家可以更加准确地表现出物体的远近大小,使画面更加真实和立体。
当物体在远处时,它们会向着两个消失点逐渐缩小;而当物体在近处时,它们会向着两个消失点逐渐放大。
这种透视效果使画面中的物体呈现出透视效果,让观者感受到空间的深度和立体感。
值得注意的是,大远小的两点透视并非只适用于绘画领域,实际上在建筑设计中也有着广泛的应用。
通过大远小的两点透视原理,建筑师可以更加准确地表现出建筑物在空间中的位置和大小,帮助客户更好地理解设计方案。
第二篇示例:大远小是一种常见的透视法,也称为成角透视,它主要通过将物体绘制在不同远近距离上,来表现物体的大小差异。
在这种透视法中,远处的物体看起来比较小,而近处的物体看起来比较大。
本文将介绍大远小的两点透视原理。
我们需要了解两点透视的基本概念。
在二维平面上,我们可以通过两点来确定一个透视系,分别称为透视中心点1和透视中心点2。
这两个点会决定物体在透视图中的大小和位置。
当物体远离透视中心点时,它看起来会比较小;而当物体靠近透视中心点时,它看起来会比较大。
通过调整物体与两个透视中心点的距离,我们可以实现大远小的效果。
大远小的透视法在绘画、建筑和设计中都有广泛的应用。
在绘画中,通过运用大远小的原理,可以增强画面的立体感和深度感,使观众感受到空间的远近和真实性。
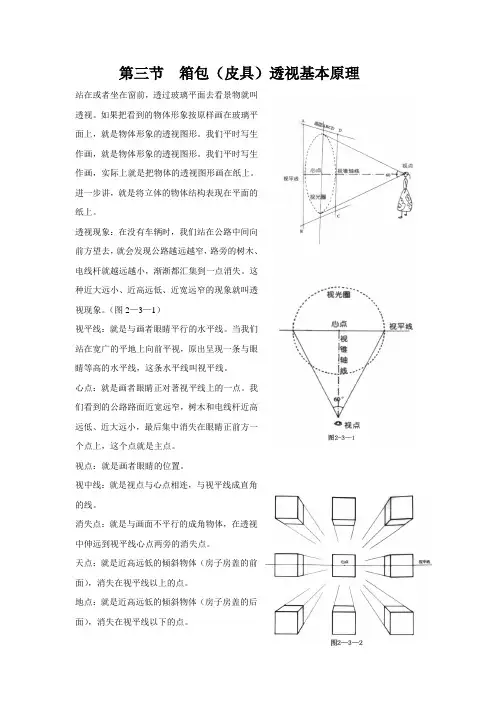
第三节箱包(皮具)透视基本原理站在或者坐在窗前,透过玻璃平面去看景物就叫透视。
如果把看到的物体形象按原样画在玻璃平面上,就是物体形象的透视图形。
我们平时写生作画,就是物体形象的透视图形。
我们平时写生作画,实际上就是把物体的透视图形画在纸上。
进一步讲,就是将立体的物体结构表现在平面的纸上。
透视现象:在没有车辆时,我们站在公路中间向前方望去,就会发现公路越远越窄,路旁的树木、电线杆就越远越小,渐渐都汇集到一点消失。
这种近大远小、近高远低、近宽远窄的现象就叫透视现象。
(图2—3—1)视平线:就是与画者眼睛平行的水平线。
当我们站在宽广的平地上向前平视,原出呈现一条与眼睛等高的水平线,这条水平线叫视平线。
心点:就是画者眼睛正对著视平线上的一点。
我们看到的公路路面近宽远窄,树木和电线杆近高远低、近大远小,最后集中消失在眼睛正前方一个点上,这个点就是主点。
视点:就是画者眼睛的位置。
视中线:就是视点与心点相连,与视平线成直角的线。
消失点:就是与画面不平行的成角物体,在透视中伸远到视平线心点两旁的消失点。
天点:就是近高远低的倾斜物体(房子房盖的前面),消失在视平线以上的点。
地点:就是近高远低的倾斜物体(房子房盖的后面),消失在视平线以下的点。
平行透视:就是有一面与画面成平行的正方形或长方形物体的透视。
这种透视有整齐、平展、稳定、庄严的感觉。
我们以正方形六面体为例,只要六面体中一个面与画面平行时,其它面则逐渐向主点消失,这种透视现象叫平行透视。
平行透视只有一个消失点即心点。
(图2—3—2)在方形物体的平行透视中,最少可以看到一个面,最多可以看到三个面。
(图2—3—3)成角透视:就是任何一面都不与平行的正方形成长方形的物体透视。
这种透视能使构图较有变化。
一个方形物体,它的每一个面都不和画面平行,而且形成一定的角度,并向两侧的点消失,这种透视现象叫成角透视。
成角透视有两个消失点叫余点,余点都在视平线上。
绘画时如果将余点画到视平线以上或者以下都是不对的。

透视技术的原理和应用1. 原理介绍透视技术是一种利用光学原理和数学计算方法的技术,它可以通过对物体进行透视变换,使其在图像上呈现出与实际相同的远近和大小关系。
透视技术的原理主要包括以下几个方面:1.1 光学原理透视技术的基础是光学原理,即光线在传播过程中会发生折射和反射。
透视技术根据观察者和物体之间的距离及其在图像上的位置,通过计算光线的折射和反射角度,确定物体在图像上的呈现形态。
1.2 数学计算透视技术还涉及到一些数学计算,包括透视投影和透视校正。
透视投影是将三维物体投影到二维图像平面上的过程,通过计算物体到图像平面的距离和角度,确定物体在图像上的位置和大小。
透视校正是对已经进行了透视投影的图像进行反向计算,恢复物体在三维空间中的原始形态。
2. 应用领域透视技术在许多领域都有广泛的应用,以下列举了一些常见的应用场景:2.1 建筑设计在建筑设计中,透视技术可以帮助设计师将建筑物的外观形态呈现在平面图或立体模型上。
通过对建筑物进行透视投影,可以更直观地展示其外观特征和空间布局,有助于设计师进行优化和调整。
2.2 游戏开发在游戏开发中,透视技术是实现虚拟世界的重要手段之一。
通过对游戏场景和角色进行透视投影和透视校正,可以使玩家在游戏中获得更真实的视觉体验,增强游戏的沉浸感和代入感。
2.3 艺术绘画透视技术在艺术绘画中有着重要的应用。
通过掌握透视原理,艺术家可以更准确地描绘物体的远近关系和形态变化,使画作更具立体感和逼真度。
2.4 医学影像在医学影像领域,透视技术可以用于对骨骼结构、器官位置和病变情况进行定位和分析。
通过透视投影和透视校正,可以使医生更准确地诊断和治疗疾病。
2.5 工程测量透视技术在工程测量中有着广泛的应用。
通过对测量对象进行透视投影和透视校正,可以得到其真实的尺寸和形态信息。
工程师可以基于此进行设计和施工规划,提高工程的精度和效率。
3. 总结透视技术是一种利用光学原理和数学计算方法的技术,通过对物体进行透视变换,使其在图像上呈现出与实际相同的远近和大小关系。

生活中透视现象的例子
透视现象是指由于人眼对距离、位置、大小等方面的感知错觉而
出现的现象。
在生活中,透视现象的例子有很多,以下是几个常见的
示例:
1. 远近景混淆:当我们在看远处的景象时,背景的物体会显得比
前景的物体更小,而且似乎更遥远。
这是因为人眼会把背景的景物和
观察者看到的前景景物放在一起比较,从而产生错觉。
2. 楼房高低错觉:观察一个高楼时,我们会发现楼顶看起来比基
础区域小,这是因为物体距离远了,人眼会对大小做出误判。
3. 直线变形:在拍照时,有时会发现直线看起来并不是真的直线,而是有些弯曲,这是因为摄影机镜头的设计和原理。
人眼会根据物体
形状、角度和位置,与相机的焦距、角度、光圈等因素相互作用,从
而产生透视错觉。
4. 驾驶中的远近错觉:在驾车过程中,我们看到道路上的直线很长,但很快就越来越短,这是因为我们在行驶中离景物的距离发生了
变化,而人眼会根据这个变化来调整其观察角度,从而达到远近景的
了解。
以上是一些生活中透视现象的例子。
这些现象可能会导致我们对
物体的大小、位置和形状等产生误解,但只要有足够的认知和观察力,我们就可以有效地矫正这些错觉。

物理中透视原理的应用1. 简介透视原理是物理学中的一个重要概念,它描述了光线在通过不同介质时会发生折射现象。
透视原理在日常生活中有许多应用,包括图像形成、眼镜设计、相机镜头等。
本文将介绍透视原理的基本概念,并探讨其在各个领域中的应用。
2. 图像形成透视原理在图像形成中起到了重要的作用。
当光线通过一个凸透镜时,会根据透视原理将光线汇聚到一个焦点上,从而形成一个清晰的图像。
这一现象被应用在相机镜头中,使得相机能够捕捉到物体的清晰图像。
透视原理也被应用在眼睛中,使得人们能够看到清晰的图像。
3. 眼镜设计透视原理在眼镜设计中也发挥着重要的作用。
许多人在中年以后都会出现视力下降的问题,这时候他们需要佩戴眼镜来帮助他们看清楚物体。
眼镜的设计就是根据透视原理来进行的,根据人的眼睛的折射率来确定适合的镜片度数,以使得眼镜可以帮助人们看到清晰的图像。
4. 相机镜头透视原理在相机镜头的设计中也起着重要的作用。
相机镜头利用透视原理将图像聚焦在感光元件上,从而捕捉到清晰的图像。
不同的镜头有不同的焦距,这决定了拍摄到的图像的视角。
透视原理的应用使得相机能够捕捉到真实且清晰的图像。
5. 影视制作透视原理在影视制作中也扮演着重要的角色。
电影摄影师通过合理应用透视原理,可以通过改变镜头的焦距和角度来创造出不同的视觉效果。
例如,通过使用广角镜头和逆透视的手法,可以使得物体看起来更加庞大和壮观。
透视原理的应用为影视制作提供了更多的创造空间。
6. 艺术绘画透视原理在艺术绘画中也是一个重要的概念。
艺术家可以通过运用透视原理来创造出具有立体感的画作。
透视原理可以帮助艺术家将远近的景物呈现在画作中,使得观众可以感受到画面的深度和立体感。
透视原理的应用使得艺术作品更加生动和真实。
7. 综述透视原理是物理学中一个重要的概念,它描述了光线在经过不同介质时的折射现象。
透视原理在图像形成、眼镜设计、相机镜头、影视制作和艺术绘画等领域中都有重要的应用。
透视基本原理
透视是一种视觉现象,它是由于人眼看到的物体在不同的距离上有不同的大小而引起的。
这种现象可以通过光线的反射和折射来解释。
当我们看一个远处的物体时,光线会经过眼睛的晶状体并聚焦在视网膜上,形成一个小的像。
而当我们看一个近处的物体时,光线会经过晶状体的弯曲而聚焦在视网膜上,形成一个较大的像。
由于物体在不同的距离上有不同的大小,我们在接收到这些像的信息后就会产生一个错觉,即远处的物体比近处的物体要小。
这个错觉是由我们的大脑自动产生的,以帮助我们对物体的距离和深度进行判断。
它是基于我们的经验和观察得出的结论。
透视原理也被广泛应用于绘画和摄影艺术中。
艺术家可以利用透视原理来创造出更加真实和立体的作品,使观众产生一种身临其境的感觉。
总的来说,透视基本原理是通过物体在不同距离上的大小差异,以及大脑的错觉判断,使我们能够对物体的距离和深度进行正确的感知。
透视知识点总结一、透视的基本原理透视是一种通过观察客观事物的外在表象去深入分析其规律和本质的认识方法。
透视能够揭示事物的内在关系和发展规律,从而洞察事物的本质属性和特征,揭示事物的本质属性和规律性。
透视的基本原理包括以下几个方面:1. 事物的内在联系透视认为事物的表层现象和外在表象是其内在联系的表现。
分析事物的外在现象不能满足对事物认识的要求,必须深入事物的内在联系,揭示事物的内在规律和本质特征。
2. 规律性的揭示透视认为事物的表象和表现形式都蕴含着一定的规律性。
通过透视可以发现事物内在的联系和规律性,揭示事物的内在规律和本质属性。
3. 对事物本质属性的把握透视的目的是要把握事物的本质属性和本质规律。
通过透视可以深入剖析事物的本质属性,揭示事物的根本特征和基本规律。
二、透视的应用领域透视是一种认识方法,应用广泛。
透视的应用领域主要包括科学研究、社会实践、哲学思考等方面。
1. 科学研究在科学研究中,透视是分析事物内在联系和规律性的重要手段。
通过透视可以深入剖析事物的本质属性和规律特征,从而推动科学研究的深入发展。
2. 社会实践在社会实践中,透视能够帮助人们认识社会运行的规律性和本质属性,为社会管理和发展提供科学依据。
3. 哲学思考在哲学思考中,透视是认识事物的重要方法。
通过透视可以把握事物的本质属性和发展规律,从而深刻理解世界的运行和发展。
三、透视的实践方法透视是一种认识方法,也是一种实践方法。
透视的实践方法包括以下几个方面:1. 深入观察深入观察事物的外在表象,发现事物的内在联系和规律性,为透视提供基本材料。
2. 综合分析综合分析事物的各个方面,揭示事物的内在联系和规律性,从而对事物进行深入剖析。
3. 辩证思维运用辩证思维分析事物的矛盾和运动规律,发现事物的内在联系和本质属性。
四、透视的意义和价值透视是认识事物的重要方法,具有重要的意义和价值。
1. 透视对于认识世界具有重要的指导意义。
通过透视可以深入剖析事物的内在联系和规律性,帮助人们认识事物的本质属性和特征。
透视的知识点在我们的日常生活中,“透视”这个词并不陌生。
无论是在绘画、摄影,还是在建筑设计、医学影像等领域,透视都扮演着重要的角色。
那么,究竟什么是透视?透视又包含了哪些关键的知识点呢?让我们一起来深入探究一下。
首先,我们来理解一下透视的基本概念。
简单来说,透视就是一种在平面上表现物体空间关系和立体感的方法。
通过透视,我们能够让二维的画面呈现出三维的效果,使观众产生一种身临其境的感觉。
在透视中,有几个重要的元素需要我们了解。
第一个是“视点”,也就是观察者眼睛的位置。
视点的高低、远近都会影响到我们所看到的景象。
比如,当我们站在低处看一个高楼时,看到的楼顶面积相对较小;而当我们站在高处看时,楼顶面积就会显得更大。
第二个重要元素是“视线”,也就是从视点出发,经过物体上的点所连成的线。
视线决定了我们看到物体的角度和形状。
第三个元素是“消失点”,这是透视中非常关键的概念。
当一组平行的直线向远方延伸时,在视觉上会汇聚于一点,这个点就被称为消失点。
常见的消失点有一点透视、两点透视和三点透视。
一点透视也叫平行透视,通常在我们面对一个规整的正方体,且其正面与我们平行时出现。
此时,只有一个消失点,所有的横线都是平行的,而竖线都垂直于画面。
两点透视则更加常见,当我们从一个角度观察一个物体时,就会出现两个消失点。
比如观察一个建筑物的一角,建筑物的两条棱边会分别向左右两个方向延伸并汇聚于消失点。
三点透视则在观察高大的建筑物或者俯瞰、仰视的场景中经常用到,它有三个消失点,除了左右两个消失点外,还有一个垂直方向的消失点。
了解了这些基本元素后,我们来看看透视在绘画中的应用。
对于绘画初学者来说,掌握透视是画出逼真画面的关键。
比如在画一幅街景时,如果不运用透视原理,街道可能会显得扁平、没有深度。
而通过合理设置消失点和线条的走向,就能让街道看起来有远有近,建筑物有高有低,整个画面更具立体感和真实感。
在摄影中,透视同样起着重要的作用。
透视的基本原理透视的基本术语1,视平线:就是与画者眼睛平行的水平线。
2,心点:就是画者眼睛正对着视平线上的一点。
3,视点:就是画者眼睛的位置。
4,视中线:就是视点与心点相连,与视平线成直角的线。
5,消失点:就是与画面不平行的成角物体,在透视中伸远到视平线心点两旁的消失点。
6,天点:就是近高远低的倾斜物体(房子房盖的前面),消失在视平线以上的点。
7,地点:就是近高远低的倾斜物休(房子房盖的后面),消失在视平线以下的点。
8,平行透视:就是有一面与画面成平行的正方形或长方形物体的透视。
这种透视有整齐、平展、稳定、庄严的感觉。
9,成角透视:就是任何一面都不与平行的正方形成长方形的物体透视。
这种透视能使构图较有变化。
透视的画法在素描中最基本的形体是立方体。
素描时,大多是以对三个面所进行的观察方法来决定立方体的表现。
另外,利用面与面的分界线所造成的角度,也能暗示出物体的深度,这就涉及到透视规律。
透视分一点透视(又称平行透视),两点透视(又称成角透视)及三点透视三类。
一点透视就是说立方体放在一个水平面上,前方的面(正面)的四边分别与画纸四边平行时,上部朝纵深的平行直线与眼睛的高度一致,消失成为一点,而正面则为正方形.两点透视就是把立方体画到画面上,立方体的四个面相对于画面倾斜成一定角度时,往纵深平行的直线产生了两个消失点。
在这种情况下,与上下两个水平面相垂直的平行线也产生了长度的缩小,但是不带有消失点.三点透视就是立方体相对于画面,其面及棱线都不平行时,面的边线可以延伸为三个消失点,用俯视或仰视等去看立方体就会形成三点透视。
圆及圆柱体透视图(一)为正圆,A=B,a=b。
图(二)为圆的透视图,视觉上A=B,但a<b,这是透视原理。
圆也成了椭圆。
且里面和弧长小于外面的弧长。
外弧弯曲度大一点,里弧变曲度小一点。
圆柱体透视:和前面的圆相比较,里面的圆当然是被缩小了,但仍然是完全的相似形。
两个椭圆是平行的面,但里面的那个被缩小了,此时,椭圆的长轴(未绘)与长方体的边不平行。