小波分析第四讲_小波与滤波器组

格式：ppt
大小：1.07 MB
文档页数：20

下载文档原格式

小波分析第四讲_小波与滤波器组

设数字滤波器信号dwt的三级分解算法树型结构小波变换的时频分析小波与滤波器组信号dwt的三级分解算法等效的简化结构小波变换与滤波器组小波变换的时频分析小波与滤波器组的频率特性分解算法中滤波器组的频域分析小波与滤波器组信号dwt的分布小波与滤波器组信号时域表达的时频分辨率信号频域表达的时频分辨率小波变换与滤波器组小波与滤波器组信号stft的时频分辨率信号dwt的时频分辨率小波变换的时频分析小波与滤波器组小波基函数具有非唯一性这使得小波分的信号采用不同的小波基信号从而使得变换后的小波系数更稀散更加易于信号分析和处理
∑
k
c j [k] ⋅ 2 ϕ(2 j t − k) +
小波与滤波器组
∑
k
d j [k] ⋅ 2 j / 2ψ (2 j t − k)
小波变换与滤波器组
离散小波变换的分解算法
c j [ k ] = x (t ), ϕ j ,k (t ) = ∫ x (t ) ⋅ 2 j / 2 ϕ ( 2 j t − k )dt
小波与滤波器组
小波变换与滤波器组
小波变换的时频分析
H0(z) H0(z) H0 (z) c+1[k] J H1(z) ↓2 ↓2 H1 (z) ↓2 ↓2 H1(z) ↓2 d −2[k] [k J d −1[k] J d [k] J ↓2 c −2[k] J
信号DWT的三级分解算法树型结构的三级分解算法树型结构信号
d j [ k ] = x (t ),ψ j , k (t ) = ∫ x (t ) ⋅ 2 j / 2ψ ( 2 j t − k )dt
c j [ k ] = ∑ h[i − 2k ] ⋅ ∫ x(t ) ⋅ 2 ( j +1) / 2 ϕ ( 2 j +1 t − i )dt

小波与滤波器组：Wavelets and Filter Banks(PPT-15)

0 1
12
Then, x–1 = [1 -1 1 -1]
a b = [1 -1 1 -1] A–1 c d
x0 x1 x2 x3
PDE
f(x) = ∑ ckφ(x – k)
k p-1 i=0
Assume f(x) has polynomial behavior near boundaries ∑ αixi = f(x) = ∑ ckφ(x – k)
Symmetric extension of finite-length signal X(ω) = B(ω)e-iωβ
10
The output: Y(ω) = H(ω)X(ω) W W H H W H H W W H W H
W = whole-point symmetry H = half-point symmetry
n
x[n]e-i N n Want real-valued results.
14
2πk
complex-valued
0
N-1 n=0
1 m
2N-1
N-1
N
m
2N-1
2N
DFT of this extended signal: ∑ x[n]e
2πk –i 2N n
+ ∑
N-1
LOOMOON
n=N
2πk
k
{φ ( - k)} orthonormal ∑ αi ∫ φ(x – k)xidx = ck
i=0 p-1
LOMON
ik
13
0 1 m p-1 0 0 0 0 1 o 1 2 1 1 m
α0 α1 o αp-1 =
c0 c1 o cp-1

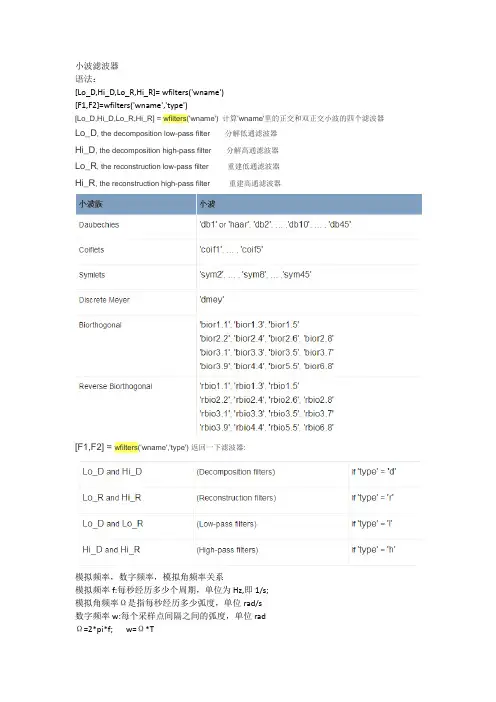
小波滤波器

小波滤波器语法：[Lo_D,Hi_D,Lo_R,Hi_R]= wfilters('wname')[F1,F2]=wfilters('wname','type')[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('wname') 计算'wname'里的正交和双正交小波的四个滤波器Lo_D, the decomposition low-pass filter 分解低通滤波器Hi_D, the decomposition high-pass filter 分解高通滤波器Lo_R, the reconstruction low-pass filter 重建低通滤波器Hi_R, the reconstruction high-pass filter 重建高通滤波器[F1,F2] = wfilters('wname','type') 返回一下滤波器:模拟频率，数字频率，模拟角频率关系模拟频率f:每秒经历多少个周期，单位为Hz,即1/s;模拟角频率Ω是指每秒经历多少弧度，单位rad/s数字频率w:每个采样点间隔之间的弧度，单位radΩ=2*pi*f; w=Ω*TIIR数字滤波器设计方法：先根据已知带通参数求出最佳滤波器阶数和截止频率[n,Wn]=buttord(Wp,Ws,Rp,Rs);[n,Wn]=buttord(Wp,Ws,Rp,Rs,'s');[b,a]=butter(n,Wn,'ftype','s')Wp为0-1之间，Ws为阻带角频率，0-1之间。

Rp为通带波纹，或者通带衰减，Rs为阻带衰减。

给出的是模拟频率fp1通带截止频率，fp2阻带截止频率，则Wp=fp1*2/fs,Ws=fp2*2/fs。

传统FIR滤波器函数FIRl是采用经典窗函数设计线性相位FIR数字滤波器，且具有标准低通、带通、高通和带阻等类型。

小波滤波

1， N1(t)= 0,

0 t<1
others
=N m(t) *N1(t) 故 N m+1(t)
一、连续小波滤波
3.Mexico草帽小波 Mexico草帽小波是Gauss函数 et 2 /2 的二次导数，它由下式给出

(t )
2 3
(1 t ) e
1/4 2
t 2 /2
（7）小波去噪程序
%应用db5作为小波函数进行3层分解 %利用无偏似然估计阈值 %对100.dat from MIT-BIH-DB的单导联数据进行去噪处理 clear;clc load('D:/matlab/matlab7.2/work/M.mat'); E=M(:,2); E=E'; n=size(E); s=E(1:2000); %小波分解 [C L]=wavedec(E,3,'db5'); % 从c中提取尺度3下的近似小波系数 cA3=appcoef(C,L,'db5',3); %从信号c中提取尺度1,2,3下的细节小波系数 cD1=detcoef(C,L,1); cD2=detcoef(C,L,2); cD3=detcoef(C,L,3);

其中的系数是为了满足 (t )的归一化要求
一、连续小波滤波
4.Morlet小波 morlet小波是经常用到的一种复值小波，其定义如下

(t )
-1/4
(e
j 0t
e
2 0 /2
) e
t 2 /2
一、连续小波滤波

根据内积的定义
1 * x(t),g(t) x ( )g ( )d 2 式②做给出的小波变换便可被写成

小波变换的滤波器实现

小波变换的应用领域
信号处理
小波变换在信号处理领域应用广泛，如语音、图像、雷达、地震等信号的分析和处理。
通信领域
小波变换在通信领域主要用于信号调制、解调、信道均衡等方面。
ABCD
图像处理
小波变换在图像处理中主要用于图像压缩、图像去噪、图像增强等方面。
金融领域
小波变换在金融领域主要用于金融数据分析、股票市场预测等方面。
02
滤波器的基本概念
滤波器的定义
滤波器
一个系统或电路，用于允许一部分频率通过而阻止另一部分频率通过。
数字滤波器
在数字信号处理中，滤波器通常由一组数字系数定义，用于修改输入信号的频谱。
滤波器的分类
01
低通滤波器
允许低频信号通过，抑制高频信号。
带通滤波器
允许某一频段的信号通过，抑制该频段以外的信号。
计算复杂度
小波变换的计算复杂度较高，对于大规模数据实时处理存在挑战。
选择合适的小波基函数
选择合适的小波基函数是关键，需要根据具体应用场景进行选择和调整。
信号重构精度
小波变换的信号重构精度受到小波基函数和分解层数的影响，需要权衡精度和计算复杂度。
边界效应
小波变换在处理信号边界时可能会出现边界效应，需要进行特殊处理以减小影响。
根据具体应用需求，选择合适的小波基函数和分解层数，以实现最佳的信号处理效果。
设计滤波器时需要考虑信号的频谱特性、噪声水平、动态范围等因素，以确保滤波器能够有效地提取或抑制特定频率范围的信号。
常用的滤波器设计方法包括基于规则的滤波器和自适应滤波器，其中自适应滤波器可以根据输入信号自动调整参数，具有更好的适应性。
小波变换的特点

小波分析全章节讲解

虽然时变信号的频率特性随着时间而改变，但是这种改变是渐变的而非突变的，也就是说，在一个特定的足够小的区间（窗）内，可以认为信号的特性是不变的，信号是局部稳定的或准平稳的。
（二）加窗时频分析 1.时窗处理将信号在时域内进行分段，等效于用位置不同的窗函数 g ( t ) 与原信号 f ( t ) 相乘的结果，如下图所示。在时域内，时间函数一般选取具有能量局部化的函数。先选定一个基本窗函数 g ( t ) ，然后将 g ( t ) 沿时间轴平移得到一组窗函数，
en , em 0, m n (m n) 1, m n
对应的傅里叶展开式为
f

f , en en
n 1
规范正交性存在于原基底与对偶基底之间，展开式也相应的由原基底和对偶基底构成，这种基称为双正交基，与互为对偶基底。
（6）框架 { 设H为Hilbert空间， k } 为H中的一个函数序列，若 f H ，都存在实数A,B使得
小波分析的应用领域十分广泛，它包括：数学领域的许多学科；信号分析、图象处理；量子力学、理论物理；军事电子对抗与武器的智能化；计算机分类与识别；音乐与语言的人工合成；医学成像与诊断；地震勘探数据处理；大型机械的故障诊断等方面；例如：在数学方面，它已用于数值分析、构造快速数值方法、曲线曲面构造、微分方程求解、控制论等。在信号分析方面的滤波、去噪声、压缩、传递等。在图象处理方面的图象压缩、分类、识别与诊断，去污等。在医学成像方面的减少B超、CT、核磁共振成像的时间，提高分辨率等。

f (t ) e
j t
d t f ( t ), e
j t

小波变换与小波滤波解析

17
小波尺度和信号频率的关系
大尺度小尺度
信号的低频信号的高频
18
1.6 离散小波变换（DWT）
在每个可能的缩放因子和平移参数下计算小波系数，其计算量相当大，将产生惊人的数据量，而且有许多数据是无用的。
如果缩放因子和平移参数都选择为2j（j>0且为
整数）的倍数，即只选择部分缩放因子和平移参数来进行计算，就会使分析的数据量大大减少。
ECG signal 100.dat 1
0.8
0.6
0.4
Voltage / mV
0.2
0 28 1
1
1
1
1
1
1
8
-0.2
-0.4
-0.6
-0.8
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
Time / s
在实际工程应用中，通常所分析的信号具有非线性，非平稳,并且奇异点较多的特点。含噪的一维信号模型可表示为：
26
1.7 小波重构
H′ L′
H′
S L′
小波重构算法示意图
27
1.7 小波重构
(1) 重构近似信号与细节信号由小波分解的近似系数和细节系数可以重构出原
始信号。同样，可由近似系数和细节系数分别重构出信号
的近似值或细节值，这时只要近似系数或细节系数置为零即可。
28
1.7 小波重构
H′ 0 约 500个 0
23
图（a）信号分解； (b) 小波分树；（c）小波分解树 24
1.6 离散小波变换（DWT）
在使用滤波器对真实的数字信号进行变换时，得到的数据将是原始数据的两倍。

基于小波分析的数字滤波器设计

基于小波分析的数字滤波器设计
近年来，随着计算机技术和信息处理技术的发展，数字滤波器受到了越来越多的关注。

数字滤波器是一种常用的信号处理技术，用于消除频率信号中的噪声，以获得清晰的输出信号。

由于数字滤波器的复杂性，设计一个高性能的滤波器可能是非常耗时的，而小波分析则可以弥补这一短板。

小波分析是一种信号变换技术，可以将信号进行频域分解，以获得信号的完整信息。

同时，小波分析也可以有效地减少信号中的噪声和抖动，从而获得清晰的信号。

因此，将小波分析和数字滤波器结合起来，可以有效地设计出一个高性能的数字滤波器。

首先，在小波变换之前，我们需要对信号进行采样，以确保我们能够获得足够的信息。

然后，我们可以将采样后的信号送入小波变换过程，以获得信号的频域分解。

接下来，我们可以根据获得的信息，设计出一个最佳的数字滤波器，以最大程度地消除信号中的噪声。

最后，使用一种最佳系数设计方法，将设计出的滤波器应用到采样信号上，以获得最终的滤波器输出信号。

本文介绍了基于小波分析的数字滤波器设计的过程。

首先，利用小波变换技术对信号进行频域分解，以获得完整的信号信息，其次，使用最佳系数设计方法设计出一个高性能的数字滤波器，然后将该滤波器应用于采样信号上，最后得到的信号即为滤波器的最终输出。

通过结合小波分析和数字滤波器，能够有效地提升信号处理的性能，实现更高效、准确的信号处理。

因此，小波分析是一种有效的方法，可以帮助我们设计出更加高效、准确的数字滤波器，并有效地消除频率信号中的噪声，从而获得更加清晰的信号输出。

在未来，小波分析和数字滤波器将继续弥补彼此的短板，提供更好的信号处理解决方案。

《小波分析方法》课件

论文和研究报告
介绍一些发表在期刊和会议上的相关论文和研究报告
小波分析工具和库
提供一些开放源代码的小波分析工具和库的信息
Matlab工具箱
介绍基于Matlab的小波分析工具箱，讲解如何使用该工具箱进行小波分析
小结和展望
1 小波分析方法的优点和局限性
总结小波分析方法相较于其他方法的优点并讨论其局限性
2 未来的研究和应用方向
展望小波分析方法在未来可能的研究方向和应用领域
参考资料
相关领域的经典书籍和教材
推荐一些与小波分析相关的经典书籍和教材
信号去噪和压缩
学习如何使用小波分析方法对信号进行去噪和压缩处理
图像处理
探索小波分析在图像处理中的广泛应用
音频处理
了解如何利用小波分析进行音频特征提取和音频效果处理
视频处理
发现小波分析在视频编解码和视频特征提取中的应用
小波分析算法实现
1
Python和其他编程语言
2
探讨使用Python和其他编程语言实现小波分析的库和方法
《小波分析方法》PPT课件
本课程将介绍小波分析方法的基本概念和应用场景，帮助您掌握信号分析的强大工具。让我们一起开启这个精彩的学习之旅吧！
课程介绍
内容和目标
了解本课程将涵盖的内容和学习目标
小波分析方法
掌握小波分析方法的基本概念和它在实际应用中的价值
信号分析基础
1 信号的分类
了解不同类型的信号及其特点
2 傅里叶分析方法
介绍傅里叶分析方法的原理和局限性
3 小波分析方法
探讨小波分析方法相较于傅里叶分析的优点和适用性
小波分析的数学基础
滤波器组和小波变换

小波滤波

一、连续小波滤波
几种常见的小波 1. Haar小波 Haar小波是一步连续的小波，它是被Haar于 1910年所提出，其定义为

1 (t ) 1 0
0 x 1/ 2 1/ 2 x 1 elsewise
一、连续小波滤波
2.二次B样条小波样条函数是一类分段光滑的函数，m阶B样条 N m+1(t) 是由Haar尺度函数 N (t)做m次自卷积后所得到的 1 函数。由于
选取的算法是：
（4）阈值函数和阈值的选取
(2) Stein无偏似然估计阈值(’rigrsure’) 对于给定一个阈值t，得到它的似然估计，再将非似然的t最小化，就得到了所选的阈值。 (3) 启发式阈值(‘heursure’) 它是前两种阈值的综合，是最优预测变量阈值选择，如果信噪比很小时，无偏似然估计的误差交大，此时，采用固定阈值。令：
(1) 对含噪信号进行预处理,并进行小波分解。选择小波确定分解的层数N,然后对信号s进行N层分解。
四、一维信号利用小波除噪的步骤
(2) 小波分解的高频系数的阈值量化。对第一层到第N层高频系数，选择软阈值或硬阈值量化处理。 (３) 一维小波重构。根据小波分解的第N层低频系数和第一层到第N层的高频系数，进行一维重构。在上面的步骤中，最为关键的就是如何选取阈值和如何阈值量化，从某种意义上讲，它直接影响信号去噪的质量。
（2）小波分解示意图：
s CA1 CA2 CA3 CD3 CD2 CD1
小波分解的结构示意图
小波分解系数示意图
（3）一维信号利用小波除噪的步骤
1.小波变换去噪的流程示意图：
含噪信号小波变换多尺度分解各尺度小波系数除噪小波逆变换重构信号除噪后的信号

利用小波分析的滤波器设计方法研究

利用小波分析的滤波器设计方法研究在信号处理领域中，滤波器是一个重要的工具。

滤波器用于去除信号中不必要的成分，同时保留有用的部分。

不同类型的滤波器可以应用于不同类型的信号。

在本文中，我们将讨论一种利用小波分析的滤波器设计方法。

小波分析是一种信号处理技术，它将信号分解为不同频率的小波组件。

这些小波组件在时间和频率上都是局部化的。

因此，小波分析不仅可以提供关于信号频域特性的信息，而且还提供有关信号时域特性的信息。

在滤波器设计中，我们可以利用小波分析的这些特性来切割信号，去除不必要的成分。

与传统的滤波器设计方法相比，小波分析的滤波器可以提供更好的局部化性能和可定制化性能。

以下是小波分析的滤波器设计方法的一些关键方面：1. 小波选择小波分析的滤波器设计需要选择适当的小波。

常见的小波有Haar、Daubechies 等。

每个小波都有不同的频率和时域特性，因此选择适当的小波对于滤波器设计非常重要。

2. 滤波器类型小波分析的滤波器可以分为低通滤波器和高通滤波器。

低通滤波器用于去除高频成分，高通滤波器用于去除低频成分。

根据信号的特性，我们可以选择适当的滤波器类型。

3. 滤波器设计滤波器的设计需要确定滤波器系数。

滤波器系数决定了滤波器对信号的影响程度。

滤波器系数的确定可以通过拟合方法、最小二乘法等。

4. 滤波器实现滤波器实现可以通过快速小波变换（FWT）实现。

FWT是一种高效的小波变换方法，它可以将信号分解成小波系数。

通过对小波系数进行滤波，我们可以去除信号中不必要的成分。

在实际应用中，小波分析的滤波器设计方法已经被广泛应用于信号处理领域。

例如，在医学领域，小波分析的低通滤波器可以用于去除心电图信号中的基线漂移。

在音频领域，小波分析的高通滤波器可以用于去除低频噪声。

总之，小波分析的滤波器设计方法是一种非常有效的信号处理技术。

通过选择适当的小波、滤波器类型和滤波器系数，我们可以根据信号的特性定制滤波器。

这种定制化的滤波器可以提供更好的局部化性能和可定制化性能，从而更好地满足实际应用的需求。

小波变换中的滤波器设计和参数调整方法详解

小波变换中的滤波器设计和参数调整方法详解小波变换（Wavelet Transform）是一种在信号处理和图像处理领域广泛应用的数学工具，它可以将信号分解成不同频率的子信号，并提供了一种有效的方式来分析和处理信号。

在小波变换中，滤波器设计和参数调整是非常重要的步骤，本文将详细介绍这两个方面的方法。

一、滤波器设计在小波变换中，滤波器是用来分解信号和重构信号的关键组成部分。

滤波器的设计可以根据不同的需求和应用来进行选择和调整。

1. 低通滤波器（Low-pass Filter）低通滤波器用于提取信号中的低频成分，通常被称为近似系数（Approximation Coefficients）。

设计低通滤波器的常用方法是通过选择合适的滤波器响应函数，如Butterworth滤波器、Chebyshev滤波器或FIR滤波器。

这些滤波器可以通过调整截止频率、阶数和滤波器类型来满足不同的需求。

2. 高通滤波器（High-pass Filter）高通滤波器用于提取信号中的高频成分，通常被称为细节系数（Detail Coefficients）。

设计高通滤波器的方法与低通滤波器类似，只是需要调整滤波器的频率响应和特性以适应高频信号的提取。

3. 带通滤波器（Band-pass Filter）带通滤波器用于提取信号中的特定频率范围内的成分，可以通过将低通滤波器和高通滤波器组合而成。

带通滤波器的设计通常需要考虑到滤波器的通带范围、截止频率和滤波器类型等因素。

二、参数调整方法在小波变换中，参数的选择和调整对于信号的分析和处理结果有着重要的影响。

以下是一些常用的参数调整方法：1. 尺度选择（Scale Selection）尺度选择是指选择合适的小波基函数（Wavelet Basis）来分析信号。

不同的小波基函数具有不同的特性和性能，如Haar小波、Daubechies小波和Morlet小波等。

根据信号的特点和分析的目的，可以选择合适的小波基函数来进行尺度选择。

小波分析及应用(附常用小波变换滤波器系数)

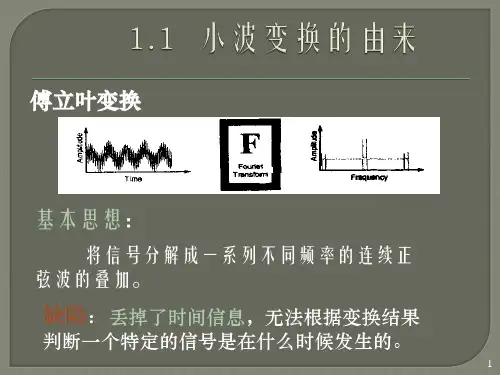
第八章小波分析及应用8.1 引言把函数分解成一系列简单基函数的表示，无论是在理论上，还是实际应用中都有重要意义。

1822年法国数学家傅里叶(J. Fourier 1768-1830)发表的研究热传导理论的“热的力学分析”，提出并证明了将周期函数展开为正弦级数的原理，奠定了傅里叶级数理论的基础[1]。

傅里叶级数理论研究的是把函数在三角函数系下的展开，使得对信号和系统的研究归结为对简单的三角函数的研究。

傅里叶级数与傅里叶变换共同组成了平常所说的傅里叶分析[2]。

傅里叶级数用于分析周期性的函数或分布，理论分析时经常假定周期是π2，定义如式(8.1-1)、(8.1-2)()()π2,02L x f ∈∀，()∑∞-∞==k ikxkec x f (8.1-1)其中 ()dx e x f c ikx k -⎰=ππ2021 (8.1-2) 然而，被分析函数的性质并不能完整地由傅里叶系数来刻划，这里有一个例子来说明[3]：从任一个平方可和的函数)(x f 出发，为了得到一个连续函数)(x g ，只需或者增大f(x)的傅里叶系数的模，或者保持它不变并适当地改变系数的位相。

因此，不可能仅根据傅里叶系数大小的阶就预知函数的性质（如大小、正则性）。

傅里叶变换的定义如式(8.1-3)、(8.1-4)()()dx e x f F x j ωω⎰∞∞-= (8.1-3)()()ωωπωd e F x f x j -∞∞-⎰=21 (8.1-4) 通过引入广义函数或分布的概念，可获得奇异函数（如冲击函数）的傅里叶变换的存在。

对于时域的常量函数，在频域将表现为冲击函数，表明具有很好的频域局部化性质。

由式(8.1-3)可知，为了得到()ωF ，必须有关于f(x)的过去和未来的所有知识，而且f(x)在时域局部值的变化会扩散到整个频域，也就是()ωF 的任意有限区域的信息都不足以确定任意小区域的f(x)。

在时域，哈尔(Haar)基是一组具有最好的时域分辨能力的正交基，它在时域上是完全局部化的，但在频域的局部化却很不好，这是由于哈尔系的两个缺点：缺乏正则性与缺乏振动性。

小波变换与滤波器组

F z
0
• ， 2 31 h n 1 , 3 , 3 , 1 • 可见 k 1 2 满足要求。而对于 4 1 1 2 1 z 1 4 z z • H z 2 0 2 2 1 1 2 F z 1 4 z z • ，，它虽满足条件1）、 2 2），但其极大值为 2 2 211 ，故不满足条件。 • 正规性条件是小波滤波器组和一般滤波器组设计中的主要区别。
，与的偶数移位交叉正交； ~ g h 当 l 为偶数时，与的奇数移位交叉正交，称双正交关系。 ~ n 2i , h n 2 j 0 g 1 • 证明：当 l 为奇数时， 0 l G z z H 1 z 两边乘以 H1z ，得到 •将 0 l G0 z H1 z z H1 z H1 z • 由于 H1 z H1 z 只有奇次项，因此当 l 为奇数时，G0 zH1z 中只有奇次项，没有偶次项，由 G0 z H1 z 的反演序列是 g0 n 与 h1 n 卷积定理知， ~ n g 的卷积，也就是 0 与 h1n 的相关。
/
• 2) 为满足 T z cz ，要求 Pz 可以是任意的，但是奇次项只有一项（与 k / 对应）非零，这样的 Pz 称为可行（Valid）Pz 。 • 3）g 0 , h0 间及 g1, h1 间存在下述正交关系
k /
• 式中 k k/ l ，当 l 为奇数时， k 为偶数；当 l 为偶数， k 为奇数。 P z H 0 z H 1 z z l H 0 z G 0 z • 证明：第一种情况 k / • 由于 Pz 只有一个奇次项 z 非零，可见当 l l k / H z G z 为奇数时 0 中只有一个偶次项 z 非 0 H0zG 零；当 l 为偶数时， 0 z 中只有一个奇次项 l k / z k k l ，便有 • 非零。令 ~ n 2 i , h n k g

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

c j [k] = ∑h0[i − 2k] ⋅ c j+1[i] d j [k] = ∑h1[i − 2k] ⋅ c j+1[i]
i
小波与滤波器组
i
小波变换与滤波器组
离散小波变换的分解算法
h0[−k]
cj+1[k]
y0[k] 2
V j+1 = V j ⊕W j
cj[k]=y0[2k]
h1[−k]
y1[k]
i
ψ ( 2 j t − k ) = ∑ h1 [i − 2 k ] 2 ⋅ ϕ ( 2 j +1 t − i )
x (t ) ∈V j +1
i
x (t ) =
∑ c j +1 [ k ] ⋅ 2
k
j/2
( j +1 ) / 2
ϕ ( 2 j +1 t − k )
Vj+1 =Vj ⊕Wj
x(t) =
信号频域表达的时频分辨率
小波变换与滤波器组
小波变换的时频分析
f
f
t
t
小波与滤波器组
信号STFT的时频分辨率的时频分辨率信号
信号DWT的时频分辨率的时频分辨率信号
小波变换与滤波器组
小波变换的时频分析小波基函数具有非唯一性，小波基函数具有非唯一性，这使得小波分析具有更广泛的适应性，析具有更广泛的适应性，可实现对于不同特性的信号采用不同的小波基信号，的信号采用不同的小波基信号，从而使得变换后的小波系数更稀散，后的小波系数更稀散，更加易于信号分析和处理。因此，小波分析有其独特的优点，特别对因此，小波分析有其独特的优点，于非平稳的信号，有着明显的优越性。于非平稳的信号，有着明显的优越性。
数字信号处理
(Digital Signal Processing) Processing)
信号与系统系列课程组国家电工电子教学基地
信号时频分析
问题的提出短时傅里叶变换小波展开与小波变换小波变换与多分辨分析小波变换与滤波器组基于小波的信号处理及应用
小波变换与滤波器组
离散小波变换的分解算法离散小波反变换的重构算法小波变换的时频分析
离散小波变换的分解算法离散小波反变换的重构算法小波变换的时频分析
小波与滤波器组
小波变换与滤波器组
离散小波变换的分解算法
ϕ(t)的MRA方程： ϕ (t ) = ∑ h0 [n] 2 ⋅ ϕ (2t − n) MRA方程方程：
n
ψ(t)的MRA方程： ψ ( t ) = ∑ h1 [ n ] 2 ⋅ ϕ ( 2t − n ) MRA方程方程：
h1[ k]
IDWT二级重构算法框图二级重构算法框图
小波与滤波器组
小波变换与滤波器组
小波变换的时频分析
信号x(t)小波变换可以由信号的抽样序列 j+1[k]经过小波变换可以由信号的抽样序列c 信号小波变换可以由信号的抽样序列经过滤波器组h − 和 − 而实现而实现，滤波器组 0[−n]和h1[−n]而实现，因此可从频域信号滤波的概念来理解信号的小波变换，的概念来理解信号的小波变换，且可从滤波器组的理论来阐述信号小波变换的时频特性。来阐述信号小波变换的时频特性。设数字滤波器h − 和 − 对应的系统函数分别为设数字滤波器 0[−n]和h1[−n]对应的系统函数分别为 H0(z)和H1(z)，频率特性分别为 0(ejΩ)和H1(ejΩ)。和，频率特性分别为H 和。
d j [ k ] = x (t ),ψ j , k (t ) = ∫ x (t ) ⋅ 2 j / 2ψ ( 2 j t − k )dt
c j [ k ] = ∑ h[i − 2k ] ⋅ ∫ x(t ) ⋅ 2 ( j +1) / 2 ϕ ( 2 j +1 t − i )dt
i
c j +1[i ] = ∫ x(t ) ⋅ 2( j +1) / 2 ϕ (2 j +1 t − i )dt
小波与滤波器组
小波变换与滤波器组
信号的DWT并不是直接由ϕ(t)与ψ(t)经信号内积来实现，并不是直接由经信号内积来实现，信号的与经信号内积来实现而是利用h 来实现。而是利用 0[n]和h1[n]来实现。其将信号的小波展开系数 j[k] 和来实现其将信号的小波展开系数c 看作是离散信号，看作是数字滤波器，和dj[k]看作是离散信号， h0[n]和h1[n]看作是数字滤波器，从看作是离散信号和看作是数字滤波器而建立小波变换与滤波器组(filter bank)之间的关系，由滤波之间的关系，而建立小波变换与滤波器组之间的关系器组的理论来实现信号小波分析。器组的理论来实现信号小波分析。
小波与滤波器组
小波变换与滤波器组
小波变换的时频分析
H0(z) H0(z) H0 (z) c+1[k] J H1(z) ↓2 ↓2 H1 (z) ↓2 ↓2 H1(z) ↓2 d −2[k] [k J d −1[k] J d [k] J ↓2 c −2[k] J
信号DWT的三级分解算法树型结构的三级分解算法树型结构信号
2
dj[k]=y1[2k]
∑ h 0 [ i − k ] ⋅ c j +1 [ i ] i y 1 [ k ] = ∑ h1 [i − k ] ⋅ c j +1 [i ]
y 0 [k ] =
i
小波与滤波器组
小波变换与滤波器组
离散小波变换的分解算法
V j +1 = V j ⊕ W j = V j −1 ⊕ W j −1 ⊕ W j
J −1
H (1) ( z ) = H 0 ( z ) H 0 ( z 2 ) H 1 ( z 4 )
(1)
(2)
H ( 2) ( z ) = H 0 ( z ) H 1 ( z 2 ) dJ −1[k] (W )
(3)
H ( 3) ( z ) = H 1 ( z ) dJ [k] ( WJ )
信号DWT的三级分解算法等效的简化结构的三级分解算法等效的简化结构信号
∑
k
c j [k] ⋅ 2 ϕ(2 j t − k) +
小波与滤波器组
∑
k
d j [k] ⋅ 2 j / 2ψ (2 j t − k)
小波变换与滤波器组
离散小波变换的分解算法
c j [ k ] = x (t ), ϕ j ,k (t ) = ∫ x (t ) ⋅ 2 j / 2 ϕ ( 2 j t − k )dt
cj [k]
2
h0 [ k]
+
d j [k]
2
cj+1[k] [k
h1[k]
IDWT一级重构算法框图一级重构算法框图
小波与滤波器组
小波变换与滤波器组
离散小波反变换的重构算法
cj−1[k]
↑2 h0[k]
+
d j−1[k]
↑2
c j [k]
↑2
h0[k ]
h1[ k]
+
dj[k]
↑2
cj+1[k]
V j +1 = V j ⊕ W j
x ( t ) = ∑ c j +1 [ k ] ⋅ 2
k
( j +1) / 2
ϕ ( 2 j +1 t − k )
x(t) = ∑cj [k]⋅ 2 ϕ(2 j t −k) + ∑d j [k]⋅ 2 j / 2ψ(2 j t −k)
j /2 k k
x(t) =
小波与滤波器组
小波变换与滤波器组
数字滤波器h 数字滤波器 0[-n]和h1[-n]的频率特性和的频率特性
分解算法中滤波器组的频域分析
小波与滤波器组
小波变换与滤波器组
小波变换的时频分析
信号DWT的分布信号的分布
小波与滤波器组
小波变换与滤波器组
小波变换的时频分析
f
f
t
t
小波与滤波器组
信号时域表达的时频分辨率
小波与滤波器组
小波变换与滤波器组
小波变换的时频分析
H ( 0) ( z ) = H 0 ( z ) H 0 ( z 2 ) H 0 ( z 4 )
H ( V +1 ) J c +1 [k] J H H H
(0)
(z) (z) (z) (z)
↓8 ↓8 ↓4 ↓2
cJ −2[k] dJ −2[k]
( VJ −2 ) (WJ −2 )
n
t →(2 j t − k)
ϕ ( 2 j t − k ) = ∑ h 0 [ n ] 2 ⋅ ϕ ( 2 j +1 t − 2 k − n )
n
ψ (2 j t − k ) =
h1 [ n ] 2 ⋅ ϕ ( 2 j +1 t − 2 k − n ) ∑
n
小波与滤波器组
小波变换与滤波器组
离散小波变换的分解算法 i = 2k + n ϕ (2 j t − k ) = ∑ h0 [i − 2k ] 2 ⋅ ϕ (2 j +1 t − i )
h0[−k]
↓2
cj−1[k]
h0[−k]
cj+1[k]
h1[−k]
↓2
cj [k]
h1[−k]
↓2
d j−1[k]
dj [k]
↓2
小波变换的分解(Analysis)算法（Mallat算法）算法（算法）小波变换的分解算法算法
小波与滤波器组
小波变换与滤波器组
离散小波反变换的重构算法
x (t ) ∈V j +1

小波分析第四讲_小波与滤波器组

合集下载