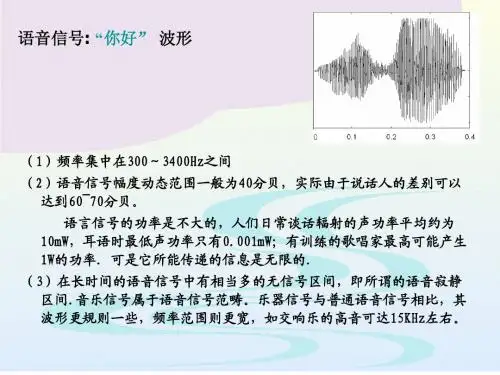
脉冲幅度调制(PAM)及系统实验

实验二：抽样定理和脉冲调幅（PAM）实验一、实验目的通过本实验，学生应达到以下要求：1、观察并了解PAM信号形成、平顶展宽、解调和滤波等过程；2、验证并理解抽样定理，掌握对频谱混叠现象的分析方法；3、观察时分多路系统中非理想信道之间的路际串话现象，分析并掌握其形成原因。

二、实验内容本实验课完成以下实验内容：采用专用集成抽样保持开关完成对输入信号的抽样；多种抽样时隙的产生；采用低通滤波器完成对PAM信号的解调；测试出入信号频率与抽样频率之间的关系，观察频谱混叠现象，验证抽样定理；多路脉冲条幅（PAM）；观察并测试时分多路PAM信号和高频串话。

三、实验原理在通信技术中为了获取最大的经济效益，就必须充分利用信道的传输能力，扩大通信容量。

因此，采取多路化制式是极为重要的通信手段。

最常用的多路复用体制是频分多路复用( FDM) 通信系统和时分多路复用( TDM) 通信系统。

频分多路技术是利用不同频率的正弦载波对基带信号进行调制，把各路基带信号频谱搬移到不同的频段上，在同一信道上传输。

利用抽样脉冲把一个连续信号变为离散时间样值的过程称为抽样，抽样后的信号好称为脉冲调幅信号。

在满足抽样定理的条件下，抽样信号保留了原信号的全部信息。

抽样定理：fs>2fh,才能从抽样信号中可以无失真的恢复出原信号。

抽样定理在通信系统、信息传输理论方面占有十分重要的地位。

数字通信系统是以此定理作为理论基础的。

在工作设备中，抽样过程是模拟信号数字化的第一步。

抽样性能的优劣关系到整个系统的性能指标。

抽样量化编码信道解码滤波收定时发定时PAM语音信号语音信号PAM图2-1 单路PCM系统示意图作为例子，图2-1示意地画出了传输一路语音信号的PCM系统。

从图中可以看出要实现对语音的PCM编码，首先就要对语音信号进行抽样，然后才能进行量化和编码。

因此，抽样过程是语音信号数字化的重要环节，也是一切模拟信号数字化的重要环节。

为了让实验者形象地观察抽样过程，加深对抽样定理的理解，本实验提供了一种典型的抽样电路。

实验二：抽样定理和脉冲调幅（PAM）实验一、实验目的通过本实验，学生应达到以下要求：1、观察并了解PAM信号形成、平顶展宽、解调和滤波等过程；2、验证并理解抽样定理，掌握对频谱混叠现象的分析方法；3、观察时分多路系统中非理想信道之间的路际串话现象，分析并掌握其形成原因。

二、实验内容本实验课完成以下实验内容：采用专用集成抽样保持开关完成对输入信号的抽样；多种抽样时隙的产生；采用低通滤波器完成对PAM信号的解调；测试出入信号频率与抽样频率之间的关系，观察频谱混叠现象，验证抽样定理；多路脉冲条幅（PAM）；观察并测试时分多路PAM信号和高频串话。

三、实验原理在通信技术中为了获取最大的经济效益，就必须充分利用信道的传输能力，扩大通信容量。

因此，采取多路化制式是极为重要的通信手段。

最常用的多路复用体制是频分多路复用( FDM) 通信系统和时分多路复用( TDM) 通信系统。

频分多路技术是利用不同频率的正弦载波对基带信号进行调制，把各路基带信号频谱搬移到不同的频段上，在同一信道上传输。

利用抽样脉冲把一个连续信号变为离散时间样值的过程称为抽样，抽样后的信号好称为脉冲调幅信号。

在满足抽样定理的条件下，抽样信号保留了原信号的全部信息。

抽样定理：fs>2fh,才能从抽样信号中可以无失真的恢复出原信号。

抽样定理在通信系统、信息传输理论方面占有十分重要的地位。

数字通信系统是以此定理作为理论基础的。

在工作设备中，抽样过程是模拟信号数字化的第一步。

抽样性能的优劣关系到整个系统的性能指标。

抽样量化编码信道解码滤波收定时发定时PAM语音信号语音信号PAM图2-1 单路PCM系统示意图作为例子，图2-1示意地画出了传输一路语音信号的PCM系统。

从图中可以看出要实现对语音的PCM编码，首先就要对语音信号进行抽样，然后才能进行量化和编码。

因此，抽样过程是语音信号数字化的重要环节，也是一切模拟信号数字化的重要环节。

为了让实验者形象地观察抽样过程，加深对抽样定理的理解，本实验提供了一种典型的抽样电路。

实验三抽样定理和 PAM 调制解调实验一、实验目的1、通过脉冲幅度调制实验,使学生能加深理解脉冲幅度调制的原理。

2、通过对电路组成、波形和所测数据的分析,加深理解这种调制方式的优缺点。

二、实验内容1、观察模拟输入正弦波信号、抽样时钟的波形和脉冲幅度调制信号,并注意观察它们之间的相互关系及特点。

2、改变模拟输入信号或抽样时钟的频率,多次观察波形。

三、实验器材1、信号源模块一块2、①号模块一块3、 60M双踪示波器一台4、连接线若干四、实验原理 (一基本原理 1、抽样定理抽样定理表明:一个频带限制在 (0, H f 内的时间连续信号 ( m t , 如果以T ≤ Hf 21秒的间隔对它进行等间隔抽样,则 ( m t 将被所得到的抽样值完全确定。

假定将信号 ( m t 和周期为 T 的冲激函数 t (T 相乘, 如图 3-1所示。

乘积便是均匀间隔为 T 秒的冲激序列, 这些冲激序列的强度等于相应瞬时上 ( m t 的值, 它表示对函数 ( m t 的抽样。

若用 ( m t s 表示此抽样函数,则有:( ( ( s T m t m t t δ=图 3-1 抽样与恢复假设 ( m t 、( T t δ和 ( s m t 的频谱分别为( M ω、( T δω和( s M ω。

按照频率卷积定理, ( m t ( T t δ的傅立叶变换是( M ω和( T δω的卷积:[]1( ( ( 2s T M M ωωδωπ=* 因为 2( T Ts n n Tπδδωω∞=-∞=-∑Ts πω2=所以 1( ( ( s T s n M M n Tωωδωω∞=-∞⎡⎤=*-⎢⎥⎣⎦∑ 由卷积关系,上式可写成1( (s s n M M n T ωωω∞=-∞=-∑ 该式表明,已抽样信号 ( m t s 的频谱( M s ω是无穷多个间隔为ωs 的( M ω相迭加而成。

这就意味着( M s ω中包含( M ω的全部信息。

需要注意,若抽样间隔 T 变得大于Hf 21,则( M ω和( T δω的卷积在相邻的周期内存在重叠(亦称混叠,因此不能由 ( M s ω恢复( M ω。

实验二：抽样定理和脉冲调幅（PAM）实验一、实验目的通过本实验，学生应达到以下要求：1、观察并了解PAM信号形成、平顶展宽、解调和滤波等过程；2、验证并理解抽样定理，掌握对频谱混叠现象的分析方法；3、观察时分多路系统中非理想信道之间的路际串话现象，分析并掌握其形成原因。

二、实验内容本实验课完成以下实验内容：采用专用集成抽样保持开关完成对输入信号的抽样；多种抽样时隙的产生；采用低通滤波器完成对PAM信号的解调；测试出入信号频率与抽样频率之间的关系，观察频谱混叠现象，验证抽样定理；多路脉冲条幅（PAM）；观察并测试时分多路PAM信号和高频串话。

三、实验原理在通信技术中为了获取最大的经济效益，就必须充分利用信道的传输能力，扩大通信容量。

因此，采取多路化制式是极为重要的通信手段。

最常用的多路复用体制是频分多路复用( FDM) 通信系统和时分多路复用( TDM) 通信系统。

频分多路技术是利用不同频率的正弦载波对基带信号进行调制，把各路基带信号频谱搬移到不同的频段上，在同一信道上传输。

利用抽样脉冲把一个连续信号变为离散时间样值的过程称为抽样，抽样后的信号好称为脉冲调幅信号。

在满足抽样定理的条件下，抽样信号保留了原信号的全部信息。

抽样定理：fs>2fh,才能从抽样信号中可以无失真的恢复出原信号。

抽样定理在通信系统、信息传输理论方面占有十分重要的地位。

数字通信系统是以此定理作为理论基础的。

在工作设备中，抽样过程是模拟信号数字化的第一步。

抽样性能的优劣关系到整个系统的性能指标。

抽样量化编码信道解码滤波收定时发定时PAM语音信号语音信号PAM图2-1 单路PCM系统示意图作为例子，图2-1示意地画出了传输一路语音信号的PCM系统。

从图中可以看出要实现对语音的PCM编码，首先就要对语音信号进行抽样，然后才能进行量化和编码。

因此，抽样过程是语音信号数字化的重要环节，也是一切模拟信号数字化的重要环节。

为了让实验者形象地观察抽样过程，加深对抽样定理的理解，本实验提供了一种典型的抽样电路。

实验四 抽样定理和PAM 调制解调实验一、实验目的1．通过脉冲幅度调制实验，使学生能加深理解脉冲幅度调制的原理。

2．通过对电路组成、波形和所测数据的分析，加深理解这种调制方式的优缺点。

二、实验内容1．观察模拟输入正弦波信号、抽样时钟的波形和脉冲幅度调制信号，并注意观察它们之间的相互关系及特点。

2． 改变模拟输入信号或抽样时钟的频率，多次观察波形。

三、实验器材1．信号源模块 一块 2．①号模块 一块 3．20M 双踪示波器 一台 4．连接线 若干四、实验原理（一）基本原理 1．抽样定理抽样定理表明：一个频带限制在（0，H f ）内的时间连续信号()m t ，如果以T≤Hf 21秒的间隔对它进行等间隔抽样，则()m t 将被所得到的抽样值完全确定。

假定将信号()m t 和周期为T 的冲激函数）t (T δ相乘，如图1所示。

乘积便是均匀间隔为T 秒的冲激序列，这些冲激序列的强度等于相应瞬时上()m t 的值，它表示对函数()m t 的抽样。

若用()m t s 表示此抽样函数，则有：()()()s T m t m t t δ=图1 抽样与恢复假设()m t 、()T t δ和()s m t 的频谱分别为()M ω、()T δω和()s M ω。

有1()()s s n M M n T ωωω∞=-∞=-∑该式表明，已抽样信号()m t s 的频谱()M s ω是无穷多个间隔为ωs 的()M ω相迭加而成。

这就意味着()M s ω中包含()M ω的全部信息。

上面讨论了低通型连续信号的抽样。

如果连续信号的频带不是限于0与H f 之间，而是限制在L f （信号的最低频率）与H f （信号的最高频率）之间（带通型连续信号），那么，其抽样频率sf 并不要求达到H f 2，而是达到2B 即可，即要求抽样频率为带通信号带宽的两倍。

2．脉冲振幅调制（PAM ）所谓脉冲振幅调制，即是脉冲载波的幅度随输入信号变化的一种调制方式。

电子信息工程系实验报告课程名称：现代通信 实验项目名称：实验二 抽样定理和脉冲调幅（PAM ）实验 实验时间班级：电信092 姓名： 学号：910706220一、实 验 目 的:1.验证抽样定理；2.观察了解PAM 信号形成过程，平顶展宽解调过程。

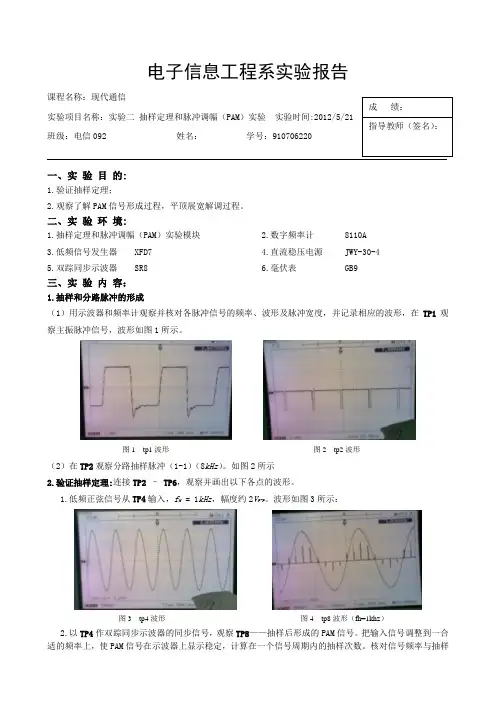
二、实 验 环 境:1.抽样定理和脉冲调幅（PAM ）实验模块2.数字频率计8110A 3.低频信号发生器 XFD7 4.直流稳压电源JWY-30-4 5.双踪同步示波器 SR8 6.毫伏表 GB9三、实 验 内 容：1.抽样和分路脉冲的形成（1）用示波器和频率计观察并核对各脉冲信号的频率、波形及脉冲宽度，并记录相应的波形，在TP1观察主振脉冲信号，波形如图1所示。

图1 tp1波形 图2 tp2波形（2）在TP2观察分路抽样脉冲（1-1）（8kHz ）。

如图2所示2.验证抽样定理:连接TP2 – TP6，观察并画出以下各点的波形。

1.低频正弦信号从TP4输入，f H = 1kHz ，幅度约2V P-P 。

波形如图3所示：图3 tp4波形 图4 tp8波形（fh=1khz ） 2.以TP4作双踪同步示波器的同步信号，观察TP8——抽样后形成的PAM 信号。

把输入信号调整到一合适的频率上，使PAM信号在示波器上显示稳定，计算在一个信号周期内的抽样次数。

核对信号频率与抽样频率的关系。

观察波形如图4所示：3.连接TP8 –TP14，在TP15观察经低通滤波器和放大器的解调信号。

测量其频率为1005Hz，确定和输入信号的关系如图5所示：图5 tp15波形（fh=1khz）图6tp4（fh=6khz）4.改变f H，令f H = 6kHz，重复步骤2，3项内容。

以TP4作双踪同步示波器的同步信号，观察TP8——抽样后形成的PAM信号。

把输入信号调整到一合适的频率上，使PAM信号在示波器上显示稳定，计算在一个信号周期内的抽样次数。

核对信号频率与抽样频率的关系。

观察波形如图7所示：连接TP8 –TP14，在TP15观察经低通滤波器和放大器的解调信号。

抽样定理和脉冲调幅(PAM)实验抽样定理，也称为奈奎斯特-香农定理或奈斯凯-香农定理，是信号处理中的一条基本定理，它表明，如果我们想要完全恢复连续的信号，我们必须将信号进行采样，采样频率必须要大于信号中频率最高的成分的两倍。

抽样定理告诉我们，如果我们使用低于两倍信号最高频率的采样频率，则不能完整地恢复原始信号。

因此，抽样定理是数字信号处理的基础之一。

脉冲调幅（PAM）是数字通信的一种基本模式，其通过将模拟信号转换为数字信号来完成模拟通信与数字通信之间的转换。

PAM是一种基本的数字化模拟调制技术，它将模拟信号进行采样并将其转换为数字信号，在数字信号中，每个样本由一个固定数量的二进制数表示。

在PAM中，我们使用一个调制脉冲来调制数据信号，这样可以将数据信号从一个信号空间映射到另一个信号空间，因此可以实现数字化通信。

在实际应用中，抽样定理和脉冲调幅（PAM）通常被用于数字通信和数字信号处理方面。

为了理解抽样定理和脉冲调幅（PAM）如何工作，我们可以进行以下实验：实验1：抽样定理实验在这个实验中，我们需要一个函数生成器（signal generator）和一个示波器（oscilloscope）来生成和观察信号。

设置函数生成器以产生一个正弦波信号，然后使用示波器来查看该信号。

以5kHz的频率采样信号，观察它的样本的数量和质量。

接下来，将抽样频率调整为10kHz并观察示波器上的波形，你会发现它看起来更平滑。

继续增加采样率以尝试找到一个极限值，达到这个极限值之后，再增加采样率不会对信号的质量产生任何显著的改进。

实验2：脉冲调幅实验在这个实验中，我们需要一个数字信号生成器（digital signal generator）、一个数字信号记录仪（digital signal recorder）和一个示波器。

设置数字信号生成器以产生一个正弦波数据信号，然后使用数字信号记录仪来记录该信号。

接下来，使用示波器来查看该记录的数字信号。

实验六 PAM 系统中的码间干扰（课程设计）一、实验目的1、了解脉冲幅度调制（PAM ）系统中引起的码间干扰（ISI ）问题；2、利用MATLAB 仿真PAM 系统。

二、实验原理在脉冲幅度调制（PAM ）系统中，一个离散时间消息是在一条通信信道上是用调制一个星期重复的脉冲来传送的。

取决于信道的带宽限制和这个脉冲形状的时间特性，被调制的这个脉冲所发送的每个信息样本可以在相邻的消息样本之间无干扰地被接收到。

然而，如果传输信道的带宽限制造成了传送脉冲在时间上弥撒，那么就能发生显著的码间干扰（ISI ）。

这个练习要研究在PAM 系统内所引起的ISI 的有关问题。

考虑一种简单的二进制通信系统，其中“1”是用传送脉冲p (t )来表示，而“0”则用传送脉冲的负值，即－p (t )来表示。

这称为双极性（antipodal ）信令。

p (t )函数可以表示为⎩⎨⎧<-=t,0||,/||1)(其余Tt T t t p 这些脉冲传输速率是每秒b f 个脉冲，称之为二进制PAM 系统的比特率。

这个练习中，假定1.0=T ，可考虑两种可能的比特率值，即T f b /1=和)2/(1T f b =。

三、实验内容在时间样本[-T:dt:T]，dt ＝T/10上产生脉冲p (t )，确定在传送波形中没有任何码间干扰的最大b f 值。

这就是说，在信号)/()(1∑=-=N k b k f k t p a t y 中N 个脉冲不重叠的最大b f 值是什么？在该比特率下所取的并且位于脉冲峰值的样本不受码间干扰影响的最大b f 值是什么，也即?)0()/)(()/(1p f k n p f n y N k b b =-=∑=参考：可以考虑用眼图来估计脉冲形状并决定所产生码间干扰程度。

一张眼图是这样展现出来的：产生一个随机二进制序列，并用等于示波器水平扫描速度整数倍的比特率在示波器上展示所得到的信号。

在示波屏上全部脉冲形状都互相重叠在一起。

实验二第一部分1.脉冲幅度调制实验步骤用示波器在TP601处观察，以该点信号输出幅度不失真时为好，如有削顶失真则减小外加信号源的输出幅度或调节W108。

在TPP603处观察其取样脉冲信号。

改变CA601处的电容，再用示波器观察TP602该点波形。

做详细记录、绘图。

2.PAM通信系统实验步骤(1)将K602的2端和3端相连，为CPLD产生的8KHz抽样时钟脉冲，用示波器观测TP601～TP604各点波形，并做详细记录、绘图。

(2)将K602的1端和2端相连，然后改变CA601的电容，即改变抽样频率f sr，使f＞f sr、 f c =2f sr、f c＜2f sr，在TP603处用示波器观测系统输出波形，以判断和验证取样定理在系统中的正确性，同时做记录和绘图，记下在系统通信状态下的奈奎斯特速率。

(3)在TP111处用示波器观察话音输出波形，通过喇叭听话音，感性判断该系统对话音信号的传输质量。

3.CA601上插电容，可改变抽样时钟。

电容在5600pf～0.1 f 之间。

五.测量点说明TP601：若外加信号幅度过大，则被限幅电路限幅成方波了，因此信号波形幅度尽量小一些。

方法是：调节通信话路终端发送放大电路中的电位器 W108。

TP602：抽样脉冲波形输出，其抽样脉冲波形由抽样时钟电路(在TP603处观察)决定，在抽样时钟电路里，在CA601中插上不同大小的电容，可改变抽样时钟的频率。

电容值在5600pf~0.1μf 之间选取。

TP603：抽样时钟信号输出，抽样频率由CA601上的电容大小决定，用频率计测量其频率的大小。

电容值在5600pf～0.1μf 之间选取；另一种抽样时钟为CPLD可编程模块产生的8KHz时钟脉冲，由开关K602选择。

TP604：收端PAM调制信号，由开关K601的1脚与2脚相接。

开关的设置：K601：取样与解调。

K602：取样脉冲选择，1—2：555定时器产生的脉冲；2—3：电路内部产生的8KHz脉冲。

《通信原理》实验报告实验三：抽样定理和PAM调制解调实验系别：信息科学与工程学院专业班级：通信1003 班学生姓名：揭芳073同组学生：杨亦奥成绩：指导教师：惠龙飞（实验时间：20 12 年12 月7 日——20 12 年12 月7 日）华中科技大学武昌分校一、实验目的1、 通过脉冲幅度调制实验，使学生能加深理解脉冲幅度调制的原理。

2、 通过实验，了解了自然抽样和平顶抽样的区别3、 对抽样定理的更深一步的了解4、 通过对电路组成、波形和所测数据的分析，加深理解这种调制方式的优缺点。

二、实验内容1、 观察模拟输入正弦波信号、抽样时钟的波形和脉冲幅度调制信号，并注意观察它们之间的相互关系及特点。

2、 改变模拟输入信号或抽样时钟的频率，多次观察波形。

三、实验器材1、 信号源模块 一块2、 ①号模块 一块3、 20M 双踪示波器 一台4、 连接线 若干四、实验原理（一）基本原理 1、抽样定理抽样定理表明：一个频带限制在（0，H f ）内的时间连续信号()m t ，如果以T ≤Hf 21秒的间隔对它进行等间隔抽样，则()m t 将被所得到的抽样值完全确定。

假定将信号()m t 和周期为T 的冲激函数）t (T δ相乘，如图3-1所示。

乘积便是均匀间隔为T 秒的冲激序列，这些冲激序列的强度等于相应瞬时上()m t 的值，它表示对函数()m t 的抽样。

若用()m t s 表示此抽样函数，则有：()()()s T m t m t t δ=图3-1 抽样与恢复假设()m t 、()T t δ和()s m t 的频谱分别为()M ω、()T δω和()s M ω。

按照频率卷积定理，()m t ()T t δ的傅立叶变换是()M ω和()T δω的卷积：[]1()()()2s T M M ωωδωπ=* 因为 2()T Ts n n Tπδδωω∞=-∞=-∑Ts πω2=所以 1()()()s T s n M M n T ωωδωω∞=-∞⎡⎤=*-⎢⎥⎣⎦∑由卷积关系，上式可写成1()()s s n M M n T ωωω∞=-∞=-∑该式表明，已抽样信号()m t s 的频谱()M s ω是无穷多个间隔为ωs 的()M ω相迭加而成。

南昌大学实验报告学生姓名：学号：专业班级：实验类型：■验证□综合□设计□创新实验日期：实验成绩：实验四抽样定理与PAM系统实训一、实验目的1.熟通过对模拟信号抽样的实验,加深对抽样定理的理解；2.通过PAM调制实验，使学生能加深理解脉冲幅度调制的特点；3.通过对电路组成、波形和所测数据的分析，了解PAM调制方式的优缺点。

二、实验原理1.取样（抽样、采样）（1）取样取样是把时间连续的模拟信号变换为时间离散信号的过程。

（2）抽样定理一个频带限制在(0,f H) 内的时间连续信号m(t)，如果以≦1/2f H每秒的间隔对它进行等间隔抽样，则m(t)将被所得到的抽样值完全确定。

（3）取样分类①理想取样、自然取样、平顶取样；②低通取样和带通取样。

2.脉冲振幅调制电路原理（PAM）（1）脉冲幅度调制系统系统由输入电路、高速电子开关电路、脉冲发生电路、解调滤波电路、功放输出电路等五部分组成。

图 1 脉冲振幅调制电路原理框图（2）取样电路取样电路是用4066模拟门电路实现。

当取样脉冲为高电位时，取出信号样值；当取样脉冲为低电位，输出电压为0。

图 2 抽样电路图 3 低通滤波电路三、实验步骤1.函数信号发生器产生2KHz（2V）模拟信号送入SP301，记fs；2.555电路模块输出抽样脉冲，送入SP304，连接SP304和SP302，记fc；3.分别观察fc>>2fs，fc=2fs，fc<2fs各点波形；4.连接SP204 与SP301、SP303H 与SP306、SP305 与TP207，把扬声器J204开关置到1、2 位置，触发SW201 开关，变化SP302 的输入时钟信号频率，听辨音乐信号的质量.四、实验内容及现象1.测量点波形图 4 TP301 模拟信号输入图 5 TP302 抽样时钟波形(555稍有失真) fc=图 6 TP303 抽样信号输出1图7 TP304 模拟信号还原输出1图8 TP303 抽样信号输出2图9 TP304 模拟信号还原输出2图10 TP303 抽样信号输出3图11 TP304 模拟信号还原输出32.电路Multisim仿真图12 PAM调制解调仿真电路图13 模拟信号输入图14 抽样脉冲波形图15 PAM信号图16 低通滤波器特性图17 还原波形 更多学习资料请见我的个人主页：落寂花溅泪。

电子信息工程学系实验报告课程名称：通信原理实验项目名称：实验2 抽样定理和脉冲调幅（PAM）实验实验时间：2012.5.21班级：电信091 姓名：林杨亮学号：910706104实验目的:1、验证抽样定理；2、观察了解PAM信号形成过程，平顶展宽解调过程。

实验原理:利用抽样脉冲把一个连续信号变为离散时间样值的过程称为抽样，抽样后的信号好称为脉冲调幅信号。

在满足抽样定理的条件下，抽样信号保留了原信号的全部信息。

抽样定理：fs>2fh,才能从抽样信号中可以无失真的恢复出原信号。

分路抽样电路的作用是：将在时间上连续的语音信号经脉冲抽样形成时间上离散的脉冲调幅信号。

N路抽样脉冲在时间上是互不相交，顺序排列的，各路的抽样信号在多路汇接的公共负载上相加便形成合路的脉冲调幅信号，本实验设置了两路抽样电路。

多路脉冲调幅系统中的路际串话，在一个理想的传输系统中，各路PAM 信号应是严格地限制在本路时隙中的矩形脉冲。

但如果传输PAM信号的通道频带是有限的，则PAM信号就会出现拖尾现象。

实验内容及过程：1.抽样和分路脉冲的形成用示波器和频率计观察并核对各脉冲信号的频率、波形及脉冲宽度，并记录相应的波形。

（1）在TP1观察主振脉冲信号。

（2）在TP2观察分路抽样脉冲（8kHz）。

抽样和分路脉冲的形成波形如图1、图2所示。

由图1可知，主振脉冲信号的频率为2.048KHz，脉冲宽度为240ns。

由图2可知，分路抽样脉冲频率为8KHz，其脉冲宽度为10us。

图1 主振脉冲信号波形图2 分路抽样脉冲波形2.验证抽样定理连接TP2–TP6，观察并画出以下各点的波形。

（1）低频正弦信号从TP4输入，f H = 1kHz，幅度约2V P-P。

（2）以TP4作双踪同步示波器的同步信号，观察TP8——抽样后形成的PAM信号。

把输入信号调整到一合适的频率上，使PAM信号在示波器上显示稳定，计算在一个信号周期内的抽样次数。

核对信号频率与抽样频率的关系。