当前位置：文档之家 › 统计学抽样推断计算题答案课件

统计学抽样推断计算题答案课件

  • 格式：ppt
  • 大小：142.00 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

《统计抽样推断》课件

《统计抽样推断》课件


实例二：产品质量检测抽样设计
总结词
严谨且准确
VS
详细描述
产品质量检测抽样设计是确保产品质量的 重要环节。通过严谨的抽样设计和统计分 析，能够准确地评估产品的质量状况，及 时发现并解决潜在的质量问题。
实例三：社会现象研究抽样设计
总结词
客观且公正
详细描述
社会现象研究抽样设计在社会科学研究中具 有广泛的应用。通过客观公正的抽样方法， 能够有效地揭示社会现象的内在规律，为政 策制定和社会管理提供科学依据。
02
03
非随机抽样
样本容量
如果样本不是随机抽取的，那么 样本可能不能代表总体，从而导 致抽样误差。
样本容量的大小也会影响抽样误 差，一般来说，样本容量越大， 抽样误差越小。
抽样误差的估计
标准误差
标准误差是衡量抽样误差的一个常用指标，它表示样 本均值的分布情况。
变异系数
变异系数是标准误差与样本均值之比，用于比较不同 样本的标准误差。
《统计抽样推断》ppt课件
目录
• 抽样的基本概念 • 抽样方法 • 样本统计量 • 抽样误差 • 置信区间和假设检验 • 实例分析
01
抽样的基本概念
抽样的定义与目的
定义
抽样是从总体中选取一部分个体进行 研究的过程。
目的
通过对样本的观察和分析，推断总体 的特征和规律。
抽样的分类
随机抽样
按照随机原则从总体中抽取样 本，每个个体被选中的机会相
置信区间
通过置信区间可以估计样本均值与总体均值之间的差 距，从而了解抽样误差的大小。
降低抽样误差的方法
增加样本容量 随机抽样 分层抽样 重复抽样
增加样本容量可以减少抽样误差，因为更多的样本可以提供更 准确的信息。
统计学基础课件(第六章抽样推断)

统计学基础课件(第六章抽样推断)


Fundamentals of Statistics
统计是指这种偶然性代表性误差。 即按随机原则抽样时，在没有登记性误差和系统性误 差的条件下单纯由于不同的随机样本得出不同估计量 而产生的误差。抽样误差是抽样调查所固有的，是无 法避免与消除的，但可以运用数学方法计算其数量界 限，并通过抽样设计程序控制其范围，所以这种抽样 误差也称为可控制误差。 需要指出，抽样误差不是 固定不变的数，它的数值是随样本不同而变化的，所 以它也是随机变量。
重复抽样 AA AB AC AD BA BB BC BD CA CB CC CD DA DB DC DD
N n = 42 =16 (个样本)
Fundamentals of Statistics
统计学基础
第六章 抽样推断
不重复抽样
N（N-1）（N-2）……. 4×3 = 12(个样本)
Fundamentals of Statistics
Fundamentals of Statistics
统计学基础
第六章 抽样推断
本章主要内容 •抽样推断概述 •抽样误差 •抽样估计的方法 •样本容量的确定
Fundamentals of Statistics
统计学基础
第第一六章节抽样推抽断样推断概述
一、抽样推断的概念和特点 概念
抽样推断是在抽样调查的基础上，用样 本实际资料计算样本指标，并据以推算总 体相应的数量特征的一种统计分析方法。
代表性误差的发生有以下两种情况：
一种是由于违反抽样调查的随机原则，如有意地多选较好的 单位或较坏的单位进行调查。这样做，所据以计算的抽样指标 必然出现偏高或偏低现象，造成系统性的误差。系统性误差和 登记性误差都是不应当发生的，是可以也应该采取措施避免发 生或将其减小到最小限度。
抽样推断培训课件(doc 9页)

抽样推断培训课件(doc 9页)

抽样推断培训课件(doc 9页)第七章抽样推断一、本章复习脉络二、本章复习要点1．抽样推断的意义：抽样推断是在抽样调查的基础上，利用样本的实际资料计算样本指标，并据以推算总体相应数量特征的一种统计分析方法。

抽样推断是在根据随机原则从总体中抽取部分实际数据的基础上，运用数理统计方法，对总体某一现象的数量性作出具有一定可靠程度的估计判断。

2．抽样推断的特点：①它是由部分推算整体的一种研究方法；②它是建立在随机抽样的基础上；③它是运用概率估计方法；④其误差可以事先计算并加以控制。

3．全及总体（总体）：指所要认识的研究对象全体，它是由所研究范围内具有某种共同性质的全体单位所组成的集合体。

一般用N表示。

4．样本总体：又称子样，它是从全及总体中随机抽取出来，作为代表这一总体的那部分单位组成的集合体。

一般用n表示。

作为推断对象的总体是确定的，而且是唯一的。

作为观察对象的样本不是确定的，也不是唯一的，而是可变的。

5．参数：由总体各单位的标志值或标志属性决定的全及指标称为参数。

常用的总体参数有14．抽样极限误差：是指抽样指标与总体指标之间误差可允许的最大范围。

它等于样本指15．抽样估计的置信度：它表明抽样指标和总体指标的误差不超过一定范围的概率有多大，各种概率保证程度和抽样误差的概率度t是密切联系，并随t增大而增大。

它是t的函数，用F(t)表示。

概率：指在随机事件进行大量试验中，某种文件出现的可能性大小，它通常可以用某种事件出现的频率来表示。

抽样误差范围和估计置信度是密切不可分离的，而且抽样误差范围小，则估计的置信度也愈小。

16．抽样估计：利用实际调查计算的样本指标值来估计相应的总体指标的数值。

总体指标是表明总体数量特征的参数，也称为参数估计。

17．点估计：根据总体指标的结构形式设计样本指标（称统计量）作为总体参数的估计量，并以样本指标的实际值直接作为相应总体参数的估计值。

18．区间估计：根据给定的概率保证程度的要求，利用实际抽样资料，指出总体被估计值的上限和下限，即指出总体参数可能存在的区间范围，而不是直接给出总体参数的估计值。

财务管理 统计学 第八章 抽样推断 ppt课件

财务管理 统计学 第八章 抽样推断 ppt课件


应用
仅适用于单位数不多、标志变异较 小、分布较均匀的总体
是最简单、最基本、最符合随机原则， 但同时也是抽样误差最大的抽样组织形式
财务管理 统计学 第八章 抽样推断
11
2.类型抽样
——将总体全部单位分类，形成若干个类型组， 然后从各类型中分别抽取样本单位组成样本。
N1
n1
总体
N
N2
n2
··· ···
5
抽样估计的应用
不可能进行全面调查时 不必要进行全面调查时 检查生产过程正常与否 对全面调查资料进行补充修正时
财务管理 统计学 第八章 抽样推断
6
二、若干基本概念
（一）总体与样本 总体：研究对象的全体。 个体：组成总体的每个元素。 样本：从总体中抽取的一部分个体。 样本容量：样本中个体的个数。 一般说来，总体是唯一的，而样本是不唯一 样本容量大于30的称为大样本,反之,即为小样
➢ 统计推断：根据抽样调查所获得的信息，对总体的 数量特征作出具有一定程度的估计和推断。
财务管理 统计学 第八章 抽样推断
4
（二）特点 按随机原则（等可能性原则）抽取调查单位 根据部分推断总体的数量特征 抽样推断的结果具有一定的可靠性和准确性，
抽样误差可以事先计算和控制
财务管理 统计学 第八章 抽样推断
（总体单位按某一标志排序）
按无关标志排队，其抽样效果相当于简单随机抽样； 按有关标志排队，其抽样效果相当于类型抽样。
财务管理 统计学 第八章 抽样推断
13
4.整群抽样（集团抽样） — 将总体全部单位分为若干“群”，然
后随机抽取一部分“群”，被抽中群体的所 有单位构成样本
例：总体群数R=16 样本群数r=4
统计学课件：抽样推断

统计学课件：抽样推断


3.当总体X~N（, 2）,从中抽取容量为n的样本，则
n
2
(n 1)s2
2
~
（2 n-1）; 2
(xi x)2
i 1
2
~
（2 n-1）
4. 2—分布的性质 （1）分布可加性 若X ~ 2(n1)，Y~ 2(n2 )， X，Y独立，则 X +Y ~ 2(n1+n2 ) （2）期望与方差 若X~ 2(n)，则 E(X)= n，D(X)=2n
3、进行产品质量检验 4、进行假设检验
（一）总体和样本 1、总体 总体也称全及总体，指所有认识的研究对象全体，它是
有所研究范围内具有某种共同性质的全体单位所组成的 集合体。 一般用英文字母大写N来表示总体的单位数。 2、样本 样本又称子样，它是从全及总体中随机抽取出来，作为 代表这一总体的那部分单位组成的集合体。 一般用英文小写字母n来表示样本的单位数。
5. 分位点 设X ~ 2(n)，若对于：0<<1，
存在 2 (n) 0 满足
P{X 2 (n)} ,
则称 2 (n) 为 2 (n) 分布的上分位点。
2
(n
)
（二）t 分布
若X 服从N (0,1)，Y 服从自由度为n的 2分布, 且X 和Y 独立，则 X
Y /n 服从自由度为n的 t分布。
1、全及指标 根据各单位的标志值或标志属性计算的，反映总体
数量特征的综合指标称为全及指标，又称为参数。
设总体变量 X 为: X1, X 2 ,X N 则有:
X X XF N F
2 X X 2 X X 2 F
N
F
设总体 N 个单位,有 N1 个单位具有某种性质, N0 个单位不具有某种性质,
《抽样推断》课件 (2)

《抽样推断》课件 (2)


参数估计
通过样本数据得到总体参数的估计值。
1
点估计
用单个统计量估计总体参数。
2
区间估计
用一个区间估计总体参数，包含真实参数的可能范围。
3
最大似然估计
选择使样本数据出现的概率最大的参数估计值。
置信区间的计算
置信区间提供了一个总体参数的范围估计。
计算方法
正态分布假设
根据样本数据和置信水平， 使用统计方法计算置信区间。
《抽样推断》PPT课件 (2)
抽样推断是统计学的重要概念之一，通过从总体中选取一部分样本，对总体 的特征进行推断。本课件将介绍抽样推断的概念、抽样方法、样本容量的确 定、参数估计、置信区间的计算、假设检验的基本原理以及实例分析。
抽样推断的概念
抽样推断是从样本数据中，通过统计方法推断总体的特征。借助抽样推断，我们能够在研究中得 到有关总体的重要信息，而无需对整个总体进行研究。
3 分层抽样
4 整群抽样
将总体划分为若干层，每层内进行简单 随机抽样。
将总体划分为若干群，随机抽取群内的 全部个体作为样本。
样本容量的确定
样本容量的大小对抽样推断的准确性有重要影响。
总体大小
总体越大，需要的样本容 量越大。
可接受的抽
置信水平
置信水平越高，需要的样 本容量越大。
在满足一定条件下，可以使 用正态分布进行置信区间的 计算。
置信水平
置信区间给出的范围包含了 真实总体参数的概率。
假设检验的基本原理
假设检验用于对总体参数的某个假设进行验证。
原假设
对总体参数的一个特定 值或范围的假设。
备择假设
与原假设相对立的假设。
检验统计量
用于比较观察到的样本 数据与原假设的预期值。
统计学抽样推断计算题答案

统计学抽样推断计算题答案


【解】五、4题 (1)
已知： x =1000小时，s＝15小时元， n=100
μ x= σ
2
n
=
s
2
n
=
15
2
100
= 1 . 5 ( 小时 )
Δ x =tμ x = 2× .5= 3(小时) 1
x± x =1000 ± Δ 3 = [997, 1003]小时
【解】五、4题 (1)
n 1= t σ Δ
要求：1）计算样本平均数和抽样平均误差； 2）以95.45%的可靠性估计该厂工人的 月平均工资和工资总额的区间。
样本平均数和方差计算表
月平均 工人数 工资(元) (人) 524 4 534 6 540 9 550 10 560 8 580 6 600 4 660 3 50 合计 xf 2096 3204 4860 5500 4480 3480 2400 1980 28000 (x-x) f 5184 4056 3600 1000 0 2400 6400 30000 52640
2 1 2 2
n2=
t σ
2
2 2
(0.5Δ1 )
=4n1
=4× 100=400(只)
平均工资的置信区间为：
［550.82，569.18］元
工资总额的置信区间为： ［550.82×1500，569.18× 1500］元
即为：［826230，853770］元
五、2题
从一批袋装食品中，按简单随机重复 抽样方法抽取50 包检查，结果如下：
每包重量(克) 90-95 95-100 100-105 105-110 包数(包) 2 3 35 10
【解】五、3题 (2)
已知， p＝10／100＝10%
第七章 抽样推断 (《统计学》PPT课件)

第七章 抽样推断 (《统计学》PPT课件)


接作为相应全及指标的估计值。
2.定义：设x_
表示总体平均数
__
X
的估计值，p^ 表示
总体成数P的估计值，则有：
__ _
X x
或
^
Pp
27
第四节 抽样估计
二、总体参数的点估计
3. 性质：
用抽样指标估计总体指标时，要求抽样指标
的平均数等于被估计的总体指标；E（
_
x）
__
X
_
E（ p） P
用抽样指标估计总体指标时，要求当样本容 量n充分大时抽样指标充分靠近总体指标；
6
第一节 抽样推断概述
二、有关抽样的基本范畴
2.指标
：根据全及总体各个单位的标志值或标 志特征计算的，用来反映全及总体某种属性的综合 指标；
：由样本总体各单位标志值或标志特征 计算出的综合指标。
注：对于一个确定的问题，全及指标是唯一的， 样本指标不是唯一确定的，即样本指标的随机变量。
7
抽样推断
2.种类：
根据抽样资料计算样本指标，并以此直接作 为相应全及指标的估计值；
根据给定的概率保证程度的要求，利用实 际抽样资料，求出总体被估计值的上限和下限，即给 出总体参数可能存在的区间范围，而不是直接给出总 体参数的估计值。
26
第四节 抽样估计
二、总体参数的点估计
根据抽样资料计算样本指标，并以此直
n
N
22
第三节 抽样误差
三、抽样极限误差
在抽样推断中可允许的误差范围，等于样本指 标可允许变动的上限或下限与总体指标之差的绝对值。
2.计算公式：
_ __
_
__ _
抽样平均数极限误差： 或
_ x- X
《统计基础》教学课件07抽样推断

《统计基础》教学课件07抽样推断

参加俱乐部。所以，贫困阶层在样本中缺乏其 应有的代表性。
不重复不遗漏！
8-21
任务二 计算抽样误差
统计误差
➢调查样本所得结果与总体真实数值之间的差异
登记性误差：观察、测量、登记差错或得到虚假信息
抽样误差
系统误差：未遵循随机原则
代表性误差
随机误差：偶然性因素引起
8-22
任务二 计算抽样误差
抽样平均误差
➢总体/全及总体（N）
• 含义：所要认识对象的全体 ➢样本/抽样总体（n）
• 含义
• 从总体中随机抽取出来的一部分单位组成的集合体 • 30个以上为大样本，30个以下为小样本
总体是唯一确定的，而样本不是唯一确定的！
8-6
基本概念
概念 单位数目 平均数
成数 方差 标准差
唯一确定
总体指标 N
随机变量
简单随机抽样 分层抽样 等距抽样 整群抽样
多阶段抽样
简单随机抽样
➢ 含义
• 完全随机地抽取调查单位。 【情境】某高校市场营
➢ 方法
• 直接抽选法 • 抽签法
将总体单位编号，从中随机 抽取号签作为样本。
• 随机数字表法
➢ 特点
销专业约1000名学生， 若要了解他们的就业倾 向，如何从中抽取200 名学生作为样本？
8-18
小结
抽样方法 简单随机 抽样分源自抽样定义具体方法完全随机地抽选样本
直接抽选法 抽签法 随机数字表法
先按某一标志分组，再在各组 等比例抽样
中随机抽取样本
不等比例抽样
特点
各单位需均匀分布 需要事先编号 不能充分利用信息
组内差异小，组间差 异大
将按某一标志排序，再按固定 无关标志排序抽样
抽样推断-37页PPT文档资料

抽样推断-37页PPT文档资料


x :抽样平均数的抽样误极差限 p : 抽 样 成 数 的 抽 样 极 限差误
x

xX
xXx
x
x
P pP ppPpp
26
(xx,xx)或（ pp,pp）称为置. 信区
23.09.2019
第二节 抽样误差 五、抽样误差的概率度
用 除以 (或者 除 用以 )，得到 t， t数 就值 称
样本又称子样，是从全及总体中随机抽取出来，作为代表 这一总体的那部分单位组成的集合体，一般用n表示。
总 体N （唯一）
7
样 本n （非唯一）
23.09.2019
第一节 统计推断概述 四、抽样推断中的基本概念
（二）总体指标和样本指标
总体指标是根据总体各单位的标志值或标志 特征计算的，反映总体数量特征的综合指标， 称为全及指标，由总体各单位的标志值或标 志特征所决定，全及指标的指标值是确定的， 唯一的，所以又称为参数。
15
23.09.2019
不同抽样方法的样本个数
重复抽样
考虑顺序 BnN=Nn
抽样方法
不考虑顺序 D n N C n N n 1 ( N n 1 ） n N ! n （ 2 ) N
不重复抽样
考虑顺序 A n N N ( N 1 ) ( N n 1 )
n
d.可以通过调整样本单位数n来控制抽样平均误差。
23
23.09.2019
第二节 抽样误差
抽样平均误差的计算
重复抽样
不重复抽样
样本平均数 的平均误差

2

x
nn
2 (1n)
x
nN
样本成数 的平均误差
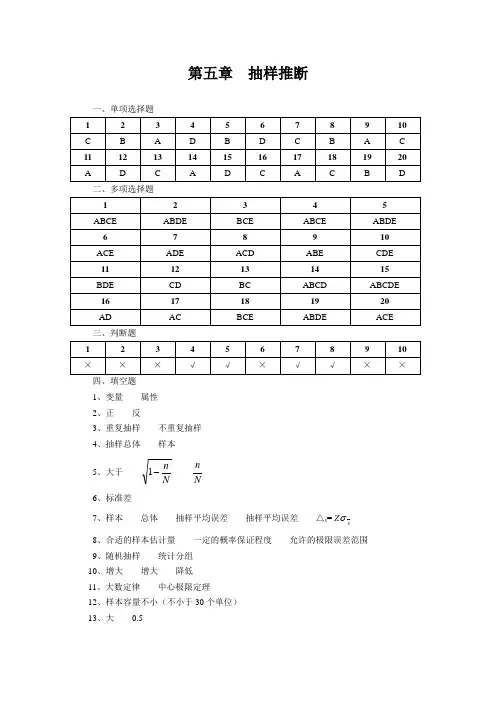
统计学 第五章 抽样推断课后答案

统计学 第五章 抽样推断课后答案

第五章 抽样推断一、单项选择题 1 2 3 4 5 6 7 8 9 10 C B A D B D C B A C 11 12 13 14 15 16 17 18 19 20 ADCADCACBD二、多项选择题1 2 3 4 5 ABCE ABDE BCE ABCE ABDE 6 7 8 9 10 ACE ADE ACD ABE CDE 11 12 13 14 15 BDE CD BC ABCD ABCDE 16 17 18 19 20 AD ACBCEABDEACE三、判断题 1 2 3 4 5 6 7 8 9 10 ×××√√×√√××四、填空题 1、变量 属性 2、正 反3、重复抽样 不重复抽样4、抽样总体 样本5、大于 N n -1 Nn 6、标准差7、样本 总体 抽样平均误差 抽样平均误差 △x = Z x σ 8、合适的样本估计量 一定的概率保证程度 允许的极限误差范围 9、随机抽样 统计分组 10、增大 增大 降低 11、大数定律 中心极限定理 12、样本容量不小（不小于30个单位） 13、大 0.514、缩小33（即0.5774） 扩大 1.1180 15、估计量（或统计量） 参数 五、简答题（略） 六、计算题1、已知条件：P = 0.5 ，n = 100 且重复抽样 求：p ≤0.45的概率 解：Z =1100)5.01(5.05.045.0)1(=-⨯-=--nP P P p则F (Z = 1) = 0.6827 所以p ≤0.45的概率为：26827.01-= 0.15865 2、解E (x 1) = E （0.5X 1 + 0.3X 2 + 0.2X 3） = 0.5 E (X ) + 0.3 E (X ) + 0.2E (X ) = E (X ) = XE (x 2) = E （0.5X 1 + 0.25X 2 + 0.25X 3）= 0.5 E (X ) + 0.25 E (X ) + 0.25E (X )= E (X ) = XE (x 3) = E （0.4X 1 + 0.3X 2 + 0.3X 3） = 0.4 E (X ) + 0.3 E (X ) + 0.3E (X ) = E (X ) = X 所以x 1、x 2、x 3都是X 的无偏估计量。

统计-抽样推断PPT课件


➢按等价公式计算：
x
2 2.5 1.12(岁)
n
2
2 ( X X ) 2 ( 2 2 0 ) 2 ( 2 2 2 1 ) 2 ( 2 2 2 3 ) 2 ( 2 2 2 4 ) 2 2 2 . 5
N
4
.
12
• 对上述公式的验证——
例：有甲乙丙丁四个人，年龄分别为20、21、23、24岁，现随机抽 2人调查年龄，试计算抽样平均误差。
由 xt x
X
xtx，把有关数据代 结 该论 批入： 茶： 叶以达9到9.了73重%的量概规率格认。为
1. 3 5 3 0 0 . 0 8 X 7 1 5 6 0 3 0 . 0 .3 876
即15 ： 0.0 4X150.5（ 6 克） .
24
练习
某灯泡厂某月生产灯泡400万个，随机抽取400个进行检验， 得资料如下表：
20
-2
4
甲，乙
20，21
20.5
-1.5
2.25
甲，丙
20，23
21.5
-0.5
0.25
甲，丁
20，24
22
0
0
乙，甲
21，20
20.5
-1.5
2.25
乙，乙
21，21
21
-1
1
乙，丙
21，23
22
0
乙，丁
21，24
22.5
0.5
丙，甲
23，20
21.5
-0.5
丙，乙
23，21
22
0
丙，丙
23，23
.
4
第二节 抽样推断的相关概念
一、总体（又称全及总体）

统计学 抽样推断课件

x
p
p
p
三、抽样估计与推算
总体参数的点估计 抽样估计的精度 抽样估计的置信度 总体参数的区间估计
1、总体参数的点估计
参数点估计的基本特点是，根据总体指标 的结构形式设计样本指标（称统计量）作 为总体参数的估计量，并以样本指标的实 际值直接作为相应总体参数的估计值。 优良估计总标准有三个方面：无偏性 、一 致性 、有效性
课堂练习
15.进行简单随机重复抽样，假定抽样单位增加3倍，则 抽样平均误差将发生如何变化？如果要求抽样误差减少 20%，其样本单位数应如何调整？ 16.某工厂有1500个工人，用简单随机重复抽样的方法 抽出50个工人作为样本，调查其工资水平，如下表：
月工资水平（元） 524 534 540 550 560 580 600 660
课堂练习
8.假定10亿人口大国和100万人口小国的居民年龄变异程 度相同。现在各自用重复抽样的方法抽取本国的1%人口计 算平均年龄，问两国平均年龄抽样平均误差是否相同，或 哪国比较大？ 9.参数估计的优良标准是什么？抽样平均数和抽样成数估 计是否符合优良估计标准，试加以说明。 10.什么是概率度？什么是置信度？这两者有什么关系？ 11.类型抽样中的分组和整群抽样中的分群有什么不同意 义和不同要求？ 12.试比较等距抽样中按无关标志和按有关标志排队的优 缺点，比较有标志排队中半距起点固定间隔取样和随机起 点对称等距取样的优缺点。
教学重点与难点
一、有关抽样的基本概念——总体和样本、 参数和统计量、样本容量和样本个数重复 抽样和不重复抽样。 二、抽样误差的意义及其影响因素、抽样 极限误差、抽样平均误差、抽样估计等内 容。
教学内容
一、抽样推断的基础 二、抽样推断与误差 三、抽样估计与推算

统计抽样推断PPT课件


2021/5/4
3
第3页/共60页
第一节 抽样推断的意义
3、特点： (1)它是由部分推断整体的一种认识方法。 (2)抽样推断建立在随机取样的基础上。
(3)抽样推断运用概率估计的方法。 (4)抽样推断的抽样误差是不可避免的， 但可以事先计算并加以控制。
2021/5/4
4
第4页/共60页
二、统计推断内容
则：
x
n
300 15(小时) 400
x
2 1 n
n N
3002 1 400 13.42(小时) 400 2000
计算结果表明：根据部分产品推断全部产品的平均使用寿命 时，采用不重复抽样比重复抽样的平均误差要小。
2021/5/4
28
第28页/共60页
抽样成数平均误差的计算公式
N
n N
C1N
C1N
Cn1
(N n 1)！ n!(N 1)!
PNn C1N C1N1 C1N2 C1Nn1 N (N 1) (N 2) (N n 1)
C
n N
PNn n!
N(N
1)( N
2)(N n!
n 1)
N! n!(N n)!
15
数据对研究对象整体的数量特征取值给出 估计方法。
假设检验：由对部分进行观测取得的 数据对研究对象的数量规律性是否具有某 种指定特征进行检验。
2021/5/4
6
第6页/共60页
统计推断的过程
总体
2021/5/4
样
样本统计量
本
如：样本的平均
数、比例、方差
7
第7页/共60页
三、有关抽样的基本概念
(一)全及总体和样本总体

统计学基础课件(第六章抽样推断)


统计学基础
第六章 抽样推断
其中一类是登记性误差，即在调查过程中由于观察、 测量、登记、计算上的差错所引起的误差，这类误差 是所有统计调查都可能发生的。
另一类是代表性误差，即样本各单位的结构不足以 代表总体而引起的误差。
Fundamentals of Statistics
统计学基础
第六章 抽样推断
第六章 抽样推断
第六章 抽样推断
Fundamentals of Statistics
统计学基础
第六章 抽样推断
教学目的与要求：
抽样估计是抽样调查的继续， 它提供了一套利用抽样资料来 估计总体数量特征的方法。通 过本章的学习，要理解和掌握 抽样估计的概念、特点，抽样 误差的含义、计算方法，抽样 估计的置信度，推断总体参数 的方法，能结合实际资料进行 抽样估计。
（只有两种表现）
Fundamentals of Statistics
总体成数
P=
N1 N
成数标准差 p
P 1 P 统计学基础
第六章 抽样推断
样本指标是根据样本各单位标志值或标志属性
计算的综合指标。
x
=
∑x n
研究数 样本平均数
x
=
∑xf ∑f
量标志
样本标准差
x
2
x
n
x
x
2
x
f
f
研究品 质标志
含义： 抽样极限误差是指样本指标和总体指标之间抽
样误差的可能范围。由于总体指标是一个确定的 数，而样本指标则是围绕着总体指标左右变动的 量，它与总体指标可能产生正离差，也可能产生 负离差，样本指标变动的上限或下限与总体指标 之差的绝对值就可以表示抽样误差的可能范围， 我们将这种以绝对值形式表示的抽样误差可能范 围称为抽样极限误差。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

能范围是［2920，3080］元。 统计学抽样推断计算题答案
【解】五、3题 (2)
已知， p＝10／100＝10%
P1 － (P)p1 － (p)0.9× 0.1
μp=
= n
=
=3%
n
100
Δp=μtp=2× 3%6= %
p± Δ p= 1% 0± 6%4% =1[% ,6 ]
统计学抽样推断计算题答案
五、3题
某地区1997年随机抽取100户农户， 测得户平均年收入为3000元，标准差为 400元，其中有10户的户均年收入在6000 元以上。若以95.45%(t=2)的概率保证程度， 试估计： (1) 该地区农户户均年收入的可能范围； (2) 在全部农户中，户均年收入在6000
元以上的户数所占比重的可能范围。
统计学抽样推断计算题答案
【解】五、2题
p＝45／50＝90%，
p1(－ p) 0.9× 00.1
μp=
= n
=4.2% 4 50
Δpp = =2t× 4 μ .2= 48.4% 8
p± Δp9= % 0± 8.4% 8 ⇒ 置 信 区 :[8.1 5 间 % 2， 9 为 .8 4% 8 ]
统计学抽样推断计算题答案
Σf
50
μ=
σ2 =
s2 =
10.58=24.59(
元
)
x n n 50
统计学抽样推断计算题答案
【解】五、1题 (2)
Δ=μt=2× 4.5= 99.1(8元 ) xx x±Δ=56± 09.18 x
平均工资的置信区间为：
［550.82，569.18］元
工资总额的置信区间为：
［550.82×1500，569.18× 1500］元 即为：［826230，853770］元
t2σ 2
n1=
Δ
2 1
t 2σ 2 n2= (0.5Δ1)2 =4n1
=4×100=400(只)
统计学抽样推断计算题答案
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
统计学抽样推断计算题答案
统计学抽样推断计算题答案
【解】五、3题 (1)
已知：
x
=3000元，s=400元， n=100， t=2
μ=
04(0元 )
x n n 100
Δx=μ tx=2× 4= 08(0 元 )
x±Δ =300± 080 x
=[292， 0308]0( 元 )
即该地区农户户平均年收入的可
10 5500
8 4480
6 3480
4 2400
3 1980
50 28000
统计学抽样推断计算题答案
(x-x)2f
5184 4056 3600 1000
0 2400 6400 30000 52640
【解】五、1题 (1)
x=Σx=f280=0506（ 0 元 ） Σf 50
s2=Σ(xx)2f =526= 41005.82
统计学抽样推断计算题答案
【解】五、4题 (1)
已知：x =1000小时，s＝15小时元， n=100
μx=
σ2 =
n
s2 =
n
152=1.5(小时 ) 100
Δx=μ tx=2× 1.5=3(小)时
x±Δ =100± 03 x
=[997, 100]3小时
统计学抽样推断计算题答案
【解】五、4题 (1)
统计学抽样推断计算题答案
五、2题
从一批袋装食品中，按简单随机重复抽样方法抽 取50 包检查，结果如下：
每包重量(克) 90-95 95-100 100-105 105-110 包数(包) 2 3 35 10
要求：以95.45%(t=2)的概率保证程 度估计该批食品重量在100克 以上的合格率范围。
五、4 题
4．从某厂生产的一批灯泡中，随机重复 抽取100只，检查结果是：100只灯泡 的平均使用寿命为1000小时，标准差 为15小时。要求：
(1) 试以95.45%(t=2)的概率保证程度推断 该批灯泡的平均使用寿命区间；
(2) 假定其他条件不变，如果将抽样极限 误差减少为原来的二分之一，则应抽 取多少只灯泡进行检查？
第七章 抽样推断习题
任课教师：汤来香
统计学抽样推断计算题答案
五、计算题
1．某工厂有1500个工人，用简单随机重 复抽样的方法，抽出50个工人作为样 本，调查其工资水平，如下表：
月平均 工资(元) 524 534 540 550 560 580 600 660 工人数
(人) 4 6 9 10 8 6 4 3
要求：1）计算样本平均数和抽样平均误差； 2）以95.45%的可靠性估计该厂工人的
月平均工资和工资总额的区间。
统计学抽样推断计算题答案
样本平均数和方差计算表
月平均 工 资 (元 )
524 534 540 550 560 580 600 660 合计
工人数
(人 )
xf
4 2096
6 3204
9 4860