原子核物理及辐射探测学 1-4章答案

第一章 习题答案1-1 当电子的速度为18105.2-⨯ms 时，它的动能和总能量各为多少？答：总能量 ()MeV ....c v c m mc E e 924003521511012222=⎪⎭⎫ ⎝⎛-=-==；动能 ()MeV c v c m T e 413.011122=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--= 1-2.将α粒子的速度加速至光速的0.95时，α粒子的质量为多少？答：α粒子的静止质量()()()u M m M m e 0026.44940.9314,244,224,20=∆+=≈-= α粒子的质量 g u m m 2322010128.28186.1295.010026.41-⨯==-=-=βα1-4 kg 1的水从C 00升高到C 0100，质量增加了多少？答：kg 1的水从C 00升高到C 0100需做功为J t cm E 510184.41001184.4⨯=⨯⨯=∆=∆。

()kg c E m 1228521065.4100.310184.4-⨯=⨯⨯=∆=∆ 1-5 已知：()();054325239;050786238239238u .U M u .U M ==()()u .U M ;u .U M 045582236043944235236235==试计算U-239,U-236最后一个中子的结合能。

答：最后一个中子的结合能()()()[]MeV .uc .c ,M m ,M ,B n n 774845126023992238922399222==⋅-+=()()()[]MeV .uc .c ,M m ,M ,B n n 54556007027023692235922369222==⋅-+= 也可用书中的质量剩余()A ,Z ∆：()()()()MeV ....,n ,,B n 806457250071830747239922389223992=-+=∆-∆+∆= ()()()()MeV ....,n ,,B n 545644242071891640236922359223692=-+=∆-∆+∆=其差别是由于数据的新旧和给出的精度不同而引起的。

西南科技大学最新原子核物理及辐射探测学_1-10章答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN西南科技大学 原子核物理与辐射探测学1-10章课后习题答案第一章 习题答案1-1 当电子的速度为18105.2-⨯ms 时，它的动能和总能量各为多少？答：总能量()MeV....c vc m mc E e 924003521511012222=⎪⎭⎫ ⎝⎛-=-==；动能()MeV c vc m T e 413.011122=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--= 1-2.将α粒子的速度加速至光速的0.95时，α粒子的质量为多少？答：α粒子的静止质量 ()()()u M m M m e 0026.44940.9314,244,224,20=∆+=≈-= α粒子的质量g u m m 2322010128.28186.1295.010026.41-⨯==-=-=βα1-4 kg 1的水从C 00升高到C 0100，质量增加了多少？答：kg 1的水从C 00升高到C 0100需做功为J t cm E 510184.41001184.4⨯=⨯⨯=∆=∆。

()kg c E m 1228521065.4100.310184.4-⨯=⨯⨯=∆=∆ 1-5 已知：()();054325239;050786238239238u .U M u .U M ==()()u .U M;u .U M045582236043944235236235==试计算U-239,U-236最后一个中子的结合能。

答：最后一个中子的结合能()()()[]MeV.uc .c ,M m ,M ,B n n 774845126023992238922399222==⋅-+=()()()[]MeV .uc .c ,M m ,M ,B n n 54556007027023692235922369222==⋅-+=也可用书中的质量剩余()A ,Z ∆：()()()()MeV....,n ,,B n 806457250071830747239922389223992=-+=∆-∆+∆= ()()()()MeV ....,n ,,B n 545644242071891640236922359223692=-+=∆-∆+∆=其差别是由于数据的新旧和给出的精度不同而引起的。

<<核辐射探测作业答案>>第一章作业答案 α在铝中的射程3．从重带电粒子在物质中的射程和在物质中的平均速度公式，估算4MeV 的非相对论α粒子在硅中慢化到速度等于零（假定慢化是匀速的）所需的阻止时间（4MeV α粒子在硅中的射程为17.8㎝）。

解：依题意慢化是均减速的，有均减速运动公式： 依题已知：17.8s R cm α== 由2212E E m v v m αααααα=⇒= 可得：82.5610t s -=⨯ 这里 2727132271044 1.6610() 6.646510()44 1.60101.38910()m u kg kg E MeV Jv v m s ααα------==⨯⨯=⨯==⨯⨯==⨯4．10MeV 的氘核与10MeV 的电子穿过铅时，它们的辐射损失率之比是多少？20MeV 的电子穿过铅时，辐射损失率和电离损失率之比是多少？ 解：由22rad dE z E dx m⎛⎫∝ ⎪⎝⎭5．能量为13.7MeV 的α粒子射到铝箔上，试问铝箔的厚度多大时穿过铝箔的α粒子的能量等于7.0MeV? 解：13.7MeV 的α粒子在铝箔中的射程1R α，7.0MeV α粒子在铝箔中的射程2R α之差即为穿过铝箔的厚度d 由 6．当电子在铝中的辐射损失是全部能量损失的1/4时，试估计电子的动能。

27MeV 的电子在铝中的总能量损失率是多少？ 解：不考虑轨道电子屏蔽时 考虑电子屏蔽时12312232634(1)1()[ln((83))]1371841314 6.02310277.3107.9510[((8313)0.06] 3.03/() 3.03/0.437 6.93() 3.03 6.939.9610/e rad e ion z z NE dE r z dx MeV cmdEdx dEMeV cm dx ----+-=+=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯+=-===+=≈和7.当快电子穿过厚为0.40㎝的某物质层后，其能量平均减少了25%.若已知电子的能量损失基本上是辐射损失，试求电子的辐射长度。

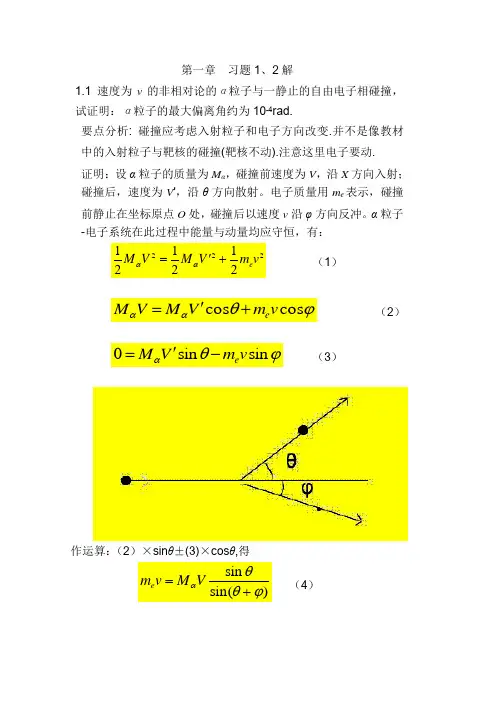
第一章 习题1、2解1.1 速度为v 的非相对论的α粒子与一静止的自由电子相碰撞，试证明：α粒子的最大偏离角约为10-4rad.要点分析: 碰撞应考虑入射粒子和电子方向改变.并不是像教材中的入射粒子与靶核的碰撞(靶核不动).注意这里电子要动. 证明：设α粒子的质量为M α，碰撞前速度为V ，沿X 方向入射；碰撞后，速度为V '，沿θ方向散射。

电子质量用m e 表示，碰撞前静止在坐标原点O 处，碰撞后以速度v 沿φ方向反冲。

α粒子-电子系统在此过程中能量与动量均应守恒，有：222212121v m V M V M e+'=αα （1） ϕθααcos cos v m V M V M e +'= （2）ϕθαsin sin 0v m V M e -'= （3）作运算：（2）×sin θ±(3)×cos θ,得)sin(sin ϕθθα+=VM v m e （4）（5）再将（4）、（5）二式与（1）式联立，消去Ｖ’与v，化简上式，得（６）θϕμϕθμ222sin sin )(sin +=+（７）视θ为φ的函数θ（φ），对（7）式求θ的极值，有令sin2(θ+φ)-sin2φ=0 即2cos(θ+2φ)sin θ=0 （1）若 sin θ=0,则 θ=0（极小） （8）（2）若cos(θ+2φ)=0则 θ=90º-2φ （9）将（9）式代入（7）式，有θϕμϕμ2202)(90sin sin sin +=-由此可得θ≈10-4弧度（极大）此题得证。

1.2（1）动能为5.00MeV 的α粒子被金核以90°散射时，它的瞄准距离（碰撞参数）为多大？（2）如果金箔厚1.0 μm ，则入射α粒子束以大于90°散射（称为背散射）的粒子数是全部入射粒子的百分之几？要点分析:第二问是90°～180°范围的积分.关键要知道n , 注意推导出n 值.其他值从书中参考列表中找.解：（1）依金的原子序数Z 2=79答：散射角为90º所对所对应的瞄准距离为22.8fm. (2)解: 第二问解的要点是注意将大于90°的散射全部积分出来. (问题不知道nA,但可从密度与原子量关系找出)从书后物质密度表和原子量表中查出Z Au =79,A Au =197,ρAu =1.888×104kg/m 3 依: θa 2sin即单位体积内的粒子数为密度除以摩尔质量数乘以阿伏加德罗常数。

第一章射线与物质的相互作用1.不同射线在同一物质中的射程问题如果已知质子在某一物质中的射程和能量关系曲线，能否从这一曲线求得d（氘核）与t （氚核）在同一物质中的射程值？如能够，请说明如何计算？解：P12”利用Bethe 公式，也可以推算不同带点例子在某一种吸收材料的射程。

”根据公式：)()(22vR M M v R b ab b a a Z Z ，可求出。

步骤：1先求其初速度。

2查出速度相同的粒子在同一材料的射程。

3带入公式。

2：阻止时间计算：请估算4MeV α粒子在硅中的阻止时间。

已知4MeV α粒子的射程为17.8μm 。

解：解：由题意得4MeV 粒子在硅中的射程为17.8um由T ≌1.2×107R E Ma，Ma=4得T ≌1.2×107×17.8×106×44s＝2.136×1012s3：能量损失率计算课本3题，第一小问错误，应该改为“电离损失率之比”。

更具公式 1.12-重带点粒子电离能量损失率精确表达式。

及公式 1.12-电子由于电离和激发引起的电离能量损失率公式。

代参数入求解。

第二小问：快电子的电离能量损失率与辐射能量损失率计算：()20822.34700700()rad ion dE E Z dx dE dx 4光电子能量：光电子能量：（带入B K ）康普顿反冲电子能量：200.511m c Mevie hv E220200(1cos )2.04(1cos20) 4.16160.060.3947(1cos )0.511 2.04(1cos20)0.511 2.040.06Er Ee Mev m c Er 5:Y 射线束的吸收解：由题意可得线性吸收系数10.6cm ，311.2/pb g cm 12220.6 5.3610/11.2/m pbcm cm gg cm 质量吸收系数由r N 可得吸收截面：12322230.61.84103.2810/r cm cmN cm 其中N 为吸收物质单位体积中的原子数2233.2810/N cm 0()t I t I e 要求射到容器外时强度减弱99.9%()0.1%0.001t I t e I 即t=5In10=11.513cm6：已知)1()(tιe A t f t 是自变量。

核辐射物理及探测学习题集第⼀章习题1-1 当电⼦的速度为2.5×108m ·s -1时, 它的动能和总能量各为多少MeV? 1-2 将α粒⼦的速度加速⾄光速的0.95时, α粒⼦的质量为多少u? 合多少g?1-3 t=25℃, p=1.013×105Pa 时, S+O 2→SO 2的反应热q=296.9kJ ·mol -1, 试计算⽣成1molSO 2时体系的质量亏损。

1-4 1kg 的⽔从0℃升温⾄100℃, 质量增加了多少? 1-5 试计算239U, 236U 最后⼀个中⼦的结合能。

已知：()MeV 307.47238,92=?；()MeV 572.50239,92=?；()MeV 916.40235,92=?；()MeV 442.42236,92=?。

1-6 当质⼦在球形核⾥均匀分布时，原⼦核的库仑能为RZ Z e E c 024)1(53πε-=Z 为核电荷数，R 为核半径，0r 取m 15105.1-?。

试计算C 13和N 13核的库仑能之差。

1-7 已知：()MeV 125.313,6=?；()MeV 346.513,7=?。

计算C 13和N 13核的结合能之差； 1-8 利⽤结合能半经验公式，计算236U, 239U 最后⼀个中⼦的结合能, 并把结果与1-5题的结果进⾏⽐较1-9 计算K 42原⼦核每⼀个核⼦的平均结合能？1-10利⽤结合能半经验公式计算64Cu, 107Ag, 140Ce, 238U 核的质量, 并把计算值与下列实验值进⾏⽐较, 说明质量公式的应⽤范围。

u Cu M 929756.63)(64=；u Ag M 905091.106)(107=；u Ce M 905484.139)(140=；u U M 050786.238)(238=；1-10利⽤结合能半经验公式计算64Cu, 107Ag, 140Ce, 238U 核的质量, 并把计算值与下列实验值进⾏⽐较, 说明质量公式的应⽤范围。