反比例函数概念

反比例函数概念
Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
知识点一：反比例函数的有关概念
1. 定义：一般地，形如（为常数，）的函数称为反比例函数。

还可以写成
知识点二：反比例函数的基本性质
1、反比例函数的图像：
反比例函数的图像是双曲线，是轴对称图形（对称轴是或）；（为常数，）中自变量，函数值，所以双曲线是不经过原点，断开的两个分支，延伸部分逐渐靠近坐标轴，但是永远不与坐标轴相交；
2、作图方法：描点法
①列表（应以O为中心，沿O的两边分别取三对或以上互为相反的数）
②描点（有小到大的顺序）
③连线（从左到右光滑的曲线）
3、反比例函数的几何意义：
反比例函数（）中比例系数的几何意义是：过双曲线（）上任意引轴轴的垂线，所得矩形面积为。

4、反比例函数的基本性质
反比例函数
的取值质①、的取值范围是；的取值范围是
②、函数图像分别在第一、三象限，在每个象限内，随着的增大而减小
③、对称轴为直线
④、若点在反比例函数图像上，则点也一定在此反比例函数图像上。

①、的取值范围是；的取值范围是
②、函数图像分别在第二、四象限，在每个象限内，随着的增大而增大
③、对称轴为直线
④、若点在反比例函数图像上，则点也一定在此反比例函数图像上。

5、反比例函数解析式的确定：利用待定系数法（只需一对对应值或图像上一个点的坐标即可求出。

课题反比例函数的复习教学目标 1.系统复习本章节的知识体系及知识内容。

重难点透视1．反比例函数的应用教学内容知识整理1.反比例函数的概念:一般地,形如kyx=(k为常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数,自变量x的取值范围是不等于0的一切实数.2.确定反比例函数的解析式:设反比例函数的解析式为kyx=,代入自变量与函数值,解方程求出k的值,得出解析式.三种表达式：①kyx=②xy=k ③1y kx-=3．反比例函数的图像和性质当k>0时，函数的图像分别位于一、三象限，在每一个象限内，y随x的增大而减小；当k<0时，函数的图像分别位于二、四象限，在每一个象限内，y随x的增大而增大；反比例函数的图像是轴对称图形。

当k>0时，对称轴是y=x;当k<0时，对称轴是y=-x;反比例函数的图像是中心对称图形，对称中心是原点。

4.|k|的意义：反比例函数上的点与x轴和y轴围成的矩形的面积。

例题：如图，点A在双曲线上，点B在双曲线y＝上，且AB∥x轴，C、D在x轴上，若四边形ABCD 为矩形，则它的面积为．基础训练1、计算：sin45°+cos230°﹣+2sin60°．2、如图,已知点A. B分别在反比例函数1yx=(x>0),4-yx=的图象上,且OA⊥OB,则OBOA的值为( )A. 2B. 2C. 3D.43、若直线y=m(m为常数)与函数2(2)8(2)x xyxx⎧≤⎪=⎨>⎪⎩的图象有三个不同的交点，则常数m的取值范围_________.4、如图,已知函数3yx=-与y=ax2+bx+c(a>0,b>0)的图象相交于点P,且点P的纵坐标为1,则关于x的方程23ax bxx++=的解是_____________.5、已知,抛物线y=ax2+2ax+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧。

反比例函数概念与性质反比例函数的概念与性质一、反比例函数的概念1.反比例函数可以写成y=k/x的形式，其中自变量x的指数为-1.在解决有关自变量指数问题时，应特别注意系数。

2.反比例函数也可以写成xy=k的形式，用它可以迅速地求出反比例函数解析式中的k，从而得到反比例函数的解析式。

3.反比例函数的自变量不能为0，故函数图象与x轴、y轴无交点。

二、反比例函数的图象1.在用描点法画反比例函数的图象时，应注意自变量x的取值不能为0，且x应对称取点（关于原点对称）。

2.反比例函数的图象是双曲线。

随着k的增大，图象的弯曲度越小，曲线越平直；随着k的减小，图象的弯曲度越大。

3.反比例函数的图象与坐标轴没有交点，称两条坐标轴是双曲线的渐近线。

当k>0时，图象的两支分别位于第一、第三象限内，在每个象限内，y随x的增大而减小；当k<0时，图象的两支分别位于第二、第四象限内，在每个象限内，y随x的增大而增大。

4.反比例函数的图象关于原点对称，即若（a，b）在双曲线的一支上，则（-a，-b）在另一支上。

5.反比例函数的k值的几何意义是：如图1，设点P（a，b）是双曲线上任意一点，作PA⊥x轴于A点，PB⊥y轴于B 点，则矩形PBOA的面积是k；如图2，由双曲线的对称性可知，P关于原点的对称点Q也在双曲线上，作QC⊥XXX的延长线于C，则三角形PQC的面积也是k。

6.反比例函数的增减性需要将两个分支分别讨论，不能一概而论。

7.直线y=k与双曲线y=k/x的关系：当k>0时，两图象必有两个交点，且这两个交点关于原点成中心对称；当k=0时，两图象有一个公共点O；当k<0时，两图象没有交点。

8.反比例函数与一次函数的联系：当k=0时，反比例函数变为一次函数y=0.求反比例函数的解析式的方法主要有三种：待定系数法、反比例函数k的几何意义、实际问题。

四、反比例函数解析式的确定一、反比例函数的定义：反比例函数是指函数表达式为y=k/x的函数，其中k为非零常数。

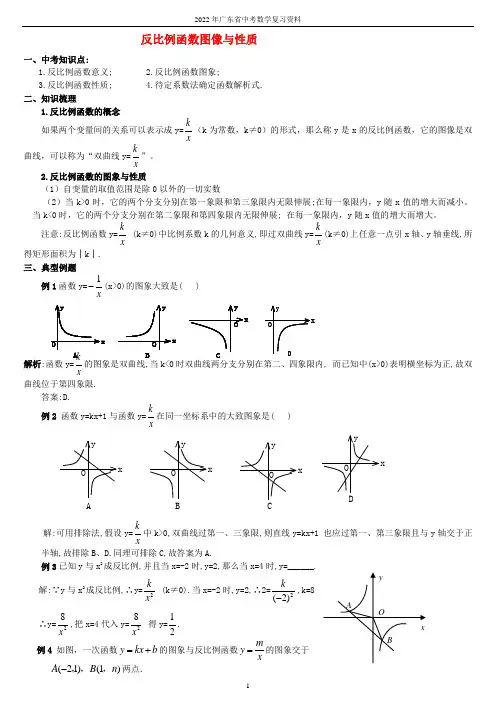
反比例函数的概念及基本性质教学目标掌握反比例函数的概念、性质、图象，熟悉反比例函数与一次函数的关系 重难点分析重点：1、反比例函数的概念； 2、反比例函数的图形特征。

难点：1、求反比例函数的解析式； 2、根据图形特征比较大小。

知识点梳理1、反比例函数的概念：一般地，如果两个变量x ，y 之间的关系可以表示成xk y =(k 为常数，0≠k )的形式，那么称y 是x 的反比例函数。

一般形式：xk y = (k 为常数，)注意：（1）等号左边是函数y ，等号右边是一个分式，分子是不为零的常数k(也叫做比例系数k)，分母中含有自变量x ，且x 的指数是1，若写成1-=kx y 。

则x 的指数是－1。

（2）比例系数是反比例函数定义的一个重要组成部分。

（3）自变量x 的取值范围是的一切实数。

（4）函数y 的取值范围也是一切非零实数。

2、待定系数法求反比例函数的解析式。

3、反比例函数图象（双曲线）的画法：（1）列表；（2）描点；（3）连线。

4、反比例函数的性质：（1）当0>k 时，函数的图象在第一、三象限，在每个象限内，曲线从左向右下降，也就是说，在每个象限内，y 随x 的增大而减小；（2）当0<k 时，函数的图象在第二、四象限，在每个象限内，曲线从左向右上升．也就是说，在每个象限内，随的增大而增大。

知识点1：反比例函数的概念【例1】判断下列说法是否正确1．如果y 是x 的反比例函数，那么当x 增大时，y 就减小 【 】 2．当x 与y 乘积一定时，y 就是x 的反比例函数，x 也是y 的反比例函数 【 】 3．如果一个函数不是正比例函数，就是反比例函数 【 】 4．y 与2x 成反比例时，y 与x 并不成反比例 【 】 5．y 与x 2成反比例时，y 与x 也成反比例 【 】 6．已知y 与x 成反比例，又知当2=x 时，3=y ，则y 与x 的函数关系式是6xy = 【 】 【随堂练习】1、已知三角形的面积是定值S ，则三角形的高h 与底a 的函数关系式是h =__________，这时h 是a 的__________。

反比例函数知识点：1.定义：形如y ＝xk （k 为常数，k ≠0）的函数称为反比例函数。

其中x 是自变量，y 是函数，自变量x 的取值是不等于0的一切实数。

说明：1）y 的取值范围是一切非零的实数。

2）反比例函数可以理解为两个变量的乘积是一个不为0的常数，因此其解析式也可以写成xy=k ；1-=kx y ；xk y 1=（k 为常数，k ≠0） 3）反比例函数y ＝xk （k 为常数，k ≠0）的左边是函数，右边是分母为自变量x 的分式，也就是说，分母不能是多项式，只能是x 的一次单项式，如xy 1=，x y 213=等都是反比例函数，但21+=x y 就不是关于x 的反比例函数。

2. 用待定系数法求反比例函数的解析式由于反比例函数y ＝xk 只有一个待定系数，因此只需要知道一组对应值，就可以求出k 的值，从而确定其解析式。

3. 反比例函数的画法：1）列表；2）描点；3）连线注：（1）列表取值时，x ≠0，因为x ＝0函数无意义，为了使描出的点具有代表性，可以“0”为中心，向两边对称式取值，即正、负数各一半，且互为相反数，这样也便于求y 值（2）由于函数图象的特征还不清楚，所以要尽量多取一些数值，多描一些点，这样便于连线，使画出的图象更精确（3）连线时要用平滑的曲线按照自变量从小到大的顺序连接，切忌画成折线（4）由于x ≠0，k ≠0，所以y ≠0，函数图象永远不会与x 轴、y 轴相交，只是无限靠近两坐标轴4. 图像：反比例函数的图像属于双曲线。

反比例函数的图象既是轴对称图形又是中心对称图形。

有两条对称轴：直线y=x 和 y= －x ；对称中心是：原点5. 性质:说明：1）反比例函数的增减性不连续，在讨论函数增减问题时，必须有“在每一个象限内”这一条件。

2）反比例函数图像的两个分只可以无限地接近x 轴、y 轴，但与x 轴、y 轴没有交点。

3）越大，图象的弯曲度越小，曲线越平直． 越小，图象的弯曲度越大．4）对称性：图象关于原点对称，即若（a ，b ）在双曲线的一支上，则（，）在双曲线的另一支上．图象关于直线对称，即若（a ，b ）在双曲线的一支上，则（，）和（，） 在双曲线的另一支上．6. 反比例函数y ＝xk （k ≠0）中的比例系数k 的几何意义表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积。

第一讲：反比例函数概念 一、一般地，形如xky =（k 为常数，且0≠k ）的函数称为反比例函数。

注意：①分母中含有自变量x ，且指数为1.②比例系数0≠k③自变量x 的取值为一切非零实数。

反比例函数表达式的三种形式① xky =②kx y =1-③ k xy =二、求函数解析式的方法：待定系数法 对于解析式xky =，中只有一个待定系数，因此只需要一对对应的x 、y 的值即可。

例1：下列函数中，是反比例函数的有①x y 5=； ②x y 4.0=； ③2x y =； ④2=xy ； ⑤πx y =； ⑥xy 5-=；⑦12-=x y ； ⑧31-=xy ； ⑨)0(2≠=a a xay 为常数且； ⑩x y 52-=；例2：如果函数222-+=k kkx y 是反比例函数，那么k =________，此函数的解析式是 ；如果自变量取值为—1时，函数值为2，次反比例函数的关系式是 ； 例3：计划修建铁路1200km ，那么铺轨天数y （天）是每日铺轨量x 的反比例函数吗？ 解：因为 ，所以y 是x 的反比例函数；例4：一块长方形花圃，长为a 米，宽为b 米，面积为8平方米，那么，列出a 关于b 的函数关系式为例5：在某一电路中，保持电压V （伏特）不变，电流I （安培）与电阻R （欧姆）成反比例，当电阻R=5时，电流I=2安培。

（1）求I 与R 之间的函数关系式；（2）当电流I=0.5安培时，求电阻R 的值。

思考：你还能举出哪些生活中的反比例函数例子？提升训练：1.已知：,21y y y +=1y 与2x 成正比例，2y 与x 成反比例，且当3,1==y x ；当1,1=-=y x ，求21-=x 时，y 的值？2.已知y 与x-1成反比例，并且x ＝-2时y ＝7，求：(1)求y 和x 之间的函数关系式； (2)当x=8时，求y 的值(3)y ＝-2时，x 的值。

3.已知y ＝y 1－y 2，y 1与x 成正比例，y 与x 成反比例，且当x ＝1时，y ＝－14，x ＝4时，y ＝3．求(1)y 与x 之间的函数关系式．(2)自变量x 的取值范围．(3)当x ＝14时，y 的值．第二讲：反比例函数的图像和性质 1.通过描点法画x y 2=和xy 3-=的函数图像 2.反比例函数的图像是双曲线。

反比例函数（1）【考点聚焦】1、反比例函数的定义：如果两个变量％、y间的关系可以表示成的形式，则称y是％的反比例函数.2、反比例函数的三种等价形式：3、反比例函数的图像y = kx（k为常数，k牛0）中k与函数图像的关系: k的符号，决定了双曲线的位置：按要求将下面两幅图补充完整.k > 0 k < 04、反比例函数的图像与性质：在反比例函数中，当k > 0时，图像位于，且在每一个象限内，函数y的值随X值的增大而；当k < 0时，图像位于且在每一个象限内，函数y的值随X值的增大而.5、对称性：（1）关于对称，是；（2）若点Q, b）在图象上时，则也在图像上；【典例剖析】考点题型1：反比例函数的定义例1、若y = m—1）x m2-2是J关于x的反比例函数关系式，则m =，此函数关系式为.变式训练：）x m-3是反比例函数，求m的值.1、已知函数y = m+2考点题型2：图像例2、（七中）在—3、—2、—1、0、1、2这六个数中，随机取出一■个数，记为a ,那么2a-3使得关于x的反比例函数y = -------------- 经过第二、四象限，且使得关于x的方程xax + 2 - 1--- ——1 = 有整数解的概率为___________________ .x—1 1 —x变式训练：G, y），B（2, y），C（- 3, y）在双曲线y - a2 H—上，则y、y、y的大1、若点A小关 1 2 3 x123系是.（1） 求一次函数的解析式；2、（锦江区二诊）在一个不透明的盒子里，装有三个分别写有数字1，2，3的小球，它们 的形状、大小、质地等完全相同，先从盒子里随机取出一个小球，记下数字后放回盒子， 摇匀后再随机取出1个小球，记下数字，前后两次的数字分别记为％ , J ,并以此确定点 P Q,y ）,那么点P 在函数y =2图象上的概率为.x考点题型3：增减性例3、如图，一次函数y = kx +b （k 、b 为常数，且k 丰0）和反比例函数y = 4Q > 0）的 x6y=一的图象交于A 、B 两点.已知当x > 1时y1> y 2；当 0 < x < 1 时，y 1 <y 2 .（2） 已知双曲线在第一象限上有一点C 到y 轴的距离为3，求A ABC 的面积.考点题型4：对称性）与双曲线y =—交于A Q , y）和B Q , y）两点，则x 例4、直线y = kh > 011 223 x y - 9 x y =1 2 2 1 -----------------------------变式训练：11、反比例函数y =--的图象的对称中心的坐标是x考点题型5：求解析式（3,0）,点B 例5、如图，已知在直角梯形OABC中，CB // x轴，点C落在y轴上，点A（2,2）,k将AB绕点B逆时针旋转90°,点A落在双曲线y =-的图象上点A，则k的值变式训练：___ …… c （ 20 _31、如图，矩形AOCB的两边OC、OA分别位于X轴、y轴上，点B的坐标为—-—,5 ID是AB边上一点，将AADO沿直线OD翻折，使点A恰好落在对角线OB上的E点处，k若E点在反比例函数y =—的图象上，则k =.X限＞ 0）2、（成外）如图，等边A OAB和等边A AFE的一边都在％轴上双曲线y = k经过。

反比例函数复习讲义 知识点一：反比例函数的概念一般地，如果两个变量x 、y 之间的关系可以表示成ky x=（k 为常数，）的形式，那么称y 是x 的反比例函数． 注：（1）反比例函数k y x =中的k x是一个分式,自变量x ≠0, k y x =也可写成1y kx -=或xy k =，其中k ≠0；（2）在反比例函数1y kx -=（k ≠0）中，x 的指数是－1。

如，5y x=也写成：15y x -=； （3）在反比例函数k y x =（k ≠0）中要注意分母x 的指数为1，如21y x=就不是反比例函数。

知识点二：反比例函数的图象 反比例函数(0)ky k x=≠的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限或第二、四象限．它们关于原点对称，反比例函数的图象与x 轴、y 轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远不与坐标轴相交． 注：（1）观察反比例函数(0)ky k x=≠的图象可得：x 和y 的值都不能为0，并且图象既是轴对称图形，又是中心对称图形，它有两条对称轴，对称中心是坐标原点． （2）用描点法画反比例函数y= kx的图象时，应注意自变量x 的取值不能为0，一般应从1或-1开始对称取点.（3）在一个反比例函数图象上任取两点P ，Q ，过点P ，Q 分别作x 轴，y 轴的平行线，与两坐标轴分别围成的矩形面积为S 1，S 2 则S 1＝S 2． 知识点三：反比例函数的性质 1．图象位置与函数性质当k>0时，x 、y 同号，图象在第一、三象限，且在每个象限内，y 随x 的增大而减小；当k<0时，x 、y 异号，图象在第二、四象限，且在每个象限内，y 随x 的增大而增大.2．若点(a,b)在反比例函数(0)ky k x=≠的图象上，则点（-a,-b ）也在此图象上，故反比例函数的图象关于原点对称；3．正比例函数与反比例函数的性质比较。

正比例函数反比例函数解析式图 像 直线有两个分支组成的曲线（双曲线）位 置k ＞0，一、三象限； k ＜0，二、四象限 k ＞0，一、三象限 k ＜0，二、四象限增减性k ＞0，y 随x 的增大而增大 k ＜0，y 随x 的增大而减小k ＞0，在每个象限，y 随x 的增大而减小 k ＜0，在每个象限，y 随x 的增大而增大4．反比例函数y=x 中k 的意义 反比例函数y = k x (k ≠0)中比例系数k 的几何意义,即过双曲线y = kx(k ≠0)上任意一点引x 轴、y 轴垂线,所得矩形面积为│k │.知识点四：反比例函数解析式的确定反比例函数解析式的确定方法是待定系数法.由于在反比例函数关系式(0)ky k x=≠中，只有一个待定系数k ，确定了k 的值，也就确定了反比例函数，因此只需给出一组x 、y 的对应值或图象上点的坐标，代入(0)ky k x=≠中即可求出k 的值，从而确定反比例函数的解析式．知识点五：应用反比例函数解决实际问题须注意以下几点1．反比例函数在现实世界中普遍存在，在应用反比例函数知识解决实际问题时，要注意将实际问题转化为数学问题。

反比例的所有概念和性质反比例是指两个变量之间存在一种相互制约的关系，当其中一个变量增大时，另一个变量会相应地减小，反之亦然。

在数学中，反比例通常用一个函数来表示，即y = k/x，其中k表示一个常数。

反比例的概念和性质如下：1. 反比例函数的定义：反比例函数是一种形式为y = k/x的函数，其中k为常数。

当x不等于零时，函数是定义良好的。

2. 反比例函数的图像：反比例函数的图像呈现出一种特殊的形态，即一个双曲线。

随着自变量x趋近于零，因变量y趋近于无穷大；随着自变量x趋近于无穷大，因变量y趋近于零。

3. 反比例的变化趋势：反比例的关系是由两个变量之间的相互制约所决定的。

当其中一个变量增大时，另一个变量会相应地减小；当其中一个变量减小时，另一个变量会相应地增大。

这种变化趋势与正比例关系相反。

4. 反比例的例子：反比例关系在现实生活中有许多实际应用，例如弹簧刚度与其伸长长度的关系、密度与体积的关系、速度与时间的关系等等。

5. 反比例的性质：反比例具有以下性质：a. 零点：反比例函数的图像经过坐标轴的原点。

b. 单调性：反比例函数在自变量的正值区间上是单调递减的，在自变量的负值区间上是单调递增的。

c. 渐进线：反比例函数的图像有两条渐近线，即y轴和x轴。

当自变量趋近于无穷大时，函数的图像趋近于x轴；当因变量趋近于无穷大时，函数的图像趋近于y轴。

d. 定比关系：反比例函数中，y/x的值始终等于常数k，即y = k/x。

6. 反比例的应用：反比例关系在实际生活中有广泛的应用，例如电阻和电流的关系、速度和时间的关系、浓度和体积的关系等等。

这些应用可以通过反比例关系来描述和解释。

7. 反比例的变种：在一些情况下，变量之间的关系可能不是严格的反比例，而是近似反比例。

在这种情况下，函数可能具有形式为y = k/x^n的一般反比例关系，其中n为正整数。

8. 反比例与正比例的关系：反比例和正比例是两个相关但相反的概念。

反比例函数知识要点1. 反比例函数的概念： 一般地，函数x k y =（k 是常数，且k ≠0）叫做反比例函数。

注意：（1）常数K 称为反比例系数，K 是非零常数；（2）解析式有三种表达式： ①xk y =（k ≠0）；②xy=k （k ≠0）；③1-=kx y （k ≠0） 2.反比例函数的图像： 3.反比例函数xk y =（k ≠0）的性质： （1）当K ＞0时，图像的两个分支分别在第一、三象限，在每一象限内，y 随x 的增大而减小；（2）当K ＜0时，图像的两个分支分别在第二、四象限，在每一象限内，y 随x 的增大而增大；（3）反比例函数的图像：①关于原点成中心对称；②关于直线x y =成轴对称；③关于直线x y -=成轴对称；4. 反比例函数面积的基本模型：①如图，过双曲线x k y =上任意一点P(X ，y)，作x 轴（或y 轴）的垂线，则S ∆OMN=2|K |; ②如图，过双曲线x k y =上任意一点P(X ，y)，作x 轴、y 轴的垂线，则S 矩形AOBP=|K|；反比例函数 xk y =（k 是常数，且k ≠0） K 的符号K ＞0K ＜0 图像（双曲线）这两条曲线只能无限接近于两坐标轴， 不能与其相交。

基础知识检测（一）填空1. 当m= 时，函数y=()的变化范围是时，函数值是反比例函数。

当y x m m 1-x 3-12≤≤+- . 2. 写出一个反比例函数，当x （x ＞0）增大时，y 反而减小，此函数的解析式是 ；已知反比例函数xk y -=4，当k 时，函数图像位于第一、三象限；当k 时，在每个象限内，y 随x 的增大而增大。

3. 在函数y=xa 12--(a 为常数)的图像上有三点（x1，y1）、（x2，y2）、（x3，y3），且x1＜x2＜0＜x3，则函数y1，y2，y3的关系是 。

4. 已知反比例函数x k y =（k ≠0）的图像经过P(1,3)点，则反比例函数的解析式为 。

反比例函数的概念及图像和性质★反比例函数的概念１.反比例函数：如果两个变量ｘ、y 之间的关系可以表示成y=k x（k•为常数，k ≠０）的形式，那么称y 是ｘ的反比例函数．２.反比例函数解析式的变形:反比例函数y=k x（k ≠0）还可以写成1-=kx y (k ≠0）或k xy =(k ≠０). 注意:（１）k 为常数,ｋ≠0;（２)k x中分母x 的指数为1； (3)自变量x 的取值范围是x ≠０的一切实数;(4)因变量ｙ的取值范围是y ≠0的一切实数．例1．若函数1322)(+--=m mx m m y 是反比例函数，则m 的值是?【变式训练】１．函数122-++=m m x m y 是反比例函数，求解析式.2.已知函数122)(--+=m m x m m y .(1)若y 是x 的正比例函数，求m 的值；（2)若y 是x 的反比例函数,求m 的值，并写出此时y 与x 的函数关系式.例 2.已知y y y y 121,+=与x 2成正比例，y 2与x 成反比例，且1=x 时，1;3-==x y 时,1=y ，求当21-=x 时y 的值。

【变式训练】已知y y y 21-=,y 1与x 成反比例,y 2与2-x 成正比例,并且当3=x 时，5=y ；当1=x 时，1-=y ,求 y 与x 之间的函数关系式。

例3.在平行四边形ABCD 中，E AD AB ,6,8==为AB 上一动点（不与B A 、重合)，设DE x AE ,=的延长线交CB 的延长线于点F ,设y CF =,求y 与x 之间的函数关系,并写出自变量x 的取值范围。

【变式训练】如图，平行四边形ABCD 中,E cm BC cm AB ,1,4==是CD 边上一动点,BC AE 、的延长线交于F 点,设ycm BF xcm DE ==，.求y 与x 之间的函数关系式,并写出自变量x 的取值范围。

A DEB C F★反比例函数图像和性质利用画函数图象的方法,可以画出反比例函数的图象,它的图象是双曲线,①当0>k 时,函数的图象在第一、三象限，在每个象限内,曲线从左到右下降,也就是在每个象限内,y 随x 的增加而减小;②当0<k 时,函数的图象在第二、四象限，在每个象限内,曲线从左到右上升，也就是在每个象限内，y 随x 的增加而增大.4.画反比例函数的图象时要注意的问题：（1）画反比例函数图象的方法是描点法;（2）画反比例函数的图象要注意自变量的取值范围是0≠x ,因此,不能把两个分支连接起来;(3)由于在反比例函数中，x 和y 的值都不能为0，所以，画出的双曲线的两个分支要分别体现出无限的接近坐标轴,但永远不能达到x 轴和y 轴的变化趋势.例1.已知反比例22223-+-+=m m x m m y 的图像的两个分支分布在第二、四象限，求m 的值【变式训练】1.已知反比例函数72)2(---=m xx m y 的图像位于第一、三象限，求ｍ的值。

反比例函数的概念与性质反比例函数是数学中常见的一类函数，其表达形式为y = k/x，其中k是一个非零常数，x和y分别表示自变量和因变量。

概念：反比例函数是一种特殊的函数，其特点是自变量和因变量呈反比关系。

当自变量的值增大时，因变量的值就会减小；反之，当自变量的值减小时，因变量的值就会增大。

这种函数在实际问题中往往具有很重要的意义。

性质一：定义域和值域反比例函数的定义域为除了x=0以外的所有实数，因为分母不能为零；而值域则为除了y=0以外的所有实数。

性质二：图像特征反比例函数的图像是一个开口向下或者开口向上的双曲线。

这是因为当x的绝对值趋近于无穷大时，y的值会趋近于0，而当x的绝对值趋近于0时，y的值会趋近于无穷大。

性质三：关于坐标轴的对称性反比例函数的图像关于原点对称。

也就是说，如果一个点（x，y）在函数的图像上，那么对应的点（-x，-y）也在图像上。

这是因为当自变量取相反数时，函数的值也会取相反数。

性质四：零点问题反比例函数的零点是x等于k的时候，因为此时分母为0，因变量为零。

换句话说，当x等于k时，函数的图像与x轴相交，这是图像的一个特殊点。

性质五：渐近线反比例函数的图像会有两条渐近线，分别是x轴和y轴。

当x趋近于正无穷或者负无穷时，函数的值会趋近于0，也就是说，函数的图像会无限接近x轴。

同样地，当y趋近于正无穷或者负无穷时，函数的值会趋近于0，函数的图像会无限接近y轴。

结论：反比例函数是一种重要的函数类型，在实际问题中经常出现。

了解反比例函数的概念和性质可以帮助我们更好地理解数学中的种种问题，同时也有助于我们在实际生活中解决各种与反比关系相关的情况。

反比例函数的基本概念与应用反比例函数是数学中常见的一种函数关系，也被称为倒数函数。

它是指当自变量x的取值趋近于无穷大或者无穷小时，函数值y趋近于零。

反比例函数可以表示为y = k/x，其中k为常数。

反比例函数的特点是随着自变量的增大，函数值会逐渐变小；而随着自变量的减小，函数值会逐渐变大。

反比例函数与比例函数相对，比例函数表示为y = kx，在反比例函数中，自变量与函数值呈现一种“反”关系。

反比例函数可以在多个领域中进行应用。

下面将重点介绍反比例函数在物理学和经济学中的应用。

一、反比例函数在物理学中的应用1. 物体均匀运动的速度与时间的关系在物理学中，物体的速度与时间呈现反比例关系。

当一个物体以匀速运动时，在相同的时间间隔内，它所走过的距离与所用的时间成反比。

即速度v与时间t的关系可以表示为v = k/t，其中k为常数。

例如，一辆汽车以恒定的速度行驶，它所走过的路程与所用的时间成反比。

当时间t增加时，速度v减小，反之亦然。

根据反比例函数的特点，我们可以推断出物体的速度与时间之间的关系。

通过对反比例函数进行实际测量和计算，可以得出物体在不同时间点的速度，进而分析和预测物体的运动情况。

2. 电阻与电流的关系在电学中，电阻与电流呈现反比例关系。

根据欧姆定律，电阻R与电流I之间的关系可以表示为R = k/I，其中k为常数。

当电流增大时，电阻减小；当电流减小时，电阻增大。

这种反比例关系使得电阻器、电阻器组和电路等可以通过调节电流来改变阻力，实现对电能的控制。

反比例函数在电路分析和设计中具有重要的作用，通过它可以确定不同电路元件的阻抗、电流和电压之间的关系，为电路的运行和优化提供了理论支持。

二、反比例函数在经济学中的应用1. 物价与需求的关系在经济学中，物价与需求之间呈现反比例关系。

根据供需关系理论，当市场上某种商品或服务的需求量增加时，其价格往往会下降；当需求量减少时，价格则会上升。

这种反比例关系可以通过需求曲线来表示。