2017-2018学年浙江省舟山中学高一下学期开学考试数学试题+Word版含解析

浙江省舟山市高一下学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共10题；共20分)1. （2分） (2015高三上·廊坊期末) 已知集合A={1，2，3}，B={2，3，4}，全集U=A∪B，则集合∁U（A∩B）中元素的个数是（）A . 1B . 2C . 3D . 42. （2分） (2016高一下·双峰期中) ﹣495°与下列哪个角的终边相同（）A . 135°B . 45°C . 225°D . ﹣225°3. （2分） (2017高一上·钦州港月考) 下列函数在（0,＋∞）上是增函数的是（）A .B .C .D .4. （2分） (2017高二下·穆棱期末) 已知角的顶点是坐标原点，始边是轴正半轴，终边过点，则（）A .B .C .D .5. （2分）已知，则角是（）A . 第一或第二象限B . 第二或第三象限C . 第三或第四象限D . 第一或第四象限6. （2分） (2019高三上·天津期末) 已知，则的大小关系为（）A .B .C .D .7. （2分） (2016·安徽模拟) 已知，则（）A . f（2）＞f（e）＞f（3）B . f（3）＞f（e）＞f（2）C . f（3）＞f（2）＞f（e）D . f（e）＞f（3）＞f（2）8. （2分）直线λx+y+λ﹣2=0不过第三象限，则λ的取值范围是（）A . [0，1]B . [0，2]C . （﹣∞，4]D . [4，+∞）9. （2分） (2019高三上·衡水月考) 函数的图象大致为（）A .B .C .D .10. （2分）(2018·临川模拟) 已知函数，若方程在上有两个不同的实根，则实数的取值范围是（）A .B .C .D .二、填空题 (共5题；共5分)11. （1分） (2018高一下·汕头期末) 如果，且是第四象限的角，那么 =________。

浙江省舟山市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题；共24分)1. （2分）下列函数中，最小正周期为π且图象关于y轴对称的函数是（）A . y=sinx+cosxB . y=sinx•cosxC . y=sin2x+cos2xD . y=sinx (2x+)2. （2分）(2018·辽宁模拟) 是双曲线的左右焦点，过且斜率为1的直线与两条渐近线分别交于两点，若，则双曲线的离心率为（）A .B .C .D .3. （2分） (2019高一上·锡林浩特月考) 已知集合，，则为（）A . 或B . 或C . 或D . 或4. （2分） (2015高二上·孟津期末) △ABC满足，∠BAC=30°，设M是△ABC内的一点（不在边界上），定义f（M）=（x，y，z），其中x，y，z分别表示△MBC，△MCA，△MAB的面积，若f（M）=（x，y，），则的最小值为（）A . 9B . 8C . 18D . 165. （2分）等比数列｛an}中, a2=9,a5=243,则S4= （）A . 81B . 120C . 168D . 1926. （2分） (2016高一下·奉新期末) 在△ABC中，角A，B，C所对的边分别为a，b，c，若A，B，C成等差数列，且b=1，则△ABC面积的最大值为（）A .B .C .D . 17. （2分）(2017·沈阳模拟) 设实数x，y满足约束条件，则目标函数z=x﹣3y的取值范围为（）A . [﹣12，1]B . [﹣12，0]C . [﹣2，4]D . [1，4]8. （2分） (2016高二上·嘉峪关期中) 不等式x（3﹣x）≥0的解集是（）A . {x|x≤0或x≥3}B . {x|0≤x≤3}C . {x|x≥3}D . {x|x≤3}9. （2分）要得到函数y=sinx的图象，只需将函数的图象（）A . 向右平移个单位B . 向右平移个单位C . 向左平移个单位D . 向左平移个单位10. （2分）(2018·株洲模拟) 已知的图像关于点对称，且在区间上单调，则的值为（）A . 1B . 2C .D .11. （2分） (2015高二下·宜昌期中) 若，是夹角为60°的两个单位向量，则 =2 + ；=﹣3 +2 的夹角为（）A . 60°B . 30°C . 150°D . 120°12. （2分）已知集合M={0，2}，数列{an}满足an∈M（n=1，2，3，…），设W= + +…+ ，则W 一定不属于区间（）A . [0，1）B . （0，1]C . [ ，）D . （， ]二、填空题 (共4题；共4分)13. （1分） (2017高一下·东丰期末) 已知变量满足约束条件，则的最大值为________14. （1分） (2016高一下·南汇期末) 化简sin2α+sin2β﹣sin2αsin2β+cos2αcos2β=________．15. （1分） (2018高二上·牡丹江期中) 已知抛物线，作直线，与抛物线交于两点，为坐标原点且，并且已知动圆的圆心在抛物线上，且过定点，若动圆与轴交于两点，且，则的最小值为________16. （1分） (2018高二上·新乡月考) 在△ABC中，已知(b＋c)∶(c＋a)∶(a＋b)＝4∶5∶6，给出下列结论：①由已知条件，这个三角形被唯一确定；②△ABC一定是钝角三角形；③sinA∶sinB∶sinC＝7∶5∶3；④若b＋c＝8，则△ABC的面积是 .其中正确结论的序号是________ .三、解答题 (共6题；共55分)17. （10分） (2020高一下·林州月考) 已知函数 .（1）求的单调递减区间；（2）若，求的最大值和最小值.18. （10分）(2016·赤峰模拟) 在△ABC中，内角A，B，C对边分别为a，b，c，且c＜a，已知 =﹣2，tanB=2 ，b=3．（1）求a和c的值；（2）求sin（B﹣C）的值．19. （10分）(2017·嘉兴模拟) 已知，（1）求函数y=f（x）的单调递增区间；（2）设△ABC的内角A满足f（A）=2，而，求边BC的最小值．20. （10分）(2020·化州模拟) 已知等差数列{an}的前n项和为Sn ， a4＝9，S3＝15.（1）求Sn；（2）设数列的前n项和为Tn，证明： .21. （10分） (2016·运城模拟) 在△ABC中，角A，B，C的对边分别为a，b，c，满足2acosB=2c﹣b．（1）求角A；（2）若△ABC的面积为，且a= ，请判断△ABC的形状，并说明理由．22. （5分） (2018高二上·新乡月考) 在等差数列中， , .(Ⅰ)求数列的通项；(Ⅱ)令，证明：数列为等比数列；（Ⅲ）求数列的前项和 .参考答案一、选择题 (共12题；共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题；共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题；共55分) 17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、21-1、21-2、22-1、。

2017-2018学年浙江省舟山中学高一下学期开学考试语 文注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第I 卷（选择题）一、选择题1．下列各句中，没有错别字且加点字的注音全部正确的一项是（ ） A. 《古文观止》是由康熙年间两位名不见经传．（zhuàn）的选家所编，他们披沙拣金，遴．(lín)选了二百多篇百读不厌的佳作。

B. 北京画院配合“明清人物画”展览的微信导览，对展品均有详实的资料解读，而回顾古人、追本溯．(shuî)源的方式，可以让人在时空转换中汲．(jí)取传统书画的艺术养分。

C. 如果不顺着领导的“杆儿”爬，会招致领导怨怼，“顺杆爬”者自然趋之若鹜，可见欲摒．(b ĭng)除此种陋习，实在需要上位者能做到豁．(huî)达大度，广开言路。

D. 母亲生前没有给我留下过什么隽．(juàn)永的哲言，或要我恪．(kè)守的教诲，只是在她去世之后，她艰忍的意志和毫不张扬的爱，在我的印象中愈加鲜明深刻。

2．下列各句中，没有语病的一句是（ ）A. 腾讯无人机在研发初期，定位就与现在占市场主流的航拍型无人机不同，他们的目标用户是大众消费群体，期望赢得更多的客户。

B. “共享快递箱”将逐步取代传统快递所使用的纸箱外包装，通过上门送件的快递员或自提网点，在用户签收快件后对漂流箱进行回收再利用，其旨在推进“绿色快递”服务。

C. 用制度保障生态文明建设，是一项在“保护优先”价值取向下制定游戏规则的创新性工作，是对现有制度安排的发展、改革与继承。

浙江省舟山中学高一第二学期数学期末复习试卷一、选择题：1. 已知AM 是ABC ∆的BC 边上的中线，若→-AB =→a 、=→-AC →b ，则→-AM 等于 。

A.)(21→→-b a B.)(21→→--b aC.)(21→→+b a D.)(21→→+-b a2. 点A 分→-BC 所成的比为2，则下列结论正确的是 。

A.点A 分→-CB 的比为2 B.点B 分→-AC 的比为32 C.点C 分→-BA 的比为3D.点C 分→-AB 的比为31-3. 按向量→a 将点)3,2(-平移到点)2,1(-，则按向量→a 将点)3,2(-平移到 。

A.)4,3(-B.)2,1(-C.)3,4(-D.)1,2(-4. 函数)3sin(2)(π+=kx x f 与函数)6tan(3)(π-=kx x g 的周期之和为π2，则正实数k 的值为 。

A.23B.2C.25 D.35. 已知]23,[,31sin ππ∈-=x x ，则x 等于 。

A.)31arcsin(-B.31arcsin -πC.31arcsin +πD.31arcsin2-π 6. 已知平行四边形ABCD 满足条件0)()(=-⋅+→-→-→-→-AD AB AD AB ，则该四边形是 。

A.矩形B.菱形C.正方形D.任意平行四边形 7. 已知向量)8,(),,2(x b x a ==→→，若||||→→→→⋅=⋅b a b a ，则x 的值是 。

A.4- B.4 C.0 D.16 8. 与向量)8,6(-=→a 垂直的单位向量坐标为 。

A.)6,8(或)6,8(--B.)8,6(-或)8,6(-C.)53,54(或)53,54(--D.)54,53(-或)54,53(-9. 已知函数B x A y ++=)sin(ϕϖ的一部分图象如右图所示，如果2||,0,0πϕϖ<>>A ，则 。

A.4=AB.1=ϖC.6πϕ=D.4=B10. 角α满足条件0cos sin ,02sin <+>ααα，则α在A.第一象限B.第二象限C.第三象限D.第四象限11．在△ABC 中，∠C=90°，),3,2(),1,(==k 则k 的值是 （ ）A ．5B ．－5C ．23D ．23-12．)(x f 是定义在R 上的以3为周期的奇函数，且0)2(=f 在区间（0，6）内解的个数的最小值是（ ） A ．2 B ．3C ．4D ．5二、填空题： 13.已知)45,43(ππα∈，135)4sin(=-πα，则αs i n 的值为__________________________； 14.函数3tan -=x y 的定义域是_____________________________________________；15.已知向量→a 与→b 的夹角为︒120，且5||,3||==→→b a ，则→b 在→a 方向上的投影是________； 16在教学楼的楼顶看奥林匹克大楼楼顶的仰角为︒125.7，看楼底的俯角为︒565.26，已知教学楼的高为24米，则奥林匹克大楼高为______________米（精确到米，计算时可参考以下数据：5.0565.26tan ,125.0125.7tan =︒=︒）；17方程a x x =+cos 3sin 有解，则实数a 的取值范围是___________________________； 18给出下列命题： ①函数)225sin(x y -=π是偶函数； ②函数)4sin(π+=x y 在闭区间]2,2[ππ-上是增函数； ③直线8π=x 是函数)452sin(π+=x y 图象的一条对称轴； ④将函数)32cos(π-=x y 的图象向左平移3π单位，得到函数x y 2cos =的图象； 其中正确的命题的序号是： ； 三、解答题：19求函数3cos 52cos )(+-=x x x f 的最大、最小值，并求取得此最值时相应的x 的取值集合； 20已知51cos sin ,02=+<<-x x x π. （I ）求sin x －cos x 的值； （Ⅱ）求xx x x x x cot tan 2cos 2cos 2sin 22sin 322++-的值. 21已知a 、b 、c 分别是ABC ∆的三个内角A 、B 、C 所对的边【Ⅰ】若ABC ∆面积,60,2,23︒===∆A c S ABC 求a 、b 的值；【Ⅱ】若B c a cos =，且A c b sin =，试判断ABC ∆的形状．22.已知ABC ∆三个顶点的坐标分别为)1,4(A 、)2,0(B 、)10,8(-C 【Ⅰ】若AD 是BC 边上的高，求向量→-AD 的坐标； 【Ⅱ】若点E 在AC 边上，且ABC ABE S S ∆∆=31，求E 的坐标； 23.如图 ，在同一平面内，向量→a 与单位向量→i 、→j 的夹角分别为︒30、︒60，已知4||=→a . 【Ⅰ】以→i 和→j 为基底，表示→a ；【Ⅱ】若→→→+=j i b 3，求→a 与→b 的夹角θ的值；24.某校在申办国家级示范校期间，征得一块形状为扇形的土地用于建设田径场，如下图所示，已知扇形角32π=∠AOB ，半径120=OA 米，按要求准备在该地截出内接矩形MNPQ ，并保证矩形的一边平行于扇形弦AB ，设θ=∠P O A ，记y PQ =.【Ⅰ】以θ为自变量，写出y 关于θ的函数关系式；【Ⅱ】当θ为何值时，矩形田径场的面积最大，并求最大面积；参考答案一、选择题：CDAACBBCCCAD 二、填空题： 13．26-14.32k x k ππππ+≤<+ 15.52-16.30 17.[-2,2] 18.①③三、解答题： 19、min max 2()1;2()9x k k Z f x k k Z f πππ=∈=-=+∈=时20、（1）75-（2）108125- 21、①1,b a ==②等腰直角三角形。

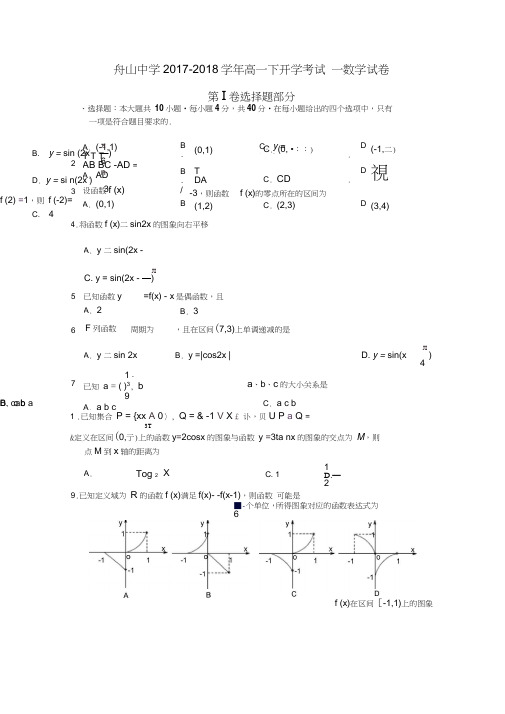
舟山中学2017-2018学年高一下开学考试 一数学试卷第I 卷选择题部分、选择题：本大题共 10小题•每小题4分，共40分•在每小题给出的四个选项中，只有 一项是符合题目要求的.1 .已知集合 P = {xx A 0〉, Q = & -1 V X £ 讣，贝U P a Q =3T&定义在区间(0,亍)上的函数y =2cosx 的图象与函数 y =3ta nx 的图象的交点为 M ，则点M 到x 轴的距离为 1 D.—2f (x)在区间［-1,1)上的图象2. 3. A . (-1,1)T T T AB BC -AD =A . AD 设函数f (x) A . (0,1) B.(0,1) C . (0,•：：) D .(-1,二)B . T DAC . CD D .視/ -3，则函数 f (x)的零点所在的区间为B . (1,2)C . (2,3)D .(3,4)4.将函数f (x)二sin2x 的图象向右平移A . y 二sin(2x -5.JIC. y = sin(2x - —)=f(x) - x 是偶函数，且B . 3已知函数yA . 2 JI B. y = sin (2x —) 6 nD . y = si n(2x )3 f (2) =1，则 f (-2)= C. 46. F 列函数中,周期为，且在区间(7,3)上单调递减的是 7. A . y 二sin 2x B . y =|cos2x |C . y = tan(x JID. y = sin(x)41 -已知 a = ( )3, b 9 A . a b ca 、b 、c 的大小关系是B. cab C . a c bD . c b aA .C. 1XTog 2 ■-个单位，所得图象对应的函数表达式为69.已知定义域为 R 的函数f (x)满足f(x)- -f(x-1)，则函数 可能是10.如图，在平面内，AABC是边长为3的正三角形，四边形EFGH是边长为1且以C为中心的正方形,,M j为边GF的中点，点N是边EF上的动点，当正方形EFGH绕中心C 转动时，AN CM的最大值为7A.-4 c 32 1 C. 4 二、填空题：本大题共 11 •计算：cos 2 23 COS 267°= D 3 2 第n 卷非选择题部分7小题，多空题每题 6分，单空题每题 4分，共36 分. ;tan 240° = _____________ . 12•已知幕函数y = f(x)的图象过点(4,)，则log 3 f (3)二 1的 f(1-2x)定义域为 T T T T 〔I 2T OA, OB , OC 满足 OA OB OC ，则4 4 4 H 4 3 3 彳」ACL14•若两个非零向量 a,b 满足」a p=|a-b 戶2| b 戶2，则向量a b 与a-b 的夹角的大小 为 , a-b 在b 方向上的投影为 _______________________________________ . 13.已知不共线的三个向量 15•函数f(x)二Asin(「x 「:)(其中A 0^ 0^ (0/ ))的图象如图所示，则函 2 ,方程 f (x)二 m (其中、.2 m ：2) 在 [0, 2二]内 数f(x)的解析式为 所有解的和为 _______ (x-1)2 2x 值，则实数a 的取值范围是 2 216•已知函数f (x)=< x _0 3 xn ，若f(x)在区间佝a F )上既有最大值又有最小 17 •设关于 x 的方程x -ax-2=0和x -x-1-a=0的实根分别为 为兀 和X3N ，若 % ：：： X 3 ：：： X 2 ：：：%,则实数a 的取值范围是 • 三、解答题：本大题共 5小题，共74分，解答时应写出文字说明、证明过程或演算步骤.18.(本题14分)已知函数f(x)=2sin(2 x - ) m,( m R)的最小值为1.6(I)求m 的值； (n)求函数f (x)的最小正周期和单调递增区间 19.(本题 15分 (I)若 (n)若,b , c 是 |艸4，且b//a ，，求向量b -(2a 3c)，求 a c .)已知向量司一平面内的三个向量，其中a = (1,，3).的坐标；彳+20.(本题15分)已知函数f(x) =(2x-1)(2八-3)7,其中a是常数•(I)若a = 6，且f (x) _ 0 ,求实数x的取值范围；(n)若方程f (x) = 0有两个不相等实根，求实数a的取值范围.421.(本题15分)已知函数f (x^ log 2 (a )，其中a为实数.x —2(I)若a =1,求函数f(x)的定义域；(n)若关于x的不等式f(x) ・log2(2a，2-x)对任意［3,6］恒成立，求实数a的取值范围•22.(本题15 分)设函数f(x) =x2-ax - b,(a,b・ R)(i)若f (x)在区间［0,1］上的最大值为b，求a的取值范围；(n)若f(x)在区间［1,2］上有零点，求a2・2b2 -4b的最小值.舟山中学2017-2018学年高一下开学考试一数学答案一、选择题BDBCD ADBCA二、填空题11.1 31 i12. -，-)2 213.214. 60 -1二915. f (x)二2sin(3 x )4 2116. (-；,0)217. (-1,1)三、解答题18. 解：(I) f(x)min =-2 m =1,m = 31 川川1)5分(n) f(x) =2sin(2x ) • 3,T =，「川川(丨9分,6JI JI JI JI JI由2k 2x 2k ，得k x ^k ,(k Z)2 6 2 6 3所以，单调递增区间为[k ,k ],(k Z)................... 4•分6 319.解：(I)令b =乜=('$3・)，则.23^4，得・2= 4•■二2, ............................................ -3-分(其他解法酌情给分)b 車2,2，或厂(一2，一2'3)(n) , (a c) _ (2a-3c) (a c) (2a-3c) =0, .................. -0•分2 2a c = 2a -3c 2 4 _3 2=2 ................... 5•分-120.（其他解法酌情给分）22.解：(I)由已知, 2 (2x)2-5 2x_3 _02 x1_3或2x .................... 分3解得：x _ log23.x的取值范围是［log 2 3, • ：：) ................. 7•分(n) f (x) =(2x-1) (2x 3_3) _a =2 (2x)2一5 2x3_a ,令t =：2x，则方程f (x) =0有两个不相等的实根等价于方程22t -5t • 3 - a = 0有两个不相等的正实根t1 ,21 •分t2 ,22.22.:0 则有讥1 +t 2 A 0二t 1 t ^> 0(-5)2 _8 (3_a) >05>0 23—a °x +2(i) a = 1 , . f (x) = log 2 -x —2由口 0x -2解得：x ” -2或x 2■ f (x)的定义域为x ・(-=-2)(2「：)........4_ 、(n)由题意log 2(a )・log 2(2a-x 2)对任意［3,6］恒成立,x —24即 0 ：：： 2a • 2 - x ：：： a 在 x • ［3,6］恒成立,x-22 a ：4川"I 川15分(其他解法酌情给分)21. (其他解法酌情给分(本题满分14分) 15•分解: ••分解：（I ）因为/'⑴的图彖是开口向上的抛物线，所以在区间［0,1］上的最大值必是/（0）和/（I ）中较大者，而/（0）= b ,所以只要/（O ）n/（1）, 即 bnl-a + b,得 a^l......... 4 分（II ）设方程*-ax + b = 0的两根是旺，且所以夕 +2胪-4Z> = (Xj +XJ)2 -k2Xj 2x 22 -4X J X 2= x/- 2X ,X 2 + x 22 + 2X J 2X 22 = (2X 22 + l)x/ - 2x 2x x + x 22遇+时命）*-肃沖一缶’当且仅当"寻时取等号.X 2设如十亦计 则^>=HP 27T =T 2~r =1 \ '头+1&右亍）-由叫《2,畤存I ，因此& + l ）F （M-】 = 3,11分此时 X 2 = 1 ,由 X| =■—-知斗=-所以出I Xl =|*L X 2= 1时，a 2 + 2b 2 一 4b 取得最小值|・12分。

2017-2018学年高一下学期期中数学试卷一、选择题（共12小题，每小题5分，满分60分）1．下列说法中正确的是（）A．共线向量的夹角为0°或180°B．长度相等的向量叫做相等向量C．共线向量就是向量所在的直线在同一直线上D．零向量没有方向2．下列函数中为奇函数的是（）A．y=sin|x| B．y=sin2x C．y=﹣sinx+2 D．y=sinx+13．已知角的终边经过点（4，﹣3），则tanα=（）A．B．﹣ C．D．﹣4．函数y=cos（4x﹣π）的最小正周期是（）A．4πB．2πC．πD．5．在直角坐标系中，直线3x+y﹣3=0的倾斜角是（）A．B．C． D．6．函数的单调递减区间（）A．（k∈Z）B．（k∈Z）C．（k∈Z）D．（k∈Z）7．函数y=3sin（2x+）+2图象的一条对称轴方程是（）A．x=﹣B．x=0 C．x=πD．8．下列选项中叙述正确的是（）A．终边不同的角同一三角函数值可以相等B．三角形的内角是第一象限角或第二象限角C．第一象限是锐角D．第二象限的角比第一象限的角大9．如果点P（sinθcosθ，2cosθ）位于第二象限，那么角θ所在象限是（）A．第一象限 B．第二象限 C．第三象限 D．第四象限10．向量+++化简后等于（）A．B．C．D．11．已知函数y=Asin（ωx+φ）+B的一部分图象如图所示，如果A＞0，ω＞0，|φ|＜，则（）A．A=4 B．ω=1 C．φ=D．B=412．给出下列说法：①终边相同的角同一三角函数值相等；②在三角形中，若sinA=sinB，则有A=B；③不论是用角度制还是用弧度制度量一个角，它们与扇形的半径的大小无关；④若sinα=sinβ，则α与β的终边相同；⑤若cos θ＜0，则θ是第二或第三象限的角．其中正确说法的个数是（）A．1 B．2 C．3 D．4二、填空（本大题共4小题，每小题5分，共20分．）13．以点（0，2）和（4，0）为端点的线段的中垂线的方程是．14．圆x2+y2=4上的点到直线3x+4y﹣25=0的距离最小值为．15．已知=， =， =， =， =，则+++﹣= ．16．已知tan（）=，tan（）=﹣，则tan（）= ．三、解答题（本大题共6小题，17题10分其余每题12分共70分）17．已知角α的终边经过一点P（5a，﹣12a）（a＞0），求2sinα+cosα的值．18．已知△ABC的三个顶点A（0，4），B（﹣2，6），C（8，2）；（1）求AB边的中线所在直线方程．（2）求AC的中垂线方程．19．若圆经过点A（2，0），B（4，0），C（1，2），求这个圆的方程．20．已知cosα=，cos（α﹣β）=，且0＜β＜α＜，（1）求tan2α的值；（2）求cosβ的值．21．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，（Ⅰ）求函数的解析式；（Ⅱ）求函数的对称轴方程和对称中心坐标．22．已知函数f（x）=sin2ωx+sinωx•cosωx﹣1（ω＞0）的周期为π．（1）当x∈[0，]时，求f（x）的取值范围；（2）求函数f（x）的单调递增区间．2017-2018学年高一下学期期中数学试卷参考答案与试题解析一、选择题（共12小题，每小题5分，满分60分）1．下列说法中正确的是（）A．共线向量的夹角为0°或180°B．长度相等的向量叫做相等向量C．共线向量就是向量所在的直线在同一直线上D．零向量没有方向【考点】向量的物理背景与概念．【分析】根据共线向量、平行向量、相等向量以及零向量的概念便可判断每个说法的正误，从而找出正确选项．【解答】解：A．共线向量的方向相同或相反；方向相同时，夹角为0°，相反时的夹角为180°，∴该说法正确；B．长度相等，方向相同的向量叫做相等向量，∴该说法错误；C．平行向量也叫共线向量，∴共线向量不是向量所在直线在同一直线上；∴该说法错误；D．零向量的方向任意，并不是没有方向，∴该说法错误．故选：A．2．下列函数中为奇函数的是（）A．y=sin|x| B．y=sin2x C．y=﹣sinx+2 D．y=sinx+1【考点】函数奇偶性的判断．【分析】要探讨函数的奇偶性，先求函数的定义域，判断其是否关于原点对称，然后探讨f（﹣x）与f（x）的关系，即可得函数的奇偶性．【解答】解：选项A，定义域为R，sin|﹣x|=sin|x|，故y=sin|x|为偶函数．选项B，定义域为R，sin（﹣2x）=﹣sin2x，故y=sin2x为奇函数．选项C，定义域为R，﹣sin（﹣x）+2=sinx+2，故y=sinx+2为非奇非偶函数偶函数．选项D，定义域为R，sin（﹣x）+1=﹣sinx+1，故y=sinx+1为非奇非偶函数，故选：B．3．已知角的终边经过点（4，﹣3），则tanα=（）A．B．﹣ C．D．﹣【考点】任意角的三角函数的定义．【分析】根据三角函数的定义进行求解即可．【解答】解：∵角α的终边经过点P（4，﹣3），∴tanα==，故选：B．4．函数y=cos（4x﹣π）的最小正周期是（）A．4πB．2πC．πD．【考点】三角函数的周期性及其求法．【分析】根据余弦函数的最小正周期的求法，将ω=4代入T=即可得到答案．【解答】解：∵y=cos（4x﹣π），∴最小正周期T==．故选：D．5．在直角坐标系中，直线3x+y﹣3=0的倾斜角是（）A．B．C． D．【考点】直线的倾斜角．【分析】由已知方程得到直线的斜率，根据斜率对于得到倾斜角．【解答】解：由已知直线的方程得到直线的斜率为﹣，设倾斜角为α，则tanα=﹣，α∈[0，π），所以α=；故选：D．6．函数的单调递减区间（）A．（k∈Z）B．（k∈Z）C．（k∈Z）D．（k∈Z）【考点】正弦函数的单调性．【分析】利用y=sinx的单调性，求出函数的单调递减区间，进而可求函数的单调递减区间．【解答】解：利用y=sinx的单调递减区间，可得∴∴函数的单调递减区间（k∈Z）故选D．7．函数y=3sin（2x+）+2图象的一条对称轴方程是（）A．x=﹣B．x=0 C．x=πD．【考点】正弦函数的图象．【分析】利用正弦函数的图象的对称性，求得y=3sin（2x+）+2图象的一条对称轴方程．【解答】解：∵对于函数y=3sin（2x+）+2图象，令2x+=kπ+，求得x=+，可得函数图象的一条对称轴方程为x=π，故选：C．8．下列选项中叙述正确的是（）A．终边不同的角同一三角函数值可以相等B．三角形的内角是第一象限角或第二象限角C．第一象限是锐角D．第二象限的角比第一象限的角大【考点】命题的真假判断与应用．【分析】分别举例说明四个选项的正误得答案．【解答】解：对于A，终边不同的角同一三角函数值可以相等，正确，如；对于B，三角形的内角是第一象限角或第二象限角，错误，如是终边在坐标轴上的角；对于C，第一象限是锐角，错误，如是第一象限角，不是锐角；对于D，第二象限的角比第一象限的角大，错误，如是第二象限角，是第一象限角，但．故选：A．9．如果点P（sinθcosθ，2cosθ）位于第二象限，那么角θ所在象限是（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】三角函数的化简求值．【分析】根据象限得出sinθ，cosθ的符号，得出θ的象限．【解答】解：∵P（sinθcosθ，2cosθ）位于第二象限，∴sinθcosθ＜0，cosθ＞0，∴sinθ＜0，∴θ是第四象限角．故选：D．10．向量+++化简后等于（）A．B．C．D．【考点】向量加减混合运算及其几何意义．【分析】利用向量的三角形法则与多边形法则即可得出．【解答】解：向量+++=，故选：D．11．已知函数y=Asin（ωx+φ）+B的一部分图象如图所示，如果A＞0，ω＞0，|φ|＜，则（）A．A=4 B．ω=1 C．φ=D．B=4【考点】由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】先根据函数的最大值和最小值求得A和B，然后利用图象中﹣求得函数的周期，求得ω，最后根据x=时取最大值，求得φ．【解答】解：如图根据函数的最大值和最小值得求得A=2，B=2函数的周期为（﹣）×4=π，即π=，ω=2当x=时取最大值，即sin（2×+φ）=1，2×+φ=2kπ+φ=2kπ﹣∵∴φ=故选C．12．给出下列说法：①终边相同的角同一三角函数值相等；②在三角形中，若sinA=sinB，则有A=B；③不论是用角度制还是用弧度制度量一个角，它们与扇形的半径的大小无关；④若sinα=sinβ，则α与β的终边相同；⑤若cos θ＜0，则θ是第二或第三象限的角．其中正确说法的个数是（）A．1 B．2 C．3 D．4【考点】任意角的概念．【分析】由任意角的三角函数的定义，三角函数值与象限角的关系，即可得出结论．【解答】解：①由任意角的三角函数的定义知，终边相同的角的三角函数值相等，正确．②在三角形中，若sinA=sinB，则有A=B，故正确；③不论是用角度制还是用弧度制度量一个角，它们与扇形的半径的大小无关，正确，④若sinα=sinβ，则α与β的终边相同或终边关于y轴对称，故不正确．⑤若cosα＜0，则α是第二或第三象限角或α的终边落在x轴的非正半轴上，故不正确．其中正确的个数为3个，故选：C．二、填空（本大题共4小题，每小题5分，共20分．）13．以点（0，2）和（4，0）为端点的线段的中垂线的方程是2x﹣y﹣3=0 ．【考点】待定系数法求直线方程．【分析】先求出线段AB的中垂线的斜率，再求出线段AB的中点的坐标，点斜式写出AB的中垂线得方程，并化为一般式．【解答】解：设A（0，2）、B（4，0）．=﹣，所以线段AB的中垂线得斜率k=2，又线段AB的中点为（2，1），直线AB的斜率 kAB所以线段AB的中垂线得方程为y﹣1=2（x﹣2）即2x﹣y﹣3=0，故答案为：2x﹣y﹣3=0．14．圆x2+y2=4上的点到直线3x+4y﹣25=0的距离最小值为 3 ．【考点】直线与圆的位置关系．【分析】圆心（0，0）到直线3x+4y﹣25=0的距离d==5，圆x2+y2=4上的点到直线3x+4y﹣25=0距离的最小值是AC=5﹣r，从而可求．【解答】解：∵圆心（0，0）到直线3x+4y﹣25=0的距离d==5，∴圆x2+y2=4上的点到直线3x+4y﹣25=0距离的最小值是AC=5﹣r=5﹣2=3故答案为：3．15．已知=， =， =， =， =，则+++﹣= ．【考点】向量的加法及其几何意义．【分析】利用向量的三角形法则与多边形法则即可得出．【解答】解： +++﹣=+++﹣=﹣=，故答案为：．16．已知tan（）=，tan（）=﹣，则tan（）= 1 ．【考点】两角和与差的正切函数．【分析】观察三个函数中的角，发现=﹣（），故tan（）的值可以用正切的差角公式求值【解答】解：∵=﹣（），∴tan（）===1故答案为1三、解答题（本大题共6小题，17题10分其余每题12分共70分）17．已知角α的终边经过一点P（5a，﹣12a）（a＞0），求2sinα+cosα的值．【考点】任意角的三角函数的定义．【分析】利用三角函数的定义可求得sinα与cosα，从而可得2sinα+cosα．【解答】解：由已知r==13a…∴sinα=﹣，cosα=，…∴2sinα+cosα=﹣…18．已知△ABC的三个顶点A（0，4），B（﹣2，6），C（8，2）；（1）求AB边的中线所在直线方程．（2）求AC的中垂线方程．【考点】待定系数法求直线方程．【分析】（1）利用中点坐标公式、斜截式即可得出．（2）利用斜率计算公式、相互垂直的直线斜率之间的关系、斜截式即可得出．【解答】解：（1）∵线段AB的中点为（﹣1，5），∴AB边的中线所在直线方程是=，即x+3y﹣14=0．（2）AC的中点为（4.3）==﹣，∵KAC∴y﹣3=4（x﹣4）即y=4x﹣13，∴AC的中垂线方程为y=4x﹣13．19．若圆经过点A（2，0），B（4，0），C（1，2），求这个圆的方程．【考点】圆的一般方程．【分析】设出圆的一般式方程，把三个点的坐标代入，求解关于D、E、F的方程组得答案．【解答】解：设圆的方程为x2+y2+Dx+Ey+F=0，则，解得．∴圆的方程为：．20．已知cosα=，cos（α﹣β）=，且0＜β＜α＜，（1）求tan2α的值；（2）求cosβ的值．【考点】二倍角的正切；两角和与差的余弦函数．【分析】（1）利用已知及同角三角函数基本关系式可求sinα，进而可求tanα，利用二倍角的正切函数公式可求tan2α的值．（2）由0＜β＜α＜，得0＜α﹣β＜，利用同角三角函数基本关系式可求sin（α﹣β），由β=α﹣（α﹣β）利用两角差的余弦函数公式即可计算求值．【解答】解：（1）∵由cosα=，0＜α＜，得sinα===，∴得tan=∴于是tan2α==﹣．…（2）由0＜β＜α＜，得0＜α﹣β＜，又∵cos（α﹣β）=，∴sin（α﹣β）==，由β=α﹣（α﹣β）得：cosβ=cos[α﹣（α﹣β）]=cosαcos（α﹣β）+sinαsin（α﹣β）==．…21．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，（Ⅰ）求函数的解析式；（Ⅱ）求函数的对称轴方程和对称中心坐标．【考点】由y=Asin（ωx+φ）的部分图象确定其解析式；正弦函数的图象．【分析】（Ⅰ）由函数的最值求出A，由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．（Ⅱ）利用正弦函数的图象的对称性，求得函数的对称轴方程和对称中心坐标．【解答】解：（Ⅰ）由函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象，可得A=2， ==+，∴ω=2．再根据五点法作图可得2•（﹣）+φ=，∴φ=，函数f（x）=2sin（2x+）．（Ⅱ）由2x+=kπ+，求得x=﹣，可得函数的图象的对称轴方程为x=﹣，k∈Z．令2x+=kπ，求得x=﹣，可得函数的图象的对称轴中心为（﹣，0），k∈Z．22．已知函数f（x）=sin2ωx+sinωx•cosωx﹣1（ω＞0）的周期为π．（1）当x∈[0，]时，求f（x）的取值范围；（2）求函数f（x）的单调递增区间．【考点】三角函数中的恒等变换应用；正弦函数的图象．【分析】（1）利用降幂公式降幂，再由辅助角公式化简，由x的范围求得相位的范围，则函数的取值范围可求；（2）利用复合函数的单调性求得原函数的单调区间．【解答】解：（1）f（x）=sin2ωx+sinωx•cosωx﹣1==．∵ω＞0，∴T=，则ω=1．∴函数f（x）=sin（2x﹣）﹣．由0，得，∴，∴．∴f（x）的取值范围[﹣1，]；（2）令，得：，（k∈Z），∴f（x）的单调递增区间为[kπ﹣，kπ+]，（k∈Z）．。

浙江省舟山中学2018年高一下学期期中考试数 学班级 姓名 本试题卷分选择题和非选择题两部分。

全卷共4页，满分110分，考试时间120分钟。

请考生按规定用笔将所有试题的答案涂、写在答题纸上。

选择题部分（共30分）注意事项：1.答题前，考生务必将自己的班级、姓名、学号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。

2.每小题选出答案后，用2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

不能答在试题卷上。

一、选择题：本大题共10小题，每小题3分，共30分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．数列,8,5,2,1-的一个通项公式为（ ▲ ） A ．43-=n a n B ．43+-=n a n C ．(1)(34)n n a n =--D ．1(1)(34)n n a n -=-- 2．不等式)13)(12(>+-x x 的解集是（ ▲ ） A ．1{|3x x <-或1}2x > B ．}2131|{<<-x x C ．1{|}2x x > D ．1{|}3x x >-3．在数列}{n a 中，12a =,1221n n a a +-=，则1a 的值为（ ▲ ）A ．49B ．50C ．51D ．52 4．在小时候，我们就用手指练习过数数，一个小朋友 按如图所示的规则练习数数，数到2012时对应的 指头是 （ ▲ ） A ．大拇指 B ．食指 C ．中指 D ．无名指5．在ABC ∆中， 30,5,15===A BC AC ，则AB 等于 （ ▲ ）A ．52B ．5C ．52或5D ．以上都不对 6．1)(2-+=ax ax x f 在R 上满足0)(<x f ，则a 的取值范围是 （ ▲ ） A ．0≤aB ．04≤<-aC ．04<<-aD ． 4-<a7．在等差数列}{n a 中，0,01110><a a ，且1011a a >，n S 为数列}{n a 的前n 项和，则使0>n S 的n 的最小值为 （ ▲ ） A ．10 B ．11 C ．20 D ．21 8．在右侧表格中，每格填上一个数字后，使每一横行 成等差数列，每一纵列成等比数列，则c b a ++的 值为 （ ▲ ） A ．1 B ．2 C ．3 D ．4 9．若)0,0(22>>=+b a b a ，则b a 21+的最小值为（ ▲ ）A ．5B ．29C ．3D ．410．设n n a a a S +++= 21,*N n ∈，下列给出两个结论：① 若2121-=-n n S ，则}{n a 是等比数列；② 若)2)(1(6++=n n n a a S ，则满足条件的2a 的最小取值为2-；那么（ ▲ ）A ．①正确，②错误B ．①错误，②正确C ．①②都正确D ．①②都错误非选择题部分（共80分）注意事项：1.用黑色字迹的签字笔或钢笔将答案写在答题纸上，不能答在试题卷上。

浙江省舟山市高一下学期期中数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题；共25分)1. （2分） (2018高二上·拉萨月考) 直线在轴上的截距为________．斜率________2. （1分）(2018·兴化模拟) 经过点且圆心是直线与直线的交点的圆的标准方程为________．3. （1分）在△ABC中，a=1，b=2，cosC=， sinA=________4. （1分） EC垂直Rt△ABC的两条直角边，D是斜边AB的中点，AC=6，BC=8，EC=12，则DE的长为________．5. （1分）直线的倾斜角θ=________．6. （1分） (2016高一下·奉新期末) 在△ABC中，∠A=60°，AC=1，△ABC的面积为，则BC的长为________．7. （1分）两条平行直线3x+4y﹣12=0与ax+8y+11=0间的距离是________8. （2分）(2017·温州模拟) 圆x2+y2﹣2y﹣3=0的圆心坐标是________，半径________．9. （1分）已知三棱锥P﹣ABC的所有顶点都在球O的球面上，△ABC是边长为2的正三角形，PC为球O的直径，且PC=4，则此三棱锥的体积为________．10. （1分）已知直线l1：ax+3y﹣1=0，，且l1⊥l2 ，则a=________．11. （10分）综合题。

（1）求过A（1，2）和两点的直线的截距方程；（2）求斜率为且与坐标轴围成的三角形面积是4的直线方程．12. （1分） (2016高一下·大丰期中) 在平面直角坐标系xOy中，圆C的方程为x2+y2﹣8x+15=0，若直线y=kx﹣2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的最大值是________．13. （1分） (2016高二下·深圳期中) 一个长方体高为5，底面长方形对角线长为12，则它外接球的表面积为________．14. （1分）已知圆，直线与的交点为点，过点向圆作两条切线，分别与圆相切于两点，则 ________.二、解答题 (共6题；共55分)15. （10分） (2018高一下·榆林期中) 三角形的三个顶点是．（1）求边所在的直线的方程；（2）求的面积．16. （5分）(2017·宜宾模拟) 如图，在多面体ABCDEF中，底面ABCD为正方形，平面AED⊥平面ABCD，AB=EA= ED，EF∥BD（ I）证明：AE⊥CD（ II）在棱ED上是否存在点M，使得直线AM与平面EFBD所成角的正弦值为？若存在，确定点M的位置；若不存在，请说明理由．17. （15分）(2013·江苏理) 如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50m/min．在甲出发2min后，乙从A乘缆车到B，在B处停留1min后，再从B匀速步行到C．假设缆车匀速直线运动的速度为130m/min，山路AC长为1260m，经测量，cosA= ，cosC=（1）求索道AB的长；（2）问乙出发多少分钟后，乙在缆车上与甲的距离最短？（3）为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？18. （5分） (2019高二上·兴宁期中) 如图，四棱锥的底面是正方形，，点在棱上.（Ⅰ）求证：；（Ⅱ）当且为的中点时，求与平面所成的角的大小.19. （5分）如图，地面上有一旗杆，为了测量它的高度，在地面上选一条基线，测得，在处测得点的仰角为，在处测得点的仰角为，同时可测得，求旗杆的高度．20. （15分） (2017高一下·盐城期末) 如图，已知动直线l过点，且与圆O：x2+y2=1交于A、B 两点．（1）若直线l的斜率为，求△OAB的面积；（2）若直线l的斜率为0，点C是圆O上任意一点，求CA2+CB2的取值范围；（3）是否存在一个定点Q（不同于点P），对于任意不与y轴重合的直线l，都有PQ平分∠AQB，若存在，求出定点Q的坐标；若不存在，请说明理由．参考答案一、填空题 (共14题；共25分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、11-2、12-1、13-1、14-1、二、解答题 (共6题；共55分) 15-1、15-2、16-1、17-1、17-2、17-3、18-1、19-1、20-1、20-2、20-3、。

浙江省舟山中学2017-2018学年高一下学期开学考试语文试题1.下列各句中，没有错别字且加点字的注音全部正确的一项是（）A.《古文观止》是由康熙年间两位名不见经传．（zhuàn）的选家所编，他们披沙拣金，遴．(l ín)选了二百多篇百读不厌的佳作。

B.北京画院配合“明清人物画”展览的微信导览，对展品均有详实的资料解读，而回顾古人、追本溯．(shuò)源的方式，可以让人在时空转换中汲．(jí)取传统书画的艺术养分。

C.如果不顺着领导的“杆儿”爬，会招致领导怨怼，“顺杆爬”者自然趋之若鹜，可见欲摒．(bĭng)除此种陋习，实在需要上位者能做到豁．(huò)达大度，广开言路。

D.母亲生前没有给我留下过什么隽．(juàn)永的哲言，或要我恪．(kè)守的教诲，只是在她去世之后，她艰忍的意志和毫不张扬的爱，在我的印象中愈加鲜明深刻。

阅读下面的文字，完成2～3题。

【甲】众所周知，中华民族在古代曾经以造纸术、指南针、火药和印刷术这四大发明闻名于世，可为什么科学和工业革命没有在近代的中国发生？20世纪英国著名科技史学家李约瑟到中国考察，他满心赞叹又充满困惑。

然而．．放眼今日中国，一轮新的科技创新热潮正如．火如荼．．．席卷神州大地……神舟飞天创造了“中国高度”，蛟龙潜海成就了“中国深度”，高铁奔腾刷新了“中国速度”，“中国天眼”拓宽了“中国维度”。

【乙】而高铁、支付宝、共享单车和网购更被称作中国“新四大发明”，还有已经领先全球的超级计算机、量子卫星……高精尖科技创新成果不断出现。

从基础建设到消费方式，从商业理念到经济业态，“新四大发明”折射出“中国式”创新的澎湃动能。

这种动能正方兴未艾．．．．，它让我国完全拥有自主知识产权的“复兴号”飞驰，令“墨子号”量子卫星腾飞。

【丙】如今，越来越多的“发明”，在“一带一路”沿线国家备受青睐，带来久违的感觉，独特的味道。

2017-2018学年浙江省舟山中学高考数学仿真试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个是符合题目要求的.1．集合A={0，2，3}，B={x|y=3x﹣x0}，则A∩B=（）A．{0}B．{8，26}C．{8}D．{2，3}2．若函数f（x）=3sin（2x+θ）（0＜θ＜π）是偶函数，则f（x）在[0，π]上的递增区间是（）A．[0，] B．[，π] C．[，]D．[，π]3．已知a，b是两条互相垂直的异面直线，下列说法中不正确的是（）A．存在平面α，使得a⊂α且b⊥αB．存在平面β，使得b⊂β且a∥βC．若点A，B分别在直线a，b上，且满足AB⊥b，则一定有AB⊥aD．过空间某点不一定存在与直线a，b都平行的平面4．设F1、F2是双曲线﹣=1（a＞0，b＞0）的左、右焦点，P为双曲线左支上任意一点，若|PF2|=2|PF1|，∠F1PF2=60°，则双曲线离心率等于（）A．B．C． +D．﹣5．已知各项均为正数的等比数列{a n}满足a7=a6+2a5，若存在两项a m，a n使得的最小值为（）A．B．C．D．6．已知x，y满足的最大值为3a+9，最小值为3a﹣3．则a的取值范围是（）A．[0，1]B．[﹣1，1] C．[﹣1，0] D．（﹣∞，﹣1]∪[1，+∞）7．设双曲线=1（a＞0，b＞0）的右焦点为F，过点F与x轴垂直的直线l交两渐近线于A，B两点，与双曲线的其中一个交点为P，设坐标原点为O，若（m，n∈R），且mn=，则该双曲线的渐近线为（）A．B．C． D．8．若函数f（x）=x2+ax+b有两个零点x1，x2，且3＜x1＜x2＜5，那么f（3），f（5）（）A．只有一个小于1 B．都小于1C．都大于1 D．至少有一个小于1二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.9．若点A（0，1）落在圆C：x2+y2+2x﹣4y+k=0（C为圆心）的外部，则|AC|=，实数k的取值范围是．10．设，为单位向量，且，的夹角为60°，若=+3，=2，则|+|等于，向量在方向上的投影为．11．一个棱锥的三视图如图所示，则该棱锥的所有棱长之和等于，棱锥的体积等于．12．已知数列{a n}为首项为a的等差数列，数列{+2n}是公比为q的等比数列，则q=，实数a的取值范围是．13．抛物线x2=﹣8y的准线交y轴于点A，过A作直线交抛物线于M，N两点，点B在抛物线的对称轴上，若（2+）⊥，则||的取值范围是．14．如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE．若M为线段A1C的中点，则在△ADE翻折过程中，下列正确的是．（写出所有正确的的编号）①线段BM的长是定值；②点M在某个球面上运动；③存在某个位置，使DE⊥A1C；④存在某个位置，使MB∥平面A1DE．15．△ABC中，AB=5，AC=2，BC上的高AH=4，=x+y，则=．三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.16．在△ABC中，角A，B，C所对的边分别为a，b，c，满足=，b=，cos2C=．（Ⅰ）求B，a的值；（Ⅱ）若A＞，如图，D为边BC中点，P是边AB上动点，求|CP|+|PD|的最小值．17．如图，已知长方形ABCD中，AB=2，AD=1，M为DC的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．（Ⅰ）求证：AD⊥BM；（Ⅱ）若=λ（0＜λ＜1），当二面角E﹣AM﹣D大小为时，求λ的值．18．已知数列{a n}的前n项和记为S n，且满足S n=2a n﹣n（n∈N*）．（1）求a1，a2的值，并证明：数列{a n+1}是等比数列；（2）证明：．19．已知中心在原点O的椭圆左，右焦点分别为F1，F2，F2（1，0），且椭圆过点（1，）（1）求椭圆的方程；（2）过F2的直线l与椭圆交于不同的两点A，B，则△F1AB的内切圆的面积是否存在最大值？若存在，求出这个最大值及此时的直线方程；若不存在，请说明理由．20．已知函数f（x）=ax2+bx+c，当|x|≤1时，|f（x）|≤1恒成立．（Ⅰ）若a=1，b=c，求实数b的取值范围；（Ⅱ）若g（x）=|cx2﹣bx+a|，当|x|≤1时，求g（x）的最大值．2016年浙江省舟山中学高考数学仿真试卷（理科）参考答案与试题解析一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一个是符合题目要求的.1．集合A={0，2，3}，B={x|y=3x﹣x0}，则A∩B=（）A．{0}B．{8，26}C．{8}D．{2，3}【考点】交集及其运算．【分析】求出B中x的范围确定出B，找出A与B的交集即可．【解答】解：∵A={0，2，3}，B={x|y=3x﹣x0}={x|x≠0}，∴A∩B={2，3}，故选：D．2．若函数f（x）=3sin（2x+θ）（0＜θ＜π）是偶函数，则f（x）在[0，π]上的递增区间是（）A．[0，] B．[，π] C．[，]D．[，π]【考点】正弦函数的奇偶性．【分析】利用诱导公式，余弦函数的单调性，得出结论．【解答】解：∵函数f（x）=3sin（2x+θ）（0＜θ＜π）是偶函数，∴φ=，f（x）=3sin（2x+）=3cos2x，令2kπ﹣π≤2x≤2kπ，求得kπ﹣≤x≤kπ，可得函数f（x）的增区间为[kπ﹣，kπ]，k∈Z．则f（x）在[0，π]上的递增区间为[，π]，故选：B．3．已知a，b是两条互相垂直的异面直线，下列说法中不正确的是（）A．存在平面α，使得a⊂α且b⊥αB．存在平面β，使得b⊂β且a∥βC．若点A，B分别在直线a，b上，且满足AB⊥b，则一定有AB⊥aD．过空间某点不一定存在与直线a，b都平行的平面【考点】空间中直线与平面之间的位置关系．【分析】根据异面直线的性质进行逐项分析判断．【解答】解：对于A，设a，b的公垂线为AB，其中A∈a，B∈b．过B作a的平行线a′，设直线a与a′确定的平面为平面α，则AB⊂α，a⊂α，a′⊂α，∵b⊥AB，b⊥a，∴b⊥α．故A正确；对于B，过b上一点C作a′∥a，设b与a′所确定的平面为β，则a∥β，故B正确．对于C，设a，b的公垂线为CB，且C∈a，B∈b．在a上取异于C的点A，则b⊥平面ABC，∴AB⊥b，但显然AB与a不垂直，故C错误；对于D，当空间一点在直线a或直线b上时，显然不存在与直线a，b都平行的平面，故D 正确．故选：C．4．设F1、F2是双曲线﹣=1（a＞0，b＞0）的左、右焦点，P为双曲线左支上任意一点，若|PF2|=2|PF1|，∠F1PF2=60°，则双曲线离心率等于（）A．B．C． +D．﹣【考点】双曲线的简单性质．【分析】运用双曲线的定义和三角形的余弦定理，结合双曲线的离心率公式，计算即可得到所求值．【解答】解：由双曲线的定义可得，|PF2|﹣|PF1|=2a，由|PF2|=2|PF1|，可得|PF2|=4a，|PF1|=2a，在△PF1F2中，由余弦定理可得|F1F2|2=|PF2|2+|PF1|2﹣2|PF2|•|PF1|cos∠F1PF2，即为4c2=16a2+4a2﹣2•4a•2a•=12a2，即有c=a，则e==．故选：B．5．已知各项均为正数的等比数列{a n}满足a7=a6+2a5，若存在两项a m，a n使得的最小值为（）A．B．C．D．【考点】基本不等式；等比数列的通项公式．【分析】由a7=a6+2a5求得q=2，代入求得m+n=6，利用基本不等式求出它的最小值．【解答】解：由各项均为正数的等比数列{a n}满足a7=a6+2a5，可得，∴q2﹣q﹣2=0，∴q=2．∵，∴q m+n﹣2=16，∴2m+n﹣2=24，∴m+n=6，∴，当且仅当=时，等号成立．故的最小值等于，故选A．6．已知x，y满足的最大值为3a+9，最小值为3a﹣3．则a的取值范围是（）A．[0，1]B．[﹣1，1] C．[﹣1，0] D．（﹣∞，﹣1]∪[1，+∞）【考点】简单线性规划．【分析】作出x、y满足约束条件图形，由图形判断出最优解，列出关于a的不等关系，再由不等式求出a的取值范围即可．【解答】解：画出x、y满足约束条件所围成的图形，有3个顶点（3，9），（3，﹣3），（﹣3，3），把它们分别代入ax+y得（3，9）⇒z=3a+9（3，﹣3）⇒z=3a﹣3（﹣3，3）⇒z=﹣3a+3由题意得，解得﹣1≤a≤1．故选B．7．设双曲线=1（a＞0，b＞0）的右焦点为F，过点F与x轴垂直的直线l交两渐近线于A，B两点，与双曲线的其中一个交点为P，设坐标原点为O，若（m，n∈R），且mn=，则该双曲线的渐近线为（）A．B．C． D．【考点】双曲线的简单性质．【分析】求出A、C坐标，然后求出P的坐标，代入双曲线方程，利用mn=，即可求出双曲线的离心率，即可求出双曲线的渐近线方程．【解答】解：由题意可知A（c，），B（c，），代入=（（m+n）c，（m﹣n）），得P（（m+n）c，（m﹣n）），代入双曲线方程=1，整理可得4e2mn=1，因为mn=，所以可得e=，所以=，所以1+=，所以=，所以双曲线的渐近线方程为y=±x，故选：B．8．若函数f（x）=x2+ax+b有两个零点x1，x2，且3＜x1＜x2＜5，那么f（3），f（5）（）A．只有一个小于1 B．都小于1C．都大于1 D．至少有一个小于1【考点】二次函数的性质．【分析】由题意可得f（x）=（x﹣x1）（x﹣x2），利用基本不等式可得f（3）•f（5）＜1，从而得出结论．【解答】解：由题意可得函数f（x）=（x﹣x1）（x﹣x2），∴f（3）=（3﹣x1）（3﹣x2）=（x1﹣3）（x2﹣3），f（5）=（5﹣x1）（5﹣x2），∴f（3）•f（5）=（x1﹣3）（x2﹣3）（5﹣x1）（5﹣x2）=[（x1﹣3）（5﹣x1）][（x2﹣3）（5﹣x2）]＜（）2（）2=1×1=1，即f（3）•f（5）＜1．故f（3），f（5）两个函数值中至少有一个小于1，故选：D．二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.9．若点A（0，1）落在圆C：x2+y2+2x﹣4y+k=0（C为圆心）的外部，则|AC|=，实数k的取值范围是（3，5）．【考点】圆与圆的位置关系及其判定．【分析】求出圆的圆心坐标，利用距离公式求解|AC|，列出不等式求解实数k的取值范围．【解答】解：圆C：x2+y2+2x﹣4y+k=0，C为圆心（﹣1，2），半径为：．则|AC|==．点A（0，1）落在圆C：x2+y2+2x﹣4y+k=0（C为圆心）的外部，，可得：k∈（3，5）．故答案为：10．设，为单位向量，且，的夹角为60°，若=+3，=2，则|+|等于3，向量在方向上的投影为．【考点】平面向量数量积的运算．【分析】根据向量的数量的运算和向量模的即可求出，利用向量在向量方向上的投影公式求得答案．【解答】解：∵设，为单位向量，且，的夹角为60°，=+3，=2，∴|+|2=2+2+||||cos60°=1+1+1=3，∴|+|=，∴+=3+3=3（+），∴|+|=3，∵•=（+3）•2=6•+22=6×1×1×+2=5，||=|2|=2，∴向量在方向上的投影为=，故答案为：，．11．一个棱锥的三视图如图所示，则该棱锥的所有棱长之和等于4+4，棱锥的体积等于．【考点】由三视图求面积、体积．【分析】由三视图知几何体是一个三棱锥，在对应的正方体中作出此三棱锥，利用正方体的长度和位置关系求出各个棱长，利用分割法和椎体的体积公式求出此三棱锥的体积． 【解答】解：由三视图知几何体是一个三棱锥A ﹣BCD ，如图：图中的正方体的棱长是2，其中A 、B 、E 、F 分别是对应边的中点，C 、D 是对应面的中心，由图得，AB ⊥平面CDE ，AB=CD=2，CF=AE=BE=1，又BF=，则BC==，即AD=BD=AC=BC=所以棱锥的各棱长之和：4+4，又DE=EC=BF=，CD=2，所以几何体的体积V=V A ﹣DEC +V B ﹣DEC =2×=2×=，故答案为：．12．已知数列{a n }为首项为a 的等差数列，数列{+2n }是公比为q 的等比数列，则q= 1，或2 ，实数a 的取值范围是 a ≠﹣1 ． 【考点】等比数列的通项公式．【分析】利用等差数列与等比数列的通项公式、分类讨论即可得出． 【解答】解：设等差数列{a n }的公差为d ， ∴a 2+2=a +2+d ，a 4+4=a +3d +4，a 8+8=a +7d +8， ∵数列{+2n }是公比为q 的等比数列，∴（a+3d+4）2=（a+2+d）（a+7d+8），化为：d=﹣1或d=a．①d=﹣1时，a2+2=a+1，a4+4=a+1，a8+8=a+1，a≠﹣1时，q=1．②d=a，a2+2=2a+2，a4+4=4a+4，a8+8=8a+8，a≠﹣1时，q=2．综上可得：q=1，2，a≠﹣1．故答案分别为：q=1，2；a≠﹣1．13．抛物线x2=﹣8y的准线交y轴于点A，过A作直线交抛物线于M，N两点，点B在抛物线的对称轴上，若（2+）⊥，则||的取值范围是（6，+∞）．【考点】抛物线的简单性质．【分析】由题意可设直线MN的方程为y=kx+2，M （x1，x2），N（x2，y2），MN 的中点E （x0，y0），联立方程可得x2+8kx+16=0，由△＞0可求k的范围，由方程的根与系数关系及中点坐标公式可求MN的中点E，由即BE⊥MN即M在MN的垂直平分线，则MN的垂直平分线与y轴的交点即是B，令x=0可求B的纵坐标，结合K的范围可求||的范围【解答】解：由题意可得A（0，2），直线MN的斜率k存在且k≠0设直线MN的方程为y=kx+2，M （x1，x2），N（x2，y2），MN 的中点E（x0，y0），联立方程可得x2+8kx+16=0则可得，△=64k2﹣64＞0，即k2＞1，x1+x2=﹣8k，y1+y2=k（x1+x2）+4=4﹣8k2∴x0=（x1+x2）=﹣4k，y0=（y1+y2）=2﹣4k2即E（﹣4k，2﹣4k2）又2+=2+2=2，∵（2+）⊥，即BE⊥MN即M在MN的垂直平分线则MN的垂直平分线y+4k2﹣2=﹣（x+4k）与y轴的交点即是B，令x=0可得，y=﹣2﹣4k2则||=2+4k2＞6故答案为（6，+∞）．14．如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻折成△A1DE．若M为线段A1C的中点，则在△ADE翻折过程中，下列正确的是①②④．（写出所有正确的的编号）①线段BM的长是定值；②点M在某个球面上运动；③存在某个位置，使DE⊥A1C；④存在某个位置，使MB∥平面A1DE．【考点】的真假判断与应用．【分析】取CD中点F，连接MF，BF，则平面MBF∥平面A1DE，可得④正确；由余弦定理可得MB2=MF2+FB2﹣2MF•FB•cos∠MFB，所以MB是定值，M是在以B为球心，MB 为半径的球上，可得①②正确．A1C在平面ABCD中的射影为AC，AC与DE不垂直，可得③不正确．【解答】解：①取CD中点F，连接MF，BF，则MF∥DA1，BF∥DE，∴平面MBF∥平面A1DE，∴MB∥平面A1DE，故D正确由∠A1DE=∠MFB，MF=A1D=定值，FB=DE=定值，由余弦定理可得MB2=MF2+FB2﹣2MF•FB•cos∠MFB，所以MB是定值，故①正确．②∵B是定点，∴M是在以B为球心，MB为半径的球上，故②正确，③∵A1C在平面ABCD中的射影为AC，AC与DE不垂直，∴存在某个位置，使DE⊥A1C不正确，故③错误．④取CD中点F，连接MF，BF，则平面MBF∥平面A1DE，可得④正确；故正确的有：①②④，故答案为：①②④．15．△ABC中，AB=5，AC=2，BC上的高AH=4，=x+y，则=．【考点】平面向量的基本定理及其意义．【分析】可过H作AC的平行线交AB于D，作AB的平行线，交AC于E，这样根据正弦定理及平行线的知识、三角函数的诱导公式即可得出，而由条件容易求出cosC，cosB的值，进而得出．由向量加法的平行四边形法则及向量数乘的几何意义可得到，进而可以求出x，y，从而得出的值．【解答】解：如图，过H分别作AC，AB的平行线，分别交AB于D，AC于E；则四边形ADHE为平行四边形；由正弦定理，；在Rt△ABH中，AB=5，AH=4；∴BH=3，cosB=；同理cosC=；∴；∵=；又；∴；∴．故答案为：．三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.16．在△ABC中，角A，B，C所对的边分别为a，b，c，满足=，b=，cos2C=．（Ⅰ）求B，a的值；（Ⅱ）若A＞，如图，D为边BC中点，P是边AB上动点，求|CP|+|PD|的最小值．【考点】余弦定理；正弦定理．【分析】（Ⅰ）已知等式利用正弦定理化简，整理得到关系式，再利用余弦定理表示出cosB，将得出关系式代入求出cosB的值，确定出B的度数，由题意确定出sinC的值，再由b与sinB的值，利用正弦定理求出c的值，再利用余弦定理求出a的值即可；（Ⅱ）由A＞，知a=2，作C关于AB的对称点C′，连C′D，C′P，C′B，如图所示，由余弦定理求出C′D的长，利用两点之间线段最短即可确定出|CP|+|PD|的最小值．【解答】解：（Ⅰ）已知等式利用正弦定理化简得：==，整理得：a2+c2﹣b2=ac，∴cosB==，∵B为△ABC的内角，∴B=；由cos2C=，得到sinC=，∵b=，sinB=，由正弦定理得：=，即=，解得：c=3，由b2=a2+c2﹣ac，得7=a2+9﹣3a，即a2﹣3a+2=0，解得：a=1或a=2；（Ⅱ）由A＞，知a=2，作C关于AB的对称点C′，连C′D，C′P，C′B，由余弦定理得：|C′D|2=|BD|2+|BC′|2+|BD|•|BC′|=12+22+2=7，|CP|+|PD|=|C′P|+|PD|≥|C′D|=，当C′，P，D共线时取等号，则CP+PD的最小值为．17．如图，已知长方形ABCD中，AB=2，AD=1，M为DC的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．（Ⅰ）求证：AD⊥BM；（Ⅱ）若=λ（0＜λ＜1），当二面角E﹣AM﹣D大小为时，求λ的值．【考点】二面角的平面角及求法；空间中直线与直线之间的位置关系．【分析】（Ⅰ）推导出BM⊥AM，从而BM⊥平面ADM，由此能证明AD⊥BM．（Ⅱ）法一：过点E作MB的平行线交DM于F，过点F作AM的垂线，垂足为H，连接HE，则∠EHF即为二面角E﹣AM﹣D的平面角，由此能求出当二面角E﹣AM﹣D大小为时λ的值．法二：以M为原点，MA，MB 所在直线为x 轴，y 轴，建立空间直角坐标系，利用向量法能求出当二面角E﹣AM﹣D大小为时λ的值．【解答】证明：（Ⅰ）∵，∴BM⊥AM，又平面ADM⊥平面ABCM，平面ADM∩平面ABCM=AM，BM⊂平面ABCM，∴BM⊥平面ADM．又AD⊂平面ADM，∴AD⊥BM．解：（Ⅱ）（方法一）过点E作MB的平行线交DM于F，由BM⊥平面ADM，得EF⊥平面ADM，在平面ADM中过点F作AM的垂线，垂足为H，连接HE，则∠EHF即为二面角E﹣AM﹣D的平面角，大小为．设FM=x，则，在Rt△FHM 中，由∠EFH=90°，∠EHF=60°，则．由EF∥MB，MB=2，则，即，解得x=4﹣2．故当二面角E﹣AM﹣D 大小为时，，即．（方法二）以M为原点，MA，MB 所在直线为x 轴，y 轴，建立如图所示空间直角坐标系，M（0，0，0），，，，且，所以，，设平面EAM 的法向量为，则，，所以，．又平面DAM 的法向量为，所以，，解得，或（舍去）．所以，．18．已知数列{a n }的前n 项和记为S n ，且满足S n =2a n ﹣n （n ∈N *）． （1）求a 1，a 2的值，并证明：数列{a n +1}是等比数列； （2）证明：．【考点】数列的求和． 【分析】（1）分别令n=1，2，计算即可得到所求；由当n ≥2时，S n =2a n ﹣n ，S n ﹣1=2a n ﹣1﹣（n ﹣1），相减再由构造数列，即可得证；（2）先证得﹣•≤＜，累加再由不等式的性质，即可得证．【解答】解：（1）当n=1时，2a 1﹣1=S 1，解得a 1=1， 当n=2时，S 2=2a 2﹣2⇒a 1+a 2=2a 2﹣2⇒a 2=a 1+2=3， 当n ≥2时，S n =2a n ﹣n ，S n ﹣1=2a n ﹣1﹣（n ﹣1）， 两式相减得：a n =2a n ﹣2a n ﹣1﹣1， 即a n =2a n ﹣1+1，两边同加1得到：a n +1=2（a n ﹣1+1）， 所以{a n +1}是以a 1+1=2为首项，2为公比的等比数列，所以；（2）证明：，，求和得到不等式：，因为，所以原不等式成立．19．已知中心在原点O 的椭圆左，右焦点分别为F 1，F 2，F 2（1，0），且椭圆过点（1，） （1）求椭圆的方程；（2）过F 2的直线l 与椭圆交于不同的两点A ，B ，则△F 1AB 的内切圆的面积是否存在最大值？若存在，求出这个最大值及此时的直线方程；若不存在，请说明理由．【考点】椭圆的简单性质． 【分析】（1）方法一、求得c=1，将已知点代入椭圆方程，解方程可得a ，b ，进而得到椭圆方程；方法二、运用椭圆的定义，结合两点的距离公式，求得a=2，再由a ，b ，c 的关系，可得b ，进而得到椭圆方程；（2）设A（x1，y1），B（x2，y2），不妨设y1＞0，y2＜0，设△F1AB的内切圆的半径R，可得三角形的面积为4R，可设直线l的方程为x=my+1，代入椭圆方程，运用韦达定理，再由三角形的面积公式，化简整理，运用换元法和对勾函数的单调性，即可得到所求最大值及此时直线的方程．【解答】解：（1）法一：由题意可设椭圆方程为+=1（a＞b＞0）．由题意可得c=1，即a2﹣b2=1，将（1，）代入椭圆方程可得+=1，解得a=2，b=，可得椭圆方程为+=1；法二：直接用椭圆的定义，由椭圆的焦点为（﹣1，0），（1，0）且过（1，），可得，即a=2，c=1，b==，得到椭圆方程为为+=1．（2）设A（x1，y1），B（x2，y2），不妨设y1＞0，y2＜0，设△F1AB的内切圆的半径R，由椭圆的定义可得△F1AB的周长为4a=8，可得，因此△F1AB面积最大，R就最大，由题知，直线l的斜率不为零，可设直线l的方程为x=my+1，由得（4+3m2）y2+6my﹣9=0，得y1+y2=﹣，y1y2=﹣，则S=|F1F2|•（y1﹣y2）===，令t=，则m2=t2﹣1，代入得=≤=3，即当t=1，m=0时，S≤3，又因为S=4R，所以R max=，这时所求内切圆面积的最大值为πR2=，故存在直线方程为x=1，△F1AB内切圆面积的最大值为．20．已知函数f（x）=ax2+bx+c，当|x|≤1时，|f（x）|≤1恒成立．（Ⅰ）若a=1，b=c，求实数b的取值范围；（Ⅱ）若g（x）=|cx2﹣bx+a|，当|x|≤1时，求g（x）的最大值．【考点】二次函数的性质；分段函数的应用．【分析】（Ⅰ）若a=1，b=c，则|f（1）|=|1+b+b|≤1，f（x）的对称轴，进而求得实数b的取值范围；（Ⅱ）由当|x|≤1时，|f（x）|≤1恒成立，可知|f（﹣1）|≤1，|f（0）|≤1，|f（1）|≤1，利用放缩法，可得当x=0时，g（x）=|﹣x2+2|取到最大值2．【解答】解：（Ⅰ）由a=1且b=c，得，…当x=1时，|f（1）|=|1+b+b|≤1，得﹣1≤b≤0．…故f（x）的对称轴，所以当|x|≤1时，，…解得…综上，实数b的取值范围为．…（Ⅱ）由当|x|≤1时，|f（x）|≤1恒成立，可知|f（﹣1）|≤1，|f（0）|≤1，|f（1）|≤1，…且由f（﹣1）=a﹣b+c，f（0）=c，f（1）=a+b+c，解得，，c=f（0）．…故≤1+1=2…且当a=2，b=0，c=﹣1时，若|x|≤1，则|f（x）|=|2x2﹣1|≤1恒成立，且当x=0时，g（x）=|﹣x2+2|取到最大值2．所以，g（x）的最大值为2．…2016年8月2日。