最新人教版高中数学必修3第三章《频率与概率》课后训练

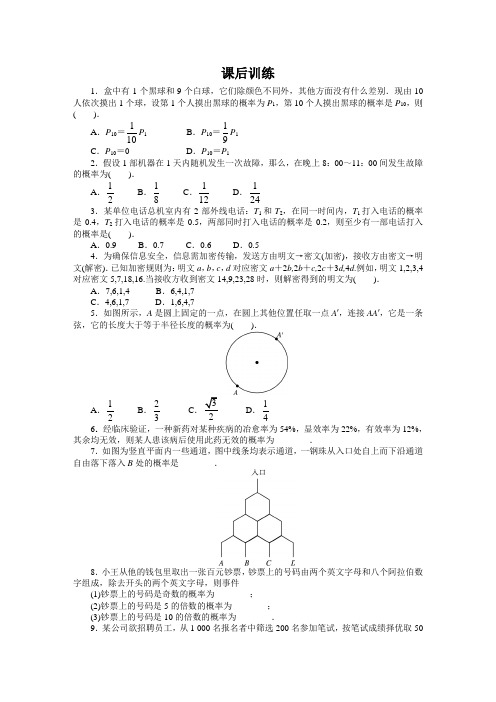
课后训练1．盒中有1个黑球和9个白球，它们除颜色不同外，其他方面没有什么差别．现由10人依次摸出1个球，设第1个人摸出黑球的概率为P 1，第10个人摸出黑球的概率是P 10，则( )．A ．P 10＝110P 1 B ．P 10＝19P 1 C ．P 10＝0 D ．P 10＝P 12．假设1部机器在1天内随机发生一次故障，那么，在晚上8：00～11：00间发生故障的概率为( )．A ．12 B ．18 C ．112 D ．1243．某单位电话总机室内有2部外线电话：T 1和T 2，在同一时间内，T 1打入电话的概率是0.4，T 2打入电话的概率是0.5，两部同时打入电话的概率是0.2，则至少有一部电话打入的概率是( )．A ．0.9B ．0.7C ．0.6D ．0.54．为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)．已知加密规则为：明文a ，b ，c ，d 对应密文a ＋2b,2b ＋c,2c ＋3d,4d .例如，明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时，则解密得到的明文为( )．A ．7,6,1,4B ．6,4,1,7C ．4,6,1,7D ．1,6,4,75．如图所示，A 是圆上固定的一点，在圆上其他位置任取一点A ′，连接AA ′，它是一条弦，它的长度大于等于半径长度的概率为( )．A ．12 B ．23 C D ．14 6．经临床验证，一种新药对某种疾病的冶愈率为54%，显效率为22%，有效率为12%，其余均无效，则某人患该病后使用此药无效的概率为________．7．如图为竖直平面内一些通道，图中线条均表示通道，一钢珠从入口处自上而下沿通道自由落下落入B 处的概率是________．8．小王从他的钱包里取出一张百元钞票，钞票上的号码由两个英文字母和八个阿拉伯数字组成，除去开头的两个英文字母，则事件(1)钞票上的号码是奇数的概率为________； (2)钞票上的号码是5的倍数的概率为________； (3)钞票上的号码是10的倍数的概率为________．9．某公司欲招聘员工，从1 000名报名者中筛选200名参加笔试，按笔试成绩择优取50名面试，再从面试对象中聘用20名员工．(1)求每个报名者能被聘用的概率；(3)若公司从聘用的4男2女中选派两人参加某项培训，则选派结果为一男一女的概率是多少？(4)若公司通知张三和李四必须在某天7：00～8：00到达面试地点，并且先到者先面试(不用等待)，每人面试的时间为20 min，求李四到达面试地点时张三正在里面面试的概率．参考答案1. 答案：D 摸球和抽签是相同的，虽然摸球的顺序有先后，但摸到的可能性是相同的．2. 答案：B3. 答案：B 利用概率的一般加法公式，得所求的概率为0.4＋0.5－0.2＝0.7.4. 答案：B 设明文为a ，b ，c ，d ，则依题意得214292323428a b b c c d d +=⎧⎪+=⎪⎨+=⎪⎪=⎩，，，，解得6417.a b c d =⎧⎪=⎪⎨=⎪⎪=⎩，，，5. 答案：B 记事件A ＝{弦的长度大于等于半径长度}，则事件A 的区域为优弧A 1′OA 2′的弧长23l ，试验的基本事件的区域长度为圆的周长l.所以223()3l P A l ==.6. 答案：12% 无效的概率P ＝1－54%－22%－12%＝12%.7. 答案：38根据古典概型的公式求解，基本事件总数为8条路，能够到达B 处的有3条路，可画出树状图考虑．所以一钢珠从入口处自上而下沿通道自由落下落入B 处的概率是38. 8. 答案：12 15 110 (1)钞票上的号码的奇偶性是由个位数字决定的，所以号码是奇数的概率是51102=. (2)个位数字是0或5时，号码是5的倍数，所以号码是5的倍数的概率是21105=. (3)个位数字是0时，号码是10的倍数，所以号码是10的倍数的概率是110.9. 答案：解：(1)每个报名者能被聘用的概率为：200.021000=； (2)估计这24人中能进入面试的人数为：50246200⨯=人； 故预测面试的切线分数大约是80分； (3)815； (4)设张三和李四到达的时间分别为7时x 分和7时y 分， 由题意得：060060020x y y x ≤≤⎧⎪≤≤⎨⎪≤-≤⎩，，， 如图所示，由几何概型公式，得所求概率为60602404025606018⨯÷-⨯÷=⨯.。

一、选择题1．第24届国际数学大会会标是以我国古代数学家赵爽的弦图为基础进行设计的.如图，会标是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形的一个锐角为θ，且πsin 2sin 52θθ⎛⎫++= ⎪⎝⎭.若在大正方形内随机取一点，则该点取自小正方形区域的概率为（ ）.A ．14B ．15C ．25D ．352．“哥德巴赫猜想”是近代三大数学难题之一，其内容是：一个大于2的偶数都可以写成两个质数(素数)之和，也就是我们所谓的“1+1”问题.它是1742年由数学家哥德巴赫提出的，我国数学家潘承洞、王元、陈景润等在哥德巴赫猜想的证明中做出相当好的成绩.若将6拆成两个正整数的和，则拆成的和式中，加数全部为质数的概率为（ ） A ．15B ．13C ．35D ．233．将一枚质地均匀的硬币连掷三次，设事件A ：恰有1次正面向上；事件B ：恰有2次正面向上，则()P A B +=（ ） A ．23B ．14C ．38D ．344．若数列{a n }满足a 1＝1，a 2＝1，a n +2＝a n +a n +1，则称数列{a n }为斐波那契数列，斐波那契螺旋线是根据斐波那契数列画出来的螺旋曲线，自然界中存在许多斐波那契螺旋线的图案，是自然界最完美的经典黄金比例.作图规则是在以斐波那契数为边的正方形拼成的长方形中画一个圆心角为90°的扇形，连起来的弧线就是斐波那契螺旋线，如图所示的7个正方形的边长分别为a 1，a 2，…，a 7，在长方形ABCD 内任取一点，则该点不在任何一个扇形内的概率为（ ）A ．1103156π-B ．14π-C ．17126π-D ．681237π-5．类比“赵爽弦图”，可类似地构造如图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设2AD BD =，若在大等边三角形中随机取一点，则此点取自小等边三角形的概率是（ ）A ．14B ．13C ．17D ．4136．甲乙两艘轮船都要在某个泊位停靠，甲停靠的时间为4小时，乙停靠的时间为6小时，假定他们在一昼夜的时间段中随机到达，则这两艘船停靠泊位时都不需要等待的概率为（ ）A ．916B ．58C ．181288D ．5127．某研究机构在对具有线性相关的两个变量x 和y 进行统计分析时，得到如下数据：x 4 6 8 10 12 y12356由表中数据求得y 关于的回归方程为，则在这些样本点中任取一点，该点落在回归直线下方的概率为（ ） A ．25B ．35 C ．34D ．128．从含有2件正品和1件次品的产品中任取2件，恰有1件次品的概率是（ ） A ．16B ．13C ．12D ．239．从分别写有1，2，3，4的4张卡片中随机抽取1张，放回后再随机抽取1张，则抽得的第一张卡片上的数不小于第二张卡片上的数的概率为 A ．25B ．35C ．38D ．5810．圆周率π是一个在数学及物理学中普遍存在的数学常数，它既常用又神秘，古今中外很多数学家曾研究它的计算方法.下面做一个游戏：让大家各自随意写下两个小于1的正数然后请他们各自检查一下，所得的两数与1是否能构成一个锐角三角形的三边，最后把结论告诉你，只需将每个人的结论记录下来就能算出圆周率的近似值.假设有n 个人说“能”，而有m 个人说“不能”，那么应用你学过的知识可算得圆周率π的近似值为（） A ．mm n+ B ．nm n+ C ．4mm n+ D ．4nm n+11．如图所示的图形中，每个三角形上各有一个数字，若六个三角形上的数字之和为26，则称该图形是“和谐图形”.已知其中四个三角形上的数字之和为20，现从1、2、3、4、5中任取两个数字标在另外两个三角形上，则恰好使该图形为“和谐图形”的概率为（ ）A ．310B ．15C ．110D ．32012．勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线，它由德国机械工程专家，机构运动学家勒洛首先发现，其作法是：以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形，现在勒洛三角形中随机取一点，则此点取自正三角形外的概率为（ ）A ()3323π- B ()323π-C ()323π+ D ()23323ππ-+二、填空题13．辛普森悖论(Simpson’sParadox)有人译为辛普森诡论，在统计学中亦有人称为“逆论”，甚至有人视之为“魔术”.辛普森悖论为英国统计学家E .H .辛普森(E.H.Simpson)于1951年提出的，辛普森悖论的内容大意是“在某个条件下的两组数据，分别讨论时都会满足某种性质，可是一旦合并考虑，却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论：关于某高校法学院和商学院新学期已完成的招生情况，现有如下数据： 某高校申请人数性别 录取率 法学院200人男50%女 70% 商学院300人男60% 女90% ①法学院的录取率小于商学院的录取率；②这两个学院所有男生的录取率小于这两个学院所有女生的录取率； ③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率； ④法学院的录取率不一定小于这两个学院所有学生的录取率. 其中，所有正确结论的序号是___________.14．住在同一城市的甲、乙两位合伙人,约定在当天下午4.00-5：00间在某个咖啡馆相见商谈合作事宜，他们约好当其中一人先到后最多等对方10分钟,若等不到则可以离去,则这两人能相见的概率为__________．15．一个多面体的直观图和三视图所示，M 是AB 的中点，一只蝴蝶在几何体ADF BCE -内自由飞翔，由它飞入几何体F AMCD -内的概率为______．16．乒乓球赛规定：一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换，每次发球，胜方得1分，负方得0分．设在甲、乙的比赛中，每次发球，甲发球得1分的概率为35，乙发球得1分的概率为23，各次发球的胜负结果相互独立，甲、乙的一局比赛中，甲先发球.则开始第4次发球时，甲、乙的比分为1比2的概率为________.17．若某学校要从5名男同学和2名女同学中选出3人参加社会考察活动，则选出的同学中男女生均不少于1名的概率是_____.18．在区间[-1,2]上随机取一个数x,则x ∈[0,1]的概率为 .19．设{}{}1,3,5,7,2,4,6a b ∈∈，则函数()log a bf x x =是增函数的概率为__________．20．在边长为2的正△ABC 所在平面内，以A 3AB ，AC 于D ，E.若在△ABC 内任丢一粒豆子，则豆子落在扇形ADE 内的概率是________．三、解答题21．某中学刚搬迁到新校区，学校考虑，若非住校生上学路上单程所需时间人均超过20分钟，则学校推迟5分钟上课.为此，校方随机抽取100个非住校生，调查其上学路上单程所需时间（单位：分钟），根据所得数据绘制成如下频率分布直方图，其中时间分组为[)0,10，[)10,20，[)20,30，[)30,40，[]40,50.（1）求频率分布直方图中a的值；（2）从统计学的角度说明学校是否需要推迟5分钟上课；（3）若从样本单程时间不小于30分钟的学生中，随机抽取2人，求这两个学生的单程时30,40上的概率.间均落在[)22．甲、乙两家商场对同一种商品开展促销活动，对购买该商品的顾客两家商场的奖励方案如下：甲商场：顾客转动如图所示圆盘，当指针指向阴影部分(图中四个阴影部分均为扇形，且每个扇形圆心角均为15︒，边界忽略不计)即为中奖.乙商场：从装有3个白球3个红球的盒子中一次性摸出2个球(球除颜色外不加区分)，如果摸到的是2个红球，即为中奖.问：购买该商品的顾客在哪家商场中奖的可能性大？23．某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.已知这100位顾客中一次购物量超过10件的顾客占40%.一次购物量1至5件6至10件11至15件16至20件21件及以上顾客数(人)x3025y5结算时间(分钟/人)12345（1）确定,x y的值，并估计顾客一次购物的结算时间的平均值；（2）求一位顾客一次购物的结算时间不超过3分钟的概率.(将频率视为概率)24．安庆市某中学教研室从高二年级随机抽取了50名学生的十月份语文成绩（满分100分，成绩均为不低于40分的整数），得到如图所示的频率分布直方图.（1）若该校高二年级共有学生1000人，试估计十月份月考语文成绩不低于60分的人数； （2）为提高学生学习语文的兴趣，学校决定在随机抽取的50名学生中成立“二帮一”小组，即从成绩[]90,100中选两位同学，共同帮助[)40,50中的某一位同学.已知甲同学的成绩为42分，乙同学的成绩为95分，求甲乙恰好被安排在同一小组的概率.25．手机运动计步已经成为一种新时尚.某单位统计了职工一天行走步数（单位：百步），绘制出如下频率分布直方图：（1）求直方图中a 的值，并由频率分布直方图估计该单位职工一天步行数的中位数； （2）若该单位有职工200人，试估计职工一天行走步数不大于13000的人数； （3）在（2）的条件下，该单位从行走步数大于15000的3组职工中用分层抽样的方法选取6人参加远足拉练活动，再从6人中选取2人担任领队，求这两人均来自区间150,(170]的概率.26．已知集合{(,)|[0,2],[1,1]}M x y x y =∈∈-. （1）若,x y Z ∈，求0x y +≥的概率； （2）若,x y R ∈，求0x y +≥的概率.【参考答案】***试卷处理标记，请不要删除一、选择题1．B 解析：B 【分析】根据πsin 2sin 52θθ⎛⎫++= ⎪⎝⎭，可以求得sin()1θϕ+=，tan 2ϕ=，求出小正方形的边长和直角三角形两直角边的长，进而得到大正方形的边长，然后根据几何概型概率公式求解即可． 【详解】 由πsin 2sin 52θθ⎛⎫++= ⎪⎝⎭可得sin 2cos 5θθ+=， 即5sin()5θϕ+=，即sin()1θϕ+=，且tan 2ϕ=，所以2πθϕ+=，所以直角三角形较大的锐角为ϕ，较小的锐角为θ，如图，设小正方形的边长为a ，直角三角形较大的锐角为θ、较大的锐角为为ϕ， 较小的直角的边长b ，则直角三角形较大的直角边长为+a b ，∵tan 2a bbϕ+==， ∴a b =，∴22(2)5a a a +=， 由几何概型概率公式可得，所求概率为2215(5)P a ==． 故选：B ． 【点睛】解答几何概型概率的关键是分清概率是属于长度型的、面积型的、还是体积型的，然后再根据题意求出表示基本事件的点构成的线段的长度（或区域的面积、空间几何体的体积），最后根据公式计算即可．2．A解析：A 【分析】列出所有可以表示成和为6的正整数式子，找到加数全部为质数的只有336+=，利用古典概型求解即可. 【详解】6拆成两个正整数的和含有的基本事件有:(1,5),(2,4),(3,3), (4,2),(5,1), 而加数全为质数的有(3,3), 根据古典概型知，所求概率为15P =. 故选：A. 【点睛】本题主要考查了古典概型，基本事件，属于容易题.3．D解析：D 【分析】根据题意，列举出所有的基本事件，再分别找出满足事件A 与事件B 的事件个数，分别求出其概率，最后再相加即可. 【详解】根据题意，将一枚质地均匀的硬币连掷三次，可能出现的情况有以下8种：（正正正），（正正反），（正反正），（正反反），（反正正），（反正反），（反反正），（反反反）.满足事件A ：恰有1次正面向上的基本事件有（正反反），（反正反），（反反正）三种，故3()8P A =；满足事件B ：恰有2次正面向上的基本事件有（正正反），（正反正），（反正正）三种，故3()8P B =；因此，3()()()4P A B P A P B +=+=. 故选：D. 【点睛】本题主要考查利用列举法计算基本事件的个数以及求解事件发生的概率.4．D解析：D 【分析】由题意求得数列{}n a 的前8项，求得长方形ABCD 的面积，再求出6个扇形的面积和，由测度比是面积比得答案． 【详解】由题意可得，数列{}n a 的前8项依次为：1，1，2，3，5，8，13，21．∴长方形ABCD 的面积为1321273⨯=．6个扇形的面积之和为222222(1235813)684ππ+++++=．∴所求概率681273P π=-．故选：D ． 【点睛】本题考查几何概型概率的求法，考查扇形面积公式的应用，是基础题．5．C解析：C 【分析】由题意求出AB =，所求概率即为DEF ABCS P S=，即可得解.【详解】由题意易知120ADB ∠=，AF FD BD ==，由余弦定理得22222cos1207AB AD BD AD BD BD =+-⋅⋅=即AB =，所以AB =，则所求概率为217DEF ABCSFD P SAB ⎛⎫=== ⎪⎝⎭. 故选：C. 【点睛】本题考查了几何概型概率的求法和余弦定理的应用，属于中档题.6．C解析：C 【分析】设甲、乙到达的时间分别为,x y ，列出所有基本事件的约束条件，同时列出两艘船停靠泊位时都不需要等待的约束条件，利用线性规划做出平面区域，利用几何概型概率关系转化为面积比. 【详解】设甲、乙到达的时间分别为,x y ，则所有基本事件的构成的区域024{|}024x x y ≤≤⎧Ω=⎨≤≤⎩， 则这两艘船停靠泊位时都不需要等待包含的基本事件构成的区域024024{(,)|}46x y A x y y x x y ≤≤⎧⎪≤≤⎪=⎨≥+⎪⎪≥+⎩，做出Ω构成的区域，其面积为224=576，阴影部分为集合A 构成的区域，面积为221(2018)3622+=， 这两艘船停靠泊位时都不需要等待的概率362181()576288P A ==. 故选:C.【点睛】本题考查利用线性规划做出事件对应的平面区域，再利用几何概型概率公式求出事件的概率，属于中档题.7．A解析：A 【分析】求出样本点的中心，求出ˆa的值，得到回归方程得到5个点中落在回归直线下方的有(6,2)，(8,3)，共2个，求出概率即可．【详解】8x =， 3.4y =，故3.40.658ˆa=⨯+，解得： 1.8a =-， 则0.65.8ˆ1yx =-， 故5个点中落在回归直线下方的有(6,2)，(8,3)，共2个， 故所求概率是25p =， 故选：A ． 【点睛】本题考查回归方程概念、概率的计算以及样本点的中心，考查数据处理能力，是一道基础题．8．D解析：D 【分析】设正品为12,a a ，次品为b ，列出所有的基本事件，根据古典概型求解即可. 【详解】设正品为12,a a ，次品为b ,任取两件所有的基本事件为12(,)a a ，1(,)a b ，2(,)a b 共3个基本事件， 其中恰有1件次品的基本事件为1(,)a b ，2(,)a b ，共2个， 所以23P =， 故选：D 【点睛】本题主要考查了古典概型，基本事件的概念，属于容易题.9．D解析：D 【分析】直接列举出所有的抽取情况，再列举出符合题意的事件数，即可计算出概率。

第一、二、三章滚动训练 （时间：100分钟,满分:100分）一、选择题（12×4分=48分）读下图的程序框图，完成1—2题.1.(2007广东佛山模拟)循环体执行的次数是（ ）A.50B.49C.100D.99 解析：∵i=i+2∴当2+2n≥100时，循环结束，此时n=49. 答案：B2.(2007广东佛山模拟)程序输出的结果是（ ）A.5 049B.4 850C.2 450D.2 550 解析：sum=0+2+4+6+…+98=2 450. 答案：C3.下列哪组数的最大公约数与1 855,1 120的最大公约数不同（ ）A.1 120，735B.385，350C.385，735D.1 855，325 解析：（1 855，1 120）→(1 120，735)→(735,385)→(385,350)→(350,35)→(35,315)→…→(35,35). 答案：D4.下列程序的运行结果是（ ） S=0for i=1∶1∶100 S=S+i endA.5 050B.2 525C.5 000D.1 010 解析：此程序为求1+2+…+100的值，故为5 050. 答案：A5.从3台甲型号彩电和2台乙型号彩电中任取2台，其中两个型号的彩电齐全的概率是（ ） A.51 B.52 C.53 D.54解析：记3台甲型号彩电分别为1、2、3，2台乙型号彩电分别为a,b ，则从5台彩电中任取2台，共有（1，2），（1，3），（2，3），（a,b ）,(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)10种情况，其中两个型号齐全的有6种情况，故概率为53106 . 答案：C6.(2007山东烟台模拟)先将一个棱长为3的正方体木块的六个面分别涂上六种颜色，再将该正方体均匀切割成棱长为1的小正方体，现从切好的小正方体中任取一块，所得的小正方体中六个面均没有涂色的有（ ）A.4个B.3个C.2个D.1个解析：棱长为3的正方体可切成27个棱长为1的小正方体，只有中间层的中间的1个小正方体六个面均没有涂色.本题是与立体几何结合的空间思维题. 答案：D7.甲、乙两人随意入住两间空房，则每人各住一间的概率是（ ） A.31 B.41 C.21D.无法确定 解析：记两个房间分别为1，2，则住房情况有以下4种情况：第1种：甲住1，乙住2；第2种：乙住1，甲住2；第3种：甲、乙都住1，2空；第4种：1空，甲、乙都住2，则每人各住一间的概率为42=21. 答案：C8.为考察某种皮鞋的各种尺码的销售情况，以某天销售40双皮鞋作为一个样本，把它按尺码分成5组，第3组的频率为0.25,第1，2，4组的频数分别为6，7，9，若第5组表示的是40—42码的皮鞋，则售出的200双皮鞋中含有40—42码的皮鞋有（ ）A.50双B.40双C.20双D.30双 解析：根据题意可知第3组的频数为40×0.25=10.则第5组的频数为8，频率为8÷40=0.2.故售出200双皮鞋，含有40—42码的皮鞋有200×0.2=40(双). 答案：B9.(2007江苏南京模拟)在箱子中装有十张卡片，分别写有1到10的十个整数，从箱子中任意取出一张卡片，把它上面的数字记为x ，然后再放回箱子中，第二次再从箱子中任意取出一张卡片，把它上面的数字记为y,则x+y 是10的倍数的概率为（ ） A.21 B.41 C.51 D.101 解析：先后两次抽取卡片，每次都有1—10这十种结果，故形成有序数对（x,y ）共有100个（图表法）.x+y 是10的倍数，它包含下列10个数对：（1，9），（2，8），（3，7），（4，6），（5，5），（6，4），（7，3），（8，2），（9，1），（10，10）. 故x+y 是10的倍数的概率为10110010 . 答案：D10.在5件产品中，有3件一等品，2件二等品.从中任取2件,那么以107为概率的事件是（ ） A.都不是一等品 B.恰有一件一等品 C.至少有一件二等品 D.至少有一件一等品 解析：记3件一等品分别为a 1,a 2,a 3,2件二等品分别为b 1,b 2,从中任取2件,则基本事件空间为{(a 1,a 2),(a 1,a 3),(a 2,a 3),(b 1,b 2),(a 1,b 1),(a 1,b 2),(a 2,b 1),(a 2,b 2),(a 3,b 1),(a 3,b 2)}.则A 、B 、C 、D4个选项的概率分别为109,107,53,101. 答案：C11.已知变量a 、b 已被赋值，要交换a 、b 的值，采用的算法是（ ） A.a=b,b=a B.a=c,b=a,c=bC.a=c,b=a,c=aD.c=a,a=b,b=c 答案：D12.(2007广东潮州模拟，9)如图，设M 是半径为R 的圆周上一个定点，在圆周上等可能地任取一点N ，连结MN ，则弦MN 的长超过R 2的概率为（ ）A.51 B.41 C.31 D.21 答案：D二、填空题（4×4分=16分）13.如图，程序运行结束后，输出的结果为____________.（填分数形式）解析：21+41+61+242581=. 答案：242514.在区间[1,3]上任取一个数，则这个数大于等于1.5的概率为____________. 解析：概率为P=25.1]3,1[]3,5.1[=的长度的长度=0.75. 答案：0.7515.某工人师傅欲用系统抽样的方法从1 503个机器零件（编号为0001—1 503）中抽取35个零件，在确定分段时，要使分段的间隔数量大，则至少应从总体中剔除的个数是____________，此时分段的间隔数是____________.解析：1 503除以35商42余33，所以剔除个数为33，分段间隔数为42. 答案：33 4216.在圆x 2+y 2-2x-2y+1=0内随机投点，则点与圆心距离小于31的概率是____________. 解析：圆的方程写成标准式为(x-1)2+(y-1)2=1,则圆心为(1,1),圆的半径为1. 当点投在以（1，1）为圆心，半径为31的圆内时，点与圆心的距离小于31,其概率为P=911)31(22=⨯⨯ππ.答案：91 三、解答题（四个大题共计36分）17.（8分）给出30个数：1，2，4，7，……其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，依次类推.要计算这30个数的和，现已给出了该问题算法的程序框图（如图所示），（1）请在图中判断框内①处和执行框中②处填上合适的语句，使之能完成该题算法功能. （2）根据程序框图写出程序.解析：（1）①处应填i ＞30; ②处应填p=p+i; (2)程序如下： i=1; p=1; s=0;while i ＜=30 s=s+p; p=p+i; i=i+1; end s18.(8分)袋中有红、黄、白3种颜色的球各1个，从中每次任取1个球，按照放回抽样方法抽取3次.求：（1）3个全是红球的概率； （2）3个颜色全相同的概率； （3）3个颜色不全相同的概率； （4）3个颜色全不相同的概率.解析：（1）由题意可知事件共27个基本事件，设全是红球的概率为A ，则P （A ）=271; (2)设3个颜色全相同的概率为B,因为3个颜色全相同，只能是全红或全黄或全白，则 P （B ）=91273=; （3）3个颜色不全相同的对立事件为3个颜色全相同，设3个颜色不全相同的事件为C ， 则P （C ）=1-P （B ）=98911=-; （4）记红、黄、白三个球分别为1，2，3，则3个颜色全不相同的事件为{1，2，3}，{1，3，2}，{2，1，3}，{2，3，1}，{3，1，2}，{3，2，1}，所以此事件的概率为92276=.（1）若已知y 与x 之间具有线性相关关系，求回归直线方程； （2）若气温为18℃，求大气压强； （3）若大气压强为1 000 hPa ，求气温. 解析：（1）设^^x b a y +=.⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=∑∑==xb y a x n x y nx y x b n i i n i i i ^^2121^ 用计算器求得a≈997.4,b≈0.56. 所以^y =0.56x+997.4.（2）x=18 ℃时，大气压强为0.56×18+997.4=1 007.48 hPa. (3)y=1 000hPa 时，气温为56.04.9971000-≈4.643 (℃).（1）列出样本的频率分布表； （2）画出频率分布直方图；（3）估计身高小于134 cm 的男孩约占多少百分比？(2)频率分布直方图如下图所示：（3）P(身高＜134 cm)=0.042+0.067+0.083=0.192.。

A级：基础巩固练一、选择题1．已知某种彩票发行1000000张，中奖率为0.001，则下列说法正确的是() A．买1张肯定不中奖B．买1000张一定能中奖C．买1000张也不一定能中奖D．买1000张一定恰有1张能中奖答案 C解析买1张，可能中奖，也可能不中奖，所以A选项错误；买1000张这样的彩票，可能中奖，也可能不中奖，所以B选项错误；买1000张也不一定能中奖，所以C选项正确；买1000张这样的彩票，可能有1张中奖，也可能多张中奖，也可能1张也不中奖，所以D选项错误．故选C.2．随着互联网的普及，网上购物已逐渐成为消费时尚，欲了解消费者对网上购物的满意情况，某公司随机对4500名网上购物消费者进行了调查(每名消费者限选一种情况回答)，统计结果如表：满意情况不满意比较满意满意非常满意人数200n 21001000“满意”的概率是()A.715 B.25 C.1115 D.1315答案 C解析由题意，n＝4500－200－2100－1000＝1200，所以对网上购物“比较满意”或“满意”的人数为1200＋2100＝3300，所以在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率为33004500＝1115.故选C.3．蜜蜂包括小蜜蜂和黑小蜜蜂等很多种类，在我国的云南及周边各省都有分布．春暖花开的时候是放蜂的大好季节．养蜂人甲在某地区放养了9000只小蜜蜂和1000只黑小蜜蜂，养蜂人乙在同一地区放养了1000只小蜜蜂和9000只黑小蜜蜂．某中学生物小组在上述地区捕获了1只黑小蜜蜂．那么，生物小组的同学认为这只黑小蜜蜂是哪位养蜂人放养的比较合理()A．甲B．乙C．甲和乙D．以上都对答案 B解析 从放蜂人甲放的蜜蜂中，捕获一只小蜜蜂是黑小蜜蜂的概率为110，而从放蜂人乙放的蜜蜂中，捕获一只小蜜蜂是黑小蜜蜂的概率为910，所以，现在捕获的这只小蜜蜂是放蜂人乙放养的可能性较大．故选B.4．在下列各事件中，发生的可能性最大的为( ) A ．任意买1张电影票，座位号是奇数 B ．掷1枚骰子，点数小于等于2C ．有10000张彩票，其中100张是获奖彩票，从中随机买1张是获奖彩票D ．一袋中装有8个红球，2个白球，从中随机摸出1个球是红球 答案 D解析 概率分别是P A ＝12，P B ＝13，P C ＝1100，P D ＝45，故选D. 5．甲、乙两人做游戏，下列游戏中不公平的是( )A ．抛一枚骰子，向上的点数为奇数则甲胜，向上的点数为偶数则乙胜B ．同时抛掷两枚硬币，恰有一枚正面向上则甲胜，两枚都是正面向上则乙胜C ．从一副不含大、小王的扑克牌中抽一张，扑克牌是红色则甲胜，是黑色则乙胜D ．甲、乙两人各写一个数字，若是同奇或同偶则甲胜，否则乙胜 答案 B解析 A 项，P (点数为奇数)＝P (点数为偶数)＝12；B 项，P (恰有一枚正面向上)＝12，P (两枚都正面向上)＝14；C 项，P (牌色为红)＝P (牌色为黑)＝12；D 项，P (同奇或同偶)＝P (奇偶不同)＝12.二、填空题6．如果从一个不透明的口袋中摸出白球的概率为16，已知袋中白球有3个，那么袋中球的总个数为________．答案 18解析 设袋中有x 个球，因为摸出白球的概率为16，且袋中白球有3个，所以3x ＝16.所以x ＝18.7．一个袋中装有数量差别较大的白球和黑球，从中任取一球，取出的是白球，估计袋中数量少的球是________．答案黑球解析根据极大似然法，知袋中数量较多的是白球，因此黑球数量较少．8．①一年按365天计算，两名学生的生日相同的概率是1 365；②如果买彩票中奖的概率是0.001，那么买1000张彩票一定能中奖；③乒乓球比赛前，决定谁先发球，抽签方法是从1～10共10个数字中各抽取1个，再比较大小，这种抽签方法是公平的；④昨天没有下雨，则说明昨天气象局的天气预报“降水概率为90%”是错误的．其中正确的有________(填序号)．答案①③解析对于②，买1000张彩票不一定中奖，故②错误；对于④，降水概率为90%只能说明下雨的可能性很大，但也可能不下雨，故④错误．三、解答题9．为了估计水库中鱼的尾数，可以使用以下的方法：先从水库中捕出一定数量的鱼，例如2000尾，给每尾鱼作上记号，不影响其存活，然后放回水库，经过适当时间，让其和水库中其余的鱼充分混合，再从水库中捕出一定数量的鱼，例如500尾，查看其中有记号的鱼，设有40尾，试根据上述数据，估计水库内鱼的尾数．解设水库中鱼的尾数为n，n是未知的，现在要估计n的值．假定每尾鱼被捕的可能性是相等的，从水库中任捕一尾，设事件A＝{带有记号的鱼}，由概率的统计定义可知P(A)＝2000 n.①第二次从水库中捕出500尾，观察每尾鱼上是否有记号，共需观察500次，其中带有记号的鱼有40尾，即事件A发生的频数m＝40，P(A)≈40 500.②由①②两式，得2000n≈40500，解得n≈25000.所以，估计水库中有鱼25000尾．B级：能力提升练10．设人的某一特征(眼睛的大小)是由他的一对基因所决定的，以d表示显性基因，r表示隐性基因，则具有dd基因的人为纯显性，具有rr基因的人为纯隐性，具有rd基因的人为混合性，纯显性与混合性的人都显露显性基因决定的某一特征，孩子从父母身上各得到一个基因，假定父母都是混合性，问：(1)1个孩子由显性决定特征的概率是多少？(2)“该父母生的2个孩子中至少有1个由显性决定特征”，这种说法正确吗？解 如图，由图可知，他们的孩子可能的基因有4种，即dd ，dr ，rd ，rr ，它们的概率分别为14，14，14，14.(1)当基因为dd ，dr ，rd 时，孩子显露显性基因决定的特征，所以他们的1个孩子由显性决定特征的概率是34.(2)这种说法不正确，2个孩子中每个由显性决定特征的概率均相等，为34.。

课后导练基础达标1.（2007山东潍坊模拟）随机事件A 的概率nm满足（ ） A.n m =0 B.n m =1 C.0＜n m ＜1 D.0≤nm ≤1 解析：由概率的统计定义知随机事件A 的概率一定在［0，1］内，即选D. 答案：D2.抛掷一枚硬币出现“正面向上”的概率为0.5是指（ ）A.正面向上的可能性是50%B.在100次抛掷中恰有50次正面向上C.无论抛掷多少次,总有50次正面向上D.以上说法都不正确 答案：A3.在20瓶饮料中,有2瓶已过了保质期,从中任取一瓶,取到已过保质期饮料的概率是（ ） A.0.1 B.0.05 C.0.01 D.0.5 答案：A4.若在同等条件下进行n 次重复试验得到某个事件A 发生的频率f(n)，则随着n 的逐渐增大，有（ ）A.f(n)与某个常数相等B.f(n)与某个常数的差逐渐减小C.f(n)与某个常数的差的绝对值逐渐减小D.f(n)在某个常数的附近摆动并趋于稳定解析：对于一个事件而言，概率是一个常数，而频率则随着试验次数的变化而变化，试验次数越多，频率就越接近于事件的概率，但并不是试验次数越多，所得频率就一定更接近概率值.答案：D5.下列结论正确的是（ ）A.对事件A 的概率P （A ）必有0＜P(A)＜1B.若事件A 的概率P （A ）=0.999，则事件A 是必然事件C.用某种药物对患有胃溃疡的500名病人治疗，结果有380人有明显的疗效，现有胃溃疡的病人服用此药，则估计其会有明显疗效可能性为76%D.某奖券中奖率为50%，则某人购买此奖券10张，一定有5张中奖 解析：A 中应有0≤P(A)≤1，B 中若A 为必然事件则P （A ）=1，在D 中，某人购买此奖券10张，有可能无一张中奖，也有可能有1张或2张、或3张或4张中奖，故选C. 答案：C6.某人将一枚硬币连掷了10次，正面朝上出现了6次，若用A 表示正面朝上这一事件，则A 的（ ） A.概率为53 B.频率为53C.频率为 6D.概率接近0.6解析：依据频率与概率的关系知应选B. 答案：B7.下列说法正确的是（ ） A.必然事件的概率是1B.某事件发生的概率是1.1C.“若平面α∩平面β=m,n ∥α,n ∥β，则m ∥n”是随机事件D.以上都不正确 答案：A8.某市的天气预报中，有“降水概率预报”，例如预报“明天降水概率为90%”，这是指（ ） A.明天该地区约有90%的地方会降水，其余地方不降水 B.明天该地区约90%的时间会降水，其余时间不降水C.气象台的专家中，有90%认为明天会降水，其余的专家认为不降水D.明天该地区降水的可能性为90 %解析：概率是随机事件发生可能性大小的度量，故选D. 答案：D9.孟德尔豌豆试验中，用纯黄色圆粒和纯绿色皱粒作杂交，则子二代结果的性状是黄色圆粒，黄色皱粒，绿色圆粒，绿色皱粒的比例约为（ ）A.1∶1∶1∶1B.1∶3∶3∶1C.9∶3∶3∶1D.1∶3∶3∶9解析：纯黄色圆粒XXYY ，纯绿色皱粒xxyy ，则豌豆杂交试验的子一代结果的性状是纯黄答案：C10.一家保险公司想了解汽车的挡风玻璃破碎的概率，公司收集了20 000部汽车，时间是从某年的5月1日到下一年的5月1日，共发现有600部汽车的挡风玻璃破碎，则一部汽车在一年时间里挡风玻璃破碎的概率近似为___________. 解析：频率是概率的近似值，故其概率近似等于20000600 n m =0.03. 答案：0.03 综合运用11.一个口袋内装有已有编号的大小相同的1个白球和2个黑球，从中任意摸出2球，摸出的2球全是黑球的概率是___________.解析：摸出的小球所有可能情况为（白，黑1），（白，黑2），（黑1，黑2），故摸出的2球全是黑球的概率是31. 答案：31 12.下列说法：其中不正确的说法是（ ）①既然抛掷硬币出现正面的概率为0.5，那么连续两次抛掷一枚质地均匀的硬币，一定是一次正面朝上，一次反面朝上 ②如果某种彩票的中奖概率为101，那么买1 000张这种彩票一定能中奖 ③在乒乓球、排球等比赛中，裁判通过让运动员猜上抛均匀塑料圆板着地是正面还是反面来决定哪一方先发球，这样做不公平④一个骰子掷一次得到2点的概率是61，这说明一个骰子掷6次会出现一次2点 A.①②③④ B.①②④ C.③④ D.③ 答案：A（1）将各次记录击中飞碟的频率填入表中. （2）这个运动员击中飞碟的概率约为多少？ 解析：（1）射击次数为100，击中飞碟数是81，故击中飞碟的频率是0.810.同理可求得下面的频率依次是0.792，0.820，0.820，0.793，0.794，0.807；（2）击中飞碟的频率稳定在0.81，故这个运动员击中飞碟的概率约为0.82. 14.先后抛掷2枚均匀的硬币.（1）一共可能出现多少种不同的结果？（2）出现“1枚正面，1枚反面”的结果有多少种？ 解析：（1）由题意可知，可能出现的结果有： “第1枚正面，第2枚正面”； “第1枚正面，第2枚反面”； “第1枚反面，第2枚正面”； “第1枚反面，第2枚反面”.即一共可能出现“2枚正面”“2枚反面”“第1枚正面，第2枚反面”“第1枚反面，第2枚正面”四种不同的结果.（2）由（1）得出现“1枚正面，1枚反面”的结果有“第1枚正面，第2枚反面”与“第1枚反面，第2枚正面”2种. 拓展探究15.某教授为了测试贫困地区和发达地区的同龄儿童的智力,出了10个智力题,每个题10分,然后作了统计,下表是统计结果：（1）利用计算器计算两地区参加测试的儿童中得60分以上的频率; （2）求两个地区参加测试的儿童得60分以上的概率; （3）分析贫富差距为什么会带来人的智力的差别. 解析：（1）贫困地区发达地区（2）概率分别为0.5和0.55;（3）经济上的贫困导致该地区生活水平落后,儿童的健康和发育会受到一定的影响;另外经济落后也会使教育事业发展落后,这都是贫富不同带来的智力差别的原因.。

一、选择题1．七巧板是我们祖先的一项创造，被誉为“东方魔板”，它是由五块等腰直角三角形（两块全等的小三角形、一块中三角形和两块全等的大三角形）、一块正方形和一块平行四边形组成的．如图是一个用七巧板拼成的正方形，现从该正方形中任取一点，则此点取自黑色部分的概率是A ．316B ．38C ．14D ．182．福建省第十六届运动会将于2018年在宁德召开，组委会预备在会议期间从3女2男共5名志愿者中任选2名志愿者参考接待工作，则选到的都是女性志愿者的概率为（ ）A ．110B ．310C ．12D ．353．如图是一边长为8的正方形苗圃图案，中间黑色大圆与正方形的内切圆共圆心，圆与圆之间是相切的，且中间黑色大圆的半径是黑色小圆半径的2倍.若在正方形图案上随机取一点，则该点取自黑色区域的概率为（ ）A ．8πB ．16π C ．18π-D ．116π-4．中国古代十进制的算筹计数法，在数学史上是一个伟大的创造，算筹实际上是一根根同长短的小木棍．如图，是利用算筹表示数1－9的一种方法．例如：3可表示为“≡”，26可表示为“=⊥”，现有6根算筹，据此表示方法，若算筹不能剩余，则可以用1－9这9个数字表示两位数中，能被3整除的概率是（ ）A ．518B ．718C ．716D ．5165．盒中有形状、大小都相同的2个红色球和3个黄色球，从中取出一个球，观察颜色后放回并往盒中加入同色球4个，再从盒中取出一个球，则此时取出黄色球的概率为（ ） A ．35B ．79C ．715D ．31456．据《孙子算经》中记载，中国古代诸侯的等级从低到高分为：男、子、伯、侯、公，共五级，若给获得巨大贡献的7人进行封爵，要求每个等级至少有一人，至多有两人，则伯爵恰有两人的概率为（ ） A ．310B ．25C ．825D ．357．将一枚质地均匀的硬币连掷三次，设事件A ：恰有1次正面向上；事件B ：恰有2次正面向上，则()P A B +=（ ） A ．23B ．14C ．38D ．348．如图，正方形ABNH 、DEFM 的面积相等，23CN NG AB ==，向多边形ABCDEFGH 内投一点，则该点落在阴影部分内的概率为（ ）A ．12B ．34C ．27D ．389．类比“赵爽弦图”，可类似地构造如图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设2AD BD =，若在大等边三角形中随机取一点，则此点取自小等边三角形的概率是（ ）A ．14B ．13C ．17D ．41310．已知三棱锥P ﹣ABC 的6条棱中，有2条长为1，有4条长为2，则从中任意取出的两条，这两条棱长度相等的概率为（ ） A ．815B ．715C ．45D ．3511．从一口袋中有放回地每次摸出1个球，摸出一个白球的概率为0.4，摸出一个黑球的概率为0.5，若摸球3次，则恰好有2次摸出白球的概率为 A ．0.24B ．0.26C ．0.288D ．0.29212．勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线，它由德国机械工程专家，机构运动学家勒洛首先发现，其作法是：以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形，现在勒洛三角形中随机取一点，则此点取自正三角形外的概率为（ ）A ．()23323ππ-- B ．()323π-C ．()323π+ D ．()23323ππ-+二、填空题13．如图，在边长为1的正方形中随机撒一粒黄豆，则它落在阴影部分的概率为_______.14．2020年初，湖北成为全国新冠疫情最严重的省份，面临医务人员不足，医疗物资紧缺等诸多困难，全国人民心系湖北，志愿者纷纷驰援.若某医疗团队从3名男医生和2名女医生志愿者中，随机选取2名医生赴湖北支援，则至少有1名女医生被选中的概率为__________.15．将一颗质地均匀的骰子(一种各个面上分别标有1，2，3，4，5，6个点的正方体玩具)先后抛掷2次，则出现向上的点数之和小于10的概率是________．16．五位德国游客与七位英国游客在游船上任意站成一排拍照，则五位德国游客互不相邻的概率为_______.17．在区间[2,4]-上随机地取一个实数x ，若实数x 满足||x m ≤的概率为23，则m =_______.18．已知四棱锥P ABCD -的所有顶点都在球O 的球面上，PA ⊥底面ABCD ，底面ABCD 为正方形， 2.PA AB ==现在球O 的内部任取一点，则该点取自四棱锥P ABCD -的内部的概率为______．19．从1，2，3，4中任取两个不同的数，则取出的2个数之差的绝对值小于或等于2的概率为__________．20．4位同学各自在周六、周日两天中任选一天参加公益活动，则周六、周日都有同学参加公益活动的概率是________三、解答题21．某电视台“挑战主持人”节目的挑战者闯第一关需要回答三个问题，其中前两个问题回答正确各得10分，回答不正确得0分，第三个问题回答正确得20分，回答不正确得10-分．如果一位挑战者回答前两个问题正确的概率都是23，回答第三个问题正确的概率为12，且各题回答正确与否相互之间没有影响．若这位挑战者回答这三个问题的总分不低于10分就算闯关成功．（1）求至少回答对一个问题的概率．（2）求这位挑战者回答这三个问题的总得分X 的分布列． （3）求这位挑战者闯关成功的概率．22．新冠病毒肆虐全球，尽快结束疫情是人类共同的期待，疫苗是终结新冠疫情最有力的科技武器，为确保疫苗安全性和有效性，任何疫苗在投入使用前都要经过一系列的检测及临床试验，周期较长.我国某院士领衔开发的重组新冠疫苗在动物猕猴身上进行首次临床试验.相关试验数据统计如下：已知从所有参加试验的猕猴中任取一只，取到“注射重组新冠疫苗”猕猴的概率为5 12.（1）根据以上试验数据判断，能否有99.9%以上的把握认为“注射重组新冠疫苗”有效？（2）若从上述已感染新冠病毒的猕猴中任取三只进行病理分析，求至少取到两只注射了重组新冠疫苗的猕猴的概率.附：22(),()()()()n ad bcK n a b c da b a c c d b d-==+++ ++++23．一个盒子里装有m个均匀的红球和n个均匀的白球，每个球被取到的概率相等，已知从盒子里一次随机取出1个球，取到的球是红球的概率为13，从盒子里一次随机取出2个球，取到的球至少有1个是白球的概率为10 11.（1）求m，n的值；（2）若一次从盒子里随机取出3个球，求取到的白球个数不小于红球个数的概率. 24．一次考试结束后，随机抽查了某校高三（1）班5名同学的数学与物理成绩如下表：（Ⅰ）分别求这5名同学数学与物理成绩的平均分与方差，并估计该班数学与物理成绩那科更稳定；（Ⅱ）从以上5名同学中选2人参加一项活动，求选中的学生中至少有一个物理成绩高于90分的概率.25．为了弘扬中华民族传统文化，某中学高二年级举行了“爱我中华，传诵经典”的考试，并从中随机抽取了60名学生的成绩（满分100分）作为样本，其中成绩不低于80分的学生被评为优秀生，得到成绩分布的频率分布直方图如图所示.（1）若该年级共有1000名学生，试利用样本估计该年级这次考试中优秀生人数； （2）试估计这次参加考试的学生的平均成绩（同一组数据用该组区间中点值作代表）； （3）若在样本中，利用分层抽样从成绩不低于70分的学生中随机抽取6人，再从中抽取2人赠送一套国学经典典籍，试求恰好抽中2名优秀生的概率.26．2020年寒假期间新冠肺炎肆虐，全国人民众志成城抗疫情.某市要求全体市民在家隔离，同时决定全市所有学校推迟开学.某区教育局为了让学生“停课不停学”，要求学校各科老师每天在网上授课辅导，每天共200分钟.教育局为了了解高三学生网上学习情况，上课几天后在全区高三学生中采取随机抽样的方法抽取了80名学生（其中男女生恰好各占一半）进行问卷调查，按男女生分为两组，再将每组学生在线学习时间（分钟）分为5组[0,40]，(40,80]，(80,120]，(120,160]，(160,200]得到如图所示的频率分布直方图.全区高三学生有3000人（男女生人数大致相等），以频率估计概率回答下列问题：（1）估计全区高三学生中网上学习时间不超过40分钟的人数；（2）在调查的80名高三学生且学习时间不超过40分钟的学生中，男女生按分层抽样的方法抽取6人.若从这6人中随机抽取2人进行电话访谈，求至少抽到1名男生的概率.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【解析】设2AB =，则1BC CD DE EF ====.∴1124BCI S ∆==，112242BCI EFGHS S ∆==⨯=平行四边形 ∴所求的概率为113422216P +==⨯ 故选A. 2．B解析：B 【解析】设3名女志愿者为,,A B C ，2名男志愿者为,a b ，任取2人共有,,,,,,,,,Aa Ab Ba Bb Ca Cb AB AC BC ab ，共10种情况，都是女性的情况有,,AB AC BC三种情况，故选到的都是女性志愿者的概率为310，故选B. 3．C解析：C 【分析】设黑色小圆的半径为r ，则黑色大圆的半径为2r ，由题意求得r ，进一步求出黑色区域的面积，由测度比是面积比得答案． 【详解】解：设黑色小圆的半径为r ，则黑色大圆的半径为2r ， 由题意可知，88r =，即1r =．∴图中黑色区域的面积为222884412648ππππ⨯-⨯+⨯⨯+⨯=-，又正方形的面积为64．∴在正方形图案上随机取一点，则该点取自黑色区域的概率为6481648ππ-=-． 故选：C ． 【点睛】本题考查几何概型的概率的求法，考查数形结合的解题思想方法，属于中档题．4．D解析：D 【分析】根据题意把6根算筹所能表示的两位数列举出来后，计算哪些能被3整除即可得概率． 【详解】1根算筹只能表示1,2根根算筹可以表示2和6,3根算筹可以表示3和7,4根算筹可以表示4和8,5根算筹可以表示5和9，因此6根算筹表示的两位数有15,19,51,91,24,28,64,68,42,82,46,86,37,33,73,77共16个，其中15,51,24,42,33共5个可以被3整除， 所以所求概率为516P =．故选：D．【点睛】本题考查古典概型，考查中国古代数学文化，解题关键是用列举法写出6根算筹所能表示的两位数．5．A解析：A【分析】若取出的是红色球，再从盒中取出一个球，则此时取出黄色球的概率为：139 25P=⨯，若取出的是黄色球，再从盒中取出一个球，则此时取出黄色球的概率为：237 59P=⨯，由此能求出再从盒中取出一个球，则此时取出黄色球的概率.【详解】盒中有形状、大小都相同的2个红色球和3个黄色球，从中取出一个球，观察颜色后放回并往盒中加入同色球4个，若取出的是红色球，再从盒中取出一个球，则此时取出黄色球的概率为：1329 515 2P=⨯=，若取出的是黄色球，再从盒中取出一个球，则此时取出黄色球的概率为：2377 5915P=⨯=，∴再从盒中取出一个球，则此时取出黄色球的概率为：1221573155P P P=+=+=，故选：A.【点睛】本题考查概率的求法，考查相互独立事件概率乘法公式、互斥事件概率计算公式等基础知识，考查运算求解能力，属于中档题.6．B解析：B【分析】根据部分平均分组分配的方法可求得分法总数和伯爵恰有两人的分法数，根据古典概型概率公式可求得结果.【详解】7人进行封爵，每个等级至少一人，至多两人，则共有2211225575327555322322C C C C C C AAA A A⋅=种分法；其中伯爵恰有两人的分法有2211142247532247543232C C C CC A C C AA A⋅=种分法，∴伯爵恰有两人的概率2247542257552225C C A p C C A A ==.故选：B . 【点睛】本题考查数学史与古典概型概率问题的求解，关键是能够利用排列组合中不平均分组分配的方法确定分法总数和符合题意的分法数.7．D解析：D 【分析】根据题意，列举出所有的基本事件，再分别找出满足事件A 与事件B 的事件个数，分别求出其概率，最后再相加即可. 【详解】根据题意，将一枚质地均匀的硬币连掷三次，可能出现的情况有以下8种：（正正正），（正正反），（正反正），（正反反），（反正正），（反正反），（反反正），（反反反）.满足事件A ：恰有1次正面向上的基本事件有（正反反），（反正反），（反反正）三种，故3()8P A =；满足事件B ：恰有2次正面向上的基本事件有（正正反），（正反正），（反正正）三种，故3()8P B =；因此，3()()()4P A B P A P B +=+=. 故选：D. 【点睛】本题主要考查利用列举法计算基本事件的个数以及求解事件发生的概率.8．C解析：C 【分析】由正方形ABNH 、DEFM 的面积相等，可得两正方形边长相等，设边长为3，由23CN NG AB ==，可得正方形MCNG 的边长为2，分别求出阴影部分的面积及多边形ABCDEFGH 的面积，由测度比为面积比得答案. 【详解】如图所示，由正方形ABNH 、DEFM 的面积相等，可得两正方形边长相等， 设边长为3，由23CN NG AB ==，可得正方形MCNG 的边长为2， 则阴影部分的面积为224⨯=，多边形ABCDEFGH 的面积为2332214⨯⨯-⨯=. 则向多边形ABCDEFGH 内投一点，则该点落在阴影部分内的概率为42147=. 故选：C.【点睛】本题主要考查了几何概型的概率的求法，关键是求出多边形ABCDEFGH 的面积，着重考查了推理与运算能力，以及数形结合的应用，属于基础题.9．C解析：C 【分析】 由题意求出7AB BD =，所求概率即为DEF ABCS P S=，即可得解.【详解】由题意易知120ADB ∠=，AF FD BD ==，由余弦定理得22222cos1207AB AD BD AD BD BD =+-⋅⋅=即7AB BD =，所以7AB FD =，则所求概率为217DEF ABCSFD P SAB ⎛⎫=== ⎪⎝⎭. 故选：C. 【点睛】本题考查了几何概型概率的求法和余弦定理的应用，属于中档题.10．B解析：B 【分析】从中任意取出的两条，基本事件总数2615n C ==，这两条棱长度相等包含的基本事件个数22247m C C =+=，由此能求出这两条棱长度相等的概率． 【详解】解：三棱锥P ABC -的6条棱中，有2条长为1，有4条长为2，从中任意取出的两条，基本事件总数2615n C ==，这两条棱长度相等包含的基本事件个数22247m C C =+=， ∴这两条棱长度相等的概率715m p n ==． 故选：B ．【点睛】本题考查概率的求法，考查古典概型、排列组合等基础知识，考查运算求解能力，是基础题．11．C解析：C 【分析】首先分析可能的情况：（白，非白，白）、（白，白，非白）、（非白，白，白），然后计算相应概率. 【详解】因为摸一次球，是白球的概率是0.4，不是白球的概率是0.6， 所以0.40.60.40.40.40.60.60.40.40.288P =⨯⨯+⨯⨯+⨯⨯=， 故选C. 【点睛】本题考查有放回问题的概率计算，难度一般.12．A解析：A 【分析】设2BC =，将圆心角为3π的扇形面积减去等边三角形的面积可得出弓形的面积，由此计算出图中“勒洛三角形”的面积，然后利用几何概型的概率公式可计算出所求事件的概率. 【详解】如下图所示，设2BC =，则以点B 为圆心的扇形面积为2122=233ππ⨯⨯， 等边ABC ∆的面积为212sin 323π⨯⨯=，其中一个弓形的面积为233π-， 所以，勒洛三角形的面积可视为一个扇形面积加上两个弓形的面积，即222322333πππ⎛⎫+⨯-=- ⎪⎝⎭， ∴在勒洛三角形中随机取一点，此点取自正三角形外部的概率()()323312323πππ--=--，故选A.【点睛】本题考查几何概型概率的计算，解题的关键就是要求出图形相应区域的面积，解题时要熟悉一些常见平面图形的面积计算方法，考查计算能力，属于中等题.二、填空题13．【分析】利用定积分求得阴影部分的面积然后利用几何概型的概率计算公式即可求解【详解】由题意结合定积分可得阴影部分的面积为由几何概型的计算公式可得黄豆在阴影部分的概率为【点睛】本题主要考查了定积分的几何解析：1 3【分析】利用定积分求得阴影部分的面积，然后利用几何概型的概率计算公式，即可求解．【详解】由题意，结合定积分可得阴影部分的面积为311221 (1()|33S dx x x=-=-=⎰，由几何概型的计算公式可得，黄豆在阴影部分的概率为113113 p==⨯．【点睛】本题主要考查了定积分的几何意义求解阴影部分的面积，以及几何概型及其概率的计算问题，其中解答中利用定积分的几何意义求得阴影部分的面积是解答的关键，着重考查了推理与计算能力，属于基础题．14．【分析】基本事件总数选中的都是男医生包含的基本事件个数根据对立事件的概率能求出选中的至少有1名女医生的概率【详解】因为医疗团队从3名男医生和2名女医生志愿者所以随机选取2名医生赴湖北支援共有个基本事解析：7 10【分析】基本事件总数2510n C==，选中的都是男医生包含的基本事件个数233m C==，根据对立事件的概率能求出选中的至少有1名女医生的概率.【详解】因为医疗团队从3名男医生和2名女医生志愿者，所以随机选取2名医生赴湖北支援共有2510n C==个基本事件，又因为选中的都是男医生包含的基本事件个数233m C==，所以至少有1名女医生被选中的概率为3711010 P=-=.故答案为：7 10【点睛】本题主要考查了排列组合，古典概型，对立事件，属于中档题.15．【解析】基本事件总数为36点数之和小于10的基本事件共有30种所以所求概率为【考点】古典概型【名师点睛】概率问题的考查侧重于对古典概型和对立事件的概率的考查属于简单题江苏对古典概型概率的考查注重事件解析：56【解析】基本事件总数为36，点数之和小于10的基本事件共有30种，所以所求概率为305.366= 【考点】古典概型【名师点睛】概率问题的考查，侧重于对古典概型和对立事件的概率的考查，属于简单题.江苏对古典概型概率的考查，注重事件本身的理解，淡化计数方法.因此先明确所求事件本身的含义，然后一般利用枚举法、树形图解决计数问题，而当正面问题比较复杂时，往往利用对立事件的概率公式进行求解.16．【分析】基本事件总数五位德国游客互不相邻包含的基本事件个数为：由此能求出五位德国游客互不相邻的概率【详解】解：五位德国游客与七位英国游客在游船上任意站成一排拍照基本事件总数五位德国游客互不相邻包含的 解析：799【分析】基本事件总数1212n A =，五位德国游客互不相邻包含的基本事件个数为：7578m A A =，由此能求出五位德国游客互不相邻的概率． 【详解】解：五位德国游客与七位英国游客在游船上任意站成一排拍照，基本事件总数1212n A =，五位德国游客互不相邻包含的基本事件个数为：7578m A A =， ∴五位德国游客互不相邻的概率为75781212799A A m p n A ===．故答案为：799．【点睛】本题考查概率的求法，考查古典概型等基础知识，考查运算求解能力，属于基础题．17．2【分析】画出数轴利用满足的概率可以求出的值即可【详解】如图所示区间的长度是6在区间上随机地取一个数若满足的概率为则有解得故答案是：2【点睛】该题考查的是有关长度型几何概型的问题涉及到的知识点有长度解析：2 【分析】画出数轴，利用x 满足||x m ≤的概率，可以求出m 的值即可.【详解】 如图所示，区间[2,4]-的长度是6，在区间[2,4]-上随机地取一个数x ， 若x 满足||x m ≤的概率为23， 则有2263m =，解得2m =， 故答案是：2. 【点睛】该题考查的是有关长度型几何概型的问题，涉及到的知识点有长度型几何概型的概率公式，属于简单题目.18．【分析】根据条件求出四棱锥的条件和球的体积结合几何概型的概率公式进行求解即可【详解】四棱锥扩展为正方体则正方体的对角线的长是外接球的直径即即则四棱锥的条件球的体积为则该点取自四棱锥的内部的概率故答案 23【分析】根据条件求出四棱锥的条件和球的体积，结合几何概型的概率公式进行求解即可． 【详解】四棱锥P ABCD -扩展为正方体， 则正方体的对角线的长是外接球的直径， 即32R =，即3R =则四棱锥的条件1822233V =⨯⨯⨯=，球的体积为34(3)433ππ⨯=， 则该点取自四棱锥P ABCD -的内部的概率823343P π==， 故答案为239π【点睛】本题主要考查几何概型的概率的计算，结合条件求出四棱锥和球的体积是解决本题的关键．本题考查了几何概型概率的求法；在利用几何概型的概率公式来求其概率时，几何“测度”可以是长度、面积、体积、角度等，其中对于几何度量为长度，面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的，而对于角度而言，则是过角的顶点的一条射线落在Ω的区域（事实也是角）任一位置是等可能的．19．【解析】【分析】由题意从中任取两个不同的数共有中不同的取法再找出取出的2个数之差的绝对值大于2的只有取得到两个数只有一种取法利用对立事件的概率计算公式即可求解【详解】由题意从中任取两个不同的数共有中解析：5 6【解析】【分析】由题意，从1,2,3,4中任取两个不同的数，共有246C=中不同的取法，再找出取出的2个数之差的绝对值大于2的只有取得到两个数只有一种取法，利用对立事件的概率计算公式，即可求解.【详解】由题意，从1,2,3,4中任取两个不同的数，共有246C=中不同的取法，其中取出的2个数之差的绝对值大于2的只有取得到两个数为1,4时，只有一种取法，所以取出的2个数之差的绝对值小于或等于2的概率为15166 P=-=.【点睛】本题主要考查了古典概型及其概率的计算问题，其中解答中认真审题，找出基本时间的总数和所求事件的对立事件的个数，利用对立时间的概率计算公式求解是解答的关键，着重考查了分析问题和解答问题的能力.20．78【分析】求得4位同学各自在周六周日两天中任选一天参加公益活动周六周日都有同学参加公益活动的情况利用古典概型概率公式求解即可【详解】4位同学各自在周六周日两天中任选一天参加公益活动共有24=16种解析：【分析】求得4位同学各自在周六、周日两天中任选一天参加公益活动、周六、周日都有同学参加公益活动的情况，利用古典概型概率公式求解即可．【详解】4位同学各自在周六、周日两天中任选一天参加公益活动，共有24=16种情况，周六、周日都有同学参加公益活动，共有24﹣2=16﹣2=14种情况，∴所求概率为=．故答案为：．【点睛】有关古典概型的概率问题，关键是正确求出基本事件总数和所求事件包含的基本事件数：1．基本事件总数较少时，用列举法把所有基本事件一一列出时，要做到不重复、不遗漏，可借助“树状图”列举；2．注意区分排列与组合，以及计数原理的正确使用．三、解答题21．（Ⅰ）1718；（Ⅱ）见解析；（Ⅲ）1318.【解析】试题分析：（Ⅰ）由题意结合对立事件概率公式可得至少回答对一个问题的概率为17 18.（Ⅱ）这位挑战者回答这三个问题的总得分X的所有可能取值为10,0,10,20,30,40-.计算各个分值相应的概率值即可求得总得分X的分布列；（Ⅲ）结合(Ⅱ)中计算得出的概率值可得这位挑战者闯关成功的概率值为13 18.试题（Ⅰ）设至少回答对一个问题为事件A,则()11117 133218P A=-⨯⨯=.（Ⅱ）这位挑战者回答这三个问题的总得分X的所有可能取值为10,0,10,20,30,40-.根据题意,()11111033218P X=-=⨯⨯=, ()2112023329P X==⨯⨯⨯=,()2212103329P X==⨯⨯=,()11112033218P X==⨯⨯=,()21123023329P X==⨯⨯⨯=,()2212403329P X==⨯⨯=.随机变量X的分布列是:（Ⅲ）设这位挑战者闯关成功为事件B ,则()2122139189918P B =+++=. 22．（1）有99.9%以上的把握认为“注射重组新冠疫苗”有效；（2）13203. 【分析】（1）先求出,x y ，再根据独立性检验可得结论； （2）由组合的应用和古典概率公式可求得其概率. 【详解】 （1）由题知2056012y +=，即5y =，∴25x =，35A =，25B =， ∴2260(1052520)10815.42910.828352530307K ⨯⨯-⨯==≈>⨯⨯⨯，故有99.9%以上的把握认为“注射重组新冠疫苗”有效；（2）由题知试验样本中已感染新冠病毒的猕猴有30只，其中注射了重组新冠疫苗的猕猴有5只，则213525533013203C C C P C +==. 【点睛】本题考查补全列联表，独立性检验，以及组合的应用和古典概率公式，求解时注意“至少”，“至多”等，属于中档题. 23．（1）4m =，8n =（2）4255【分析】（1）设该盒子里有红球m 个，白球n 个，利用古典概型、对立事件概率计算公式列出方程组，能求出m ，n ．（2） “一次从盒子里任取3个球，取到的白球个数不少于红球个数”分为“一次从盒子里任取3个球，取到的白球个数为3个”和“一次从盒子里任取3个球，取到的白球个数为2个，红球数为1个”，由此能求出取到的白球个数不小于红球个数的概率． 【详解】解：（1）设该盒子里有红球m 个，白球n 个.根据题意得221310111m m n m m n C C +⎧=⎪+⎪⎨⎪-=⎪⎩， 解方程组得4m =，8n =， 故红球有4个，白球有8个.（2）设“一次从盒子里任取3个球，取到的白球个数不少于红球个数”为事件A .设“一次从盒子里任取3个球，取到的白球个数为3个”为事件B ，则3831214()55C P B C ==设“一次从盒子里任取3个球，取到的白球个数为2个，红球个数为1个”为事件C ，则。

第三章频率与概率级基础巩固一、选择题．每道选择题有个选择支，其中只有个选择支是正确的．某次考试共有道选择题，某人说：“每个选择支正确的概率是，我每题都选择第一个选择支，则一定有道题选择结果正确”这句话)( )．错误．正确．无法解释．不一定[解析]道题选择结果可能都正确，也可能都错误，还可能仅道题正确，或仅道题正确．．抛掷一枚质地均匀的硬币，如果连续抛掷次，那么第次出现正面朝上的概率是)( )．．)．．)[解析]抛掷一枚质地均匀的硬币，如果连续抛掷次，每一次出现正面朝上的概率均为.．成语“千载难逢”意思是说某事)( )．一千年中只能发生一次．一千年中一次也不能发生．发生的概率很小．为不可能事件，根本不会发生[解析]根据概率的意义可知选项、、都不正确．．一个保险推销员对人们说：“人有可能得病，也有可能不得病，因此，得病与不得病的概率各占.”他的说法)( )．正确．不正确．有时正确，有时不正确．应由气候条件确定[解析]在大多数时候，人是不得病的．得病与不得病的概率不相等，故选．．下列结论正确的是)( )．事件的概率为()，则必有<()<．事件的概率()＝，则事件是必然事件．用某种药物对患有胃溃疡的名病人治疗，结果有人有明显的疗效，现在胃溃疡的病人服用此药，则估计有明显疗效的可能性为．某奖券中奖率为，则某人购买此券张，一定有张中奖[解析]不正确，因为≤()≤；若是必然事件，则()＝，故不正确；对于，奖券中奖率为，若某人购买此券张，则可能会有张中奖，所以不正确，故选．．给出下列三个说法，其中正确的个数为)( )①设有一批产品，已知其次品率为，则从中任取件，必有件是次品；②做次抛硬币的试验，结果次出现正面，因此出现正面的概率是；③随机事件发生的频率就是这个随机事件发生的概率．．个．个．个．个[解析]频率是事件发生的次数与试验次数的比值；当很大时，可以将事件发生的频率作为事件发生的概率的近似值，故选．二、填空题．已知随机事件发生的频率是，事件出现了次，那么共进行了次试验)[解析]设共进行了次试验，则＝，解得＝.．某人进行打靶练习，共射击次，其中有次环，次环，次环，次脱靶，在这次练习中，这个人中靶的频率是，中环的概率是) [解析]打靶次，次中靶，故中靶的概率为＝，其中次中环，故中环的频率是＝.三、解答题．某出版社对某教辅图书的写作风格进行了次“读者问卷调查”，结果如下：)()读者对此教辅图书满意的概率()约是多少？()根据()()说明读者对此教辅图书满意情况．[解析]()表中各个频率依次是、、、.()由第()问的结果，知某出版社在次“读者问卷调查”中，收到的反馈信息是“读者对某教辅图书满意的概率约是()＝.”用百分数表示就是()＝.()由()、()可以看出，读者对此教辅图书满意程度较高，且呈上升趋势．．为了估计某自然保护区中天鹅的数量，可以使用以下方法：先从该保护区中捕出一定数量的天鹅，例如只，给每只天鹅做上记号，不影响其存活，然后放回保护区，经过适当的时间，让其和保护区中其余的天鹅充分混合，再从保护区中捕出一定数量的天鹅，例如只，。

课后训练1．一个战士一次射击，命中环数大于8，大于5，小于4，小于6这四个事件中，互斥事件有()．A．2对B．4对C．6对D．3对2．从装有数十个红球和数十个白球的罐子里任取两个球，下列情况中是互斥而不是对立的两个事件是()．A．至少有一个红球，至少有一个白球B．恰有一个红球，都是白球C．至少有一个红球，都是白球D．至多有一个红球，都是红球3．从装有5只红球、5只白球的袋中任意取出3只球，有事件：①“取出2只红球和1只白球”与“取出1只红球和2只白球”；②“取出2只红球和1只白球”与“取出3只红球”；③“取出3只红球”与“取出3只球中至少有1只白球”；④“取出3只红球”与“取出3只白球”．其中是对立事件的有()．A．①②B．②③C．③④D．③4．在第3,6,16路公共汽车的一个停靠站，假定这个车站只能停靠一辆汽车，有一位乘客需5分钟之内赶到厂里，他可乘3路或6路车到厂里．已知3路车、6路车在5分钟内到此车站的概率分别为0.2和0.6，则此乘客在5分钟内能乘到所需车的概率为()．A．0.2 B．0.6 C．0.8 D．0.125．甲，乙两人下象棋，两人下成和棋的概率是12，乙获胜的概率是13，则乙输的概率是________．6(1)(2)至少3人排队等候的概率是________．7．袋中有12个小球，分别为红球、黑球、黄球、绿球．从中任取一球，得到红球的概率为13；得到黑球或黄球的概率是512；得到黄球或绿球的概率也为512；试求得到黑球、黄球、绿球的概率各是多少？8．有朋自远方来，他乘飞机，火车，汽车，轮船来的概率分别为0.4,0.3,0.2,0.1.(1)求他乘飞机或火车来的概率；(2)求他不乘汽车来的概率．(2)求年降雨量在[150,200)或[250,300)范围内的概率；(3)求年降雨量不在[150,300)范围内的概率；(4)求年降雨量在[100,300)范围内的概率．参考答案1.答案：D解析：按照互斥事件的定义，两个事件不可能同时发生，所以命中环数大于8与命中环数小于4是互斥事件；命中环数大于8与命中环数小于6是互斥事件；命中环数大于5与命中环数小于4是互斥事件．2. 答案：B解析：对于A ，至少有一个红球，另一个可能为白球；至少有一个白球，另一个可能为红球，故两事件可能同时发生，所以不是互斥事件．对于B ，恰有一个红球，则另一个必是白球；与“都是白球”是互斥事件，而任选两球还有“都是红球”的情形，故两事件不是对立事件．对于C ，至少有一个红球为“都是红球”或“一红一白”与“都是白球”显然是对立事件．对于D ，至多有一个红球为“都是白球”或“一红一白”与“都是红球”是对立事件．故选B.3. 答案：D解析：从袋中任取3只球，可能取到的情况有：“3只红球”，“2只红球1只白球”，“1只红球2只白球”，“3只白球”，由此可知①、②中的两个事件都不是对立事件．对于③，“取出的3只球中至少有1只白球”包含“2只红球1只白球”，“1只红球2只白球”，“3只白球”三种情况，故是对立事件．4. 答案：C解析：乘客在一个停靠站乘3路车与其乘6路车是不可能同时发生的，是互斥事件，所以所求的概率是0.20＋0.60＝0.80.5. 答案：16解析：乙输的对立事件是乙获胜或两人下成和棋，因此可使用概率加法公式和对立事件的概率公式求解．设事件A ＝“乙获胜”，B ＝“两人下成和棋”，C ＝“乙输”，则()13P A ＝，()12P B ＝.∴P (A ∪B )＝P (A )＋P (B )＝115236+=. ∴P (C )＝1－P (A ∪B )＝51166-=. 6. 答案：(1)0.56 (2)0.44解析：记事件在窗口等候的人数为0,1,2,3,4,5人及5人以上分别为A ，B ，C ，D ，E ，F .(1)至多2人排队等候的概率是P (A ∪B ∪C )＝P (A )＋P (B )＋P (C )＝0.1＋0.16＋0.3＝0.56.(2)解法一：至少3人排队等候的概率是P (D ∪E ∪F )＝P (D )＋P (E )＋P (F )＝0.3＋0.1＋0.04＝0.44.解法二：因为至少3人排队等候与至多2人排队等候是对立事件，故由对立事件的概率公式知，至少3人排队等候的概率是P (D ∪E ∪F )＝1－P (A ∪B ∪C )＝1－0.56＝0.44.∴至多2人排队等候的概率是0.56，至少3人排队等候的概率是0.44.7. 解：从袋中任取一球，记事件“摸得红球”、“摸得黑球”、“摸得黄球”、“摸得绿球”分别为A ，B ，C ，D ，则A ，B ，C ，D 是彼此互斥事件． 由题知1,35,125,121,P A P B C P C D P A B C D ⎧()=⎪⎪⎪()=⎪⎨⎪()=⎪⎪⎪()=⎩∴5,125,1211. 3P B P CP C P DP B P C P D⎧()+()=⎪⎪⎪()+()=⎨⎪⎪+()+()+()=⎪⎩∴1,41,61.4 P BP CP D⎧()=⎪⎪⎪()=⎨⎪⎪()=⎪⎩答：得到黑球、黄球、绿球的概率各是14，16，14.8.解：记“他乘飞机来”为事件A，“他乘火车来”为事件B，“他乘汽车来”为事件C，“他乘轮船来”为事件D.由于事件A，B，C，D不可能两两同时发生，所以它们彼此互斥．依题意，有P(A)＝0.4，P(B)＝0.3，P(C)＝0.2，P(D)＝0.1.(1)记“他乘飞机或火车来”为事件E，则E＝A∪B.由于事件A与事件B互斥，所以P(E)＝P(A∪B)＝P(A)＋P(B)＝0.4＋0.3＝0.7.即他乘飞机或火车来的概率为0.7.(2)记“他不乘汽车来”为事件F，则事件C与事件F是对立事件，所以P(F)＝1－P(C)＝1－0.2＝0.8.9.解：(1)P1＝0.12＋0.25＝0.37；(2)P2＝0.25＋0.14＝0.39；(3)P3＝1－(0.25＋0.16＋0.14)＝0.45；(4)P4＝0.12＋0.25＋0.16＋0.14＝0.67.。

亲爱的同学：这份试卷将再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光……学习资料专题3.1.3 频率与概率课时过关·能力提升1下列说法:①频率反映随机事件发生的频繁程度,概率反映随机事件发生的可能性大小;②做n 次随机试验,事件A发生m次,则事件A发生的频其中正确的个数是()A.1B.2C.3D.4.2某人将一枚质地均匀的硬币连续抛掷了10次,正面朝上的情形出现了6次,则正面朝上的()A.概率为0.6B.频率为0.6C.频率为6D.概率接近于0.6.3下列结论正确的是()A.对事件A的概率P(A)必有0<P(A)<1B.若事件A的概率P(A)=0.999,则事件A是必然事件C.用某种药物治疗患有胃溃疡的500名病人,结果有380人有明显的疗效.现有胃溃疡的病人服用此药,则估计其会有明显疗效的可能性为76%D.某奖券中奖率为50%,则某人购买此奖券10张,一定有5张中奖项中,应有0≤P(A)≤1;B项中,若A为必然事件,则P(A)=1;D项中,某人购买此奖券10张,有可能都不中奖,也有可能部分或全部中奖,故选C.4某厂生产的产品的次品率为2%,估算该厂生产的4 000件产品中合格品的件数约为() A.80 B.3 920 C.3 900 D.3 8902%,则合格品率是1-2%=98%,因此合格品的件数大约是4 000×98%=3 920.5某气象台的天气预报中预测某地明天降雨的概率为10%,则()A.该地明天降雨的可能性是10%B.10%太小,该地明天不可能降雨C.该地明天有10%的区域降雨D.降雨概率为10%没有什么意义10%是说明降雨的可能性是10%.6在给病人动手术之前,外科医生会告知病人或家属一些情况,其中有一项是说这种手术的成功率大约是99%.下列解释正确的是()A.100个手术有99个手术成功,有1个手术失败B.这个手术一定成功C.99%的医生能做这个手术,另外1%的医生不能做这个手术D.这个手术成功的可能性是99%99%,说明手术成功的可能性是99%.72014年12月份,某市共有7天为雨雪天气,设雨雪天气为事件A,则事件A出现的频数为,事件A出现的频率为.,12月份共31天,事件A出现的天数为7,即为频数,故事件A出现的频率为f n(A)8如果袋中装有数量差别很大的白球和黑球(除颜色外其他都相同),从中任取一球,取了10次有9次是白球,估计袋中数量最多的是.10次有9次是白球,则取出白球的频率,因此,估计袋中数量最多的是白球.9在高考数学试题中,有12道选择题,每道选择题有4个选项,其中只有1个选项是正确的,则随机选择其中一个选项正确的概率,答对的概率12道选择题,即进行了12次试验,每个结果都是随机的,那么答对3道题的可能性较大,但是并不一定答对3道题.也可能都选错,或有1,2,3,4,…甚至12个题都选择正确.10某市2012~2015年新生儿出生数及其中女婴数(单位:人)如下表:(1)试计算女婴各年出生的频率(精确到0.001);(2)该市女婴出生的概率约是多少?年女婴出生的频率≈0.524.同理可求得2013年、2014年和2015年女婴出生的频率分别约为0.521,0.513,0.513;(2)各年女婴出生的频率在0.51~0.53之间,故该市女婴出生的概率约为0.52.11今天电视台的天气预报说:今晚阴有雨,明天白天降雨概率是60%.请回答下列问题:(1)明天白天运输部门能否抢运粮食?(2)如果明天抢运的是石灰和白糖,能否在白天进行?.在降雨概率为60%时,仍可以抢运粮食,毕竟还有40%的无雨概率,不过要采取防雨措施.(2)因为石灰和白糖属于易溶物质,最好暂时不运,否则必须采取严密的防雨措施.★12在如图两个转盘进行“配紫色”的游戏,规则如下:分别旋转两个转盘,当一个转盘转出“红色”,另一个转出“蓝色”,则可配成紫色.若能配成紫色,甲得1分,否则乙得1分.这个游戏对双方公平吗?为什么?若认为不公平,如何修改规定才能使该游戏对双方公平?:只有当其中一个转盘转出了“红色”,另一个转盘转出“蓝色”,才可以配成紫色.由图可见配成紫色的概率1分,否则乙得1分,因此该游戏对甲不公平.要想使游戏对双方公平,可重新规定若配成紫色甲得2分,否则乙得1分.。