高等流体力学
- 格式:docx
- 大小:78.58 KB
- 文档页数:3


高等流体力学高等流体力学是研究流体运动的一门学科,涉及到流体的物理、数学和工程学知识。
在高等流体力学的研究中,我们需要了解流体的性质、流体流动的基本方程和变量,以及流体在不同条件下的行为。
在高等流体力学的研究中,我们主要关注流体穿过各种障碍物时的流动和流体的稳定性问题。
首先,我们需要了解导致流体流动的原因。
在我们的日常生活中,我们可以看到流体穿过各种障碍物时的流动,如水管中的水流、喷泉中的水流、空气穿过机翼时的流动等。
这些流体流动受到各种因素的影响,如流体的黏性、密度、速度、压力等等。
流体在不同条件下的行为是高等流体力学研究的重点。
在流体力学中,我们可以使用流体的基本方程来描述流体在不同条件下的行为。
这些方程包括连续性方程、动量方程和能量方程。
这些方程可以帮助我们理解流体在不同情况下的行为,并预测流体的运动趋势。
在高等流体力学的研究中,我们需要探讨流体流动的稳定性问题。
流体流动的稳定性是指流体流动是否会在运动中不断扰动并最终变为混沌状态。
在高等流体力学的研究中,我们需要通过分析流体在不同条件下的稳定性来预测流体流动的发展趋势。
在高等流体力学的研究中,我们还需要掌握一些数值方法和实验技术。
数值方法可以帮助我们模拟流体流动的行为,并预测流体的运动趋势。
实验技术可以帮助我们验证理论和预测,并提供流体性质和流体流动的数据。
总之,高等流体力学是一门复杂而有关键性的学科。
通过研究流体运动的基本方程和变量,以及探索流体流动的稳定性问题,我们可以更深刻的理解流体的性质和行为,并用数值方法和实验技术来验证我们的理论和预测。
在高等流体力学的研究中,有一些流体流动的现象和实际应用十分广泛。
下面我们将一一探讨。
首先,是流体的湍流流动。
湍流是流体流动的一种不稳定状态,流体在湍流状态下会出现不规则的涡旋和强烈的乱流。
湍流的出现是由于流体在高速流动或流动中受到障碍物的影响而产生的。
在许多实际应用中,如机械运动、空气动力学和海洋运动等,湍流是一个非常重要的研究对象。




高等流体力学授课提纲第一章概论§1.1 流体力学的研究对象§1.2 流体力学发展简史§1.3 流体力学的研究方法§1.3.1 一般处理途径§1.3.2 应用数学过程§1.3.3 流体力学方法论:一般方法§1.3.4 流体力学方法论:特殊方法●Lagrange描述和Euler描述●无量纲化●线性化●分离变量法●积分变换法●保角映射法●奇点法(孤立奇点法、分布奇点法、Green函数法)●控制体积法●微元法第一章概论§1.1 流体力学的研究对象(1)物质四态:●四态:固态—液态—气态—等离子态;等离子体=电离气体●界限:彼此无明确界限(高温下的沥青;冰川),取决于时间尺度;●流体力学的具体研究对象:液体、气体、等离子体(电磁流体力学、等离子体物理学);●液体与气体的差别:液体—有固定容积、有自由面、不易压缩、有表面张力;气体—无固定容积、无自由面、易压缩、无表面张力。
(2)流体的基本性质:易流动性:静止流体无剪切抗力;压缩性(膨胀性):压差、温差引起的体积改变,判据:马赫数;粘性:运动流体对剪切的抗力,判据:雷诺数;热传导性:温差引起的热量传递,普朗特数。
(3)流体的分类:i)按有无粘性、热传导性分:真实流体(有粘性、有热传导、与固体有粘附性无温差);理想流体(无粘性、无热传导、与固体无粘附性有温差);ii)按压缩性分:不可压缩流体,可压缩流体;iii)按本构关系分:牛顿流体(牛顿粘性定律成立),非牛顿流体(牛顿粘性定律不成立),下分纯粘性流体(拟塑性流体,涨塑性流体);粘塑性流体(非宾汉流体、宾汉流体);时间依存性流体(触变流体、振凝流体);粘弹性流体拟塑性流体(剪切流动化流体):剪切应力随剪切速度增加而减小,如淀粉浆糊、玻璃溶液、高分子流体、纤维树脂;涨塑性流体(剪切粘稠化流体):剪切应力随剪切速度增加而减小,如淀粉中加水、某些水-砂混合物;粘塑性(非宾汉和宾汉流体):存在屈服应力,小于该应力无流动,如粘土泥浆、沥青、油漆、润滑脂等,所有粘塑性流体为非宾汉流体,宾汉流体为近似;触变流体(摇溶流体):粘性或剪切应力随时间减小,如加入高分子物质的油、粘土悬浊液;振凝流体:粘性或剪切应力随时间增大,如矿石浆料、膨润土溶胶、五氧化钒溶液等;粘弹性流体:兼有粘性和弹性性质的流体,能量不像弹性体守恒,也不像纯粘性体全部耗散。

第 1 页 共 1 页第 1 页 共 1 页 扩散:指流体在没有对流混合情况下,流体由分子的随机运动引起的质量传递的一种性质。
本构方程:是反应物体的外部效应与内部结构之间关系的方程。
对运动的粘性流体而言,外部黏性应力与内部变形速度之间的关系成为本构方程。
变形速度张量:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=zz zy zx yz yy yx xz xy xx s εεεεεεεεε,,,,,,,其中,z y v x u zz yy xx ∂∂=∂∂=∂∂=ωεεε,,, ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂==x v y u yx xy 21εε,⎪⎭⎫ ⎝⎛∂∂+∂∂==z u x zx xz ωεε21,⎪⎪⎭⎫ ⎝⎛∂∂+∂∂==y z v zy yz ωεε21 雷诺应力:在不可压缩流体的雷诺方程中,j -u u i ''ρ称为雷诺应力(i ,j=1,2,3)当i=j 时为法相雷诺应力,不等时称为切向雷诺应力。
镜像法:是确定干扰后流场的方法之一,是一种特别的奇点法。
粘性:流体微团发生相对滑移时产生切向阻力的性质。
不可压缩流体:0=DtD ρ的流体称为不可压缩流体。
不可压缩均质流体:C =ρ 可压缩流体:密度随温度和压强变化的流体称为可压缩流体。
紊流:是一种随机的三维非定常有旋流动。
紊流的基本特征:1,不规则流动状态;2,参数随时间空间随机变化;3,空间分布大小形状各不相同漩涡;4,具有瞬息万变的流动特征;5,流动参数符合概率规律;6,相邻参数有关联。
流体:通常说能流动的物质为流体,液体和气体易流动,我们把液体和气体称之为流体。
严格地说:在任何微小剪切力的持续作用下,能够连续不断变形的物质称为流体,流体显然不能保持一定的形状,即具有流动性。
耗散函数:ij ij x u p ∂∂'称为耗散函数Γ,Γ表示单位时间内单位体积流体由机械能耗散成热能 ij ij ij i jij x u V div x u p ∂∂⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=∂∂=Γμεδμμ232'' 应力张量:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=zz zy zx yz yy yx xz xy xx p p p p p p p p p p ,,,,,,称为应力张量,它是描述运动黏性流体内任一点应力状态的物理量。


概念第一章绪论连续介质:但流体力学研究的是流体的宏观运动,不以分子作为流动的基本单元,而是以流体质点为基本单元,把流场看做是由无数流体质点组成的连续体。
流体质点:流场中一个体积很小并可以忽略其几何尺寸,但与分子相比,这个体积可容纳足够多的分子数目的流体元,有一个稳定的平均特性,即满足大数定律理想流体:忽略流体黏性的流体,即μ=0.可压缩流体与不可压缩流体:简单地讲,密度为常数的流体为不可压缩流体,如水、石油及低速流动的气体。
反之,密度不为常数的流体为可压缩流体。
牛顿流体与非牛顿流体:根据流体流动时切应力与流速梯度之间的关系,即牛顿内摩擦定律。
凡是符合牛顿内摩擦定律的成为牛顿流体,如水、空气、石油等。
否则为非牛顿流体,如污泥、泥石流、生物流体、高分子溶液等动力粘度与运动粘度:动力粘度又成为动力黏度系数,动力黏度是流体固有的属性。
运动粘度又称为运动粘性系数,运动黏性系数则取决于流体的运动状态体积力与表面力:体积力亦称质量力,是一种非接触力,即外立场对流体的作用,且外立场作用于流体每一质点上,如重力、惯性力、离心力。
表面力是一种表面接触力,指流体与流体之间或流体与物体之间的相互作用,主要指压力、切应力、阻力等定常流与非定常流:又称恒定流与非恒定流。
若流场中流体质点的所有运动要素均不随时间变化,则这种流动称为定常流;反之只要有一个运动要素随时间变化则为非定常流大气层分为5层:对流层、同温层、中间层、电离层及外逸层第二章流体运动学描述流体质点的位置、速度及加速度的两种方法,即拉格朗日法和欧拉法质点导数:亦称随体导数,表示流体质点的物理量对时间的变化率,亦即跟随流体质点求导数那布拉P9流体质点的运动轨迹称为迹线流线:此曲线上任一点的切线方向就是该点流速方向依照一定次序经过流场中某一固定点的各个质点连线称为脉线,也叫序线。
流体线:在流场中任意指定的一段线,该段线在运动过程中始终保持由原来那些规定的质点所组成。




高等流体力学第一章 流体力学的基本概念连续介质:流体是由一个紧挨着一个的连续的质点所组成的,没有任何空隙的连续体,即所谓的连续介质。
流体质点:是指微小体积内所有流体分子的总和。
欧拉法质点加速度:zuu y u u x u u t u dt du a x z x y x x x x x ∂∂+∂∂+∂∂+∂∂==zu u yu u xu u tu dtdu a y zy yy xy y y ∂∂+∂∂+∂∂+∂∂==zu u y u u x u u t u dt du a z z z y z x z z z ∂∂+∂∂+∂∂+∂∂==质点的随体导数:质点携带的物理量随时间的变化率称为质点的随体导数,用dtd表示。
在欧拉法描述中的任意物理量Q 的质点随体导数表述如下:kQu t Q dt dQ k ∂∂+∂∂= 式中Q 可以是标量、矢量、张量。
质点的随体导数公式对任意物理量都成立,故将质点的随体导数的运算符号表示如下:ku t dt d k ∂∂+∂∂= 其中t ∂∂称为局部随体导数,ku k ∂∂称为对流随体导数,即在欧拉法描述的流动中,物理量的质点随体导数等于局部随体导数与对流随体导数之和。
体积分的随体导数:()dV divv dt d dV v div t dS u dV t dV dt d v v n s v v ⎥⎦⎤⎢⎣⎡Φ+Φ=⎥⎦⎤⎢⎣⎡Φ+∂Φ∂=Φ+∂Φ∂=Φ⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰()dV adivv dt da dV av div t a dS au dV t a adV dt d v v n s v v ⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+∂∂=+∂∂=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ 变形率张量: 11ε 12ε13εD ij = 21ε 22ε 23ε31ε 32ε 33ε其中ii ε表示所在方向的线性变形率,其余ij ε(j i ≠)为角变形率。
D ij 为变形张量。
⎪⎪⎭⎫⎝⎛∂∂+∂∂=i j j i ij x u x u 21ε 旋转角速度: 0 z ω- y ωR ij =z ω 0 x ω-y ω- x ω 0z ω=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂y u x u x y 21y ω=⎪⎭⎫⎝⎛∂∂-∂∂x u z u z x 21x ω=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂z u y u y z 21 判断有旋流和无旋流:x ω=y ω=z ω=0,z ω=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂y u x u x y 21=0,y ω=⎪⎭⎫⎝⎛∂∂-∂∂x u z u z x 21=0 x ω=⎪⎪⎭⎫⎝⎛∂∂-∂∂z u y u y z 21=0 ,y u x u x y ∂∂=∂∂x u z u z x ∂∂=∂∂,z u y u yz ∂∂=∂∂ 涡量与速度环量的关系:涡量,流体力学中多用涡量来表示流体微团的旋转。


《高等流体力学》考试大纲一、参考教材1.《高等工程流体力学》,张铭远、景思睿、李国君,高等教育出版社2012年5月第一版2.《高等流体力学》,刘应中、缪国平编,上海交通大学出版社2000年6月第一版二、考核要求《高等流体力学》是一门综合性较强的交叉学科,要求考生系统掌握高等流体力学学科的基本理论、基本原理和方法,掌握高等流体力学中的思维特点和综合分析方法。
能够运用所学的基础理论、基本知识和基本方法分析和解决有关理论问题和实际问题。
三、考试内容、比例1.流体力学的基础知识(约占20%)掌握拉格朗日参考系与欧拉参考系的主要概念以及他们之间的区别与内在联系,了解迹线、流线及脉线的区别,能够掌握物质导数的应用,学会微团流体运动分析,了解有旋运动的基本概念,掌握物质积分的随体导数,明白应力张量的意义,掌握本构方程。
2.流体力学的基本方程(约占33%)掌握连续方程、N-S方程、能量方程、总能量方程、机械能方程、内能方程并能做到熟练应用。
了解不可压缩流体与布西内斯克近似,明白不可压缩流动的成立条件,掌握布西内斯克近似,重要掌握边界条件。
3.涡量动力学(约占7%)阐明涡量场的运动学性质特点,掌握开尔文定理的实质,重点掌握涡量动力学方程,希尔球涡和兰金涡,掌握涡量场和散度场的诱导速度场,能够区分直线涡丝和圆形涡丝,阐明涡层的定义。
4.理想流体动力学基础(约占20%)掌握理想流体流动与高雷诺数流动,熟练掌握欧拉方程的应用,会在流线坐标系中使用欧拉方程,重点掌握伯努利方程及其在不同形势下的方程。
了解在非惯性系中的两种方程。
4.不可压缩平面势流(约占7%)掌握流函数、势函数与拉普拉斯方程,明白复位势能与复速度的概念,阐明基本流动与圆柱绕流的概念,重点掌握布拉休斯公式,掌握镜像法,掌握平面定理与圆定理,重点掌握保角变换。
5.其他(约占13%)掌握不可压缩空间轴对称势流手段和研究方法,了解N-S方程的精确解,阐明小雷诺数流动的概念,掌握不可压缩层边界层流动,明白流动不稳定性及其概念,掌握湍流的研究方法,了解理想的一维可压缩流动,了解理想流体的平面可压缩流动。




内容提纲边界层及其方程层流边界层流动转捩湍流边界层结构流动分离、二次流动与旋涡能源动力领域流动问题的主要特征全三维非定常粘性☐高雷诺数,边界层☐边界层:层流、转捩、湍流(紊流),分离流动,旋涡运动叶轮机械(透平和压气机等)大多由单个或多个级组成。
每个级含有一排静子叶片列和一排转子叶片列。
在级内的气流场中,一般至少有以下几种流动现象发生:1、前缘马蹄涡;2、通道涡;3、顶部间隙涡;4、边界层转捩;5、叶片尾迹;6、旋涡、尾迹等与叶片列周期性非定常相互作用。
☐激波、激波与边界层相互作用边界层流动边界层边界层概念:粘性很小的流体以大雷诺数运动时,在大部分流场上可以略去粘性的作用;但在物面附近的很薄的一层流体内必须考虑粘性作用。
这一薄层流体称为边界层。
平板边界层示意图 有边界的流动图谱如右上图所示:流动分为三个区:边界层,尾迹区,位流区(外部势流区)二维平板的边界层微分方程设直匀流 以零迎角平行流过一块长度为 的平板,如左下图所示,人为规定,当某个y 处的速度达到层外自由流的99%时,这一点到物体表面的距离(即y )称为边界层在改点的厚度,记为 。
显然,边界层的厚度是与X 有关的,所以可以写成 。
υ∞l δδ(x )平板边界层边界层的厚度 很小,满足此关系式:在忽略质量力的前提下,粘性平面不可压流的运动方程加上连续方程是:用边界层条件式 上式,y 的数值限制在边界层之内,即经过数量级分析,上面方程组化为:的物理意义:在边界层内,沿物体表面的发法线方向压强是不变的,亦即等于边界层处自由流的压强。
卡门动量积分关系解采用动量积分法得出控制面ABCD 的动量变化:其中: 为边界层边界上的流速。
作用在AB,BC,CD,AD 四个面上的力在x 方向上投影的合力的冲量是:根据动量定理得:δ(x )l δ(x )<<222222221()1()0u u u p u u u t x y x x y p u t x y y x y u x y υνρυυυυυυνρυ⎫∂∂∂∂∂∂++=-++⎪∂∂∂∂∂∂⎪⎪∂∂∂∂∂∂⎪++=-++⎬∂∂∂∂∂∂⎪⎪∂∂+=⎪∂∂⎪⎭l δ(x )<<0y δ≤≤22100u u u p u u t x y x y p y u x y υνρυ⎫∂∂∂∂∂++=-+⎪∂∂∂∂∂⎪⎪∂=⎬∂⎪⎪∂∂+=⎪∂∂⎭0p y ∂=∂200()d d dt dx dy dy dx dxδδδρυυρυ⋅⋅-⋅⋅⎰⎰δυ()w dp dt dx dxδτ-⋅+⋅200()w d d dpdy dy dx dx dx δδδρυυρυδτ⋅-⋅⋅=-⋅+⎰⎰即定常流动的边界层动量积分关系式,也叫卡门-波尔豪森(Karman-Pohlhausen )动量积分关系式。
高等流体力学复习题
1. 试给出以下各术语的定义
流体,质量力,面力,物质体,控制体,随体导数,无粘流动,无旋流动,等熵流动,不可压缩流动,激波,接触面,简单区及简单波。
流体:液体和气体的总称,是由大量的不断热运动,而且无固定平衡位置的分子组成的。
基本特征是流动性、粘性及压缩性。
质量力: 是指作用于隔离体内每一流体质点上的力,它的大小与质量成正比。
重力、惯性力
面力::又称面积力,是毗邻流体或其它物体,作用在隔离体表面上的直接施加的接触力。
它的大小与作用面积成比例。
剪力、拉力、压力
物质体:相同质点组成的体积(面、线) 控制体:控制体是指流场中某一确定的空间区域,这个区域的周界称为控制面。
控制体的形状根据流动情况和边界位置任意选定。
当选定之后,控制体的形状和位置相对于所选定的坐标系来讲是固定不变的,但它所包含的流体的量是时时刻刻改变的。
如果这个坐标系是固定的就称为固定控制体,如果坐标系本身也在运动,则称为运动控制体。
随流导数:
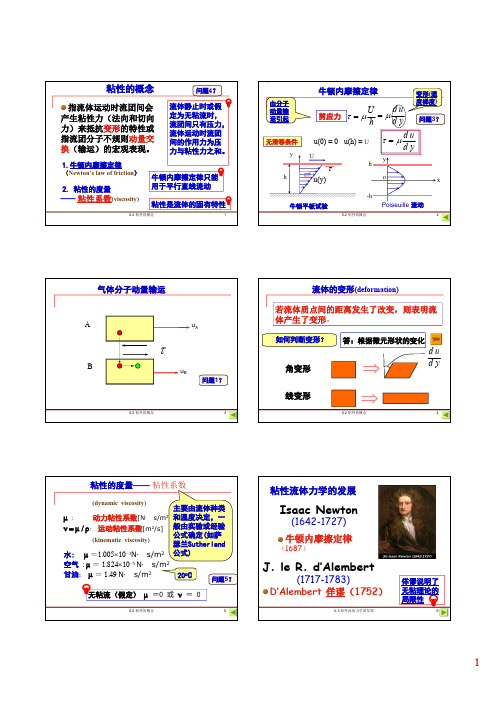
2. A body V of density ρis submerged in a fluid of density a ρ. Show that the net force on the body is given by
dv dA dv V S V a G T G ⎰⎰⎰-=+)(ρρρ(Archimede ’s
principle ).
ρa ρ
V
S
G
3. 试给出使流体中的涡旋发生变化的五个因素;哪几个因素可使无涡旋的流体中产生涡旋?结合工程或自然界中的例子加以说明。
4.速度为U 的直匀流流过二强度为Q ,分别位于(0,0),
(L,0)处的点汇。
(1) 求驻点位置;
(2) 画出流线(包括流入点汇的流线,驻点附近的
流线)的示意图。
5. 无粘不可压流中,设某时刻t ,沿某一封闭流体周线L 的环量为Г(t)。
试从N-S 方程出发,推导Г(t)对时间的导数的表达式。
并从而证明当流体为无粘、正压,外力有单值势函数时,该式可简化为Kalvin 的环量守恒定理,t
D D Γ=0。
6. 流体中的一球面按规律)(t R R =膨胀,请确定球所受的压力(忽略质量力)。
7.二维超音速流流过波形壁,壁面坐标l x h y w ⋅=π2cos ,设1<<l
h 。
(1) 试求出流动的速度位(表示为l h M u ,,,∞∞的函数);
(2) 求壁面压强系数的表达式;
(3) 求波峰、波谷处的压强值。
h l
x
y
∞∞>u M 1
w
y
8.等截面管内为空气。
t=0时,气体静止,压强处处相同,各热力学参数已知。
外界大气压为a p
(已知),
其小于管内的空气的压强。
设t=0时突然打开左边的阀门。
写出求解管内气体流动的详细过程(文字描述,例如,如何推进求解,有那些不同区域,各区域内流动、
热力学参数如何确定等等;画出特征线);描述管内气体流动随时间的变化情况。
∞
9. 用控制体上的运动方程,导出激波关系式1-4(写出所作的假设和详细推导过程)。
a p。