MATLAB在化学试验设计与数据处理中的应用

物理化学实验中常用的数据处理软件及在化学中常见应用方法随着计算机技术的不断发展，数据处理软件在物理化学实验中的应用越来越普遍。

这些软件可以帮助实验人员处理实验数据，提高实验效率和准确度。

本文将介绍几种常用的数据处理软件及在化学中常见的应用方法。

一、常用的数据处理软件1. ExcelExcel是微软公司开发的一款电子表格软件，广泛应用于各个领域。

在物理化学实验中，Excel可以用来制作数据图表、计算平均值和标准偏差、进行线性回归等。

对于数据量较小的实验，Excel是一个简单易用的数据处理工具。

2. OriginOrigin是一款专业的科学数据分析和绘图软件，主要应用于科学研究、工程设计和教学等领域。

在物理化学实验中，Origin可以用来制作各种类型的图表、进行数据拟合和统计分析等。

Origin的功能非常强大，但学习起来也比较复杂。

3. MatlabMatlab是一款用于数学计算、数据分析和可视化的软件，被广泛应用于科学研究、工程设计和金融分析等领域。

在物理化学实验中，Matlab可以用来进行数据处理、信号处理和图像处理等。

Matlab的功能非常强大，但学习起来也比较困难。

二、在化学中的应用方法1. 数据图表的制作在物理化学实验中，数据图表是非常重要的，可以帮助实验人员更直观地了解实验结果。

在Excel中，可以选择不同的图表类型，如折线图、柱状图、散点图等，来展示实验数据。

在Origin中，可以制作更复杂的图表，如等高线图、三维图等，以展示更多的信息。

在Matlab中，可以利用其强大的绘图功能，制作各种复杂的图表。

2. 数据拟合和统计分析在物理化学实验中，常常需要对实验数据进行拟合和统计分析。

在Excel中，可以使用函数进行线性回归、非线性拟合和数据统计等。

在Origin中，可以使用各种拟合和统计分析工具，如最小二乘法拟合、方差分析等。

在Matlab中，可以使用其强大的数学计算和统计分析功能，进行各种数据拟合和统计分析。

熟悉化学实验数据处理软件使用化学实验数据处理软件的使用引言：随着科技的不断发展，化学实验数据处理软件在实验室中的应用越来越广泛。

这些软件不仅可以帮助实验人员处理数据，还能提供数据分析、绘图和报告撰写等功能，极大地提高了实验效率和数据准确性。

本文将介绍化学实验数据处理软件的使用方法，帮助读者更好地掌握该技能。

一、化学实验数据处理软件的概述化学实验数据处理软件是专门为化学领域设计开发的软件，主要用于处理实验数据、进行数据分析和撰写实验报告。

目前市场上常见的化学实验数据处理软件有Origin、MATLAB、Excel等，它们都具有强大的功能和灵活的数据处理方式。

二、化学实验数据的导入首先，我们需要将实验数据导入到软件中进行处理。

通常情况下，实验数据可以以表格的形式存储在电子文件中，如Excel表格或CSV文件。

对于Excel表格，可以通过直接复制粘贴的方式将数据导入到软件中。

首先选中需要导入的数据区域，然后将其复制到剪贴板中。

接着，在软件中选择相应的导入数据方式，并将剪贴板中的数据粘贴到软件中。

对于CSV文件，可以在软件中选择打开文件的方式，并选择相应的文件路径和格式进行导入。

三、数据的处理和分析一旦数据被导入到软件中，就可以进行数据的处理和分析。

化学实验数据处理软件通常提供了多种数据处理方法和函数，可以根据实验目的进行选择。

1. 数据清理与筛选：在导入的数据中，常常会出现一些异常值或不符合实验要求的数据。

我们可以通过软件提供的数据清理和筛选功能，对这些数据进行处理和排除。

2. 数据处理和计算：化学实验数据处理软件提供了多种数据计算和处理方法。

比如，可以进行数据的加减乘除运算，求平均值、标准差、方差等统计值的计算，还可以进行数据的拟合和回归分析等。

3. 数据分析和绘图：化学实验数据处理软件还提供了强大的数据分析和绘图功能。

可以进行数据的统计分析、频率分布分析、相关性分析和趋势分析等。

同时，该软件还支持各种图表和图像的绘制，如线图、柱状图、散点图、饼图等。

MATLAB在化学工程实验数据处理中的应用随着我国高科技人才的不断出现，各行业的高新技术也逐渐兴起。

对于我国以往的化学工程，化学人员需要进行大量的复杂的数据处理，以及相当有难度的化学实验，这样的做法既浪费时间又浪费资源。

因此，在化学工程中进行不断的创新与改革，是我国化学工程技术人员需要研究的重要课题。

而MATLAB的出现，是化学工程中的重大创新软件。

化学工程人员将MATLAB软件运用到化学工程实验中，可以大大提高数据处理效率，并且节省了很多的人力物力等资源。

此软件被广泛的运用到化学工程的各种试验中。

本文就针对MATLAN在化学工程与工艺实验数据处理中的应用进行深入的分析与探讨。

0 前言化学工程与工艺学科是我国重要的学科之一，在化学工程中，化学实验起着重要的作用。

化学实验的好坏严重影响着化学工程的建设。

而数据处理过程又是化学实验中的重要组成部分。

对程序中的数据进行有效的处理有助于化学实验的研究与开发。

然而以往的数据处理方法基本上都是人工处理，这种处理方法既浪费时间又浪费资源。

因此，开发新的化学数据处理方法成为我国化学工程研究的重点，而MATLAB软件就是新型化学数据处理方法之一，也对化学工业的发展起到巨大的作用，它能有效地将繁琐的计算步骤化解成简单的计算，提高工作效率，让实验数据的准确性达到最高值，避免误差的产生。

MATLAB软件最早由美国的Mathworks公司提出，其主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。

它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案，并在很大程度上摆脱了传统非交互式程序设计语言的编辑模式，代表了当今国际科学计算软件的先进水平。

近年来MATLAB软件逐渐被用于化学工程与工艺实验的数据处理中，极大地提高了数据处理的效率。

Matlab 光谱特征波长提取在科学研究和工程应用中，光谱数据的处理和分析是非常重要的。

光谱特征波长提取是其中一个关键步骤，它可以帮助我们从复杂的光谱曲线中提取出重要的信息。

在本文中，我将深入探讨 Matlab 中光谱特征波长提取的方法和应用。

1. 光谱特征波长提取的意义光谱特征波长是指在光谱曲线中具有特殊意义或特定信息的波长点。

通过提取这些特征波长，我们可以更好地理解样品的化学成分、光学性质以及其他重要参数。

而 Matlab 作为一款强大的科学计算软件，提供了多种方法来进行光谱特征波长的提取和分析。

2. 光谱数据的预处理在进行光谱特征波长提取之前，我们通常需要对光谱数据进行预处理。

这包括数据的平滑处理、背景校正、波长校准等。

通过 Matlab 中的信号处理工具箱和光谱分析工具箱，我们可以方便地实现这些预处理步骤，保证数据的质量和准确性。

3. 常用的特征波长提取方法在 Matlab 中，有多种常用的方法可以用来提取光谱的特征波长。

其中，最常见的包括峰值检测、波峰波谷法、偏最小二乘法（PLS）、系数相关法等。

这些方法可以根据光谱数据的特点和需要，灵活地选择和组合，以获得更准确和全面的特征波长信息。

4. 实际案例分析举个例子，假设我们有一组光谱数据，对应某种药物的药效成分。

我们希望从中提取出与药效相关的特征波长。

我们可以通过 Matlab 对数据进行预处理，比如去除背景信号和噪音。

可以利用峰值检测和偏最小二乘法，提取出与药效相关的特征波长点。

结合实验结果和化学知识，对这些特征波长进行解释和分析。

5. 个人观点和总结在我看来，光谱特征波长提取是光谱分析中非常重要的一个环节。

通过合理选用方法和工具，我们可以更准确、更全面地获取光谱信息，从而更好地理解样品的特性和性能。

而 Matlab 作为一款功能强大、灵活多样的工具，为光谱特征波长提取提供了良好的支持和便利。

光谱特征波长提取是光谱分析中的一个重要步骤，在科学研究和工程应用中具有广泛的应用前景。

matlab在化学中的应用
Matlab在化学中有着广泛的应用，包括但不限于以下几方面：
1. 数据处理与分析：Matlab可以用于处理和分析化学实验中的各种数据，如光谱数据、质谱数据、色谱数据等。

通过编写脚本，可以快速地进行数据预处理、信号处理、统计分析等操作，以提高数据处理和分析的效率和精度。

2. 模拟与建模：Matlab可以用于建立化学系统的数学模型，并进行模拟和预测。

通过编写脚本，可以建立反应动力学模型、传质模型、热力学模型等，从而预测化学反应的速率、产物产率、热力学性质等。

3. 图像处理与可视化：Matlab可以用于图像处理和可视化，在化学实验中，可以用Matlab来处理和分析光学显微镜图像、扫描电镜图像、X射线衍射图像等。

通过编写脚本，可以对图像进行处理、分割、分析、可视化等，以提高数据分析和结果展示的质量。

4. 优化与控制：Matlab可以用于化学过程的优化和控制，在化学反应过程中，可以利用Matlab来优化反应条件、控制反应进程，从而提高反应产率和效率。

总之，Matlab在化学中的应用是非常广泛的，并且随着Matlab技术的不断发展和创新，其应用领域也不断扩大和深化。

晋中学院本科毕业论文（设计）题目计算机在化学中的应用-利用MATLAB求解化学计算题院系化学化工学院专业化学姓名学号0909111113学习年限2009年9月至2013年7月指导教师申请学位学士学位2013年5 月15日计算机在化学中的应用——利用MATLAB求解化学计算题摘要：MATLAB是由美国Math works公司发布的主要面对科学计算、可视化以及交互式程序设计计算环境。

它能有效地解决数值线性代数、数值逼近、最优化等科学和工程问题。

编制程序方便，求解化学计算题高效快速。

本文分别以结构、分析、化工三方面的典型例题，来说明MATLAB在化学中的应用。

关键词：MATLAB；化学计算题；计算应用；结构；分析；化工Applications of MATLAB in Chemistry—Use MATLAB SolvingChemical Calculation ProblemsAuthor’s Name：Lijiajia Tutor: DongtaoABSTRACT：MATLAB, released by the America Mathwoks Company, is the computing environment mainly in the face of scientific computing, visualization and interactive programming. It can efficiently solve problems in science and engineering such as numerical linear algebra, digital approximation, and optimization. It also has characters of convenient programming and efficiently and quickly solving chemical calculation problems. This paper will explain MATLAB in the application of chemistry by referencing typical examples about structural chemistry, analytical chemistry and chemical industry.KEYWORDS：MATLAB；Chemical calculation problems；Computing applications；Structural chemistry；Analytical chemistry ；Chemical industry目录1 MATLAB简介 (1)1.1MATLAB的简要发展 (1)1.2 MATLAB的功能介绍 (1)2 MATLAB在化学中的应用 (2)2.1 MATLAB在结构化学计算中的应用—休克尔分子轨道的计算 (2)2.2 MATLAB在分析化学中的应用—计算溶液的pH (3)2.2.1 一元强酸（碱）中H+的计算 (3)2.2.2 一元弱酸（碱）溶液pH的计算 (4)2.3 MATLAB在化工计算中的应用—解非线性方程（组） (6)2.3.1 解非线性方程 (6)2.3.2 解非线性方程组 (7)3结语 (8)注释 (9)参考文献 (10)致谢 (11)1 MALAB简介1.1MATLAB的发展历史MATLAB是Math works公司推出的适用于科学和工程计算的数学软件系统，MATLAB即Matrix（矩阵）和Laboratory（实验室）的简称，雏形是Cleve Moler教授为学生编写的用于Linspack和Eispack的接口程序。

硕士研究生课程论文（或读书报告）课程名称： MATLAB程序设计与应用题目： MATLAB在化学工程中的应用题目类型：课程论文学院：化学工程学院专业名称：化学工程姓名：学号：任课教师：提交时间：2013 年11 月21 日摘要本文以在化学科研与教学遇到的各种科学计算、作图、数据处理为核心，简述了MATLAB在这些方面的运用情况，及其处理数据的高效、直观性。

阐述了MATLAB在处理数据与其他数据处理软件的不同之处，突出其优越性。

MATLAB不仅是一种方便的科学计算软件，还是一种优秀的计算机语言。

与其他语言显著不同点在于：1）MATLAB能够直接对矩阵操作；2）MATLAB能够直接使用复数。

这让其在化学数据处理方面，化学计算方面具有更见广泛的应用。

能够帮助广大化学工作者轻易的解决在各化学分支遇到的各种复杂的作图、科学计算和数据处理问题。

ABSTRACTBased in the chemical research and teaching the various scientific computation, mapping, data processing as the core, the MATLAB in these aspects of the application, and its data processing and efficient, intuitive. Elaborated the MATLAB in the processing of data and other data processing software is different, highlighting its superiority. MATLAB is not only a convenient scientific calculation software, is a good computer language. Other languages with significantly different point depends on: 1) MATLAB can directly on the matrix operation;2) MATLAB can be directly used in the plural. This makes the chemical data analysis chemical calculation has more extensive application. To help the majority of chemical workers easily in the branch of chemistry that encountered in a variety of complex mapping, scientific computing and data analysis.1 引言本文通过对MATLAB在化学各分支的广泛应用。

两种常用软件在夫兰克-赫兹实验数据处理中的应用与比较夫兰克-赫兹实验的原理和意义夫兰克-赫兹实验是揭示原子内部电子能级的实验之一。

这一实验首先由德国物理学家弗兰克和赫兹于1914 年发现。

它的实验过程中电子在真空中沿着管子快速运动并轰击到一个阳极上，通过调节阴极与阳极之间的电压、电流和管子内部的气压等物理参数，可以测量到电子的动能和穿过阳极时释放的电子的能量。

这些数据可以推导出气体中的电子能级。

夫兰克-赫兹实验对于研究原子和分子的结构有巨大的贡献，它让人类能够更加全面理解原子结构的本质，从而推动了物理学和化学学科的发展。

两种常用软件在夫兰克-赫兹实验数据处理中的应用在夫兰克-赫兹实验中，数据的处理和分析至关重要。

为此，科学家开发了许多种不同的软件用于对实验数据进行分析和处理。

其中，比较常用的包括Origin 和MATLAB 两种软件。

Origin 是由美国公司OriginLab 开发的一款实验数据处理软件，它的主要功能在于数据预处理、绘图和分析。

在夫兰克-赫兹实验中，Origin可以用于对实验数据进行处理和可视化分析。

它可以帮助用户进行数据的可视化分析，产生出直观的图像来更好地理解实验结果。

此外，Origin 在帮助处理实验数据时支持多种曲线拟合方法，如线性拟合、多项式拟合和非线性拟合等。

使用Origin 可以完成诸如拟合、求导、积分等操作。

MATLAB (Matrix Laboratory) 是一种计算机语言与开发环境，主要用于数学计算、绘图、算法开发、数据分析以及应用程序创建等领域。

在夫兰克-赫兹实验中，MATLAB 可以用于对实验数据进行处理和分析。

与Origin 不同的是，MATLAB 拥有更强大和灵活的计算能力，能够处理较大规模、较复杂的数据，并支持多种编程语言和自定义算法的设计。

在使用MATLAB 进行数据处理时，用户可以自行编写代码并使用相应的算法，来完成数据的处理和统计分析。

两种常用软件的比较Origin 和MATLAB 两种软件虽然用于实验数据处理和分析有相似之处，但仍有明显的区别。

MATLAB 在实际问题中的分析与应用自20世纪80年代以来，出现了多种科学计算语言，亦称数学软件，比较流行的有MATLAB 、Mathematical 、Maple 等。

因为他们具有功能强、效率高、简单易学等特点，在在许多领域等到广泛应用。

MATLAB 便是一种影响大、流行广的科学计算语言。

MATLAB 的语法规则简单，更加贴近人的思维方式。

MATLAB 是英文Matrix Laboratory(矩阵实验室)的缩写。

自1984年由美国Math Works 公司推向市场以来，得到了广泛的应用和发展。

在欧美各高等院校MATLAB 已经成为线性代数、自动控制理论、数字信号处理、时间序列分析、动态系统仿真、图像处理等诸多课程的基本教学工具，成为大学生、硕士生以及博士生必须掌握的基本技能。

在设计研究单位和工业部门，MATLAB 已被广泛的应用于研究和解决各种具体的工程问题。

近年来，MATLAB 在我国也开始流行，应用MATLAB 的单位和个人急剧增加。

可以预见，MATLAB 将在我国科学研究和工程应用中发挥越来越大的作用。

Mat lab 是当前数值计算方面应用地非常广泛的一种计算机软件，特别是在工程应用求解中发挥了重要作用。

其所具有的浅显易懂的编程语言、强大的绘图功能、大量的内部函数等都深深地吸引了我认真地去学习它。

同时在上《过程装备力学基础》时，其中涉及有很多的问题是超越方程、微积分的问题，难以用普通的线性方法求解，而Mat lab 在此方面有强大的功能，特别是超越方程的精确求解以及图形的绘制方面。

数学当中的绘制函数图象、绘制立体图形的交线（如绘制两个等直径圆柱体的交线）、求多项式的根等问题，这些问题如果依靠我们人工进行操作，则需要很多的时间和精力，当我们掌握了基本原理后，借助于MATLAB 进行解决则会大大提高效率和精确度。

仅举一些运用MATLAB 的例子。

常用控制命令：click ：%清屏； clear ：%清变量； save ：%保存变量； load ：%导入变量 一、利用公式直接进行赋值计算本金P 以每年n 次，每次i%的增值率（n 与i 的乘积为每年增值额的百分比）增加，当增加到r ×P 时所花费的时间T 为：（利用复利计息公式可得到下式）)01.01ln(ln )01.01(i n rT i P P r nT +=⇒+=⨯（12,5.0,2===n i r ）MATLAB 的表达形式及结果如下： >> r=2;i=0.5;n=12; %变量赋值 >> T=log(r)/(n*log(1+0.01*i)) 计算结果显示为：T = 11.5813即所花费的时间为T=11.5813 年。

利用matlab对连续搅拌反应釜机理建模-概述说明以及解释1.引言1.1 概述连续搅拌反应釜是化工领域常见的反应设备，其在化学工程中具有重要的应用。

通过对连续搅拌反应釜的研究与分析，可以深入了解复杂的化学反应机理和反应过程，从而实现对反应条件的优化和控制。

本文将利用Matlab对连续搅拌反应釜的机理进行建模，并探讨该模型的验证与应用。

通过建立数学模型，可以帮助工程师和研究人员更好地理解反应过程中的物质转化规律，进而实现对反应釜的优化设计和运行控制。

通过本文的研究，将有助于提高连续搅拌反应釜的反应效率和产品质量，推动化工领域的发展，为相关行业提供更加可靠和有效的解决方案。

1.2 文章结构:本文共分为三个主要部分，分别是引言、正文和结论。

在引言部分，将会概述本文的研究背景和意义，介绍文章的结构和目的。

正文部分将着重介绍连续搅拌反应釜的基本原理，以及利用Matlab 进行机理建模的方法和过程。

同时，将会详细讨论模型验证与应用的重要性和效果。

结论部分将总结研究的成果和收获，同时也会讨论研究的局限性和不足之处。

最后，展望未来研究的方向和可能的发展趋势。

1.3 目的：本文旨在利用Matlab软件对连续搅拌反应釜进行机理建模，以探索反应过程中的动态行为和特性。

通过建立数学模型，我们可以更好地理解反应的动态过程，预测反应物的转化情况以及产物的生成速率，探究影响反应效率和产物选择性的因素。

通过对模型的验证和应用，我们可以优化搅拌反应釜的操作条件，提高反应效率和产物质量，为工业生产提供重要的理论支持和技术指导。

通过本研究，还可为未来深入探讨反应机理和优化工艺提供基础。

2.正文2.1 连续搅拌反应釜的基本原理连续搅拌反应釜是一种常见的化工反应设备，其主要工作原理是通过搅拌将反应物料充分混合，从而提高反应速率和产物收率。

在连续搅拌反应釜中，反应物料被持续地输入，同时产物被持续地输出，使得反应过程能够连续进行。

这种反应器通常具有良好的温度控制和搅拌效果，适用于各种液相或气液相反应。

matlab应用领域和行业Matlab是一款功能强大的数学软件，广泛应用于各个领域和行业。

本文将介绍Matlab在不同应用领域和行业中的具体应用。

1. 科学研究领域：Matlab在科学研究中有着广泛的应用，例如物理学、化学、生物学等。

在物理学中，Matlab可以用于求解微分方程、模拟物理实验、数据分析等。

在化学中，Matlab可以用于分子模拟、化学反应动力学研究等。

在生物学中，Matlab可以用于基因分析、蛋白质结构预测、生物图像处理等。

2. 工程设计领域：Matlab在工程设计中也被广泛应用。

例如，在电气工程中，Matlab可以用于电路设计、信号处理、嵌入式系统开发等。

在机械工程中，Matlab可以用于机械结构设计、动力学仿真、优化设计等。

在土木工程中，Matlab可以用于结构分析、地震工程、水资源管理等。

3. 金融领域：Matlab在金融领域有着重要的应用价值。

例如，在量化投资中，Matlab可以用于数据分析、金融模型建立、交易策略优化等。

在金融风险管理中，Matlab可以用于风险评估、投资组合优化、衍生品定价等。

在金融工程中，Matlab可以用于金融工具设计、金融市场预测等。

4. 数据分析领域：Matlab在数据分析中有着强大的功能和灵活性。

例如，在大数据分析中，Matlab可以用于数据清洗、数据可视化、机器学习等。

在统计分析中，Matlab可以用于假设检验、回归分析、时间序列分析等。

在图像处理中，Matlab可以用于图像增强、图像分割、目标识别等。

5. 教育领域：Matlab在教育领域中也发挥着重要的作用。

例如，在高校教学中，Matlab可以用于数学建模、科学计算、工程实践等。

在培训机构中，Matlab可以用于编程教学、数据分析培训等。

6. 生产制造领域：Matlab在生产制造领域也有着广泛的应用。

例如，在自动化控制中，Matlab可以用于系统建模、控制设计、仿真验证等。

在质量控制中，Matlab可以用于过程监控、异常检测、质量优化等。

Matlab是一种专业的数学计算软件，广泛应用于科学计算、工程计算和数据分析等领域。

而洛伦兹分布曲线则是一种常见的拟合曲线模型，用于描述数据分布中的两个峰。

在Matlab中进行两个峰的洛伦兹拟合，既可以帮助我们更好地理解数据分布，也可以为相关研究提供重要的参考。

二、洛伦兹分布曲线的原理1. 洛伦兹分布模型基本原理洛伦兹分布曲线是一种常见的拟合曲线模型，通常用于描述数据分布中存在的两个峰。

它的表达式为：f(x) = (A1/π) / ((x-x01)2 +(A1/2)2) + (A2/π) / ((x-x02)2 + (A2/2)2)，其中A1、A2分别为两个峰的振幅，x01、x02为两个峰的位置参数。

2. 洛伦兹分布曲线的特点洛伦兹分布曲线的特点是在两个峰周围呈现出类似钟形的分布，常用于描述共振峰、峰形分析等。

在进行数据拟合时，洛伦兹分布曲线能够较好地符合实际情况。

三、在Matlab中实现两个峰的洛伦兹拟合1. 准备数据我们需要准备包含两个峰的数据，可以是实验数据、模拟数据或者其他形式的数据。

这些数据需要包含两个明显的峰，并且能够充分反映2. 使用Matlab进行洛伦兹拟合在Matlab中，可以使用curve fitting工具箱中的fit函数进行洛伦兹拟合。

具体步骤为：首先导入数据，然后选择洛伦兹曲线模型，并调整参数以进行拟合，最后得到拟合结果并进行分析。

3. 结果分析与优化在得到拟合结果后，需要对结果进行分析，确保拟合曲线与原始数据相符合，并对拟合参数进行优化，以提高拟合的精度和稳定性。

四、应用范例与实例1. 共振频率的测量在物理实验中，常需要测量共振频率，并对共振峰进行分析。

此时可以使用洛伦兹拟合来提取出共振峰的位置和振幅，从而得到更精确的测量结果。

2. 化学分析中的应用在化学分析中，常需要对光谱数据进行拟合分析，以提取出各种峰的位置和强度。

洛伦兹拟合能够帮助分析师更好地理解光谱数据，并得到准确的分析结果。

实验设计与数据处理 作业（武汉工程大学）
第 页
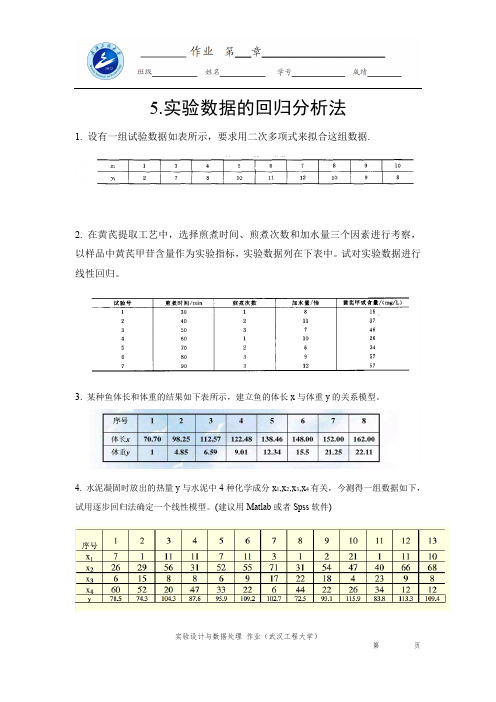
5.实验数据的回归分析法
1. 设有一组试验数据如表所示，要求用二次多项式来拟合这组数据.
2. 在黄芪提取工艺中，选择煎煮时间、煎煮次数和加水量三个因素进行考察，以样品中黄芪甲苷含量作为实验指标，实验数据列在下表中。

试对实验数据进行线性回归。

3.某种鱼体长和体重的结果如下表所示，建立鱼的体长x 与体重y 的关系模型。

4. 水泥凝固时放出的热量y 与水泥中4种化学成分x 1,x 2,x 3,x 4
有关，今测得一组数据如下，试用逐步回归法确定一个线性模型。

(
建议用Matlab 或者Spss 软件)。

MATLAB在化学工程中的应用与优化化学工程是一门研究化学过程和化学反应的学科，其应用领域涉及化工生产、能源开发、环境保护等多个方面。

为了提高生产效率、减少资源浪费，化学工程师们经常需要使用各种工具和方法进行过程模拟和优化。

而MATLAB作为一种功能强大的科学计算软件，提供了丰富的工具箱和函数，因此在化学工程中有着广泛的应用和巨大的优势。

一、过程模拟和优化在化学工程中，过程模拟是基础且必要的步骤。

通过建立数学模型，可以预测化学反应过程中的物质转化率、反应速率等重要参数，进而精确地设计反应器、控制温度、压力等操作条件。

而MATLAB提供了丰富的数值计算和仿真工具，可以帮助化学工程师实现精确的过程模拟。

MATLAB中强大的数值计算功能使得化学反应动力学的模拟变得相对简单。

通过使用ODE（Ordinary Differential Equations）工具箱，可以方便地求解化学反应过程中的微分方程。

在反应动力学已知的情况下，使用MATLAB建立反应速率方程，并将其嵌入微分方程求解器中，可以精确地模拟出化学反应的时间演化。

此外，MATLAB还提供了动态过程模拟工具Simulink，化学工程师可以通过直观的图形界面搭建反应器、换热器等各种装置，并通过连接传感器和执行器模拟现实过程中的动态变化。

化学工程中经常需要进行各种操作条件的优化，如反应温度、反应物物料比等。

MATLAB中的优化工具箱正好能够满足这一需求。

通过建立合适的优化目标函数和约束条件，化学工程师可以使用MATLAB的优化算法（如遗传算法、粒子群优化等）找到最优的操作条件。

这种基于数值计算的优化方法不仅节省了时间和资源，而且在复杂的多变量问题中也有着较好的表现。

二、参数估计和反馈控制在实际的化学工程中，往往难以获得准确的动力学参数，这给过程模拟与优化带来了很大的挑战。

然而，MATLAB提供了丰富的参数估计工具箱，化学工程师可以通过实验数据对动力学参数进行估计，从而提高模型的准确性。

北 京 化 工 大 学实 验 报 告课程名称： 化工原理实验 实验日期： 2008.10.29 班 级： 化工0602 姓 名：许兵兵学 号： 200611048 同 组 人 ：汤全鑫 阮大江 阳笑天流体流动阻力的测定摘要● 测定层流状态下直管段的摩擦阻力系数（光滑管、粗糙管和层流管）。

● 测定湍流状态不同（ε/d）条件下直管段的摩擦阻力系数（突然扩大管）。

● 测定湍流状态下管道局部的阻力系数的局部阻力损失。

● 本次实验数据的处理与图形的拟合利用Matlab 完成。

关键词流体流动阻力 雷诺数 阻力系数 实验数据 Matlab一、实验目的1、掌握直管摩擦阻力系数的测量的一般方法；2、测定直管的摩擦阻力系数λ以及突扩管的局部阻力系数ζ；3、测定层流管的摩擦阻力4、验证湍流区内λ、Re 和相对粗糙度的函数关系5、将所得光滑管的Re -λ方程与Blasius 方程相比较。

二、实验原理不可压缩流体（如水），在圆形直管中作稳定流动时，由于粘性和涡流的作用产生摩擦阻力；流体在流过突然扩大和弯头等管件时，由于流体运动的速度和方向突然发生变化，产生局部阻力。

影响流体流动阻力的因素较多，在工程研究中，利用因次分析法简化实验，引入无因此数群雷 诺 数：μρdu =Re相对粗糙度： d ε管路长径比： d l可导出：2)(Re,2u d d l p⋅⋅=∆εφρ这样，可通过实验方法直接测定直管摩擦阻力系数与压头损失之间的关系：22u d l pH f ⋅⋅=∆=λρ因此，通过改变流体的流速可测定出不同Re 下的摩擦阻力系数，即可得出一定相对粗糙度的管子的λ—Re 关系。

在湍流区内，λ = f（Re ，ε/ d ），对于光滑管大量实验证明，当Re 在3×103至105的范围内，λ与Re 的关系遵循Blasius 关系式，即：25.0Re 3163.0=λ对于层流时的摩擦阻力系数，由哈根—泊谡叶公式和范宁公式，对比可得：Re 64=λ局部阻力：f H =22u ⋅ξ [J/kg]三、装置和流程四、操作步骤1、启动水泵，打开光滑管路的开关阀及压降的切换阀，关闭其它管路的开关阀和切换阀；2、排尽体系空气，使流体在管中连续流动。