射频低通滤波器设计示例

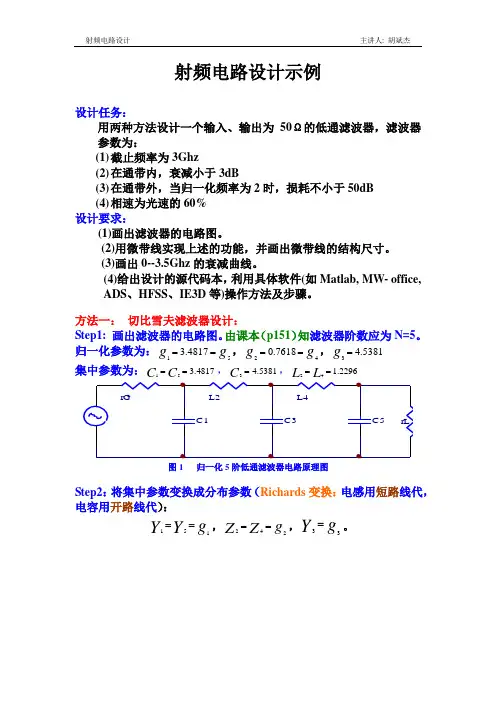
射频电路设计示例设计任务：用两种方法设计一个输入、输出为50Ω的低通滤波器，滤波器参数为：(1) 截止频率为3Ghz(2) 在通带内，衰减小于3dB(3) 在通带外，当归一化频率为2时，损耗不小于50dB (4) 相速为光速的60% 设计要求：(1)画出滤波器的电路图。

(2)用微带线实现上述的功能，并画出微带线的结构尺寸。

(3)画出0--3.5Ghz 的衰减曲线。

(4)给出设计的源代码本，利用具体软件(如Matlab, MW- office, ADS 、HFSS 、IE3D 等)操作方法及步骤。

方法一： 切比雪夫滤波器设计： Step1: 画出滤波器的电路图。

由课本（p151）知滤波器阶数应为N=5。

归一化参数为：g g 514817.3==，g g 427618.0==，5381.43=g 集中参数为：4817.351==C C ，5381.43=C ，2296.142==L L图1 归一化5阶低通滤波器电路原理图Step2：将集中参数变换成分布参数（Richards 变换：电感用短路线代，电容用开路线代）：gY Y 151==，g Z Z 242==，g Y 33=。

图2 （O.C ＝开路线，S.C=短路线）Step3：将串联线段变为并联线段—Kuroda 规则（P162表5.6）。

首先在滤波器的输入、输出端口引入两个单位元件。

因为单位元件与信号源及负载的阻抗都是匹配的，所以到入它们并不影响滤波器的特性。

对第一个并联的短线和最后一个并联短线应用Kuroda 规则-1后得：2872.12872.014817.31121=+=+==N N ， 2231.02872.14817.31''21＝⨯==Z Z UE UE7769.02872.1151＝==''Z Z S S图4 配置第一套单位元件后将并联短路线换为串联短路线因为这个电路中有四个串联短线，所以仍然无法实现。

滤波器（Filter ）（一）滤波器之种类以信号被滤掉的频率范围来区分，可分为「低通」（Lowpass）、「高通」（Highpass）、「带通」（Bandpass）及「带阻」（Bandstop）四种。

若以滤波器原型之频率响应来分，则常见有「巴特沃斯型」（Butter-worth）、「切比雪夫I型」（Tchebeshev Type-I）、「切比雪夫II型」（Tchebyshev Type-II）及「椭圆型」（Elliptic）等几类。

若以使用组件型态来分，则可分为「主动型」（Active）及「被动型」（Passive)两类。

其中「被动型」又可分为「L-C型」（L-C Lumped）及「传输线型」（Transmission line）。

而「传输线型」以其结构不同又可分为「平行耦合型」（Parallel Coupled）、「交叉指型」（Interdigital）、「梳型」（Combline）及「发针型」（Hairpin-line）等不同型态。

这里以较为常使用的「巴特沃斯型」（Butterworth）、「柴比雪夫I 型」（Tchebeshev Type-I）为例，说明其设计方法。

（二）「低通滤波器」设计方法(A) 「巴特沃斯型」（Butterworth Lowpass Filter ）步骤一：决定规格。

电路特性阻抗（Impedance ）: Zo (ohm) 通带截止频率（Cutoff Frequency ）: fc (Hz) 阻带起始频率（Stopband Frequency ）: fx (Hz)通带衰减量（Maximum Attenuation at cutoff frequency ）: Ap (dB) 阻带衰减量（Minimum Attenuation at stopband frequency ）：Ax(dB)步骤二：计算组件级数（Order of elements ，N ）。

⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--⋅≥c x Ap Ax f f N log 110110log 5.010/10/ ， N 取最接近的整数。

利用双绞线与低通滤波器抑制射频干扰和电磁干扰引言“The Twist”指双绞线，Alexander Graham Bell于1881年申请该项专利。

而该项技术一直沿用到今天，原因是它提供了诸多便利。

此外，随着现场可编程门阵列(FPGA)器件处理能力的逐渐强大，结合电路仿真及滤波器设计软件，使得双绞线在数据通信领域的应用也越来越普遍。

FPGA为设计工程师提供了强大、灵活的控制能力，特别是那些无法获取专用集成电路(ASIC)的小批量设计项目，可以利用FPGA实现设计;许多大批量生产的产品，在项目设计初期也利用FPGA进行原型开发，并定制芯片之前对新功能进行测试。

FPGA的强大之处在于复杂的数字处理功能，而一些模拟信号则会受限于数字噪声的干扰。

需要外部提供模拟放大，以及失调、滤波和信号处理，确保FPGA满足系统的整体需求。

本文讨论了如何将双绞线与低通滤波器相结合，抑制射频干扰(RFI)和电磁干扰(EMI)。

我们还介绍了如何利用高精度电阻排设计定制化差分放大器，消除信号干扰并改善FPGA系统的性能。

在我们选择频响特性时，利用高精度电阻设置增益和共模抑制比。

双绞线的重要性双绞线对数据通信有着重大意义，能够大幅降低串扰、RFI和EMI。

互联网和计算机的普及带动了双绞线应用的普及，许多人误以为双绞线是项新发明，实际情况并非如此。

图1所示是Alexander Graham Bell早在1881年就已申请的专利副本，他描述了多对双绞线之间的相互影响。

图1. Alexander Graham Bell于1881年获得美国专利244,426Bell先生指出：多个电路通过两条线连接——一条直通线和一条返回线，构成一个金属线导电回路。

当金属线导电回路置于其它电路附近时，如果周边电路在两条线上感应信号不同，则金属线所连接的电话及其它电气设备就会感应干扰信号;显而易见，如果在直通线和返回线上产生相同影响，则其中一条导线产生的电流将抵消另一条导线产生的电流。

巴特沃斯低通滤波器仿真实验一、实验目的掌握巴特沃斯低通滤波器的设计方法及原理二、滤波器设计的具体指标1.截止频率GHz c 5.2=ω。

2.在GHz 4=ω处的插入损耗必须大于20dB 。

3.阻抗为Ω50，采用6阶巴特沃兹低通原型，最高实际线阻抗为120Ω，最低实际阻抗为20Ω，采用的基片参数为02.0tan ,2.4,58.1===δεr mm d ，铜导体的厚度为mm t 035.0=。

三、巴特沃斯滤波器的特性巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦，没有起伏，而在阻频带则逐渐下降为零。

在振幅的对数对角频率的波得图上，从某一边界角频率开始，振 幅随着角频率的增加而逐步减少，趋向负无穷大。

一阶巴特沃斯滤波器的衰减率为每倍频6分贝，每十倍频20分贝。

二阶巴特沃滤波器的衰减率为每倍频12分贝、 三阶巴特沃斯滤波器的衰减率为每倍频18分贝、如此类推。

巴特沃斯滤波器的振幅对角频率单调下降，并且也是唯一的无论阶数，振幅对角频率曲线都保持同样的形状的滤波器。

只不过滤波器阶数越高，在阻频带振幅衰减速度越快。

其他滤波器高阶的振幅对角频率图和低级数的振幅对角频率有不同的形状。

四、滤波器设计步骤1.确定低通原型元器件值。

2.采用阻抗和频率定标公式，用低阻抗和高阻抗线段代替串联电感和并联电容。

所需微带线的电长度l β，以及实际微带线宽w 和线长l 可由ADS 软件中的lineCalc 工具计算得到。

3.根据得到的线宽和线长进行建模并仿真计算。

计算如下：6.015.241||=-=-c w w ，由下图1.1看出，对于n=6的曲线，当6.0)1|(|=-cw w 时，LA<20dB,故最大平坦滤波器级数n=6。

4.根据下表设计滤波器的参数n表示巴特沃斯低通滤波器的阶数，g参数表示巴特沃兹滤波器低通原型元器件值。

五、实验结果原理图如下图所示：各元件的设置情况如下：第一个微带线和最后一个微带线，长等于16.772200 mm，宽等于3.114450 mm。

║260 物联网：ADS 射频电路仿真与实例详解 5式（11.7）和（11.8）中，L 和C 是低通滤波器原型的元器件值，R S 是滤波器阻抗。

2．阶梯阻抗低通滤波器的设计下面设计微带线阶梯阻抗低通滤波器，设计的详细过程可以参阅人民邮电出版社出版的《射频电路理论与设计》。

要求截止频率为3GHz ，通带内波纹为0.5dB ，在6GHz 处具有不小于30dB 的衰减，系统阻抗为50Ω。

选微带线特性阻抗最大值h Z =120Ω，特性阻抗最小值l Z =15Ω。

设计微带线阶梯阻抗低通滤波器的步骤如下。

（1）根据波纹为0.5dB 切比雪夫滤波器衰减随频率的对应关系，滤波器需为5阶，对应的切比雪夫低通滤波器原型元器件值为111.7058g C ==221.2296g L ==332.5408g C ==441.2296g L ==551.7058g C == （2）利用式（11.7）和（11.8）计算可以得到 1 1.70581518029.350l ⨯=⨯≈︒πβ 2 1.22965018029.4120l ⨯=⨯≈︒πβ 3 2.54081518043.750l ⨯=⨯≈︒πβ 4 1.22965018029.4120l ⨯=⨯≈︒πβ 5 1.70581518029.350l ⨯=⨯≈︒πβ （3）低通滤波器电路的示意图如图11.3所示，其中图11.3（a ）为由低通滤波器原型元器件值构成的低通滤波器，图11.3（b ）为微带线阶梯阻抗低通滤波器。

图11.3 低通滤波器电路的示意图11.1.2 微带阶梯阻抗低通滤波器原理图的仿真由上面微带线阶梯阻抗低通滤波器的理论基础，我们得到了微带线阶梯阻抗低通滤波器第11章 分布参数低通滤波器的仿真 261║的电路基本结构，本节学习如何利用ADS微带线的计算工具完成微带线的计算，以及如何设计并仿真微带线阶梯阻抗低通滤波器的原理图。

微带线阶梯阻抗低通滤波器的设计指标如下。

低通滤波器设计制作一、实验目标及目的：1设计一个截止频率为9200Hz 的低通滤波器 2掌握滤波器的设计制作方法 3掌握滤波器截止频率的测量方法 4掌握测试报告文档处理方法 二、测试仪器1、GWinsTEKGOS-620双踪示波器2、函数信号发生器3、示波器测试笔2个 三、滤波器的设计制作步骤1首先给出低通滤波器的电路图和频谱特性。

2根据低通滤波器的截止频率10200Hz ，选定合适的电容和电阻。

3根据选定的参数用Matlab 进行仿真。

4制作电路板。

5完成测试。

6撰写测试报告。

四、滤波器的设计制作1低通滤波器的电路图和频谱特性1）理想低通滤波器概念：频谱函数为()()0-2=cj t H j G e ωωωω的系统称为理想低通滤波器。

其幅频特性和相频特性如图1所示。

图1理想低通滤波器的幅频特性和相频特性这里，c ω是理想低通滤波器的截止频率。

理想低通滤波器将高于c ω的信号完全衰减，而允许低于c ω的信号通过。

2）通频带概念：能使信号通过的频率范围称为通带。

理想低通滤波器的通频带为c ω3）阻带概念：阻止信号通过的频率范围称为阻带。

2实际低通滤波器：尽管理想低通滤波器具有理想的频率选择特性，但在实际应用中无法实现，我们只能用一些可实现的系统来近似它。

实际低通滤波器截止频率：用来说明电路频率特性指标的特殊频率。

当保持电路输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍所对应的频率称为其截止频率。

3低通滤波器的电路图 低通滤波器的电路图如下：4低通滤波器的频谱函数5参数选定+0u6 MATLAB仿真如下：r=4000;c=3900e-12;f=1000:1:30000; a=1./(2.*pi*r*c);b=1.+(f./a).^2;H=1./(b.^0.5);plot(f,H)运行后结果：四、电路板制作1、电阻R及电容C参数的选取C3900=ΩpFR=4000制做的电路板如图：图（一）五、频谱函数测试 1、测试步骤（1）按下示波器电源“power ”； （2）扫描时间“TIME/DIV ”达到0.2ms ； （3）将示波器“MODE ”达到“CH1”； （4）将“VOLTS/DIS ”达到“1”； （5）将打到AC;(6)将同轴测试电缆连接到“CH1”上，测试笔上的开关推到“X1” 校准如下图（二）：图（二）（7）同理对“CH2”通道进行校准； 校准如下图（三）ACGND DC图（三） 2、滤波器测试（1）用导线接滤波器的输入端，另一端插入接信号信号发生器的输出端；（2）将示波器的同轴测试电缆CH2上的鳄鱼夹接滤波器的“地端”，测试钩接“输出”；（3）将示波器“MODE ”打到“DUAL ”，调节频率旋钮，观察波形； （4）根据规定当输出的()ωj H 为最大()ωj H 的0.707倍时所对应的频率即为截止频率 。

经典滤波器设计范文一、FIR滤波器设计FIR（Finite Impulse Response）滤波器是一种常用的数字滤波器，其特点是抗混叠性能好、线性相位响应、易于设计等。

FIR滤波器的设计通常分为两个步骤：滤波器的理想频率响应设计和具体的滤波器系数设计。

1.理想频率响应设计理想的低通FIR滤波器频率响应为单位脉冲响应的离散傅里叶变换，即H(e^jω) = sum(h(n)e^(-jωn))，其中h(n)为滤波器的单位脉冲响应。

通过将理想频率响应转换为时域单位脉冲响应，可以得到容纳在有限长度L的FIR滤波器中。

其中单位脉冲响应为：h(n) = (ω_0π)^-1 * sin(ω_0n)/(nπ)，其中ω_0为截止频率。

2.系数设计对于FIR滤波器，系数设计是指对滤波器的单位脉冲响应进行窗函数的处理。

窗函数可以选择矩形窗、汉宁窗、海明窗等。

二、IIR滤波器设计IIR（Infinite Impulse Response）滤波器是另一种常用的数字滤波器，其特点是滤波器具有无限长度的单位脉冲响应。

与FIR滤波器不同，IIR滤波器的设计指标更多地侧重于滤波器的幅频响应与相位响应的设计。

1.巴特沃斯滤波器设计巴特沃斯滤波器是一种IIR滤波器的设计方法，其特点是在通带中具有均匀响应，即幅频特性较为平坦。

巴特沃斯滤波器设计的关键是选择滤波器阶数和截止频率。

2.预畸变滤波器设计预畸变滤波器是为了使滤波器的相频特性更加平坦而设计的，其主要应用在通信系统中。

预畸变滤波器一般采用线性相位结构，在设计时需要考虑相位补偿。

三、其他滤波器设计方法除了上述的FIR和IIR滤波器设计方法外，还有一些其他的滤波器设计方法，如小波滤波器设计、自适应滤波器设计等。

1.小波滤波器设计小波滤波器是在小波变换领域中常用的滤波器设计方法。

小波滤波器具有多尺度分析的特点，可以提供多分辨率的信号处理。

2.自适应滤波器设计自适应滤波器是根据输入信号的特性进行动态调整的一种滤波器设计方法。

射频电路切比雪夫低通滤波器
射频电路中的切比雪夫低通滤波器是一种常见的滤波器类型，
它在射频通信系统中起着重要的作用。

切比雪夫滤波器是一种具有
截止频率特性的滤波器，其特点是在通带和阻带上都能提供较为陡
峭的过渡。

下面我将从不同的角度来介绍切比雪夫低通滤波器。

首先，从理论角度来看，切比雪夫滤波器是一种以俄罗斯数学
家切比雪夫命名的滤波器类型，其特点是在通带内具有波纹的频率
响应。

这意味着在通带内会有波纹存在，但是可以实现更为陡峭的
截止特性。

切比雪夫滤波器的设计是基于切比雪夫多项式，这些多
项式在滤波器设计中起着关键作用。

其次，从实际应用角度来看，切比雪夫低通滤波器在射频电路
中被广泛应用于需要较为陡峭的截止特性的场合。

例如，在无线通
信系统中，需要对信号进行滤波以去除不需要的频率成分，切比雪
夫低通滤波器可以提供较为理想的滤波效果。

此外，在雷达系统、
射频前端等领域，切比雪夫低通滤波器也有着重要的应用。

此外，从设计角度来看，切比雪夫低通滤波器的设计需要考虑
到滤波器的阶数、通带波纹、截止频率等参数。

在实际设计过程中，
工程师需要权衡这些参数，以满足具体的系统要求。

通常情况下，增加滤波器的阶数可以提高滤波器的性能，但也会增加设计的复杂度和成本。

总的来说，切比雪夫低通滤波器作为射频电路中常用的滤波器类型，具有较为陡峭的截止特性和波纹的通带特性，适用于需要严格滤波要求的场合。

在实际应用中，工程师需要根据具体的系统要求进行设计和选择，以实现最佳的滤波效果。

1、低通滤波器（LPF）低通滤波器是用来通过低频信号，衰减或抑制高频信号。

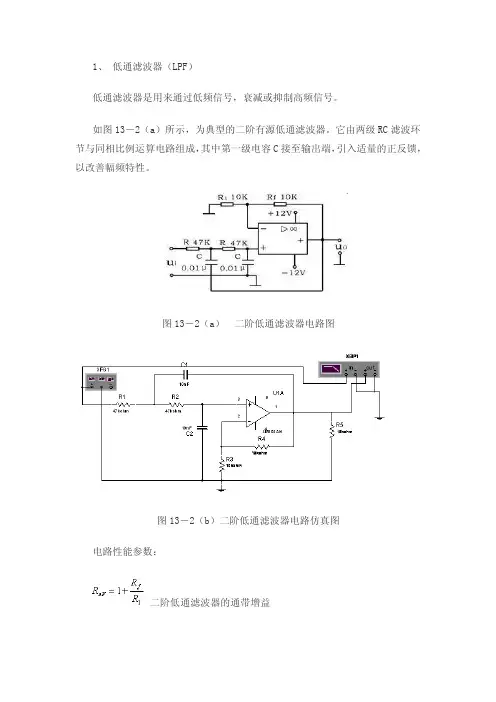
如图13－2（a）所示，为典型的二阶有源低通滤波器。

它由两级RC滤波环节与同相比例运算电路组成，其中第一级电容C接至输出端，引入适量的正反馈，以改善幅频特性。

图13－2（a）二阶低通滤波器电路图图13－2（b）二阶低通滤波器电路仿真图电路性能参数：二阶低通滤波器的通带增益截止频率，它是二阶低通滤波器通带与阻带的界限频率。

品质因数，它的大小影响低通滤波器在截止频率处幅频特性的形状。

2、高通滤波器（HPF）与低通滤波器相反，高通滤波器用来通过高频信号，衰减或抑制低频信号。

只要将图13－2低通滤波电路中起滤波作用的电阻、电容互换，即可变成二阶有源高通滤波器，如图13－3所示。

高通滤波器性能与低通滤波器相反，其频率响应和低通滤波器是“镜象”关系，仿照LPH分析方法，不难求得HPF的幅频特性。

图13－3 二阶高通滤波器电路图电路性能参数A uf、f0、Q各量的函义同二阶低通滤波器3、带通滤波器（BPF）图13-4 二阶带通滤波器这种滤波器的作用是只允许在某一个通频带范围内的信号通过，而比通频带下限频率低和比上限频率高的信号均加以衰减或抑制。

这种滤波器的作用是只允许在某一个通频带范围内的信号通过，而比通频带下限频率低和比上限频率高的信号均加以衰减或抑制。

典型的带通滤波器可以从二阶低通滤波器中将其中一级改成高通而成。

如图13－4所示。

电路性能参数：通带增益中心频率通带宽度选择性此电路的优点是改变R f和R4的比例就可改变频宽而不影响中心频率。

4、带阻滤波器（BEF）如图13－5所示，这种电路的性能和带通滤波器相反，即在规定的频带内，信号不能通过（或受到很大衰减或抑制），而在其余频率范围，信号则能顺利通过。

在双T网络后加一级同相比例运算电路就构成了基本的二阶有源BEF。

(a) 电路图 (b) 频率特性图13－5 二阶带阻滤波器OPA2111的四阶低通滤波器，截止频率10HZ永磁交流伺服电机位置反馈传感器检测相位与电机磁极相位的对齐方式2008-11-07 来源：internet 浏览：504主流的伺服电机位置反馈元件包括增量式编码器，绝对式编码器，正余弦编码器，旋转变压器等。

射频系统仿真实验报告射频滤波器设计姓名：学号：一、设计要求设计一个三阶原型Butterworth 低通滤波器。

要求：H f =10GHz ，电长度4πθ=。

二、设计方案在三阶原型Butterworth 低通滤波器的基础上，采用kuroda 变换。

变为可实现的结构。

1) 三阶原型Butterworth 低通滤波器：注：并联元件的单位是电纳，串联元件的单位是电抗2) 传输线实现集总参数的电感电容：θtg jZ jX Z L L 0== （8λ的短路线） θjtg 记为S θtg jY jB Y c c 0== （8λ的开路传输线）3) 插入单位元件后再进行Kuroda 规则变换。

目的是变成可实现的物理结构。

采用如下变换：取121Z Z Z N +=时两者等效。

所以Z=1的单位元件并联Y=1的8λ开路传输线变为：Z=1/2的8λ短路传输线和Z=1/2的单位元件相串联。

上图交换为如下：4) 再插入一个单位元件，如下图：⇔利用Kuroda 规则：取121Z Z Z N +=即可。

所以Z=1的单位元件串联Z=1/2的8λ短路传输线变为：并联的Y=3的8λ开路传输线和Z=1.5的单位元件。

所以Z=1/2的单位元件串联Z=2的8λ短路传输线变为：并联的Y=8/5的8λ开路传输线和Z=2.5的单位元件。

整个电路如下图：5) 阻抗交换：采用8λ开路传输线单位值Ω⨯50。

∴ 变换后特征阻抗为：⇔0.333333 16.66671.5 75.0000 0.625 31.25002.5 125.0000 1 50.00006) 物理尺寸计算得到另外4段微带线尺寸如下：归一化值 Z 的特征阻抗宽度W 长度P 单位：mil 频率：10GHz 电长度：45°1/3 Ω67.16 126.6 103.098 1.5 Ω75 15.0051 110.234 5/8 Ω25.31 58.2277 105.493 2.5 Ω125 4.3755113.6 1Ω5029.9473107.84三、仿真分析①Project 导航条内。

低通滤波器应用实例简介低通滤波器是一种常见的信号处理技术，它可以将高频信号滤除，只保留低频信号。

在实际应用中，低通滤波器有着广泛的应用，例如音频处理、图像处理、通信系统等领域。

本文将介绍低通滤波器的基本原理和应用实例。

基本原理低通滤波器的基本原理是通过设置一个截止频率，将高于截止频率的信号滤除。

滤波器通常使用一组滤波器系数或滤波器的频率响应来实现。

常用的低通滤波器包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器等。

巴特沃斯滤波器是一种理想的低通滤波器，它具有平坦的通带和陡峭的阻带。

切比雪夫滤波器是一种具有过渡带纹波的低通滤波器，可以通过调整纹波大小来权衡通带和阻带的性能。

椭圆滤波器是一种具有过渡带纹波和陡峭阻带的低通滤波器，它可以提供更好的性能，但通常比其他滤波器更复杂。

应用实例音频处理在音频处理中，低通滤波器可以用于降低高频噪声或滤除音频信号中的高频成分。

例如，在音乐录音中，可以使用低通滤波器来滤除录音设备本身的噪声或过滤掉高频演奏器乐器的噪声。

另外，低通滤波器也常用于语音处理中，可以用来提取语音信号的低频成分，以便进行语音识别或语音合成等任务。

图像处理在图像处理中，低通滤波器可以用于图像平滑或去除图像噪声。

通过对图像进行低通滤波，可以降低图像的高频细节，使得图像看起来更加平滑。

这在一些图像处理任务中非常有用，例如边缘检测、图像增强等。

同时，低通滤波器也可以用来去除图像中的噪声，例如椒盐噪声或高斯噪声。

通信系统在通信系统中，低通滤波器常用于信号调制和解调。

在信号调制过程中，低通滤波器用于限制载波信号的带宽，以便将调制的信息嵌入到载波信号中。

而在信号解调过程中，低通滤波器则用于滤除调制信号带外的噪声和干扰，以恢复原始的调制信息。

总结低通滤波器是一种重要的信号处理技术，具有广泛的应用。

本文简要介绍了低通滤波器的基本原理和应用实例，包括音频处理、图像处理和通信系统。

通过合理选择合适的滤波器类型和参数，可以根据实际需求实现信号的滤波和处理。

低通滤波器设计范文1.理想低通滤波器设计方法：理想低通滤波器是一种理论上的滤波器，可以完全传递低于截止频率的信号，而完全阻碍高于截止频率的信号。

它的频率响应是一个矩形函数。

这种滤波器的设计方法包括：-频域设计方法：使用傅立叶变换将输入信号与理想低通滤波器的频率响应相乘，然后再进行反傅立叶变换得到滤波器的时域响应。

这种方法可以得到理论上最佳的低通滤波器设计，但是在实际应用中由于输入信号和滤波器的长度有限，会产生频谱泄漏和振铃等现象。

- 时域设计方法：通过直接设计滤波器的时域冲激响应或单位脉冲响应。

这种方法包括窗函数法、布莱克曼窗法、Cauer窗法等。

2.模拟滤波器设计方法：模拟低通滤波器设计通常使用传统的模拟滤波器结构，如巴特沃斯、切比雪夫和椭圆滤波器等。

这些滤波器结构都有各自的特点和设计要求，可以根据实际需求选择合适的滤波器结构。

3.数字滤波器设计方法：数字低通滤波器设计通常使用数字滤波器结构或算法来实现。

常见的数字滤波器设计方法包括：-FIR（有限脉冲响应）滤波器设计：FIR滤波器是一种线性相位滤波器，可以通过设计其冲激响应来实现低通滤波。

常用的设计方法有窗函数法、最小二乘法等。

-IIR（无限脉冲响应）滤波器设计：IIR滤波器是一种递归滤波器，可以通过设计其差分方程的系数来实现低通滤波。

常用的设计方法有巴特沃斯滤波器设计、切比雪夫滤波器设计等。

在实际应用中，低通滤波器的设计通常需要考虑多个因素，包括滤波器的通带、阻带和过渡带的特性，滤波器的幅频响应、相频响应和群延迟等参数，以及设计的难易程度和实现的复杂度等。

根据不同的应用需求和设计指标，可以选择合适的滤波器设计方法和技术。

需要注意的是，滤波器的设计过程并非一次成功，通常需要进行多次优化和调整，以达到设计要求。

同时，为了验证滤波器的设计效果，还需要进行频率响应测试、时域响应测试和系统性能评估等工作。

因此，低通滤波器的设计是一个相对复杂和繁琐的过程，需要设计者具备相应的理论知识和实践经验。

实验三射频滤波器实验一实验目的1．掌握射频低通、带通滤波器的工作原理2．学习使用ADS软件进行滤波器的设计、优化和仿真3．学会使用AV3620矢量网络分析仪测试滤波器的幅频特性二实验原理1 低通滤波器集总元件低通原型滤波器是设计微波滤波器的基础。

一般低通原型滤波器的两种可行结构如图3-1所示，它是个LC梯型网络，两端各接纯电阻负载，（a）与（b）两电路互为对偶，即串联电感与并联电容存在对换关系。

图3-1 低通原型滤波器的电路低通原型的频率响应通常有最平坦响应和等波纹响应两种。

最平坦型滤波器的衰减曲线中没有任何波纹，所以称为最大平滑滤波器，也称巴特沃斯滤波器。

其衰减函数为()2210lg 1n A L =+εΩ （3-1） 其中归一化频率'1ω'ωΩ=。

等波纹型滤波器的频率响应在通带内有规律性的起伏，且幅度相等，故称为等波纹型，也称为切比雪夫响应。

其衰减函数为()2210lg 1A n L T ⎡⎤=+εΩ⎣⎦ （3-2）与巴特沃斯低通原型相比较，对于给定的通带衰减和滤波器节数，切比雪夫低通原型的阻带衰减斜率陡峭得多。

2 带通滤波器发卡式滤波器是半波长耦合微带滤波器的一种变形结构，是把半波长耦合谐振器折合成“U ”字形构成的。

发卡式滤波器是由若干个发卡式谐振器并排排列组合而成，这些谐振器之间主要是通过其边缘区域的电磁场相互交叉耦合的。

因此，这部分区域决定了发卡式滤波器之间的耦合特性和耦合强度。

在每个谐振器两臂的开放端，电场强度分布达到最大；而在其两臂的中间部分，磁场强度分布达到最大。

如图3-2所示，根据谐振器间的相对位置，发卡式谐振器可以分为四种基本耦合结构：电耦合、磁耦合、第一及第二类混合耦合。

图中，a 为谐振器臂长，b 为臂间距，w 为线宽，s 为两谐振器间距，d 为两谐振器偏移距离。

图3-2 微带型发卡式谐振器的4类基本耦合结构对于相同的微带线结构，如果两个谐振器的s 和d 减小，其耦合性能必定增强。