江苏省前黄高级中学2008届高三调研数学试题

2008届全国百套高考数学模拟试题分类汇编02函数二、填空题1、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)三位同学在研究函数 f (x ) = x1 + | x |(x ∈R ) 时，分别给出下面三个结论：① 函数 f (x ) 的值域为 (－1,1)② 若x 1≠x 2，则一定有f (x 1)≠f (x 2)③ 若规定 f 1(x ) = f (x )，f n +1(x ) = f [ f n (x )]，则 f n (x ) = x1 + n | x | 对任意 n ∈N *恒成立. 你认为上述三个结论中正确的个数有 答案：3.2、(江苏省启东中学2008年高三综合测试一)已知函数()3x f x =的反函数是1()f x -且1(18)23a f a -=+则=______________答案：23、(江苏省启东中学高三综合测试二)给出下列图象其中可能为函数f (x )＝x 4＋ax 3＋bx 2＋cx ＋d (a ，b ，c ，d ∈R)的图象的是_____. 答案：①③4、(江苏省启东中学高三综合测试二)已知f (x )=a ｘ（ａ＞1），ｇ（ｘ）＝ｂｘ（ｂ＞1），当f (x 1)＝g (ｘ2)＝2时，有ｘ1＞ｘ2，则a,ｂ的大小关系是 . 答案：a ＜b5、(江苏省启东中学高三综合测试四)已知函数⎩⎨⎧≤>=)0(2)0(log )(3x x x x f x，则 )]91([f f = 答案：146、(江西省五校2008届高三开学联考)设{x }表示离x 最近的整数，即若x m <-21≤21+m (m ∈Z )，则{x } = m ．给出下列关于函数|}{|)(x x x f -=的四个命题： ①函数)(x f y =的定义域是R ，值域是[0，21]； ②函数)(x f y =的图像关于直线2kx =(k ∈Z )对称； ③函数)(x f y =是周期函数，最小正周期是1； ④函数)(x f y =是连续函数，但不可导．其中真命题是 __________ ． 答案：①②③④7、(四川省巴蜀联盟2008届高三年级第二次联考)已知函数y =[0,)+∞，则实数m 的取值范围是 答案：(0,1][9,)+∞8、(陕西长安二中2008届高三第一学期第二次月考)函数)1lg ()(2--=ax x x f 在区间),1(+∞上单调增函数，则a 的取值范围是________。

全国名校高考数学专题训练05平面向量(选择题)1、 (江苏省启东中学高三综合测试三)将抛物线y 2=4x 沿向量a 平移得到抛物线y 2-4y=4x, 则向量a 为A. (-1,2)B. (1, -2)C. (-4,2)D. (4, -2) 答案：A2、 (江苏省启东中学高三综合测试四)将直线/： y = 2x 按。

=(3, 0)平移得到直线〃，则 的方程为() A. y = 2x-3 B y = 2x +3 C. y = 2(.x - 3) D. y = 2(.x + 3)答案:C3、 (江苏省启东中学高三综合测试四)在AOAB 中，OA=a, OB =b, M 为OB 的中点，N 为4、 (安徽省皖南八校2008届高三第一次联考)已知向量a = (2,3). b = (-1,2),若ma+tib 与a-2b 共线，则竺等于()nA. ------- ；B. — ；C. — 2 ；D. 2 ；2 2答案：A5、 (江西省五校2008届高三开学联考)已知向量云，传|=1，对任意 垢R ，恒有修一 te \ ^\ a — e \,则K. a -Le B. e_L(。

一。

) C. Q J_(Q —e) D. (o + e)_L(。

一e) 答案：B6、 (江西省五校2008届高三开学联考)点0为AABC 内一点，且存在正数 九,％,%使4汤+人2商+ 4无 二6,设AAOB, AAOC 的面积分别为Si 、S 2,则S 】： S2 = A.入1：入2B.入2：入3C.入 3：入 2D. A. 2： X 1 答案：c7、 (四川省成都市新都一中高2008级一诊适应性测试)已知两个非零向量 —► — —► ——» —»—► 2 —* 2所的中点，ON,，/交于点只则AP - 1 2 ,( 1 2 , )2 1 , 2 1 , A. 一 a 一 bB. ——bC. —ci 一— bD. — — — b3 3 3 3333 3答案：B—>—>a^b,a + b = (-3,6),a-b = (-3,2),贝U Q -b =( )答案：c8、（四川省成都市一诊）在四边形ABCD中，是“四边形ABCD为梯形”的A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件答案：A AB = 2DC n 四边形ABCD为梯形，但反之不成立.选A9、（四川省乐山市2008届第一次调研考试）如图，半圆的直径AB=6, 0为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，贝|J（P4+PB）PC的最小值为( )A. ? ；B. 9；C. —? ；D. —9；答案：C10、（四川省乐山市2008届第一次调研考试）在平面直角坐标系中，分别是与*成轴正方向同向的单位向量，平面内三点A、B、C满足，AB=4i+3j, AC=ki-^j当A、B、C 三点构成直角三角形时，实数k的可能值的个数为（）A. 1 个；B. 2 个；C. 3 个；D. 4 个；答案：C11、（四川省成都市新都一中高2008级12月月考）若y=sz'〃（一§工一号）的图像按照向量a 平移后得到y=sin{-\ x）的图象，则。

江苏省常州市前黄实验学校高三数学理测试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 两条直线l1：y=kx+1+2k,l2：y=－x+2的交点在直线x－y=0的上方,则k的取值范围是( ）A．(－,) B．(－∞,－)∪(,+∞) C．(－∞,－)∪(,+∞) D．(－,)参考答案：C2. 已知命题，则为（）A．B．C．D．参考答案：C3. 在极坐标系中，圆的垂直于极轴的两条切线方程分别为（A）（B）（C）（D）参考答案：B4. f（x）=﹣+log2x的一个零点落在下列哪个区间( )A．（0，1）B．（1，2）C．（2，3）D．（3，4）参考答案：B【考点】函数零点的判定定理．【专题】计算题．【分析】根据函数的实根存在定理，要验证函数的零点的位置，只要求出函数在区间的两个端点上的函数值，得到结果．【解答】解：根据函数的实根存在定理得到f（1）?f（2）＜0．故选B．【点评】本题考查函数零点的判定定理，本题解题的关键是做出区间的两个端点的函数值，本题是一个基础题．5. 若过点的直线与圆x2+y2=4有公共点，则该直线的倾斜角的取值范围是（）A．B．C．D．参考答案：B【考点】直线与圆的位置关系．【分析】当过点的直线与圆x2+y2=4相切时，设斜率为k，由圆心到直线的距离等于半径求得k的范围，即可求得该直线的倾斜角的取值范围．【解答】解：当过点的直线与圆x2+y2=4相切时，设斜率为k，则此直线方程为y+2=k（x+2），即 kx﹣y+2k﹣2=0．由圆心到直线的距离等于半径可得=2，求得k=0或 k=，故直线的倾斜角的取值范围是[0，]，故选：B．【点评】本题主要考查直线和圆相切的性质，点到直线的距离公式的应用，属于基础题．6. 已知是方程的根，是方程的根，则（）A．2009 B．2010 C．2011D．2012参考答案：D方程为，方程为。

江苏省前黄高级中学2008届第一学期期末考试数学（理科）试卷命题人 孙东升 罗利平 审核 张国良 李学富说明：本试卷分第І卷（选择题）和第П卷（非选择题）两部分。

满分160分。

考试时间120分钟。

第І卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分。

1、已知甲、乙两个样本（样本容量一样大），若甲样本的方差是0.4，乙样本的方差是0.2, 那么比较甲、乙两个样本的波动大小的结果是 （ ） A ．甲样本的波动比乙大 B ．乙样本的波动比甲大 C ．甲、乙的波动一样大 D ．无法比较2、 “3x >”是“24x >”的 （ ）A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分也不必要条件3、已知向量()()8,3,,2,6,5m a n b ==，若//m n ，则a b +的值为 （ ）A ．0B ．52C ．8D ．2124、复数z 满足方程224z i z i ++-=，z 对应点的轨迹是 （ ）A ．一条直线B ．椭圆C ．一个圆D ．线段5、已知在平行六面体1111ABCD A BC D -中，14,3,5,90AB AD AA BAD ===∠=， 1160BAA DAA ∠=∠= ，则1AC 等于（ ）AB ．85C． D ．506、已知32()26f x x x m =-+（m 为常数），在[2,2]-上有最大值3，那么此函数在[2,2]-上的最小值为 （ ） A ．37- B ． 29- C ． 5- D ． 11-7、已知椭圆22ax +y 2=1（a>1）的两个焦点为F 1、F 2，P 为椭圆上一点，且∠F 1PF 2=60°，则|PF 1|·|PF 2|的值为 （ ） A ．1B ．31 C ．34 D ．32 8、函数322()f x x ax bx a =+++在1x =时有极值10，则a 的值为 （ ） A ．43a a ==-或 B ．4a = C ．43a a =-=或 D ．3a =-9、已知点F 1、F 2分别是双曲线2222by a x -=1的左、右焦点，过F 1且垂直于x 轴的直线与双曲线交于A 、B 两点，若△ABF 2为锐角三角形，则该双曲线的离心率e 的取值范围是 （ ） A ．（1，+∞）B ．（1，3）C ．（2－1，1+2）D ．（1，1+2）10、过抛物线x y =2的焦点F 的直线m 的倾斜角m ,4πθ≥交抛物线于A 、B 两点，且A 点在x轴上方，则|FA|的取值范围是（ ）A ．]221,41(+B ．)1,41[C ．]1,41(D ．),21(+∞第П卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分。

全国名校高考专题训练06不等式一、选择题1、(江苏省启东中学高三综合测试二)在R 上定义运算).1(:y x y x -=⊗⊗若不等式1)()(<+⊗-a x a x 对任意实数x 成立，则A.11<<-aB.20<<aC.2321<<-a D.2123<<-a 答案：C2、(江苏省启东中学高三综合测试二)已知a ，b ，c ，d 均为实数，有下列命题：0,0,0)2(;0,00)1(>->->>->->ad bc bda c ab b d dc ad bc ab 则若则，若其中正确命题的个数是则若,0,,0)3(>>->-ab bda c ad bcA. 0B. 1C. 2D. 3 答案：D3、(江苏省启东中学高三综合测试二) ab>ac 是b>c 的A.充分不必要条件B. 必要不充分条件C.充要条件D.即不充分也不必要条件 答案：D4、(江苏省启东中学高三综合测试三)当x>1时，不等式x+11-x ≥a 恒成立，则实数a 的取值范围是A ．(－∞,2]B ．[2,+∞)C ．[3,+∞)D ．(－∞,3]答案：D5、(江苏省启东中学高三综合测试四)不等式xx 1log 2-≥1的解集为 ( ) A ．(]1,-∞- B ．[)∞+-,1 C ．[)0,1- D ．(]()∞+-∞-,01, 答案：C6、(江西省五校2008届高三开学联考)已知正整数b a ,满足304＝＋b a ，使得ba 11+取最小值时，则实数对（),b a 是（ ）A ．(5，10）B ．（6，6）C ．（10，5）D ．（7，2）答案：A7、(江西省五校2008届高三开学联考)设2sin1sin 2sin 222n n na =++⋅⋅⋅+ , 则对任意正整数,()m n m n > , 都成立的是A ．||2n m m n a a ⋅-<B ．||2n m m n a a -->C ．1||2n m n a a -<D ．1||2n m n a a -> 答案：C12sin(1)sin(2)sin ||||222n m n n mn n ma a ++++-=++⋅⋅⋅+ 12sin(1)sin(2)sin ||||||222n n mn n m ++++≤++⋅⋅⋅+ 1112111111122||||||12222212n m n n m n m ++++-<++⋅⋅⋅+==--12n < . 故应选C . 8、(陕西长安二中2008届高三第一学期第二次月考)设1212121<⎪⎭⎫⎝⎛<⎪⎭⎫ ⎝⎛<ab，那么( )A.ab a b a a <<B.b a a a b a << C 。

江苏省前黄高级中学2012～2013学年第一学期期中统考高三数学模拟试题一（理科）一．填空题（本大题共14小题，每小题5分，计70分）1. 已知集合{}{}12,1A x x B x x =-=<≤≤,则)(B C A R =2. 若“2230x x -->”是“x a <”的必要不充分条件，则a 的最大值为3. 已知2)4tan(=+πx ，则x x2tan tan 的值为4. 若 △ABC 内接于以O 为圆心，1为半径的圆，且 3450OA OB OC ++=，则 OC AB ⋅的值为5. 已知实数y x ,满足线性约束条件⎪⎩⎪⎨⎧≤--≥-+≥+-0520402y x y x y x ，目标函数)(R a ax y z ∈-=，若z 取最大值时的唯一最优解是(1,3)，则实数a 的取值范围是 ．6. 已知二次函数2()41f x ax x c =-++的值域是[1,＋∞)，则1a ＋9c 的最小值是 ．7. 已知奇函数()f x 的图像关于直线2x =-对称，当[]0,2x ∈时，()2f x x =，则(9)f -＝ ； 8．已知等比数列{a n }的公比q ＝－12，S n 为其前n 项和，则S 4a 4＝ ．9． 在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知a ＝1，A ＝60°，c ＝33，则△ABC 的面积为 ． 10．已知函数,0()(2),0xe xf x k x k x ⎧≤=⎨-+>⎩是R 上的增函数，则实数k 的取值范围是 ．11. 在等差数列{}n a 中，52=a ，216=a ，记数列⎭⎬⎫⎩⎨⎧n a 1的前n 项和为n S ，若1512mS S nn ≤-+对+∈N n 恒成立，则正整数m 的最小值为12. 设等差数列{a n }的前n 项和为S n ，若存在正整数m ，n (m <n )，使得S m ＝S n ，则S m ＋n ＝0.类比上述结论，设正项等比数列{b n }的前n 项积为T n ，若存在正整数m ，n (m <n )，使得T m ＝T n ，则T m ＋n ＝________.13．如图，A ，B 是半径为1的圆O 上两点，且∠AOB ＝π3，若点C 是圆O 上任意一点，则→OA ▪→BC 的取值范围为 ．14. 设m N ∈，若函数()21010f x x m x m =---+存在整数零点，则m 的取值集合为 ．二.解答题（解答应写出文字说明、证明过程或演算步骤） 15．（本题满分14分）在ABC ∆中，A,B,C 的对边分别为a,b,c,且acosC,bcos B,ccos A 成等差数列。

2008年全国高考模拟精选试题2008届江苏省前黄高级中学高三期中试卷测试题 2019.91,如图，在注射器中加入少量Na2SO3晶体，并吸入少量浓硫酸（以不接触纸条为准）。

则下列有关说法正确的是A．蓝色石蕊试纸先变红后褪色B．品红试纸、沾有KMnO4溶液滤纸均褪色都能证明SO2的漂白性C．湿润淀粉KI试纸未变蓝说明SO2的氧化性弱于I2D．NaOH溶液可用于除去实验中多余的SO22,下列离子方程式正确的是A．碳酸氢钠溶液与足量氢氧化钡溶液混合：HCO3－＋Ba2＋＋OH－=BaCO3↓＋H2OB．亚硫酸氢铵和少量氢氧化钠溶液的反应：NH4＋＋OH－＝NH3↑＋H2O C．足量的溴化亚铁和少量的氯气反应：2Fe2＋＋4Br－＋3Cl2＝3Fe3＋＋2Br2＋6Cl－D．碳酸氢钙溶液中加入足量的氢氧化钠溶液：2HCO3－＋Ca2＋＋2OH－＝CO32-＋CaCO3↓＋2H2O3,钡在氧气中燃烧时得到一种钡的氧化物晶体, 结构如下图所示, 有关说法正确的是A．该晶体属于离子晶体 B．晶体的化学式为Ba2O2C．该晶体晶胞结构与CsCl相似 D．与每个Ba2+距离相等且最近的Ba2+共有12个4,将2.5g碳酸钠、碳酸氢钠和氢氧化钠的固体混合物完全溶解于水，制成稀溶液，然后向该溶液中逐滴加入1mol·L-1的盐酸，所加入盐酸的体积与产生CO2的体积（标准状况）关系如下图所示：（1）写出OA段所发生反应的离子方程式____ _______________________________。

（2）当加入35mL盐酸时，产生CO2的体积为___________mL（标准状况）。

（3）计算原混合物中NaOH的质量及碳酸钠的质量分数。

5,化学是一门以实验为基础的自然科学，化学实验在化学学习中具有极其重要的作用。

(1)下列关于实验的叙述正确的有 (填序号)。

①在气体发生装置上直接点燃一氧化碳气体时，必需要先检验一氧化碳气体的纯度。

一、填空题：
1．2．3．4．
5．6．7．8．
9．10．11．12．
13．14．
二、解答题：
15。(本题满分14分)在锐角△ABC中，角A、B、C的对边分别为a、b、c，且满足 .
（Ⅰ）求角B的大小；(7分)
（Ⅱ）设 ,试求 的取值范围. (7分)
16．(本题满分14分)已知函数 的定义域为 ，且同时满足：① ；② 恒成立；③若 ，则有 ．试求:
5．已知数列 对任意的 满足 ，且 ，那么 等于。
6． 。
7.在△ABC中，BC=1， ，当△ABC的面积等于 时， __。
8．已知 ，sin( )=－ sin 则cos =。
9．已知 ，则下列四个命题：① ；② ；③ ；④ 中为真命题的序号为。
10．已知 ，若关于x的方程 的取值范围是。
11．已知命题 与命题
（I） 的值；
（II）函数 的最值．
17．(本题满分16分) 已知数列 的各项均为正数，它的前n项和Sn满足 ，并且 成等比数列.
（I）求数列 的通项公式；
（II）设 为数列 的前n项和，求 .
18．(本题满分16分)定义在 上的函数 ，如果满足：对任意 ，存在常数 ，都有 成立，则称 是 上的有界函数，其中 称为函数 的上界.
16．解：(I) 在条件③中,令 ，得 ，即 ，·········2分
又 时， 恒成立， ． ················4分
（II）设 ，当 时，有 ················5分
，················7分
∴ ，
由 ， 得 ，················9分
故由条件②得, ，
当a1=2时， 不成立；舍去.······························9分

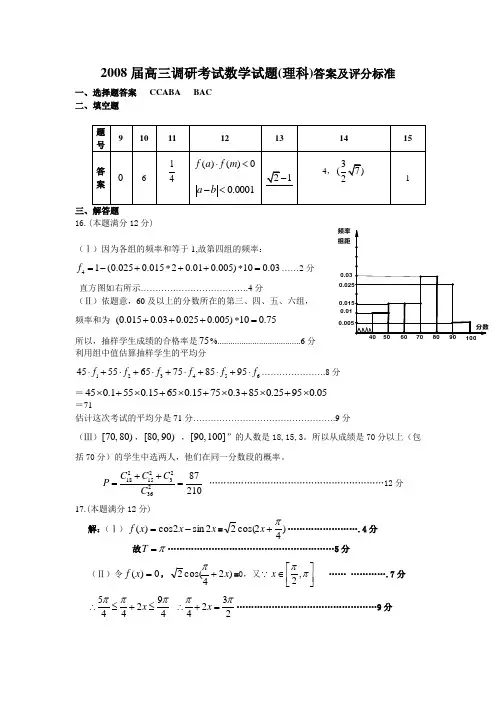
0.030.01频率组距2008届高三调研考试数学试题(理科)答案及评分标准一、选择题答案 CCABA BAC 二、填空题三、解答题16.(本题满分12分)（Ⅰ）因为各组的频率和等于1,故第四组的频率：41(0.0250.01520.010.005)100.03f =-+*++*=……2分直方图如右所示……………………………….4分（Ⅱ）依题意，60及以上的分数所在的第三、四、五、六组， 频率和为 (0.0150.030.0250.005)100.75+++*=所以，抽样学生成绩的合格率是75%......................................6分 利用组中值估算抽样学生的平均分123456455565758595f f f f f f ⋅+⋅+⋅+⋅+⋅+⋅………………….8分＝450.1550.15650.15750.3850.25950.05⨯+⨯+⨯+⨯+⨯+⨯ ＝71估计这次考试的平均分是71分………………………………………….9分（Ⅲ）[70,80)，[80,90) ，[90,100]”的人数是18,15,3。

所以从成绩是70分以上（包括70分）的学生中选两人，他们在同一分数段的概率。

22218153236C C C P C ++==87210 ……………………………………………………12分 17.(本题满分12分)解：（Ⅰ）x x x f 2sin 2cos )(-==)42cos(2π+x …………………….4分故π=T …………………………………………………5分 （Ⅱ）令0)(=x f ，)24cos(2x +π=0，又 ,2x ππ⎡⎤∈⎢⎥⎣⎦…… ………….7分 592444x πππ∴≤+≤ 3242x ππ∴+=…………………………………………9分故58x π=函数)(x f 的零点是58x π= ……………. 12分 18．(本题满分12分)证（Ⅰ）因为AB ⊥侧面11BB C C ，故1AB BC ⊥ 在1BC C 中，1111,2,3BC CC BB BCCπ===∠=由余弦定理有1BC == 故有 222111BC BC CC C B BC += ∴⊥而 BC AB B = 且,AB BC ⊂平面ABC∴1C B ABC ⊥平面（Ⅱ）由11,,,,EA EB AB EB ABAE A AB AE ABE ⊥⊥=⊂平面从而1B E ABE ⊥平面 且BE ABE ⊂平面 故1BE B E ⊥不妨设 CE x =，则12C E x =-，则221BE x x =+-又1123B C C π∠= 则2211B E x x =++在1Rt BEB 中有 22114x x x x +++-+= 从而1x =±（舍负）故E 为1CC 的中点时，1EA EB ⊥法二：以B 为原点1,,BC BC BA 为,,x y z 轴，设CE x =，则11(0,0,0),(1),(2B E x B A -- 由1EA EB ⊥得 10EA EB ⋅=即11(1,2)(,0)2211(1)(2)022x x x x x x x --=⎫--=⎪⎪⎭化简整理得 2320x x -+= 1x = 或 x = 当2x =时E 与1C 重合不满足题意EC 1B 1A 1CBA111当1x =时E 为1CC 的中点 故E 为1CC 的中点使1EA EB ⊥（Ⅲ）取1EB 的中点D ，1A E 的中点F ，1BB 的中点N ，1AB 的中点M 连DF 则11//DF A B ，连DN 则//DN BE ，连MN 则11//MN A B 连MF 则//MF BE ，且MNDF 为矩形，//MD AE 又1111,A B EB BE EB ⊥⊥ 故MDF ∠为所求二面角的平面角在Rt DFM 中，111(22DF A B BCE==∆为正三角形）111222MF BE CE === 1tan 2MDF ∴∠== 法二：由已知1111,EA EB B A EB ⊥⊥， 所以二面角11A EB A --的平面角θ的大小为向量11B A与EA 的夹角因为11B A BA ==1(2EA=-- 故 11112cos tan 3EA B A EA B A θθ⋅==⇒=⋅.19. (本题满分14分)解：(Ⅰ)依题意知，直线l 的方程为：1x =-．点R 是线段FP 的中点，且RQ ⊥FP ，∴RQ 是线段FP 的垂直平分线．…………………….2分∴PQ 是点Q 到直线l 的距离．∵点Q 在线段FP 的垂直平分线，∴PQ QF =．…………4分 故动点Q 的轨迹E 是以F 为焦点，l 为准线的抛物线，其方程为：24(0)y x x =>．…………………………………………………….7分(Ⅱ) 设()()B B A A y x B y x A ,,,，()()N N M M y x N y x M ,,，，直线AB 的方程为)1(-=x k y…………………………………………………….8分则⎪⎩⎪⎨⎧==)2(4)1(422BB AA x y x y（1）—（2）得k y y B A 4=+，即ky M 2=，……………………………………9分代入方程)1(-=x k y ，解得122+=kx M ．所以点Ｍ的坐标为222(1,)k k+．……………………………………10分同理可得：N 的坐标为2(21,2)k k +-．直线MN 的斜率为21kkx x y y k N M N M MN -=--=，方程为 )12(1222---=+k x kkk y ，整理得)3()1(2-=-x k k y ，………………12分 显然，不论k 为何值，(3,0)均满足方程，所以直线MN 恒过定点R (3,0)． (14)20. (本题满分14分) .解:11n na kn a +=+ 故2211a a k a ==+,．……………………………………1分 又因为()211111,,2n n n n n a a a a a a n N n +--+==+∈≥则3121a a a a =22a +,即3322221,21,2a aa k a k a a =+=+∴=又．………………………3分 所以212,1k a k k +==∴=, ……………………………………4 (2)11,n na n a +=+ 121121n n n n n a a a a a a a a ---=⋅⋅⋅⋅⋅⋅⋅⋅=()1...21!n n n ⋅-⋅⋅⋅= ……………………………………6 因为()()11!n n a x g x n -=-=1n nx -所以,当1x =时,()()()11123 (2)n n f x f n +==++++=.................................7 当1x ≠时,()21123...n f x x x nx -=++++. (1)()1x ⋅得()()23123...1n n xf x x x x n x nx -=++++-+……(2) ()()()()2112:11...n n x f x x x x nx ---=++++-=11nn x nx x--- ()()2111nn x nx f x xx -∴=--- ……………………………9 综上所述:2(1),12()1,1(1)1n nn n x f x x nx x x x+⎧=⎪⎪=⎨-⎪-≠⎪--⎩ ……………………………10 (3)因为()()()212221211212nnn n f n -∴=-=-+-- 又()333n g n=,易验证当1,2n =,3时不等式不成立; ……………………………11 假设()3n k k =≥,不等式成立,即()3121kkk >-+ 两边乘以3得:()()111331232131222k k k k k k k k k +++>-+=⋅++--+又因为()()()131222233223220k k k k k k k k k +--⋅+=--+=-+>所以()11113213122221k k k k k k k k k ++++>⋅++--+>⋅+即1n k =+时不等式成立.故不等式恒成立. (14)21. (本题满分14分) 解：(Ⅰ)()ln(1)(1),x f x a e a x =+-+(1)()(1)011x xx xae a e f x a e e-+-'∴=-+=<++恒成立,………………………… 所以函数()f x 在(,)-∞+∞上是单调减函数. …………………………4分(Ⅱ) 证明:据题意1,12233(()),(,()),(,())A x f x B x f x C x f x 且x 1<x 2<x 3,由(Ⅰ)知f (x 1)>f (x 2)>f (x 3), x 2=231x x +…………………………6分 12123232(,()()),(,()()BA x x f x f x BC x x f x f x ∴=--=--12321232()()[()()][()()]BA BC x x x x f x f x f x f x ∴⋅=--+--…………………8分123212320,0,()()0,()()0x x x x f x f x f x f x -<->->-<0,(,)2BA BC B ππ∴⋅<∴∠∈即⊿ABC 是钝角三角形……………………………………..9分(Ⅲ)假设⊿ABC 为等腰三角形，则只能是BA BC =即2132()()()f x f x f x =+3212132ln(1)2(1)[ln(1)(1)(1)()x x x a e a x a e e a x x ⇔+-+=++-++ 321222ln(1)2(1)[ln(1)(1)2(1)x x x a e a x a e e a x ⇔+-+=++-+3212ln(1)ln(1)(1)x x x e e e ⇔+=++31332122122(1)(1)(1)2x x x x x x x x x e e e e e e e e +⇔+=++⇔+=++3212x x x e e e ⇔=+ ① …………………………………………..12分而事实上, 3122xx x e e e +≥= ②由于31xxe e <,故(2)式等号不成立.这与(1)式矛盾. 所以⊿ABC 不可能为等腰三角形..14分222212123232()[()()]()[()()]x x f x f x x x f x f x -+-=-+-即：2221321232[()()][()()]x x x x f x f x f x f x -=-∴-=-。

江苏省前黄高级中学2009届高三数学调研考试理科试卷2008.10.23 命题人：李学富一、填空题：本大题共14小题，每小题6分，计84分.不需写出解答过程,请把答案写在答题纸的指定位置上. 1．已知全集{12345}U =，，，，，集合2{|320}A x x x =-+=，{|2}B x x a a A ==∈，， 则集合()U A B ð= 。

2．函数2(sin cos )y x x =+的最小正周期为 ． 3．在等比数列｛n a ｝中,若7944,1a a a ⋅==,则12a 的值是 .。

4．若1a = ,b = 且()a b a -⊥ ,则a 与b的夹角为 .。

5．已知数列{}n a 对任意的*p q ∈N ，满足p q p q a a a +=+，且26a =-，那么10a 等于 。

6．23sin 702cos 10-=-。

7. 在△ABC 中，BC=1，3π=∠B ，当△ABC 的面积等于3时，=C tan __ 。

8．已知βα,⎪⎭⎫ ⎝⎛∈ππ,43，sin(βα+)=－,53 sin ,13124=⎪⎭⎫ ⎝⎛-πβ则cos ⎪⎭⎫⎝⎛+4πα= 。

9．已知576*,)}({S S S n N n a d S n n >>∈且项和的前的等差数列是公差为，则下列四个命题：①0<d ；②011>S ；③012<S ；④013>S 中为真命题的序号为 。

10．已知kxx x x f ++-=22|1|)(，若关于x 的方程k x x x f 则上有两个解在,,)2,0(0)(21=的取值范围是 。

11．已知命题21:"[1,2],ln 0"2p x x x a ∀∈--≥与命题2:",2860"q x R x ax a ∃∈+--=都是真命题，则实数a 的取值范围是 ．12．如图1，设P 、Q 为△ABC 内的两点，且2155AP AB AC =+ ， AQ =23AB +14AC ,则△ABP的面积与△ABQ 的面积之比为 ．13．已知等比数列{}n a 中21a =，则其前3项的和3S 的取值范围是 。

OBxyC A江苏省前黄高级中学2012～2013学年第一学期期中统考高三数学模拟试题二（理科）一．填空题（本大题共14小题，每小题5分，计70分）1、若2{|228},{|log 1}xA xB x x =≤≤=>，则A B = ___ ___.2、存在实数x ，使得0342<+-b bx x 成立，则b 的取值范围是___ __.3、已知数列{}n a 为等差数列，且17134a a a π++=，则212tan()a a += ___ ___.4、已知向量(1)(1)a n b n ==-，，，，若2a b - 与b 垂直，则a = ___ ___. 5、△ABC 中，三内角A 、B 、C 所对边的长分别为a 、b 、c ，已知60B =︒，不等式2680x x -+->的解集为{|}x a x c <<，则b =___ ___. 6、已知函数()3sin()6f x x πω=-(0)ω>和()3cos(2)g x x ϕ=+的图象的对称中心完全相同，[0,]2x π∈，则()f x 的取值范围是___ ___.7、数列{}n a 的前n 项和是n S ，若数列{}n a 的各项按如下规则排列：11212312341, , , , , , , , , , , 23344455556，若10k S <，110k S +≥，则k a = 8、若函数()4ln f x x =，点(,)P x y 在曲线'()y f x =上运动，作PM x ⊥轴，垂足为M ，则△POM （O 为坐标原点）的周长的最小值为___ ___.9、已知函数()sin (0)f x x ωω=>在[0,1]内至少有5个最小值点,则正整数ω的最小值为__ ____. 10、如果实数⎪⎩⎪⎨⎧≥≥≤+0012,y x y x y x 满足，则31624--+x y x 的最大值为___ __.11、已知||2||0a b =≠ ，且关于x 的函数3211()||32f x x a x a bx =++⋅在R 上有极值，则a 与b 的夹角范围为____ __. 12、如果关于x 的方程213ax x +=在区间(0,)+∞上有且仅有一个解，那么实数a 的取值范围为_____ _． 13、当n 为正整数时，函数()N n 表示n 的最大奇因数,如(3)3,(10)5,N N ==⋅⋅⋅,设(1)(2)(3)(4)...(21)(2)nnn S N N N N N N =+++++-+,则n S = ． 14. 若已知0,,>c b a ，则bcab cb a 2222+++的最小值为 .二.解答题（解答应写出文字说明、证明过程或演算步骤）15. （本题满分14分）已知向量p ＝(sin x ，3cos x )，q ＝(cos x ，cos x )，定义函数()f x ＝p q ⋅(1)求()f x 的最小正周期T ；(2)若△ABC 的三边长,,a b c 成等比数列，且22c ac a bc +-=，求边a 所对角A 以及()f A 的大小.16．（本题满分14分）如图，在直角坐标系xOy 中，锐角ABC ∆内接于圆.122=+y x 已知BC 平行于x 轴，AB 所在直线方程为)0(>+=k m kx y ，记角A 、B 、C 所对的边分别是a 、b 、c .（1）若,23222bc a ac k -+=求B C A 2sin 2cos 2++的值； （2）若,2=k 记),23(),20(πβπβπαα<<=∠<<=∠xOB xOA 求)sin(βα+的值。

2008年全国高考模拟精选试题2008届江苏省前黄高级中学高三期中试卷 测试题 2019.91,下列离子方程式正确的是（ ） A ．石灰石溶于盐酸：CO + 2H +＝H 2O + CO 2↑B ．溴化亚铁溶液中通入足量的氯气：2Fe 2+ + 4Br -+ 3Cl 2＝2Fe 3+ +2 Br 2 + 6Cl －C ．在硫酸氢钾溶液中加入氢氧化钡溶液至pH ＝7： Ba 2＋+2OH －+2H ＋+SO ＝BaSO 4↓+2H 2OD ．Fe 3O 4溶于稀HNO 3中：Fe 3O 4 + 8H + ＝Fe 2+ + 2Fe 3+ + 4H 2O2,粗盐中含有可溶性杂质CaCl 2、MgCl 2和Na 2SO 4，若要得到纯净的NaCl 固体，有如下实验操作：①加入过量Ba(OH)2溶液 ②加入过量NaOH 溶液 ③加入过量BaCl 2溶液 ④加入过量Na 2CO 3溶液 ⑤加入过量盐酸 ⑥过滤 ⑦蒸发结晶。

正确的实验操作顺序是（ ） A ．③②④⑥⑤⑦ B ．③④②⑤⑦C ．②③④⑤⑥⑦D ．①④⑥⑤⑦3,目前一种新型抗酸剂能迅速改善和缓解胃酸过多的症状，它主要由碳酸镁、氢氧化镁和氢氧化铝组成(说明：Mg(OH)2在高温下分解为MgO)。

现按如下步骤测定药剂中三种主要成分的配比：①取药剂样品，研磨后，加入50mL3.6 mol ·L -1盐酸，正好完全反应并收集得到标准状况下224mL 气体②过滤，弃去其中不溶性物质(其余成分不参与反应)-23-24③取②中滤液，加入足量的NaOH溶液后，过滤、洗涤、灼烧，所得固体2.4g。

试求该药剂中三种主要成分的物质的量之比。

4, 标况下，在100 mL0.1mol·L－1某NaOH溶液中通入一定量CO2后，再向所得溶液中滴加某浓度的稀盐酸，滴加盐酸的体积与生成气体的情况如图所示。

(假设生成的CO2全部逸出)。

求：（1）该稀盐酸物质的量浓度c(HCl)。

08届高三数学上学期教学调研测试数 学2008.1一填空题（本大题共14小题海小题5分,共70分） 1•设集合 A 二{1,2,3},集合 B 二{2,3,4},则 A 「B =▲.2•函数y 二sinx-cosx 的最小正周期是 __________ ▲ _______ . 3•计算2 =▲ ______1+i4.函数y = x —a 的图象关于直线 x =3对称.则a = _______ ▲ 5•命题“ x • R, x 2 • 2x • 2乞0 ”的否定是 __________ ▲ _________ 6•右图为80辆汽车通过某一段公路时的时速的频率分布直方图 ，则时速在［50,60）的汽车大约有▲ 辆•7•把一根匀均匀木棒随机地按任意点拆成两段 ，则“其中一段的长度大于另一段长度的 2倍”的概率为▲ _________&函数y = x - 2sin x 在（0,二）上的单调递增区间为▲9•圆x 2 y 2 -6x-4y *12=0上一点到直线3x ・4y -2=0的距离的最小值为 厶 10. 一个几何体的三视图及其尺寸如右图所示 11. 一个算法的流程图如图所示，则输出 S 为主挖图 左视图12.已知向量 a,b,c 满足：a =1, b =2,c=a+b ，且c X a ,则a 与b 的夹角大小是1 2 —13 .已知 一 一=1（m0, n • 0）,当mn 取得最小值 时，直线 y = --,2x ・2与曲线m n3▲ cm（单位：cm ）,则该几何体的体积是 ▲14•在计算“ 1 2 2 3 - n(n 1)”时，某同学学到了如下一种方法: x x y y—+ 4=1的交点个数为 ______________ ▲ ____1先改写第 k 项：k(k 1) [k(k 1)(k2)—(k —1)k(k 1)],由此得311 2 (1 2 3-0 1 2),3 12 3 (2 3 4 -1 2 3),3 1n(n 1) [n(n 1)(n 2) _(n -1)n(n 1)].31相加，得 1 22 3 n(n 1) n(n 1)(n 2).类比上述方法，请你计算“ 1汉2域3十2汉3汉4+…宀n(n +1)(n+2) ”，其结果为▲ 二、解答题(本大题共 6小题，共90分，解答时应写出文字说明、证明过程或演算步骤) 15. (本小题满分14分)在 ABC 中，角A 、B 、C 的对边分别为a,b,c ，已知向量(n)若b x 3a,试判断 ABC 的形状。

④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三棱锥．
其中真命题的编号是_____________
答案：①④
32、正三角形 的边长为 ，将它沿高 翻折成直二面角 ，则三棱锥 的外接球的表面积为。
答案：5π
33、(湖北省随州市2008年高三五月模拟)三角形 的 边在平面 内， 在平面 外， 和 分别与面 成 的角，且面 与面 成 的二面角，那么 的值为。
其中真命题的编号是（写出所有真命题的编号）
答案：①③④
26、(河南省开封市2008届高三年级第一次质量检)已知直线二面角 大小为100°，过空间一点P作直线m，若m与 所成角都为40°，则这样的直线共有条数为。
答案：3
27、(河南省濮阳市2008年高三摸底考试)过球面上A，B，C三点的截面和球心的距离等于半径的一半，且AB＝BC＝CA＝3，则球的半径是_______________．
本题考查二面角、球的基本知识及其运用.
解析：设球心为O，根据几何知识可得∠AOB＝180°－120°＝60°
从而A、B两点的球面距离为5× ＝
答案：
7、(安徽省巢湖市2008届高三第二次教学质量检测)边长为 的等边三角形内任一点到三边距离之和为定值，这个定值等于_____；将这个结论推广到空间是：棱长为 的正四面体内任一点到各面距离之和等于.
2008届全国百套高考数学模拟试题分类汇编
07立体几何
二、填空题
1、(江苏省启东中学2008年高三综合测试一)与不共面的四点距离都相等的平面共有______个。
答案：7
2、(江苏省启东中学2008年高三综合测试一)已知线段AB在平面 外，AB两点到平面 的距离分别是1和3，则线段AB中点到平面 的距离是__________.

江苏省前黄高级中学数列多选题试题含答案一、数列多选题1．已知等比数列{}n a 的公比为q ，前n 项和0n S >，设2132n n n b a a ++=-，记{}n b 的前n 项和为n T ，则下列判断正确的是（ ） A ．若1q =，则n n T S = B ．若2q >，则n n T S > C ．若14q =-，则n n T S > D ．若34q =-，则n n T S > 【答案】BD 【分析】先求得q 的取值范围，根据q 的取值范围进行分类讨论，利用差比较法比较出n T 和n S 的大小关系. 【详解】由于{}n a 是等比数列，0n S >，所以110,0a S q =>≠， 当1q =时，10n S na =>，符合题意； 当1q ≠时，()1101n n a q S q-=>-，即101nq q ->-，上式等价于1010n q q ⎧->⎨->⎩①或1010n q q ⎧-<⎨-<⎩②.解②得1q >.解①，由于n 可能是奇数，也可能是偶数，所以()()1,00,1q ∈-.综上所述，q 的取值范围是()()1,00,-+∞.2213322n n n n b a a a q q ++⎛⎫=-=- ⎪⎝⎭，所以232n n T q q S ⎛⎫=- ⎪⎝⎭，所以()2311222n n n n T S S q q S q q ⎛⎫⎛⎫-=⋅--=⋅+⋅- ⎪ ⎪⎝⎭⎝⎭，而0n S >，且()()1,00,q ∈-⋃+∞.所以，当112q -<<-，或2q >时，0n n T S ->，即n n T S >，故BD 选项正确，C 选项错误. 当12(0)2q q -<<≠时，0n n T S -<，即n n T S <. 当12q =-或2q 时，0,n n n n T S T S -==，A 选项错误.综上所述，正确的选项为BD. 故选：BD 【点睛】本小题主要考查等比数列的前n 项和公式，考查差比较法比较大小，考查化归与转化的数学思想方法，考查分类讨论的数学思想方法，属于中档题.2．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一列数：1，1，2，3，5，…，其中从第三项起，每个数等于它前面两个数的和，后来人们把这样的一列数组成的数列{}n a 称为“斐波那契数列”，记n S 为数列{}n a 的前n 项和，则下列结论正确的是（ ） A ．68a = B ．954S =C ．135********a a a a a ++++=D ．22212201920202019a a a a a +++= 【答案】ACD 【分析】由题意可得数列{}n a 满足递推关系12211,1,(3)n n n a a a a a n --===+≥，依次判断四个选项，即可得正确答案. 【详解】对于A ，写出数列的前6项为1,1,2,3,5,8，故A 正确； 对于B ，911235813+21+3488S =++++++=，故B 错误；对于C ，由12a a =，342a a a =-，564a a a =-，……，201920202018a a a =-，可得：13520192426486202020182020a a a a a a a a a a a a a a +++⋅⋅⋅+=+-+-+-++-=，故C正确.对于D ，斐波那契数列总有21n n n a a a ++=+，则2121a a a =，()222312321a a a a a a a a =-=-，()233423423a a a a a a a a =-=-，……，()220182018201920172018201920172018a a a a a a a a =-=-，220192019202020192018a a a a a =-，可得22212201920202019201920202019a a a a a a a a+++==，故D 正确；故选：ACD. 【点睛】本题以“斐波那契数列”为背景，考查数列的递推关系及性质，考查方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意递推关系的灵活转换，属于中档题.3．设数列{}{},n n a b 的前n 项和分别为,n n S T ，1121,n n n S S S n++==，且212n n n n a b a a ++=，则下列结论正确的是（ ） A ．20202020a =B ．()12n n n S +=C ．()112n b n n =-+D ．1334n T n ≤-< 【答案】ABD 【分析】可由累乘法求得n S 的通项公式，再由()12n n n S +=得出n a n =，代入212n n n n a b a a ++=中可得()112n b n n =++.由裂项相消法求出n T ，利用数列的单调性证明1334n T n ≤-<.【详解】 由题意得，12n n S n S n++=， ∴当2n ≥时，121121112n n n n n S S S n n S S S S S n n ---+=⋅⋅⋅⋅⋅=⋅⋅⋅⋅--()13112n n +⋅=，且当1n =时也成立， ∴ ()12n n n S +=，易得n a n =，∴ 20202020a =，故,A B 正确； ∴ ()()()211111112222n n b n n n n n n +⎛⎫==+=+- ⎪+++⎝⎭，∴11111111111111112324351122212n T n n n n n n n n ⎛⎫⎛⎫=+-+-+-++-+-=++-- ⎪ ⎪-++++⎝⎭⎝⎭3111342124n n n n ⎛⎫=+-+<+ ⎪++⎝⎭， 又n T n -随着n 的增加而增加， ∴1113n T n T -≥-=，∴1334n T n ≤-<，C 错误，D 正确， 故选：ABD. 【点睛】使用裂项法求和时，要注意正负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消去的项，未被消去的项有前后对称的特点，实质上造成正负相消是此法的根源与目的．4．已知数列{}n a 满足11a =，()111n n na n a +-+=，*n N ∈，其前n 项和为n S ，则下列选项中正确的是（ ）A ．数列{}n a 是公差为2的等差数列B ．满足100n S <的n 的最大值是9C ．n S 除以4的余数只能为0或1D ．2n n S na = 【答案】ABC 【分析】根据题意对()111n n na n a +-+=变形得()1111111n n a a n n n n n n +=-+-=++，进而根据累加法求得()*21n a n n N =-∈，再依次讨论各选项即可得答案.【详解】解：因为()111n n na n a +-+=，故等式两边同除以()1n n +得：()1111111n n a a n n n n n n +=-+-=++， 所以()1111111n n a a n n n n n n -=-----=，()()12111221211n n a a n n n n n n --=------=--，，2111121122a a =-⨯-= 故根据累加法得：()11121n a a n nn =-≥-， 由于11a =，故()212n a n n =-≥，检验11a =满足， 故()*21n a n n N=-∈所以数列{}n a 是公差为2的等差数列，故A 选项正确； 由等差数列前n 项和公式得：()21212n n n S n +-==，故2100n n S =<，解得：10n <，故满足100n S <的n 的最大值是9，故B 选项正确； 对于C 选项，当*21,n k k N =-∈时，22441n n k S k ==-+，此时n S 除以4的余数只能为1；当*2,n k k N =∈时，224n n k S ==，此时n S 除以4的余数只能0，故C 选项正确；对于D 选项，222n S n =，()2212n n n n n n a =-=-，显然2n n S na ≠，故D 选项错误.故选：ABC 【点睛】本题考查累加法求通项公式，裂项求和法，等差数列的相关公式应用，考查运算求解能力，是中档题.本题解题的关键在于整理变形已知表达式得()1111111n n a a n n n n n n +=-+-=++，进而根据累加法求得通项公式.5．记数列{}n a 的前n 项和为n S ，*n ∈N ，下列四个命题中不正确的有（ ） A ．若0q ≠，且对于*212,n n n n a a a ++∀∈=N ，则数列{}n a 为等比数列B ．若nn S Aq B =+（非零常数q ，A ，B 满足1q ≠，0A B +=），则数列{}n a 为等比数列C ．若数列{}n a 为等比数列，则232,,,n n n n n S S S S S --仍为等比数列D ．设数列{}n a 是等比数列，若123a a a <<，则{}n a 为递增数列 【答案】AC 【分析】若0n a =，满足对于*212,n n n n a a a ++∀∈=N ，但数列{}n a 不是等比数列，可判断A ；利用n a 与n S 的关系，可求得数列{}n a 的通项公式，可判断B ；若数列{}n a 为等比数列，当公比1q =-，且n 为偶数时，此时232,,,n n n n n S S S S S --均为0，可判断C ；设数列{}n a 是等比数列，且公比为q ，若123a a a <<，即1211a a q a q <<，分类讨论10a >与10a <两种情况，可判断D ； 【详解】对于A ，若0n a =，满足对于*212,n n n n a a a ++∀∈=N ，但数列{}n a 不是等比数列，故A 错误；对于B ，当2n ≥时，()111(1)nn n n n n a S S Aq B AqB Aq q ---=-=+-+=-且1q ≠；当1n =时，0A B +=，则()111a S Aq B A q ==+=-符合上式，故数列{}n a 是首项为()1A q -公比为q 的等比数列，故B 正确；对于C ，若数列{}n a 为等比数列，当公比1q =-，且n 为偶数时，此时232,,,n n n n n S S S S S --均为0，不为等比数列，故C 错误；对于D ，设数列{}n a 是等比数列，且公比为q ，若123a a a <<，即1211a a q a q <<，若10a >，可得21q q <<，即1q >，则{}n a 为递增数列；若10a <，可得21q q >>，即01q <<，则{}n a 为递增数列；故D 正确；故选：AC 【点睛】结论点睛：本题考查等比数列通项公式及和的性质，等比数列和的性质：公比为1q ≠-的等比数列{}n a 的前n 项和为n S ，则232,,,n n n n n S S S S S --仍成等比数列，其公比为n q ；同理等差数列和的性质：公差为d 的等差数列{}n a 的前n 项和为n S ，数列232,,,m m m m m S S S S S --构成等差数列，公差为md ，考查学生的分析能力，属于中档题.6．已知数列{}n a ，下列结论正确的有（ ） A ．若12a ＝，11n n a a n +++＝，则20211a ＝.B ．若11132n n a a a ++＝，＝，则71457a =C ．若12nn S =3+，则数列{}n a 是等比数列 D ．若11212n n n a a a a ++＝，＝()*n N ∈，则15215a ＝ 【答案】AB 【分析】直接利用叠加法可判断选项A ，从而判断，利用构造新数列可求出B,D 中数列的通项公式，可判断，选项C 求出数列的前3项从而可判断. 【详解】选项A. 由11n n a a n +=++，即11n n a a n +-=+ 则()()()()19191818120207121a a a a a a a a a a =-+-+-++-+20191822211=+++++=故A 正确.选项B. 由132n n a a +=+，得()1311n n a a +=++，所以数列{}1n a +是以112a +=为首项，3为公比的等比数列.则1123n n a -+=⨯，即1231n n a -=⨯-，所以672311457a =⨯-=，故B 正确.选项C. 由12nn S =3+，可得当1n =时，11722a =+=3 当2n =时，得2211193622a S S ⎛⎫⎛⎫=-=+-+= ⎪ ⎪⎝⎭⎝⎭， 当3n =时，得332112791822a S S ⎛⎫⎛⎫=-=+-+= ⎪ ⎪⎝⎭⎝⎭， 显然2213a a a ≠，所以数列{}n a 不是等比数列，故C 错误. 选项D. 由122nn n a a a +=+，可得11112n n a a +-= 所以数列1n a ⎧⎫⎨⎬⎩⎭是以1为首项，12为公差的等差数列.所以()1111122n n n a +=+-=，则1511826a ==，即1518a =，故D 错误. 故选：AB 【点睛】关键点睛：本题考查利用递推关系求数列的通项公式，解答的关键是掌握求数列通项公式的常见方法，由叠加法可得()()()()19191818120207121a a a a a a a a a a =-+-+-++-+，利用构造新数列()1311n n a a +=++，11112n n a a +-=解决问题，属于中档题.7．（多选）设数列{}n a 是等差数列，公差为d ，n S 是其前n 项和，10a >且69S S =，则（ ） A ．0d > B ．80a =C ．7S 或8S 为n S 的最大值D ．56S S >【答案】BC 【分析】根据69S S =得到80a =，再根据10a >得到0d <，可得数列{}n a 是单调递减的等差数列，所以7S 或8S 为n S 的最大值，根据6560S S a -=>得65S S >，故BC 正确. 【详解】由69S S =得，960S S -=， 即7890a a a ++=，又7982a a a +=，830a ∴=，80a ∴=，∴B 正确；由8170a a d =+=，得17a d =-，又10a >，0d ∴<， ∴数列{}n a 是单调递减的等差数列，()()0,70,9n n a n N n a n N n **⎧>∈≤⎪∴⎨<∈≥⎪⎩， 7S ∴或8S 为n S 的最大值，∴A 错误，C 正确； 6560S S a -=>，65S S ∴>，所以D 错误.故选：BC ． 【点睛】关键点点睛：根据等差中项推出80a =，进而推出0d <是解题关键.8．已知等差数列{}n a 的公差0d ≠，前n 项和为n S ，且112n n n S a a +=⋅-，则（ ）A ．12d =B ．11a =C ．数列{}n a 中可以取出无穷多项构成等比数列D ．设(1)nn n b a =-⋅，数列{}n b 的前n 项和为n T ，则2n T n =【答案】AC 【分析】利用已知条件可得11212n n n S a a +++=-与已知条件两式相减，结合{}n a 是等差数列，可求d的值即可判断选项A ，令1n =即可求1a 的值，可判断选项B ，分别计算{}n a 的通项即可判断选项C ，分别讨论两种情况下21212n n b b -+=，即可求2n T 可判断选项D. 【详解】 因为112n n n S a a +=-，所以11212n n n S a a +++=-， 两式相减，得()11212n n n n n a a a a da ++++=-=， 因为0d ≠，所以21d =，12d =，故选项 A 正确； 当1n =时，1111122a a a ⎛⎫=+- ⎪⎝⎭，易解得11a =或112a =-，故选项B 不正确；由选项A 、B 可知，当112a =-，12d =时，()1111222n na n =-+-⨯=-，{}n a 可取遍所有正整数，所以可取出无穷多项成等比数列，同理当()()1111122n a n n =+-⨯=+时也可以取出无穷多项成等比数列，故选项C 正确； 当()112n a n =+时，()221212n n b a n ==+，()212112112n n b a n n --=-=--+=-， 因为21221212n n n n b b a a --+=-+=， 所以()()()212342122n n n n T b b b b b b -=++++++=， 当12n n a =-时，2212112n n b a n n ==⨯-=-，2121213122n n n b a n ---⎛⎫=-=--=-⎪⎝⎭， 所以22131122n n b b n n -+=-+-=， 此时()()()22212223212n n n n n nT b b b b b b ---=++++++=， 所以2n T n ≠，故选项D 不正确． 故选：AC. 【点睛】方法点睛：数列求和的方法（1）倒序相加法：如果一个数列{}n a 的前n 项中首末两端等距离的两项的和相等或等于同一个常数，那么求这个数列的前n 项和即可以用倒序相加法（2）错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前n 项和即可以用错位相减法来求；（3）裂项相消法：把数列的通项拆成两项之差，在求和时，中间的一些项可相互抵消，从而求得其和；（4）分组转化法：一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组转换法分别求和再相加减；（5）并项求和法：一个数列的前n 项和可以两两结合求解，则称之为并项求和，形如()()1nn a f n =-类型，可采用两项合并求解.二、平面向量多选题9．如图，A ､B 分别是射线OM ､ON 上的点，下列以O 为起点的向量中，终点落在阴影区域内的向量是（ ）A ．2OA OB + B ．1123OA OB +C ．3143OA OB + D ．3145OA OB + 【答案】AC 【分析】利用向量共线的条件可得：当点P 在直线AB 上时，等价于存在唯一的一对有序实数u ，v ，使得OP uOA vOB =+成立，且u +v =1.可以证明点P 位于阴影区域内等价于：OP uOA vOB =+，且u >0，v >0，u +v >1.据此即可判断出答案. 【详解】由向量共线的条件可得：当点P 在直线AB 上时，存在唯一的一对有序实数u ，v ，使得OP uOA vOB =+成立，且u +v =1.可以证明点P 位于阴影区域内等价于： OP uOA vOB =+，且u >0，v >0，u +v >1. 证明如下：如图所示，点P 是阴影区域内的任意一点，过点P 作PE //ON ，PF //OM ，分别交OM ，ON 于点E ，F ；PE 交AB 于点P ′，过点P ′作P ′F ′//OM 交ON 于点F ′，则存在唯一一对实数(x ，y )，(u ′，v ′)，使得OP xOE yOF u OA v OB ''''=+=+，且u ′+v ′=1，u ′，v ′唯一；同理存在唯一一对实数x ′，y ′使得OP x OE y OF uOA vOB =+=+''， 而x ′=x ，y ′>y ，∴u =u ′，v >v ′，∴u +v >u ′+v ′=1，对于A ，∵1+2>1，根据以上结论，∴点P 位于阴影区域内，故A 正确； 对于B ，因为11123+<，所以点P 不位于阴影区域内，故B 不正确； 对于C ，因为311314312+=>，所以点P 位于阴影区域内，故C 正确； 对于D ，因为311914520+=<，所以点P 不位于阴影区域内，故D 不正确； 故选：AC. 【点睛】关键点点睛：利用结论：①点P 在直线AB 上等价于存在唯一的一对有序实数u ，v ，使得OP uOA vOB =+成立，且u +v =1；②点P 位于阴影区域内等价于OP uOA vOB =+，且u >0，v >0，u +v >1求解是解题的关键.10．关于平面向量有下列四个命题，其中正确的命题为（ ）A ．若a b a c ⋅=⋅，则b c =；B ．已知(,3)a k =，(2,6)b =-，若//a b ，则1k =-；C ．非零向量a 和b ，满足||||||a b a b ==-，则a 与a b +的夹角为30º；D ．0||||||||a b a b a b a b ⎛⎫⎛⎫+⋅-= ⎪ ⎪⎝⎭⎝⎭【答案】BCD 【分析】通过举反例知A 不成立，由平行向量的坐标对应成比例知B 正确，由向量加减法的意义知，C 正确，通过化简计算得D 正确．【详解】对A ，当0a = 时，可得到A 不成立；对B ，//a b 时，有326k =-，1k ∴=-，故B 正确． 对C ，当||||||a b a b ==-时，a 、b 、a b -这三个向量平移后构成一个等边三角形， a b + 是这个等边三角形一条角平分线，故C 正确．对D ，22()()()()110||||||||||||a b a b a b a a a b b b +⋅-=-=-=，故D 正确． 故选：BCD ．【点睛】本题考查两个向量的数量积公式，两个向量加减法的几何意义，以及共线向量的坐标特点．属于基础题．。

江苏省前黄高级中学联考试卷2007/9命题人：汪静珍杨晓霞张一玮第一部分：听力（每小题1分，共20分）第一节：听下面5段对话，选择正确答案。

每段对话只听一遍。

1. What will the man give the woman?A. some moneyB. some thingsC. some help2. How long is the man‟s trip?A. one dayB. two daysC. three days3. What is the possible relationship between the two?A. a doctor and a patientB. a drug-store assistant and a customerC. aircrew and a passenger4. What is the woman‟s point to violence?A. She is for it.B. She is against it.C. She has nothing to say.5. Is the woman as confident in raising payment as the man?A. Yes.B. No.C. It is hard to see.第二节：听下面4段对话或独白，选择正确答案。

每段材料听两遍。

听第6段材料，回答第6至7题。

6. How much is a nickel?A. 5 centsB. 10 centsC. 15 cents7. How many dimes are there in a dollar?A. 20B. 10C. 5听第7段材料，回答第8至10题。

8. Where is the “Rumble in Bronx” on?A. At the Hospital CinemaB. At the Capital CinemaC. At the Riddle Cinema9. When is the fixed time to go?A. Wednesday eveningB. Thursday eveningC. Tuesday evening10. Where will they meet?A. At the number 223 bus stopB. At the number 332 bus stopC. At the number 323 bus stop听第8段材料，回答第11至13题。

08届高三第三次联考数学试卷08届高三第三次联考数学试卷本试卷分选择题和非选择题两部分,共4页,满分150,考试时间120分钟,答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的班级.姓名.座位号填写在答题卷的密封线内.所有题目必须用黑色字迹的钢笔或签字笔答在答题卷上,否则答案无效.一.选择题:(本大题共8小题,每小题5分,共40分．在每小题列出的四个选项中,选出符合题目要求的一项)．1.设集合,集合,那么下列结论正确的是: ( )A．B. C. D.2.设,则对任意实数,是的( )A. 充分必要条件B. 充分而不必要条件C. 必要而不充分条件D. 既不充分也不必要条件3.方程一定有解,则的取值范围是( )A．B．C．D．以上都不对4.如果执行下面的程序框图,那么输出的( )．Ａ．2450 Ｂ.2500 Ｃ．2550 Ｄ．26525.将函数的图象先向左平移,然后将所得图象上所有的点的横坐标变为原来的倍(纵坐标不变),则所得到的图象对应的函数解析式为( )．A．B．C．D．6.等差数列{an}.{bn}的前n项和分别为Sn.Tn,且,则使得为整数的正整数n的个数是()A．3 B．4 C．5 D．67.右图是一个正方体,它的展开图可能是下面四个展开图中的( )A．B．C．D．8. 如图,设P.Q为△ABC内的两点,且, ＝＋,则△ABP的面积与△ABQ的面积之比为( )A． B．C．D．第8题第Ⅱ卷(非选择题,共100分)二．填空题:(本大题共6小题,每小题5分,满分30分)．9.化简: ．10. 一物体在力F(_)=4_+2(力的单位:N)的作用下,沿着与力F相同的方向,从_=0处运动到_=5处(单位:m),则力F(_)所作的功___________11.已知点的坐标满足条件,点为坐标原点,那么的最大值等于_______,最小值等于____________.12.从装有个球(其中个白球,1个黑球)的口袋中取出个球,共有种取法.在这种取法中,可以分成两类:一类是取出的个球全部为白球,共有,即有等式:成立.试根据上述思想化简下列式子:..▲选做题:以下三小题请选做其中两题,若三小题都做的,只计前两小题得分.13.如图,在△ABC中,AB＝AC,∠C＝720,⊙O过A.B两点且与BC相切于点B,与AC交于点D,连结BD,若BC＝,则AC＝.14.极坐标方程化为直角坐标方程是,它表示的图形是 __15.设_,y均为正实数,且,则_y的最小值为三.解答题:(本大题共6小题,共80分,解答应写出文字说明,证明过程或演算步骤).16.(本小题满分12分)已知函数(Ⅰ)求函数的最小正周期和单调递减区间;(Ⅱ)在所给坐标系中画出函数在区间的图象(只作图不写过程).17.(本小题满分14分)将一颗骰子先后抛掷2次,观察向上的点数,问:(1)两数之和为8的概率;(2)两数之和是3的倍数的概率;(3)两数之积是6的倍数的概率.(4)以第一次向上点数为横坐标_,第二次向上的点数为纵坐标y的点(_,y)在圆_2+y2=25的内部的概率.18.(本小题满分14分)已知函数图像上的点处的切线方程为．(1)若函数在时有极值,求的表达式;19.(本题满分14分)如图,在矩形中,是的中点,以为折痕将向上折起,使为,且平面平面．(Ⅰ)求证:;(Ⅱ)求直线与平面所成角的正弦值．20. (本小题满分14分)如图,矩形的两条对角线相交于点,边所在直线的方程为, 点在边所在直线上．(I)求边所在直线的方程;(II)求矩形外接圆的方程;20题(III)若动圆过点,且与矩形的外接圆外切,求动圆的圆心的方程．21.(本小题满分14分)已知(m为常数,m_gt;0且)设是首项为4,公差为2的等差数列.(Ⅰ)求证:数列{an}是等比数列;(Ⅱ)若bn=an·,且数列{bn}的前n项和Sn,当时,求Sn;(Ⅲ)若cn=,问是否存在m,使得{cn}中每一项恒小于它后面的项?若存在,求出m 的范围;若不存在,说明理由.(2)函数在区间上单调递增,求实数的取值范围.参考答案一:选择题题号12345678答案代号CAACCBAB二．填空题: 9 . 2 10. 11. ,12 . 6013. 2 14.(或) , 两条直线15. 161.C; ,2.A; 显然为奇函数,且单调递增.于是若,则,有,即,从而有.反之,若,则,推出,即.故选A.3.A; 由 , 知 ;4.C; 05.C;6.B;, ;7.A 把握住4,6,8三个面有一个共同的顶点这一个特点8.B; 如下图,设,,则．由平行四边形法则,知NP∥AB,所以＝,同理可得．故,选B．9.2(略)10.60; 力F(_)所作的功为11. 从图中看出 ,所以选A12.;根据题中的信息,可以把左边的式子归纳为从个球(n个白球,k个黑球)中取出m个球,可分为:没有黑球,一个黑球,……,k个黑球等类,故有种取法.13.2; 由已知得, ,解得14.;两条直线;由 ,得 , ,,;两条直线15.16;由可化为_y =8+_+y,_,y均为正实数_y =8+_+y(当且仅当_=y等号成立)即_y-2-8可解得,即_y16故_y的最小值为16.三.解答题:16.(本小题满分12分)解:………………3分(Ⅰ)函数的最小正周期,………………5分令,∴函数的单调递减区间为…………7分(Ⅱ)---------------12分17.(本小题满分14分)解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件-----------1分(1)记〝两数之和为8〞为事件A,则事件A中含有5个基本事件,所以P(A)=;答:两数之和为6的概率为.--------------------------------------- 4分(2)记〝两数之和是3的倍数〞为事件B,则事件B中含有12个基本事件,所以P(B)=;答:两数之和是3的倍数的概率为.-------------------------------7分(2)记〝向上的两数之积是6的倍数〞为事件C,则事件C中含有其中的15个等可能基本事件,所以P(C)=,答:两数之积是6的倍数的概率为.-------------------------------10分(3)基本事件总数为36,点(_,y),在圆_2+y2=25的内部记为事件D,则D包含13个事件,所以P(D)=.答:点(_,y)在圆_2+y2=25的内部的概率.----------------------14分18.(本小题满分13分)解:, -----------------2分因为函数在处的切线斜率为-3,所以,即,------------------------3分又得.------------------------4分(1)函数在时有极值,所以,-------5分解得,------------------------------------------7分所以．------------------------------------8分(2)因为函数在区间上单调递增,所以导函数在区间上的值恒大于或等于零,------------------------------------10分则得,所以实数的取值范围为．----------------------------------13分19.(本小题满分13分)解(Ⅰ)在中,,在中,,∵,∴．---------------------------2分∵平面平面,且交线为,∴平面．∵平面,∴．------------------------------------5分(Ⅱ)设与相交于点,由(Ⅰ)知,∵,∴平面,∵平面,∴平面平面,且交线为,---------7分如图19-2,作,垂足为,则平面,连结,则是直线与平面所成的角．-------------------9分由平面几何的知识可知,∴．--------------11分在中,,在中,,可求得．∴．------------------------------------------------------------------------13分20.(本题满分14分)【解析】(I)因为边所在直线的方程为,且与垂直,所以直线的斜率为．又因为点在直线上,所以边所在直线的方程为．．-----------------3分(II)由解得点的坐标为,------------4分因为矩形两条对角线的交点为．所以为矩形外接圆的圆心．-----------------6分又．从而矩形外接圆的方程为．----------------------9分(III)因为动圆过点,所以是该圆的半径,又因为动圆与圆外切, 所以,即．------------------------11分故点的轨迹是以为焦点,实轴长为的双曲线的左支．因为实半轴长,半焦距．所以虚半轴长．从而动圆的圆心的轨迹方程为．-----------------14分21.(本小题满分14分)解:(Ⅰ)由题意即∴……………………2分∴∵m_gt;0且,∴m2为非零常数,∴数列{an}是以m4为首项,m2为公比的等比数列…………4分(Ⅱ)由题意,当∴①…………6分①式两端同乘以2,得②…………7分②－①并整理,得=-----------------------------------------------10分(Ⅲ)由题意要使对一切成立,即对一切成立,①当m_gt;1时, 成立;…………12分②当0_lt;m_lt;1时,∴对一切成立,只需,解得, 考虑到0_lt;m_lt;1, ∴0_lt;m_lt;综上,当0_lt;m_lt;或m_gt;1时,数列{cn }中每一项恒小于它后面的项. ----------14分。