德萨格定理在初等几何中的应用

笛沙格定理在初等数学中的简单应用1 序言17世纪法国数学家笛沙格，他是射影几何的奠基人，在射影几何方面的工作具有创造性成 就．他年轻时不仅做过工程师还做过建筑师，在学术研究方面他也不赞成为理论而搞理论，更注重于将理论应用于实际．但由于笛沙格当时的手稿写作手法晦涩难懂并且当时正值欧洲文艺复兴后，解析几何、微积分等学科的产生和发展，使得人们热衷于新兴领域，而传统数学几何学发展相对滞后，基于各种原因在很长一段时期内笛沙格的研究被人们所忽略，直到200多年后笛沙格的射影几何学术思想才引起人们的普遍重视，他的重要理论才得以被人们所认知．2 预备知识2.1 笛沙格定理内容及特例[1](P58-59)笛沙格定理两个三角形ABC 和'''C B A 中,若对应顶点的连线'AA ,'BB ,'CC 共点,则对应边的交点'','',''B A AB R A C CA Q C B BC P ⨯=⨯=⨯=共线.(图1) 笛沙格定理的逆定理设两个三角形中三对对应边的交点共线，则三对对应顶点的连线共点. 常见笛沙格定理的特殊情况 1 有一对对应点重合 见图2 2 有两对对应顶点重合 见图３(图2) (图3) 定理拓展在平面几何中适用笛沙格定理，拓展到空间几何学，他同样适用.如图（4）,（5）所示:(图4) (图5)2.2 笛沙格定理的证明 定理的证明有若干种方法，而且方法涉及面很广，在此选取较容易理解的两种方法和大家一起来分享.1 线性代方法证明[1](P59)2 应用梅涅劳定理证明 证明 （如图1）对于''C OB ∆及截线BCP1''''-=⋅⋅CO CC PC P B BB OB 对于''B OA ∆及截线BAR1''''-=⋅⋅BOBB RB R A AA OA对于''C OA ∆及截线ACQ1''''-=⋅⋅C C COQ A QC OA AA 三式相乘得1''''''-=⋅⋅QA QC RB R A PC P B 对于'''C B A ∆用梅涅劳定理可得PQR 三点共线.3 笛沙格定理的重要地位3.1 笛沙格定理在高等几何中的重要性笛沙格定理是《高等几何》中的重要定理，它是平面（二维）射影几何的重要基础之一，高等几何的许多定理都是以它为基础，他也是许多初等数学中定理和命题的理论依据,由此还可以推出一系列几何命题．而且定理在空间几何中也有部分的应用.3.2 高等几何与初等几何的联系高等几何不仅是对初等几何理论的提高，同时也是对初等几何的延伸与拓广。

关于点共线、线共点问题的多种证法学生姓名：贾娟 指导教师：杨慧摘要： 在初等几何中，我们常常会遇到点共线、线共点这方面的问题。

而射影几何的基本不变性是点线的结合性，因此点共线、线共点问题是射影几何的主要研究对象之一。

对于点共线、线共点问题的解决方法也有很多，本文则主要探讨的是利用射影几何方法与初等几何方法解决这类问题，通过比较发现具体问题用哪种方法更合适，以及解题时需要注意的问题。

关键词： 射影变换 德萨格定理 完全四点形 赛瓦定理 一维基本形的透视对应作为师范类院校的学生，将来若想成为一名合格的中学数学教师，就必须在学习解析几何的基础上再进一步学习高等几何。

而高等几何对中学数学教师几何基础的培养、解题观点的提高、思维方法的多样性等都起着重要的指导作用。

对于高等几何到来说，尤其是其中的射影几何，既包含了解析几何中主要研究图形性质的内容，也融合了欧氏几何中主要研究空间几何结构的内容。

因此，学习高等几何知识，不仅使我们开阔了几何学的视野，也让我们更好地理解、把握了初等几何的本质。

比如初等几何中点共线、线共点的问题，在中学数学教学中既是一个重点也是一个难点。

如果只是用初等几何方法去解决，有时会很复杂，相反若要用射影几何中的知识如完全四点形的调和性质、德萨格定理及其逆定理、一维基本形的透视对应性质等知识点来解决，会更简便。

这样也为我们提供了多种解决初等几何问题的研究方法。

用高等几何的观点指导初等几何的教学内容，进而不断地改进初等几何的教学方式，这样也有助于提高中学几何的教学质量。

1.主要定义及定理 一维基本形的透视对应：定义1如果一个点列与一个线束的元素之间建立了一一对应且对应元素是结合的，则这个对应叫做点列与线束之间的透视对应。

同理，如果两个点列与同一线束成透视对应，则这两个点列叫做透视点列；如果两个线束与同一点列成透视对应，则这两个线束叫透视线束。

由此可知，两个成透视对应的点列，其对应点之连线共点。

Desargues定理及其逆定理的应用一(Desargues定理及其逆定理的应用Desargues定理的内容从完整的角度讲,包括Desargues定理及其逆定理。

它是高等几何中最重要的定理之一,高等几何中许多定理及命题都以它为根据。

我们知道,在初等几何中有许多需要证明“点共线”或“线共点”的问题,这类问题用初等方法去证明往往较复杂,但用Desargues定理去证明却很容易。

因此,对于初等几何中的某些定理或命题而言,Desargues定理除可以给它们提供一种高等数学的证明方法外,还可以在用初等方法证明它们之前,起到先“验证”的作用。

1.1定理背景德莎格(Desargues),1591年2月21日生于法国里昂的一个教会会员家庭,一生主要在巴黎从事学术研究活动,晚年隐居老家里昂,1661年10月卒于里昂。

作为一个普通教会会员家庭的九个孩子之一的笛沙格,早年曾在其家庭所在地里昂接受基础教育,并在里昂主管区基督教会的教士税务局收过杂税。

他在那时,也曾写过如何教儿童唱歌的文章。

笛沙格青年时期还参过军,当过军官,同时担任过法国军事工程师和建筑师。

他在青壮年时期长期定居巴黎,并从1626年11月开始长期从事几何透视法的研究工作和学术活动。

他曾在巴黎免费给别人讲课,以鼓励世人钻研数学,给他的同行以深刻的印象。

他曾建议市政府建设大型机器以便将水源分流,使其在城市里得以充分利用。

笛沙格一来提高塞纳河水的水位,生中无论在数学领域还是在其他方面都有许多成就。

他关心如何改进艺术家、工程师和石匠的教育技巧与方法。

他在学术研究方面不赞成为理论而搞理论,更注重于将理论应用于实际。

笛沙格的学术活动与事业生涯主要在巴黎,他在那里结识了笛卡尔、梅森、费尔玛、帕斯卡等数学界名流。

笛沙格还经常参加由梅森发起与组织的梅森学会的定期学术讨论会,在数学思想方面受到当时的数学家及其数学潮流的诸多影响。

他在数学方面的初期工作是编辑了许多有用的数学知识及其数学定理,并将它们传授给渴望学习数学的人。

德沙格定理证明【实用版】目录1.引言：介绍德沙格定理2.德沙格定理的证明方法3.结论：总结德沙格定理的证明及其意义正文1.引言：德沙格定理是图论中的一个重要定理，它描述了在一个无向树中，存在一个点，该点到其他所有点的距离之和最小。

这个定理对于解决最短路径问题具有重要的意义。

本文将介绍德沙格定理的证明方法。

2.德沙格定理的证明方法：证明德沙格定理的一个有效方法是使用数学归纳法。

首先，我们需要明确几个概念。

- 无向树：一个无向树是一个连通的无向图，其中没有环。

- 度：一个节点的度是与其相连的边的数量。

- 度数为 2 的节点：一个度数为 2 的节点是与恰好两个其他节点相连的节点。

现在，我们开始证明德沙格定理。

（1）当无向树的度数为 2 时，显然存在一个点，该点到其他所有点的距离之和最小。

（2）假设在度数为 k 的无向树中，存在一个点，该点到其他所有点的距离之和最小。

我们需要证明，在度数为 k+1 的无向树中，也存在这样的点。

在度数为 k+1 的无向树中，新增的节点将与原有的 k 个节点相连。

这 k 个节点中，一定存在度数为 2 的节点。

否则，这 k 个节点的度数均为 3 或以上，那么它们的度数之和至少为 2k+3，与无向树度数为 k+1 矛盾。

因此，在度数为 k+1 的无向树中，新增节点与度数为 2 的节点相连。

根据归纳假设，度数为 2 的节点到其他所有点的距离之和最小。

所以，在新增节点与度数为 2 的节点相连的情况下，新增节点到其他所有点的距离之和最小。

综上所述，对于任意度数的无向树，都存在一个点，该点到其他所有点的距离之和最小。

这就是德沙格定理。

3.结论：德沙格定理证明了在一个无向树中，存在一个点，该点到其他所有点的距离之和最小。

天津师范大学本科毕业论文（设计）题目：笛沙格定理在初等几何中的应用学院：数学科学学院学生姓名：朱保军学号：09505011专业：数学与应用数学年级：2009级完成日期：2013年5月13日指导教师：武猛笛沙格定理在初等几何中的应用摘要：笛沙格定理是射影平面上的重要定理．许多定理以它为依据,利用它也可以证明初等几何中一些共线或共点问题．本文将抓住笛沙格定理的精髓：两个对应三点形、透视轴、透视中心．通过笛沙格定理的介绍,展示其图形之美．之后，着重介绍其在几何作图、共线问题、共点问题、动态问题中的应用．而且,还可轻易看出在初等几何中一些繁琐证明或难以得证的问题,通过笛沙格定理便一目了然．本文必将充分展示出笛沙格定理在初等几何中的重要作用,给初等几何中一些共线或共点问题带来简易之路．关键词：透视轴；透视中心；笛沙格定理；共点问题；共线问题The Application of the Desargues Theorem to ElementaryGeometryAbstract:The Desargues theorem is an important theorem on the projective plane. Many theorems are based on it, using it can also prove some collinear or concurrent problems in the elementary geometry. This thesis will grasp the Desargues theorem’s pith that there are two corresponding triangles, perspective axis, perspective centre. By the introduction of the Desargues theorem, showing the beauty of its picture. After that, we focus on the application to geometric drawing, collinear, concurrent, dynamic problems. Moreover, we can easily see some problems of complex proof or hard-to-get proof in the elementary geometry, but they will be clear at a glance by the Desargues theorem. This thesis is bound to fully show the important role of the Desargues theorem in the elementary geometry. What’s more, it will simplify the way to the some problems of the collinear or concurrent in the elementary geometry.Key words:perspective axis; perspective centre; Desargues theorem; concurrent; collinear目录1 引言．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(1)2 笛沙格定理相关概念及其定理．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(2) 2.1 基本概念．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(2) 2.2 笛沙格定理．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(3) 2.3 笛沙格逆定理．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(4) 2.4 推论．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(5)2.5 笛沙格构图．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(6)3 笛沙格定理在初等几何中的应用．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(7) 3.1 几何作图．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(7) 3.2 共线问题．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(7) 3.3 共点问题．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．.．．．．．．(9) 3.4 动态问题．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(10) 3.5 三维拓展．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(12) 参考文献．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．(14)1 引言吉拉德·笛沙格（Girard Desargues）,法国里昂, 1591年出生,1661年逝世于里昂,法国建筑师、工程师和著名数学家,射影几何学创始人之一．笛沙格在射影几何方面硕果累累,率先提出无穷远元素、调和点组、对合等新的概念,以及射影几何学中著名定理——笛沙格定理．在当时人才辈出的时代,笛沙格以其独创精神,脱颖而出,得到了费马、笛卡尔、帕斯卡等数学界名流的赏识．但是,那个年代盛行的是解析几何,笛沙格依然敢于开创射影几何的新领域,不畏众多人的反对和批评,坚持创作并大量出版．但作品并没有引起多大的关注,直到1845年,沙勒偶然发现了笛沙格著作的手抄本——《试论圆锥曲线和平面的相交所得结果的初稿》，才引起人们广泛关注,从那时起,这本书被列为近世几何的经典著作．笛沙格定理是射影几何学中四大定理之一．我们定义射影几何是研究图形的射影性质，即它们经过射影变换后，依然保持不变图形性质的几何学分支学科．射影几何起着一个特殊的作用，它能把几何学中的射影几何、仿射几何、欧式几何联系起来，使几何学成为一个完整系统．而且，射影几何有着广泛的应用，在绘画、摄影、航空、测量等方面尤为突出．射影几何的发展也是长期研究形成的，它最早开始于绘画．它的发展得助于欧洲文艺复兴时期透视学的快速发展．那时，学者在绘画和建筑方面非常痴迷，大力研究在平面上如何表现实物的图形．学者发现，一个画家将一个事物画在一张纸上，眼睛好比投影中心，把事物投影到纸上，然后再画出来．在画的过程中，有些元素的相对大小和位置关系，有的变了，有的没变．学者在这方面大力研究，因而渐渐的产生了新的概念和理论，最终，形成了射影几何学．在射影几何中，有一基本概念——交比，在射影变换下，交比具有不变形，利用这一性质可以推导出射影几何中许多其它重要性质．射影几何学真正成为一门学科是在十七世纪，笛沙格为射影几何学做出了杰出的贡献．人们以他的名字命名的笛沙格定理：“如果两个三点形对应顶点的连线交于一点，则对应边的交点在一直线上，反之也成立”，就是射影几何的基本定理．笛沙格定理的重要意义不仅在于它可以推出一系列射影几何命题，还在于它是平面射影几何的基础之一．许多定理以它为根据,利用它还可以证明初等几何中一些共点或共线问题,在解决初等几何问题具有独特之处．2 射影几何基本概念及定理2.1 基本概念定义 2.1 在平面内对于任何一组平行线引入唯一一点叫做无穷远点；一平面内一切无穷远点的集合组成一条直线叫做无穷远直线．我们可以看出在一组平行线交于无穷远点一点；一平面内所有直线都与无穷远直线有交点．定义 2.2 平面内不共线的三点与其每两点的连线所组成的图形叫做三点形；平,c 叫别为AB 图2-2定义2.4 共线三点12,,P P P 的单比表示为12PP P （）,定义1122()PP PP P P P=．其中1,PP2P P 是有向线段,称12,P P 为基点,P 为分点．那么，共线四点1234,,,PP P P 的交比1234(,)P P P P 等于两个单比123()PP P 与124()PP P 的比,即1231234124(,)PP P PP P P PP P =,其中12,P P 叫做基点偶,34,P P 叫做分点偶．如果1234(,)1PP P P =-,我们称4P 为123,,PP P 的第四调和点． 其中，此定义只是为了解释以下推论中的第四调和点，只需了解第四调和点即可． 定义 2.5 在射影平面里设有点，直线及其相互结合和顺序关系所组成的一个命O ,图2-3 情况（1） 三点形ABC 和A B C '''分别在两个不同的平面π和π'上(如图2-3)．因为AA BB O ''= ,所以,,,A B A B ''和O 共面,二直线AB 和A B ''必相交,交点N 在平面π和π'的交线上．同理,BC 与B C ''相交,AC 与A C ''相交,且相应的交点,L M 都在二平面π和π'的交线上．于是,,L M N 三点共线．情况（2） 三点形ABC 和A B C '''在同一平面π内（如图2-4）．通过O 作不在平面π内的直线d ,在直线d 上任取两点D 和D ',且不与O 点重合．因为AA DD O ''= ,所以我们可知,,,A A D D ''共面,且D A ''与DA 相交,我们记DA D A A ''''= ,同理我们可知, DB D B B ''''= ,DC D C C ''''= ．三点形A B C ''''''所在的平面与平面π不同（例如A ''不在π内）．由于三点形DBC 与D B C '''不同在一平面内,,,DD BB CC '''都通过点O ,且记BC即L 在''与平面M ,N 连线交于一点．由于三线性与三点形实际上是一种图形．则可得如下定理．定理2.3(笛沙格逆定理) 如果两个三点形对应边的交点在一直线上,则对应顶点的连线交于一点．笛沙格定理与其逆定理是对偶命题,由对偶原则知,笛沙格定理成立,则其逆定理也成立,这为笛沙格逆定理的证明起到了事半功倍之效．由笛沙格及其逆定理说明,若两三点形有透视中心,则必有透视轴．反之,若有透视轴则必有透视中心．其中,这样的两个三点形叫做透视三点形．我们必须指出，笛沙格定理的证明，要先证空间的情况,因当两个三点形在同一平面时,进行证明时要借助空间作图,否则是不能证明的．所以只就平面射影几何而言,笛沙格定理必须选作公理．笛沙格定理的证明还有很多种,可参考福建师大数学系陈圣德的证法[4]．本文用的是综合法,证明有点繁难,但这是几何证明题的基本方法,应当熟练掌握．同时,笛沙格定理与笛沙格逆定理都可以用代数法证明．P．,可得,P的''', 'A B C AB'' AA',DD,A A'的图2-52.5 笛沙格构图笛沙格定理构图一共包含十个点和十条直线（如图2-6）．3 笛沙格定理在初等几何中的应用3.1 几何作图例1 在一张纸上,设给定点P 与不通过P 的二直线a ,b ,不许求出a ,b 的交点而得到P 与a ,b 交点的连线．仅用直尺作图．作图 取不在,a b 上的一点Q （Q 与P 不同）,通过Q 作三直线,,r s t 与a 的交点顺次为123,,,A A A 与b 的交点顺次为123,,,B B B 连接1PA 交s 于H ,连接1PB 交s 于K ,连接33,,KB HA 并设33KB HA R = ,连接PR （如图3-1）．,即直线点形11A B P 和33A B R ,根据笛沙格逆定理即得．3.2 共线问题例2 证明三角形的垂心,重心,外心三点在一条直线上．证明 已知三角形ABC ,依据几何作图作出其垂心R ,重心S ,外心T ,其中,M N 分别为,BC AC 中点(如图3-2),下面证明三点,,R S T 共线．在三点形ABR 和MNT 中,根据几何作图性质可知,//AB MN ,//AR MT ,//BR NT ,即两个三点形ABR 和MNT 对应边的交点都为无穷远点,从而它们的交点都在无穷远直线上．根据笛沙格逆定理,两个三点形ABR和MNT对应顶点,,AM BN RT的连线交于一点S．即三点,,R S T共线．证毕．此题是,的中图3-3AD MN BC,即两个三点形的对应顶证明如图3-3,在三点形ACN和DBM中,////点共点(此点即为无穷远点)．我们根据笛沙格定理知它们对应顶点的交点为,,AC DB O AN DM Q CN BM P === 共线．此题在初等几何中应用的完美,这是1998年初中数学竞赛加试题中的第二题,现用笛沙格定理直接便可知,十分简单方便．一般情况下，共线问题也可转化为共点问题．如例3，证,,P Q O 三点共线，也就是证直线PO 通过直线,AN DM 的交点Q ．依然如图3-3．选取三点形PNM 和OAD ,它们对应边的交点,,////PN OA C PM OD B MN AD BC == (即MN 与AD 的交点在直Q ．即,连接//HN ,沙格逆定理,此两个三点形对应顶点,,FH LN GE 交于一点M ,即三点,,L M N 共线．证毕．此题中巧妙的选取了三点形FLG 和HNE ,使得对应边平行,此题类似与证明三角形的三中线共点,有异曲同工之妙．例5 设直线p 交三角形ABC 的三边,,AB BC CA 分别于,,,L M N ,AM BN R = ,,AM CL T BN CL S == 如图3-5,证明：,,AS BT CR 共点．证明 选取三点形ABC 和STR ,因为这两个三点形对应边的交点AB ST L = ，AC SR N = ，BC TR M = 在直线p 上,根据笛沙格逆定理,所以此两个三点形对应顶点AS ,,BT CR 共点．证毕．证沙．即6、例OW 上1211112R A ,2R B 分别交,OY OZ 于22,,P Q 依题作图,即证1122,,PQ PQ AB 三直线共点．从而，将此动态问题转化为三线共点问题．如图3-6．选取三点形111PQ R 和222P Q R ,其两个三点形的对应顶点显然交于一点O ,由笛沙格定理知,三点形111PQ R 和222P Q R 的对应边的交点1122,PQ PQ S = 1122,PR P R A = 1122Q R Q R B = 共线．即1122,,PQ PQ AB 三直线共点S ．证毕．T,X''2R证图3-7此外,此题也可选取三点形11X X P '和22X X P '',根据笛沙格逆定理即证．我们观察例6、例7,在初等几何中,解决此类问题较为复杂,但笛沙格定理的出现便化繁为简,通俗易懂．3.5 三维拓展之上,介绍的都是在射影平面上的笛沙格定理,即二维射影几何．此外,笛沙格定理在三维射影空间中也成立．,Q 另一X ,由,D =P R图3-8方法（二） 选取三点形PQA 和RST ,其对应边,,PQ RS X PA RT P ==QA ST Q = 的交点共线．由笛沙格逆定理知,三点形PQA 和RST 对应点的交点PR , ,QS AT 共点T ．即证．此题还可用三点形CAD 和XPR 、三点形ABD 和QXS 用笛沙格定理分别证明．由此可见，笛沙格定理在三维射影几何中仍然可用, 关键是找好对应三点形．综上所诉,在利用笛沙格定理或逆定理证明三线共点或三点共线问题时,关键是准确地找到两个对应三点形,而且要调整好对应顶点的顺序．以便达到证明的目的．共线问题和共点问题一般可以转化．在都适用时，一般共线问题用笛沙格定理，共点问题用笛沙格逆定理．当然，我们也要具体问题具体分析．此外,笛沙格定理在初等几何中的应用非常简单易懂实用,可以化简初等几何中繁琐的步骤，为几何的证明开辟了一条快捷之路．参考文献[1] 梅向明,刘增贤,王汇淳,等．高等几何[M]．北京:高等教育出版社, 2000：1-43．[2] 梁宗巨．数学家传略辞典[M]．山东：山东教育出版社 ,1989年：21-42．[3] 金福．笛沙格及其射影几何学奠基性工作[J]．自然辨证法通讯,2005,27（1）：79-85．[4] 陈圣德．笛沙格定理的几种证法及其应用[J]．中学数学，1981(1)：14-17．[5] 1998年初中数学竞赛．中等数学[J]．1998(3):32-33．[6] 郭李芢．几何画板轨迹功能在三维曲面绘制中的应用[J]．钦州学院学报, 2008, 23(6): 5-9．[7] 梅向明,刘增贤．高等几何学习指导与习题选解[M]．北京：高等教育出版社,2003:16-23．[8] 周纪安,聂子青,金家瑞,等．天津师范大学数学系[M]．天津：天津师范大学,1985:18．[9] 刘胜利．几何画板课件制作教程[M]．北京：科学出版社,2004：8-45．[10] 周兴和．高等几何[M]．北京：科学出版社,2007：53-60．[11] 钟集．高等几何[M]．北京：高等教育出版社,1983:24-28．[12] 刘增贤,门树慧．高等几何学导引[M]．北京：科学技术文献出版社，1987:83-88．[13] 朱德祥．高等几何［M］．北京：高等教育出版社,1987：60．[14] 王家烨，金福．射影几何创始人——笛沙格[J]．数学通报，1994(3):46．[15] 姜子英．试谈高等几何在初等几何中的应用[J]．阜阳师范学院学报，1988(1):77-83．。

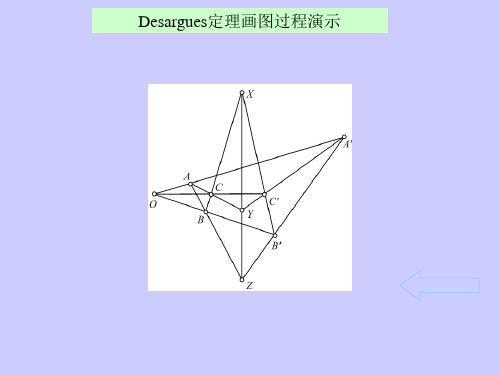
一．Desargues定理及其逆定理的应用Desargues定理的内容从完整的角度讲,包括Desargues定理及其逆定理。

它是高等几何中最重要的定理之一,高等几何中许多定理及命题都以它为根据。

我们知道,在初等几何中有许多需要证明“点共线”或“线共点”的问题,这类问题用初等方法去证明往往较复杂,但用Desargues定理去证明却很容易。

因此,对于初等几何中的某些定理或命题而言,Desargues定理除可以给它们提供一种高等数学的证明方法外,还可以在用初等方法证明它们之前,起到先“验证”的作用。

1.1定理背景德莎格(Desargues),1591年2月21日生于法国里昂的一个教会会员家庭,一生主要在巴黎从事学术研究活动,晚年隐居老家里昂,1661年10月卒于里昂。

作为一个普通教会会员家庭的九个孩子之一的笛沙格,早年曾在其家庭所在地里昂接受基础教育,并在里昂主管区基督教会的教士税务局收过杂税。

他在那时,也曾写过如何教儿童唱歌的文章。

笛沙格青年时期还参过军,当过军官,同时担任过法国军事工程师和建筑师。

他在青壮年时期长期定居巴黎,并从1626年11月开始长期从事几何透视法的研究工作和学术活动。

他曾在巴黎免费给别人讲课,以鼓励世人钻研数学,给他的同行以深刻的印象。

他曾建议市政府建设大型机器来提高塞纳河水的水位,以便将水源分流,使其在城市里得以充分利用。

笛沙格一生中无论在数学领域还是在其他方面都有许多成就。

他关心如何改进艺术家、工程师和石匠的教育技巧与方法。

他在学术研究方面不赞成为理论而搞理论,更注重于将理论应用于实际。

笛沙格的学术活动与事业生涯主要在巴黎,他在那里结识了笛卡尔、梅森、费尔玛、帕斯卡等数学界名流。

笛沙格还经常参加由梅森发起与组织的梅森学会的定期学术讨论会,在数学思想方面受到当时的数学家及其数学潮流的诸多影响。

他在数学方面的初期工作是编辑了许多有用的数学知识及其数学定理,并将它们传授给渴望学习数学的人。

德沙格定理证明引言德沙格定理是数学中的一个重要定理，它在代数几何中有着广泛的应用。

本文将对德沙格定理进行证明，并探讨其在代数几何中的重要性。

德沙格定理简介德沙格定理（Desargues’ theorem）是由法国数学家德沙格（Girard Desargues）在17世纪提出的。

它是射影几何学中的一个基本定理，描述了两个三角形在射影平面上透视时的一些性质。

定理表述德沙格定理可以用以下方式表述：定理：如果两个三角形的对应边的交点共线，那么这两个三角形是透视的。

证明为了证明德沙格定理，我们需要从几何的角度出发，使用一些基本的几何定理和性质。

准备工作首先，设有两个三角形ABC和A’B’C’，它们的对应边的交点分别为D、E和F。

我们需要证明D、E和F是共线的。

证明思路我们可以通过构造辅助线来证明D、E和F共线。

具体的证明思路如下：1.连接线段AD和A’D’，线段BE和B’E’，以及线段CF和C’F’。

2.根据线段AD和A’D’的交点D，线段BE和B’E’的交点E，以及线段CF和C’F’的交点F，我们可以构造一个新的三角形DEF。

3.根据对应边的交点共线的条件，我们知道三角形ABC和A’B’C’是透视的，因此线段AD、BE和CF是共线的。

4.同样地，根据对应边的交点共线的条件，我们可以得知线段A’D’、B’E’和C’F’也是共线的。

5.根据射影几何学中的一条基本定理，如果两个三角形的对应边的交点共线，那么这两个三角形是透视的。

因此，我们可以得出结论：三角形DEF是透视于三角形ABC和A’B’C’。

证明过程下面，我们将详细阐述证明过程。

证明步骤一：连接线段AD和A’D’根据准备工作中的设定，我们连接线段AD和A’D’。

证明步骤二：连接线段BE和B’E’同样地，我们连接线段BE和B’E’。

证明步骤三：连接线段CF和C’F’再次，我们连接线段CF和C’F’。

证明步骤四：构造新的三角形DEF根据线段AD和A’D’的交点D，线段BE和B’E’的交点E，以及线段CF和C’F’的交点F，我们可以构造一个新的三角形DEF。

用代数法证明德萨格定理正如古希腊数学家埃拉托斯特罗所说，“几何是由定义、公理和定理组成的，而它们唯一正确的证明方法便是通过数学证明来实现。

”在几何中，德萨格定理是一个非常重要的定理，它说明当一个三角形的三条边满足特定的因素时，它的内角一定有两个是相等的。

由于它的定义及其简单的形式，这个定理极其容易被接受，并且被证明是准确的。

然而，对于这个定理的数学证明却难以实现，有些人甚至认为它是数学证明的一个极大挑战。

因此，试图用代数法证明德萨格定理，可以算是一次充满挑战的尝试。

首先，要证明德萨格定理，需要明确三角形的定义。

根据定义，三角形是由三条边构成的，每条边对应一个内角，外角之和为1800。

接下来，我们需要列出定义和公理以便下面证明德萨格定理。

定义有：（1）三角形由三条边构成（2）每条边对应一个内角（3）外角之和为1800公理有：（1）当a，b，c为两条边之和大于第三边的三角形时，两个内角相等（2）当a，b，c同时都为正数时，a＞b＞c（3）a＋b＞c继续，我们将要证明德萨格定理，即当a，b，c为两条边之和大于第三边的三角形时，两个内角相等。

由定义可知，外角之和为1800，设三角形的三条边分别为a，b，c，则外角之和可表示为：α+β+γ=1800 。

假定a，b，c为两条边之和大于第三边的三角形，即a＋b＞c，据此，我们可以用代数计算出α，β，γ的值：α= arcsin（c/a）+ arcsin（c/b）β= arcsin（a/c）+ arcsin（b/c）γ= 1800-α-β由此，我们可以得出以下定理：当a＋b＞c时，α＝β＝γ/2，即两个内角相等。

最后，我们来证明此定理。

设α＝β＝θ，γ＝2θ，则有1800＝α＋β＋γ＝θ＋θ＋2θ＝4θ，即θ＝1800/4＝450，则α＝β＝450。

因此，当a＋b＞c时，α＝β＝γ/2，即两个内角相等，也就是说，用代数法证明德萨格定理的结论是正确的。

总结一下，本文讨论了如何用代数法证明德萨格定理。