大学物理学实验指导书_4

目录实验一电势差计测电动势 (1)实验二用电流场模拟静电场 (4)实验三电子束实验 (5)实验四霍耳效应法测量磁场 (8)实验四磁阻效应综合实验 (12)实验五分光计的使用和光栅测波长 (22)实验六光电效应 (28)实验七密立根油滴实验——电子电荷的测定 (31)实验七弗兰克—赫兹实验 (33)实验一 电势差计测电动势【实验原理】详见教材：《结构化大学物理实验》P.208−212。

仔细研读原理后回答以下问题： 问题1：能用电压表直接测出电池的电动势吗？为什么？问题2：箱式电势差计的工作原理图里有几个补偿回路？所测电动势的精度和什么有关？ 问题3：为什么温差电偶能用作温度计？补充内容：（一）本实验用高精度的1.0185V 稳压电源代替标准电池，虽然重复性较差，但比较环保，常温下也可以忽略温度对)(t E s 的影响。

（二）测量温差电动势时，因为实验装置的冷端为环境温度，误差较大，所以只测量t E ~关系，写出方程t E E θ+=0（三）UJ31电势差计中的一些参数1. 可测范围：0.001—170.00mV ；分两档，×1档为0.001—17.000mV （最小分度1μV ），×10档为0.01—170.00mV （最小分度10μV ）。

2. 准确度等级为0.05级，基本误差为(0.05%)x x U U U ∆=±+∆。

式中，x U 是被测电动势值（即示值），U ∆取值倍率为×10时，5=∆U μV ；倍率为×1时，5.0=∆U μV 。

【实验目的】（一）掌握电势差计的工作原理和结构特点。

（二）了解温差电偶的测温原理。

【实验内容】（一）电势差计的调节；（二）测温差电偶（铜-康铜）的温差电动势。

【实验器材】箱式电势差计，直流稳压工作电源，灵敏电流计，高精度1.0185V 标准电源，铜—康铜温差热电偶，加热装置。

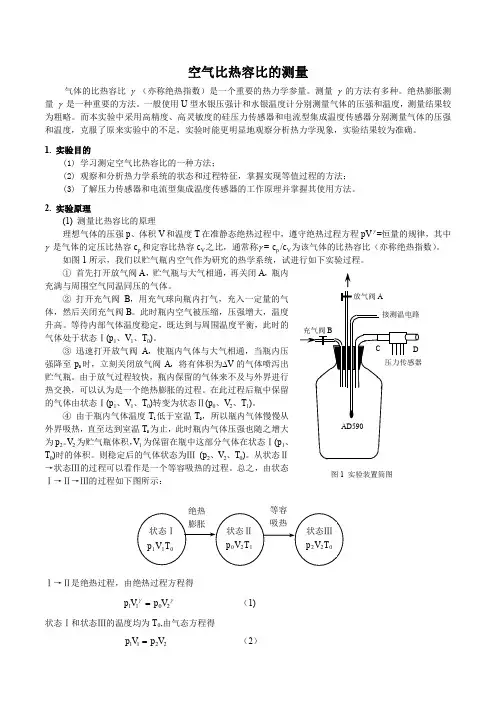
【实验步骤及操作】（一）电势差的调节图10-1 UJ31型电势差计面板图1. 面板中各旋钮、开关介绍2．把S R旋至标准的电动势值的位置。

大学物理实验指导书--9个项目 -实验一多普勒效应综合实验【实验目的】 1、测量超声接收器运动速度与接收频率之间的关系，验证多普勒效应。

2、由f－V关系直线的斜率求声速。

【实验原理】根据声波的多普勒效应公式，当声源与接收器之间有相对运动时，接收器接收到的频率f为：f = f0（u+V1cosα1）/（u�CV2cosα2）（1）式中f0为声源发射频率，u为声速，V1为接收器运动速率，α1为声源与接收器连线与接收器运动方向之间的夹角，V2为声源运动速率，α2为声源与接收器连线与声源运动方向之间的夹角。

若声源保持不动，运动物体上的接收器沿声源与接收器连线方向以速度V运动，则从（1）式可得接收器接收到的频率应为：f = f0（1+V/u）（2）当接收器向着声源运动时，V取正，反之取负。

若f0保持不变，以光电门测量物体的运动速度，并由仪器对接收器接收到的频率自动计数，根据（2）式，作f ―V关系图可直观验证多普勒效应，且由实验点作直线，其斜率应为 k=f0/u ，由此可计算出声速 u=f0/k 。

由（2）式可解出：V = u（f/f0 �C 1）（3）若已知声速u及声源频率f0 ，通过设置使仪器以某种时间间隔对接收器接收到的频率f采样计数，由微处理器按（3）式计算出接收器运动速度，由显示屏显示V－t关系图，或调阅有关测量数据，即可得出物体在运动过程中的速度变化情况，进而对物体运动状况及规律进行研究。

【仪器安装】图1 多普勒效应验证实验及测量小车水平运动安装示意如图1所示。

所有需固定的附件均安装在导轨上，并在两侧的安装槽上固定。

调节水平超声发射器的高度，使其与超声接收器（已固定在小车上）在同一个平面上，再调整红外接收器高度和方向，使其与红外发射器（已固定在小车上）在同一轴线上。

将组件电缆接入实验仪的对应接口上。

安装完毕后，让电磁铁吸住小车，给小车上的传感器充电，第一次充电时间约6～8秒，充满后(仪器面板充电灯变绿色)可以持续使用4～5分钟。

大学物理实验I指导书(2024秋季普通班)一、教学内容1. 实验原理：介绍测量物体质量、密度和比热容的基本原理，如阿基米德原理、密度的定义以及比热容的计算公式等。

2. 实验步骤：详细说明实验操作的顺序，包括仪器的安装、调节、测量和数据记录等。

3. 实验数据处理：教授如何对实验数据进行处理，包括误差分析、数据拟合等。

4. 实验安全：强调实验过程中需要注意的安全事项，如正确使用仪器、防止实验伤害等。

二、教学目标1. 使学生掌握测量物体质量、密度和比热容的基本原理和方法。

2. 培养学生的实验操作能力，提高实验技能。

3. 培养学生的数据处理能力，使他们能够对实验数据进行合理的分析和处理。

三、教学难点与重点1. 难点：实验数据的处理和分析，包括误差分析、数据拟合等。

2. 重点：实验原理的理解和实验操作的熟练掌握。

四、教具与学具准备1. 教具：计算机、投影仪、实验仪器（如天平、密度计、热源等）。

2. 学具：实验报告册、实验讲义、测量工具（如尺子、量筒等）。

五、教学过程1. 实践情景引入：通过一个简单的实验，使学生了解测量物体质量、密度和比热容的重要性。

2. 讲解实验原理：详细讲解测量物体质量、密度和比热容的基本原理。

3. 演示实验操作：教师演示实验操作步骤，学生跟随操作。

4. 数据处理与分析：教授如何对实验数据进行处理和分析，包括误差分析、数据拟合等。

5. 实验安全讲解：强调实验过程中需要注意的安全事项。

6. 随堂练习：学生进行实验操作，教师巡回指导。

7. 例题讲解：通过例题，使学生掌握实验数据的处理方法。

六、板书设计1. 实验原理：阿基米德原理、密度的定义、比热容的计算公式。

2. 实验步骤：仪器的安装、调节、测量和数据记录。

3. 数据处理：误差分析、数据拟合。

4. 实验安全：正确使用仪器、防止实验伤害。

七、作业设计1. 题目：测量物体质量、密度和比热容的实验报告。

答案：详见实验报告。

2. 题目：根据实验数据，进行误差分析和数据拟合。

课程名称：大学物理实验授课对象：大学物理专业学生教学目标：1. 理解实验的基本原理和方法，掌握实验的基本操作技能。

2. 培养学生的观察能力、分析问题和解决问题的能力。

3. 增强学生的科学素养和实验技能，为今后的科研工作打下基础。

教学重点：1. 实验原理的理解和掌握。

2. 实验操作技能的培养。

3. 实验数据的处理和分析。

教学难点：1. 复杂实验原理的理解。

2. 实验误差的分析和处理。

教学过程：一、导入1. 介绍实验的目的和意义。

2. 强调实验操作规范和安全注意事项。

二、实验原理讲解1. 详细讲解本次实验的原理和操作步骤。

2. 分析实验中可能出现的误差和影响因素。

三、实验操作示范1. 教师现场演示实验操作，包括仪器的组装、调整和操作方法。

2. 强调操作中的关键步骤和注意事项。

四、学生分组实验1. 学生分组进行实验，每组由一名组长负责。

2. 组长组织组员按照实验步骤进行操作，教师巡回指导。

五、实验数据处理与分析1. 教师讲解实验数据的记录和处理方法。

2. 学生对实验数据进行整理和分析，得出实验结果。

六、实验报告撰写1. 教师讲解实验报告的撰写格式和内容。

2. 学生根据实验结果撰写实验报告。

七、总结与讨论1. 教师总结本次实验的收获和不足。

2. 学生讨论实验过程中遇到的问题和解决方法。

教学资源：1. 实验指导书2. 实验原理课件3. 实验数据记录表4. 实验报告模板教学评价：1. 实验操作技能：考察学生在实验过程中的操作规范和熟练程度。

2. 实验数据处理与分析：考察学生对实验数据的处理能力和分析能力。

3. 实验报告：考察学生撰写实验报告的能力。

课后作业：1. 复习本次实验的原理和操作步骤。

2. 完成实验报告的撰写。

教学时间安排：1. 导入：5分钟2. 实验原理讲解：10分钟3. 实验操作示范：15分钟4. 学生分组实验：60分钟5. 实验数据处理与分析：15分钟6. 实验报告撰写：15分钟7. 总结与讨论：10分钟教学总结：本次大学物理实验课程旨在让学生掌握实验的基本原理和操作技能，提高学生的科学素养和实验能力。

大学物理实验指导书(电子版)上海海运学院2010.05目录绪论┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 3 实验数据的处理方法┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 7实验一.长度的测量┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅9实验二.测量钢丝杨氏模量┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅11实验三.扭摆法测定物体转动惯量┅┅┅┅┅┅┅┅┅┅┅┅┅13实验四.空气比热容比测定实验┅┅┅┅┅┅┅┅┅┅┅┅┅┅17实验五.线膨胀系数测定┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 18实验六.常用电学仪器的使用┅┅┅┅┅┅┅┅┅┅┅┅┅┅- 19实验七.惠斯登电桥测电阻┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 22实验八.电位差计测电动势┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 24实验九.电表改装┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅26实验十.示波器的使用┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅28实验十一.等厚干涉的应用┅┅┅┅┅┅┅┅┅┅┅┅┅┅ 31实验十二.用光栅测定光波的波长┅┅┅┅┅┅┅┅┅┅┅┅┅┅33实验十三.旋转液体物体特性测量┅┅┅┅┅┅┅┅┅┅┅┅┅┅34实验十四.波尔共振┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅36实验十五.用梁的弯曲测量材料的杨氏模量┅┅┅┅┅┅┅┅┅┅38实验十六.仿真实验—偏振光的研究┅┅┅┅┅┅┅┅┅┅┅┅┅39实验十七.光纤传输技术┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅42实验十八.激光全息照相┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅44实验十九.迈克尔逊干涉仪的应用┅┅┅┅┅┅┅┅┅┅┅┅┅┅46实验二十.光拍法测量光速┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅49实验二十一.光电效应┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅52实验二十二.霍尔效应及其应用┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅55实验二十三.荷质比实验┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅58实验二十四.金属电子逸出功实验┅┅┅┅┅┅┅┅┅┅┅┅┅┅62实验二十五.声速测量┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅66实验二十六.夫兰克赫兹实验┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅69实验二十七.密立根油滴实验┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅73实验二十八.多量程直流电表的设计┅┅┅┅┅┅┅┅┅┅┅┅┅77绪论早在五十年代，我国物学家钱三强就指出：今天的科学技术发展可以概括为“科学技术化和技术的科学化”，也就是说：科学和技术关系越来越密切，科学与技术相互渗透。

第4章 分离变量法物理学、力学和工程技术等方面的许多问题都可归结为偏微分方程的定解问题，上一章我们已初步看到怎样把具体的物理问题表达为定解问题.下面一个重要任务是怎样去解决这些定解问题，也就是说在已经列出的方程与定解条件之后，怎样去求既满足方程又满足定解条件的解.从微积分学得知，在计算诸如多元函数的微分及重积分时总是把它们转化为单元函数的相应问题来解决.与此类似，求解偏微分方程的定解问题也是要设法把它们转化为常微分方程问题，分离变量法就是常用的一种转化手法.本章我们将通过实例来说明分离变量法的步骤和实质.在4.2我们讨论了如何处理第三类齐次边界条件（当然也包括第二类边界条件）.在4.3说明如何在极坐标系下使用分离变量法.在4.4及4.5我们讨论了如何处理非齐次方程及非齐次边界条件的问题，本章的最后还安排了两个较为综合性的例子作为总结.4.1 有界弦的自由振动为了使读者了解什么是分离变量法以及使用分离变量法应该具备什么条件，我们选取两端固定的弦的自由振动问题为例，通过具体地求解逐步回答这些问题.根据第3章所得的结论，讨论两端固定的弦的自由振动，就归结为求解下列定解问题22222000,0,0; (4.1)0,0;(4.2)(),().(4.3)x x l t t uu a x l t t x u u u u x x t ϕψ====⎧∂∂⎪=<<>∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩这个定解问题的特点是：偏微分方程是线性齐次的，边界条件也是齐次的，求解这样的问题，可以运用叠加原理.我们知道.在求解常系数线性齐次常微分方程的初值问题时，是先求出足够多个特解（它们能构成通解），再利用叠加原理作这些特解的线性组合，使满足初始条件.这就启发我们，要解问题(4.1),(4.2),(4.3)，先寻求齐次方程（4.1)的满足齐次边界条件(4.2)的足够多个具有简单形式（变量被分离的形式）的特解，再利用它们作线性组合使满足初始条件(4.3).现在我们试求方程(4.1)的变量分离形式(,)()()u x t X x T t =的非零解，并要求它满足齐次边界条件(4.2),式中(),()X x T t 分别表示仅与x 有关及仅与t 有关的待定函数. 由(,)()()u x t X x T t =得2222''()(),()''(),u uX x T t X x T t x t∂∂==∂∂代入方程(4.1)得2()()()()X x T t a X x T t ''''=或2()()()()X x T t X x a T t ''''=这个式子左端仅是x 的函数，右端仅是t 的函数，一般情况下二者不可能相等，只有当它们均为常数时才能相等.令此常数为λ，则有2()()()()X x T t X x a T t λ''''==. 这样我们得到两个常微分方程：2()()0,T t a T t λ''-= （4.4）()()0.X x X x λ''-= （4.5）再利用边界条件(4.2)，由于(,)()()u x t X x T t =)，故有(0)()0,()()0.X T t X l T t ==但()0T t ≠,因为如果()0T t ≡，则(,)0u x t ≡，这种解显然不是我们所要求的，所以(0)0,()0.X X l == （4.6）因此，要求方程（4.1）满足条件(4.2)的分离变量形式的解，就先要从方程''()()0,(0)()0X x X x X X l λ-=⎧⎨==⎩中解出()X x .现在我们就来求非零解()X x ，但要求出()X x 并不是一个简单的问题，因为方程(4.5)中含有一个待定常数λ，所以我们的任务既要确定λ取何值时方程(4.5)才有满足条件(4.6)的非零解，又要求出这个非零数()X x .这种常微分方程问题称为固有值问题，λ称为特征值（固有值，本征值），函数()X x 称为特征函数（固有函数，本征函数）.下面根据第1章所介绍的方法，我们对λ分三种情况来讨论.1°λ＞0，此时方程(4.5)的通解为().X x Be =+-由条件(4.6)得0A B +=，0.Be +=解出,A B 得0A B ==，即()0X x ≡，不符合非零解的要求，因此λ不能大于零.2°设λ=0，此时方程(4.5)的通解为()X x Ax B =+，由条件(4.6)还是得0A B ==，所以λ也不能等于零.3°设λ＜0，并令ββλ,2-=为非零实数.此时方程(4.5)的通解为()cos sin ,X x A x B x ββ=+由条件(4.6)得0,A = Bsin 0.l β=由于B 不能为零（否则()0X x ≡），所以sin 0,l β=即),,3,2,1(. ==n ln πβ（n 为负整数可以不必考虑，因为例如21,sin n B x l π-=-实际上还是2sin B x lπ'的形式）从而222,n lπλ=- （4.7）这样，我们就求出了一系列固有值及相应的固有函数：222.(1,2,3,),n n n lπλ=-=()sin(1,2,3,),n n n X x B x n lπ== （4.8）限定了λ的值后，现在再来求函数()T t ，以(4.7)式中的λ值代入方程(4.4)中得2222()()0,n a n T t T t lπ''+= 显然，其通解为''()cossin (1,2,3,).n n n n at n at T t C D n l lππ=+= （4.9）于是由(4.8)，（4.9）得到满足方程(4.1)及边界条件(4.2)的一组变量被分离的特解(,)cos sin sin(1,2,3,),n n n n at n at n x u x t C D n l l l πππ⎛⎫=+= ⎪⎝⎭(4.10)其中,n n n n n n C B C D B D ''==是任意常数，至此，我们的第一步工作已经完成了，求出了既满足方程(4.1)又满足边界条件(4.2)的无穷多个特解.为了求原定解问题的解，还需要满足条件(4.3).由(4.10)式所确定的一组函数虽然已经满足方程(4.1)及条件(4.2)，但不一定满足初始条件(4.3).为了求出原问题的解，首先我们将（4.10）中所有函数(,)n u x t 叠加起来1(,)(,)n n u x t u x t ∞==∑1c o s s i n s i n ,n nn n a n a n C t D x l l lπππ∞=⎛⎫=+ ⎪⎝⎭∑ （4.11） 如果(4.11)右端的无穷级数是收敛的，而且关于,x t 都能逐项微分两次，则它的和(,)u x t 也满足方程(4.1)和条件（4.2)（参考习题三第6题）.现在我们要适当选择,n n C D ，使函数(,)u x t 也满足初始条件（4.3），为此必须有01(,)(,0)sin(),n t n n u x t u x C x x lπϕ∞=====∑ 10sin (),n n t u n a n D x x t l lππψ∞==∂==∂∑ 因为(),()x x ϕψ是定义在[0,]l 上的函数，所在只要选取n C 为()x ϕ的傅氏正弦级数展开式的系数，n n aD lπ为()x ψ的傅氏正弦级数展开式的系数，也就是 002()sin ,2()sin .l n l nn C x xdx l ln D x xdx n a l πϕπψπ⎧=⎪⎪⎨⎪=⎪⎩⎰⎰ （4.12） 初始条件(4.3)就能满足，以(4.12)所确定的,n n C D 代入(4.11)式，即得原定解解问题的解.当然，如上所述，要使(4.11)式所确定的函数u(x,t)确定是问题(4.1)，(4.2)，(2.3)的解，除了其中的系数,n n C D 必须由(4.12)确定以外，还要求只要对函数()x ϕ及()x ψ加一些条件就能满足，可以证明（参阅复旦大学数学系编《数学物理方程》第二章§1），如果()x ϕ三次连续可微，)(x ψ二次连续可微，且(0)()(0)()(0)()0l l l ϕϕϕϕψψ''''======，则问题(4.1)，(4.2)，（4.3)的解存在.并且这个解可以用(4.11)给出，其中,n n C D 由（4.12）式确定*).从上面的运算过程可以看出，用分离变量法求解定解问题的关键步骤是确定固有函数与运用叠加原理，这些运算之所以能够进行，就是因为偏微分方程与边界条件都是齐次的，这一点希望读者一定要注意.例1 设有一根长为10个单位的弦，两端固定，初速为零，初位移为1000)10()(x x x -=ϕ，求弦作微小横向振动时的位移.解 设位移函数为(,)u x t ，它是下列定解解问题2222201000,010,0;0,0;(10),01000x x l t uu a x t t x u u x x u u t ====⎧∂∂⎪=<<>∂∂⎪⎪==⎨⎪-∂⎪==⎪∂⎩的解，这时10l =，并给定210000a =（这个数字与弦的材料、张力有关）.显然，这个问题的傅氏级数形式解可由(4.11)给出，其系数按（4.12）式为10033330,1(10)sin 5000102(1cos )50,4,5n n D n C x x xdx n n n n n ππππ==-=-⎧⎪=⎨⎪⎩⎰当为偶数 当为奇数 因此，所求的解为33041(21)(,)sin cos10(21).5(21)10n n u x t x n t n πππ∞=+=++∑ 为了加深理解，下面我们扼要地分析一下级数形式解(4.11)的物理意义，先分析一下级数中每一项(,)cos sin sin n n n a n a n u x t C t D t x l l l πππ⎛⎫=+ ⎪⎝⎭*)这里所讲的结论经适当修改即可用于下面几节将要讨论的定解问题，所以，本书中凡是用分离变量法求解的定解问题都假定它的定解条件具备一定的条件，保证定解问题的解可以表示成级数的形式，或者说可以运用叠加原理.的物理意义，分析的方法是：先固定时间t ，看看在任一指定时刻波是什么形状；再固定弦上一点，看看该点的振动规律.把括号内的式子改变一下形式，可得(,)cos()sin,n n n n u x t A t x lπωθ=-其中,.n n n n nD n aA arctg l C πωθ=== 当时间t 取定值0t 时，得(,)sin,n n u x t A x lπ'= 其中0cos()n n n n A A t ωθ'=-是一个定值，这表示在任一时刻，波0(,)n u x t 的形状都是一些正弦曲线，只是它的振幅随着时间的改变而改变.当弦上点的横坐标x 取定值0x 时，得0(,)cos(),n n n n u x t B t ωθ=-其中0sinn n n B A x l π=是一个定值.这说明弦上以0x 为横坐标的点作简谐振动，其振幅为n B ，角频率为n ω，初位相为n θ.若x 取另外一个定值时，情况也一样，只是振幅n B 不同罢了，所以(,)n u x t 表示这样一个振动波：在考察的弦上各点以同样的角频率n ω作简谐振动，各点处的初位相也相同，而各点的振幅则随点的位置改变而改变；此振动波在任一时刻的图形是一正弦曲线.这种振动波还有一个特点，即在[0,]l 范围内还有1n +个点（包括两个端点）永远保持不动，这是因为在(0,1,2,,)m mlx m n n==那些点上，sinsin 0mn x m l ππ==的缘故，这些点在物理上称为节点.这就说明(,)n u x t 的振动是在[0,]l 上的分段振动，其中有1n +个节点，人们把这种包含节点的振动波叫做驻波.另外驻波还在n 个点处振幅达到最大值（读者可自己讨论），这种使振幅达到最大值的点叫做波腹.图4-1画出了在某一时刻1,2,3n =的驻波形状.综合上述，可知(,),(1,2,3,)n u x t n =是一系列驻波，它们的频率、位相与振幅图4-1都随n 不同而不同，因此我们可以说，一维波动方程用分离变量法解出的结果(,)u x t )是由一系列驻波叠加而成的，而每一个驻波的波形由固有函数确定，它的频率由固有值确定.这完全符合实际情况，因为人们在考察弦的振动时，就发现许多驻波，它们的叠加又可以构成各种各样的波形，因此很自然地会想到用驻波的叠加表示弦振动方程的解.这就是分离变量法的物理背景.所以分离变量法也称为驻波法.4.2 有限长杆上的热传导设有一均匀细杆，长为l ，两端点的坐标为0x =与x l =，杆的侧面是绝热的，且在端点0x =处温度是零度，而在另一端x l =处杆的热量自由发散到周围温度是零度的介质中去（参考第3章1.2中第三类边界条件），已知初始温度分布为().x ϕ求杆上的温度变化规律，也就是要考虑下列定解问题：222,0,0; 2.13(,)(0,)0,(,)0;(2.14)(,0)().(2.15)u u a x l t t x u l t u t hu l t x u x x ϕ⎧∂∂=<<>⎪∂∂⎪∂⎪=+=⎨∂⎪=⎪⎪⎩（）我们仍用分离变量法来解这个问题，首先求出满足边界条件而且是变量被分离形式的特解.设(,)()()u x t X x T t =, 2()().()()T t X x a T t X x '''=上式左端不含有x ，右端不含有t ，所以只有当两端均为常数时才可能相等.令此常数为2β-，（读者可以从方程()(),X x X x λ''=结合边界条件按λ取值的三种不同情况像4.1那样讨论后得出），则有22()(),()()T t X x a T t X x β'''==- 从而得到两个线性常数微分方程222()()0,()()0.T t a T t X x X x ββ'+=''+= （4.16）解后一个方程得()cos sin ,X x A x B x ββ=+由边界条件(4.14)可知(0)0,'()()0.X X l hX l =+=从(0)0X =得 0A =，从()()0.X l hX l '+=得cos sin 0.l h l βββ+= （4.17）为了求出β，方程(4.17)可改写成tg a γγ=， （4.18）其中1,.l a hlγβ==-方程(4.18)的根可以看作是曲线1y tg γ=与直线2y a γ=交点的横坐标（图4-1），显然它们的交点有无穷多个，于是方程(4.18)有无穷多个根，由这些根可以确定出固有值β.设方程(4.18)的无穷多个正根（不取负根是因为负根与正根只差一个符号（图4-2），再根据4.1中所述的同样理由）为123,,,,,n γγγγ于是得到无穷多个固有值图4-21212,,,,nn lllγγγβββ===及相应的固有函数()sin .n n n X x B x β= （4.19）再由(4.16)中第一个方程解得22().n a tn n T t A eβ-= （4.20）由(4.19)，（4.20)两式，我们得到方程（4.13）满足边界条件(4.14)的一组特解22(,)()()sin (1,2,3,),n a tn n n n n u x t X x T t C ex n ββ-=== （4.21）其中 .n n n C A B =由于方程(4.13)与边界条件(4.14)都是齐次的，所以2211(,)(,)sin n a t n n n n n u x t u x t C e x ββ∞∞-====∑∑ （4.22）仍满足方程与边界条件，最后考虑(,)u x t 是否能满足初始条件(4.15)，从(4.22)式得1(,0)sin .n n n u x C x β∞==∑现在希望它等于已知函数()x ϕ，那么首先要问[0,]l 上定义的函数()x ϕ是否能展开为1sin nn n Cx β∞=∑级数形式，其次要问系数n C 如何确定，关于前者，只要()x ϕ在[0,]l 上满足狄氏条件就可以了，现在主要谈求系数的问题.回忆傅氏系数公式的得来是根据函数系的正交性，所以现在也要考察函数系{}sin n x β在[0,]l 上的正交性，可以证明（参阅§5.3关于固有函数正交性的证明方法）sin sin 0,.lm n x xdx m n ββ=≠⎰令 20sin ,ln n L xdx β=⎰于是把1()sin n n n x C x ϕβ∞==∑ （4.23）的两端乘上sin k x β，然后在[0,l ]上积分得()sin lkk k x xdx L C φβ=⎰即 01()sin .Lk k kC x xdx L φβ=⎰（4.24）把(4.24)代入(4.22)式即得原定解问题的解.通过上面两节的讨论，我们对分离变量法已经有了一个初步的了解，它的主要步骤大体为：一、首先将偏微分方程的定解问题通过分离变量转化为常微分方程的定解问题，这对线性齐次偏微分方程来说是可以做到的.二、确定固有值与固有函数.由于固有函数是要经过叠加的，所以用来确定固有函数的方程与条件，当函数经过叠加之后仍旧要满足，当边界条件是齐次时，求固有函数就是求一个常微分方程满足零边界条件的非零解.三、定出固有值、固有函数后，再解其他的常微分方程，把得到的解与固有函数乘起来成为(,)n u x t ，这时(,)n u x t 中还包含着任意常数.四、最后为了使解满足其余的定解条件，需要把所有的(,)n u x t 叠加起来成为级数形式，这时级数中的一系列任意常数就由其余的条件确定，在这最后的一步工作中，需要把已知函数展开为固有函数项的级数，所以，必须考虑固有函数的正交性.由本节的例子还可以看出，用分离变量法求解第三类边界条件（第二类边界条件也一样）的定解问题时，只要边界条件都是齐次的，其过程与解第一类边界条件的定解问题是相同的，但在确定固有值时，一般说来是比较复杂的.4.3 圆城内的二维拉普拉斯方程的定解问题一个半径为0ρ的薄圆盘，上下两面绝热，圆周边缘温度分布为已知，求达到稳恒状态时圆盘内的温度分布.在第3章讲过，热传导问题达到稳恒状态时温度分布与时间无关，应满足拉普拉斯方程20.u ∇=因为边界形状是个圆周，它在极坐标下的方程为0ρρ=，所以在极坐标系下边界条件可表为(),u f ρρθ==既然边界条件使用了极坐标系，所以我们将方程也采用极坐标的形式，于是有220220110,;(4.25)(,)().(4.26)u uu u f ρρρρρρρθρθθ⎧⎛⎫∂∂∂∇=+=<⎪ ⎪∂∂∂⎨⎝⎭⎪=⎩此外，因为自变量,ρθ的取值范围分别是[0,0ρ]与[0,2]π，圆盘中心点的温度决不可能是无穷的，并且（,ρθ）与（,2ρθπ+）实际上表示同一点，温度应该相同，即应该有lim u ρ→<+∞ （4.27）(,)(,2).u u ρθρθπ=+ （4.28）现在来求满足方程(4.25 )及条件(4.26)，（4.27），（4.28）的解.先令(,)()(),u R ρθρθ=Φ代入方程(4.25)得2110R R R ρρ'''''Φ+Φ+Φ=即2,R R Rρρ'''''+Φ=-Φ令比值为常数λ即得两个常微分方程0,λ''Φ+Φ=20.R R R ρρλ'''+-=再由条件(4.27)及(4.28)可得(0),R <∞(2)().θπθΦ+=Φ （4.29）这样一来，我们得到了两个常微分方程的定解问题0,(2)().λθπθ''Φ+Φ=⎧⎨Φ+=Φ⎩（4.30） 与20,(0).R R R R ρρλ'''⎧+-=⎨<∞⎩ （4.31） 先解哪能一个呢？要看哪一个可以定出固有值，由于条件(4.29)满足可加性（即所有满足(4.29)的函数叠加起来仍旧满足(4.29)，所以只能先解问题(4.30).采用与4.1中同样的方法可以得到 当0λ<时，问题(4.30)无解；当0λ=时，它的解为00()a θ'Φ=（常数）；当0λ>时，它的解为0(),n n a b θ''Φ=+且λ必须是整数n ，取1,2,3,n =（只取正整数的理由与4.1相同），则0()cos sin .n n a n b n θθθ''Φ=+至此，我们已经定出了固有值与固有函数，接下去是解问题(4.31)，其中的方程是欧拉(Euler)方程，它的通解为000ln ,R c d ρ=+当λ=0；,n n n n n R c d ρρ-=+ 当2(1,2,3,).n n λ==为了保证(0)R <∞，只有0n d = (0,1,2,),n =即 0(0,1,2,)nn R c n ρ==，因此利用叠加原理，方程(4.25)满足条件(4.27),（4.28）的解可以表示为级数01(,)(cos sin )2nn n n n a u a n b ρθρθθ∞==++∑ (2.32)此式中的2a 就是00;,n n a c ab '分别是.n n n n ac b c ''，最后为了确定系数,n n a b ，我们利用边界条件(4.26)得001()(cos sin )2nn n n n a f a n b θρθθ∞==++∑， （4.33）因此，000,,nnn n a a b ρρ就是()f θ展开为傅氏级数时的系数，即有2002002001(),1()cos ,1()sin .n n n n a f d a f n d b f n d πππθθπθθθρπθθθρπ⎧⎪=⎪⎪⎪=⎨⎪⎪=⎪⎪⎩⎰⎰⎰ （4.34） 将这些系数代入(4.32)式即得所求的解.为了以后应用起来方便，我们还可以将解(4.32)写成另一种形式.为此，将(4.34)式所确定的系数代入(4.32)式经过简化后可得201011(,)()cos ().2n n u f t n t dt πρρθθπρ∞=⎡⎤⎛⎫⎢⎥=+- ⎪⎢⎥⎝⎭⎣⎦∑⎰（4.35）利用下面已知的恒等式221111cos ()2212cos()n n k k n t k t k θθ∞=-+-=--+∑*）(1),k <*）这个恒等式的证明如下：[]∑∑∞=∞=---++=-+11)()(2121)(cos 21n n t in t in n n e e k t n k θθθ [][]∑∑∞=∞=---++=11)()(212121n n nt i n t i ke ke θθ)()()((1211)2121t i t i t i t i ke ke ke ke -------+-+=θθθθ（|K|＜1） ⎥⎦⎤⎢⎣⎡-+-----+-----+-+=)sin()cos(1)sin()cos()sin()cos(1)sin()cos(121t ik t k t ik t k t ik t k t ik t k θθθθθθθθ可将解(,)u ρθ（4.35）表达为()2220022001(,)(),.22cos()u f t dt t πρρρθρρπρρρρθ-=<+--⎰（4.36） 公式(4.36)称为圆域上的泊松公式，它的作用在于把解写成了积分形式，这样便于作理论上的研究.4.4 有界弦的强迫振动前面所讨论的偏微分方程都限于齐次的，现在要讨论非齐次方程的解法，为方便起见，以弦的强迫振动为例，所用的方法对其他类型的方程也适用.我们研究的问题是一根弦在两端固定的情况下，受强迫力作用所产生的振动现象.即要考虑下列定解问题22222000(,),0,0;(2.37)0;(2.38)(),().(2.39)x x l t t uu a f x t x l t t x u u u u x x t ϕψ====⎧∂∂⎪=+<<>∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩在现在的情况，弦的振动是由两部分干扰引起的，一是强迫力，一是初始状态，所以由物理意义可知，此时振动可以分解为仅由强近力引起的振动和仅由初始状态引起的振动的合成.由此得到启发，我们可设解为(,)(,)(,),U x t V x t W x t =+ （4.40）其中(,)V x t 表示仅由强迫力引起弦振动的位移，它满足22222000(,),0,0;0;(2.41)0.x x l t t VV a f x t x l t t x V V u V t ====⎧∂∂⎪=+<<>∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩而(,)W x t 表示仅由初始状态引起弦振动的位移，它满足.)cos(21121)cos(212)cos(21212222kt k k k t k k t k +---=⎥⎦⎤⎢⎣⎡+----+=θθθ22222000,0,0;0;(2.42)(),().x x l t t WW a x l t t x W W W W x x t φψ====⎧∂∂⎪=<<>∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩读者不难验证，若V 是(4.41)的解，W 是(4.42)的解，则U V W =+一定就是原定解问题的解.问题(4.42)可直接用分离变量法求解，因此现在的问题只要讨论如何解问题（4.41）就行了.关于问题（4.41），我们可以采用类似于线性非齐次常微分方程中所常用的参数变易法，并保持如下的设想，即这个定解问题的解可分解为无穷多个驻波的叠加，而每个驻波的波形仍然是由该振动体的固有函数所决定，这就是说，我们假设（4.41）的解具有如下的形式1(,)()sin,n n n V x t v t x lπ∞==∑ （4.43） 其中()n v t 是待定的函数，为了确定()n v t ，将自由项(,)f x t 展成的傅氏正弦级数，即1(,)()sin,n n n f x t f t x lπ∞==∑ （4.44） 其中 02()(,)sin .l n n f t f x t xdx l lπ=⎰ 将(4.43)及(4.44)代入(4.41)的第一个式了，得到222''21()()()sin 0,n n n n a n n v t v t f t x l l ππ∞=⎡⎤+-=⎢⎥⎣⎦∑ (4.45) 由此可见得222''2()()().nn n a n v t v t f t lπ+= 再将(４.41)中的初始条件代入(４.43)得'(0)0,(0)0.n n v v ==这样一来，确定函数()n v t 只需解下列定解问题：2222()()()(0)0,(0)0n n n nn a n v t v t f t l v v π⎧''+=⎪⎨⎪'==⎩ 1,2,n =. （４.46） 用拉氏变换法解出（４.46），得到()()()sintn n ln a t v t f d n a lπτττπ-=⎰*)，*)在方程（4.46）的两端取关于t 的拉氏变换，得所以，01()(,)()sin sin .t n n ln a t n v x t f d x n a l l πτπττπ∞=-⎡⎤=⎢⎥⎣⎦∑⎰ 将这个解与问题（４.42）的解加起来，就得到原定解问题（４.37），(４.38)，(４.39)的解.这里所给的求解问题(４.41)的方法，其实质是将方程的自由项及解都按齐次方程所对应的一族固有函数展开.随着方程与边界条件的不同，固有函数族也就不同，但总是把非齐次方程的解按相应的固有函数展开.所以这种方法也叫固有函数法.４.5 非齐次边界条件的处理前面所讨论的定解问题的解法，不论方程是齐次的还是非齐次的，边界条件都是齐次的.如果遇到非齐次边界条件的情况，应该如何处理？总的原则是设法将边界条件化成齐次的.具体地说，就是取一个适当的未知函数之间的代换，使对新的未知函数，边界条件是齐次的.现在以下列定解问题为例，说明选取代换的方法.设有定解问题2222212000(,),0,0;(4.47)(),();(4.48)(),().(4.x x l t t uu a f x t x l t t x u u t u u t u u x x t ϕψ====⎧∂∂⎪=+<<>∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩49)我们设法作一代换将边界条件化为齐次的，为此令(,)(,)(,).u x t V x t W x t =+ （４.50） 选取W(x,t)使V(x,t)的边界条件为齐次的，即0,0x x lVV==== （４.5１）120(),()x x lWu t Wu t ==== （４.52）也就是说，只要所选取的W 满足(４.52)就能达到我们的目的.而满足(４.52)的函数是容易找到的，例如取W 为x 的一次式，即设(,)()(),W x t A t x B t =+ 用条件(4.52)确定(),()A t B t 得2111()()(),()()A t u t u t B t u t l=-=⎡⎤⎣⎦.),()()(22222p F p U ln a p U p n n n =+π 其中U n (p),F n (p)分别为v n (t)与f n (t)的拉氏变换，解出),(1)(22222p F l n a p p U nn π+= 由于222221l n a p π+的逆拉氏变换为lat n an l ππsin，利用拉氏变换的卷积性质，即得v n (t).显然，函数211()()(,)()u t u t W x t u t x l-=+就满足(4.52)式，因而只要作代换211,u u u V u x l -⎡⎤=++⎢⎥⎣⎦（4.53）就能使新的未知函数满足齐次的边界条件.经过这个代换后，得到V 的定解问题为22212201100(,),0,0;0,0;(2.54)(),(),x x l t t VV a f x t x l t t x V V V V x x t ϕψ====⎧∂∂⎪=+<<>∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩其中211121112111()()(,)(,)();(0)(0)()()(0);(0)(0)()()(0).u t u t f x t f x t u t x l u u x x u x l u u x x u x l ϕϕψψ⎧⎡⎤''''-''⎪=-+⎢⎥⎪⎢⎥⎣⎦⎪-⎡⎤⎪=-+⎨⎢⎥⎣⎦⎪⎪⎡⎤''-⎪'=-+⎢⎥⎪⎢⎥⎣⎦⎩（4.55）问题（4.54）可用上一节的方法解出，将(4.54)的解代入(4.53)即是原问题的解.上面由(4.52)式定(,)W x t 时，取(,)W x t 为x 的一次式是为了使（4.55）中几个式子简单一些，并且(,)W x t 也容易定，但若12,,f u u 都与t 无关，则可适当的选择()W x （也与t 无关），使(,)V x t 的方程与边界条件同时都化成齐次的，这样做就可以省掉下面对(,)V x t 要进行解非齐次方程的繁重工作.这种()W x 究竟怎么找，将在后面的例题中说明.若边界条件不全是第一类的，本节的方法仍然适用，不同的只是函数(,)W x t 的形式，读者可就下列几种边界条件的情况写出相应的(,)W x t 来：1201201201(),();2(),();3(),().x x lx l x x x lu u u t u t xuu t u u t x u u u t u t xx======∂==∂∂==∂∂∂==∂∂ 以上各节我们说明了如何用分离变量法来解定解问题，为便于读者掌握此方法，现将解定解问题的主要步骤简略小结如下：一、根据边界的形状选取适当的坐标系，选取的原则是使在此坐标系中边界条件的表达式最为简单.圆、圆环、扇形等域用极坐标系较方便，圆柱形域与球域分别用柱坐标系与球坐标系较方便.二、若边界条件是非齐次的，又没有其他条件可以用来定固有函数，则不论方程是否为齐次，必须先作代换使化为具有齐次边界条件的问题，然后再求解.三、非齐次方程、齐次边界条件的定解问题（不论初始条件如何）可以分为两个定解问题，其一是具有原来初始条件的齐次方程，其二是具有齐次定解条件的非齐次方程.第一个问题用分离变量法求解，第二个问题按固有函数法求解.在结束本章之前，我们再举两个综合性的例子，目的是帮助读者掌握分离变量法的全过程.例2 求下列定解问题5)22222000,0,0;(2.56)0,;(2.57)0(2.8x x l t t uu a A x l t tx u u B u u t ====⎧∂∂⎪=+<<>∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩的解，其中,A B 均为常数.解 这个定解问题的特点是：方程及边界条件都是非齐次的.根据上述原则，首先应将边界条件化成齐次的，由于方程(2.56)的自由项及边界条件都与t 无关，所以我们有可能通过一次代换将方程与边界条件都变成齐次的，具体做法如下： 令 (,)(,)(),u x t V x t W x =+ 代入方程（4.56）得22222''().V V a W x A t x ⎡⎤∂∂=++⎢⎥∂∂⎣⎦为了使这个方程及边界条件同时化成齐次的，选()W x 满足⎪⎩⎪⎨⎧===+==BW W A x W a l x X ,0,0)(''02（4.59） (4.59)是一个二阶常系数线性非齐次方程的边值问题，它的解可以通过两次积分求得222().22A Al B W x x x a al ⎛⎫=-++ ⎪⎝⎭ 求出函数()W x 之后，再由（4.58）可知函数(,)V x t 为下列定解问题的解.22222000,0,0;(4.60)00;(4.61)(),0.(4.62)x x l t t VV a x l t tx V V V V W x t ====⎧∂∂⎪=<<>∂∂⎪⎪==⎨⎪∂⎪=-=⎪∂⎩采用分离变量法，令(,)()()V x t X x T t =,代入(4.60)得2,XT a X T ''''=或22.X T X a Tβ''''==- 由此得到2220,(4.63)0.(4.64)X X T a T ββ''+=''+=由(4.63)及(4.61)可以确定固有值与固有函数为2222.n l πβ=()sin .n n X x x lπ=再由(4.64)得()cossin ,n n n n a n aT t C t D t l lππ=+ 利用（4.62）中第二个条件可得0n D =.于是定解问题（4.60）,(4.61),(4.62)的解可表示为1(,)cossin .n n n a n V x t C t x l lππ∞==∑ 代入(4.62)中第一个条件得1()sin,n n n W x C x lπ∞=-=∑ 即2221sin .22nn A Al B n x x C x a a l l π∞=⎛⎫-+= ⎪⎝⎭∑ 由傅氏级数的系数公式可得22202sin .22l n A Al B n C x x xdx l a a l l π⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦⎰ 2222002sinsin llAn A B n x xdx x xdx a ll a l l ππ⎛⎫=-+ ⎪⎝⎭⎰⎰2223322222cos Al Al B n a n n a n ππππ⎛⎫=-++ ⎪⎝⎭（4.65）因此，原定解解问题的解为2221(,)cos sin ,22n n A Al B n a n u x t x x C t x a a l l l ππ∞=⎛⎫=-+++ ⎪⎝⎭∑其中n C 由(4.65)确定. 例3在环形域a b ≤内求解下列定解问题22222212();0,0.a b u u x y x y ⎧∂∂+=-⎪∂∂⎪⎨⎪==⎪⎩解 由于求解区域是环形区域，所以我们选用平面极坐标系，利用直角坐标与极坐标系之间的关系cos ,sin ,x y ρθρθ=⎧⎨=⎩ 可将上述定解问题用极坐标,ρθ表示出来22211()122cos 2,;(4.66)0,0.(4.67)a b u ua b u u ρρρρθρρρρρθρ==⎧∂∂∂+=<<⎪∂∂∂⎪⎨∂⎪==⎪∂⎩这是一个非齐次方程附有齐次边界条件的定解问题，采用4.4所述的固有函数法，并注意在4.3中得到的关于圆域内拉普拉斯方程所对应的固有函数，可令问题（4.66）,(4.67)的解为(,)()cos ()sin ,n n n u A n B n ρθρθρθ∞==+⎡⎤⎣⎦∑代入(4.66)并整理得到22''''''222011()()()cos ()()()sin 12cos ,n n n n n n n n n A A A n B B B n ρρρθρρρθρθρρρρ∞=⎫⎧⎡⎤⎡⎤⎪⎪+-++-=⎨⎬⎢⎥⎢⎥⎪⎣⎦⎣⎦⎪⎩⎭∑比较两端关于cos ,sin n n θθ的系数可得'''2222214()()()12,A A A ρρρρρρ+-= (4.68)2''''21()()()0(2),nnn n A A A n ρρρρρ+-=≠ (4.69)2'''21()()()0.nnn n B B B ρρρρρ+-= (4.70)再由条件(4.67)得()()0,n n A a B a == (4.71)()()0.n n A b B b ''== (4.72)由(4.69)，(4.70),(4.71),(4.72)可知()0(2),()0.n n A n B ρρ≡≠≡下面的任务就是要确定2().A ρ方程(4.68)是一个非齐次的欧拉方程，它的通解为224212(),A C C ρρρρ-=++由条件(4.71),(4.72)确定12,C C 得661442,a b C a b +=+4422244(2).a b a b C a b-=-+ 因此664422224244442(2)(),a b a b a b A a b a bρρρρ-+-=--+++ 原定解问题的解为()66244222444441(,)2(2)()cos 2.u a b a b a b a b a bρθρρρθ-⎡⎤=-++--+⎣⎦+习 题 四1、设弦的两端固定于0x =及x l =，弦的初始位移如图所示，初速度为零，又没有外力作用，求弦作横向振动时的位移函数(,)u x t .2、就下列初始条件及边界条件解弦振动方程(,0)0,u x =(,0)(),(0,)(,)0.u x x l x tu t u l t ∂=-∂== 3、就下列初始条件及边界条件解弦振动方程01,0211,1;2t x x u x x =⎧<≤⎪⎪=⎨⎪-<<⎪⎩01(1);0.t x x ux x t u u ===∂=-∂== 4、解出习题三中第2题.5、试求适合于下列初始条件及边界条件的一维热传导方程的解00(),0.t x x t u x l x u u ====-==6、解一维热传导方程，其初始条件及边界条件为00,0,0.t x x tu x u u xx====∂∂==∂∂7、一根长为l 的细杆表面绝缘，其初始温度分布如图所示，由0t =开始两端温度保持于零度，求杆上温度分布.8、试解出具有放射衰变的热传导方程2220,xu u a Ae x tα-∂∂-+=∂∂ 已知边界条件为00,0,x x l u u ====初始条件为0t u T ==,T 为常数9、求下列定解问题22200;0;0x x l t u u a A t x u u u ===⎧∂∂=+⎪∂⎪⎪==⎨⎪=⎪⎪⎩的解.10、求满足下列定解条件的一维热传导方程的解010,5,x x l u u ==== 0,t u ks k ==为常数11、试确定下列定解问题22200();,;()x x l t u u a f x t x u A u B u g x ===⎧∂∂=+⎪∂∂⎪⎪==⎨⎪=⎪⎪⎩解的一般形式.12、求稳恒状态下，由直线120,,0,x x l y y l ====所围矩形板内各点的温度，假设在10,,0x x l y ===三边上温度保持为零度，2y l =这边上各点温度为(),x ϕ其中1(0)()0.l ϕϕ== 13、一半径为a 的半圆形平板，其圆周边界上的温度保持(,)()u a T θθπθ=-，而直径边界上温度保持为零度，板的侧面绿缘，试求稳恒状态下的温度分布规律(,).u ρθ14、一圆环形平板，内半径为1r ，外半径为2r ，侧面绝缘，如内圆温度保持零度，外圆温度保持1度，试求稳恒状态下的温度分布规律(,).u r θ 15、如何解下列定解问题2222212000();,;(),().x x l t t uu a f x t x u M u M u u x x t ϕψ====⎧∂∂⎪=+∂∂⎪⎪==⎨⎪∂⎪==⎪∂⎩16、在矩形域内求下列定解问题2120120(,);(),();(),().x x a y y b u f x y u y u y u x u x ϕϕψψ====⎧∇=⎪⎪==⎨⎪==⎪⎩ 的解.17、在扇形区域内求下列定解问题200;0;()a a u u u u f θθρθ===⎧∇=⎪⎪==⎨⎪=⎪⎩ 的解.18、在矩形域0,0x a y b ≤≤≤≤内求拉普拉斯方程的解，使满足边界的条件：000,;0,0.x x a y y b u u Ay uu y y ====⎧==⎪∂∂⎨==⎪∂∂⎩19、把高频输电线充电到具有电压E ，然后一端短路封闭，另一端仍保持断开，求以后的电压分布.20、求矩形膜振动的位移，即解下列定解问题22222220000;0;0;()(),0.x x a y y b y t u uu a tx y uu u u u u xy x a y b t ======⎧⎛⎫∂∂∂=+⎪ ⎪∂∂∂⎝⎭⎪⎪==⎪⎨==⎪⎪∂⎪=--=⎪∂⎩。

大学物理实验指导书云南大学软件学院目录1.课程基本信息 (2)2.课程简介 (2)3.教学目的与基本要求 (2)4.考核方式和成绩评定办法 (3)5.参考文献 (3)6.实验指导 (4)6.1测量及误差分析 (4)6.2质点运动学 (9)6.3质点动力学 (11)6.4静电场 (13)6.5磁场 (18)6.6电量测量.................................. 错误!未定义书签。

6.7波的叠加.................................. 错误!未定义书签。

6.8示波器.................................... 错误!未定义书签。

6.9传感器.................................... 错误!未定义书签。

6.10光的干涉与衍射.......................... 错误!未定义书签。

1. 课程基本信息名称：大学物理实验/College Physics Lab课程性质：学科基础总学时/学分： 32/12. 课程简介本实验课程根据教育部《非物理类理工学科大学物理实验课程教学基本要求》并结合软件学院人才培养目标开展教学。

本实验课程内容包括：•测量误差的基础知识、用计算机处理实验数据的基本方法，以及基本物理量的测量方法，并加强数字化测量技术的应用。

•结合软件学院的专业特点，通过计算机模拟和实际操作掌握误差分析方法、质点运动学、质点动力学、振动与波、电场、磁场、光的干涉与衍射等基本原理。

•学习常用物理实验方法，实验室常用仪器的性能，常用实验操作技术及仪器正确调节，学习简单的计算机模拟。

3. 教学目的与基本要求本实验课培养学生初步掌握实验科学的思想和方法，提高其分析能力和创新能力；培养理论联系实际的科学作风，认真严谨的科学态度，积极主动的探索精神，团结协作的职业素养。

使之加深对物理学基本概念、基本理论的理解，掌握运用物理学基本原理分析和解决问题的科学方法。