南京理工大学普通物理(A)考研真题2004——2010年

南京理工大学课程考试答案及评分标准课程号-课序号： 11120804 课程名称： 大学物理（上） 学分： 3.5 考试方式： 闭卷笔试 满分分值： 100 考试时间： 120 分钟一、选择题（每题2分，共24分）1、（B ）；2、（C ）；3、（A ）；4、（D ）；5、（B ）；6、（A ） 二、填空题（每题2分，共24分）1、（1）2/5.2s m a =；（2）s m /0.3=υ；2、（3）00044R V ==ωω；（4）2023mV A =；3、（5）⎥⎦⎤⎢⎣⎡-±--=3)2(cos 0ππωu x L t A y 反；（6）2k L x 0λ±=； 4、（7）R i 22+； （8）等温过程； 5、（9）K T 200'2=；（10）K T 750'1= 6、（11）21σσ-=；（12）22σσ=（参考分数）三、（10分）解：（1） gdx gdm df lm λμμλ⋅-=⋅-==,mgl l g gdx x xdf dM M l μμλμλ2120-=⋅-=⋅-=-==⎰⎰⎰ （5分）（2）（一）用动量矩定律： 0021ωωωI I I Mt -=-= （2分） g l mgl ml M I t μωμωω3223120020=⨯=-= （3分）（二）亦可用转动定律： l g I M 23μα-== （2分）t αωω+=0 （2分）gl t μωαω3200=-= （1分）四、（10分）解：（1）ππω====Ts T m A 2,2,12.0 （2分） 0=t 时，0,000>=υx 所以有 )35(3ππϕor -= （2分）))(3cos(12.0m t x ππ-= （2分）（2）由图可知： ;6532πππθ∆=+= （2分）s t 65==ωθ∆∆ （2分）五、（10分）解：（1）P -V 图； （4分）（2）)(4052102010013.12)(351212J V V P A =⨯⨯⨯⨯=-=-； （1分） ;023=A （1分）)(280821ln ln 333131J R V P R V V RT A -=⎪⎭⎫ ⎝⎛== （1分）（3）)124428084052J A （＝－＝总 （1分）)(1418227)(1122121J R V P R V P R T T C Q P =⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛=-= （1分）%8.81418212441===Q A η （1分）六、解：（10分）（1）dr r Qq dr r q V R R RA ⎰++⎰=∞321202044πεπε （4分） 302010444R Qq R q R qπεπεπε++-=（1分）（或由电荷分布q Q q q +-,,产生的电势叠加302010444321R Qq R q R q V V V V A A A A πεπεπε++-=++=）（2）0,44020=+=+=∞∞⎰V rQq dr r Q q V rP πεπε （3分）)(l 题五图所以 rQ q q V V q A p p 0004)()(πε+=-=∞∞ （2分）七、解：（12分）（1）无介质板时，dSC 00ε=（2分）有介质板 ⎪⎪⎭⎫⎝⎛+=+=+=r r r S d S dS d C C C εεεεεε122211100021 （2分） d S C r r )1(20+=εεε dS C C C r r )1()1(00+-=-=εεε∆ （2分）（2） W W W A -==0∆ （2分）CQ C Q 22202-= （2分） 204)1(Q Sd r r εεε-=（2分）。

2 e j30° 3
∴h(t) = 2 k1 ieαt cos(ωt +θ1) = 2×
2 e−500t cos(500 3
3t + 30°)ε (t) =
4 e−500t cos(500 3
3t + 30)ε (t)
∴单位冲激响应：
版权所有 ，翻版必究 正版用户可享受免费更新服务，包括最新的试题解答，及错误改正，敬请联系： 10 ，预祝大家顺利考上南京理工大学！
图1 解析：如图所示以节点 5 为参考节点， 列写节点电压方程：
⎧(1+ 2 + 3)Un1 −Un2 − 3Un4 = 0 ⎪⎪⎪⎨U−Un3n1=+8U(1+ 6 + 4)Un2 − 4Un4 − 6Un3 = 4 × 4 ⎪⎩−2Un1 − 4Un2 − 7Un3 + (2 + 4 + 7)Un4 = 7I −16
（2）如果电流 I2 = 0 A,则 R1 为何值？
（3）如果 R1 为非线性电阻，U1 = I12 ，求此时 I1 。
解析：（1）由已知条件可知仅 R1 发生变化，其它部分不变，画出从 R1 两端看进去的戴维南
等效电路图，如上图右所示，则有Uoc = I1(R1 + Req ) ，代入已知条件有
⎧U ⎪
− 90°
= 100∠0°
I1
=
Uc 30 + jωL
=
100∠0° 30 + 40 j
=
2∠ − 53.1°
由 KVL 可得
版权所有 ，翻版必究 正版用户可享受免费更新服务，包括最新的试题解答，及错误改正，敬请联系： 8 ，预祝大家顺利考上南京理工大学！

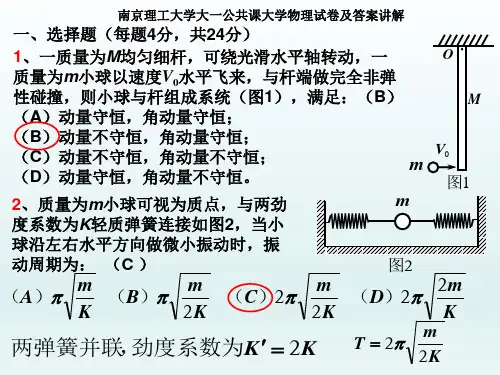
2011级大物试卷及答案一、选择题（每题2分，共20分）1、一质点从静止出发绕半径为R 的圆周作匀变速圆周运动，角加速度为α，当该质点走完一圈回到出发点时，所经历的时间为 （ B ）（A ）R 221α； （B ）απ4； （C ）απ2； （D ）条件不够不能确定。

2、有一个小球，置于一个光滑的水平桌面上，有一绳其一端连接此小球，另一端穿过桌面中心的小孔，该小球原以角速度ω在距孔为r 的圆周上转动，今将绳从小孔缓慢往下拉的过程中，则对小球下列叙述正确的是 （ C ） （A ）角动量、动能、动量都不变； （B ）角动量、动能、动量都改变； （C ）角动量不变，动能、动量都改变； （D ）角动量和动量不变，动能改变。

3、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图1。

今使棒从水平位置由静止开始下落。

在棒摆动到竖直位置的过程中，则应 （ A ） （A ）角速度从小到大，角加速度从大到小； （B ）角速度从小到大，角加速度从小到大； （C ）角速度从大到小，角加速度从大到小； （D ）角速度从大到小，角加速度从小到大。

4、一简谐振动曲线如图2所示，则振动周期为 （ D ） （A ）2.62s ； （B ）0.42s ； （C ）0.38s ； （D ）2.40s5、传播速度为100m/s ，频率为50Hz 的平面简谐波，在波线上相距为0.5m 的两点之间的位相差为 （ C ）（A ）3π； （B ）6π； （C ）2π； （D ）4π。

6、如图3所示，设某热力学系统经历一个准静态过程b →c →a ，a ，b 两点在同一条绝热线上，则该系统在b →c →a 过程中 （ D ） （A ）只吸热，不放热； （B ）只放热，不吸热；（C ）有的阶段吸热，有的阶段放热，吸收的热量等于放出的热量； （D ）有的阶段吸热，有的阶段放热，吸收的热量大于放出的热量； （E ）有的阶段吸热，有的阶段放热，吸收的热量小于放出的热量。

南京理⼯⼤学现代物理复习题复习题⼀、相对论1、关于同时相对性，以下结论中正确的是（ C ）（A ）在⼀惯性系同时发⽣的两个事件，在另⼀惯性系⼀定不同时发⽣；（B ）在⼀惯性系不同地点同时发⽣的两个事件，在另⼀惯性系⼀定同时发⽣；（C ）在⼀惯性系同⼀地点同时发⽣的两个事件，在另⼀惯性系⼀定同时发⽣；（D ）在⼀惯性系不同地点不同时发⽣的两个事件，在另⼀惯性系⼀定不同时发⽣。

2、两个惯性系S 和S '，沿X (X ')轴⽅向相对运动，相对速度为u 。

设在S '系中某点先后发⽣的两个事件，⽤固定于该系的钟测出两事件的时间间隔为0τ，⽽⽤固定在S 系的钟测出这两个事件的时间间隔为τ，⼜在S '系的X '轴上静⽌放置⼀固有长度为0l 的细杆，从S 系测得此杆的长度为l ，则（ D ）（A ）0ττ<，0l l <；（B ）0ττ<，0l l >；（C ）0ττ>，0l l >；（D ）0ττ>，0l l < 3、粒⼦的静质量为0m ，速率为υ，则该物体相对论性的物质波波长为（12）。

（12）υυυλ0221m c h m h-== 4、某物体，静⽌时测得其质量为m 0，体积为V 0、，寿命为τ0，当此物体以u 速度运动时，测得其质量密度为（14），寿命为（15）。

（14）220011c u V m -；（15）2201c u-τ；5、若⼀个光⼦的能量等于⼀个电⼦的静能，则该光⼦的波长约为（15） nm 。

（15）2.4×10 -36、设某微观粒⼦的总能量是它的静⽌能量的k 倍，则其运动速度的⼤⼩为（ A ）（A ）12-k k c ；（B ）21k k c -；（C ）1-k c ；（D ）)2(1++k k k c7、+π介⼦是⼀种不稳定的粒⼦，平均寿命是s 8106.2-?（在与它相对静⽌的参照系中测得）。

ez 30 （W/m2）
三、 （10 分）频率为
f 1.8 GHz、x
方向极化的均匀平面波在媒质（ r
1 ， r 81 ，
4 S/m）中沿 z 方向传播，电场强度的幅度为 0.5V/m。试求：
1．该媒质中波的衰减常数、相移常数； 2．电场强度和磁场强度的瞬时值表达式。
3
R( N )
垂直极化波斜入射时，反射系数为 试求： 1．入射角 i ；
2 cos i 1 cos i 2 1
2 sin i 2 sin i 。
2．反射波的坡印廷矢量均值的大小 | Sav | ； 3．折射波的极化类型。
10 1 1 0.70 14 c 先求：
2
2
；
g
波导波长：

1 c
2
1.43 14.3 mm
；
5
v p TE10
波速：
v 1 c
2
Hale Waihona Puke 1.43c1 2
r 2 1 2 1 1 | Sav | RN E0 N 2 1 8 所以


mW/m
2
3. 由于折射波中，既有平行极化波，又有垂直极化波，但二者的幅度已不相等，因此，折射 波应为椭圆极化波。 六、 （14 分）空气填充的矩形金属波导，尺寸为 74 mm2，电磁波工作频率为 30GHz， （1） 该电磁波能否在波导中传输； （2）若能传输，求波导波长、波速以及基模状态下的波阻抗； （3）若波导长度为 50mm，求电磁波传输后的相移。 解：电磁波工作频率 30GHz，得 电磁波波长为：

（5）测量结果表示为N 真 =（1900.0±2.1）×10-2mm；（ （6）测量结果表示为N 真 =（1900±2）×10-2mm。（
18、（1）在弦线上驻实验中音叉共振时，若音叉的固有频率为 100Hz，则低 频讯号发生器输出的频率为 100Hz。（ ）
（2）在弦线上驻实验中测量波长λ，半波数取得多，λ的测量精度就能 提高。（ ） （3）在转动惯量实验中，承物台是否水平对测量误差不会产生影响。 （ ） （4） 在测量线膨胀系数很小的材料时， 可以适当增加光杠杆的放大倍数， 提高测量精度。（ ） 二、 填空题（30 分，每空 1.5 分） 。 。
二、填空题 30 分（每空 1.5 分） 1、 u= �σ2 (n) + μ2 j 。 承物台是否水平 30 。 μ= �⅀σ2 (n) + ∑ μ2 j a<<g ， 。
2、 u m <0.086、u D <0.023、u h <0.1 。 3、 4、 K= ，
太大
。
5、 辉度调节、 x、y位移 。 6、 f x ：f y = 1:3 7、_传热速率_， 6、 桥臂 ， 接触 ， fy= 1000 HZ。
第四步（2 分） k=－2.26 J=2.35×10-3kg·m2 4、(1) （5 分） 答案：4.712
（2）（5 分） 答案：1.8×104
南京理工大学物理实验中心
砝码质量 m(g) 30.0 40.0 50.0 60.0 t 1 (s) 1.702 1.478 1.323 1.261
M 作用下 t 2 (s) 3.184 2.756 2.457 2.303 β(s-2) 3.007 4.050 5.154 6.149 t 1 (s) 0.648 0.549 0.502 0.449

[][]的平均值为多少？态上力学量）在少？（体系能量的平均值为多出现的概率是多少可测得哪些值？各个值态的体系进行能量测量）对处于求（是正的实数。

，其中，的矩阵表示分别为：学量及力系哈密顿量算符为态空间中得基矢，体和、中，态十一、已经体系处于状的可能值是多少？下，力学量）（）（十、求在状态的几率为多少？的值为的本征态，求在此态中）如果粒子处于的本征值和本征态；（）表象中，求（九、在）能量至一级修正。

（示；）微扰哈密顿的矩阵表。

写出（《，其中矩阵表示为八、体系哈密顿算符的分）能量至二级修正值。

（为实数。

用微扰公式求，且七、在能量表象中分）。

（。

证明，六、设分）。

（中算符的表示为五、试证明在动量表象分）（的本征值和本征函数。

分量四、求角动量的分的可微函数，试证明：是三、设分）彼此正交。

（同能级的束缚态波函数）中运动，证明属于不（二、粒子在一维势场分）流密度。

（计算其几率密度和几率的粒子处于定态波函数一、质量为试题（量子力学）年硕士研究生入学考试南京理工大学A A H AHS L J Y S Y S S S S S S H b a E E a E b b a E H i S S pi xI z pf i q f pq q q f i p q x V erm Z Z Z Z y x y x Z y x Z ikrZψψαωαωϕϕϕϕϕϕψϕθχϕθχψααααββαβαϕ3)2(?1010100001ˆ200020001ˆˆˆ212121-ˆˆˆ),(),(231222ˆ,ˆ1ˆ2112002002ˆ15,,ˆ152ˆ,2ˆ100115ˆ15-i ˆ)15.(2)(,)(,,1515,12004003213211121-1021020102012⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫⎝⎛=++=+=⎥⎦⎤⎢⎣⎡+==⎪⎪⎪⎭⎫⎝⎛=≠⎪⎪⎭⎫+ ⎝⎛+=-==⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=∂∂=∂∂====ψ南京理工大学2005年硕士研究生入学考试试题[][]()()面。

A．反射光为偏振光，折射光为部分偏振光；
B．反射光为部分偏振光，折射光为偏振光；
C．反射光和折射光都为部分偏振光； D．反射光和折射光都为偏振光。
8．一宇航员要到离地球为 5 光年的星球去旅行，如果宇航员希望把这距离缩短为 3
光年，则他所乘的火箭相对于地球的速度应是：（c 表示真空中光速） （ ）
A．υ=c/2； B．υ=3c/5； C．υ=4c/5； D．υ=9c/10。
碰撞过程。
10．不确定关系 x px h 表示在 x 方向上
（）
A．粒子位置不能准确确定； B．粒子动量不能准确确定；
C．粒子位置和动量都不能准确确定； D．粒子位置和动量不能同时准确确定。
共2页
word 格式-可编辑-感谢下载支持
二．填空题（每空 2 分，共 30 分） 1．一载流导线被弯曲成如图 3 形状，电流由无限远处流来，又
流向无限远处。则圆心 O 点处磁感应强度大小为 （1） ，
方向为 （2） 。
I 2．磁感应强度为 B 的均匀磁场，充满在半径为 R 的圆柱体体内, R
在柱内、外分别放有两个静止点电荷 qA 和 qB，距离轴心的距
o
I
离为 rA，rB。若圆柱体内 B 的大小以速率 dB dt 变化，则点电荷
图3
qA 和 qB 受到的作用力分别为 （3） ， （4） 。
9、光电效应和康普顿效应都为电子与光子的相互作用过程，在以下几种理解中，
关于这两个过程理解正确的是
（）
A．两种效应中电子与光子两者组成系统都不服从能量守恒定律；
B．两种效应都相当于电子与光子的弹性碰撞过程；
C．两种效应都属于电子吸收光子的过程；
D．光电效应是电子吸收光子的过程，康普顿效应则等效于光子和自由电子的弹性

势；（2）从距球心为 rp(rp R3) 的P点移动点电荷 q0 至无穷远
的过程中，电场力所做的功（图8）。
解（: 1）VA
R2 R1
q
4 0r 2 dr
qQ
R3 4 0r 2 dr
Q B
Aq
q
q
qQ
4 0 R1 4 0 R2 4 0 R3
R2 O
R1
R3
P
图8
或由电荷分布产生的电势叠加
q
F (3 4x) ma
a F (3 4x) 3 4 3 2.5m/s2
mm
6
F (3 4x) m d m d dx m d
dt dx dt
dx
1 m 2 3x 2 x2
2
（2 3x 2x2） 3m/s
m
2、在光滑的水平桌面上开一小孔。今有质量m的小球以细轻绳
系着，绳穿过小孔下垂，如图4。小球原以速率 υ0 沿半径R0在桌 面回转。在回转过程中将绳缓缓下拖，当小球的回转半径缩短为
0.12m，周期为2s，初始时 x =0.06m，并向 x 轴正向运动。求：
（1）物体的运动方程；（2）物体从初始时刻运动到平衡位置所
需要最短时间；（3）物体在平衡位置时所具有的机械能（图7）。
A
t0 A
O 图7
x
（3）E
Ek
E P max
1 2
k A2
1 2
m 2 A2
1 2 2 (0.12)2 0.0144 2
2
五、（10分）一摩尔的双原子理想气体，初始时压强为2atm，体
积为20l，先等压膨胀至原体积2倍，再等容冷却至原来温度，最
后等温压缩回到初态。求：（1）作出该循环的P-V图；（2）气

南京理工大学2004硕士研究生入学考试工程光学试题分析一、在国际标准单位制下，一单色平面光波的表示式为：)]1063(102exp[)232(8600t y x i y x E ⨯-+⨯+-=π式中：0x ，0y 分别是直角坐标系中x 轴和y 轴方向的单位矢量，求：1、画图示意出该光波的传播方向和偏振方向；2、该光波的振幅和频率；3、该光波的相速度和波长。

解：∵ 该平面光波在自由空间沿xy 平面传播的表达式为)]1063(102exp[)232(8600t y x i y x E ⨯-+⨯+-=π∴ 光波传播方向单位矢量：)0,23,21(0=k ，即在xy 平面内与x 轴成︒60 偏振方向为E 的方向，即与x 轴成︒150（如图中所示）∵ s rad /1012214⨯==ππνω∴ 光波的频率Hz 14106⨯=ν， m V A /4=光波的波长：nm C CT 500106103148=⨯⨯===νλ又∵ s rad kV /101214⨯==πω，6104⨯=πk∴ 相速度s m V /1038⨯=二、已知红宝石的折射率为76.1=n ，要使线偏振光的激光通过红宝石棒时在棒的端面没有反射损失，且光束在棒内沿棒轴方向传播，问：1、光束的入射角1ϕ为多少？00.10=n2、棒端面对棒轴的倾角α应该取多大？3、入射光的振动方向如何？解：（1）要使线偏振光的激光通过红宝石棒时在棒的端面没有反射损失那么边界条件应使得在入射点处的入射角为布儒斯特角（反射波只有s分量，而实际的线偏光中恰好没有s 分量）∴ ︒≈⇒=6.34sin 101ϕϕnn × （2）由于进入棒的光束在沿棒轴方向传播，根据折射定律可以知道： ︒≈⇒=⇒=--=2.71sin cos cos )2sin(sin 1010αϕαααππϕn n n n n ×（3）为达到题目中所提出的要求，入射光中应该只含有p 分量，即入射光在p 方向振动。

[][]的平均值为多少？态上力学量）在少？（体系能量的平均值为多出现的概率是多少可测得哪些值？各个值态的体系进行能量测量）对处于求（是正的实数。

，其中，的矩阵表示分别为：学量及力系哈密顿量算符为态空间中得基矢，体和、中，态十一、已经体系处于状的可能值是多少？下，力学量）（）（十、求在状态的几率为多少？的值为的本征态，求在此态中）如果粒子处于的本征值和本征态；（）表象中，求（九、在）能量至一级修正。

（示；）微扰哈密顿的矩阵表。

写出（《，其中矩阵表示为八、体系哈密顿算符的分）能量至二级修正值。

（为实数。

用微扰公式求，且七、在能量表象中分）。

（。

证明，六、设分）。

（中算符的表示为五、试证明在动量表象分）（的本征值和本征函数。

分量四、求角动量的分的可微函数，试证明：是三、设分）彼此正交。

（同能级的束缚态波函数）中运动，证明属于不（二、粒子在一维势场分）流密度。

（计算其几率密度和几率的粒子处于定态波函数一、质量为试题（量子力学）年硕士研究生入学考试南京理工大学A A H A HS L J Y S Y S S S S S S H b a E E a E b b a E H i S S pi x I z pf i q f p q q q f i p q x V e rm Z Z Z Z y x y x Z y x Zikr Z ψψαωαωϕϕϕϕϕϕψϕθχϕθχψααααββαβαϕ3)2(?1010100001ˆ200020001ˆˆˆ212121-ˆˆˆ),(),(231222ˆ,ˆ1ˆ2112002002ˆ15,,ˆ152ˆ,2ˆ100115ˆ15-i ˆ)15.(2)(,)(,,1515,12004003213211121-1021020102012⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=++=+=⎥⎦⎤⎢⎣⎡+==⎪⎪⎪⎭⎫ ⎝⎛=≠⎪⎪⎭⎫+ ⎝⎛+=-==⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=∂∂=∂∂====ψ南京理工大学2005年硕士研究生入学考试试题[][]()()面。

10年南京大学研究生入学考试试题-物理学专业-普通物理甲试题：1、如果地球的自转可以使地球赤道上的物体漂浮起来，那么一天将有多长？2、两个质点质量均为m，由一个长为L的轻杆连接为一刚体。

一开始刚体静止于光滑水平面上，现已垂直于轻杆的冲量I作用于其中一个质点上，求刚体以后的运动情况。

3.一作小角度摆动的单摆，质量为M，摆长为L ，弦线质量可忽略，在铅垂平面内自由摆动，初振幅为θ0若非常缓慢地将摆长缩短为L/2（一个周期内摆长的相对变化很小），试问单摆长振幅为原来θ0的几倍？4气缸内有单原子理想气体，若绝热压缩使其体积减半，问气体分子的平均速率为原来平均速率的几倍？若为双原子气体时又为几倍？5体积为V1+V2的绝热容器被一隔板分成体积为V1和V2的两部分。

体积为V1的部分有1ｍｏｌ理想气体，体积为V2的部分是真空。

当隔板抽掉后，气体膨胀充满整个空间。

问在这一过程中气体温度变化多少，熵的变化多少？6.设有一个内外半径分别为R1和R2的均匀带电薄圆环，电荷面密度为σ。

求圆环中轴线上各点的场强和电势。

7.两个相距很远的导体球，半径分别为R和ｒ（Ｒ＞ｒ），埋在相对介电常数为εr的电介质中，小球带正电荷Q。

现用一根细导线连接两个球。

（a）求两个球上的电荷分布；（b）求系统的电容；（c）求系统的静电能。

8.有一无限长薄铜片，厚度可忽略，宽度为d。

电流I沿着长边方向流过，电流在铜片上均匀分布。

（a）求铜片平面内右侧空间各点的磁感应强度；（b）在铜片平面内有一边长为a的正方形线圈，距铜片的距离也为a（如下图所示），求穿过线圈的磁通量。

9.彩虹的形成是由于日光遇到天空中细小的水珠时，光线被折射进水珠，并在水珠内反射，由于白光中不同波长的光线折射率不一样，不同颜色的光线离开水珠时便分开了。

我们通常看到的彩虹是水珠内一次反射光形成的。

定义进入水珠，又经过水珠内反射，再折射进空气的光线与入射到水珠的光线的夹角为偏向角。

彩虹出现在一次反射光最小偏向角的方向上。

【电光】南理工2004年《微波技术》A卷（附答案）分析（教师组卷、存档用）一.简答题 (10分)1.试给出微波的频率和波长 (在自由空间) 范围.2.(1) 传输线中的不同模式具有各自不同的特点, 简述圆波导中TE11,TM01和TE01模的不同特点;(2) 在以下的三种工程应用中, 应各自选择何种模式作为其工作模式最为有利? (a) 毫米波长距离多径通讯; (b) 机械扫描雷达天线用的旋转关节 (rotating joints); (c) 极化衰减器.3.为了降低矩形波导中主模的截止频率, 可以采取哪些措施?4.在何种情况下可以忽略微带线的辐射损耗? (Radiation loss)二.(1) 画出矩形波导中TE02模和TM21模的横截面场分布示意图. (5分)(2) 根据主模的壁电流分布特点, 试简单阐述波导测量线的工作原理.（5分)(3) 如果提供一台信号源, 一付波导测量线和选频放大器, 请简述驻波和波导波长的测量方法. (5分)三.波导衰减器可以用图(1)所示的一段截止波导构成.假设波导宽边a=22.86cm,工作频率为12GHz. 试求解以下问题: (15分)(1) 两段波导中主模的截止频率;(2) 如果衰减量为50dB, 问中间的截止波导的长度为多少毫米？四. 微波器件的散射参数可以用矢量网络分析仪测量得到, 其外部特性便可以用散射参数来表示. 下面是测量所得的某二端口微波器件的S-参数: (10分)据此S-参量, 请确定该二端口器件的如下外部特性参量:(1) 插入相移θ;(2) 输入驻波比;(3) 插入衰减(dB).五．假设一个50Ω的微带线，衬底介电常数为2.33, 衬底厚度为1.27mm, 导带宽度为3.913mm, 工作频率为2.5GHz. 试求：（15分）（１）有效介电常数；（２）波导波长；（３）如果根据上述参数设计一微带线谐振器，请问其长度如何选择？ []32320.320.880.880.32j j j j e e s e e ππππ=六．用Smith 圆图求图 (2) 所示无耗传输线的以下参量：（20 分）(1) 传输线上的驻波比和终端负载处的电压反射系数；(2) 该传输线的输入阻抗；(3) 若相邻两波节点的间距为60mm, 试求终端负载到第一个电压波腹点和第一个电压波节点的实际距离；(4) 给出第一个电压波腹点和波节点处的输入阻抗值(非归一化值)．图(2)七．魔Ｔ(Magic T) 是一种应用非常广泛的无源微波器件，图(3) 所示是其结构示意图．如果微波信号分别从Ｅ臂和Ｈ臂输入，试分析能量的输出特性，并画出各端口的电场分布图．（15分）图(3)Z in ? L= 0.32λZ L =60+j50Ω Z 0=50Ω微波技术试题答案及评分标准一. 简答题（10分，每小题2.5分）1. 微波的频率范围: 300MHz ~ 300GHz , 在自由空间的波长为1m~1mm 。