电子技术第14章

教案：苏科版九年级物理第14章第4节欧姆定律的应用一、教学内容1. 欧姆定律的表述及意义；2. 欧姆定律的应用场景；3. 电阻的计算与测量；4. 电流、电压、电阻三者之间的关系；5. 实际电路中欧姆定律的应用。

二、教学目标1. 使学生理解欧姆定律的表述及意义，能够运用欧姆定律解决实际问题；2. 培养学生运用物理知识解决生活问题的能力；3. 培养学生合作探究、动手实践的能力。

三、教学难点与重点1. 欧姆定律的应用场景；2. 电阻的计算与测量方法；3. 电流、电压、电阻之间的关系；4. 实际电路中欧姆定律的应用。

四、教具与学具准备1. 教具：多媒体课件、实验器材（电阻、电流表、电压表、导线、电源等）；2. 学具：笔记本、笔、实验报告单。

五、教学过程1. 实践情景引入：通过展示一个充电器，让学生思考：充电器的工作原理是什么？电流、电压、电阻之间有什么关系？2. 知识讲解：讲解欧姆定律的表述及意义，电流、电压、电阻之间的关系，电阻的计算与测量方法。

3. 例题讲解：给出一个实际电路问题，如：一个电阻值为R的电阻，两端电压为U，通过电阻的电流为I，求电阻的值。

4. 随堂练习：让学生根据欧姆定律，计算给定电压和电流下的电阻值。

5. 实验环节：让学生分组进行实验，测量不同电压和电流下的电阻值，验证欧姆定律。

六、板书设计欧姆定律：U = IR电阻的计算与测量：R = U / I七、作业设计1. 请简述欧姆定律的表述及意义；2. 请解释电流、电压、电阻之间的关系；3. 根据欧姆定律，计算给定电压和电流下的电阻值；4. 请举例说明欧姆定律在生活中的应用。

八、课后反思及拓展延伸本节课通过引入实践情景，让学生思考电流、电压、电阻之间的关系，通过例题讲解、随堂练习、实验环节，让学生深入理解欧姆定律，并能够运用欧姆定律解决实际问题。

在教学过程中，要注意引导学生思考欧姆定律在生活中的应用，提高学生的学习兴趣和积极性。

在课后，可以让学生进一步探究欧姆定律在其他领域的应用，如：电子技术、电力工程等。

第14章晶体管起放大作用的外部条件，发射结必须正向偏置，集电结反向偏置。

晶体管放大作用的实质是利用晶体管工作在放大区的电流分配关系实现能量转换。

2．晶体管的电流分配关系晶体管工作在放大区时，其各极电流关系如下：C B I I β≈(1)E B C B I I I I β=+=+C C BB I I I I ββ∆==∆3．晶体管的特性曲线和三个工作区域 （1）晶体管的输入特性曲线：晶体管的输入特性曲线反映了当UCE 等于某个电压时，B I 和BE U 之间的关系。

晶体管的输入特性也存在一个死区电压。

当发射结处于的正向偏压大于死区电压时，晶体管才会出现B I ，且B I 随BE U 线性变化。

（2）晶体管的输出特性曲线：晶体管的输出特性曲线反映当B I 为某个值时，C I 随CE U 变化的关系曲线。

在不同的B I 下，输出特性曲线是一组曲线。

B I =0以下区域为截止区，当CE U 比较小的区域为饱和区。

输出特性曲线近于水平部分为放大区。

（3）晶体管的三个区域：晶体管的发射结正偏，集电结反偏，晶体管工作在放大区。

此时，C I =b I β，C I 与b I 成线性正比关系，对应于曲线簇平行等距的部分。

晶体管发射结正偏压小于开启电压，或者反偏压，集电结反偏压，晶体管处于截止工作状态，对应输出特性曲线的截止区。

此时，B I =0，C I =CEO I 。

晶体管发射结和集电结都处于正向偏置，即CE U 很小时，晶体管工作在饱和区。

此时，C I 虽然很大，但C I ≠b I β。

即晶体管处于失控状态，集电极电流C I 不受输入基极电流B I 的控制。

14．3 典型例题例14．1 二极管电路如例14．1图所示，试判断二极管是导通还是截止，并确定各电路的输出电压值。

设二极管导通电压D U =0.7V 。

25610VD1(a)(b)(c)(d)例14.1图解：○1图（a ）电路中的二极管所加正偏压为2V ，大于DU =0.7V ，二极管处于导通状态，则输出电压0U =A U —D U =2V —0.7V=1.3V 。

模拟电子技术基础目录模拟电子技术基础目录模拟电子技术基础目录前言教学建议第1章半导体二极管及其应用1.1 半导体物理基础知识1.1.1 本征半导体1.1.2 杂质半导体1.2 pn结1.2.1 pn结的形成1.2.2 pn结的单向导电性1.2.3 pn结的反向击穿特性1.2.4 pn结的电容特性1.3 半导体二极管及其基本电路1.3.1 半导体二极管的伏安特性曲线1.3.2 半导体二极管的主要参数1.3.3 半导体二极管的电路模型1.3.4 二极管基本应用电路1.4 特殊二极管1.4.1 稳压二极管.1.4.2 变容二极管1.4.3 光电二极管1.4.4 发光二极管思考题习题第2章双极型晶体管及其放大电路2.1 双极型晶体管的工作原理2.1.1 双极型晶体管的结构2.1.2 双极型晶体管的工作原理2.2 晶体管的特性曲线2.2.1 共射极输出特性曲线2.2.2 共射极输入特性曲线2.2.3 温度对晶体管特性的影响2.2.4 晶体管的主要参数2.3 晶体管放大电路的放大原理2.3.1 放大电路的组成2.3.2 静态工作点的作用2.3.3 晶体管放大电路的放大原理2.3.4 基本放大电路的组成原则2.3.5 直流通路和交流通路2.4 放大电路的静态分析和设计2.4.1 晶体管的直流模型及静态工作点的估算2.4.2 静态工作点的图解分析法2.4.3 晶体管工作状态的判断方法2.4.4 放大状态下的直流偏置电路2.5 共射放大电路的动态分析和设计2.5.1 交流图解分析法2.5.2 放大电路的动态范围和非线性失真2.5.3 晶体管的交流小信号模型2.5.4 等效电路法分析共射放大电路2.5.5 共射放大电路的设计实例2.6 共集放大电路（射极输出器）2.7 共基放大电路2.8 多级放大电路2.8.1 级间耦合方式2.8.2 多级放大电路的性能指标计算2.8.3 常见的组合放大电路思考题习题第3章场效应晶体管及其放大电路3.1 场效应晶体管3.1.1 结型场效应管3.1.2 绝缘栅场效应管3.1.3 场效应管的参数3.2 场效应管工作状态分析及其偏置电路3.2.1 场效应管工作状态分析3.2.2 场效应管的偏置电路3.3 场效应管放大电路3.3.1 场效应管的低频小信号模型3.3.2 共源放大电路3.3.3 共漏放大电路思考题习题第4章放大电路的频率响应和噪声4.1 放大电路的频率响应和频率失真4.1.1 放大电路的幅频响应和幅频失真4.1.2 放大电路的相频响应和相频失真4.1.3 波特图4.2 晶体管的高频小信号模型和高频参数4.2.1 晶体管的高频小信号模型4.2.2 晶体管的高频参数4.3 晶体管放大电路的频率响应4.3.1 共射放大电路的频率响应4.3.2 共基、共集放大器的频率响应4.4 场效应管放大电路的频率响应4.4.1 场效应管的高频小信号等效电路4.4.2 共源放大电路的频率响应4.5 多级放大器的频率响应4.5.1 多级放大电路的上限频率4.5.2 多级放大电路的下限频率4.6 放大电路的噪声4.6.1 电子元件的噪声4.6.2 噪声的度量思考题习题第5章集成运算放大电路5.1 集成运算放大电路的特点5.2 电流源电路5.3 以电流源为有源负载的放大电路5.4 差动放大电路5.4.1 零点漂移现象5.4.2 差动放大电路的工作原理及性能分析5.4.3 具有电流源的差动放大电路5.4.4 差动放大电路的大信号分析5.4.5 差动放大电路的失调和温漂5.5 复合管及其放大电路5.6 集成运算放大电路的输出级电路5.7 集成运算放大电路举例5.7.1 双极型集成运算放大电路f0075.7.2 cmos集成运算放大电路mc145735.8 集成运算放大电路的外部特性及其理想化5.8.1 集成运放的模型5.8.2 集成运放的主要性能指标5.8.3 理想集成运算放大电路思考题习题第6章反馈6.1 反馈的基本概念及类型6.1.1 反馈的概念6.1.2 反馈放大电路的基本框图6.1.3 负反馈放大电路的基本方程6.1.4 负反馈放大电路的组态和四种基本类型6.2 负反馈对放大电路性能的影响6.2.1 稳定放大倍数6.2.2 展宽通频带6.2.3 减小非线性失真6.2.4 减少反馈环内的干扰和噪声6.2.5 改变输入电阻和输出电阻6.3 深度负反馈放大电路的近似计算6.3.1 深负反馈放大电路近似计算的一般方法6.3.2 深负反馈放大电路的近似计算6.4 负反馈放大电路的稳定性6.4.1 负反馈放大电路的自激振荡6.4.2 负反馈放大电路稳定性的判断6.4.3 负反馈放大电路自激振荡的消除方法思考题习题第7章集成运算放大器的应用7.1 基本运算电路7.1.1 比例运算电路7.1.2 求和运算电路7.1.3 积分和微分运算电路7.1.4 对数和反对数运算电路7.2 电压比较器7.2.1 电压比较器概述7.2.2 单门限比较器7.2.3 迟滞比较器7.2.4 窗口比较器7.3 弛张振荡器7.4 精密二极管电路7.4.1 精密整流电路7.4.2 峰值检波电路7.5 有源滤波器7.5.1 滤波电路的作用与分类7.5.2 一阶有源滤波器7.5.3 二阶有源滤波器7.5.4 开关电容滤波器思考题习题第8章功率放大电路8.1 功率放大电路的特点与分类8.2 甲类功率放大电路8.3 互补推挽乙类功率放大电路8.3.1 双电源互补推挽乙类功率放大电路8.3.2 单电源互补推挽乙类功率放大电路8.3.3 采用复合管的准互补推挽功率放大电路8.4 集成功率放大器8.5 功率器件8.5.1 双极型大功率晶体管8.5.2 功率mos器件8.5.3 绝缘栅双极型功率管及功率模块8.5.4 功率管的保护思考题习题第9章直流稳压电源9.1 直流电源的组成9.2 整流电路9.2.1 单相半波整流电路9.2.2 单相全波整流电路9.2.3 单相桥式整流电路9.2.4 倍压整流电路9.3 滤波电路9.3.1 电容滤波电路9.3.2 电感滤波电路9.3.3 复合型滤波电路9.4 稳压电路9.4.1 稳压电路的主要指标9.4.2 线性串联型直流稳压电路9.4.3 开关型直流稳压电路思考题习题第10章可编程模拟器件与电子电路仿真软件10.1 在系统可编程模拟电路原理与应用10.1.1 isppac10的结构和原理10.1.2 其他isppac器件的结构和原理10.1.3 isppac的典型应用10.2 multisim软件及其应用10.2.1 multisim 8的基本界面10.2.2 元件库10.2.3 仿真仪器10.2.4 仿真分析方法10.2.5 在模拟电路设计中的应用思考题习题第11章集成逻辑门电路11.1 双极型晶体管的开关特性11.2 mos管的开关特性11.3 ttl门电路11.3.1 ttl标准系列与非门11.3.2 其他类型的ttl标准系列门电路11.3.3 ttl其他系列门电路11.4 ecl门电路简介11.5 cmos门11.5.1 cmos反相器11.5.2 其他类型的cmos电路11.5.3 使用cmos集成电路的注意事项11.5.4 cmos其他系列门电路11.6 cmos电路与ttl电路的连接思考题习题参考文献延伸阅读：模拟电子技术基础50问1、空穴是一种载流子吗？空穴导电时电子运动吗？答：不是，但是在它的运动中可以将其等效为载流子。

第一章 习题与思考题◇ 习题 1-1欲使二极管具有良好的单向导电性，管子的正向电阻和反向电阻分别为大一些好，还是小一些好？ 解：二极管的正向电阻愈小愈好，反向电阻愈大愈好。

理想二极管的正向电阻等于零，反向电阻等于无穷大。

◇ 题 1-4已知在图P1-4中，u1=10sin ωt(V)，R L ＝1k Ω，试对应地画出二极管的电流i D 、电压u0的波形，并在波形图上标出幅值，设二极管的正向压降和反向电流可以忽略。

解：波形见图。

◇ 习题 1-5欲使稳压管具有良好稳压特性，它的工作电流I Z 、动态内阻r Z 以及温度系数a u 等各项参数，大一些好还是小一些好？解：动态内阻r Z 愈小，则当稳压管的电流变化时稳压管的电压变化量愈小，即稳压性能愈好。

一般来说，对同一个稳压管而言，工作电流I Z 愈大，则其动态内阻r Z 愈小，稳压性能也愈好。

但应注意不要超过其额定功耗，以免损坏稳压管。

温度系数a U 的绝对值愈小，表示当温度变化时，稳压管的电压变化的百分比愈小，则稳压性能愈好。

◇ 习题 1-7 在图P1-7 中，已知电源电压V=10V ，R=200Ω，R L =1 k Ω,稳压管的U Z =6V ，试求： ① 稳压管中的电流I Z =?② 当电流电压V 升高到12V ，I Z 将变为多少？ ③当V 仍为10V ，但R L 改为2 k Ω时，I Z 将变为多少？ 解：① mA mA mA k VV V R U R U U IL Z Z Z1462016200610=-=Ω-Ω-=--=② mA mA mA k VV V R U R U U IL Z Z Z2463016200612=-=Ω-Ω-=--=③ mA mA mA k VV V R U R U U IL Z Z Z1732026200610=-=Ω-Ω-=--=◇ 习题 1-8 设有两个相同型号的稳压管，稳压仁政值均为6V ，当工作在正向时管压降均为0.7V ，如果将它们用不同的方法串联后接入电路，可能得到几种不同的稳压值？试画出各种不同的串联方法。

第 14 章半导体器件一、选择题1、对半导体而言，其正确的说法是( )。

(1) P 型半导体中由于多数载流子为空穴，所以它带正电。

(2) N 型半导体中由于多数载流子为自由电子，所以它带负电。

(3) P 型半导体和 N 型半导体本身都不带电。

2、在图 14-1 所示电路中，Uo 为 ( ) 。

(1) -12V (2) -9V (3) -3VR- 0V D Z11V 3kΩ-9VUo DZ2U o + + R- -图14-1 图14-2 图14-33、在图 14-2 所示电路中，二极管 D1、D2、D3 的工作状态为( ) 。

(1) D1、D2 截止， D3 导通 (2) D1 截至， D2、D3 导通 (3) D1、D2、D3 均导通4、在图 14-3 所示电路中，稳压二极管 Dz1 和 Dz2 的稳定电压分别为 5V 和 7V，其正向压降可忽略不计，则 Uo 为( ) 。

(1) 5V (2) 7V (3) 0V5、在放大电路中，若测得某晶体管的三个极的电位分别为 6V，1.2V 和 1V，则该管为( )。

(1) NPN 型硅管 (2) PNP 型锗管 (3) NPN 型锗管6、对某电路的一个 NPN 型的硅管进行测试，测得 UBE>0，UBC>0，UCE>0，则此管工作在 ( ) 。

(1)放大区 (2)饱和区 (3) 截至区7、晶体管的控制方式为( ) 。

(1)输入电流控制输出电压 (2)输入电流控制输出电流 (3)输入电压控制输出电压二、判断题1、晶体管处于放大区，其 PN 结一定正偏。

( )2、三极管由二极管构成的，三极管具有放大作用，故二极管也具有放大作用。

( )3、二极管正向导通，反向截止，当反向电压等于反向击穿电压时，二极管失效了，故所有的二极管都不可能工作在反向击穿区。

( )三、填空题1、若本征半导体中掺入某 5 价杂质元素，可成为，其多数载流子为。

若在本征半导体中掺入某 3 价杂质元素，可成为，其少数载流子为。

模拟电子技术基础第四版清华大学电子学教研组编童诗白华成英主编自测题与习题解答山东大学物理与微电子学院目录第 1 章常用半导体器件‥‥‥‥‥‥‥‥‥‥3第 2 章基本放大电路‥‥‥‥‥‥‥‥‥‥‥14第 3 章多级放大电路‥‥‥‥‥‥‥‥‥‥‥31第 4 章集成运算放大电路‥‥‥‥‥‥‥‥‥41第 5 章放大电路的频率响应‥‥‥‥‥‥‥‥50第 6 章放大电路中的反馈‥‥‥‥‥‥‥‥‥60第 7 章信号的运算和处理‥‥‥‥‥‥‥‥‥74第 8 章波形的发生和信号的转换‥‥‥‥‥‥90第 9 章功率放大电路‥‥‥‥‥‥‥‥‥‥‥114第 10 章直流电源‥‥‥‥‥‥‥‥‥‥‥‥‥126第 1 章常用半导体器件自测题一、判断下列说法是否正确，用“×”和“√”表示判断结果填入空内。

(1)在 N 型半导体中如果掺入足够量的三价元素，可将其改型为 P 型半导体。

( √ )(2)因为 N 型半导体的多子是自由电子，所以它带负电。

( × )(3)PN 结在无光照、无外加电压时，结电流为零。

( √ )(4)处于放大状态的晶体管，集电极电流是多子漂移运动形成的。

( × )(5)结型场效应管外加的栅一源电压应使栅一源间的耗尽层承受反向电压，才能保证其R GS 大的特点。

( √ )(6)若耗尽型 N 沟道 MOS 管的U GS 大于零，则其输入电阻会明显变小。

( × )二、选择正确答案填入空内。

(l) PN 结加正向电压时，空间电荷区将 A 。

A.变窄B.基本不变C.变宽(2)稳压管的稳压区是其工作在 C 。

A.正向导通B.反向截止C.反向击穿(3)当晶体管工作在放大区时，发射结电压和集电结电压应为 B 。

A.前者反偏、后者也反偏B.前者正偏、后者反偏C.前者正偏、后者也正偏(4) U GS=0V 时，能够工作在恒流区的场效应管有 A 、C 。

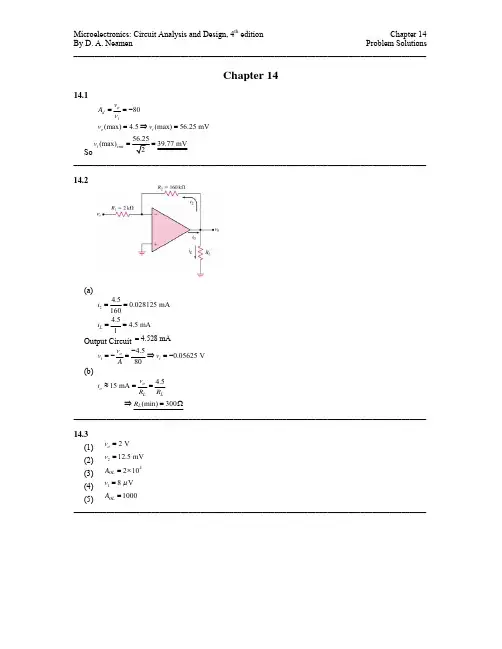
A.结型管B.增强型 MOS 管C.耗尽型 MOS 管三、写出图Tl.3 所示各电路的输出电压值，设二极管导通电压U D=0.7V。

Chapter 1414.1 80(max) 4.5(max)56.25 mV o d io i v A v v v ==−=⇒=So(max)i rms v = ______________________________________________________________________________________14.2(a) 2 4.50.028125 mA 1604.5 4.5 mA 1L i i ==== Output Circuit 4.528 mA = 4.50.05625 V 80o i i v v v A −=−=⇒=−(b) 4.515 mA (min)300o o L L L v i R R R ≈==⇒=Ω______________________________________________________________________________________14.3 (1)2 V o v = (2)212.5 mV v = (3)4210OL A =× (4) 18 V v μ=(5)1000OL A =______________________________________________________________________________________14.4(a) ()42857.216.512012−=−=−=∞R R A CL 42376.211042857.22142857.215−=+−=CL A ()%0224.0%10042857.2142857.2142376.21−=×−−−− (b) ()634146.142.812012−=−=−=∞R R A CL 63186.1410634146.151634146.145−=+−=CL A ()%0156.0%100634146.14634146.1463186.14−=×−−−− ______________________________________________________________________________________14.5(a) (i) 90863.710291176.7191176.71028.647118.647144=×+=×⎟⎠⎞⎜⎝⎛+++=CL A (ii) %03956.0%10091176.791176.790863.7−=×− (b) (i) 84966.71091176.7191176.73=+=CL A (ii) %785.0%10091176.791176.784966.7−=×− ______________________________________________________________________________________14.6(a) 12091.151050005.1102110.15121241231212=⇒⎟⎠⎞⎜⎝⎛×+−=×⎟⎠⎞⎜⎝⎛++−=−−R R R R R R R R R R (b) 1160.1510512091.16112091.154−=×+−=CL A ______________________________________________________________________________________14.7()()5109991.890190900001.01×=⇒+=−OL OLA A ______________________________________________________________________________________14.8()()499911110002.01=⇒+=−=OL OLCL A A A ______________________________________________________________________________________14.9(a) ()()001.0121001.0121012±±=+=R R A 02.10979.2021.210max ==A 98.9021.2179.209min ==A So 02.1098.9≤≤A (b) 009.101002.11102.104max =+=A 969.91098.10198.94min =+=A So 009.10969.9≤≤A ______________________________________________________________________________________14.1010110012010011212and so that 111I L iL I i v v v v v v A R R R v v A v v v R R R R R −−=+=−=−⎛⎞+=++⎜⎟⎝⎠1vSo 01201211111I L i v v R R A R R R ⎡⎤⎛⎞=−+++⎢⎥⎜⎟⎝⎠⎣⎦ Then 012012(1/)11111CL I L i v R A v R A R R R −==⎡⎤⎛⎞+++⎢⎥⎜⎟⎝⎠⎣⎦ From Equation (14.20) for and L R =∞00R =02(1)1111L if i A R R R +=+⋅ a. For1 k i R =Ω 33(1/20)11111100201001100.05[0.01 1.0610]CL A −−=⎡⎤⎛⎞+++⎜⎟⎢⎥⎝⎠⎣⎦−=+×or3 4.521111090.8 1100CL if if A R R ⇒=−+=+⇒=Ω b. For10 k i R =Ω 34(1/20)111111002010010100.05[0.01 1.610]CL A −−=⎡⎤⎛⎞+++⎜⎟⎢⎥⎝⎠⎣⎦−=+× or 4.92CL A ⇒=−31111098.9 10100if if R R +=+⇒=Ω c. For100 k i R =Ω 35(1/20)1111110020100100100.05[0.01710]CL A −−=⎡⎤⎛⎞+++⎜⎟⎢⎥⎝⎠⎣⎦−=+×or 3 4.9651111099.8 100100CL if if A R R ⇒=−+=+⇒=Ω ______________________________________________________________________________________14.1121211111o CL i OL R R v A v R A R ⎛⎞+⎜⎟⎝⎠==⎡⎤⎛⎞++⎢⎥⎜⎟⎝⎠⎣⎦ For the ideal: 210.10150.002R R ⎛⎞+==⎜⎟⎝⎠0 ()(0.10)(10.001)0.0999ov actual =−= So 0.09995049.9510.0021(50)OL A ==+which yields 1000OLA = ______________________________________________________________________________________14.12From Equation (14.18) 211121111OL o o vf L o A R R v A v R R R ⎛⎞−−⎜⎟⎝⎠==⎛⎞++⎜⎟⎝⎠ Or 331131151011100(4.9999910)111 1.111011004.50449510o o v v v v ⎛⎞×−−⎜⎟−×⎝⎠=⋅=⎛⎞++⎜⎟⎝⎠=−×⋅1v ⋅ Now 11111i v v i K v R v −=≡Then 11i v v KR v −=1 which yields 111i v v KR =+ Now, from Equation (14.20) 3311510111011101001101005.001110(0.1)(0.01)45.154951.11K ⎡⎤+×+⎢⎥=+⎢⎥⎢⎥++⎢⎥⎣⎦⎡⎤×=+=⎢⎥⎣⎦Then ()()145.15495101452.5495i i v v v ==+We find31 4.50449510452.5495i o v v ⎡⎤=−×⎢⎥⎣⎦ Or 119.9536o vf i v A v ==− For the second stage,L R =∞ 332131111151011100 4.9504851011110011151049.6148511010011001(49.61485)(10)1497.1485o o o o v v K v v v v KR ⎛⎞×−−⎜⎟⎝⎠′′=⋅=−⎛⎞+⎜⎟⎝⎠⎡⎤⎢⎥+×≡+=⎢⎥⎢⎥+⎢⎥⎣⎦′===++1v ×⋅ Then 321 4.950485109.95776497.1485o o v v −×==−So 2(9.9536)(9.95776)99.12o vf vf iv A A v ==−−⇒= ______________________________________________________________________________________14.13a.10113120I i v v v v v R R R R −−++=+ (1) 0131223111I i i v v v R R R R R R R ⎡⎤++=+⎢⎥++⎣⎦00001020L d L v v A v v v R R R −−++= (2) or 010*******L dL A v v v R R R R R ⎡⎤++=+⎢⎥⎣⎦ 13I d i i v v v R R R ⎛⎞−=⋅⎜⎟+⎝⎠ (3)So substituting numbers:011110201040401020I v v v 1⎡⎤++=+⎢⎥+⎣⎦+ (1)or10[0.15833][0.025][0.03333]I v v v =+ 410(10)11110.540400.5d v v v ⎡⎤++=+⎢⎥⎣⎦ (2) or[][]()4013.0250.025210dv v =+×v ()11200.66671020I d v v v v −⎛⎞=⋅=⎜⎟+⎝⎠I v − (3)So[][]()()()4013.0250.0252100.6667I v v v =+×−1v (2) or []44013.025 1.33310 1.33310I v v =×−×v ) From (1):()(100.15790.2105I v v v =+ Then []()()44003403.025 1.33310 1.333100.15790.21052.107810 1.052410I I I v v v v v v =×−×+⎡⎤⎣⎦⎡⎤⎡⎤×=×⎣⎦⎣⎦or 0 4.993CL I v A v == To find:if R Use Equation (14.27) ()31210.50.5114010110.50.50.51104014040(40)(1.5125){(0.125)(1.5125)0.0003125}25I d I d i v v i v ⎛⎞++⎜⎟⎝⎠⎧⎫⎛⎞⎛⎞=+++−−⎨⎬⎜⎟⎜⎟⎝⎠⎝⎠⎩⎭=−v −or (1.5125){0.18875}25I I d i v =−v I Nowand(20)d I i I v i R i ==1(20)I I v v i =− So(1.5125)[(20)][0.18875]25(20)[505.3](0.18875)I I I I I i v i i i v =−⋅−= or 2677 k I I v i =Ω Now 102677 2.687 M if if R R =+⇒=ΩTo determine 0:f R Using Equation (14.36)30200111110400.5111020L f i A R R R R R ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⋅=⋅′⎢⎥⎢⎥++⎢⎥⎢⎥⎣⎦⎣⎦or0 3.5 f R ′=Ω Then 0 1 k f R =ΩΩ0 3.49 f R ⇒=Ωb. Using Equation (14.16) 35(10)(0.05)%10CL CL CL CL dA dA A A ⎛⎞=−⇒=−⎜⎟⎝⎠ ______________________________________________________________________________________14.14(a)(b) (i)()o O I OL O i O I R A R υυυυυ−−=− ⎟⎟⎠⎞⎜⎜⎝⎛++=+o OL o iO o I OL i IR A R R R A R 11υυυ ⎟⎟⎠⎞⎜⎜⎝⎛×++=⎟⎟⎠⎞⎜⎜⎝⎛×+110511101110510133O I υυ()(33100011.5100001.5×=×O I υυ) 9998.0=IO υυ (ii) ()ix o x OL x x R V R V A V I +−−= 101110511113+×+=++==i o OL of x x R R A R V IΩ≅2.0of R______________________________________________________________________________________14.151011210121201040111201040201040I I I I v v v v v v v v v v −−−+=⎡⎤++=++⎢⎥⎣⎦ andso that 00L v A =−1v 010L v v A =−Then 1203200120000117(0.05)(0.10)4040210[2.5087510]1.993 3.9862 1.9930.352I I I I v v v v v v v v v %v v −⎧⎫⎛⎞+=−+⋅⎨⎬⎜⎟×⎝⎠⎩⎭=−×⇒=−−ΔΔ−=⇒= ______________________________________________________________________________________14.16224040.840105B v v v ⎛⎞⎛⎞===⎜⎟⎜⎟+⎝⎠⎝⎠2v (1) 011040A A v v v v −−= 011110401040A v v v ⎛⎞+=+⎜⎟⎝⎠ (2)10(0.1)(0.025)(0.125)A v v v += 000()L d L B A v A v A v v ==−(3)or002020020[0.8]0.80.8L A A LA L v A v v v v v A v v v A =−−=−⇒=−Then 01020120320021(0.1)(0.025)(0.125)0.80.125(0.1)(0.1)0.02510[2.512510]3.98010.01990.49754L d d d v v v v A v v v v v A v v A %A −⎡⎤+=−⎢⎥⎣⎦⎡⎤−=−+⎢⎥⎣⎦=−×⇒==−Δ⇒=⇒ ______________________________________________________________________________________14.17a. Considering the second op-amp and Equation (14.20), we have 211111001010.101100.1(0.1)(11)10.1if R ⎡⎤⎢⎥+=+⋅=+⎢⎥⎢⎥+⎢⎥⎣⎦ So 20.0109 k if R =ΩThe effective load on the first op-amp is then 120.10.1109 k L if R R =+=Ω Again using Equation (14.20), we have 11100111110.0170.11090.101110111.01710.11091if R ++=+⋅=+++ so that 99.1 if R =Ω b. To determine 0:f RFor the first op-amp, we can write, using Equation (14.36) 020101111100401111||10||L f i A R R R R R ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⋅=⋅⎢⎥⎢⎥++⎢⎥⎢⎥⎣⎦⎣⎦ which yields010.021 k f R =Ω For the second op-amp, then020*******()||11000.1011(0.121)||10L f f i A R R R R R R ⎡⎤⎢⎥⎢⎥=⋅⎢⎥+⎢⎥+⎣⎦⎡⎤⎢⎥⎢⎥=⋅⎢⎥+⎢⎥⎣⎦ or018.4 f R =Ω c. To find the gain, consider the second op-amp.0122202()0.10.1d d d i v v v v v R −−−−+= (1) 010221110.10.1100.10.1d v v v ⎛⎞+++=−⎜⎟⎝⎠ or 01202(10)(20.1)(10)d v v v +=−02020220()00.1L d d v A v v v R −−−+= (2) 0202202210010110.10.1(11)(90)0d d v v v v v ⎛⎞−−+⎜⎟⎝⎠−==−or 202(0.1222)d v v = Then Equation (1) becomes010202(10)(0.1222)(20.1)(10)v v v += or0102(1.246)v v =− Now consider the first op-amp.1110()11I d d d i v v v v v R −−−−+=1 (1) 10111(1)(1)1101I d v v v ⎛⎞+++=−⎜⎟⎝⎠1(1)(2.1)(1)v v v +=− or101I d 010*******()00.11091L d d v v A v v v R −−−++= (2) 011011111100100.11091111(11.017)(99)0d d v v v v ⎛⎞⎛++−−=⎜⎟⎜⎝⎠⎝−=⎞⎟⎠−or 101(0.1113)d v v = Then Equation (1) becomes0101(1)(0.1113)(2.1)I v v v += or01(1.234)I v v =− We had0102(1.246)v v =− So02(1.246)(1.234)I v v = or 020.650I v v =d. Ideal021Iv v = So ratio of actual to ideal0.650.=______________________________________________________________________________________14.18(a) For the op-amp. 60310L dB A f ⋅= 6341050 Hz 210dB f ==× For the closed-loop amplifier. 631040 kHz 25dB f == (b) Open-loop amplifier.444310A f f ==×=10 Closed-loop amplifier330.2524.255dB dB f f f f −===⇒______________________________________________________________________________________14.19dB,100=o A 510=⇒o A dB,38=A 43.79=A Then 2451011043.79⎟⎟⎠⎞⎜⎜⎝⎛+=PD f 94.743.79101054=⇒≅PD PD f f Hz Hz()()551094.794.710×==GBW ______________________________________________________________________________________14.20(a) 11151501112=⎟⎠⎞⎜⎝⎛+=⎟⎟⎠⎞⎜⎜⎝⎛+=R R A CLO kHz()10911102.1336=⇒=×=−−dB dB T f f f (b) ()()()()⎥⎦⎤⎢⎣⎡±±+=05.011505.011501CLO A ()05.1225.145.1571max =+=CLO A ()05.1075.155.1421min =+=CLO A Then05.1205.10≤≤CLO AkHz ()6.9905.12102.1336=⇒=×=−−dB dB T f f f kHz()4.11905.10102.1336=⇒=×=−−dB dB T f f f Then kHz4.1196.993≤≤−dB f ______________________________________________________________________________________14.21The open loop gain can be written as 006()11510L PD A A f f f j j f =⎛⎞⎛⎞+⋅+⋅⎜⎟⎜⎟×⎝⎠⎝⎠ where 50210.A =× The closed-loop response is 001L CL LA A A β=+ At low frequency, 552101001(210β×=+×) So that39.99510.β−=× Assuming the second pole is the same for both the open-loop and closed-loop, then116tan tan 510PD f f f φ−−⎛⎞⎛⎞=−−⎜⎟⎜⎟×⎝⎠⎝⎠ For a phase margin of80 ,°100.φ=−°So 1610090tan 510f −⎛⎞−=−−⎜⎟×⎝⎠ or58.81610 Hz f =× Then051L A == or 558.81610 1.969610PD f ×≅× or 4.48 HzPD f = ______________________________________________________________________________________14.22(a) 1st stage33(10) 1 100dB dB f MHz f kHz −−=⇒= 2nd stage33(50) 1 20dB dB f MHz f kHz −−=⇒= Bandwidth of overall system20 kHz ≅(b) If each stage has the same gain, so 250022.36K K =⇒= Then bandwidth of each stage33(22.36) 1 44.7dB dB f MHz f kHz −−=⇒= ______________________________________________________________________________________14.23(a) 9978.91051110.101141212−=×+−=⎟⎠⎞⎜⎝⎛++−=O CLO A R R R R A kHz()033.1509978.9105.1336=⇒=×=−−dB dB T f f f (b) ()34.9999978.93−=−=CLO A At ; dB f −364.706234.999==⇒CL AThen 323310033.150134.99964.706⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛×+=−dB f 49.7664.70634.99910033.1501323233=⇒⎟⎠⎞⎜⎝⎛=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛×+−−dB dB f f kHz ______________________________________________________________________________________14.24466333(510)1020 (25)1040 1PD PD dB dB vov v dB f f Hzf f kHzA A A fj f −−−×=⇒=⇒==⇒=+ At 30.520 dB f f k −==Hz22.36v AAt 3280 dB f f k −==Hz11.18v A = ______________________________________________________________________________________14.25 36(2010)1050vf vf MAX MAX A A ×⋅=⇒= ______________________________________________________________________________________14.26(a) ()159521052max 6max =⇒×==f V SR f PO ππkHz (b) ()5.5305.12105max 6max =⇒×=f f πkHz (c) ()99.14.02105max 6max =⇒×=f f πMHz ______________________________________________________________________________________14.27a. Using Equation (14.55), 6038102(25010)P V π×=× or 0 5.09 V P V =b.Period 6311410 s 25010T f −===××One-fourth period 1 sμ= 00Slope 8 V/s 18 VP P V SR s V μμ===⇒= ______________________________________________________________________________________14.28 PO V SR f π2max = V/s()()531054.71012102×=×=πSR Or V/754.0=SR μs______________________________________________________________________________________14.29(a) 0.521063.0102063max =⇒×=×=PO POV V f πV (b) ()87.231020210336=××=πPO V V ______________________________________________________________________________________14.30For input (a), maximum output is 5 V. 1 V/μs S R =soFor input (b), maximum output is 2 V.For input (c), maximum output is 0.5 V so the output is______________________________________________________________________________________14.31 For input (a),01max 3 V.v =Then02max 3(3)9 V v ==For input (b),01max 1.5 V.v =Then()02max 31.5 4.5V v ==______________________________________________________________________________________14.32111exp ,BE S T V I I V ⎛⎞=⎜⎟⎝⎠ 222exp BE S T V I I V ⎛⎞=⎜⎟⎝⎠ Want so12,I I = 1411214212510(1)exp 1510(1)exp (1)exp (1)BE T BE T BE BE T V x V I I V x V V V x x V −−⎛⎞×+⎜⎟⎝⎠==⎛⎞×−⎜⎟⎝⎠⎛⎞−+=⎜⎟−⎝⎠Or 211exp exp 10.0025exp 1.100.026OS BE BE T T V V V x x V ⎛⎞⎛−+==⎜⎟⎜−⎝⎠⎝⎛⎞==⎜⎟⎝⎠V ⎞⎟⎠Now 1(1)(1.10)x x +=−⇒ 0.0476 4.76%x =⇒______________________________________________________________________________________14.33(a) Balanced circuit, A154105−×=S I (b) From Eq. (14.62), 51=CE υV, 4.42.16.52=−=CE υV⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+⋅=++802.111204.41806.011205143S S I I()()015.1036667.10075.1041667.143⋅=S S I I 1544310939.40123.1−×=⇒=S S S I I I A (c) 51=CE υV, 1.35.26.52=−=CE υV ⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+⋅=++805.211201.31806.011205143S S I I()()03125.1025833.10075.1041667.143⋅=S S I I 1544310811.403937.1−×=⇒=S S S I I I A ______________________________________________________________________________________14.34μ150=n K A/V 2()()μx x x K n 30011501150=−−+=ΔA/V2 ⎟⎟⎠⎞⎜⎜⎝⎛Δ=n n n Q OS K K K I V 221()01837.08165.015030015022002110153=⇒=⎟⎠⎞⎜⎝⎛=×−x x x ______________________________________________________________________________________14.35(a) V()()3310603001021030−−×±−=×±−=O υ So 240.0360.0−≤≤−O υV (b) V()06.0310*******±−=×±−=−O υ So 94.206.3−≤≤−O υ V______________________________________________________________________________________14.36()2sin 2530±−=t O ωυmV06.0sin 75.0±−=t O ωυVSo ()(06.0sin 75.006.0sin 75.0)+−≤≤−−t t O ωυω V______________________________________________________________________________________14.373840.510510 10I A −−×==×Also 01i o o dV I I C V Idt t dt C C =⇒==∫⋅Then 836510511010t t s −−×=⇒=×0______________________________________________________________________________________14.38(a) (31010011±⎟⎠⎞⎜⎝⎛+=O υ) mV, 33331≤≤−O υmV ()33310502±±⎟⎠⎞⎜⎝⎛−=O υ mV, 1801802≤≤−O υmV (b) ()()310111±=O υ mV, 143771≤≤⇒O υmV()730314352−=+−=O υmV()37037752−=−−=O υmVSo 37.073.02−≤≤−O υV(c) ()()3100111±=O υ mV133.1067.11≤≤O υV()68.5003.0133.152−=+−=O υV()32.5003.0067.152−=−−=O υVSo 32.568.52−≤≤−O υV______________________________________________________________________________________14.39 due to 0v I v 01(0.5)10.9545 V 1.1v ⎛⎞=+=⎜⎟⎝⎠ Wiper arm at (using superposition) 10 V,V +=151154||0.0909(10)(10)||0.0909100.090R R v R R R ⎛⎞⎛⎞==⎜⎟⎜⎟++⎝⎠⎝⎠= Then 011(0.090)0.0901v ⎛⎞=−=−⎜⎟⎝⎠Wiper arm in center, and10v =020v = Wiper arm at10 V,V −=−10.090v =− So030.090v = Finally, total output (from superposition)0:v Wiper arm at,V + 00.8645 Vv = Wiper arm in center, 00.9545 V v = Wiper arm at,V − 0 1.0445 V v = ______________________________________________________________________________________14.40 a.120.5||250.490 k R R ′′===Ω or 12490 R R ′′==Ωb. From Equation (14.75), 6114621412510(0.026) ln (0.125)21012510(0.026) ln (0.125)2.210R R −−−−⎛⎞×′+⎜⎟×⎝⎠⎛⎞×′=+⎜⎟×⎝⎠12210.586452(0.125)0.583974(0.125)0.002478(0.125)()R R R R ′′+=+′′=−So210.0198 k 19.8 R R ′′−=Ω⇒Ω Then 2121(1)0.0198(1)(0.5)(1)(50)(0.5)(50)0.0198(0.5)(1)(50)(0.5)(50)25(1)250.019850.5500.550(0.550)(2525)(25)(50.550)0.0198(50.550)(0.550)x x x xR x R R R R x R R xR x x x x x x x xx x x x x x −×−=+−+−−=+−+−−=−++−−−=−+{}{}{}{}22222250.50.5505050.5500.019825.252525252500250.50.019825.25250025000.50.019998 1.98 1.981.98 2.980.4802x x x x x x x x x x x x x x x x x −+−−+=+−−−=+−−=+−−+==So 0.183x = and 10.81x −=7ΩΩ ______________________________________________________________________________________14.411122||150.5||150.4839 k ||350.5||350.4930 k R R R R ′===′=== From Equation (14.75), 121122341221121112222211222(0.026) ln (0.026) ln (0.026) ln (0.026) ln 1(0.026) ln (0.4930)1(0.9815)C C C C S S C C C C C C C C C C C C C C i i i R i R I I i i R i R i i i R i R i i R i i i i i ⎛⎞⎛⎞′′+=+⎜⎟⎜⎟⎝⎠⎝⎠⎛⎞′′=−⎜⎟⎝⎠′⎛⎞⎡⎤′=−⋅⎜⎟⎢⎥′⎝⎠⎣⎦⎛⎞=−⎜⎟⎝⎠⎡⎤⎛⎞⎢⎥⎜⎟⎝⎠⎣⎦ By trial and error: 1252 A C i μ= and 2248 A C i μ=or 12 1.0155C C i i = ______________________________________________________________________________________14.42(a) ()()()2.010********=×=−A O μυV Insert resistor3R ()()09.92020011022.03362=⇒⎟⎠⎞⎜⎝⎛+×−=−=−R R A O μυk Ω (b) ()()()16.010200108.0368.0=××=−A O μυV ()()09.29202001105.016.03365.0=⇒⎟⎠⎞⎜⎝⎛+×−=−=−R R A O μυk Ω ______________________________________________________________________________________14.43(a) V ()()3.010*********−=××−=−=−R I B O υ(b) ()5.03.002.015150−=−−=O υV (c) ()1.03.002.015150−=−−−=O υV (d) ()3.13.01.015150−=−−=O υV ______________________________________________________________________________________14.44(a) V ()()15.010250106.036=××=−O υ(b) ()()478.015.0008.041=+=O υV(c) ()()0065.015.00035.041=+−=O υV(d) ()()15.0sin 205.015.0sin 005.041+=+=t t O ωωυ (V)______________________________________________________________________________________14.45a.For 2 1 A,B I μ= then()(6401010v −=−) or00.010 Vv =− b. If a 10 resistor is included in the feedback loop k ΩNow021(10)(10)0B B v I I =−+= Circuit is compensated if12.B B I I =______________________________________________________________________________________14.46From Equation (14.83), we haveΩ 020S v R I = where and 240 k R =0 3 A.S I μ= Then()(3604010310v −=××) or 00.12 V v = ______________________________________________________________________________________14.47a. Assume all bias currents are in the same direction and into each op-amp.()()()6501101100 k 10100.1 V B v I v −=Ω=⇒=Then ()()()()()(020******* k 0.15105100.50.05B v v I −=−+Ω=−+×=−+)or 020.45 V v =− b. Connect resistor to noninverting terminal of first op-amp, and310||1009.09 k R ==ΩΩ resistor to noninverting terminal of second op-amp.310||508.33 k R ==______________________________________________________________________________________14.48a. For a constant current through a capacitor. 001 t v I C =∫dt or 60060.110(0.1)10v t v −−×=⋅⇒=t b.At10 s,t =0 1 V v = c. Then 1240010010(10)10v t v −−−×=⋅⇒=t At10 s,t =0 1 mV v = ______________________________________________________________________________________14.49(a) V()()15.010********=××=−O υ 15.02=O υV ()()()09.010*******.02020363−=××+−=−O υV (b) 33.85010==A R k Ω 102020==B R k Ω(c) V()()015.0103.01050631±=××±=−O υ 015.02±=O υVV()()021.0015.0103.01020633±=±××±=−O υ______________________________________________________________________________________14.50a. Using Equation (14.79),Circuit (a),()()()()63630500.81050100.8102510150v −−⎛⎞=××−××+⎜⎟⎝⎠ or 00v = Circuit (b),()()()()636302500.81050100.81010150410 1.6v −−−⎛⎞=××−×+⎜⎟⎝⎠=×− or 0 1.56 V v =− b. Assume 10.7 AB I μ= and 20.9 A,B I μ= then using Equation (14.79): Circuit (a),()()()()63630500.71050100.91025101500.0350.045v −−⎛⎞=××−××+⎜⎟⎝⎠=− or00.010 V v =−Circuit (b), ()()()()63660500.71050100.910101500.035 1.8v −−⎛⎞=××−×+⎜⎟⎝⎠=− or 0 1.765 Vv =−______________________________________________________________________________________14.51(a) For : OS V ()333101001±=±⎟⎠⎞⎜⎝⎛+=O υmV For : B I ()()()043.010*******.0max 36=××=−O υ V()()()037.010*******.0max 36=××=−OυVSo 764≤≤O υmV(b) For : OS V 33±=O υmV For : VOS I ()()006.010*******.036±=××±=−O υSo 3939≤≤−O υmV(c) ()039.02.0101001±⎟⎠⎞⎜⎝⎛+=O υ So 239.2161.2≤≤O υV______________________________________________________________________________________14.52a. 2(15)0.010 V i i R R R ⎛⎞=⎜⎟+⎝⎠ 22150.00066671515(10.0006667)0.0006667 R R =+−= Then 222.48 M R =Ωb.11||15||10 6 k i F R R R R ==⇒=Ω ______________________________________________________________________________________14.53a. Assume the offset voltage polarities are such as to produce the worst case values, but the bias currents are in the same direction.Use superposition:Offset voltages 010********||1(10)110 mV ||1050||(5)(110)1(10)10||610 mV v v v v ⎛⎞=+==⎜⎟⎝⎠⎛⎞=++⎜⎟⎝⎠⇒=Bias Currents: 6301(100 k )(210)(10010)0.2 V B v I −=Ω=××= Then6302(5)(0.2)(210)(5010)0.9 V v −=−+××=− Worst case: is positive and is negative, then01v 02v 010.31 V v = and 021.51 V v =−b. Compensation network:If we want20 mV and 10 V 8.33(10)0.0208.33B B C C R V V R R R ++⎛⎞==⎜⎟+⎝⎠⎛⎞=⎜⎟+⎝⎠ or 4.15 M C R ≅Ω______________________________________________________________________________________14.54(a) Offset voltage: ()122105011±=±⎟⎠⎞⎜⎝⎛+=O υmV 142122±=±±=O υmV ()()()16221220203±=±+±⎟⎠⎞⎜⎝⎛−=O υmV Bias current:V()()0105.010501021.0361=××=−O υ or V ()()0095.010501019.0361=××=−O υ 12O O υυ= ()()()()0042.010201021.0113613+−=××+−=−O O O υυυor()()0038.010201019.013613+−=××+−=−O O O υυυ By superposition5.225.21≤≤−O υmV5.245.42≤≤−O υmV7.103.223≤≤−O υmV(b) Bias currents:()()()110501002.010*******±=⇒××±=×±=−O OS O I υυmV()()()4.010201002.010*******±=⇒××±=×±=−O OS O I υυmVBy superposition: ()4.02213±±±=O O υυ13131≤≤−O υmV15152≤≤−O υmV4.174.173≤≤−O υmV______________________________________________________________________________________14.55For circuit (a), effect of bias current:390(5010)(10010) 5 mV v −=××⇒ Effect of offset voltage 050(2)1 4 mV 50v ⎛⎞=+=⎜⎟⎝⎠ So net output voltage is09 mV v = For circuit (b), effect of bias current:Let then from Equation (14.79),2550 nA,B I =1450 nA,B I = 93960250(45010)(5010)(55010)(10)1502.2510 1.1v −−−⎛⎞=××−×+⎜⎟⎝⎠=×− or0 1.0775 V v =− If the offset voltage is negative, then0(2)(2)4mV v =−=− So the net output voltage is 0 1.0815 Vv =− _____________________________________________________________________________________14.56a. At so the output voltage for each circuit is25C,T =°0 2 mV S V = 0 4 mV v = b. Forthe offset voltage for is 50C,T =° 0 2 mV (0.0067)(25) 2.1675 mV S V =+= so the output voltage for each circuit is 0 4.335 mVv = ______________________________________________________________________________________14.57 a. At then25C,T =°0 1 mV,S V = 010150(1)1 6 mV 10v v ⎛⎞=+⇒=⎜⎟⎝⎠and 020********(1)120206(4)(1)(4)28 mV v v v ⎛⎞⎛⎞=+++⎜⎟⎜⎟⎝⎠⎝⎠=+⇒= b. Atthen 50C,T =°01(0.0033)(25) 1.0825 mV,S V =+= 0101(1.0825)(6) 6.495 mV v v =⇒=and 02(6.495)(4)(1.0825)(4)v =+ or 0230.31 mVv = ______________________________________________________________________________________14.580025C;500 nA,200 nA50C,500 nA (8 nA /C)(25C)700 nA200 nA (2 nA /C)(25C)250 nA B S B S I I I I °==°=+°°==+°°= a. Circuit (a): For ,B I bias current cancellation, 00v =Circuit (b): For ,B I Equation (14.79), 93960050(50010)(5010)(50010)(10)1500.025 1.000.975 V v v −−⎛⎞=××−×+⎜⎟⎝⎠=−⇒=− b. Due to offset bias currents.Circuit (a): 930(20010)(5010)0.010 V v −=××⇒=0vCircuit (b): 21Let 600 nA400 nA B B I I == Then93960050(40010)(5010)(60010)(10)1500.020 1.20 1.18 V v v −−⎛⎞=××−×+⎜⎟⎝⎠=−⇒=−c. Circuit (a): Due to ,B I 0v = Circuit (b): Due to ,B I93960050(70010)(5010)(70010)(10)1500.035 1.40 1.365 V v v −−⎛⎞=××−×+⎜⎟⎝⎠=−⇒=−Circuit (a): Due to 0,S I930(25010)(5010)0.0125 V v v −=××⇒=0Circuit (b): Due to0,S I 21Let 825 nA575 nA B B I I == Then 93960050(57510)(5010)(82510)(10)1500.02875 1.65 1.62 Vv v −−⎛⎞=××−×+⎜⎟⎝⎠=−⇒=− ______________________________________________________________________________________14.590025C; 2 A,0.2 A 50C, 2 A (0.020 A /C)(25C 2.5 A 0.2 A (0.005 A /C)(25C)0.325 A B S B S I I I )I μμμμμμμμ°==°=+°°==+°°= a. Due to :B I (Assume bias currents into op-amp). 630101(50 k )(210)(5010)0.10 VB v I v −=Ω=××⇒= 020*********(60 k )(50 k )12020(0.1)(4)(210)(6010)(210)(6010)4B B v v I I −−⎛⎞⎛⎞=++Ω−Ω+⎜⎟⎜⎟⎝⎠⎝⎠=+××−××3 or020.12 V v = b. Due to0:S I1121st op-amp. Let 2.1 A2nd op-amp. Let 2.1 A1.9 A B B B I I I μμμ===6301101(50 k )(2.110)(5010)0.105 V B v I v −=Ω=××⇒= 020112636360601(60 k )(50 k )12020(0.105)(4)(2.110)(6010)(1.910)(5010)(4)B B v v I I −−⎛⎞⎛⎞=++Ω−Ω+⎜⎟⎜⎟⎝⎠⎝⎠=+××−×× or 020.166 V v =c. Due to :B I 63010101026363(2.510)(5010)0.125 V60601(60 k )(50 k )12020(0.125)(4)(2.510)(6010)(2.510)(5010(4)B B v v v v I I −−=××⇒=⎛⎞⎛⎞=++Ω−Ω+⎜⎟⎜⎟⎝⎠⎝⎠=+××−×× or 020.15 V v =Due to0:S I12Let 2.625 A2.3375 A B B I I μμ== 6301101(50 k )(2.662510)(5010)1.133 V B v I v −=Ω=××⇒= 020112636360601(60 k )(50 k )12020(0.133)(4)(2.662510)(6010)(2.337510)(5010)(4)B B v v I I −−⎛⎞⎛⎞=++Ω−Ω+⎜⎟⎜⎟⎝⎠⎝⎠=+××−×× or 020.224 Vv = ______________________________________________________________________________________14.60(a) 0.51050==d A For common-mode, 21I I υυ=From Chapter 9, 12431211R R R R R R A cm −⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛+= If , ()75.50015.1502==R ()85.9015.01101=−=R, ()85.9015.01103=−=R ()75.50015.1504==R Then 610046.515228.519409.115228.685.975.5075.5085.9185.975.501−×=−=−++=cm A If , ()15.10015.1103==R ()25.49015.01504=−=R Then 051268.015228.520609.115228.685.975.5025.4915.10185.975.501−=−=−++=cm A If , 25.492=R 15.101=R Then 04877.085222.419409.185222.515.1025.4975.5085.9115.1025.491+=−=−++=cm A Now ()8.39051268.05log 20min 10=⎟⎠⎞⎜⎝⎛=dB CMRR dB (b) , ()5.5103.1502==R ()70.997.0101==R, ()5.4897.0504==R ()3.1003.1103==R。