工程应用数学(研究生,2013)

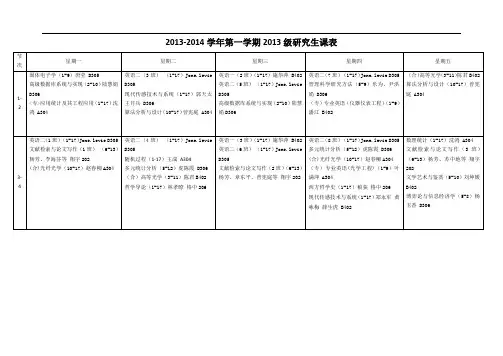
桂林电子科技大学2012～2013学年第二学期研究生课程安排表二〇一二年十二月课程安排说明一、研究生《英语I》课程安排说明：1、选课说明：机电工程学院、信息与通信学院、材料科学与工程学院的同学请在以下课号中选课：SX06003_01、SX06003_02、SX06003_03、SX06003_04、SX06003_05、SX06003_06、SX06003_07、SX06003_08其它学院的同学请在以下课号中选课：SX06003_09、SX06003_10、SX06003_11、SX06003_12、SX06003_13、SX06003_14、SX06003_15、SX06003_162、《英语I》授课内容分为听说和读写译两部分，每部分由不同的专业老师授课，网上任课老师只为实际授课老师之一。

具体安排如下：周二5、6节1-4班（听说）任课老师分别为：易永忠（2205）、黄林涛（2211）、任晓红（8507）、杨亚南（8505）（1班表示课号SX06003_01，2班表示课号SX06003_02，依此类推）5-8班（读写译）莫秀兰（6212）、李月（6312）、谷新黎（8310）、潘正芹（9106）7、8节9-12班（听说）易永忠（2205）、黄林涛（2211）、任晓红（8507）、杨亚南（8505）13-16班（读写译）莫秀兰（6212）、李月（8310）、谷新黎（8309）、潘正芹（9106）周四1、2节9-12班（读写译）韦储学（8310）、龙翔（8308）、谢玉（8309）、张燕（6212）13-16班（听说）赵明（8505）、黄悟（2205）、黄宇元（8507）、莫建萍（2211）3、4节1-4班（读写译）韦储学（8310）、龙翔（6312）、谢玉（8309）、张燕（6212）5-8班（听说）赵明（8505）、黄悟（2205）、黄宇元（8507）、莫建萍（2211）二、《中国特色社会主义理论与实践》课程安排：课号：SX09017_01 、SX09017_02、SX09017_03 2-10周星期六上午1-4节何平、李鸣、张文机电工程学院、信息与通信学院、材料科学与工程学院学生课号：SX09017_04 、SX09017_05、SX09017_06 2-10周星期六下午1-4节何平、曲宗琴、龙海平其他学院学生三、《体育》课程安排SF071111_01网球（宾金生）；SF071111_ 02普通（唐桂黔）；SF071111_03篮球（甘健辉）；SF071111_04篮球（高文强）；SF071111_05羽毛球（罗小刚）；SF071111_ 06乒乓球（韦朝贵）；SF071111_07篮球（李健）；SF071111_08羽毛球（宾苑成）；SF071111_09乒乓球（秦泽平）；SF071111_10篮球（秦小鹏）；SF071111_11排球（蓝瑞高）；SF071111_12足球（龚彦豪）；SF071111_13篮球（容贤冰）；SF071111_14定向越野（李启畅）；SF071111_ 15武术（黄程）SF071111_16网球（韦燊）；SF071111_ 17健美操（邓小兰）；SF071111_ 18健美操（黄宝叶）；SF071111_19排球（梁益军）；SF071111_ 20跆拳道（徐永峰）请各位同学严格按照上学期所选课号选课，因为《体育》两个学期只评1个成绩。

理学院
苏中地
5-15
周三5-7节
翔宇202
14
<专>矩阵论及其工程应用
1
32
大类基础课
理学院
王航平
1-12
周一9-11节
翔宇202
15
技术监督概论
1
16
公共选修课
经管学院
宋明顺
5-10
周四5-7节
A304
16
食品安全标准体系
1
16
公共选修课
生命学院
潘家荣
5-10
周三5-7节
A304
17
质检法律制度
1
1
32
公共选修课
理学院
赵承业
5-15
周四9-11节
A304
22
中国文化专题
1
16
公共选修课
人文学院
林孝暸
5-10
周三9-11节
C202
23
社会科学研究方法
1
16
公共选修课
马院
李海芬
12-17
周二9-11节
A304
24
数学思维
1
公共选修课
理学院
王航平、邹海雷
王义康
5-10
周二5-7节
A304
25
低碳发展与循环经济
材料热力学（1-12）沈杭燕D306
泛函分析（1-17）陶继成A206
材料电子学（8-18）张莉A304
法哲学和比较法学（5-15）周红阳刘义格中B109
通信测试技术（1-12）李九生赛北502
中国特色社会主义理论与实践研究（1班）（1-13）毕晓光课题组翔宇202
数学思维（5-10）王航平、邹海雷、王义康A304

1
选修
2
栾贻会 栾贻会 刘广臣
2-3
知新楼C座701
专硕二
P08019030
1
必修
2
2-3
知新楼B1230
山东大学2013－2014学年第一学期数学院、金融研究院研究生专业课课程表 概率论数理统计、金融数学与金融工程、应用统计
除注明的课程外，2013级研究生公共课、专业课上课时间：第二周周一（2013.09.16）至十八 周；考试时间：2014年1月6日－19日
C08019017 P08019007
1
必修
3
刘蕴贤
2-4 数学楼201教室
上课时间2-18周
有限差分法和 有限体积法; 差分方法及应 发展方程有限 元方法 发展 方程数值方法 自适应算法 分裂和并行算 法 区域分解与多 重网格 工程 软件与编程
1
选、必 修 必、选 修
3
刘允欣 5-7 数学楼203教室 上课时间2-18周
非线性随机分 析 非参数统计 金融数学 数理经济学
随机过程中的统 计推断、线性统 计模型 倒向随机微分
方程 随机计算 (1)：SDEs 随机计算 (2):FBSDFEs
Bayes统计
选修、 3 必修 必、选 3 修 选修 选修 选修
专硕必 修、科 选修
陈增敬 赵卫东 赵卫东 林 路
2 2 2
3
多元统计方法 生物统计
崔玉泉 胡发胜 王光辉 李国君 刘丙强
山东大学2013－2014学年第一学期数学院、金融研究院研究生专业课课程表 控制论、系统理论 7/9
除注明的课程外，2013级研究生公共课、专业课上课时间：第二周周一（2013.09.16）至十八 周；考试时间：2014年1月6日－19日

工学本科生和研究生要学的数学课程本科生：1. 微积分一般学校称之为高等数学，包括极限论、微积分、级数论、空间解析几何等内容。

2. 线性代数包括线性方程组、行列式、矩阵、二次齐式、线性空间（一般不讲）3. 概率论与数理统计包括概率论和数理统计两个部分，一般学校讲概率论较多，主要包括随机变量及数字特征。

4. 复变函数与积分变换包括解析函数、级数、共形映射、傅立叶变换和拉普拉斯变换等内容。

5. 矢量分析与场论包括梯度、散度和旋度等内容，电子信息类专业一般开设此课程。

6. 数学物理方程与特殊函数包括物理学中常见线性微分方程的分离变量法、贝塞尔函数和勒让德函数等内容。

7. 离散数学包括集合论、数论、图论、逻辑学、代数学和组合学等内容。

8. 随机过程包括泊松过程、马尔可夫过程、布朗运动等内容。

信息和通信专业学这门课。

研究生：9. 数值分析一般工科研究生都学这门课，包括插值、拟合、数值微分和数值积分等内容，很实用。

10. 最优化理论一般工科研究生都学这门课，类似数学专业的运筹学，很实用。

11. 应用泛函分析一般工科研究生都学这门课，主要提升内功。

12. 矩阵理论一般工科研究生都学这门课，线性代数的深化。

13. 数学物理方法（线性方程）电子信息类专业研究生都学这门课，解方程有特殊用途。

14. 小波分析电子信息类专业研究生学这门课，图像处理很有用。

15. 有限元方法电子信息类和工程力学类专业研究生学这门课，较为有效的计算方法。

16. 组合数学计算机专业研究生学这门课。

17. 高等数学物理方法（非线性方程）通信和光学工程类专业研究生学这门课，一般讲孤子理论。

18. 抽象代数信息和通信专业研究生学这门课，群论在信息编码和密码学中很有用。

19. 微分几何控制科学、人工智能类工科研究生学这门课。

20. 李群与李代数人工智能类工科研究生学这门课，和水泊梁山三当家一样，听起来无用，实际上有大用。

暂时想到这些，各位大神高人，欢迎您点评和补充[微笑][鼓掌]。

同上
复试：
外语听力和口语、专业口试加笔试城市规划学
复试：
外语听力和口语、专业口试加笔试环境学概论
2013年硕士研究生招生参考书目
考试科目
参考书名
出版社及年份
编者
生态学
《生态学》
高等教育出版社，2000年
李博主编
遥感概论
《遥感应用分析原理与方法》
北京：科学出版社，2003
赵英时等
水文学
《水文学原理》
中国水利水电出版社，2004
领域名称（代码）及研究方向
招生 人数
考试科目
备注
建筑与土木工程（085213）
01城市发展战略与空间管理
02城市规划与设计
环境工程（085229）
01湖泊污染控制与治理
02湖泊生态修复
2
2
①思想政治理论 ②英语（一） ③数学（二）④经济地理学
同上
①思想政治理论 ②英语（一） ③数学（二）④生态学或环境工程学
蒋展鹏主编
气候学
《气候物理学引论》
《气象学与气候学》
气象出版社，1997
高等教育出版社，1997
李晓东著
周淑贞主编
普通生物学
《普通生物学》
高等教育出版社，2005年（第二版）
吴相钰主编
自然地理学
《现代自然地理学》
高等学校教材《自然地理学》
高等教育出版社，2010
高等教育出版社，2004
王建主编
伍光和等
2013年硕士研究生招生目录
一、学术型学位专业及研究方向
学科、专业名称（代码）
研究方向
招生
人数
考 试 科 目
备注
070501 自然地理学

研究生英语（1-16周）尹祝辉3-1-402
研究生英语（1-16周）尹祝辉3-1-402
3-4
星
期
6-7
四
现代控制理论（1-8周）陈秀梅3-1-501
8-9
现代控制理论（1-8周）陈秀梅3-1-501
现代控制理论（1-8周）陈秀梅3-1-501
现代控制理论（1-8周）陈秀梅3-1-501
现代控制理论（1-8周）陈秀梅3-1-501
知识产权（11-14周）周飞跃3-2-大阶 信息检索（3-6周）江珊3-2-大阶
知识产权（11-14周）周飞跃3-2-大阶 信息检索（3-6周）江珊3-2-大阶
知识产权（11-14周）周飞跃3-2-大阶 信息检索（3-6周）江珊3-2-大阶
知识产权（11-14周）周飞跃3-2-大阶 信息检索（3-6周）江珊3-2-大阶
10-13
张云筝3-3-201
云筝3-3-201
周）张云筝3-3-201
波3-3-202
波3-3-202
周）敖云波3-3-202
中国特色社会主义理论与实践研究（1-9周）敖云 波3-3-202
1-2
3-4
研究生英语（1-16周）尹祝辉3-1-402
研究生英语（1-16周）尹祝辉3-1-402
研究生英语（1-16周）尹祝辉3-1-402
机
械振动理论（11-18周）戈新生3-1-501
机械振动理论（11-18周）戈新生3-1-501
械振动理论（11-18周）戈新生3-1-501
械振动理论（11-18周）戈新生3-1-501
设计研究方法（1-8）李洪海1-3-806
8-9
10-13
机械振动基础（11-18周）戈新生3-1-501 信息检索（3-6周）江珊3-2-大阶

，
⎜⎝ a3 ⎟⎠
⎜⎝ b3 ⎟⎠
（Ⅰ）证明二次型 f 对应的矩阵为 2αα T + ββ T ；
∫∫ x2dxdy
D
【详解】
第 3页（共 7页）
∫∫ ∫ ∫ ∫ ∫ x2dxdy =
2
dx
0
3 x
x
x
2dy
+
6
dx
2
8− x
x
x
2dy
D
3
3
∫ ∫ =
2 8x3 dx +
6 x2 (8 − 4 x)dx
03
2
3
= 32 + 384 = 416 33 3
（18）（本题满分 10 分）设奇函数 f (x) 在 [−1,1] 上具有二阶导数，且 f (1) = 1，证明：
f
(x)
=
⎧ ⎪⎪ ( x ⎨
1 − 1)α−1
,1 <
x
<
e
，若反常积分
+∞
f (x)d x 收敛，则（
⎪ ⎪⎩
x
1 lnα
+1
x
,
x≥e
1
）
(A) α < −2
【答案】D
(B) α > 2
(C) −2 < α < 0 (D) 0 < α < 2
（5）设 z = y f (xy) ，其中函数 f 可微，则 ∂z + ∂z = （ ）
=
1
确定，则
lim
n→∞
n
⎛ ⎜⎝
f
(
2 n
)
−
1⎞⎟⎠
=（

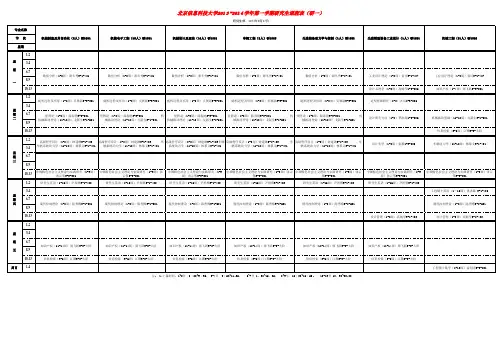
统计学硕士研究生培养方案（2013级研究生开始使用）一、专业学科、学制、学习方式一级学科名称：统计学（代码： 0270 ）二级学科名称：金融统计与风险管理（代码： 027001 ）二级学科名称：经济统计（代码： 027002 ）二级学科名称：应用统计（代码： 027003 ）二级学科名称：管理统计与决策（代码： 027004 ）二级学科名称：数量金融与保险精算（代码： 027005 ）学制：三年学习方式：全日制二、本学科情况介绍1、本学科建设时间较长，师资力量雄厚，科研实力强。

我校统计学学科作为应用数学的一个分支，建立于1958年，1994年经广州市人民政府批准成立了广州市系统工程研究所，以社会、经济、科教、环境等领域中的复杂大系统为研究对象，开展一系列统计分析研究工作。

1997年开始招收硕士生，2009年开始招收博士生。

2011年我校统计学被批准为一级学科博士和硕士授予权。

本学科现有教授11人，副教授8人，其中博士18人，博士生导师7人。

先后主持国家自然科学基金、国家社科基金、国家统计局以及国家软科学基金等30余项，省部级项目30项，合计获得科研经费1000多万元，获省部级以上科研奖励3项。

出版学术专著9部，教材12部。

在《Biometrika》《Statistica Sinica》、《中国科学》、《统计研究》、《金融研究》等重要刊物上发表了一系列重要论文。

2、主要研究方向稳定，特色鲜明，学科带头人影响大。

学科带头人长期从事数理统计、经济统计理论与方法、管理统计与决策分析的研究，取得了一批重要成果，在国内外有重要影响。

如，本学科在时间序列分析领域已成为国内主要研究中心之一，在国际上具有重大影响的第八届泛华统计国际学术会议就是2010年在我校召开的。

3、学术交流频繁，学术地位高。

五年来，本学科组织了国际国内学术会议10次，与美国、加拿大、英国、德国、香港等海外10多所高校与研究所开展了频繁的国际交流与合作，先后有20多人次参加国际会议并做大会报告。

研究生课程的数学与应用数学随着科学技术的不断发展和社会的进步，数学在现代社会中扮演着举足轻重的角色。

作为一门基础学科，数学在各个领域中的运用和拓展都极为深远。

尤其在研究生阶段，数学课程对于培养学生深厚的数学思维和解决实际问题的能力至关重要。

本文将从研究生数学课程的目标、数学的应用以及数学与应用数学的关系三个方面探讨研究生课程的数学与应用数学。

一、研究生数学课程的目标研究生数学课程的目标是培养学生掌握数学基本理论和方法，提高其数学建模和解决实际问题的能力。

首先，研究生数学课程注重学生对数学基础知识的扎实掌握。

通过学习数学分析、高等代数、概率论与数理统计等课程，培养学生对数学基本概念、定理和公式的理解和应用能力。

其次，研究生数学课程注重培养学生的数学建模和问题解决能力。

研究生是科学研究的主力军，需要能够准确地将实际问题转化为数学模型，并通过数学方法分析和解决问题。

因此，在数学建模、优化理论与方法等课程中，学生将学会如何应用数学知识解决实际问题。

最后，研究生数学课程注重提高学生的数学推理和创新能力。

数学不仅仅是一门知识，更是一种思维方式。

通过学习数学逻辑、数学分析和数学证明等课程，培养学生严谨的数学思维和创新的能力，为其日后从事科学研究和解决复杂实际问题奠定基础。

二、数学的应用领域数学作为一门应用广泛的学科，几乎渗透到了各个领域。

以下是数学在实际领域中的应用范例：1. 金融领域：数学在金融领域中有着广泛的应用，如金融衍生品定价、投资组合优化、风险管理等。

数学模型和方法为金融机构的决策提供了重要的支持。

2. 物理学领域：数学是物理学的基础，物理学中的很多理论和方程都是通过数学方法推导和证明的。

从牛顿力学到量子力学，数学在物理学的发展中起到了至关重要的作用。

3. 工程领域：工程学科中涉及到了大量的数学问题，如控制论、信号处理、最优化、统计方法等。

这些数学方法在工程领域的设计、建模和优化过程中发挥了关键的作用。

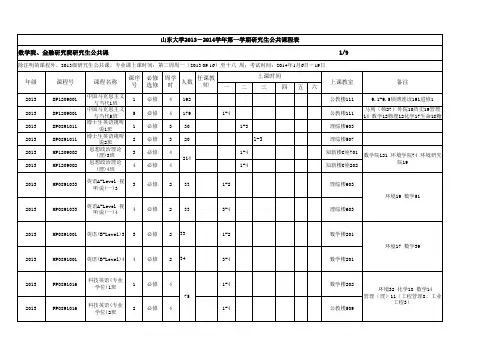
研究生课程介绍课程编码：091002课程名称：计算方法(A)Computational Methods (A)学分：3课内总学时数：72上机（实验）学时数：18课程内容简介：本课程讲授电子计算机上使用的各种基本的数值计算方法, 如插值法, 最小二乘法, 最佳一致逼近, 数值微积分, 方程求根法, 线性与非线性代数方程组解法, 矩阵特征值与特征向量求法, 常微分方程初值问题的解法, 求解数理方程定解问题的差分法, 有限元法等. 书中重点讨论了各种计算方法的构造原理和使用, 对稳定性, 收敛性, 误差估计等也作了适当讨论. 本课程适合于计算数学专业以外的理工科各专业研究生学习。

先修课：高等数学, 线性代数, C 语言或FORTRAN 语言参考书目：1. 邓建中,刘之行编, 计算方法，西安交通大学出版社，2002执笔人：梅立泉、李乃成、高静审定人：彭济根课程编码：091003课程名称：计算方法（B）Computational Methods (B)学分：3课内总学时数：54上机（实验）学时数：48课程内容简介：由于现代计算机技术的迅速发展，数值方法已成为科学研究的最重要的手段之一。

本课程在介绍数值计算的基本问题，包括浮点数、误差形成等的基础上，主要介绍：线性方程组的直接解法与迭代解法、离散数据的连续化处理（包括多项式插值、分段插值和最小二乘法）、数值积分和数值导数、非线性方程解法简介、常微分方程数值解法、以及最优化方法简介。

通过听课与相应的上机练习等途径，理解数值方法的形成原理，掌握最基本的数值方法，了解采用数值方法时应注意的主要问题，为以后在科研和工程技术工作中设计算法、应用数值软件进行数值计算奠定必要的基础。

先修课：高等数学、线性代数、算法语言（Fortran、C、C++、或Matlab 等）参考书目：1.凌永祥、陈明逵编，计算方法教程（第二版）西安交通大学出版社，2005执笔人：黄昌斌、苏剑、马军审定人：彭济根课程名称：工程优化方法及其应用Engineering Optimization Methods and Its Applications学分：2课内总学时数：40上机（实验）学时数：课程内容简介：讲述工程优化的数学基础，凸集、凸函数、凸规划的基本概念与基本理论；突出非线性规划各类算法的共性分析及其在计算机上可实现的步骤，并指出每类算法中所包含各种常用和著名算法；简介工程中常用到的几类特殊规划，如：线性规划、二次规划、几何规划和多目标规划的基本概念、常用和最新算法；简介工程优化设计应用实例（包括建立优化模型，根据模型特点构造或选用相适应的算法、计算流程图）。

21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43
新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 经济管理系 经济管理系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系
余永龙 倪永佳 周小三 王平 冯雪燕 陆 凡 戴 菁 陶周成 檀小惠 梁海滨 朱国平 张金倩 尹珺 宁丹丹 代毓杰 李浩淼 温茹 于璐 邓舒雨 李群 孙安琪 储学敏 王庭瑞
哈尔滨理工大学 广西民族大学 苏州科技学院 云南大学 上海师范大学 苏州大学 安徽师范大学 中共湖北省委党校 浙江师范大学 安徽大学 中国科技大学 上海海事大学 西南石油大学 扬州大学 上海海事大学 中国科学技术大学 上海师范大学 辽宁师范大学 合肥工业大学 赣南师范学院 浙江师范大学 河海大学 安徽师范大学
112 113 114
经济管理系 经济管理系 经济管理系
张平安 李永林 钟娇娇
青海民族大学 安徽大学 安庆师范学院
法律（非法学） 经济技术与管理 计算数学
新闻与传播 新闻与传播 新闻与传播 传播学 教育学原理 法律硕士 会计 农村与区域发展 现当代文学 文字学 古代文学 民俗学 古代文学 文字学 语言学及应用语言学 社会学 古代文学 民俗学 新闻学 教育学 文艺学 学科教学语文 社会学
44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66
2013届毕业生考取硕士研究生情况统计表
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 系别 外语系 外语系 外语系 外语系 外语系 外语系 外语系 外语系 外语系 设计艺术系 设计艺术系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 新闻传媒系 姓名 潘少兵 李蒙蒙 张滢莹 董瑞祥 邢瑞婷 柏昱君 王凯 李木子 程红 陈磊 谢朱 陈晓奕 武建树 李海平 李晨曦 毛莎莎 张颜也 刘 娇 方丹 赵谨 录取学校 大连外国语大学 西北大学 扬州大学 广州大学 西北大学 上海对外经贸大学 华中师范大学 上海师范大学 吉林大学 北京工业大学 安徽工程大学 安徽师范大学 广西民族大学 广西师范大学 华东师范大学 华东师范大学 华东师范大学 汕头大学 浙江传媒学院 南京师范大学 录取专业 汉语国际教育 翻译硕士 汉语国际教育 汉语国际教育 法律硕士 英语语言文学 汉语国际教育 日语语言文学 翻译硕士 数字媒体设计 平面设计 历史文献学 中国现当代文学 高等教育 新闻与传播 新闻与传播 国际政治 新闻传播学 新闻与媒体管理 新闻与传播

2013年研究生招生学科、专业代码册01哲学0101哲学010101 马克思主义哲学010102 中国哲学010103 外国哲学010104 逻辑学010105 伦理学010106 美学010107 宗教学010108 科学技术哲学02经济学0201理论经济学020101 政治经济学020102 经济思想史020103 经济史020104 西方经济学020105 世界经济020106 人口、资源与环境经济学0202应用经济学020201 国民经济学020202 区域经济学020203 财政学020204 金融学020205 产业经济学020206 国际贸易学020207 劳动经济学020208 统计学020209 数量经济学020210 国防经济0270统计学(0714)03法学0301法学030101 法学理论030102 法律史030103 宪法学与行政法学030104 刑法学030105 民商法学030106 诉讼法学030107 经济法学030108 环境与资源保护法学030109 国际法学030110 军事法学0302政治学030201 政治学理论030202 中外政治制度030203 科学社会主义与国际共产主义运动030204 中共党史030206 国际政治030207 国际关系030208 外交学0303社会学030301 社会学030302 人口学030303 人类学030304 民俗学0304民族学030401 民族学030402 马克思主义民族理论与政策030403 中国少数民族经济030404 中国少数民族史030405 中国少数民族艺术0305马克思主义理论030501 马克思主义基本原理030502 马克思主义发展史030503 马克思主义中国化研究030504 国外马克思主义研究030505 思想政治教育030506 中国近现代史基本问题研究0306公安学04教育学0401教育学040101 教育学原理040102 课程与教学论040103 教育史040104 比较教育学040105 学前教育学040106 高等教育学040107 成人教育学040108 职业技术教育学040109 特殊教育学040110 教育技术学040111 教育法学0402心理学040201 基础心理学040202 发展与教育心理学040203 应用心理学0403体育学040301 体育人文社会学040302 运动人体科学040303 体育教育训练学040304 民族传统体育学047101 教育经济与管理(120403)05文学0501中国语言文学050101 文艺学050102 语言学及应用语言学050103 汉语言文字学050104 中国古典文献学050105 中国古代文学050106 中国现当代文学050107 中国少数民族语言文学050108 比较文学与世界文学0502外国语言文学050201 英语语言文学050202 俄语语言文学050203 法语语言文学050204 德语语言文学050205 日语语言文学050206 印度语言文学050207 西班牙语语言文学050208 阿拉伯语语言文学050209 欧洲语言文学050210 亚非语言文学050211 外国语言学及应用语言学0503新闻传播学050301 新闻学050302 传播学06历史学0601考古学0602中国史0603世界史07理学0701数学070101 基础数学070102 计算数学070103 概率论与数理统计070104 应用数学070105 运筹学与控制论0702物理学070201 理论物理070202 粒子物理与原子核物理070203 原子与分子物理070204 等离子体物理070205 凝聚态物理070206 声学070207 光学070208 无线电物理0703化学070301 无机化学070302 分析化学070303 有机化学070304 物理化学070305 高分子化学与物理0704天文学070401 天体物理070402 天体测量与天体力学0705地理学070501 自然地理学070502 人文地理学070503 地图学与地理信息系统0706大气科学070601 气象学070602 大气物理学与大气环境0707海洋科学070701 物理海洋学070702 海洋化学070703 海洋生物学070704 海洋地质0708地球物理学070801 固体地球物理学070802 空间物理学0709地质学070901 矿物学、岩石学、矿床学070902 地球化学070903 古生物学与地层学070904 构造地质学070905 第四纪地质学0710生物学071001 植物学071002 动物学071003 生理学071004 水生生物学071005 微生物学071006 神经生物学071007 遗传学071008 发育生物学071009 细胞生物学071010 生物化学与分子生物学071011 生物物理学0711系统科学071101 系统理论071102 系统分析与集成0712科学技术史0713生态学0714统计学0771心理学(0402) 077101 基础心理学(040201) 077102 发展与教育心理学(040202) 077103 应用心理学(040203) 0772力学(0801) 077201 一般力学与力学基础(080101) 077202 固体力学(080102) 077203 流体力学(080103) 077204 工程力学(080104) 0773材料科学与工程(0805) 077301 材料物理与化学(080501) 077302 材料学(080502) 077303 材料加工工程(080503) 0774电子科学与技术(0809) 077401 物理电子学(080901) 077402 电路与系统(080902) 077403 微电子学与固体电子学(080903) 077404 电磁场与微波技术(080904) 0775计算机科学与技术(0812) 077501 计算机系统结构(081201) 077502 计算机软件与理论(081202) 077503 计算机应用技术(081203) 0776环境科学与工程(0830) 077601 环境科学(083001) 077602 环境工程(083002) 0777生物医学工程(0831) 0778基础医学(1001)077801 人体解剖与组织胚胎学 (100101) 077802 免疫学 (100102) 077803 病原生物学 (100103) 077804 病理学与病理生理学 (100104) 077805 法医学 (100105) 077806 放射医学 (100106) 0779 公共卫生与预防医学 (1004) 077901 流行病与卫生统计学 (100401) 077902 劳动卫生与环境卫生学 (100402) 077903 营养与食品卫生学 (100403) 077904 儿少卫生与妇幼保健学 (100404) 077905 卫生毒理学 (100405) 077906 军事预防医学(100406) 0780 药学(1007) 078001 药物化学 (100701) 078002 药剂学 (100702) 078003 生药学 (100703) 078004 药物分析学 (100704) 078005 微生物与生化药学 (100705) 078006 药理学 (100706) 0781 中药学 (1008) 0782 医学技术 (1010) 0783 护理学 (1011)078401 教育技术学 (040110) 078501 运动人体科学(040302) 078601 农药学(090403)08 工学0801 力学080101 一般力学与力学基础 080102 固体力学080103 流体力学080104 工程力学 0802 机械工程080201 机械制造及其自动化 080202 机械电子工程080203 机械设计及理论080204 车辆工程0803光学工程0804仪器科学与技术080401 精密仪器及机械080402 测试计量技术及仪器0805材料科学与工程080501 材料物理与化学080502 材料学080503 材料加工工程0806冶金工程080601 冶金物理化学080602 钢铁冶金080603 有色金属冶金0807动力工程及工程热物理080701 工程热物理080702 热能工程080703 动力机械及工程080704 流体机械及工程080705 制冷及低温工程080706 化工过程机械0808电气工程080801 电机与电器080802 电力系统及其自动化080803 高电压与绝缘技术080804 电力电子与电力传动080805 电工理论与新技术0809电子科学与技术080901 物理电子学080902 电路与系统080903 微电子学与固体电子学080904 电磁场与微波技术0810信息与通信工程081001 通信与信息系统081002 信号与信息处理0811控制科学与工程081101 控制理论与控制工程081102 检测技术与自动化装置081103 系统工程081104 模式识别与智能系统081105 导航、制导与控制0812计算机科学与技术081201 计算机系统结构081202 计算机软件与理论081203 计算机应用技术0813建筑学081301 建筑历史与理论081302 建筑设计及其理论081304 建筑技术科学0814土木工程081401 岩土工程081402 结构工程081403 市政工程081404 供热、供燃气、通风及空调工程081405 防灾减灾工程及防护工程081406 桥梁与隧道工程0815水利工程081501 水文学及水资源081502 水力学及河流动力学081503 水工结构工程081504 水利水电工程081505 港口、海岸及近海工程0816测绘科学与技术081601 大地测量学与测量工程081602 摄影测量与遥感081603 地图制图学与地理信息工程0817化学工程与技术081701 化学工程081702 化学工艺081703 生物化工081704 应用化学081705 工业催化0818地质资源与地质工程081801 矿产普查与勘探081802 地球探测与信息技术081803 地质工程0819矿业工程081901 采矿工程081902 矿物加工工程081903 安全技术及工程0820石油与天然气工程082001 油气井工程082002 油气田开发工程082003 油气储运工程0821纺织科学与工程082101 纺织工程082102 纺织材料与纺织品设计082103 纺织化学与染整工程082104 服装设计与工程0822轻工技术与工程082201 制浆造纸工程082202 制糖工程082203 发酵工程082204 皮革化学与工程0823交通运输工程082301 道路与铁道工程082302 交通信息工程及控制082303 交通运输规划与管理082304 载运工具运用工程0824船舶与海洋工程082401 船舶与海洋结构物设计制造082402 轮机工程082403 水声工程0825航空宇航科学与技术082501 飞行器设计082502 航空宇航推进理论与工程082503 航空宇航制造工程082504 人机与环境工程0826兵器科学与技术082601 武器系统与运用工程082602 兵器发射理论与技术082603 火炮、自动武器与弹药工程 082604 军事化学与烟火技术 0827 核科学与技术 082701 核能科学与工程 082702 核燃料循环与材料 082703 核技术及应用 082704 辐射防护及环境保护 0828 农业工程 082801 农业机械化工程 082802 农业水土工程082803 农业生物环境与能源工程 082804 农业电气化与自动化 0829 林业工程 082901 森林工程 082902 木材科学与技术 082903 林产化学加工工程 0830 环境科学与工程 083001 环境科学 083002 环境工程 0831 生物医学工程 0832 食品科学与工程 083201 食品科学083202 粮食、油脂及植物蛋白工程 083203 农产品加工及贮藏工程 083204 水产品加工及贮藏工程 0833 城乡规划学 0834 风景园林学 0835 软件工程 0836 生物工程0837 安全科学与工程 0838 公安技术0870 科学技术史 (0712) 0871 管理科学与工程 (1201) 0872 设计学 (1305)09农学0901作物学090101 作物栽培学与耕作学090102 作物遗传育种0902园艺学090201 果树学090202 蔬菜学090203 茶学0903农业资源与环境090301 土壤学090302 植物营养学0904植物保护090401 植物病理学090402 农业昆虫与害虫防治090403 农药学0905畜牧学090501 动物遗传育种与繁殖090502 动物营养与饲料科学090504 特种经济动物饲养0906兽医学090601 基础兽医学090602 预防兽医学090603 临床兽医学0907林学090701 林木遗传育种090702 森林培育090703 森林保护学090704 森林经理学090705 野生动植物保护与利用090706 园林植物与观赏园艺090707 水土保持与荒漠化防治0908水产090801 水产养殖090802 捕捞学090803 渔业资源0909草学0970科学技术史(0712)0971 环境科学与工程 (0830)097101 环境科学 (083001) 097102 环境工程(083002) 0972 食品科学与工程 (0832) 097201 食品科学 (083201) 097202 粮食、油脂及植物蛋白工程 (083202) 097203 农产品加工及贮藏工程 (083203) 097204 水产品加工及贮藏工程 (083204) 0973 风景园林学 (0834)10医学1001 基础医学 100101 人体解剖与组织胚胎学100102 免疫学100103 病原生物学100104 病理学与病理生理学100105 法医学100106 放射医学 1002 临床医学 100201 内科学 100202 儿科学 100203 老年医学 100204 神经病学100205 精神病与精神卫生学 100206 皮肤病与性病学 100207 影像医学与核医学 100208 临床检验诊断学 100210 外科学 100211 妇产科学 100212 眼科学 100213 耳鼻咽喉科学 100214 肿瘤学100215 康复医学与理疗学 100216 运动医学 100217 麻醉学 100218 急诊医学 1003口腔医学100301 口腔基础医学100302 口腔临床医学1004公共卫生与预防医学100401 流行病与卫生统计学100402 劳动卫生与环境卫生学100403 营养与食品卫生学100404 儿少卫生与妇幼保健学100405 卫生毒理学100406 军事预防医学1005中医学100501 中医基础理论100502 中医临床基础100503 中医医史文献100504 方剂学100505 中医诊断学100506 中医内科学100507 中医外科学100508 中医骨伤科学100509 中医妇科学100510 中医儿科学100511 中医五官科学100512 针灸推拿学100513 民族医学（含：藏医学、蒙医学等）1006中西医结合100601 中西医结合基础100602 中西医结合临床1007药学100701 药物化学100702 药剂学100703 生药学100704 药物分析学100705 微生物与生化药学100706 药理学1008中药学1009特种医学1010医学技术1011护理学1071科学技术史(0712) 1072生物医学工程(0831)107301 运动人体科学(040302) 107401 社会医学与卫生事业管理(120402)11军事学1101军事思想及军事历史110101 军事思想110102 军事历史1102战略学110201 军事战略学110202 战争动员学1103战役学110301 联合战役学110302 军种战役学1104战术学110401 合同战术学110402 兵种战术学1105军队指挥学110501 作战指挥学110502 军事运筹学110503 军事通信学110504 军事情报学110505 密码学1106军制学110601 军事组织编制学110602 军队管理学1107军队政治工作学1108军事后勤学110802 后方专业勤务1109军事装备学1110军事训练学12管理学1201管理科学与工程1202工商管理120201 会计学120202 企业管理120203 旅游管理120204 技术经济及管理1203农林经济管理120301 农业经济管理120302 林业经济管理1204公共管理120401 行政管理120402 社会医学与卫生事业管理120403 教育经济与管理120404 社会保障120405 土地资源管理1205图书情报与档案管理120501 图书馆学120502 情报学120503 档案学13艺术学1301艺术学理论1302音乐与舞蹈学1303戏剧与影视学1304美术学1305设计学。

哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 哲学 宗教学 宗教学 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治 国际政治
刘沁 黄笛 杨偲劢 周巍卫 周世愚 王群韬 伍翔凤 秦晋楠 刘梁 李想 李冀 方晔顿 白彦花 高旭 李红锦 冯慧羚 刘一鸣 张寰 罗宇迪 李嘉华 汪笑男 蒋季芳 王博医 李舒群 方欣捷 马鑫博 申一青 张平天 邵家毅 姚中道 彭骞 杨蕗闻 傅若兰 霍雪霏 孙婧 郑薇 王敏钊 包亦然 朱雅仪 王婉璐 伍雪骏 钱乙 孙博文 李泽 曾顺 陈琦斐 崔可忆 杨品杰 周瑜倩 张昕扬 夏布望 李艳茹 李晓杰 刘获 周冰阳 叶阳
郭留杨 陈冲 吴泽彬 常洪 李漫欣 薛非 袁会卓 何笑鸥 梁玥 范悦 赵志威 艾婧 付龙杰 陈晨曦 王竟先 傅晶雪 马千卉 廖威 黎永汉 刘彧多 蔡林泉 王殷超 孔维燃 赵义敏 余晨迪 张佳琦 魏佳林 张越 黄嘉怡 陈涵 王环宇 翟光耀 刘尚 袁文韬 张楠 徐智韬 姚帆 贠晓帆 吴昌晶 蔡政 周越 王亚平 刘明辉 邱颖骏 张云飞 杨怡然 范理思 孙振尧 陈延冰 朱佳琪 刘洋 陈江琦 张怡 张鹏浩 李屹 肖英东
李玉长 张晓慧 吴淑敏 包晓悦 曹茜茜 史少伟 王圆中 林欢彦 段维维 邵琳琳 李继东 努丽亚·卡迪尔 郑宪 孙迪 马骥飞 卢雪铮 孙斐 苏健伟 于天琳 严正达 陈磊 贺梦晨 高凯 梁千里 陆号 谢尧 钱栖榕 王沁鸥 王唱 马倩 刘星辰 侯亚杰 叶雨薇 徐斐宏 何月馨 黄莹 孙雪静 邓婉文 卢亚辉 解心怡 周杨 侯琳 侯郁聪 蔡经纬 马文轩 孙沛阳 王思渝 张巳丁 龙妍 陆元诚 陈竹茵 谢雨豪 裔传臻 马艳歌 郑晓莹 李震

维数公式（*）给出
dim(W1 W2 ) dimW1 dimW2 dim(W1 W2 ) 1.
5
为了求 W1 W2 的基，设 W1 W2 ，则由 W1
知，存在 k1 , k2 使 k11 k22 ，又由 W2 知，存在 k3 , k 4 使 k33 k44 因而， k1 , k2 , k3 , k4 应满足方程。
矩阵论复习
一、线性空间（子空间）的基与维数的求法、直和的概念 二、两个基之间过渡矩阵的求法 三、线性变换的概念及其矩阵表示
线性变换的特征值、特征向量的计算 四、特征多项式与最小多项式、Cayley-Hamilton定理
的简单应用 五、会求可逆矩阵将方阵化为Jordan标准型 六、向量与矩阵的范数、条件数的概念与计算 七、矩阵的三角分解
T的特征值问题与 A 的特征值问题是一一对应的。由于相似矩 阵有相同的特征多项式，所以我们可以把A的特征多项式
f ()det(In A) n b1n1 bn1 bn
称为T的特征多项式，于是T的特征值就是T的特征多项式的根。
10
为了求出T的特征值和特征向量，在 V n 中取一个基
B {1,2,,n}，且设T在B下的矩阵是A。 如果
6 1 6
注：把 A 相似简化为Jordan矩阵的关键是,寻找 A 关于其特
征值的各级根向量.1级根向量可以解齐次线性方程组
( A i I )x 0,i 1,2,, s
解det(I A) ( 2)3, 2 是A的三重特征值。齐次线性方程组
6 1 4 ( A 2I )x 12 2 8 x 0
7
三、线性变换的概念及其矩阵表示
定义 V n到V m的变换T 称为线性的，如果对任意的
数 k及V n中的任意向量 , , 恒有

第一部分 考研数学基本情况一．试卷分类及使用专业根据工学、经济学、管理学各学科、专业对硕士研究生入学所应具备的数学知识和能力的不同要求，硕士研究生入学统考数学试卷分为3种，其中针对工学门类的为数学一、数学二，针对经济学和管理学门类的为数学三.招生专业须使用的试卷种类规定如下：1.须使用数学一的招生专业1）工学门类中的力学、机械工程、光学工程、仪器科学与技术、冶金工程、动力工程及工程热物理、电气工程、电子科学与技术、信息与通信工程、控制科学与工程、计算机科学与技术、土木工程、水利工程、测绘科学与技术、交通运输工程、船舶与海洋工程、航空宇航科学与技术、兵器科学与技术、核科学与技术、生物医学工程等20个一级学科中所有的二级学科、专业.2）授工学学位的管理科学与工程一级学科。

2.须使用数学二的招生专业工学门类中的纺织科学与工程、轻工技术与工程、农业工程、林业工程、食品科学与工程等5个一级学科中所有的二级学科、专业。

3.须选用数学一或数学二的招生专业（由招生单位自定）工学门类中的材料科学与工程、化学工程与技术、地质资源与地质工程、矿业工程、石油与天然气工程、环境科学与工程等一级学科中对数学要求较高的二级学科、专业选用数学一，对数学要求较低的选用数学二。

4.须使用数学三的招生专业1）经济学门类的各一级学科。

2）管理学门类中的工商管理、农林经济管理一级学科。

3）授管理学学位的管理科学与工程一级学科。

二.考试形式和试卷结构1.试卷满分及考试时间试卷满分150分，考试时间为180分钟。

2.答题方式答题方式为闭卷、笔试。

3.试卷内容结构数学一： 高等数学 %56线性代数 %22概率论与数理统计 %22数学二： 高等数学 %78线性代数 %22数学三： 微积分 %56线性代数 %22概率论与数理统计 %224.试卷题型结构各卷种试卷题型结构为：单项选择题 8小题，每小题4分，共32分填空题 6小题，每小题4分，共24分解答题（包括证明题） 9大题，共94分三.考研数学全国平均成绩2006年2007年2008年2009年2010年 数学一83.0 62.2 70.7 68.1 70.9数学二91.4 72.3 85.8 77.6 64.7数学三81.2 68.6 69.4 68.3 73.4四.考研数学试题、试卷的特点及对策1.考试内容多、题量大数学一和数学三考三门课（高等数学；线性代数；概率论与数理统计），数学二考两门课（高等数学；线性代数）。

210 230 230 230 230 230 230 230 230 242 242 242 250 250 250 250 250 250 250 260 300 300 300 300 300 300 300 300 300 300 300 300 300 300 300 300 300 310 310 310 310 310 310 310 310 310 310 310 310 321 321 321 321 321 330
05 06 07 08 09 01 02 01 02 06 69 69 01 04 69 01 02 03 04 20 21 22 01 01 01 02 03 04 01 02 01 03 04 05 11 70 01 06 11 01 01 01 01 03 01 02 21 01 01 01 02 03 01 11 01
生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 生命科学学院 数学与计算科学学院 数学与计算科学学院 数学与计算科学学院 数学与计算科学学院 数学与计算科学学院 数学与计算科学学院 数学与计算科学学院 数学与计算科学学院 数学与计算科学学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 信息科学与技术学院 药学院 药学院 药学院 药学院 药学院 药学院 药学院 药学院 地理科学与规划学院 地理科学与规划学院 地理科学与规划学院 地理科学与规划学院 地理科学与规划学院

应用数学研究生考试科目一、数学专业基础课1. 高等数学：这可是重头戏呢，占的比重可不小。

一般会考查函数、极限、连续这些基础概念，就像搭房子的地基一样重要。

比如说求极限的各种方法，像洛必达法则啦，等价无穷小替换啦，那都是必须掌握的小技巧。

这部分可能会出很多选择题和计算题哦，选择题大概每题3 - 5分，出个8 - 10道很正常，计算题的话，分值可能在10 - 15分一道，来个3 - 5道也不奇怪。

2. 线性代数：矩阵、向量、线性方程组这些都是重点。

矩阵的运算、秩的概念、特征值和特征向量，听起来就很有挑战性吧，但也很有趣哦。

这部分可能选择题会出个6 - 8道，每题3 - 4分，简答题2 - 3道，每题10 - 15分。

比如说让你求一个矩阵的特征值和特征向量，那就要把公式记熟，计算准确。

3. 概率论与数理统计：概率的基本概念、随机变量、概率分布这些是关键。

像正态分布、二项分布这些常见的分布一定要滚瓜烂熟。

选择题可能会有6 - 8道，每题3 - 4分，计算和证明题2 - 3道，每题10 - 15分。

例如给你一个实际问题，让你判断是哪种概率分布，然后进行计算。

二、数学专业课1. 数学分析：这门课深入研究函数的各种性质，比如连续性、可微性、可积性。

里面的定理特别多，像拉格朗日中值定理、柯西中值定理之类的。

考试的时候，可能会出一些证明题来考查对定理的理解和运用，一道证明题分值可能在15 - 20分，出个2 - 3道，再加上一些计算题，每题10 - 15分，来个3 - 4道。

2. 高等代数：除了线性代数的基础内容，还会深入研究多项式理论、线性空间等更高级的内容。

对于多项式的整除、最大公因式这些概念，要理解透彻。

考试题型的话，选择题大概 6 - 8道，每题3 - 4分，解答题3 - 4道，每题10 - 15分。

3. 常微分方程：各种类型的微分方程的解法是重点，像一阶线性微分方程、二阶常系数线性微分方程。

考试可能会出一些求解微分方程的题目，选择题3 - 5道，每题3 - 4分，计算题3 - 4道，每题10 - 15分。