(完整版)苏教版七年级下册三角形内角和外角和.doc

1.三角形3个内角的和等于180°． 2.直角三角形两个锐角互余 3. 三角形的一个外角等于与它不相邻的 两个内角的和．
求图中的x、y的值.
112°
x ° 65°
（1）x＝ 47°
x°
（x－10）°
y°
（2）x＝ 50° y＝ 140°
动动脑
已知△ABC满足∠A＝ 是（ B ）
1∠B 2
＝
1∠C,则△ABC
3
A、锐角三角形 B、直角三角形
C、钝角三角形
D、等腰三角形
变题：若△ABC满足∠A＝2∠B ＝3∠C,则△ABC 是（ C ）
则图中有哪些互余的角？有相等的角吗？
C
解（1）∠A与∠B互余
∠A与∠ACD互余
AD
B
∠BCD与∠ACD互余
∠B与∠BCD互余
（2）∠A＝∠BCD ∠B＝∠ACD
∠ACB＝∠ADC ＝∠BDC
三角形的外角
三角形的一边与另一边 C
的延长线所组成的角，
叫做三角形的外角.
A
一边是公共边，另一边 是延长线
1
试一试
如图，AD是△ABC的角平分线，E是BC延长线上一点， ∠EAC=∠B， ∠ADE与∠DAE相等吗?为什么?
Ａ
Ｂ ＤＣ Ｅ
动动脑
如图所示，△ABC的角平分线BD、CE相交于点P， ∠A=70°.求∠BPC的度数。
A
EPD
B1
2C
动动脑
如图所示， 你能计算 ∠A ＋∠B ＋∠C＋∠D ＋∠E的值？
7.5多边形的内角和 与外角和(1)
探索活动
1、任意画一个三角形，用量角器量出三个内角 的度数，并求它们的和.
A
B

B
C D E
因为
∠ACE＝∠1+∠2，（为什么？） ∠BAF＝∠2+∠3，（为什么？） ∠CBD＝∠1+∠3，（为什么？）
三角形的一个 外角等于和它 不相邻的两个 内角的和．
所以
∠ACE+∠BAF+∠CBD =2(∠1+∠2+∠3)=2×180º ＝360º
F
A
1
三角形的三个外角和等于360º D
由三角形内角和性质易得：
A
直角边
B
直角三角形的两个锐角互为余角．
A 把△ABC的一边BC延长，得到∠ACD， 像这样，三角形一边与另一边的延长线组 成的角，叫作三角形的外角， B
对外角∠ACD而言，∠ACB是与它相邻的内角，∠A， ∠B是与它不相邻的内角．
C
D
三角形的外角与内角之间有什么样的关系呢？你能讲出道理吗？
ACD A ACD B
B C
D
与三角形的一个内角相邻 的外角有 多少个？它们之间有什么关系？
2
F
相等
A
B C D E
如图，对于△ABC每一个内角取它的一个外角，如∠ACE， ∠BAF，∠CBD，量一量这三个外角的大小，猜一猜任意三角形 的三个外角的和是多少？ F
360°
A
解：因为CD是∠ACB的角平分线， ∠ACB＝60°
1 所以 DCB ACB 30 2
因为∠A ＋∠B＋∠C＝180° B （三角形的内角和等于180°） 由∠B=50° 得∠BDC ＝100°
D
C
一个三角形的三个内角中，最多有几个直角？最多有几个钝角？
三个角都是锐角的三角形叫做 锐角三角形.如图（1） 有一个角是直角的三角形叫 做直角三角形.如图（2） 有一个角是钝角的三角形 叫钝角三角形.如图（3） 锐角三角形和钝角三角形合称斜三角形

7.5 多边形的内角和与外角和（1）
【探究三】拼图
请每位同学将课前发下的三角形纸片 的3个内角（如图）剪开，然后拼在一起， 观察它们的和是否为180°．
A
B
C
苏科版初中数学精品教学课件设计
7.5 多边形的内角和与外角和（1）
【探究四】说理
苏科版初中数学精品教学课件设计
7.5 多边形的内角和与外角和（1）
中小学精品教学资源 中小学精品教学资源
பைடு நூலகம்
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
中小学精品教学资源 中小学精品教学资源
7.5 多边形的内角和与外角和（1）
苏科版初中数学精品教学课件设计
7.5 多边形的内角和与外角和（1）
（1）小学里我们就已经知道了三角形的 三个内角的和等于多少度？
（2）你能举例说明三角形的三个内角的 和等于180°吗？
苏科版初中数学精品教学课件设计
7.5 多边形的内角和与外角和（1）
【探究一】画图、度量、计算
请每位同学在课堂笔记本上任意 画一个三角形，用量角器量出各内角 的度数，并求它们的和．
苏科版初中数学精品教学课件设计
7.5 多边形的内角和与外角和（1）
【探究二】观察 动画演示（见几何画板）
苏科版初中数学精品教学课件设计
【知识应用】牛刀小 试
课本P29练一练第1、3小题.
苏科版初中数学精品教学课件设计
7.5 多边形的内角和与外角和（1）
【例1】已知，在△ABC中，∠A＝40° ， ∠B＝∠C，求∠C的度数．

七年级下册数学第九章三角形的外角与内角摘要：一、三角形的外角与内角的基本概念二、三角形外角与内角的关系三、三角形外角与内角的性质与应用四、如何利用外角与内角解决实际问题五、总结与拓展正文：一、三角形的外角与内角的基本概念在七年级下册数学的第九章，我们将学习三角形的外角与内角。

三角形的外角是指一个三角形的一个角的外部角，而内角则是指三角形的一个角的内部角。

外角和内角是三角形的重要构成部分，它们之间的关系和性质对于我们理解和解决实际问题具有重要意义。

二、三角形外角与内角的关系根据外角和内角的定义，我们可以知道三角形的外角和内角之间存在以下关系：1.外角和等于内角和：一个三角形的一个外角与它所对应的内角之和等于180度。

2.外角大于任何一个不相邻的内角：对于一个三角形，它的任意一个外角都大于与之不相邻的内角。

三、三角形外角与内角的性质与应用掌握了三角形外角与内角的关系后，我们可以运用这些性质来解决实际问题。

例如，在解决几何图形的面积、周长等问题时，可以利用外角与内角的关系进行简化。

此外，外角与内角的关系在证明几何命题时也具有很高的实用价值。

四、如何利用外角与内角解决实际问题下面我们通过一个实例来展示如何利用外角与内角解决实际问题。

题目：已知一个三角形的两边长分别为3和4，求这个三角形的最大面积。

解：根据三角形外角与内角的关系，我们可以先求得这个三角形的一个外角，然后利用外角与内角的关系求得第三个内角，进而求得三角形的面积。

五、总结与拓展通过本章的学习，我们掌握了三角形的外角与内角的基本概念和性质，并学会了如何利用这些性质解决实际问题。

在今后的学习中，我们要不断加强对三角形外角与内角的理解，熟练运用它们的性质，提高解决实际问题的能力。

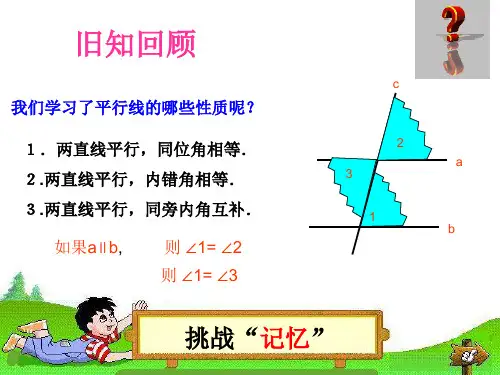
一、三角形的内角和定理三角形的内角和等于180度。

要会利用平行线性质、邻补角、平角等相关知识推出三角形内角和定理。

注：①、已知三角形的两个内角度数，可求出第三个角的度数；②、等边三角形的每一个内角都等于60度；③、如果已知等腰三角形的一个内角等于60度，那么这个等腰三角形就是等边三角形。

④、三角形中，有“大角对大边，大边对大角”性质，即度数较大的角，所对的边就较长，或较长的边，所对的角的度数较大。

例：已知等腰三角形的一个内角等于70度，则另外两个内角的度数分别是多少度?二、三角形的外角及其性质三角形的每一个内角都有相邻的两个外角，且这两个外角相等（对顶角相等）。

一共有六个外角。

其中，从与三角形的每一个内角相邻的两个外角中各取一个外角相加（一共三个外角相加），叫三角形的外角和。

根据邻补角、三角形的内角和等相关知识，可知：三角形的外角和= 360 度。

性质1、三角形的一个外角等于与它不相邻的两个内角和。

性质2、三角形的一个外角大于任何一个与它不相邻的内角。

（常用于解决角的不等关系问题）例：等腰三角形的一个外角等于100度，则这个等腰三角形的三个内角分别是多少度？注：（1）、△ABC内有一点O，连接BO、CO，则有∠BOC = ∠A + ∠ABO +∠ACO（2）、△ABC内有一点M，连接BM、CM，BO、CO分别是∠ABM 和∠ACM的平分线，则有∠BOC =(∠A +∠BMC)/2（3）、一个五角星，五个顶角的和等于180度。

（可利用性质1和三角形的内角和来加以证明）（4）、BO、CO分别是△ABC的内角平分线，BO、CO相交于点O，则∠BOC = 90°+ ∠A/2（5）、BO、CO分别是△ABC的外角平分线，BO、CO相交于点O，则∠BOC = 90°- ∠A/2（6）、BO是△ABC的内角平分线，CO是△ABC的外角平分线，BO、CO相交于点O，则∠BOC = ∠A/2（7）、①锐角三角形两条边上的高相交所成的夹角与第三边所对的角互补；②直角三角形两条边上的高相交所成的夹角与第三边所对的角相等；③钝角三角形一条钝角边上的高与钝角所对最大边上的高相交所成的夹角与另一钝角边所对的角相等，但若是两条钝角边上的高相交所成的夹角，则与第三边所对的角互补。

求∠EDF，∠DBC的度数.FFra bibliotekE DA
B
C
C
1
P
2
B
思考
1、在一个三角形的3个内角中，最多能有几个直角？ 最多能有几个钝角呢？为什么？
2、如图，在三角形纸片ABC中剪去∠C得到四边形ABDE， 且∠1+∠2=230°．求纸片中∠C的度数.
作业答案
1、60° 2、B 3、∠1+∠2=∠B+∠C
这个三角形简称共顶三角形 （或共角三角形、A字形）
锐角三角形
2
2
3
3
直角三角形
数学文化
帕斯卡(1623—1662)，法国数学家、哲学家。早在300多 年前也就是这位科学家12 岁时就已经发现这个结论。
帕斯卡
有一天他问父亲“什么是几何” ，父亲很简单地回答
说“几何就是教人在画图时能作出正确又美观的图”。 于是帕斯卡就拿了粉笔在地上画起各种图形来。画着画 着，帕斯卡发现任何一个三角形内角和都是180度；又发 现三角形三个内角的总和是两个直角。
数学文化
古希腊数学家欧几里德、泰勒斯等给予了证明。
阅读 三角形内角和定理：从历史到课堂
归纳总结：
文字语言： 三角形的内角和是180°
几何语言：
A
在△ABC中
∠A+∠B+∠C=180°（三角形内角和是180 ° ）.
B
C
练一练
1、求出图中的n、x、y的值：
A
81°
A
x°
B 72°
n°
C
(1)
(1)n=27°；
4、∠A+∠B=∠C+∠D 这个三角形简称对顶三角形 （或对角三角形、X字形、8字形）

A
3、A 2B 3C
3x
B 2x
xC
例2、如图，AC、BD相交于点O，
∠A与∠B的和等于∠C与∠D的和吗？
为什么？
O
C D
A
B
变式：如右图，∠A与∠B的和等于 ∠OCD与∠ODC的和吗？为什么？
1、如图：∠α=_____。
α
480
320
440
2、如图(1)是一个五角星，你会求∠A+ ∠B+ ∠C+ ∠D+ ∠E的值吗？
DE
F
2 G1 H
Ａ BC
考一考
1.一个三角形中最多有 1 个直角？为什么？ 2.一个三角形中最多有 1 个钝角？为什么？ 3.一个三角形中至少有 2 个锐角？为什么？
4.任意一个三角形中,最大的一个角的度数至少
为 60 °.
2、如图,某同学把一块三角形的玻璃打碎成三片,
现在他要到玻璃店去配一块形状完全一样的玻璃,
那么最省事的办法是 A.带①去 B.带②去
C.带③去 D.带①和②去
( C)
②
③
①
根据图形，你能说明“三角形3个内角的和等
于180°”吗？
三角形的内角和定理 三角形的三个内角的和等于180度。
1、n=__27__ ，x=_2_9__， y=_5_9__。
81 72
n
x
122
x
y 31
2、在直角三角形中， ∠C是直角，则 ∠A与∠B的和是多少？
重要结论：
直角三角形的两个锐角互余.
A
B
E
C
D
(1)
图(2)中的点A向下移到BE上时，五个角的 和（即∠CAD+ ∠B+ ∠C+ ∠D+ ∠E ）有无 变化？如图（2）说明你的结论的正确性。

7.5 三角形的内角和与外角和（3）
1．任意多边形的外角和等于__________．
2．（1）一个多边形，它的内角和是外角和的2倍，这个多边形的边数是（）．A．3 B．4 C．5 D．6
（2）一个多边形，它的每个内角都等于相邻外角的5倍，则这个多边形是( )
A．正五边形B．正十边形C．正十二边形D．不存在．
3．一个n边形的每一个外角都等于72°，则n = ，它的内角和是。

4．（1）n边形的内角和等于，多边形的外角和都等于．
（2）一个多边形的内角和等于它的外角和，那么这个多边形是边形．
（3）一个多边形的每个外角都是300，则这个多边形是边形．
（4）一个十边形所有内角都相等，它的每一个外角等于度．
（5）一个五边形五个外角的比是2：3：4：5：6，则这个五边形五个外角的度数分别是．
（6）多边形边数增加一条，则它的内角和增加度，外角和．
5．一个多边形的外角和是内角和的1
5
，它是几边形？
6．一个多边形的每一个外角都是72°，那么这个多边形的内角和为多少度？
7．一个多边形每一个外角都等于与它相邻的内角，这种多边形是几边形？能确定它的每一个外角的度数吗？
8、一个多边形的各个内角都相等，且一个内角是150°，你知道它是几边形吗？
9．一个零件的形状如图中阴影部分．按规定∠A应等于90º，∠B、∠C应分别是29º和21º，检验人员度量得∠BDC＝141º，就断定这个零件不合格．你能说明理
由吗？
10．若两个多边形的边数相差1，则它们的内角和、外角和分别有什么异同？
第9题图。

BΒιβλιοθήκη (A CKEF
C
试一试
1
A
BD
∵∠A+∠C+∠1=180°(三角形三个)内角的和等于180°.
∴∠A+∠C= 180°- ∠1
∵ ∠1+ ∠CBD= 180°( 平角定义)
∴ ∠CBD= 180°- ∠1
∴∠A+∠C = ∠CBD 。
结论：三角形的一个外角等于与它不相邻
的两个内角的和.
练一练
1.求图中x和y的值.
B1 O
2
∴∠A+∠B=180°－∠1. ∵ ∠C+∠D+∠2=180° ∴ ∠C+∠D=180°－∠2. 又∵ ∠1= ∠2，
C
D ∴∠A+∠B= ∠C+∠D
1.根据下图填空：
∟
做一做 81°
72° n°
x° 122° x°
(1)
(2)
(1)n= 2；7 (2)x= ； (239)y= .
y° 31°
7.5 多边形的内角和与外角和
多边形的内角和(1) ───三角形三个内角的和
三角形三个内角的和 等于180°.
结论： 三角形三个内角的和等于180°.
如图,3根木条相交得∠1、∠2.若a∥b,则 ∠1+∠2=180.理°由: 两直线平行. ,同旁内角互补
A 24
caa
议一议
B1
3C
b
把木条a绕点A转动,使它与木条b相交于点C. 木 条 a 原位置的直线记为c, 此时c∥b 根据图形,你能说明∠1+∠2+∠3=180°吗？
(3)
59
2.在直角△ABC中,∠C=90°,∠A+∠B=90°.

●●●●
知2－讲
(2)分类： 多边形按组成它的线段的条数分成三角形、四边形、五边
形……三角形是最简单的多边形. 如果一个多边形由n条 线段组成，那么这个多边形就叫做n边形.
特别解读： 多边形的三个必要条件： 1. 线段在“同一平面内”； 2. 线段“不在同一直线上”且条数不少于3； 3. 首尾依次相接.
2∶3∶4，则这个三角形是()
A
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 等腰三角形
知1－讲
解题秘方：紧扣三角形的三个内角的度数比，求出三个 内角的度数，根据三个内角的度数判断三 角形的形状．
知1－讲
另解：设三个内角分别为2x°、3x°、4x°， 则2x+3x+4x＝180. 解得x＝20.所以4x＝80. 即可求解.
所以∠OBE+∠OEB=∠C+∠D.
所
以
∠ A+∠ABC+∠C+∠D+∠FED+∠F=∠A+∠ABC+∠OB
E+∠OEB+∠FED+∠F=∠A+∠ABE+∠BEF+∠F=360°.
知2－讲
解题秘方：由于所求的六个角不在同一个多边形中， 所以考虑把它们转化到同一个多边形中. 如图7.5-6，连接BE，则这六个角的和等 于四边形ABEF的内角和.
多边形的内角 和与外角和
多边形的内角 和与外角和
三角形 多边形
三角形的内角和是180° n边形的内角和 等于(n-2)·180°
多边形的外 角和等于360°
课后作业
作业1 必做:请完成教材课后习题 补充:
作业2
知2－讲

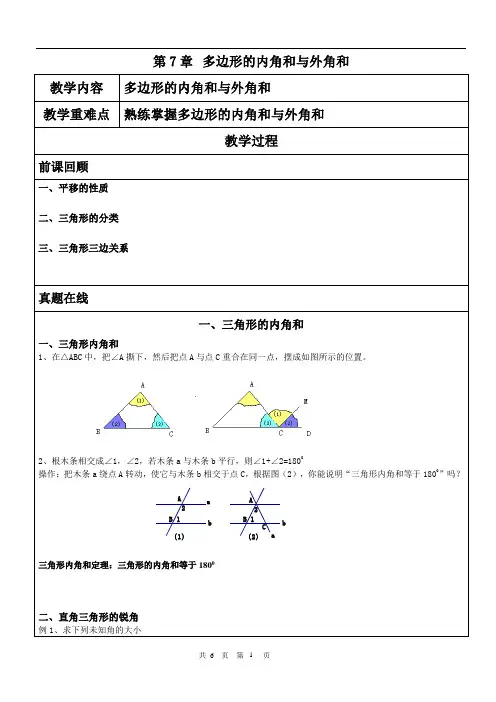
第7章多边形的内角和与外角和教学内容多边形的内角和与外角和教学重难点熟练掌握多边形的内角和与外角和教学过程前课回顾一、平移的性质二、三角形的分类三、三角形三边关系真题在线一、三角形的内角和一、三角形内角和1、在△ABC中，把∠A撕下，然后把点A与点C重合在同一点，摆成如图所示的位置。

2、根木条相交成∠1，∠2，若木条a与木条b平行，则∠1+∠2=1800操作：把木条a绕点A转动，使它与木条b相交于点C，根据图（2），你能说明“三角形内角和等于1800”吗？三角形内角和定理：三角形的内角和等于1800二、直角三角形的锐角例1、求下列未知角的大小ABab(2)1221(1)baCBAx ︒x ︒122︒1A BC D [来源:学科网]直角三角形的两个锐角互余三、三角形的外角把△ABC 的边AB 延长，得到∠CBD ，∠A 、∠C 和∠CBD 的度数的关系:学*科*网Z*X*X*K]三角形的一个外角等于与它不相邻的两个内角的和二、多边形的内角和一、多边形的有关概念（1）在平面内，由一些线段首尾顺次相接组成的图形叫做多边形.一个多边形由几条线段组成，就叫做几边形，三角形是最简单的多边形。

（2）多边形中相邻两边组成的角叫做多边形的内角.如图中的∠A 、∠B 、∠C 、∠D 、∠E 。

（3）多边形的边与它的邻边的延长线组成的角叫做多边形的外角.如图中的∠1是五边形ABCDE 的一个外角。

（4）连结多边形不相邻的两个顶点的线段，叫做多边形的对角线.从n 边形的一个顶点可以引_______条对角线，它们将n 边形分成_______•个三角形． 从n 边形一个顶点可引9条对角线，则此n 边形的边数是_______．（5）各个角都相等，各条边都相等的多边形叫做正多边形。

二、多边形的内角和1、两 个三角形有一条边相等，把它们拼在一起，构成一个四边形，则这个四边形的内角和为多少？n ︒81︒72︒y ︒31︒A BCD E2.、任意一个四边形的内角和是多少？任意一个五边形的内角和是多少？（五边形可以看作是在四边形的基础上加了一个三角形，反之，一个五边形也可以分解为3 个三角形，其中AD 、BD 这样的线段叫做对角线） 对于边数更多的多边形，可以考虑类似的方法。

数学三角形的内角和某某科技版【本讲教育信息】一. 教学内容：三角形的内角和二. 教学目标：1. 掌握三角形内角和定理及外角有关性质。

2. 掌握多边形内角和的计算公式及其应用。

3. 三角形外角和的规律及其简单应用。

三. 重、难点：1. 三角形内角和与三角形外角的有关性质的应用。

2. 多边形内角和的计算公式及其应用。

3. 三角形外角和的特点及其应用。

四. 知识要点1. 三角形的内角：（1）三角形的三个内角的和等于180°。

（2）推论：直角三角形的两个锐角互余。

2. 三角形的外角：（1）三角形的一边与另一边的延长线所组成的角，叫做三角形的外角。

图中的∠CBD称为△ABC的一个外角注意：“外角”是三角形的外角，不是它相邻内角的外角。

对三角形的外角,称某个角是某个三角形的外角,而不称三角形某个角的外角（2）三角形的一个外角等于与它不相邻的两个内角的和。

三角形的外角和等于360°。

3. 多边形的外角：（1）多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角，在每个顶点处取这个多边形的一个外角，它们的和叫做这个多边形的外角和。

（2）任意多边形的外角和等于360°。

4. 多边形的内角：n 边形的内角和等于（n －2）·180°【典型例题】例1. （1）已知四边形4个内角的度数比是1︰2︰3︰4，那么这个四边形中最大角的度数是。

（2）一个五边形的三个内角是直角，另两个内角都是n °，则n ＝。

（3）六角螺母的面是六边形，它的内角都相等，则这个六边形的每个内角是多少？（4）在四边形ABCD 中，∠A 与∠C 互补，那么∠B 与∠D 有什么关系呢？为什么？ 分析：本题考察的是多边形内角和为（n －2）·180°解：（1）四边形的内角和为360°，所以四边形中最大角为︒=+++⨯︒14443214360 （2）五边形的内角和为540°，所以︒=︒⨯+︒⨯5402903n ，解得：︒=︒135n ，即135=n（3）六边形的内角和为720°，所以其每个内角都＝︒=︒1206720 （4）四边形的内角和为360°，因为∠A 与∠C 互补，所以∠A ＋∠C ＝180°， 所以∠B ＋∠D ＝360°－180°＝180°，即∠B 与∠D 互补。

第七章 平面图形认识（二）第7课时 三角形的内角和与外角和（1）一、选择题1．△ABC 中，∠A =45°，∠B =63°，则∠C = 【 】A ．72°B ．92°C ．108°D ．180°2．将一副直角三角板如图所示放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合，则∠1的度数为 【 】A ．45°B ．60°C ．75°D ．85°3．适合条件∠A =∠B =2∠C 的△ABC 是 【 】A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定4．如图△ABC 中，∠B =30º，∠BAC =80º，AD 平分∠BAC ，则∠ADC 的度数为 【 】A ．30º；B ．40º；C ．70ºD ．80º5．如图，11002145∠=∠=o o ，，那么3∠= 【 】 A ．55° B ．65 C ．75° D ．85°二、填空题6．在直角△ABC 中，∠A =35º，则∠B = º．7．如图，AD 是△ABC 的外角平分线，∠B =︒30，∠DAE =︒65，则∠ACD 等于 ．8．如图，已知AB ∥CD ，BE 平分∠ABC ，∠CDE ＝150°，则∠C ＝__________． 9．如图，AB ∥CD ，∠B =680，∠E =200，则∠D 的度数为 ．10．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐弯的角∠A 是1200，第二次拐弯的角∠B是1500，第三次拐弯的角是∠C ，这时道路恰好和第一次拐弯之前的道路平行，则∠C = º．三、解答题11．在△ABC 中，∠B -∠A =50º，∠C -∠B =35º.求△ABC 的各角的度数．12．如图，已知DF ⊥AB 于点F ，且∠A ＝45°，∠D ＝30°，求∠ACB 的度数．13．一块三角形的材料被折断了一个角，余下的形状如图，请根据所剩的材料推算出所缺角的度数．（写第2题图 D C B A 1 2 3 第5题图 第4题图 A B C D E 第8题图 第7题图 第9题图 F E D C A B A B C 第10题图 E C F D B A第12题图出必要的文字说明及画出相应的图形）14．如图，在△ABC中，∠ABC=56º，∠ACB=44º，AD是BC边上的高，AE是△ABC的角平分线，你能求出∠DAE的度数吗？请试一试！四、拓展题15．已知∠ABC，∠ACB的平分线交于I。

B
12/11/2021
C
第八页，共三十五页。
已知：△ABC. 求证(qiúzhèng)：∠A +∠B +∠C=180°.
A
B
12/11/2021
C
第九页，共三十五页。
已知：△ABC. 求证(qiúzhèng)：∠A +∠B +∠C=180°.
A
B
12/11/2021
C
第十页，共三十五页。
已知：△ABC. 求证(qiúzhèng)：∠A +∠B +∠C=180°.
4.三角形的一个外角等于与它不相邻的两个内角的和.
（）
5.三角形的一个外角大于任何一个内角.（ ）
6.三角形的一个内角小于任何一个与它不相邻的外角.
12/11/2021
（）
第二十二页，共三十五页。
【例题(lìtí)】
【例】已知:国旗(guóqí)上的正五角星形如图所示. 求:∠A+∠B+∠C+∠D+∠E的度数.
2
∠1＋∠2＋∠3＋∠BAC＋∠ABC＋∠ACB=540°，
而∠BAC＋∠ABC＋∠ACB=180°，
∴∠1＋∠2＋∠3＝360°.
12/11/2021
第二十页，共三十五页。
方法二：
1 A4
3
B
C 2
两直线平行，同 位角相等
D
解：过A作AD平行(píngxíng)于BC.
∠3＝∠4， ∠2＝∠BAD， ∠2＋∠3＝∠BAD＋∠4.
A
B
12/11/2021
C
第五页，共三十五页。
已知：△ABC. 求证(qiúzhèng)：∠A +∠B +∠C=180°. A