费米-狄拉克分布和玻色-爱因斯坦分布的简单推导

费米狄拉克分布函数解析图像和应用文件管理序列号：[K8UY-K9IO69-O6M243-OL889-F88688]各能级被电子占据的数目服从特定的统计规律这个规律就是费米-狄拉克分布规律。

一般而言，电子占据各个能级的几率是不等的。

占据低能级的电子多而占据高能级的电子少。

统计物理学指出，电子占据能级的几率遵循费米的统计规律：在热平衡．．．状态下，能量为E 的能级被一个电子占据的几率为： f(E)称为电子的费米(费米-狄拉克)分布函数，k 、TE fermi 称为费米能级，它与物质的特性有关。

只要知道了费米能级E fermi 的数值，在一定温度下，电子在各量子态上的统计分布就完全确定了。

费米分布函数的一些特性:【根据f(E)公式来理解】第一，费米能级E fermi 是一种用来描述电子的能级填充水平的假想能级．．．．，E f 越大，表示处于高能级的电子越多；E f 越小，则表示高能级的电子越少。

(E f 反映了整体平均水平)第二，假定费米能级E f 为已知，则f(E)f(E)式可画出f(E)的曲线如图所示，但要注意因变量f(E)不像普通习惯画在纵轴，而是破天荒的画在横轴。

的能级都空着。

因而费米能级E f 是在绝对零度时电子所具有的最大能量，是能级在绝对零度时能否被占据的一个界限，因而它是一个很重要的参数。

费米分布函数变化曲线T 3>T 2>T 1>T 0第五，在T≠0K时即不处于绝对零度的前提下，若E-E f＞5kT，则f(E)＜0.007；在T≠0K 前提下，若E-E f＜-5kT，则f(E)＞0.993。

(k、T分别为波耳兹曼常数和绝对温度)可见，温度T高于绝对零度的前提下，能量比E f高5kT的能态被电子占据的几率只有0.7%，几率很小，能级几乎是空的；而能级比E f低5kT的能态被电子占据的几率是99.3%，几率很大，该能级范围几乎总有电子。

一般可以认为，在T不为绝对零度但也不很高时，能量小于E f的能态基本上为电子所占据，能量大于E f的能态基本上没有被电子占据；而电子占据费米能级E f这个能级的概率是(不论任何温度下)都是1/2。

量子力学公式
量子力学中的一些常见公式包括：
1. 薛定谔方程式：描述了量子物理学的宏观世界，即微观粒子如何随着时间的推移而演变。

其一般形式为：iℏ∂Ψ/∂t=HΨ，其中i是虚数单位，ℏ是普
朗克常数的约化常数，Ψ是波函数，H是哈密顿算符。

2. 波粒二象性：描述了物质粒子的波动性质和粒子性质之间的相互作用关系。

其表达式为λ=h/p，其中λ是波长，h是普朗克常数，p是粒子的动量。

3. 测量理论：物理量的测量和观测结果有一定的概率性和不确定性。

测量理论采用概率统计的方法来描述这种不确定性。

最常见的公式是海森堡不确定性原理：ΔxΔp≥h/4π，其中Δx和Δp分别表示位置和动量的不确定度，h 是普朗克常数。

4. 费米-狄拉克统计和玻色-爱因斯坦统计：描述了物质粒子的统计行为。

费米-狄拉克统计用于描述费米子（如电子、质子等）的行为，玻色-爱因斯坦统计用于描述玻色子（如光子、声子等）的行为。

5. 波函数的复共轭：Ψ^（r，t）。

6. 归一化条件：∫Ψ（r，t）^2d3r=1。

7. 位置算符：x。

8. 动量算符：-iℏ∇。

9. 能量算符：iℏ∂/∂t。

10. 完备性条件：∫ψn^（r）ψm（r）d3r=δnm。

以上公式仅供参考，如需更准确的信息，建议查阅量子力学相关的书籍或咨询专业人士。

说明玻尔兹曼系统玻色子系统费米子系统的区别玻尔兹曼系统和玻色子系统以及费米子系统是统计力学中的三种重要模型。

它们描述了微观粒子在宏观尺度上的行为。

本文将逐步阐述玻尔兹曼系统、玻色子系统和费米子系统的区别。

1.玻尔兹曼系统：玻尔兹曼系统是一种描述粒子统计行为的模型。

在玻尔兹曼系统中，粒子可以以任意数量存在于相同的量子态。

这意味着多个粒子可以处于相同的能量状态，也就是说，它们之间没有排斥效应。

玻尔兹曼系统中的粒子是无标识的，它们之间是可以交换的。

2.玻色子系统：玻色子系统描述了玻色子的统计行为。

玻色子是一类具有整数自旋的粒子，例如光子、声子等。

玻色子系统中，多个粒子可以同时处于相同的能量状态，它们之间没有排斥效应。

这种行为被称为玻色-爱因斯坦统计。

玻色子系统的一个重要特点是它们会聚集到基态，即粒子会尽可能地集中在能量最低的状态。

3.费米子系统：费米子系统描述了费米子的统计行为。

费米子是一类具有半整数自旋的粒子，例如电子、质子等。

费米子系统中，根据泡利不相容原理，每个能级只能有一个粒子占据，它们之间存在排斥效应。

这种行为被称为费米-狄拉克统计。

费米子系统的一个重要特点是它们填充能级从低到高，直到达到所谓的费米能级。

根据以上的描述，可以总结出玻尔兹曼系统、玻色子系统和费米子系统的区别：1.统计行为：玻尔兹曼系统中粒子之间无排斥效应，玻色子系统中多个粒子可以处于相同的能级，费米子系统中每个能级只能有一个粒子占据。

2.粒子类型：玻尔兹曼系统中的粒子是无标识的，玻色子系统中的粒子具有整数自旋，费米子系统中的粒子具有半整数自旋。

3.基态分布：玻色子系统会聚集到能量最低的状态，费米子系统填充能级从低到高。

4.波尔茨曼系统、玻色子系统和费米子系统在实际应用中有着不同的物理特性和行为模式。

综上所述，玻尔兹曼系统、玻色子系统和费米子系统在统计行为、粒子类型、基态分布等方面存在着明显的区别。

这些模型在研究微观粒子的统计性质和宏观行为时提供了重要的理论基础和工具，对于理解物质的性质和行为具有重要意义。

天津市考研物理学复习资料统计物理基础知识梳理统计物理学是物理学中的一个重要分支，研究的对象是物质的宏观统计性质以及宏观物理量的统计规律。

在天津市考研中，统计物理学作为物理学的一门必修课程，对于学生们来说是一个重要的复习内容。

本文将为大家梳理天津市考研物理学复习资料中的统计物理学的一些基础知识，希望对大家复习有所帮助。

一、热力学基础概念1. 系统和环境在热力学中，我们将要研究的对象称为系统，而与系统有能量和物质交换的外部部分则称为环境。

2. 状态量和过程量热力学中，状态量是指与系统的状态有关的物理量，如温度、压力等；而过程量则是指与系统的状态变化有关的物理量，如热量、功等。

3. 平衡态和非平衡态平衡态是指系统处于稳定状态，各个宏观性质保持不变；非平衡态则是指系统处于不稳定状态，各个宏观性质处于变化过程中。

二、统计物理学基本框架统计物理学的基本框架是建立在微观粒子的运动规律上的。

通过统计物理学的方法，我们可以将宏观物理量与微观粒子的动力学联系起来。

1. 经典统计物理学经典统计物理学适用于宏观物理系统，其中的粒子之间的相互作用是经典力学描述的。

通过经典统计物理学，我们可以计算出宏观物理量的统计规律，如分子平均速度、能量分布等。

2. 量子统计物理学量子统计物理学适用于微观粒子系统，其中的粒子之间的相互作用是量子力学描述的。

通过量子统计物理学，我们可以计算出微观粒子系统的物理量统计规律，如费米子和玻色子的分布等。

三、热力学基本定律热力学是研究能量转化和宏观性质变化的学科，其基本定律为热力学第一定律和热力学第二定律。

1. 热力学第一定律热力学第一定律也称为能量守恒定律，它指出能量的变化等于系统对外界做功和从外界吸收的热量之和。

2. 热力学第二定律热力学第二定律也称为熵增定律，它指出孤立系统的熵总是不会减小，而在实际过程中总是增大或保持不变。

四、统计物理学中的分布律统计物理学中有几个重要的分布律，它们可以用于描述微观粒子在宏观物理系统中的分布情况。

热力学中统计力学的数学基础统计力学是连接微观世界与宏观现象之间的重要桥梁。

通过统计方法，统计力学能够从大量粒子的行为中推导出热力学的基本定律和性质。

本文将重点讨论热力学中统计力学的数学基础，包括主要概念、相关数学工具及其在热力学中的应用。

一、统计力学的基本概念1.1 微观状态与宏观状态在统计力学中，物质的微观状态是描述该系统中粒子位置和动量的详细信息。

每一个微观状态都可以看作是系统的一种可能的排列组合，系统可以通过不同方式达到这些排列。

而宏观状态则是指一组微观状态所对应的宏观性质，如温度、压强和体积等。

这两个层面之间的关系是统计力学研究的核心。

1.2 配分函数配分函数是统计力学中的重要工具，用于计算系统的热力学性质。

对于一个包含粒子数量为N的系统，配分函数Z定义为所有可能微观状态能量E_i的指数形式：[ Z = _{i} e^{-E_i/(kT)} ]其中 ( k ) 是玻尔兹曼常数，( T ) 是绝对温度。

配分函数不仅可以帮助我们获得内能、熵等热力学量，还能反映出系统的概率分布特征。

二、概率论与统计分布2.1 概率分布在统计力学中，研究系统时常涉及概率分布。

最常用的几种分布包括：麦克斯韦-玻尔兹曼分布：用于描述气体分子的速度分布，适用于经典气体。

费米-狄拉克分布：适用于费米子，如电子和质子。

玻色-爱因斯坦分布：用于描述玻色子，如光子和声子。

这些概率分布为我们提供了理解不同微观粒子行为的重要框架。

2.2 大数法则与中心极限定理大数法则说明当样本容量趋向于无穷大时，样本均值趋近于总体均值。

中心极限定理则指出，不论原始数据的分布形式如何，只要样本数量足够大，样本均值会呈现正态分布。

这些理论在统计力学中非常重要，因为它们使我们能够基于有限数量粒子的行为推测整个系统的性质。

三、热力学中的重要量3.1 内能与亥姆霍兹自由能内能 ( U ) 是描述系统微观粒子总能量的重要量。

在配分函数的帮助下，我们可以通过以下公式计算内能：[ U = - ]其中 ( = )。

2001年10月9日瑞典皇家科学院宣布，将本年度诺贝尔物理学奖授予美国国家标准与技术研究所物理学家埃里克·康奈尔(E.A.Cornell)、美国麻省理工学院教授德国人沃尔夫冈·克特勒(W.Ketterle)以及美国科罗拉多大学教授卡尔·威曼(C. E. Wieman)，以表彰他们在稀薄碱金属原子气中实现了玻色－爱因斯坦凝聚以及在凝聚体性质方面的早期基础性研究。

本文将介绍玻色－爱因斯坦凝聚的研究简史以及三位获奖者的主要贡献。

玻色－爱因斯坦凝聚及其实验研究简史1924年印度物理学家玻色研究了“光子在各能级上的分布”问题，他以不同于普朗克的方式推导出普朗克黑体辐射公式。

玻色将这一结果寄给爱因斯坦，请其翻译成德文并在德国发表。

爱因斯坦意识到玻色工作的重要性，立即着手研究这一问题。

爱因斯坦于1924和1925年发表了两篇文章，将玻色对光子的统计方法推广到某类原子，并预言当这类原子的温度足够低时，所有的原子就会突然聚集在一种尽可能低的能量状态，这就是所谓的玻色－爱因斯坦凝聚(Bose－Einstein Condensation，BEC)，这时宏观量物质的状态可以用同一波函数来描写。

从理论上讲，处在这种状态的物质在性质上有别于通常的气态、液态、固态和等离子态，故有人又称其为物质的第五态。

玻色和爱因斯坦所采用的统计方法后来被称为玻色－爱因斯坦统计，而服从这种统计的粒子被统称为玻色子。

然而，并不是所有微观粒子都服从玻色－爱因斯坦统计，有一类粒子服从的是1926年诞生的费米－狄拉克统计，这类粒子被统称为费米子。

费米子不同于玻色子，它服从泡利不相容原理，即两个费米子不能占据同一个态。

利用这一点可以解释元素周期表。

费米子之间相互排斥，这是一种量子压力，它在无任何外力时也存在。

而玻色子的情况则相反，一个量子态上可以有任意多个粒子占据着。

微观粒子究竟属于哪一类是由其自旋决定的，自旋为整数的如光子、胶子等是玻色子，而为半整数的如电子、夸克等则是费米子。

量子理论的诞生和发展（13）：玻色统计和费米统计作者：张天蓉物理学中的统计规律是指粒子系统的宏观运动规律。

波尔兹曼研究的是经典粒子的统计行为，粒子系统的自由度用麦克斯韦-波尔兹曼统计方法来描述或计算。

不同于经典统计，量子力学的统计规律则有两种：玻色-爱因斯坦统计和费米-狄拉克统计。

图13-1：波色和费米提出量子统计理论的这四位物理学家，其中玻色可能是很多人不甚了解的一位。

玻色是印度人，他在一次有关光电效应的讲课中，因为犯了一个违反经典统计的“錯誤”却发现了玻色子的统计规律。

物理学中以他的名子命名玻色子，这使得他在物理学界还是挺有名的。

纳特·玻色（Nath Bose，1894年－1974年）出生于印度加尔各答，他的父亲是一名铁路工程师，他是七名孩子中的长子。

玻色在大学时曾得到几位优秀教师的赞赏和指点。

他获得数学硕士学位之后并未继续攻读博士，而是直接在加尔各答物理系担任讲师。

后来，他又到达卡大学物理系任讲师，并自学物理。

大约是在1921年，玻色讲授光电效应和黑体辐射引发的紫外灾难，他本来是想按照经典方法分析粒子的统计行为，结果犯了一个类似“掷两枚硬币，得到“正正”概率为三分之一”的错误。

然而没想到是，他的这个错误却得出了与实验相符合的结论，也就是不可区分的全同粒子所遵循的一种统计规律。

所谓“掷两枚硬币，‘正正’概率为三分之一”是错误的，意思是说当你掷两枚硬币的时候，因为每个硬币都有正反两面，实验结果就有四种情况：正正、正反、反正、反反。

也就是说，按照经典理论，这四种情况中的每一种发生的几率是一样的，即都是四分之一，但玻色所得到的结果却是三分之一。

玻色的这个“错误”之所以是“不可区分的全同粒子”的统计规律，是因为对于两个粒子而言，它们的统计行为是否可以区分或不可区分是有区别的。

假如两枚硬币不能区分谁正谁反，你掷两枚硬币所得到的正、反与反、正就是完全一样的结果。

“不可区分”的两个粒子如同“量子硬币”，它们在宏观系统中总是给我们完全一模一样的感觉。

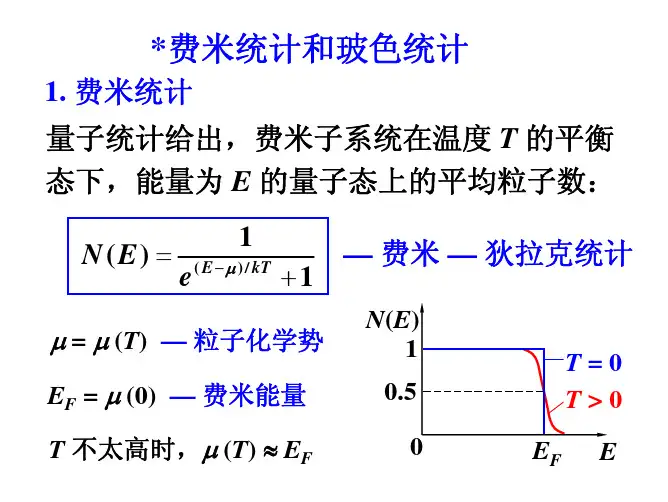
费米狄拉克分布函数费米-狄拉克分布（Fermi-Dirac distribution）全同和独立的费米子系统中粒子的最概然分布。

简称费米分布，量子统计中费米子所遵循的统计规律。

这个统计规律的命名来源于恩里科·费米和保罗·狄拉克，他们分别独立地发现了这一统计规律。

不过费米在数据定义比狄拉克稍早。

费米–狄拉克统计的适用对象是，热平衡时自旋量子数为半奇数的粒子。

除此之外，应用此统计规律的前提是，系统中各粒子之间的相互作用可以忽略不计。

费米子是自旋为半整数( 即自旋为/2，=h/2π，h是普朗克常量）的粒子，如轻子和重子，全同费米子系统中粒子不可分辨，费米子遵从泡利不相容原理，每一量子态容纳的粒子数不能超过一个。

对于粒子数、体积和总能量确定的费米子系统，当温度为T时，处在能量为E的量子态上的平均粒子数为[2]费米-狄拉克分布公式式中，k是玻耳兹曼常量，εf是化学势。

在高温和低密度条件下，费米-狄拉克分布过渡到经典的麦克斯韦-玻尔兹曼分布。

对费米-狄拉克分布公式的理解：是各能级被电子占据的数目服从的特殊的统计规律。

费米能级：用来描述电子的能级填充水平的假想能级，E越大，高能级的电子越多，反之FE反映整体平均水平）。

对于金属，绝对零度下，电子占据的最高能级就是费米能级。

费米能则越少（F级的物理意义是，该能级上的一个状态被电子占据的几率是1/2。

只要知道了它的值，在一定温度下，就能确定电子在各量子态下的统计分布。

它和温度，半导体材料的导电类型，杂质的含量以及能量零点的选取有关。

n型半导体费米能级靠近导带边，过高掺杂会进入导带。

p型半导体费米能级靠近价带边，过高掺杂会进入价带。

将半导体中大量电子的集体看成一个热力学系统，可以证明处于热平衡状态下的电子系统有统一的费米能级。

统计热力学中的量子统计统计热力学是研究大量粒子的宏观性质的科学领域。

在统计热力学中，我们通常使用经典统计力学来描述粒子的行为，但是当粒子的量子效应变得显著时，我们就需要使用量子统计力学来更准确地描述系统的行为。

量子统计力学是基于量子力学的统计理论。

在经典统计力学中，我们假设粒子之间是可区分的，即每个粒子都有明确的自己的状态。

然而，在量子统计力学中，由于粒子遵循泡利不相容原理，我们必须考虑粒子之间的不可区分性。

在量子统计力学中，我们有两种统计分布：波尔兹曼分布和费米-狄拉克分布。

波尔兹曼分布适用于玻色子，如光子和声子等，而费米-狄拉克分布适用于费米子，如电子和质子等。

波尔兹曼分布描述了玻色子的分布情况。

根据波尔兹曼分布，玻色子的能级越高，其占据的概率就越低。

这意味着玻色子可以集中在同一个能级上，形成所谓的玻色-爱因斯坦凝聚。

这种凝聚态在低温下可以观察到，如玻色-爱因斯坦凝聚体的形成。

费米-狄拉克分布描述了费米子的分布情况。

根据费米-狄拉克分布，费米子的能级越高，其占据的概率就越低。

与波尔兹曼分布不同的是，费米子不能集中在同一个能级上，由于泡利不相容原理的限制，每个能级只能容纳一个费米子。

这导致了费米子的排斥效应，使得它们在填充能级时会遵循能级的阶梯结构。

量子统计力学的一个重要应用是描述玻色子和费米子的凝聚态现象。

玻色-爱因斯坦凝聚和费米-狄拉克凝聚是两种不同的凝聚态现象。

玻色-爱因斯坦凝聚发生在玻色子之间，当玻色子的数目足够多且温度足够低时，它们会聚集在同一个能级上。

费米-狄拉克凝聚发生在费米子之间，当费米子的数目足够多且温度足够低时，它们会填充能级直到能级填满。

除了凝聚态现象，量子统计力学还可以用来解释一些奇特的现象，如量子隧穿和量子纠缠。

量子隧穿是指量子粒子在经典力学中不可能发生的现象，即粒子能够穿过经典势垒。

这种现象在量子力学中得到了解释，其中量子统计力学起到了重要的作用。

量子纠缠是指两个或多个粒子之间存在一种特殊的关联关系，即使它们之间的距离很远，它们的状态仍然是相互关联的。

粒子物理学中的基本粒子及其相互作用在我们的宇宙中，所有物质都是由基本粒子构成的。

这些基本粒子是物质的最基本单位，它们互相作用才能形成我们所看到的复杂世界。

粒子物理学研究这些基本粒子及其相互作用的规律。

首先介绍一下基本粒子的分类。

基本粒子可以分为两类：费米子和玻色子。

费米子遵循费米-狄拉克统计，满足泡利不相容原理，即同一时刻存在的两个费米子不能占据相同的量子状态。

常见的费米子有电子和质子。

玻色子遵循玻色-爱因斯坦统计，不受泡利不相容原理限制，多个玻色子能够占据相同的量子状态。

常见的玻色子有光子和重子介子等。

在标准模型中，基本粒子可以分为两类：夸克和轻子。

夸克是建筑物质的基本石头。

它们有六种不同的“口味”，即上、下、顶、底、粉、反粉。

没有单独存在的自由夸克。

轻子包括电子、中微子和它们的反粒子，它们构成了物质的基本框架。

以上是关于基本粒子的分类，接下来我们来谈谈基本粒子之间的相互作用。

强相互作用是基本粒子之间最强烈的相互作用。

它可以通过强相互作用介子交换来实现，比如介子进行核力的传递。

强相互作用也是核能源的来源，例如核融合反应中中子与氘核相撞时就会产生介子。

电磁相互作用是基本粒子之间最熟悉的相互作用之一，也是人类日常生活中最为常见的相互作用之一。

它通过光子介质来实现。

例如，光子被电子吸收，赋予了电子能量，然后电子被激发并向周围释放光子。

弱相互作用是最不为人知但也是最重要的相互作用之一。

它在自然界中发挥着重要的作用。

弱相互作用具有两个广泛影响的方面：一方面是贝塔衰变，即核内中子变成质子、电子和主题中微子的过程；另一方面是太阳能的产生，太阳产生能量的过程是由两个质子结合成氘核，通过一个介子实现的。

相比较于强相互作用、电磁相互作用和弱相互作用，引力相互作用是最弱的相互作用。

引力会将质量聚集到一起，这就是我们所熟知的万有引力定律。

在引力相互作用下，星体之间的相互作用会导致行星的运动以及整个星系的结构。

综上所述，基本粒子及其相互作用是构成宇宙的基础。

多体量子力学中的粒子统计特性研究多体量子力学是研究多个粒子之间相互作用及其宏观性质的一门学科。

在多体系统中，粒子的统计特性起着至关重要的作用。

本文将就多体量子力学中的粒子统计特性展开讨论。

首先，我们来探讨玻色子和费米子两种类型的统计特性。

根据泡利不相容原理，玻色子可以占据同一个量子态，而费米子则不能。

这一特性导致玻色统计与费米统计在宏观性质上有很大差异。

例如，在低温下，玻色子会聚集成玻色-爱因斯坦凝聚体，形成一种超流体。

而费米子由于不能占据相同的态，会呈现出费米-狄拉克气体的特性。

其次，统计力学是多体量子力学研究的重要方法之一。

基于玻尔兹曼统计或费米-狄拉克统计，可以通过分布函数来描述多体系统的状态。

例如，对于玻色子，我们可以使用玻色-爱因斯坦分布函数来描述系统的粒子分布。

而费米子则需要使用费米-狄拉克分布函数。

通过这些分布函数，可以推导出一系列宏观性质，如压力、内能等。

统计力学提供了理论框架，使得我们能够更好地理解多体量子系统的行为。

除了统计力学，量子力学中的凝聚态物理也是研究多体系统的重要方法。

凝聚态物理主要研究大量粒子组成的宏观系统，如固体、液体和气体等。

多体量子力学中的凝聚态物理研究的是在低温下，粒子之间的量子性质开始显现的系统。

例如，超导和超流现象就是典型的多体凝聚态性质。

在这些现象中，大量粒子形成了一种集体行为，表现出了与单个粒子完全不同的性质。

此外，量子计算也是多体量子力学中的重要研究领域。

量子计算利用量子叠加和量子纠缠的特性，能够以更高效的方式解决某些问题。

在量子计算中，多个量子比特的统计特性起着决定性的作用。

例如，量子比特的纠缠可以被用来实现量子门操作，从而进行复杂的计算。

多体量子力学为量子计算提供了理论基础，同时也带来了许多新的问题和挑战。

综上所述，多体量子力学中的粒子统计特性是研究多体系统行为的关键因素。

玻色子和费米子具有不同的统计特性，导致多体系统呈现出不同的宏观性质。

统计力学和凝聚态物理为我们理解多体系统提供了重要的工具和方法。

冷原子物理学中的超冷玻色气体和费米气体在冷原子物理学领域中，超冷玻色气体和费米气体是两个重要的研究对象。

这两种气体的特殊性质和行为使得它们在理论研究和实验应用中具有广泛的潜力和应用前景。

首先，我们来了解一下超冷玻色气体。

玻色气体是由具有整数自旋的玻色子组成的，其特点是可以在低温下形成基态凝聚。

在玻色气体被冷却至绝对零度附近时，它的波函数会出现集中分布，原子间发生玻色-爱因斯坦凝聚。

这种凝聚现象的发生让超冷玻色气体成为了研究量子统计行为和凝聚态物理现象的理想平台。

超冷玻色气体的研究中，最有名的莫过于玻色-爱因斯坦凝聚。

这种凝聚态现象的实现，让物理学家们可以研究超流性质、相干现象以及凝聚态中的拓扑缺陷等重要问题。

此外，超冷玻色气体还具有与光学和自旋系统之间的耦合性质，这种光-原子相互作用的巧妙平台，使得研究者们可以进一步探索量子信息处理、量子计算等相关领域。

接下来，我们转向费米气体。

费米气体由具有半整数自旋的费米子构成，根据泡利不相容原理，这些费米子不能存在于相同的量子态。

费米气体在冷却至足够低的温度时会出现费米-狄拉克凝聚，费米子会填满低能态直到费米能级，其波函数也会出现集中分布。

费米气体的研究对于理论物理学和凝聚态物理学来说具有重要意义。

费米-狄拉克凝聚是一种新奇的量子相，具有巨大的熵、寻求最大自发对称破缺等特性。

如今，研究者们通过磁光和其他技术手段来探索费米气体的性质，在高能物理、量子调控和量子模拟等领域发现了一系列新效应和新领域。

超冷玻色气体和费米气体在实验应用方面也有着广泛的应用前景。

例如，超冷玻色气体可以用于模拟物质中的相变现象，并帮助我们更好地理解复杂的凝聚态系统。

费米气体则有助于研究高能物理中的强关联现象，也可以用于制造高精度测量设备和量子计算器。

总之，在冷原子物理学中，超冷玻色气体和费米气体作为两个重要的研究对象，具有不可忽视的意义和巨大的潜力。

通过对它们的研究，我们可以进一步拓展对量子统计行为、凝聚态现象和量子信息处理的认识，也为实际应用领域提供了新的思路和技术平台。

玻色-爱因斯坦凝聚是什么样的？费米-狄拉克凝聚呢？玻色—爱因斯坦凝聚态，世界不是你想象的那样关于时间与生命的思考，是个大的命题，自古以来无数人都在发问。

类似的文章，我在《非线性变化》一书中写过。

大概就是两个观点。

一是生命的意义的不可说；二是活着比意义更重要。

当时间成为通用货币时，你将如何生活？《时间规划局》片中有个主角的朋友，主角给了他10年时间，一笔巨大的财富。

结果他用9年的时间买酒喝，暴死街头。

现实生活中呢？有人中彩票，暴富后很快又成了乞丐。

时间对于人性的贪欲从来都是残忍的。

大家慢慢体会吧。

其实我想说，黄金，金钱是生活通用货币，但人生的通用货币还真是时间。

生命在于运动，更在于探索。

每天去发现和知道新的知识，对你我来说绝对是美的享受。

玻色–爱因斯坦凝聚就是一种这样的美丽，可能我们的想象力会匮乏到领悟这样的美。

一起来认识一下吧。

玻色–爱因斯坦凝聚是玻色子原子在冷却到接近绝对零度所呈现出的一种气态的、超流性的物质状态（物态）。

1995年，麻省理工学院的沃夫冈·凯特利与科罗拉多大学鲍尔德分校的埃里克·康奈尔和卡尔·威曼使用气态的铷原子在170 nK（1.7×10?7K）的低温下首次获得了玻色-爱因斯坦凝聚。

在这种状态下，几乎全部原子都聚集到能量最低的量子态，形成一个宏观的量子状态。

这幅图像显示的是铷原子速度的分布，它证实了玻色-爱因斯坦凝聚的存在。

图中的颜色显示多少原子处于这个速度上。

红色表示只有少数原子的速度是该速度。

白色表示许多原子是这个速度。

最低速度显示白色或浅蓝色。

左图：玻色-爱因斯坦凝聚出现前。

中图：玻色-爱因斯坦凝聚刚刚出现。

右图：几乎所有剩余的原子处于玻色-爱因斯坦凝聚状态。

由于不确定性原理尖部不是无穷窄：由于原子被束缚于一个很小的空间，它们的速度必须有一个很大的范围。

从左图到右图，我们看到原子态的变化情况有很大的转折。

这里的“凝聚” 与日常生活中的凝聚不同，它表示原来不同状态的原子突然“凝聚”到同一状态（一般是基态）。

玻色-爱因斯坦统计玻色-爱因斯坦统计，适用于被称作玻色子的基本粒子的统计类别，它是指光子、介子，以及W和Z粒子。

玻色子拥有整数值的被称为自旋的量子力学特性，并且是“聚集的（gregarious）”，它的意义是能够处于同一状态的玻色子的数量是无限的。

所有传递自然界中的基本力的粒子都是玻色子。

玻色-爱因斯坦统计在统计力学中，玻色-爱因斯坦统计（更通常的被称为B-E统计）确定了在热平衡下同一的不可分辨的（indistinguishable）玻色子相对于能量状态的统计分布。

费米-狄拉克和玻色-爱因斯坦统计适用于量子效应必须考虑和粒子被看作是“不可分辨的”情况下。

如果粒子的密度N/V n q（n q为量子密度），量子效应就显现出来。

量子密度就是粒子间距等于热德•布罗意波长的时候，即粒子的波函数已经接触但还未重叠时。

量子密度依赖于温度；高温会使大多数系统处于经典的限制中，除非它们有非常高的密度比如白矮星。

费米-狄拉克统计适用于费米子（服从泡利不相容定律的粒子），玻色-爱因斯坦统计适用于玻色子。

在高温或低密度下费米-狄拉克和玻色-爱因斯坦统计都变为麦克斯韦-玻耳兹曼统计。

麦克斯韦-玻耳兹曼统计经常被描述为“可分辨的”经典粒子的统计。

换句话说，处在状态1的粒子A和处在状态2的粒子B的结构相比于粒子B是状态1和粒子A是状态2是不同的。

当沿着这条思路充分展开时，就会导出适当的（玻耳兹曼）对于能量状态的粒子分布，但由于熵也会导出非自然（non-physical）的结果，如吉布斯反论。

当认识到所有的粒子实际上都是不可分辨的，这些问题就消失了。

这些分布在高温和低密度限制下都会趋近于麦克斯韦-玻耳兹曼分布，而不需要任何额外的假设。

麦克斯韦-玻耳兹曼统计对于研究气体非常有用；F-D统计经常用于固体中的电子的研究。

同样的，它们都成为半导体设备和电子学理论的基础。

玻色子，不同于费米子，不受泡利不相容定律的影响：无限数量的粒子可以同时占据相同的状态。

课程设计题目：系综理论的讨论及运用学院：电子与信息工程学院专业：物理学师范姓名：学号：指导老师：时间：系综理论的讨论及运用姓名：摘要系综是处在相同的给定宏观条件下的大量结构完全相同的系统的集合。

它是统计物理的一个想象中的工具，而不是实际客体。

本文从概念开始讨论系综理论内容和运用。

关键词概念；系综理论；正则分布；关系；运用系综理论的基本观点是，宏观量是相应微观量的时间平均，而时间平均等价于系综平均。

系综的一个基本假设是各态历经假说：只要等待足够长的时间，宏观系统必将经历和宏观约束相应的所有可达微观态。

1 概念系统的一种可能的运动状态，可用相与中的一个相点表示，随着时间的推移，系统的运动状态改变了，相应的相点在相宇中运动，描绘出一条轨迹，由大量系统构成的系综则可表为相宇中大量相点的集合，随着时间的推移，各个相点分别沿各自的轨迹运动，类似于流体的流动。

若系统具有s个自由度，则相宇是以s个广义坐标p（详写为p、p2……ps）和s个广义动量q(详写为q1、q2……qs)为直角坐标构成的2s维空间。

在相宇内任一点（p，q）附近单位相体积元内的相点数目D（p，q，t）称为密度函数。

D(p,q,t)在整个相宇的积分等于全部相点数，即等于系综所包含的全部系统数N，与时间t无关。

定义ρ(p,q,t)=D(p,q,t)/N，称为系综的概率密度函数。

ρ（p，q，t）dpdq表示在t时刻出现在（p，q）点附近相体积元dpdq 内的相点数在全部相点数中所占的比值，即表示任一系统在t时刻其运动状态处于（p，q）附近的相体积元dpdq内的概率。

显然，概率密度函数ρ（p，q，t）满足归一化条件∫ρ（p,q,t）dpdq=1。

统计物理学的认为系统的任意宏观量I（t）是相应微观量L（p，q）在一定宏观条件下对系统一切可能的微观运动状态的统计平均值，即I （t）＝∫L（p，q）ρ（p，q，t）dpdq。

由此可见，经典统计物理的基本课题是确定各种条件下系综的概率密度函数ρ（p，q，t）ρ确定后，即可对相应的热力学系统的宏观性质，作出统计描述。