离散数学图论作业2-图的表示与图同构
- 格式:pdf
- 大小:53.38 KB
- 文档页数:2


离散数学中的图的同构与同构不变性离散数学是数学的一个分支,研究离散的结构和对象。
图论是离散数学的一个重要分支,研究图的性质和结构。
在图论中,同构和同构不变性是两个重要的概念。
一、同构的定义和性质在图论中,如果两个图具有相同的结构,即它们的顶点集和边集相同,那么这两个图就是同构的。
具体来说,对于两个图G=(V, E)和G'=(V', E'),如果存在一个双射函数f: V→V',使得对于任意的u, v∈V,(u, v)∈E当且仅当(f(u), f(v))∈E',那么图G和图G'就是同构的,记作G≅G'。
同构是图论中的一个重要概念,它可以帮助我们研究图的性质和结构。
同构关系具有以下性质:1. 同构关系是等价关系。
即对于任意的图G,它与自身是同构的;对于任意的图G和图G',如果G与G'是同构的,则G'与G也是同构的;对于任意的图G、G'和图G'',如果G与G'是同构的,G'与G''是同构的,则G与G''也是同构的。
2. 同构关系保持图的基本性质。
如果两个图是同构的,则它们具有相同的顶点数和边数。
3. 同构关系与图的表示方式有关。
同一个图可以有不同的表示方式,而不同的表示方式可能导致不同的同构判断结果。
二、同构不变性同构不变性是指图在同构变换下保持某些性质不变。
具体来说,如果两个图是同构的,那么它们在某些性质上是相同的。
同构不变性在图论中有重要的应用,可以帮助我们简化问题的分析和求解。
在图的同构不变性中,有一些重要的性质是不变的,包括:1. 度序列:图的度序列是指图中每个顶点的度按非递减顺序排列的序列。
对于同构的图,它们的度序列是相同的。
2. 连通性:图的连通性指的是图中任意两个顶点之间存在路径。
对于同构的图,它们的连通性是相同的。
3. 路径和回路:图中的路径是指顶点之间的连续边构成的序列,回路是指起点和终点相同的路径。


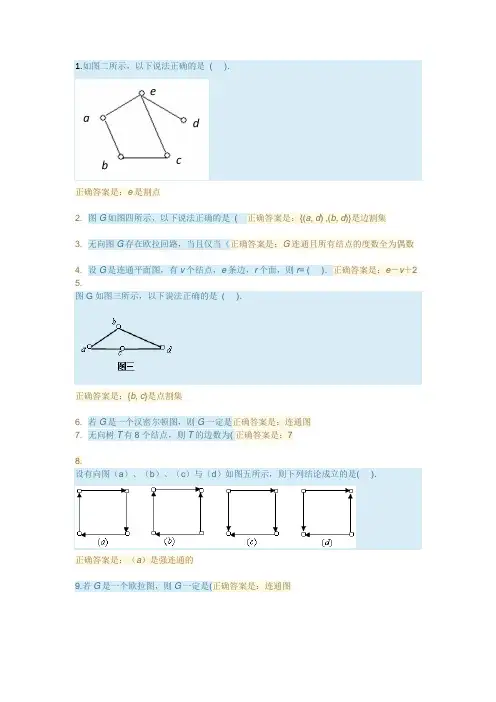
1.如图二所示,以下说法正确的是( ).正确答案是:e是割点2. 图G如图四所示,以下说法正确的是( 正确答案是:{(a, d) ,(b, d)}是边割集3. 无向图G存在欧拉回路,当且仅当(正确答案是:G连通且所有结点的度数全为偶数4. 设G是连通平面图,有v个结点,e条边,r个面,则r= ( ).正确答案是:e-v+25.图G如图三所示,以下说法正确的是( ).正确答案是:{b,c}是点割集6. 若G是一个汉密尔顿图,则G一定是正确答案是:连通图7. 无向树T有8个结点,则T的边数为( 正确答案是:78.设有向图(a)、(b)、(c)与(d)如图五所示,则下列结论成立的是( ).正确答案是:(a)是强连通的9.若G是一个欧拉图,则G一定是(正确答案是:连通图10.已知无向图G的邻接矩阵为,则G有().正确答案是:5点,7边11. 设连通平面图G的结点数为5,边数为6,则面数为4.( )正确的答案是“错”。
12. 若图G=<V, E>中具有一条汉密尔顿回路,则对于结点集V的每个非空子集S,在G中删除S中的所有结点得到的连通分支数为W,则S中结点数|S|与W满足的关系式为W|S|.( ) 正确的答案是“对”13. 如图九所示的图G不是欧拉图而是汉密尔顿图.( )正确的答案是“对”14. 设图G是有5个结点的连通图,结点度数总和为10,则可从G中删去6条边后使之变成树.正确的答案是“错”。
15. 设G是一个连通平面图,且有6个结点11条边,则G有7个面正确的答案是“对”16.设图G如图七所示,则图G的点割集是{f}.( )正确的答案是“错”17.设完全图K有n个结点(n2),m条边,当n为奇数时,K中存在欧拉回路.( 正确的答案是“对”。
18. 如图八所示的图G存在一条欧拉回路.正确的答案是“错”。
19. 无向图G的结点数比边数多1,则G是树.正确的答案是“错”。
20. 如果图G是无向图,且其结点度数均为偶数,则图G存在一条欧拉回路.(正确的答案是“错”。






离散数学中的图论入门图论是离散数学的一个重要分支,研究的对象是图。
图是由一些点和连接这些点的边组成的数学模型,可以用来描述现实世界中的各种关系和问题。
本文将介绍图论的基本概念和常见应用,帮助读者初步了解图论的入门知识。
一、图的定义与基本术语图由顶点集合和边集合组成。
顶点集合是图中的点的集合,用V表示;边集合是图中连接顶点的边的集合,用E表示。
图可以分为有向图和无向图。
有向图中的边是有方向的,表示从一个顶点指向另一个顶点的关系;无向图中的边是无方向的,表示两个顶点之间的关系。
图还可以分为简单图和多重图。
简单图中不存在重复的边和自环(起点和终点相同的边);多重图中可以存在重复的边和自环。
图中的边可以带权重,表示顶点之间的距离、代价或其他属性。
带权图可以用来解决最短路径、最小生成树等问题。
图的度是指与顶点相关联的边的数量。
对于无向图,顶点的度等于与之相连的边的数量;对于有向图,顶点的度分为入度和出度,分别表示指向该顶点的边的数量和从该顶点指出的边的数量。
二、图的表示方法图可以用邻接矩阵和邻接表两种方式进行表示。
邻接矩阵是一个二维数组,其中的元素表示两个顶点之间是否存在边。
如果顶点i和顶点j之间存在边,则邻接矩阵中第i行第j列的元素为1;否则为0。
邻接矩阵适用于稠密图,但对于稀疏图来说,会浪费较多的存储空间。
邻接表是由若干个链表构成的数组,数组的每个元素对应一个顶点,链表中存储与该顶点相连的其他顶点。
邻接表适用于稀疏图,可以有效地节省存储空间。
三、常见的图论算法与应用1. 深度优先搜索(DFS):DFS是一种用于遍历图的算法,通过递归的方式依次访问与当前顶点相邻的未访问过的顶点,直到所有顶点都被访问过为止。
DFS可以用来解决连通性、可达性等问题。
2. 广度优先搜索(BFS):BFS也是一种用于遍历图的算法,通过队列的方式按层次遍历图中的顶点。
BFS可以用来求解最短路径、网络分析等问题。
3. 最小生成树(MST):最小生成树是指在连通图中选择一棵生成树,使得树中所有边的权重之和最小。
图论中的图的同构与同构问题在图论中,同构是一个重要的概念。
图的同构指的是两个图结构完全相同,只是节点的标签或者边的标签不同。
而图的同构问题则是判断两个给定的图是否同构的问题。
本文将详细探讨图的同构与同构问题。
一、图的同构图的同构是指两个图结构完全相同,只是节点的标签或者边的标签不同。
为了更好地理解图的同构,我们先来了解一些基本概念。
1.1 图的定义在图论中,图由节点(也称为顶点)和边组成。
通常用G=(V, E)来表示一个图,其中V是节点(顶点)的集合,E是边的集合。
边可以用有序或无序对(u, v)来表示,表示节点u和v之间存在一条边。
1.2 同构图的定义给定两个图G1=(V1, E1)和G2=(V2, E2),如果存在一一对应关系f: V1→V2,使得对于每条边(u, v)∈E1,有(f(u), f(v))∈E2,则称图G1与G2同构。
其中,f被成为同构映射。
二、图的同构问题图的同构问题是判断两个给定的图是否同构的问题,它是图论中的一个经典问题。
在实际应用中,图的同构问题非常重要,对于计算机视觉、网络安全等领域都有广泛应用。
2.1 图的同构问题的定义给定两个图G1=(V1, E1)和G2=(V2, E2),判断它们是否同构。
2.2 图的同构问题的解决方法图的同构问题是一个NP问题,目前还没有确定的多项式时间解决算法。
在实际应用中,为了解决图的同构问题,通常采用以下方法:(1)特征向量法:通过计算图的特征向量,并比较两个图的特征向量来判断是否同构。
(2)图分类器法:通过训练一个图分类器,将同构和非同构的图进行分类。
(3)哈希算法法:通过为图节点和边生成一个唯一的哈希值,并比较两个图的哈希值来判断是否同构。
以上方法都有各自的优缺点,在不同的应用场景下选择合适的方法。
三、图的同构性质图的同构性质是指图的某些特征在同构映射下保持不变。
在判断图的同构性质时,可以利用这些性质来简化问题。
3.1 路径在判断图的同构性质时,路径是一个重要的性质。
离散数学中的图同构问题研究与算法分析在离散数学中,图是一种重要的数学模型,它能够描述事物之间的关系和连接。
图同构问题是图论中的一个经典问题,它要求判断两个图是否同构,即是否存在一种一对一映射将一个图的顶点和边对应到另一个图的顶点和边上,使得它们的结构完全一致。
图同构问题在实际应用中具有广泛的意义。
例如,在化学中,分子结构可以用图来表示,判断两个分子是否同构就是一个图同构问题。
在计算机科学中,网络拓扑结构的分析和路由算法的设计也需要解决图同构问题。
因此,研究图同构问题的算法和方法具有重要的理论和实际价值。
图同构问题的研究与算法分析可以从多个角度进行。
一种常见的方法是基于图的特征进行分析。
例如,可以通过计算图的度序列、邻接矩阵等特征来判断两个图是否同构。
这种方法在小规模图的同构判断中具有较高的准确性,但对于大规模图的判断效果有限。
另一种方法是基于图的结构进行分析。
这种方法主要依赖于图的子结构的匹配和比较。
例如,可以通过搜索图的所有子图并比较它们的结构来判断两个图是否同构。
这种方法的优势在于可以处理大规模图,但由于子图的数量庞大,算法的时间复杂度较高。
近年来,随着计算机科学和人工智能领域的发展,图同构问题的研究也取得了一些进展。
一些基于机器学习和深度学习的方法被引入到图同构问题的研究中。
这些方法通过学习图的特征表示和嵌入向量,利用机器学习算法来判断两个图是否同构。
这种方法在处理大规模图和复杂图的同构判断中具有一定的优势。
除了算法的研究,图同构问题还涉及到数学理论的探索。
例如,图同构问题与群论、代数理论等数学分支有着密切的联系。
一些研究者通过引入群的概念和性质,来解决图同构问题。
这种方法在理论上具有一定的深度,但在实际应用中的效果有待进一步验证。
总之,离散数学中的图同构问题是一个重要且具有挑战性的问题。
它在实际应用中具有广泛的意义,并且涉及到图论、算法和数学理论等多个领域。
目前,针对图同构问题的研究主要集中在基于图的特征、结构和机器学习等方法上。