天津市滨海新区七所重点学校2018届高三毕业班联考 数学文(word版有答案)

绝密★启用前2018年普通高等学校招生全国统一考试（天津卷）数学（文史类）本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第Ⅰ卷1至2页，第Ⅱ卷3至5页。

答卷前，考生务必将自己的姓名、准考证号填写在答题考上，并在规定位置粘贴考试用条形码。

答卷时，考生务必将答案涂写在答题卡上，答在试卷上的无效。

考试结束后，将本试卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷注意事项：1．每小题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

2．本卷共8小题，每小题5分，共40分。

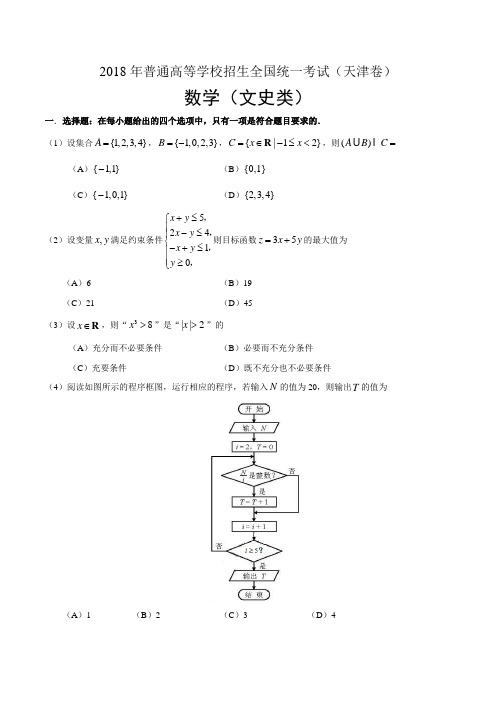
参考公式：·如果事件 A ，B 互斥，那么 P (A ∪B )=P (A )+P (B )． ·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积，h 表示棱柱的高． ·棱锥的体积公式13V Sh =，其中S 表示棱锥的底面积，h 表示棱锥的高. 一．选择题：在每小题给出的四个选项中，只有一项是符合题目要求的. （1）设集合{1,2,3,4}A =，{1,0,2,3}B =-，{|12}C x x =∈-≤<R ，则()A B C =（A ）{1,1}-（B ）{0,1}（C ）{1,0,1}-（D ）{2,3,4}（2）设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩，，，，则目标函数35z x y =+的最大值为（A ）6 （B ）19 （C ）21（D ）45（3）设x ∈R ，则“38x >”是“||2x >” 的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件（D ）既不充分也不必要条件（4）阅读如图所示的程序框图，运行相应的程序，若输入N 的值为20，则输出T 的值为（A ）1（B ）2（C ）3（D ）4（5）已知13313711log ,(),log 245a b c ===，则,,a b c 的大小关系为（A ）a b c >> （B ）b a c >> （C ）c b a >>（D ）c a b >>（6）将函数sin(2)5y x π=+的图象向右平移10π个单位长度，所得图象对应的函数 （A ）在区间[,]44ππ- 上单调递增 （B ）在区间[,0]4π上单调递减（C ）在区间[,]42ππ 上单调递增 （D ）在区间[,]2ππ 上单调递减（7）已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ，且126,d d += 则双曲线的方程为（A ）22139x y -=（B ）22193x y -=（C ）221412x y -=（D ）221124x y -= （8）在如图的平面图形中，已知 1.2,120OM ON MON ==∠=,2,2,BM MA CN NA ==则·BC OM 的值为（A ）15- （B ）9- （C ）6-（D ）0第Ⅱ卷注意事项：1．用黑色墨水的钢笔或签字笔将答案写在答题卡上。

2018年天津市滨海七所重点学校高三毕业班联考
数学试卷（文科）
一、选择题（本题共8个小题，每小题5分，共40分。

在每小题给出的四个选项中，有且只有一个是正确的）
1. 已知全集,集合,集合,则( )
A. B. C. D.
【答案】C
【解析】由题意得,选C.
2. 实数满足不等式组则目标函数的最小值是（）
A. B. C. D.
【答案】B
【解析】由约束条件画出可行域如下图，目标函数变形为，要求目标函数最小值，即求截距的最小值，所以过A(1,1)点时，，选B.
【点睛】线性规划中常见目标函数的转化公式：
（1）截距型：，与直线的截距相关联，若，当的最值情况和z的一致；若，当的最值情况和的相反；
（2）斜率型：与的斜率，常见的变形：，
，.
（3）点点距离型：表示到两点距离的平方；
3. 执行如图1所示的程序框图,若输入的值为3,则输出的值是（）
A. 1
B. 2
C. 4
D. 7
【答案】C
【解析】试题分析：第一次循环；第二次循环；第三次循环；结束循环，输出选C.
考点：循环结构流程图
【名师点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更
要通过循环规律，明确流程图研究的数学问题，是求和还是求项.
4. 若，,则的大小关系是( )。

2018年普通高等学校招生全国统一考试（天津卷）数学（文史类）一．选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．（1）设集合{1,2,3,4}A =，{1,0,2,3}B =-，{|12}C x x =∈-≤<R ，则()A B C =（A ）{1,1}- （B ）{0,1} （C ）{1,0,1}-（D ）{2,3,4}（2）设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩，，，，则目标函数35z x y =+的最大值为（A ）6 （B ）19 （C ）21（D ）45（3）设x ∈R ，则“38x >”是“||2x >”的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件（D ）既不充分也不必要条件（4）阅读如图所示的程序框图，运行相应的程序，若输入N 的值为20，则输出T 的值为（A ）1（B ）2（C ）3（D ）4（5）已知13313711log ,(),log 245a b c ===，则,,a b c 的大小关系为（A ）a b c >> （B ）b a c >> （C ）c b a >>（D ）c a b >>（6）将函数sin(2)5y x π=+的图象向右平移10π个单位长度，所得图象对应的函数 （A ）在区间[,]44ππ-上单调递增 （B ）在区间[,0]4π-上单调递减（C ）在区间[,]42ππ上单调递增 （D ）在区间[,]2ππ上单调递减（7）已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2，过右焦点且垂直于x 轴的直线与双曲线交于,A B两点．设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ，且126,d d +=则双曲线的方程为（A ）22139x y -=（B ）22193x y -= （C ）221412x y -=（D ）221124x y -= （8）在如图的平面图形中，已知1,2,120OM ON MON ==∠=,2,2,BM MA CN NA == 则·BC OM的值为（A ）15- （B ）9- （C ）6-（D ）0二．填空题：本大题共6小题，每小题5分，共30分. （9）i 是虚数单位，复数67i12i++=__________． （10）已知函数f (x )=e xln x ，f ′(x )为f (x )的导函数，则f ′（1）的值为__________．（11）如图，已知正方体ABCD –A 1B 1C 1D 1的棱长为1，则四棱锥A 1–BB 1D 1D 的体积为__________．（12）在平面直角坐标系中，经过三点（0，0），（1，1），（2，0）的圆的方程为__________．（13）已知a ，b ∈R ，且a –3b +6=0，则2a+18b的最小值为__________． （14）已知a ∈R ，函数()22220220x x a x f x x x a x ⎧++-≤⎪=⎨-+->⎪⎩，，，．若对任意x ∈［–3，+∞），f (x )≤x 恒成立，则a 的取值范围是__________．三．解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤． （15）（本小题满分13分）已知某校甲、乙、丙三个年级的学生志愿者人数分别为240，160，160．现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动．学&科网（Ⅰ）应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人？（Ⅱ）设抽出的7名同学分别用A ，B ，C ，D ，E ，F ，G 表示，现从中随机抽取2名同学承担敬老院的卫生工作．（i ）试用所给字母列举出所有可能的抽取结果；（ii ）设M 为事件“抽取的2名同学来自同一年级”，求事件M 发生的概率． （16）（本小题满分13分）在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ．已知b sin A =a cos(B –π6)． （Ⅰ）求角B 的大小；（Ⅱ）设a =2，c =3，求b 和sin(2A –B )的值． （17）（本小题满分13分）如图，在四面体ABCD 中，△ABC 是等边三角形，平面ABC ⊥平面ABD ，点M 为棱AB 的中点，AB =2，AD =23，∠BAD =90°．（Ⅰ）求证：AD ⊥BC ；（Ⅱ）求异面直线BC 与MD 所成角的余弦值； （Ⅲ）求直线CD 与平面ABD 所成角的正弦值．（18）（本小题满分13分）设{a n }是等差数列，其前n 项和为S n （n ∈N *）；{b n }是等比数列，公比大于0，其前n 项和为T n （n ∈N *）．已知b 1=1，b 3=b 2+2，b 4=a 3+a 5，b 5=a 4+2a 6． （Ⅰ）求S n 和T n ；（Ⅱ）若S n +（T 1+T 2+…+T n ）=a n +4b n ，求正整数n 的值． （19）（本小题满分14分）设椭圆22221(0)x y a b a b +=>>的右顶点为A ，上顶点为B ．已知椭圆的离心率为53，||13AB =．（I ）求椭圆的方程；（II ）设直线:(0)l y kx k =<与椭圆交于,P Q 两点，l 与直线AB 交于点M ，且点P ，M 均在第四象限．若BPM △的面积是BPQ △面积的2倍，求k 的值． （20）（本小题满分14分）设函数123()=()()()f x x t x t x t ---，其中123,,t t t ∈R ,且123,,t t t 是公差为d 的等差数列． （I ）若20,1,t d ==求曲线()y f x =在点(0,(0))f 处的切线方程； （II ）若3d =，求()f x 的极值；（III ）若曲线()y f x =与直线2()63y x t =---有三个互异的公共点，求d 的取值范围．参考答案一、（1）C （2）C （3）A （4）B （5）D （6）A （7）A （8）C 二、（9）4–i （10）e （11）13（12）2220x y x +-=（13）14（14）［18，2］三、解答题（15）（Ⅰ）解：由已知，甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2，由于采用分层抽样的方法从中抽取7名同学，因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人，2人，2人． （Ⅱ）（i ）解：从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ，B }，{A ，C }，{A ，D }，{A ，E }，{A ，F }，{A ，G }，{B ，C }，{B ，D }，{B ，E }，{B ，F }，{B ，G }，{C ，D }，{C ，E }，{C ，F }，{C ，G }，{D ，E }，{D ，F }，{D ，G }，{E ，F }，{E ，G }，{F ，G }，共21种．（ii ）解：由（Ⅰ），不妨设抽出的7名同学中，来自甲年级的是A ，B ，C ，来自乙年级的是D ，E ，来自丙年级的是F ，G ，则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ，B }，{A ，C }，{B ，C }，{D ，E }，{F ，G }，共5种． 所以，事件M 发生的概率为P （M ）=521． （16）本小题主要考查同角三角函数的基本关系，两角差的正弦与余弦公式，二倍角的正弦与余弦公式，以及正弦定理、余弦定理等基础知识，考查运算求解能力．满分13分． （Ⅰ）解：在△ABC 中，由正弦定理sin sin a b A B =，可得sin sin b A a B =，又由πsin cos()6b A a B =-，得πsin cos()6a B a B =-，即πsin cos()6B B =-，可得tan 3B =．又因为(0π)B ∈，，可得B =π3．（Ⅱ）解：在△ABC 中，由余弦定理及a =2，c =3，B =π3，有2222cos 7b a c ac B =+-=，故b =7． 由πsin cos()6b A a B =-，可得3sin 7A =．因为a <c ，故2cos 7A =．因此43sin 22sin cos 7A A A ==，21cos22cos 17A A =-=． 所以，sin(2)sin 2cos cos 2sin AB A B A B -=-=4311333727214⨯-⨯=． （17）本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识．考查空间想象能力、运算求解能力和推理论证能力．满分13分．（Ⅰ）证明：由平面ABC ⊥平面ABD ，平面ABC ∩平面ABD =AB ，AD ⊥AB ，可得AD ⊥平面ABC ，故AD ⊥BC ．（Ⅱ）解：取棱AC 的中点N ，连接MN ，ND ．又因为M 为棱AB 的中点，故MN ∥BC ．所以∠DMN （或其补角）为异面直线BC 与MD 所成的角．在Rt △DAM 中，AM =1，故DM =22=13AD AM +．因为AD ⊥平面ABC ，故AD ⊥AC ． 在Rt △DAN 中，AN =1，故DN =22=13AD AN +．在等腰三角形DMN 中，MN =1，可得1132cos 26MNDMN DM ∠==．所以，异面直线BC 与MD 所成角的余弦值为1326． （Ⅲ）解：连接CM ．因为△ABC 为等边三角形，M 为边AB 的中点，故CM ⊥AB ，CM =3．又因为平面ABC ⊥平面ABD ，而CM ⊂平面ABC ，故CM ⊥平面ABD ．所以，∠CDM 为直线CD 与平面ABD 所成的角．在Rt △CAD 中，CD =22AC AD +=4． 在Rt △CMD 中，3sin 4CM CDM CD ∠==． 所以，直线CD 与平面ABD 所成角的正弦值为34． （18）本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识．考查数列求和的基本方法和运算求解能力．满分13分．（I ）解：设等比数列{}n b 的公比为q ，由b 1=1，b 3=b 2+2，可得220q q --=． 因为0q >，可得2q =，故12n n b -=．所以，122112nn n T -==--． 设等差数列{}n a 的公差为d ．由435b a a =+，可得134a d +=．由5462b a a =+，可得131316,a d +=从而11,1a d ==，故n a n =，所以，(1)2n n n S +=． （II ）解：由（I ），有131122(12)(222)=2 2.12n nn n T T T n n n +⨯-+++=+++--=---由12()4n n n n S T T T a b ++++=+ 可得11(1)2222n n n n n n ++++--=+， 整理得2340,n n --=解得1n =-（舍），或4n =．所以n 的值为4．（19）本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识．考查用代数方法研究圆锥曲线的性质．考查运算求解能力，以及用方程思想解决问题的能力．满分14分．（I ）解：设椭圆的焦距为2c ，由已知得2259c a =，又由222a b c =+，可得23a b =．由22||13AB a b =+=,从而3,2a b ==．所以，椭圆的方程为22194x y +=． （II ）解：设点P 的坐标为11(,)x y ，点M 的坐标为22(,)x y ，由题意，210x x >>， 点Q 的坐标为11(,)x y --．由BPM △的面积是BPQ △面积的2倍，可得||=2||PM PQ ， 从而21112[()]x x x x -=--，即215x x =．学*科网 易知直线AB 的方程为236x y +=，由方程组236,,x y y kx +=⎧⎨=⎩消去y ，可得2632x k =+．由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y ，可得12694x k =+．由215x x =，可得2945(32)k k +=+，两边平方，整理得2182580k k ++=，解得89k =-，或12k =-． 当89k =-时，290x =-<，不合题意，舍去；当12k =-时，212x =，1125x =，符合题意． 所以，k 的值为12-．（20）本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法，考查函数思想和分类讨论思想，考查综合分析问题和解决问题的能力，满分14分．（Ⅰ）解：由已知，可得f (x )=x (x −1)(x +1)=x 3−x ，故()f x '=3x 2−1，因此f (0)=0，(0)f '=−1，又因为曲线y =f (x )在点(0，f (0))处的切线方程为y −f (0)=(0)f '(x −0)，故所求切线方程为x +y =0． （Ⅱ）解：由已知可得f (x )=(x −t 2+3)(x −t 2)(x −t 2−3)=(x −t 2)3−9(x −t 2)=x 3−3t 2x 2+(3t 22−9)x −t 23+9t 2． 故()f x '=3x 2−6t 2x +3t 22−9．令()f x '=0，解得x =t 2−3，或x =t 2+3．当x 变化时，()f x '，f (x )的变化如下表：x(−∞，t 2−3)t 2−3 (t 2−3，t 2+3)t 2+3 (t 2+3，+∞)()f x '+ 0 − 0 + f (x )↗极大值↘极小值↗所以函数f (x )的极大值为f (t 2−3)=(−3)3−9×(−3)=63；函数f (x )的极小值为f (t 2+3)=(3)3−9×(3)=−63．（Ⅲ）解：曲线y =f (x )与直线y =−(x −t 2)−63有三个互异的公共点等价于关于x 的方程(x −t 2+d )(x −t 2)(x −t 2 −d )+(x −t 2)+ 63=0有三个互异的实数解，令u =x −t 2，可得u 3+(1−d 2)u +63=0．学科.网设函数g (x )=x 3+(1−d 2)x +63，则曲线y =f (x )与直线y =−(x −t 2)−63有三个互异的公共点等价于函数y =g (x )有三个零点．()g'x =3x 3+(1−d 2)．当d 2≤1时，()g'x ≥0，这时()g x 在R 上单调递增，不合题意．当d 2>1时，()g'x =0，解得x 1=213d --，x 2=213d -．易得，g (x )在(−∞，x 1)上单调递增，在[x 1，x 2]上单调递减，在(x 2，+∞)上单调递增．g (x )的极大值g (x 1)=g (213d --)=32223(1)639d -+>0． g (x )的极小值g (x 2)=g (213d -)=−32223(1)639d -+． 若g (x 2)≥0，由g (x )的单调性可知函数y =g (x )至多有两个零点，不合题意．若2()0,g x <即322(1)27d ->，也就是||10d >，此时2||d x >，(||)||630,g d d =+>且312||,(2||)6||2||636210630d x g d d d -<-=--+<-+<，从而由()g x 的单调性，可知函数()y g x =在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点，符合题意．所以，d 的取值范围是(,10)(10,)-∞-+∞ ．。

绝密★启用前2018年普通高等学校招生全国统一考试（天津卷）数学（文史类）本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分,共150分,考试用时120分钟.第Ⅰ卷1至2页,第Ⅱ卷3至5页.答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码.答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效.考试结束后,将本试卷和答题卡一并交回. 祝各位考生考试顺利！第Ⅰ卷注意事项:1．每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.2．本卷共8小题,每小题5分,共40分. 参考公式:·如果事件 A ,B 互斥,那么 P (A ∪B )=P (A )+P (B )． ·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积,h 表示棱柱的高． ·棱锥的体积公式13V Sh =,其中S 表示棱锥的底面积,h 表示棱锥的高. 一．选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.（1）设集合{1,2,3,4}A =,{1,0,2,3}B =-,{|12}C x x =∈-≤<R ,则()A B C =U I （A ）{1,1}-（B ）{0,1}（C ）{1,0,1}-（D ）{2,3,4}（2）设变量,x y 满足约束条件52410x y x y x y y +≤⎧⎪-≤⎪⎨-+≤⎪⎪≥⎩，，，，则目标函数35z x y =+的最大值为（A ）6 （B ）19 （C ）21（D ）45（3）设x ∈R ,则“38x >”是“||2x >” 的（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充要条件（D ）既不充分也不必要条件（4）阅读如图所示的程序框图,运行相应的程序,若输入N 的值为20,则输出T 的值为（A ）1（B ）2（C ）3（D ）4（5）已知13313711log ,(),log 245a b c ===,则,,a b c 的大小关系为（A ）a b c >> （B ）b a c >> （C ）c b a >>（D ）c a b >>（6）将函数sin(2)5y x π=+的图象向右平移10π个单位长度,所得图象对应的函数 （A ）在区间[,]44ππ- 上单调递增 （B ）在区间[,0]4π上单调递减（C ）在区间[,]42ππ 上单调递增 （D ）在区间[,]2ππ 上单调递减（7）已知双曲线22221(0,0)x y a b a b-=>> 的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于,A B两点.设,A B 到双曲线的同一条渐近线的距离分别为1d 和2d ,且126,d d += 则双曲线的方程为（A ）22139x y -=（B ）22193x y -=（C ）221412x y -=（D ）221124x y -= （8）在如图的平面图形中,已知 1.2,120OM ON MON ==∠=o,2,2,BM MA CN NA ==u u u u r u u u r u u u r u u u r则·BC OM u u u r u u u u r 的值为（A ）15- （B ）9- （C ）6-（D ）0第Ⅱ卷注意事项:1．用黑色墨水的钢笔或签字笔将答案写在答题卡上. 2．本卷共12小题,共110分.二．填空题:本大题共6小题,每小题5分,共30分. （9）i 是虚数单位,复数67i12i++=__________． （10）已知函数f (x )=e x ln x ,f ′(x )为f (x )的导函数,则f ′（1）的值为__________．（11）如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________．（12）在平面直角坐标系中,经过三点（0,0）,（1,1）,（2,0）的圆的方程为__________． （13）已知a ,b ∈R ,且a –3b +6=0,则2a +18b的最小值为__________．（14）已知a ∈R ,函数()22220220x x a x f x x x a x ⎧++-≤⎪=⎨-+->⎪⎩，，，．若对任意x ∈［–3,+∞）,f (x )≤x 恒成立,则a 的取值范围是__________．三．解答题:本大题共6小题,共80分．解答应写出文字说明,证明过程或演算步骤． （15）（本小题满分13分）已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160．现采用分层抽样的方法从中抽取７名同学去某敬老院参加献爱心活动．（Ⅰ）应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人？（Ⅱ）设抽出的7名同学分别用A ,B ,C ,D ,E ,F ,G 表示,现从中随机抽取2名同学承担敬老院的卫生工作． （i ）试用所给字母列举出所有可能的抽取结果；（ii ）设M 为事件“抽取的2名同学来自同一年级”,求事件M 发生的概率． （16）（本小题满分13分）在△ABC 中,内角A ,B ,C 所对的边分别为a,b,c ．已知b sin A =a cos(B –π6)． （Ⅰ）求教B 的大小；（Ⅱ）设a =2,c =3,求b 和sin(2A –B )的值． （17）（本小题满分13分）如图,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB =2,AD =23,∠BAD =90°． （Ⅰ）求证:AD ⊥BC ；（Ⅱ）求异面直线BC 与MD 所成角的余弦值； （Ⅲ）求直线CD 与平面ABD 所成角的正弦值．（18）（本小题满分13分）设{a n }是等差数列,其前n 项和为S n （n ∈N *）；{b n }是等比数列,公比大于0,其前n 项和为T n （n ∈N *）．已知b 1=1,b 3=b 2+2,b 4=a 3+a 5,b 5=a 4+2a 6．（Ⅰ）求S n 和T n ；（Ⅱ）若S n +（T 1+T 2+…+T n ）=a n +4b n ,求正整数n 的值． （19）（本小题满分14分）设椭圆22221(0)x y a b a b+=>> 的右顶点为A ,上顶点为B .||AB =（I ）求椭圆的方程；（II ）设直线:(0)l y kx k =<与椭圆交于,P Q 两点,l 与直线AB 交于点M ,且点P ,M 均在第四象限.若BPM △的面积是BPQ △面积的2倍,求k 的值.（20）（本小题满分14分）设函数123()=()()()f x x t x t x t ---,其中123,,t t t ∈R ,且123,,t t t 是公差为d 的等差数列. （I ）若20,1,t d == 求曲线()y f x =在点(0,(0))f 处的切线方程； （II ）若3d =,求()f x 的极值；（III ）若曲线()y f x = 与直线 12()y x t =---有三个互异的公共点,求d 的取值范围. 参考答案一、选择题:本题考查基本知识和基本运算．每小题5分,满分40分． （1）C （2）C （3）A （4）B （5）D（6）A（7）A（8）C二、填空题:本题考查基本知识和基本运算．每小题5分,满分30分． （9）4–i（10）e （11）13（12）2220x y x +-= （13）14（14）［18,2］三、解答题（15）本小题主要考查随机抽样、用列举法计算随机事件所含的基本事件数、古典概型及其概率计算公式等基本知识．考查运用概率知识解决简单实际问题的能力．满分13分．（Ⅰ）解:由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人． （Ⅱ）（i ）解:从抽出的7名同学中随机抽取2名同学的所有可能结果为{A ,B },{A ,C },{A ,D },{A ,E },{A ,F },{A ,G },{B ,C },{B ,D },{B ,E },{B ,F },{B ,G },{C ,D },{C ,E },{C ,F },{C ,G },{D ,E },{D ,F },{D ,G },{E ,F },{E ,G },{F ,G },共21种．（ii ）解:由（Ⅰ）,不妨设抽出的7名同学中,来自甲年级的是A ,B ,C ,来自乙年级的是D ,E ,来自丙年级的是F ,G ,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A ,B },{A ,C },{B ,C },{D ,E },{F ,G },共5种．学@科网所以,事件M 发生的概率为P （M ）=521． （16）本小题主要考查同角三角函数的基本关系,两角差的正弦与余弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识,考查运算求解能力．满分13分． （Ⅰ）解:在△ABC 中,由正弦定理sin sin a b A B =,可得sin sin b A a B =,又由πsin cos()6b A a B =-,得πsin cos()6a B a B =-,即πsin cos()6B B =-,可得tan 3B =．又因为(0π)B ∈，,可得B =π3．（Ⅱ）解:在△ABC 中,由余弦定理及a =2,c =3,B =π3,有2222cos 7b a c ac B =+-=,故b =7． 由πsin cos()6b A a B =-,可得3sin 7A =．因为a <c ,故cos 7A =．因此43sin 22sin cos A A A ==,21cos22cos 17A A =-=． 所以,sin(2)sin 2cos cos2sin AB A B A B -=-=431133327⨯-⨯=．（17）本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识．考查空间想象能力、运算求解能力和推理论证能力．满分13分．（Ⅰ）由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD =AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC ． （Ⅱ）解:取棱AC 的中点N ,连接MN ,ND ．又因为M 为棱AB 的中点,故MN ∥BC ．所以∠DMN （或其补角）为异面直线BC 与MD 所成的角．在Rt △DAM 中,AM =1,故DM 22=13AD AM +AD ⊥平面ABC ,故AD ⊥AC ．在Rt △DAN 中,AN =1,故DN在等腰三角形DMN 中,MN =1,可得12cos MNDMN DM ∠==． 所以,异面直线BC 与MD（Ⅲ）解:连接CM ．因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CMABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面AB D ．所以,∠CDM 为直线CD 与平面ABD 所成的角． 在Rt △CAD 中,CD． 在Rt △CMD 中,sin CM CDM CD ∠==． 所以,直线CD 与平面ABD． （18）本小题主要考查等差数列、等比数列的通项公式及前n 项和公式等基础知识.考查数列求和的基本方法和运算求解能力.满分13分.（I ）解:设等比数列{}n b 的公比为q ,由b 1=1,b 3=b 2+2,可得220q q --=. 因为0q >,可得2q =,故12n n b -=.所以122112nn n T -==--. 设等差数列{}n a 的公差为d .由435b a a =+,可得134a d +=.由5462b a a =+,可得131316,a d += 从而11,1a d ==,故n a n =,所以(1)2n n n S +=. （II ）解:由（I ）,知13112(222)2 2.n n n T T T n n ++++=+++-=--L L由12()4n n n n S T T T a b ++++=+L 可得11(1)2222n n n n n n ++++--=+, 整理得2340,n n --= 解得1n =-（舍）,或4n =.所以n 的值为4.学&科网（19）本小题主要考查椭圆的标准方程和几何性质、直线方程等基础知识.考查用代数方法研究圆锥曲线的性质.考查运算求解能力,以及用方程思想解决问题的能力.满分14分.（I ）解:设椭圆的焦距为2c ,由已知得2259c a =,又由222a b c =+,可得23.a b =由||AB ==,从而3,2a b ==.所以,椭圆的方程为22194x y +=. （II ）解:设点P 的坐标为11(,)x y ,点M 的坐标为22(,)x y ,由题意,210x x >>, 点Q 的坐标为11(,).x y -- 由BPM △的面积是BPQ △面积的2倍,可得||=2||PM PQ , 从而21112[()]x x x x -=--,即215x x =.易知直线AB 的方程为236x y +=,由方程组236,,x y y kx +=⎧⎨=⎩ 消去y ,可得2632x k =+.由方程组221,94,x y y kx ⎧+⎪=⎨⎪=⎩消去y ,可得1x =.由215x x =,5(32)k =+,两边平方,整理得2182580k k ++=,解得89k =-,或12k =-.当89k =-时,290x =-<,不合题意,舍去；当12k =-时,212x =,1125x =,符合题意.所以,k 的值为12-.（20）本小题主要考查导数的运算、导数的几何意义、运用导数研究函数的性质等基础知识和方法,考查函数思想和分类讨论思想,考查综合分析问题和解决问题的能量,满分14分.（Ⅰ）解:由已知,可得f (x )=x (x −1)(x +1)=x 3−x ,故f ‵(x )=3x −1,因此f (0)=0,(0)f '=−1,又因为曲线y =f (x )在点(0, f (0))处的切线方程为y −f (0)= (0)f ' (x −0),故所求切线方程为x +y =0. （Ⅱ）解:由已知可得f (x )=(x −t 2+3)( x −t 2) (x −t 2−3)=( x −t 2)3−9 ( x −t 2)=x 3−3t 2x 2+(3t 22−9)x − t 22+9t 2. 故()f x '= 3x 3−6t 2x +3t 22−9.令()f x '=0,解得x = t 2或x = t 2当x 变化时,f ‵(x ),f (x )的变化如下表:所以函数f (x )的极大值为f (t 23−9×(函数小值为f (t 2)3−9×−.（III ）解:曲线y =f (x )与直线y =−(x −t 2)−有三个互异的公共点等价于关于x 的方程(x −t 2+d ) (x −t 2) (x −t 2−d )+(x −t 2有三个互异的实数解,令u = x −t 2,可得u 3+(1−d 2)u =0.设函数g (x )= x 3+(1−d 2)x 则曲线y =f (x )与直线y =−(x −t 2)−y =g (x )有三个零点.()g'x =3 x 3+(1−d 2).当d 2≤1时,()g'x ≥0,这时()g'x 在R 上单调递增,不合题意.当d 2>1时,()g'x =0,解得x 1=,x 2.易得,g (x )在(−∞,x 1)上单调递增,在[x 1, x 2]上单调递减,在(x 2, +∞)上单调递增,g (x )的极大值g (x 1)= g (+g (x )的极小值g (x 2)= g)=+若g (x 2) ≥0,由g (x )的单调性可知函数y =f (x )至多有两个零点,不合题意.若2()0,g x <即322(1)27d ->,也就是||d >此时2||d x >,(||)||0,g d d =+> 且312||,(2||)6||2||0d x g d d d -<-=--+<-<,从而由()g x 的单调性,可知函数()y g x = 在区间1122(2||,),(,),(,||)d x x x x d -内各有一个零点,符合题意.学科……网所以d 的取值范围是(,).-∞+∞U。

2018年天津市滨海七所重点学校高三毕业班联考数学试卷（理科） 评分标准一、选择题(本题共8个小题，每小题5分，共40分). CCAB BDDB 二、填空题(本大题共6小题，每小题5分，共30分).9. -5； 10.14; 11.10π3 ； 12. ]1,25[--； 13. 38； 14. 288.三.解答题(本大题6小题，共80分．解答应写出文字说明，证明过程或演算步骤．) 15. (本小题满分13分) 已知函数21)6(sin )2cos(cos 3)(2--+-=ππx x x x f . （Ⅰ）求)(x f 的单调递增区间；（Ⅱ）若63)(],4,0[=∈x f x π，求cos 2x 的值； 【解析】(Ⅰ)21)6(sin )2cos(cos 3)(2--+-=ππx x x x f 212)32cos(1cos sin 3---+=πx x x -----------------------------2分 212)32cos(12sin 23---+=πx x -----------------------------3分 )32cos(212sin 23π--=x x )2sin 232cos 21(212sin 23x x x +-=-----------------------------4分 x x 2cos 412sin 43-= )62sin(21π-=x -----------------------------5分 令226222πππππ+≤-≤-k x k ，322232ππππ+≤≤-k x k ， 36ππππ+≤≤-k x k ，-----------------------------6分所以，)(x f 的单调递增区间为：Z k k k ∈+-],3,6[ππππ---------------------------------7分 (Ⅱ)63)62sin(21)(=-=πx x f 33)62s i n (=-πx ,-----------------------------8分 ⎥⎦⎤⎢⎣⎡∈4,0πx 3626πππ≤-≤-∴x -----------------------------9分3662cos =⎪⎭⎫ ⎝⎛-∴πx -----------------------------10分 ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=∴662cos 2cos ππx x -----------------------------11分2162sin -2362cos ⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-=ππx x -----------------------------12分 632233212336-=⨯-⨯=--------------------------13分 16. (本小题满分13分)某单位年会进行抽奖活动，在抽奖箱里装有1张印有“一等奖”的卡片，2张印有“二等奖”的卡片，3张印有“新年快乐”的卡片.抽中“一等奖”获奖200元，抽中“二等奖”获奖100元，抽中“新年快乐”无奖金。

2018年天津市滨海七所重点学校高三毕业班联考数学试卷（文科） 第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知全集{}12345U =，，，，，集合{}15A =，，集合{}235B =，，，则()U C B A =（ ） A ．{}2 B ．{}23， C ．{}1 D ．{}14，2.实数x ，y 满足不等式20201x y x y y +-≥⎧⎪--≤⎨⎪≥⎩则目标函数2z x y =+的最小值是（ ）A ．2B ．3C ．4D ．53.执行如图所示的程序框图，若输入n 的值为3，则输出s 的值是（ ）A ．1B ．2C ．4D ．74.若131()2a =，13log 2b =，12log 3c =，则a ，b ，c 的大小关系是（ ）A ．b a c <<B ．b c a << C.a b c << D ．c b a << 5.设x R ∈，则“1x <”是“20x x -<”的（ ）A ．充分不必要条件B ．必要不充分条件 C.充要条件 D ．既不充分也不必要条件6.函数()sin()f x x ωϕ=+（0ω>，2πϕ<）的最小正周期是π，若其图象向左平移3π个单位后得到的函数为奇函数，则函数()f x 的图象（ ） A ．关于点(0)12π，对称 B ．关于直线12x π=对称C.关于点(0)6π，对称 D ．关于直线6x π=对称 7.已知双曲线22221x y a b -=（0a >，0b >）的两条渐近线与抛物线22y px =（0p >）的准线分别交于A ，B 两点，O 为坐标原点，若双曲线的离心率为2，ABO △的面积为，则抛物线的焦点为（ ）A ．1(0)2， B．0) C.(10)， D．0) 8.已知函数()2f x x x a x =-+，若存在(]23a ∈，，使得关于x 的函数()()y f x tf a =-有三个不同的零点，则实数t 的取值范围是（ ）A ．9584⎛⎫ ⎪⎝⎭，B ．25124⎛⎫ ⎪⎝⎭， C.918⎛⎫ ⎪⎝⎭， D ．514⎛⎫⎪⎝⎭，第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上） 9.已知i 是虚数单位，则734ii+=+ ． 10.一个几何体的三视图如图所示，则该几何体的体积为 ．11.等比数列{}n a 中，各项都是正数，且1a ，312a ，22a 成等差数列，则13141415a a a a +=+ ．12.设直线2y x a =+与圆C ：22220x y ay +--=（0a >）相交于A ，B 两点，若AB =则a = ．13.已知正实数a ，b 满足a b >，且12ab =，则22412a b a b ++-的最小值为 ．14.已知菱形ABCD 的边长为2，120BAD ∠=︒，点E 、F 分别在边BC ，CD 上，BE BC λ=，DF DC μ=，若522λμ+=，则AE AF ⋅的最小值 ． 三、解答题 （本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.） 15.从高三学生中抽取n 名学生参加数学竞赛，成绩（单位：分）的分组及各数据绘制的频率分布直方图如图所示，已知成绩的范围是区间[40100)，，且成绩在区间[7090)，的学生人数是27人，（1）求x ，n 的值；（2）若从数学成绩（单位：分）在[4060)，的学生中随机选取2人进行成绩分析 ①列出所有可能的抽取结果；②设选取的2人中,成绩都在[5060)，内为事件A ，求事件A 发生的概率.16.锐角ABC △中，a ，b ，c 分别为角A ，B ，C 的对边，4sin a B ， （1）若6a =，8b c +=，求ABC △的面积； （2）求2sin(2)3A π+的值. 17. 如图，在四棱锥P ABCD -中，底面ABCD 的边长是2的正方形，PA PD =，PA PD ⊥，F 为PB 上的点，且AF ⊥平面PBD .（1）求证：PD AB ⊥；（2）求证：平面PAD ⊥平面ABCD ； （3）求直线PB 与平面ABCD 所成角的正弦值.18. 已知(02)A -，，椭圆E ：22221x y a b+=（0a b >>F 是椭圆E 的右焦点，直线AFO 为坐标原点.（1）求椭圆的方程；（2）设过点A 的动直线l 与椭圆E 相交于P ，Q 两点，当OPQ △的面积最大时，求直线l 的方程.19. 已知数列{}n a 的前n 项和为n S ，满足21n n S a =-（*n N ∈），数列{}n b 满足()()111n n nb n b n n +-+=+（*n N ∈），且11b = （1）证明数列n b n ⎧⎫⎨⎬⎩⎭为等差数列，并求数列{}n a 和{}n b 的通项公式；（2）若12214(1)(1)(32log )(32log )n n n n n c a a -++=-++，求数列{}n c 的前n 项和2n T ；（3）若n n d a =，数列{}n d 的前n 项和为n D ，对任意的*n N ∈，都有n n D nS a ≤-，求实数a 的取值范围. 20. 已知函数1()ln xf x x ax-=+（其中0a >， 2.7e ≈）. （1）当1a =时，求函数()f x 在(1(1))f ，点处的切线方程；（2）若函数()f x 在区间[2)+∞，上为增函数，求实数a 的取值范围； （3）求证：对于任意大于1的正整数n ，都有111ln 23n n>+++.2018年天津市滨海七所重点学校高三毕业班联考数学试卷（文科）评分标准一、选择题1-5:CBCDA 6-8:BDB 二、填空题9.1i - 10.46π+114.3 三、解答题15.解：（1）由直方图可得成绩分布在区间的频率为 0.1(0.0040.0060.020.0160.03)0.024x =-++++=样本容量275010(0.030.024)n ==+（2）①成绩在区间[4050)，共有2人记为x ，y 成绩在区间[5060)，共有3人记为a ，b ，c 则从中随机选取2人所有可能的抽取结果共有10种情况：{}x y ，{}x a ，{}x b ，{}x c ，{}y a ，{}y b ，{}y c ，，{}a b ，{}a c ，{}b c ， ②“从上述5人中任选2人，都来自[5060)，分数段”为事件A ； 则事件A 包含的基本事件有{}a b ，{}a c ，{}b c ， 故所求概率3()10P A =16.（1）∵4sin a B =∴4sin sin A B B = ∵0B π<<∴sin A =∵A 是锐角∴3cos 4A = 由余弦定理2222cos a b c bc A =+-.得223362b c bc =+-277()6422b c bc bc =+-=-，∴8bc =则11sin 822ABC S bc A ==⨯=△（2）3sin 22sin cos 24A A A ===221cos 212sin 18A A =-=-= 222sin(2)sin 2cos cos2sin333A A A πππ+=+11()28=-+= 17.证明：（1）∵AF ⊥平面PBD ，PB ⊂平面PBD ， ∴PD AF ⊥ ∵PA PD ⊥PAAF A =∴PD ⊥平面PAB∵AB ⊂平面PAB ∴PD AB ⊥ （2）∵ABCD 是正方形，∴AB AD ⊥ ∵PD AB ⊥，ADPD D =，∴AB ⊥平面PAD∵AB ⊂平面ABCD ，∴平面PAD ⊥平面ABCD（3）取AD 的中点H ，连接PH ，BH ，∵PA PD =，∴PH AD ⊥ ∵平面PAD ⊥平面ABCD ，PH ⊂平面PAD 平面PAD平面ABCD AD =∴PH ⊥平面ABCD∴BH 是PB 在平面ABCD 内的射影. ∴PBH ∠就是PB 与平面ABCD 所成的角在等腰Rt PAD △中，∵2AD =，H 是AD 的中点，∴1PH = 在Rt BAH △中，∵1AH =，2AB =∴BH =PB∴sinPH PBH PB ∠===18.（1）设(0)F c ，，由条件知，2c c =⇒=又c a a =⇒=22b =，故椭圆E 的方程为22182x y +=；（2）当l x ⊥轴时，不合题意，故可设l ：2y kx =-. 222182y kx x y =-⎧⎪⎨+=⎪⎩22(14)1680k x kx ⇒+-+=， 22116(41)04k k ∆=->⇒>， 设11()P x y ，，22()Q x y ，，1221614k x x k +=+，122814x x k =+，PQ=又点O 到直线l的距离d =∴OPQ △的面积12OPQS PQ d ==△，t =，则0t >，∴2OPQ S t t==≤+△当且仅当2t t t=⇒k = 满足0∆>，∴当k =OPQ △的面积取得最大值2，此时直线l的方程为2y =-或2y x =-. 19.解（1）由1(1)(1)n n nb n b n n +-+=+两边同除以(1)n n +，得111n nb b n n+-=+， 从而数列n b n ⎧⎫⎨⎬⎩⎭为首项11b =，公差1d =的等差数列，所以n b n n =，数列{}n b 的通项公式为2n b n =， 当1n =时，11121S a a =-=，所以11a =. 当2n ≥时，21n n S a =-，1121n n S a --=-， 两式相减得12n n a a -=，又11a =，所以12nn a a -=，从而数列{}n a 为首项11a =，公比2q =的等比数列， 从而数列{}n a 的通项公式为12n n a -=. （2）14(1)(1)()(21)(23)n n n c n n -+=-++111(1)()2123n n n -=-+++ 2123212n n n T c c c c c -=++++11111135574143n n =+--+--++ 11343n =-+（3）由（1）得12n n d a n -= 221112232(1)22n n n D n n --=⨯+⨯+⨯+-+23112122232(1)2(1)22n n n n D n n n --=⨯+⨯+⨯+-+-+所以，两式相减得2112222n nn D n --=++++-12212nn n -=--所以(1)21n n D n =-+由（1）得2121n n n S a =-=-，因为对*n N ∀∈，都有n n D nS a ≤-，即(1)21(21)n n n n a -⋅+≤--恒成立， 所以21n a n ≤--恒成立， 记21n n d n =--，所以min ()n a d ≤，因为()()1121121n nn n d d n n ++⎡⎤-=-+----⎣⎦210n =->，从而数列{}n d 为递增数列所以当1n =时，n d 取最小值10d =，于是0a ≤ 20.解（1）∵1()ln xf x x x-=+， ∴21()x f x x-'=（0a >） ∴(1)0f '= ∵(1)0f =∴()f x 在点(1(1))f ，处的切线方程为0y = （2）∵1()ln xf x x ax-=+ ∴21()ax f x ax -'=（0a >） ∵海宁市()f x 在[2)+∞，上为增函数， ∴()0f x '≥对任意[2)x ∈+∞，恒成立. ∴10ax -≥对任意[2)x ∈+∞，恒成立， 即1a x≥对任意[2)x ∈+∞，恒成立. ∵[2)x ∈+∞，时，max 112x ⎛⎫= ⎪⎝⎭， ∴12a ≥，即所求正实数a 的取值范围是1[)2+∞，. （3）当1a =时，1()ln x f x x x -=+，21()x f x x-'= 当1x >时，()0f x '>，故()f x 在(1)+∞，上是增函数.。

天津塘沽一中、汉沽一中、大港一中、咸水沽一中、杨柳青一中、一百中学六校联考高三年级数学试卷（文科）本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分,共150分,考试时间120分钟。

第I 卷 (选择题，共50分)注意事项：1．答第Ⅰ卷前，请考生将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．选出答案后，用铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再填涂其它答案，不能答在试卷上。

一、选择题（本题共10个小题，每小题5分，共50分。

在每小题给出的四个选项中，有且只有一个是正确的） 1.设集合P={直线的倾斜角}，Q={两个向量的夹角}，R={两条直线的夹角}，M={直线l 1到l 2的角}则必有A. Q R=P MB. R ⊂M ⊂P ⊂QC. Q=R ⊂M=PD. R ⊂P ⊂M ⊂Q2. 在等差数列{}n a 中，若C a a a =++1383，则其前n 项和n S 的值等于5C 的是A ．15SB ．17S C ．7SD ．8S3. 若点B 分CE 的比为21-，且有BC CE λ=，则λ等于 A.２ B.12C.1D.－1 4．过点（－4，0）作直线L 与圆x 2+y 2+2x －4y －20=0交于A 、B 两点，如果|AB|=8，则L 的方程为 A ． 5x +12y+20=0 B ． 5x -12y+20=0C ． 5x -12y+20=0或x +4=0D ． 5x +12y+20=0或x +4=05.已知p, q, p+q 是等差数列,p ,q ,pq 是等比数列，则椭圆122=+qy p x 的准线方程是A.22±=yB. 22±=xC. 362±=y D. 362±=x 6. 已知命题P ：关于x 的不等式m xx x >+-2241的解集为{}R x x x ∈≠且,0|；命题Q ：xm x f )25()(--=是减函数.若P 或Q 为真命题，P 且Q 为假命题，则实数m 的取值范围是A .（1，2）B .[1，2）C .（－∞，1]D .（－∞，1）7．函数1)42(sin 2)(2-+=πx x f 是 A.周期为π的奇函数 B. 周期为π的偶函数 C. 周期为π2的奇函数 D. 周期为π2的偶函数 8. 若m x x f ++=)cos(2)(ϕω，对任意实数t 都有)()4(t f t f -=+π，且1)8(-=πf , 则实数m 的值等于 A. 1± B. 3± C. -3或1 D. -1或39. 设函数x x f m log )(=，数列{}n a 是公比为m 的等比数列，若,8)(200642=a a a f 则)()()(220062221a f a f a f +++ 的值等于A ．-1974B ．-1990C ．2182D ．218810. 函数)(||)(R x q px x x x f ∈++=是奇函数，且在R 上是增函数的充要条件是 A. p >0 ,q=0 B. p <0 ,q=0 C. p ≤0，q ＝0 D. p ≥0，q =0第Ⅱ卷 (非选择题，共100分)注意事项：1．第Ⅱ共6页，用蓝、黑色的钢笔或圆珠笔直接答在试卷中。

2018年天津市滨海七所重点学校高三毕业班联考英语试卷第I卷选择题（共115分)注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。

2．选出答案后，用铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再填涂其它答案。

第一部分：听力（共两节，满分20分）第一节（共5小题；每小题1分，满分5分）听下面五段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你将有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What does the man plan to do?A. Watch a show.B. Do an experiment.C. Attend a lecture.2.How will the man probably go to Chicago?A. By car.B. By plane.C. By bus.3.What does the man mean?A. Few people agree with his points.B. Few people know about arts.C. Few people read his article.4. What do we know about Helen?A. She is away traveling.B. She started a studio.C. She was fired.5. How many tickets does the woman have?A. 2.B. 3.C. 4.第二节（共10小题；每小题1.5分，满分15分）听下面几段材料。

每段材料后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段材料前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

2018年天津市滨海七所重点学校高三毕业班联考数学试卷（文科）一、选择题（本题共8个小题，每小题5分，共40分。

在每小题给出的四个选项中，有且只有一个是正确的）1. 已知全集,集合,集合,则( )A. B. C. D.【答案】C【解析】由题意得,选C.2. 实数满足不等式组则目标函数的最小值是（）A. B. C. D.【答案】B【解析】由约束条件画出可行域如下图，目标函数变形为，要求目标函数最小值，即求截距的最小值，所以过A(1,1)点时，，选B.【点睛】线性规划中常见目标函数的转化公式：（1）截距型：，与直线的截距相关联，若，当的最值情况和z的一致；若，当的最值情况和的相反；（2）斜率型：与的斜率，常见的变形：，，.（3）点点距离型：表示到两点距离的平方；3. 执行如图1所示的程序框图,若输入的值为3,则输出的值是（）A. 1B. 2C. 4D. 7【答案】C【解析】试题分析：第一次循环；第二次循环；第三次循环；结束循环，输出选C.考点：循环结构流程图【名师点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.4. 若，,则的大小关系是( )A. B. C. D.【答案】D【解析】，，所以，选D.5. 设，则“”是“”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】由，解得，由，可知“”是“”的充分不必要条件，选A.6. 函数的最小正周期是，若其图象向左平移个单位后得到的函数为奇函数，则函数的图象 ( )A. 关于点对称B. 关于直线对称C. 关于点对称D. 关于直线对称【答案】B【解析】最小正周期是,得，，图像向左平移个单位后得到的函数为为奇函数，所以，，所以直线是函数f(x)的对称，选B.7. 已知双曲线的两条渐近线与抛物线的准线分别交于,两点, 为坐标原点. 若双曲线的离心率为,的面积为, 则抛物线的焦点为( )A. ()B. （）C.D.【答案】D【解析】双曲线离心率抛物线的准线，，所以抛物线的焦点坐标。

2017-2018学年天津市滨海新区六所重点学校高三联考数学试卷（文科）一.选择题：本题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，有且只有一个是正确的.1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则（∁U A）∪B为（）A．{1，2，4}B．{2，3，4}C．{0，2，3，4} D．{0，2，4}2．“x＜4”是“|x﹣2|＜1”成立的（）A．充分不必要条件B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件3．阅读如图的程序框图，当程序运行后，输出S的值为（）A．57 B．119 C．120 D．2474．设实数p在[0，5]上随机地取值，使方程x2+px+1=0有实根的概率为（）A．0.6 B．0.5 C．0.4 D．0.35．若，则a，b，c大小关系为（）A．b＞c＞a B．b＞a＞c C．c＞a＞b D．a＞b＞c6．将y=sin2x+cos2x的图象向右平移个单位后，所得图象的解析式是（）A．y=sin2x﹣cos2x B．y=cos2x﹣sin2xC．y=cos2x+sin2x D．y=cosxsinx7．如图，F1、F2是双曲线=1（a＞0，b＞0）的左、右焦点，过F1的直线l与C 的左、右2个分支分别交于点A、B．若△ABF2为等边三角形，则双曲线的离心率为（）A ．4B ．C ．D ．8．设函数f （x ）=|2x ﹣1|，函数g （x ）=f （f （x ））﹣log a （x +1），（a ＞0，a ≠1）在[0，1]上有3个不同的零点，则实数a 的取值范围为（ ） A ．（1，） B ．（1，2） C ．（，2） D ．（2，+∞）二.填空题：本大题共6小题，每小题5分，共30分.把答案填在答题纸的相应横线上. 9．已知i 为虚数单位，复数z 满足z （2﹣i ）=5i ，则z 等于________． 10．已知一个几何体的三视图如图所示，则该几何体的体积为________cm 311．如图，PA 是圆O 的切线，切点为A ，PO 交圆O 于B 、C 两点，，则AC=________．12．已知各项不为0的等差数列{a n }满足，数列{b n }是等比数列，且b 7=a 7，则b 2b 8b 11的值等于________．13．已知实数a ，b 满足a ＞b ，且ab=2，则的最小值是________．14．已知菱形ABCD 的边长为2，∠BAD=120°，点E ，F 分别在边BC 、DC 上，．若，则实数λ的值为________．三.解答题：本大题6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．某厂用甲、乙两种原料生产A 、B 两种产品，已知生产1吨A 产品，1吨B 产品分别需万元？16．在△ABC中，设内角A、B、C的对边分别为a、b、c，．（Ⅰ）求角C；（Ⅱ）若且sinA=2sinB，求△ABC的面积．17．如图，在四棱锥E﹣ABCD中，底面ABCD是边长为的正方形，平面AEC⊥平面CDE，∠AEC=90°，F为DE中点，且DE=1．（Ⅰ）求证：BE∥平面ACF；（Ⅱ）求证：CD⊥DE；（Ⅲ）求FC与平面ABCD所成角的正弦值．18．设数列{a n}的前n项的和为S n，点（n，S n）在函数f（x）=2x2的图象上，数列{b n}满足：b1=a1，b n+1（a n+1﹣a n）=b n．其中n∈N*．（Ⅰ）求数列{a n}和{b n}的通项公式；（Ⅱ）设，求证：数列{c n}的前n项的和（n∈N*）．19．椭圆C： +=1（a＞b＞0）的左、右顶点的坐标分别为A（﹣2，0），B（2，0），离心率（Ⅰ）求椭圆C的方程；（Ⅱ）设椭圆C的两焦点分别为F1、F2，点P是椭圆C的上顶点，求△PF1F2内切圆方程；（Ⅲ）若直线l：y=k（x﹣1）（k≠0）与椭圆交于M、N两点，求证：直线AM与直线BN 的交点在直线x=4上．20．已知函数f（x）=kx2，g（x）=lnx（Ⅰ）求函数的单调递增区间；（Ⅱ）若不等式f（x）≥g（x）在区间（0，+∞）上恒成立，求k的取值范围；（Ⅲ）求证：．2016年天津市滨海新区六所重点学校高三联考数学试卷（文科）参考答案与试题解析一.选择题：本题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，有且只有一个是正确的.1．已知全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，4}，则（∁U A）∪B为（）A．{1，2，4}B．{2，3，4}C．{0，2，3，4} D．{0，2，4}【考点】交、并、补集的混合运算．【分析】由题意，集合∁U A={0，4}，从而求得（∁U A）∪B={0，2，4}．【解答】解：∵∁U A={0，4}，∴（∁U A）∪B={0，2，4}；故选D．2．“x＜4”是“|x﹣2|＜1”成立的（）A．充分不必要条件B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】由|x﹣2|＜1，解得1＜x＜3，即可判断出结论．【解答】解：由|x﹣2|＜1，解得1＜x＜3，∴“x＜4”是“|x﹣2|＜1”成立的必要不成立条件，故选：B．3．阅读如图的程序框图，当程序运行后，输出S的值为（）A．57 B．119 C．120 D．247【考点】程序框图．【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【解答】解：模拟执行程序框图，可得S=1，k=1k=2，S=4不满足条件k＞5，k=3，S=11不满足条件k＞5，k=4，S=26不满足条件k＞5，k=5，S=57不满足条件k＞5，k=6，S=120满足条件k＞5，退出循环，输出S的值为120．故选：C．4．设实数p在[0，5]上随机地取值，使方程x2+px+1=0有实根的概率为（）A．0.6 B．0.5 C．0.4 D．0.3【考点】几何概型．【分析】由题意知方程的判别式大于等于零求出p的范围，再判断出所求的事件符合几何概型，再由几何概型的概率公式求出所求事件的概率．【解答】解：若方程x2+px+1=0有实根，则△=p2﹣4≥0，解得，p≥2或p≤﹣2；∵记事件A：“P在[0，5]上随机地取值，关于x的方程x2+px+1=0有实数根”，由方程x2+px+1=0有实根符合几何概型，∴P（A）===0.6．故选：A．5．若，则a，b，c大小关系为（）A．b＞c＞a B．b＞a＞c C．c＞a＞b D．a＞b＞c【考点】对数值大小的比较．【分析】根据指数函数与对数函数的图象与性质，即可得出a，b，c的大小关系．【解答】解：∵a=30.1＞1，且1＜2＜π，∴0＜logπ2＜1，∴0＜b＜1；又0＜sin＜1，∴c=log2sin＜0，∴a，b，c大小关系是a＞b＞c．故选：D．6．将y=sin2x+cos2x的图象向右平移个单位后，所得图象的解析式是（）A．y=sin2x﹣cos2x B．y=cos2x﹣sin2xC．y=cos2x+sin2x D．y=cosxsinx【考点】函数y=Asin（ωx+φ）的图象变换；两角和与差的正弦函数．【分析】由条件利用函数y=Asin（ωx+φ）的图象变换规律，得出结论．【解答】解：将函数y=sin2x+cos2x=sin（2x+）的图象向右平移个单位后，所得图象对应的解析式是y=sin[2（x﹣）+]=sin（2x﹣）=sin2x﹣cos2x，故选：A．7．如图，F1、F2是双曲线=1（a＞0，b＞0）的左、右焦点，过F1的直线l与C 的左、右2个分支分别交于点A、B．若△ABF2为等边三角形，则双曲线的离心率为（）A．4 B．C．D．【考点】双曲线的简单性质．【分析】利用双曲线的定义可得可得|AF1|﹣|AF2|=2a，|BF2|﹣|BF1|=2a，利用等边三角形的定义可得：|AB|=|AF2|=|BF2|，．在△AF1F2中使用余弦定理可得：=﹣，再利用离心率的计算公式即可得出．【解答】解：∵△ABF2为等边三角形，∴|AB|=|AF2|=|BF2|，．由双曲线的定义可得|AF1|﹣|AF2|=2a，∴|BF1|=2a．又|BF2|﹣|BF1|=2a，∴|BF2|=4a．∴|AF2|=4a，|AF1|=6a．在△AF1F2中，由余弦定理可得：=﹣，∴，化为c2=7a2，∴=．故选B．8．设函数f（x）=|2x﹣1|，函数g（x）=f（f（x））﹣log a（x+1），（a＞0，a≠1）在[0，1]上有3个不同的零点，则实数a的取值范围为（）A．（1，）B．（1，2）C．（，2）D．（2，+∞）【考点】函数零点的判定定理．【分析】作出两个函数的图象，结合对数函数的单调性，利用数形结合即可得到结论．【解答】解：∵f（x）=|2x﹣1|=，∴f（f（x））=|2|2x﹣1|﹣1|=分别画出y=f（f（x））与y=log a（x+1）的图象，∵y=log a（x+1）的图象是由y=log a x的图象向左平移一个单位得到的，且过点（0，0），当x=1时，y=f（f（1））=1，此时log a（1+1）=1，解得a=2，有4个交点，当x=时，y=f（f（））=1，此时log a（+1）=1，解得a=，有2个交点，综上所述a的取值范围为（，2）故选：C．二.填空题：本大题共6小题，每小题5分，共30分.把答案填在答题纸的相应横线上. 9．已知i为虚数单位，复数z满足z（2﹣i）=5i，则z等于﹣1+2i．【考点】复数代数形式的乘除运算．【分析】利用复数的运算法则即可得出．【解答】解：∵z（2﹣i）=5i，∴z===2i﹣1，故答案为：﹣1+2i．10．已知一个几何体的三视图如图所示，则该几何体的体积为cm3【考点】由三视图求面积、体积．【分析】由三视图知几何体是一圆柱挖去一个半球，且圆柱的高为3，圆柱与球的半径都是1，代入体积公式求出圆柱的体积与半球的体积相减．【解答】解：由三视图知几何体是一圆柱挖去一个半球，且圆柱的高为3，圆柱与球的半径都是1，∴几何体的体积V=π×12×3﹣π×13=．故答案是：．11．如图，PA是圆O的切线，切点为A，PO交圆O于B、C两点，，则AC=．【考点】与圆有关的比例线段；相似三角形的性质．【分析】连接OA，则OA⊥PA，利用切割线定理，求出PO，OA，可求出∠PAB，即可求出AC．【解答】解：连接OA，则OA⊥PA．∵PA是圆O的切线，∴PA2=PB•PC，∵PA=，PB=1，∴PC=3，∴PO=2，OA=1，∴sin∠PAB=，∴∠PAB=30°，∴∠C=30°，∵BC=PC﹣PB=2，∴AC=2cos30°=故答案为：．12．已知各项不为0的等差数列{a n}满足，数列{b n}是等比数列，且b7=a7，则b2b8b11的值等于8．【考点】等差数列的通项公式．【分析】由等差数列和等比数列的通项公式和性质可得b7=a7=2，而b2b8b11=b73，代值计算可得．【解答】解：∵各项不为0的等差数列{a n}满足，∴2a7﹣a72=0，解得a7=2，∴b7=a7=2，∴b2b8b11=b6b8b7=b73=8，故答案为：8．13．已知实数a，b满足a＞b，且ab=2，则的最小值是．【考点】基本不等式．【分析】实数a，b满足a＞b，且ab=2，变形为==（a﹣b）+，再利用基本不等式的性质即可得出．【解答】解：∵实数a，b满足a＞b，且ab=2，∴==（a﹣b）+≥2=2，当且仅当，a=时取等号．∴的最小值是2．故答案为：2．14．已知菱形ABCD 的边长为2，∠BAD=120°，点E ，F 分别在边BC 、DC 上，．若，则实数λ的值为﹣．【考点】平面向量数量积的运算．【分析】利用两个向量的加减法的法则，以及其几何意义，两个向量的数量积的定义由若，求得． 【解答】解：∵=+=+， =+=+，∴•=（+）（+），=•+•+•+•， =||•||cos120°+||•||cos0°+||•||cos0°+||•||cos120°，=2×2×（﹣）+×2×2×1+×2×2×1+×2×2×（﹣）==1，解得λ=﹣， 故答案为：﹣．三.解答题：本大题6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．某厂用甲、乙两种原料生产A 、B 两种产品，已知生产1吨A 产品，1吨B 产品分别需问：在现有原料下，、产品应各生产多少吨才能使利润总额最大？利润总额最大是多少万元？【考点】简单线性规划的应用；简单线性规划．【分析】生产A 、B 产品分别为x ，y 吨，利润总额为z 元，列出约束条件，作出可行域，根据可行域寻找最优解．【解答】解：设生产A 、B 产品分别为x ，y 吨，利润总额为z 元，由题意得．目标函数为z=7x+12y．作出二元一次不等式组所表示的可行域，如图：目标函数可变形为，∵﹣＜﹣＜﹣，∴当通过图中的点A时，截距最大，即z最大．解得点A坐标为（20，24）．将点A（20，24）代入z=7x+12y得z max=7×20+12×24=428万元．答：该厂生产A，B两种产品分别为20吨、24吨时利润最大，最大利润为428万元．16．在△ABC中，设内角A、B、C的对边分别为a、b、c，．（Ⅰ）求角C；（Ⅱ）若且sinA=2sinB，求△ABC的面积．【考点】余弦定理；正弦定理．【分析】（Ⅰ）利用两角差的正弦函数，余弦函数公式化简已知可得，结合范围0＜C＜π，即可解得C的值．（Ⅱ）由正弦函数化简sinA=2sinB，可得a=2b，利用余弦定理解得b，可求a的值，利用三角形面积公式即可得解．【解答】（本题满分13分）解：（Ⅰ）因为，所以，因为在△ABC中，0＜C＜π，所以．（Ⅱ）因为sinA=2sinB，所以a=2b，因为c2=a2+b2﹣2abcosC，所以，所以b=2，所以a=4．所以．17．如图，在四棱锥E﹣ABCD中，底面ABCD是边长为的正方形，平面AEC⊥平面CDE，∠AEC=90°，F为DE中点，且DE=1．（Ⅰ）求证：BE∥平面ACF；（Ⅱ）求证：CD⊥DE；（Ⅲ）求FC与平面ABCD所成角的正弦值．【考点】直线与平面所成的角；直线与平面平行的判定．【分析】（I）连结BD和AC交于O，连结OF，由中位线定理得出BE∥OF，故BE∥平面ACF；（II）由面面垂直的性质得出AE⊥平面CDE，故而AE⊥CD，又CD⊥AD，于是CD⊥平面ADE，从而CD⊥DE；（III）过F作FM⊥AD于M，连接CM．则可证FM⊥平面ABCD，于是∠FCM为所求的线面角，利用勾股定理和相似三角形求出CF，FM，得出sin∠FCM．【解答】证明：（Ⅰ）连结BD和AC交于O，连结OF，∵ABCD为正方形，∴O为BD中点，∵F为DE中点，∴OF∥BE，又∵BE⊄平面ACF，OF⊂平面ACF，∴BE∥平面ACF．（Ⅱ）∵平面AEC⊥平面CDE，∠AEC=90°，平面AEC∩平面CDE=CE，∴AE⊥平面CDE，CD⊂平面CDE，∴AE⊥CD，∵ABCD为正方形，∴CD⊥AD，又∵AE∩AD=A，AD，AE⊂平面DAE，∴CD⊥平面DAE，∵DE⊂平面DAE，∴CD⊥DE．（Ⅲ）过F作FM⊥AD于M，连接CM．由（II）得CD⊥平面DAE，CD⊂平面ABCD，∴平面ABCD⊥平面DAE，又∴平面ABCD∩平面DAE=AD，FM⊥AD，∴FM⊥平面ABCD，∴∠FCM为FC与平面ABCD所成角，∴，DF=，DE=1，∴，AE=1，，∴FM==，∴．18．设数列{a n}的前n项的和为S n，点（n，S n）在函数f（x）=2x2的图象上，数列{b n}满足：b1=a1，b n+1（a n+1﹣a n）=b n．其中n∈N*．（Ⅰ）求数列{a n}和{b n}的通项公式；（Ⅱ）设，求证：数列{c n}的前n项的和（n∈N*）．【考点】数列与不等式的综合；数列递推式．【分析】（Ⅰ）利用与作差可知a n=4n﹣2（n≥2）进而可知a n=4n﹣2；通过代入计算可知b n+1=b n，进而计算可得结论；（Ⅱ）通过（I）可知数列{c n}的通项公式，进而利用错位相减法计算即得结论．【解答】（Ⅰ）解：由已知条件得，①当n=1时，a1=2当n≥2时，，②①﹣②得：，即a n=4n﹣2（n≥2），又a1=2，∴a n=4n﹣2；∵b1=a1，b n+1（a n+1﹣a n）=b n，∴，∴；（Ⅱ）证明：∵，∴，4T n=4+3•42+…+（2n﹣3）•4n﹣1+（2n﹣1）•4n两式相减得∴．19．椭圆C： +=1（a＞b＞0）的左、右顶点的坐标分别为A（﹣2，0），B（2，0），离心率（Ⅰ）求椭圆C的方程；（Ⅱ）设椭圆C的两焦点分别为F1、F2，点P是椭圆C的上顶点，求△PF1F2内切圆方程；（Ⅲ）若直线l：y=k（x﹣1）（k≠0）与椭圆交于M、N两点，求证：直线AM与直线BN 的交点在直线x=4上．【考点】直线与圆锥曲线的综合问题；椭圆的简单性质．【分析】（Ⅰ）根据条件便得到a=2，，从而便可得出c=，b=1，这样便得出椭圆C的方程为；（Ⅱ）根据题意便知△PF1F2内切圆的圆心在y轴上，设圆心为（0，m），m＞0，并且圆半径为m，可以得出点P，F2的坐标，从而得出直线PF2的方程为，这样即可得出圆心到该直线的距离，从而可求出m，这样便可得出内切圆的方程；（Ⅲ）可将直线l的方程带入椭圆C的方程并整理可以得到（1+4k2）x2﹣8k2x+4k2﹣4=0，可设M（x1，y1），N（x2，y2），从而由韦达定理得到．可分别写出直线AM和BN的方程，从而可分别求出这两直线与x=4的交点，从而可证明R，Q两点重合，即这两点的纵坐标相等，这样便可证出直线AM与直线BN的交点在直线x=4上：M，N都在直线l上，从而有y1=k（x1﹣1），y2=k（x1﹣1），然后证明即可．【解答】解：（Ⅰ）根据题意，a=2，；∴，∴b2=a2﹣c2=1；∴椭圆C的方程；（Ⅱ）；∴△PF1F2为等腰三角形；∴△PF1F2的内切圆的圆心在y轴上设圆心（0，m），m＞0，∴；直线PF2的方程为，内切圆与直线PF2相切，圆心到PF2的距离解得；∴△PF1F2内切圆方程为；（Ⅲ）证明：将直线l：y=k（x﹣1）代入椭圆C的方程并整理得：（1+4k2）x2﹣8k2x+4k2﹣4=0；∵直线过（1，0），∴△＞0恒成立；设直线l与椭圆C的C交点M（x1，y1），N（x2，y2）；由根与系数的关系，得；直线AM的方程为：，它与直线x=4的交点坐标为；同理可求得直线BN与直线x=4的交点坐标为；下面证明P，R两点重合，即证明P，R两点的纵坐标相等：y1=k（x1﹣1），y2=k（x2﹣1）；∴===，因此结论成立；综上可知．直线AM与直线BN的交点在直线x=4上．20．已知函数f（x）=kx2，g（x）=lnx（Ⅰ）求函数的单调递增区间；（Ⅱ）若不等式f（x）≥g（x）在区间（0，+∞）上恒成立，求k的取值范围；（Ⅲ）求证：．【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．【分析】（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的递增区间即可；（Ⅱ）分离参数，问题转化为求R（x）=的最大值，解关于导函数的方程，求出函数的单调区间，从而求出函数的最大值即可；（Ⅲ）由（Ⅱ）知，得到，（x≥2），放缩法证明即可．【解答】解：（Ⅰ）∵（x＞0）∴，令h'（x）＞0，得0＜x＜e，故函数的单调递增区间为（0，e）（Ⅱ）由，则问题转化为k大于等于R（x）的最大值，又令x0∞R'x R x）由表知当时，函数R（x）有最大值，且最大值为，因此k≥（Ⅲ）证明：由（Ⅱ）知，∴，（x≥2），10分∴，又∵=∴2016年9月7日。

2018年普通高等学校招生天津卷文史类数学试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

第Ⅰ卷1至2页，第Ⅱ卷3至10页。

考试结束后，将本试卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷（选择题 共60分）注意事项：1. 答第Ⅰ卷前，考生务必将自己的姓名、准考号、科目涂写在答题卡上。

2. 每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

答在试卷上的无效。

参考公式：如果事件A 、B 互斥，那么)()()(B P A P B A P +=+，如果事件A 、B 相互独立，那么)()()(B P A P B A P ⋅=⋅。

柱体（棱柱、圆柱）的体积公式Sh V =柱体其中S 表示柱体的底面积，h 表示柱体的高。

一. 选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 设集合{}6,5,4,3,2,1=P ，{}62≤≤∈=x R x Q ，那么下列结论正确的是 A. P Q P = B. Q Q P ≠⊃ C. Q Q P = D. ≠⊂Q P P2. 不等式21≥-xx 的解集为 A. ]0,1[- B. ),1[∞+- C. ]1,(--∞ D. ),0(]1,(∞+--∞ 3. 对任意实数a 、b 、c ，在下列命题中，真命题是 A.“bc ac >”是“b a >”的必要条件 B.“bc ac =”是“b a =”的必要条件 C.“bc ac >”是“b a >”的充分条件 D.“bc ac =”是“b a =”的充分条件4. 若平面向量与向量)2,1(-=的夹角是︒18053=，则= A. )6,3(- B. )6,3(- C. )3,6(- D. )3,6(-5. 设P 是双曲线19222=-y ax 上一点，双曲线的一条渐近线方程为023=-y x ，1F 、2FAC A 1分别是双曲线的左、右焦点。

绝密★启用前2018 年一般高等学校招生全国一致考试（天津卷）数学（文史类）本试卷分为第Ⅰ卷（选择题）和第 Ⅱ 卷（非选择题）两部分，共 150 分，考试用时 120 分钟。

第 Ⅰ卷 1至2页，第Ⅱ卷 3至5页。

答卷前，考生务势必自己的姓名、准考据号填写在答题考上，并在规定地点粘贴考试用条形码。

答卷时，考生务势必答案涂写在答题卡上，答在试卷上的无效。

考试结束后，将本试卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷注意事项：1．每题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑。

如需变动，用橡皮擦洁净后， 再选涂其余答案标号。

2．本卷共 8 小题，每题 5 分，共 40 分。

参照公式：·假如事件A ，B 互斥，那么 P(A ∪B)=P(A)+P(B)．·棱柱的体积公式 V=Sh. 此中 S 表示棱柱的底面面积， h 表示棱柱的高．1·棱锥的体积公式VSh ，此中 S 表示棱锥的底面积， h 表示棱锥的高.3一 ．选择题：在每题给出的四个选项中，只有一项为哪一项切合题目要求的 .（ 1）设会合 A {1,2,3,4} ， B {1,0,2,3} ， C { xR | 1x 2} ，则 (AU B)I C（A ） {1,1}（ B ） {0,1}（C ） { 1,0,1}（ D ） {2,3,4}x y 5，2x y 4， 3x5y 的最大值为（ 2）设变量 x, y 知足拘束条件 y 则目标函数 zx 1，y 0，（A ）6 （B ）19 （C ）21（D ）45（ 3）设x R，则“x38 ”是“ |x | 2 ”的（ A）充足而不用要条件（ B）必需而不充足条件（ C）充要条件（ D）既不充足也不用要条件（ 4）阅读以下图的程序框图，运转相应的程序，若输入N 的值为20，则输出 T 的值为（A）1（B）2（C）3（D）4（ 5）已知a log37,b(1)31,c log 11，则 a,b, c 的大小关系为2435（ A）a b c（ B）b a c（ C）c b a（ D）c a b （ 6）将函数y sin(2 x) 的图象向右平移个单位长度，所得图象对应的函数510（A）在区间（C）在区间[,]上单一递加（ B）在区间[,0]上单一递减444[,]上单一递加（ D）在区间[, ]上单一递减422（ 7）已知双曲线x2y21(a 0, b 0) 的离心率为2，过右焦点且垂直于x 轴的直线与双曲线a2b2交于 A, B 两点.设 A, B 到双曲线的同一条渐近线的距离分别为d1和 d2，且 d1d2 6, 则双曲线的方程为（A） x2y21（B） x2y21 3993（C） x2y21（D） x2y21 412124OM 1.ON2,MON 120o uuuur uuur uuur uuur（ 8）在如图的平面图形中，已知, BM2MA ,CN2NA, 则uuur uuuurBC·OM 的值为（A）（C）15（B）9 6（D）0第Ⅱ卷注意事项：1．用黑色墨水的钢笔或署名笔将答案写在答题卡上。