中国石油大学物理2-2第五章课件.pdf

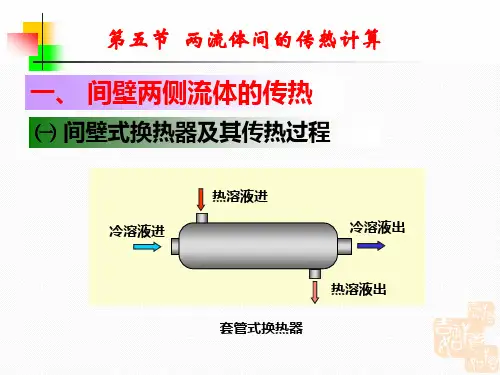
大学物理（2-2）贾翠萍2019.2.25插班： CL730学习要求听课作业出勤答疑预习石大云课堂微助教活页作业总成绩：平时成绩+考试成绩电磁学基本原理为核心第 4 篇 电磁学电磁西周青铜铭文就记载有“电”和“雷”字。

1660年，盖里克发明摩擦起电机。

1720年，格雷（研究了电的传导现象，静电感应现象。

1733年杜菲经过实验区分出正负两种电荷，同性相斥，异性相吸。

1745年，荷兰人马森布洛克发现了莱顿瓶。

公元前3世纪，古书《韩非子》就记载司南.《吕氏春秋》记有慈石召铁。

1600年,英国吉尔伯特发表了《论磁、磁体和地球作为一个巨大的磁体》1785年，库仑定律电流的磁效应1820年 奥斯特电磁感应现象1831年 法拉第研究内容电场磁场电磁感应现象及规律麦克斯韦电磁理论（电磁场的统一性）静电场的性质及规律稳恒磁场的性质及规律第12章真空中的静电场静电场 —静止电荷在空间所产生的电场本章着重研究真空中的静电场相关性质及规律。

本章内容：描述静电场的两个基本物理量：电场强度和电势。

两条基本实验定律：库仑定律和场叠加原理。

两条基本定理：高斯定理和环路定理。

一、电荷及其量子化摩檫起电感应起电 §12 .1 电荷 库仑定律电荷正负性量子性守恒性（孤立系统）运动不变性正电荷和负电荷；同性相斥，异性相吸neq =C1060217733.119-⨯=e1）当q＞＞ e 时， 电量可以认为是连续变化的。

2）夸克模型：“夸克”的电量为： 未从实验中直接发现单独存在的夸克或反夸克说明ee 3231±±或二、库仑定律1.点电荷（Point charge)带电体的几何线度比起它到其它带电体的距离小得多，这时带电体的形状和电荷在其中的分布已无关紧要，可以抽象成一个几何点，称为点电荷。

① 点电荷具有相对意义；DD②任何带电体都可看成点电荷的组合。

l理想模型2、库仑定律Fre 1q 2q rer q q kF221=在 SI 单位制中，k = 9×10 9 N · m 2 / C 222120m /N C 1085.841⋅⨯==-k πε称为真空电容率0ε041πε=k F '真空中两个静止点电荷之间的相互作用力大小，与两个点电荷的电量的乘积成正比，与它们之间距离的平方成反比。

第五章 相平衡1．Ag 2O 分解的计量方程为)g (O 21)s (Ag 2)s (O Ag 22+= 当Ag 2O(s)进行分解时，体系的组分数，自由度和可能平衡共存的最大相数各为多少？ 解：独立组分数 'C S R R =−−物种数S =3，独立化学平衡数R =1，无浓度限制关系，'0R =则 3102C =−−=.Ag 2O(s)一开始分解，就至少有三个相存在，根据相律有22321f C =−Φ+=−+=。

自由度为0时，相数最多，22024C f Φ=−+=−+=。

2．指出下列各体系的独立组分数，相数和自由度数各为若干？（1） NH 2Cl(s)部分分解为NH 3(g)和HCl(g)（2） 若在上述体系中额外再加入少量NH 3(g)（3） NHHS(s)和任意量的NH 3(g),H 2S(g)混合达到平衡。

（4） C(s)与CO(g),O 2(g)在937K 时达到平衡解：（1）NH 4Cl(s)=NH 3(g)+HCl(g)'3111C S R R =−−=−−=2Φ=(一个固相，一个气相)21221f C =−Φ+=−+=（2）若在上述体系中额外加入少量NH 3(s)，则浓度限度条件就没有了，故'3102C S R R =−−=−−=2Φ=22222f C =−Φ+=−+=（3）NH 4HS(s)=NH 3(g)+H 2S(g)'3102C S R R =−−=−−=2Φ=22222f C =−Φ+=−+=（4） 系统存在4种物质，有4个化学平衡)g (CO )g (O 21)s (C 2=+ (a))g (CO )g (O 21)g (CO 22=+ (b))g (CO )g (O )s (C 22=+ (c))g (CO 2)g (CO )s (C 2=+ (d)但（a ）+(b)=(c),(a)—(b)=(d)，所以系统中只有2个独立的化学平衡关系。

2-1 质量为m 的子弹以速率0v 水平射入沙土中，设子弹所受阻力与速度反向，大小与速度成正比，比例系数为k ，忽略子弹的重力，求：(1)子弹射入沙土后，速度大小随时间的变化关系； (2)子弹射入沙土的最大深度。

[解] 设任意时刻子弹的速度为v ，子弹进入沙土的最大深度为s ，由题意知，子弹所受的阻力 f = - kv(1) 由牛顿第二定律 tv m ma f d d ==即 tv m kv d d ==-所以t mk vv d d -= 对等式两边积分⎰⎰-=tvvt mkvv 0d d 0得 t mk v v -=0ln因此 tmk ev v -=0(2) 由牛顿第二定律 xv mvtx x v mt vm ma f d d d d d d d d ====即 xv mv kv d d =-所以 v x mk d d =-对上式两边积分 ⎰⎰=-0d d v sv x m k得到 0v s m k -=-即 kmv s 0=2-2 质量为m 的小球，在水中受到的浮力为F ，当它从静止开始沉降时，受到水的粘滞阻力为f ＝kv (k 为常数)。

若从沉降开始计时，试证明小球在水中竖直沉降的速率v 与时间的关系为⎪⎪⎭⎫ ⎝⎛--=-m kt e kF mg v 1 [证明] 任意时刻t 小球的受力如图所示，取向下为y 轴的正方向，开始沉降处为坐标原点。

由牛顿第二定律得tv mma f F mg d d ==--即 tv mma kv F mg d d ==-- 习题2－2图整理得mt kvF mg v d d =--对上式两边积分⎰⎰=--tvm tkvF mg v 00d d得 mkt Fmg kv F mg -=---ln即 ⎪⎪⎭⎫ ⎝⎛--=-m kt e kF mg v 12-3 跳伞运动员与装备的质量共为m ，从伞塔上跳出后立即张伞，受空气的阻力与速率的平方成正比，即2kv F =。

求跳伞员的运动速率v 随时间t 变化的规律和极限速率T v 。

5-1 设有一宇宙飞船，相对于地球作匀速直线运动，若在地球上测得飞船的长度为其静止长度的一半，问飞船相对地球的速度是多少?[解] 飞船静止长度0l 为其固有长度，地球上测得其长度为运动长度，由长度收缩公式，有：2)(1020l c v l l =-=解得：23=cv即：c c v 866.023==5-2 宇宙射线与大气相互作用时能产生π介子衰变，此衰变在大气上层放出μ粒子，已知μ粒子的速率为v ＝0.998c ，在实验室测得静止μ粒子的平均寿命为s 102.26-⨯，试问在8000m 高空产生的μ粒子能否飞到地面?[解] 地面上观测到的μ子平均寿命与固有寿命之间的关系21⎪⎭⎫ ⎝⎛-=c v t tμ子运行距离m 1042998.01102.2998.012620=-⨯⨯=⎪⎭⎫ ⎝⎛-==-c c v t v vt lμ子能飞到地面。

5-3 在S 系中观测到两个事件同时发生在x 轴上，其间距离为1m ，在S '系中观测这两个事件之间的距离是2m 。

求在S '中测得的这两个事件发生的时间间隔。

[解] 在S 系中两事件时间间隔,0=∆t 由Lorentz 变换222)/(1)/(1c u xcu t t c u ut x x --='--='得：⎪⎪⎪⎩⎪⎪⎪⎨⎧-∆-=-∆-∆='∆-∆=-∆-∆='∆222222)/(1)/(1)/(1)/(1c u x c u c u x c u t t c u x c u t u x x 将m 1m ,2=∆='∆x x 代入上两式，得s 1077.5,239-⨯-='∆=t c u5-4 远方一颗星体以0.80c 的速率离开我们，我们接收到它辐射来的闪光按5昼夜的周期变化，求固定在这星体上的参考系中测得的闪光周期。

[解] 所求的为固有周期0T ： 380.015)/(1220=-=-=c v T T 昼夜5-5 假设一飞船的速率可达u ＝0.5c ，它沿着广州和北京的连线飞行，已知广州到北京的直线距离为km 1089.13⨯，问飞船中的乘客观测到广州到北京的直线距离是多少? [解] 已知固有长度km 1089.130⨯=lkm 106368.15.011089.113232⨯=-⨯⨯=⎪⎭⎫ ⎝⎛-=c v l l5-6 1966～1972年间，欧洲原子核研究中心(CERN)多次测量到储存环中沿“圆形轨道”运行的μ粒子的平均寿命，在μ粒子的速率为0.9965c 时，测得的平均寿命是s 1015.266-⨯。