第二节 辐射换热计算
- 格式：ppt
- 大小：503.00 KB
- 文档页数：21
下载文档原格式
合集下载
管式加热炉第二节辐射换热计算
管式加热炉第二节辐射换热计算
在管式加热炉中，燃料燃烧产生的高温燃烧气体通过管壁对被加热物
料进行辐射传热。
辐射传热是指通过电磁波辐射的方式传递热能。
在管式
加热炉中，燃烧气体通过管壁辐射给物料，被加热物料在吸收热能后升温。
要计算管式加热炉中的第二节辐射换热，需要考虑以下几个因素：
1.辐射传热区域：将加热炉分为不同的辐射传热区域是计算辐射换热
的第一步。
在管式加热炉中，通常将管内和管外的区域划分为两个不同的
辐射传热区域。
2.燃烧气体温度：燃烧气体的温度是计算辐射换热的重要参数。
可以
通过燃烧器的设计参数和燃烧气体的化学反应等知道燃烧气体的温度。
4.吸收率：物料对辐射能量的吸收率是一个影响辐射换热的重要参数。
不同的物料对辐射能量的吸收率有所差异，需要在计算中考虑。
在进行第二节辐射换热计算时，可以使用蒙特卡洛方法或反向追踪法
等辐射传热计算方法。
这些方法需要通过数值模拟的方式计算辐射传热过
程中的能量传递。
在计算过程中，可以采用离散法将加热炉分为若干个离散的小面元，
并计算每个小面元上的辐射换热。
通过将各个小面元的辐射换热求和，可
以得到整个第二节辐射换热的结果。
在进行计算时，需要注意选择合适的模拟参数和边界条件，并进行辐
射传热过程中的能量平衡计算。
总之，计算管式加热炉中的第二节辐射换热是一个复杂的过程，需要考虑多个因素和使用适当的数值模拟方法。
希望本文对理解管式加热炉的辐射换热计算有所帮助。
辐射换热公式
辐射换热公式
辐射换热是一种物体间的热传递方式，它发生在两个物体之间，没有任何物理性的接触，而是通过空气或其他介质的中空的空间来传输热量。
两个物体之间的辐射换热取决于它们的温度差和辐射系数。
这种物理现象的发生可以用一个简单的公式来描述，即辐射换热率（以千克·度/秒为单位）= 5.67 x 10 ^ -8 x 温度差4 乘以表面积（以平方米为单位）。
其中，温度差是指两个物体的温度差的绝对值，而辐射系数是指物体表面的反射系数，越大的反射系数意味着越少的热量被辐射掉。
辐射换热具有许多优点，其中最重要的是它可以完全避免物理接触，从而避免污染和传播病毒等问题。
它还可以有效地把热量从一个物体传递到另一个物体，而不会改变任何物质。
辐射换热可以用在各种场合，比如室内暖气系统，汽车内部空调系统，家用电器，工业加热系统等等。
它的应用范围非常广泛，可以有效控制室内和室外的温度，并使空气更加清新。
总而言之，辐射换热是一种有效的热传导方式，可以有效地把热量从一个物体传递到另一个物体，而不会改变任何物质，同时又可以有效控制室内和室外的温度，使空气更加清新。
它还可以完全避免物理接触，从而避免污染和传播病毒等问题。
辐射传热的计算
当没有遮热板时，两块平壁间的辐射换热量：
Q12
A(Eb1Eb2)A T14T24
1112 1
21
在两块平壁之间加一块大小一样、表面发射率相同的遮热板 （忽略导热热阻）
辐射换热量减少为原来的 1/2，即：
112
1 2
12
A 3X 3,1A 3X 3,2A 3
根据角系数的相对性有：
A1X1,2A2X2,1
A1X1,3A3X3,1 A2X2,3A3X3,2
三个非凹表面组成的封闭辐射系统
X1
2
A1
A2 A3 2A1
X1,3
A1
A3 A2 2A1
X2,3
A2
A3 A1 2A2
黑体间的辐射换热及角系数例题讲解：
[例] 试用代数法确定如图所示
的辐射和吸收是在整个气体容积中进行的，属 于体积辐射。
(4) 气体的反射率为零
气体辐射的特点1：
在工业上常见的温度范围内，单原子气体 及空气、H2、O2、N2等结构对称的双原 子气体，无发射和吸收辐射的能力可认为 是透明体。 CO2、H2O、SO2、CH4和CO等气体都具 有辐射的本领。
例：煤和天然气的燃烧产物中常有一定浓度的CO2和
例：大气中的臭氧层能保护人类免受紫外线的伤害
气体辐射的特点3:
热射线穿过气体层时，辐射能沿途被气体 分子吸收而逐渐减弱。其减弱程度取决于 沿途碰到的气体分子数目，碰到的分子数 目越多，被吸收的辐射能也越多。因此气 体的吸收能力αg与热射线经历的行程长 度L，气体分压力p和气体温度Tg等因素有 关。
9.5 辐射传热的控制（强化与削弱）
遮热板的应用:
在现代隔热保温技术中，遮热板的应用 比较广泛。例如：
Q12
A(Eb1Eb2)A T14T24
1112 1
21
在两块平壁之间加一块大小一样、表面发射率相同的遮热板 （忽略导热热阻）
辐射换热量减少为原来的 1/2，即：
112
1 2
12
A 3X 3,1A 3X 3,2A 3
根据角系数的相对性有：
A1X1,2A2X2,1
A1X1,3A3X3,1 A2X2,3A3X3,2
三个非凹表面组成的封闭辐射系统
X1
2
A1
A2 A3 2A1
X1,3
A1
A3 A2 2A1
X2,3
A2
A3 A1 2A2
黑体间的辐射换热及角系数例题讲解：
[例] 试用代数法确定如图所示
的辐射和吸收是在整个气体容积中进行的，属 于体积辐射。
(4) 气体的反射率为零
气体辐射的特点1：
在工业上常见的温度范围内，单原子气体 及空气、H2、O2、N2等结构对称的双原 子气体，无发射和吸收辐射的能力可认为 是透明体。 CO2、H2O、SO2、CH4和CO等气体都具 有辐射的本领。
例：煤和天然气的燃烧产物中常有一定浓度的CO2和
例：大气中的臭氧层能保护人类免受紫外线的伤害
气体辐射的特点3:
热射线穿过气体层时，辐射能沿途被气体 分子吸收而逐渐减弱。其减弱程度取决于 沿途碰到的气体分子数目，碰到的分子数 目越多，被吸收的辐射能也越多。因此气 体的吸收能力αg与热射线经历的行程长 度L，气体分压力p和气体温度Tg等因素有 关。
9.5 辐射传热的控制（强化与削弱）
遮热板的应用:
在现代隔热保温技术中，遮热板的应用 比较广泛。例如：
辐射换热的计算2
（1）从温度上看，可以将其视为黑体；绝热表面的温
度与其发射率无关。 （2）从能量上看，可以将其当作反射率为1的表面。 所以重辐射表面是在一定条件下的黑体或白体。 因为重辐射面的温度与其它表面的温度不同，所以重 辐射面的存在改变了辐射能的方向分布。重辐射面的 几何形状、尺寸及相对位置将影响整个系统的辐射换
3
2 1
5 6
向外辐射的热流量；
Qi , j Ji J j 1 Fi X i , j
A为物体表面的面积。Q表示物体表 面实际向空间辐射出去的辐射能
Eb G
J
G
G
（热流量），单位为W。
通常称Eb－J为表面辐射 势差，而称 (1 ) /(F ) 为表面辐射热阻，因而有： 热流＝势差/热阻
Eb
Q J
1 A
Eb J Q 1 A
越大，表面热阻越小； 对于黑体， ＝1
图中给出了一个由多个漫灰表面构
4 3
5
成的封闭空间。
当系统处于稳定状态时，由系统空 间的辐射热平衡可以得出任何一个 表面辐射出去的热流量有如下关系：
2
6
Qi Qi , j
j 1
n
1
Qi Qi , j
j 1
n
4
Ebi J i Qi 式中， 1 i i Fi
为一ห้องสมุดไป่ตู้表面
Q1, 2 ：辐射热流 ；
Eb1 Eb2 ：辐射势差；
1 X 1, 2 A1
：辐射热阻（空间热阻、形状热阻）；
§8-2 -2
两平行黑表面间的辐射换热
X 1,2 X 2,1 1
4 4
对于两平行的黑体大平壁，由于：
A1 A2 A
辐射换热的计算
X1, 2 X1,3 1 X 2,1 X 2,3 1 X 3,1 X 3, 2 1
(1) 角系数：有两个表面，编号为1和2，其间充满透明介质，我们 把表面1对表面2的角系数X1,2定义为：把表面1发出的辐射能中落到 表面2上的百分数称为表面1对表面2的角系数，记为X12。即
X 1, 2
表面1发出的落到表面 2上的辐射能 表面1发出的辐射能
(9-1)
同理，也可以定义表面2对表面1的角系数。 在讨论角系数时，我们假设：①所研究的表面是漫射表面，② 在所研究表面的不同地点上向外发射的辐射热流密度是均匀的。因 此，物体的表面温度及黑度的改变只影响到该物体向外发射的辐射 能大小而不影响在空间的相对分布，因而不影响辐射能落到其他表 面上的百分数，于是，角系数就纯是一个几何因子，与两个表面的 温度及黑度没有关系，从而给其计算带来很大的方便。 为了讨论的方便，在研究角系数时把物体作为黑体来处理。所 得到的结论对于漫灰表面均适合。
2.
角系数性质
根据角系数的定义和诸解析式，可导出角系数的代数性质。
(1) 相对性 由式(8-2a)和(8-2b)可以看出
X d1, d 2
Lb1 cos1dA1d dA2 cos1 cos2 Eb1dA1 r2
dA1 cos1 cos2 X d 2, d 1 2 r
dA1 X d 1, d 2 dA2 X d 2, d1
(2)
微元面对微元面的角系数
如图9-2所示，黑体微元面dA1对微元面dA2的角系数记 为Xd1,d2，则根据前面的定义式有
X d1, d 2 Lb1 cos1dA1d dA2 cos1 cos2 Eb1dA1 r2
dA1 cos1 cos2 r2
辐射换热的计算2
1
空间辐射热阻。
A1 X 1,2
如果物体表面为黑体，因J=Eb，则可得
Q1,2
J1 J2 1
J1 J2 1
A1 X 1,2
A2 X 2,1
Q1,2
Eb1 Eb2 1
Eb1 Eb2 1
A1 X 1,2
A2 X 2,1
代入斯忒芬－波尔兹曼定律 Eb 0T 4 Q1,2＝A1X1,2（0 T14 T24）
§8-2 被透热介质隔开的两固体表面间 的辐射换热
§8-2 -1 黑表面间的辐射换热
两黑体之间的辐射换热量为：
Q12 A1Eb1 X 1,2 A2 Eb2 X 2,1
A1 X 1,2 (Eb1 Eb2 )
A2 X 2,1 (Eb1 Eb2 )
即：
Q12
Eb1 Eb2 1
Eb1 Eb2 1
11 1 12
A11 A1 X 1,2 A2 2
A11 A1 X 1,2 A2 2
Q1，2＝ n 0 A1 (T14 T24 )
式中εn为辐射换热系统的系统黑度
n
1
1 1
1 X 1,2
A1 A2
1
2
2
1
② 三个凸形漫灰表面间的辐射换热计算
如图所示的由三个凸形漫灰表面构成的封闭空间，它
＝ A1 0 T14 T24
1 1 1
1 2
1 2
c) 一个凸形漫灰表面对大空间的辐射换热。
这实质上是包围表面A2特别大的情
2
况。此时，除X1，2＝1之外，
A1/A2→0或者相当于ε2→1，这也就
1
是把大空间视为一个黑体。
Q1,2
A1 Eb1 Eb2 ＝ A1 0 T14 T24
传热学重点、题型讲解第九章辐射换热计算
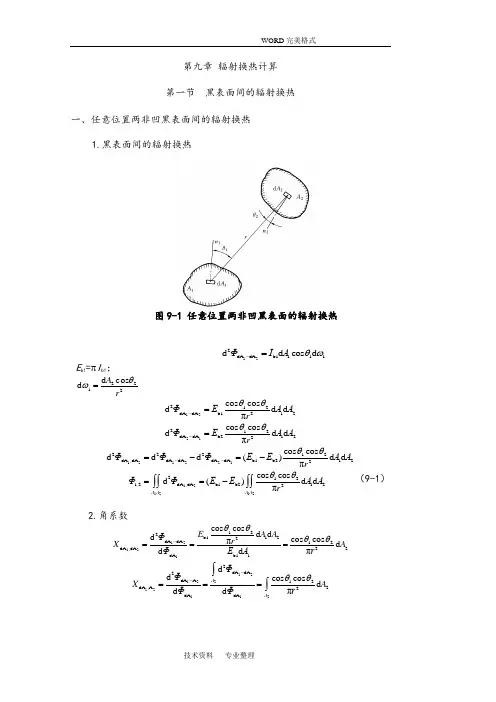
第九章 辐射换热计算 第一节 黑表面间的辐射换热一、任意位置两非凹黑表面间的辐射换热1.黑表面间的辐射换热图9-1 任意位置两非凹黑表面的辐射换热122dA dA b1111d d cos d ΦI A θω-= E b1=πI b1； 2221cos d d rA θω=12212dA dA b1122cos cos d d d πΦE A A r θθ-=21212dA dA b2122cos cos d d d πΦE A A r θθ-=12122122212dA ,dA dA dA dA dA b1b2122cos cos d d d ()d d πΦΦΦE E A A r θθ--=-=- 1212122121,2dA ,dA b1b2122cos cos d ()d d πA A A A ΦΦE E A A r θθ==-⎰⎰⎰⎰ （9-1）2.角系数12121122b1122dA dA 12dA ,dA 22dA b11cos cos d d d cos cos πd d d πE A A Φr X A ΦE A r θθθθ-===12122121122dA dA 2dA A 12dA ,A 22dA dA d d cos cos d d d πA A ΦΦX A ΦΦr θθ--===⎰⎰12121211122dA dAA A121,2122A A1dcos cos1d dπA AA AΦΦX A AΦΦA rθθ--===⎰⎰⎰⎰（9-2a）212212AAA1,2ddπcoscos121212AArAΦΦXAA⎰⎰==-θθ（9-2b）21,212,1AXAX=（9-3）3.辐射空间热阻图9-2 辐射空间热阻21,2b2b112,1b2b12,1)()(AXEEAXEEΦ-=-=（9-4）b1b21,21,211E EΦX A-=Φ1,2=（E b1－E b2）A = σb（T14- T24）A二、封闭空腔诸黑表面间的辐射换热图9-3 多个黑表面组成的空腔图9-4 三个黑表面组成空腔的辐射网络图9-5 例9-1附图：,1,2,,1ni i i i n i j j ΦΦΦΦΦ==++⋅⋅⋅⋅⋅⋅=∑将上式除以i Φ，按角系数定义，可得,1,2,n ,11ni i i i j j X X X X ==++⋅⋅⋅⋅⋅⋅=∑（9-5）∑∑∑∑====-=-==nj nj i j i nj i j i i j i nj j i i A X E A X E A X E E ΦΦ11,bj 1,bi ,bj bi 1,)(∑=-=nj j i j i i A X E A E Φ1,bj bi （9-6）【例9-1】∑=-=311,b 1b11j j j j A X E A E Φ （a ）∑=-=312,b 2b22j j j j A X E A E Φ （b ）0313,b 3b33=-=∑=j j j j A X E A E Φ （c ）02,21,22,11,1====X X X X13,23,1==X X31,313,1A X A X =32,323,2A X A X =213,11,33,223/210.252A r X X X A r ππ==⨯==13,32,31,3=++X X X5.03,3=X033,3b323,2b213,1b13b3=---A X E A X E A X E A E4b b T E σ=2424143T T T +=T 3=415.6K 或者142.6℃1b11b11,11b22,12b33,1344b11b31,3111344311b 244()()()100100473415.61 5.67()()1801.0W 2100100b ΦE A E X A E X A E X A E A E X A A T T T T AC σπ=---=-=-⎡⎤=-⎢⎥⎣⎦⎡⎤=⨯⨯⨯-=⎢⎥⎣⎦【讨论】π411212121=+=+=∑A A A A A AR 4444b1b2121,2()π 5.67 4.73 3.13)1801.0W 4/π4b E E T T ΦRσ--===⨯⨯-=∑（第二节 灰表面间的辐射换热一、有效辐射图9-6 有效辐射示意图图9-7 辐射表面热阻1.有效辐射J 1=ε1E b1＋ρ1G 1=ε1E b1＋（1－α1）G 1 W/m 2（a ）2. 辐射表面热阻11b111111G E G J A Φαε-=-= W/m 2 （b ） 1111b11b111111)(1A J E J E A Φεεεε--=--= W （9-7）二、组成封闭腔的两灰表面间的辐射换热图9-8 两个灰表面组成封闭腔的辐射换热网络图9-9 空腔与内包壁面间的辐射换热22212,1111b2b12,1111A A X A E E Φεεεε-++--=W (9-8a ))11(1)11()(2212,112b 1b 12,1-++--=εεA A X E E A Φ 1,2112()W s b b X A E E ε=- （9-8b ）)11()11(1121,212,1s -+-+=εεεX X1.无限大平行灰平壁的辐射换热A 1=A 2=A ，且X 1,2=X 2,1=1，)(111)(4241b s 212b b12,1T T A E E A Φ-=-+-=σεεε W （9-9）1121s -+=εεε2.其中一个表面为平面或凸表面的辐射换热)11(1)(22112b 1b 12,1-+-=εεA A E E A Φ W (9-10)A 2 >>A 1，且ε2的数值较大Φ1,2=ε1 A 1（E b1-E b2）W （9-11）三、封闭空腔中诸灰表面间的辐射换热1.网络法求解图9-10三个灰表面组成封闭腔辐射换热网络图9-11 例9-4附图图9-12 例题9-5附图节点1013,11312,1121111b1=-+-+-A X J J A X J J A J E εε （a ）节点2 011123,22321,2212222b2=-+-+--A X J J A X J J A J E εε （b ）节点3 011132,33231,3313333b3=-+-+--A X J J A X J J A J E εε （c ）【例9-4】X 1,2= X 2,1=0.38X 1,3=X 2,3=1-X 1,2=1-0.38=0.62计算网络中的各热阻值：A 1=A 2=π⨯0.32=0.283m 21.14283.02.02.011111=⨯-＝－A εε m -23.5283.04.04.011222=⨯=-－A εε m -23.9283.038.01112,1=⨯=A X m -27.5283.062.011123,213,1=⨯==A X A X m -2流入每个节点的电流总和等于零07.53.91.141b3121b1=-+-+-J E J J J E 07.53.93.52b3212b2=-+-+-J E J J J E 202447731067.5484b1=⨯⨯==-T E b σW/m 235445001067.5484b2=⨯⨯==-T E b σW/m24593001067.5484b3=⨯⨯==-T E b σW/m 2J 1=5129 W/m 2 J 2=2760W/m 2b1111112024451291072W 114.1E J ΦA εε--===- b22222235442760148W 1 5.3E J ΦA εε--===-312()(1072148)1220W ΦΦΦ=-+=-+=-【例9-5】1.1411111=-=A R εεm -23.512222=-=A R εεm -23.9112,12,1==A X R m -27.5113,13,23,1===A X R R m -2E b1=20244W/m 2 E b2=3544W/m 2∑++++=23,23,12,11111R R R R R R =14.1+5.243.57.57.513.911=+++m -2b1b21,2202443544682W 24.5E E ΦR --===∑J 1=E b1－Φ1,2⨯R 1=20244－682⨯14.1=10627.8 W/m 2J 2=E b2＋Φ1,2⨯R 2=3544＋682⨯5.3=7185.6 W/m 2J 3=（J 1+J 2）/2=8893.2 W/m 2J 3=G 3=E b3=σ b T 341/41/4b3388893.2629K5.6710b E T σ-⎛⎫⎛⎫=== ⎪⎪⨯⎝⎭⎝⎭2. 值解法图9-13 例9-6（a ）（b ）附图及其辐射换热网络∑==ni i j i i j j A X J G A 1,j j εα=∑=-+=ni i j i i j j j j j j A X J A E A J 1,b )1(εε（9-12）∑∑===ni i j i j n i i j i i X J A A X J 1,1,b ,1(1)nj j j j i j i i J E J X εε==+-∑（9-13）4b 1,11j j j j jni i j i T J X J σεεε⎥⎥⎦⎤⎢⎢⎣⎡-=--∑=（9-14）4111,121,231,31,b 1114212,122,232,32,b 2221,12,231()()111()()11n n n n n n n J X J X J X J X T J X J X J X J X T J X J X J X εσεεεσεε-+++⋅⋅⋅+=--+-++⋅⋅⋅+=--⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅++4,3,b 1()()11n n n n n n n J X T εσεε⎫⎪⎪⎪⎪⎬⎪⎪⎪+⋅⋅⋅+-=⎪--⎭ （9-15）ii i i i i A J E Φεε--=1b i =1，2，…n （9-16）【例9-6】1,11,21,31,400.150.540.31X X X X ====、、、；2,12,22,32,40.2500.500.25X X X X ====、、、；3,13,23,33,40.270.140.320.27X X X X ====、、、；4,14,24,34,40.310.150.540X X X X ====、、、；4432198.267.5931.054.015.010⨯⨯=---J J J J 4432183.267.5425.05.0525.0⨯⨯=--+-J J J J4432186.267.5427.068.414.027.0⨯⨯=-+--J J J J 4432184.267.55.15.254.015.031.0⨯⨯=+---J J J JJ 1=440.45 W/m 2； J 2=370.28 W/m 2； J 3=382.69 W/m 2 ; J 4=380.80 W/m 2。
辐射换热计算与规则
利用角系数的相对性、完整性及可加性，通过求解代数方程 而获得角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
图8-5 三个非凹表面组成的封闭系统
辐射换热的计算和规则
由角系数完整性
X1,2 X1,3 1 X2,1 X2,3 1 X3,1 X3,2 1
A1
A2
由角系数相对性
A3
A1X1,2 A2X2,1
辐射换热的计算和规则
辐射换热的计算和规则
9.1 辐射换热的角系数
两个表面之间的辐射换热量与两个表面之间的相对位置 有很大关系
表面相对位置的影响
❖a图中两表面无限接近，相互间的换热量最大；
❖b图中两表面位于同一平面上，相互间的辐射换热量为零。 由图可以看出，两个表面间的相对位置不同时，一个表面
发出而落到另一个表面上的辐射能的百分数随之而异，从
两微元表面角系数的相对性表达式：
d A 1X d A 1 ,d A 2 d A 2X d A 2 ,d A 1
辐射换热的计算和规则
两个有限大小表面之间角系数的相对性
1 ， 2 A 1 E b 1 X 1 ,2 A 2 E b 2 X 2 ,1
当 T1 时T2，净辐射换热量为零，即
Eb1 Eb2
则有限大小表面间角系数的相对性的表达式：
2表 面 A1的 断 面 长 度
两个非凹表面及假想面组
成的封闭系统
上述方法又被称为交叉线法。
注意：这里所谓的交叉线和不交叉线都是指虚拟 面断面的线，或者说是辅助线。
辐射换热的计算和规则
【例】求下列图形中的角系数
解： A1X1， 2A2X2， 1
X 1 ，2
X1，2
A2 A1
X 2，1
图8-5 三个非凹表面组成的封闭系统
辐射换热的计算和规则
由角系数完整性
X1,2 X1,3 1 X2,1 X2,3 1 X3,1 X3,2 1
A1
A2
由角系数相对性
A3
A1X1,2 A2X2,1
辐射换热的计算和规则
辐射换热的计算和规则
9.1 辐射换热的角系数
两个表面之间的辐射换热量与两个表面之间的相对位置 有很大关系
表面相对位置的影响
❖a图中两表面无限接近，相互间的换热量最大；
❖b图中两表面位于同一平面上，相互间的辐射换热量为零。 由图可以看出，两个表面间的相对位置不同时，一个表面
发出而落到另一个表面上的辐射能的百分数随之而异，从
两微元表面角系数的相对性表达式：
d A 1X d A 1 ,d A 2 d A 2X d A 2 ,d A 1
辐射换热的计算和规则
两个有限大小表面之间角系数的相对性
1 ， 2 A 1 E b 1 X 1 ,2 A 2 E b 2 X 2 ,1
当 T1 时T2，净辐射换热量为零，即
Eb1 Eb2
则有限大小表面间角系数的相对性的表达式：
2表 面 A1的 断 面 长 度
两个非凹表面及假想面组
成的封闭系统
上述方法又被称为交叉线法。
注意：这里所谓的交叉线和不交叉线都是指虚拟 面断面的线，或者说是辅助线。
辐射换热的计算和规则
【例】求下列图形中的角系数
解： A1X1， 2A2X2， 1
X 1 ，2
X1，2
A2 A1
X 2，1
7.2 辐射换热计算
两无限接近平面： ⒈两无限接近平面： φ11 = φ 22 = 0 一物包一物： ⒉一物包一物： φ12 = 1 φ11 = 0
A1 φ12 A1 = φ 21 A2 ⇒ φ 21 = A2
φ12 = φ 21 = 1
2.1.3 几种简单情况下的角系数
⒊形成密闭系统的三凸面： 形成密闭系统的三凸面：
平壁保温层外： 平壁保温层外： α T = 9.8 + 0.07(TW − T )
①空气作自然对流： 空气作自然对流：
圆筒壁或管道保温层外： 圆筒壁或管道保温层外：α T = 9.4 + 0.052(TW − T )
②空气沿粗糙壁面作强制对流： 空气沿粗糙壁面作强制对流：
空气流速u<5m/s： 空气流速u<5m/s： α T = 6.2 + 4.2u u<5m/s
A1φ12 = A2φ 21
2.1.2 角系数的性质
完整性（可加性）： ⒊完整性（可加性）： 若表面K=K 若表面K=K1+K2+K3，则：
φ1K = φ1K + φ1K + φ1K
1 2 3
但：
φ K1 ≠ φ K 1 + φ K 1 + φ K 1
1 2 3
2.1.3 几种简单情况下的角系数
2.1.2 角系数的性质
⒈归一性： 归一性： 如果由n个表面组成一个封闭体系， 如果由n个表面组成一个封闭体系，则其中 任意表面i对其它表面的角系数之和为1 任意表面i对其它表面的角系数之和为1 即： 或：
φ i1 + φ i 2 + ....... + φ in = 1
Σφ ij = 1
2.1.2 角系数的性质
A1 φ12 A1 = φ 21 A2 ⇒ φ 21 = A2
φ12 = φ 21 = 1
2.1.3 几种简单情况下的角系数
⒊形成密闭系统的三凸面： 形成密闭系统的三凸面：
平壁保温层外： 平壁保温层外： α T = 9.8 + 0.07(TW − T )
①空气作自然对流： 空气作自然对流：
圆筒壁或管道保温层外： 圆筒壁或管道保温层外：α T = 9.4 + 0.052(TW − T )
②空气沿粗糙壁面作强制对流： 空气沿粗糙壁面作强制对流：
空气流速u<5m/s： 空气流速u<5m/s： α T = 6.2 + 4.2u u<5m/s
A1φ12 = A2φ 21
2.1.2 角系数的性质
完整性（可加性）： ⒊完整性（可加性）： 若表面K=K 若表面K=K1+K2+K3，则：
φ1K = φ1K + φ1K + φ1K
1 2 3
但：
φ K1 ≠ φ K 1 + φ K 1 + φ K 1
1 2 3
2.1.3 几种简单情况下的角系数
2.1.2 角系数的性质
⒈归一性： 归一性： 如果由n个表面组成一个封闭体系， 如果由n个表面组成一个封闭体系，则其中 任意表面i对其它表面的角系数之和为1 任意表面i对其它表面的角系数之和为1 即： 或：
φ i1 + φ i 2 + ....... + φ in = 1
Σφ ij = 1
2.1.2 角系数的性质
《传热学》第九章 辐射换热计算
微面积dA1对表面积A2的角系数:
表面积A1对表面积A2的角系数:
仅和几何因素有关，与是否黑体无关，因而可适用于非黑体
同理可得，表面积A2对表面积A1的角系数:
由两式得出:
——角系数的互换性
3.辐射空间热阻：
任意两黑表面间的辐射换热计算式:
将上式改写为：
辐射空间热阻——
或
二、封闭空腔诸黑表面间的辐射换热
一、有效辐射
1.有效辐射：
有效辐射J ——单位时间离开单位面积表面的总辐射能
表面1本身辐射
表面1投射辐射的反射
2. 辐射表面热阻：
表面1向外界的净传热量平衡关系式：
有效辐射与投射辐射之差
对于漫射灰表面，根据基尔霍夫定律： 代入上式消去G1，得：
本身辐射与吸收辐射之差
辐射表面热阻——
二、组成封闭腔的两灰表面间的辐射换热
三表面系统的两个特例
表面3为黑体 表面3为重辐射面
表面3无表面热阻， 直接连接外源
表面3不连接外源， 成为浮动节点
四、遮热板——削弱两表面间辐射换热的方法
未加遮热板时：
加遮热板时：
遮热板辐射 网络图
进一步削弱辐射换热的措施——
1 3 1 3 , 增加总辐射热阻中 两项，即减小遮热板两侧的发射率 A3 3 A3 3
谢谢观看
常用材料：铝箔（管道外保温），镀银（保温瓶胆）
遮热板的例子
水幕墙
遮热罩式热电偶
第三节 角系数的确定方法
一、积分法确定角系数
以微表面积dA1向与之平行的直径为D的圆A2辐射的 角系数为例，对角系数进行推导：
环形微元体面积： 两微面积法向与连线夹角：
两微面积距离：
第九章—辐射换热计算
第九章 辐射换热计算重点：角系数的特点、性质及其计算，表面热阻、空间热阻及有效辐射的概念，两个及多个漫灰表面辐射换热的计算方法，辐射换热的强化与削弱，气体辐射的特点。
影响辐射换热的因素有：表面温度、表面的几何特性（大小、形状）、表面的相对位置，表面的辐射性质。
本章只对黑体表面和漫灰表面作分析。
第一节 黑表面间的辐射换热1-1 任意位置两非凹黑表面间的辐射换热 一、两黑表面间的辐射换热设有两个任意放置的非凹黑体表面，面积分别为1A 、2A ，温度分别为1T 、2T 。
从表面上分别取微元面积1dA 、2dA ，两者的距离为r ，两表面的法线与连线r 间的夹角分别为：1θ，2θ。
微面积1dA 投射到微元面积2dA 的辐射能为：111cos 121ωθd dA I b dA dA ⋅⋅⋅=Φ-黑体服从兰贝特定律：11b b I E ⋅=π ⇒ 21221c o sc o s 121dA dA rE b dA dA ⋅⋅⋅⋅=Φ-πθθ 2221cos rdA d θω=同理，从微面积2dA 投射到微元面积1dA 的辐射能为：21221cos cos 212dA dA r E b dA dA ⋅⋅⋅⋅=Φ-πθθ微面积1dA 和2dA 之间的辐射换热量为：21221cos cos 2121dA dA rE E b b dA dA ⋅⋅⋅⋅-=Φπθθ）（、 黑体表面1A 和2A 之间的辐射换热量为：⎰⎰⎰⎰⋅⋅⋅⋅-=Φ=Φ122112212122121cos cos A A b b A A dA dA dA dA r E E πθθ）（、、二、角系数（angle factor or view factor ）角系数：表示一表面发出的辐射能中直接落到另一表面上的百分数。
21、X —称为1A 对2A 的角系数，表示1A 辐射的能量落到2A 上的百分数。
12、X —称为2A 对1A 的角系数角系数中的第一个角码指发射体，第二个角码指受射体。
辐射换热的计算和规则
两微元表面角系数的相对性表达式：
d A 1X d A 1 ,d A 2 d A 2X d A 2 ,d A 1
两个有限大小表面之间角系数的相对性
1 ， 2 A 1 E b 1 X 1 ,2 A 2 E b 2 X 2 ,1
当 T1 时T2，净辐射换热量为零，即
Eb1 Eb2
则有限大小表面间角系数的相对性的表达式：
A 2X 2,1A 2aX 2a,1A 2bX 2b,1
X2,1X2a,1A A22a X2b,1
A2b A2
角系数的上述特性可以用来求解许多情况下两 表面间的角系数值
8.1.3 角系数的计算方法 直接积分法
求解角系数的方法
代数分析法
几何分析法
2、代数分析法
利用角系数的相对性、完整性及可加性，通过求解代数方 程而获得角系数的方法称为代数分析法。 (1)三个非凹表面组成的封闭系统
A1 两个非凹表面及假想面组
成的封闭系统
根据角系数的完整性：
X a b ， cd 1 X a b ， a cX a b ， b d
Xab，ac
abacbc 2ab
Xab，bd
abbdad 2ab
两个非凹表面及假想面组 成的封闭系统
(bcad)(acbd)
Xab,cd
2ab
交 叉 线 之 和 不 交 叉 线 之 和
辐射换热的计算和规则
9.1 辐射换热的角系数
两个表面之间的辐射换热量与两个表面之间的相对位置 有很大关系
表面相对位置的影响
❖a图中两表面无限接近，相互间的换热量最大； ❖b图中两表面位于同一平面上，相互间的辐射换热量为零。 由图可以看出，两个表面间的相对位置不同时，一个表面 发出而落到另一个表面上的辐射能的百分数随之而异，从 而影响到换热量。
辐射换热
A1 X1,2 = A2 X 2,1
图(c) ：X1,2 = X1,2 a
图(d) ： X1,2 = X 2,1 = 1 三个非凹表面构成的封闭空腔
A1 X 2,1 = A2 A2a = A1
A2 X 2,1 + A2 X 2,3 = A2 A3 X 3,1 + A3 X 3,2 = A3
A1 X1,2 + A1 X1,3 = A1
非凹表面1和包壳2 非凹表面1和包壳2之间的辐射换热
A1 = A2 = A
A1 ( Eb1 − Eb2 ) X1,2 = 1 Φ1,2 = 1 A1 1 + − 1 ε1 A2 ε 2 如果 A1 << A2 ，Φ = A1ε1 ( Eb1 − Eb2 ) 1,2
19
三、多个漫灰表面封闭空腔内的辐射换热
dAj cosθ j r
2
= Ebi
cosθi cosθ j πr
2
3
离开整个黑体表面i 直接投射到表面 离开整个黑体表面i 直接投射到表面j 的辐射能为 投射到表面j
Φi→ j = ∫
Aj
∫
Ai
Ebi
cosθi cosθ j πr πr
2
dAdAj i dAdAj i
= Ebi ∫
Aj
∫
cosθi cosθ j
6
3. 角系数的计算方法
主要有积分法、代数法、图解法(或投影法) 主要有积分法、代数法、图解法(或投影法)等。 （1）积分法 根据角系数表达式通过积分运算求得角系数
X i, j
1 = Ai
∫ ∫
Aj
cosθi cosθ j πr
2
Ai
【2017年整理】人体辐射换热的计算
【2017年整理】人体辐射换热的计算
人体辐射换热的计算涉及到生物热力学和热传递等领域的知识。
一种常用的方法是使用生物热产率（Metabolic Rate）和有效辐射面积等参数来估算人体的辐射换热。
以下是一个简单的计算方法：
1.生物热产率（Metabolic Rate）：生物热产率是指人体在静止状态下产生的热量，通常以单位时间内消耗的能量来表示，单位为瓦特（W）。
可以使用人的基础代谢率（BMR）来估算。
2.有效辐射面积：人体的辐射换热主要通过皮肤表面进行，有效辐射面积可以通过人体的身表面积来估算。
表面积的计算可以使用Du Bois公式等。
3.斯蒂芬-波尔兹曼定律：辐射换热可以使用斯蒂芬-波尔兹曼定律来估算，该定律表示一个黑体表面的辐射能力与其温度的四次方成正比。
这个定律可以用来计算人体的辐射换热。
具体的计算公式和参数需要根据具体的情况和所用单位进行调整。
需要注意的是，这只是一个简单的估算方法，实际的人体辐射换热计算可能会更加复杂，需要考虑多种因素，如环境温度、相对湿度等。
在实际应用中，可以使用专业的生物热力学和热传递模型进行更准确的计算。
辐射换热系数确定公式
金属与金属铸型间的辐射换热系数：
billet T 为铸锭表面温度；mold T 为金属模表面温度。
辐射换热系数由下面的计算式决定：
))((22mold billet mold billet eff rad T T T T h ++=σε
其中，σ是斯蒂芬-玻耳兹曼常数（5.669×10-8
），e f f ε是等效辐射率，计算式如下：1
11
1
-+=mold billet eff εεε 式中billet ε和mold ε分别为铸锭与金属模的辐射率。
举例：AZ31：镁合金billet ε=0.2, AA6061铝合金：mold ε=0.4。
金属与空气间的辐射换热系数：
rad h 的值由下面公式计算得出
))((22air m etal air m etal rad T T T T h ++=σε
ε：金属的辐射率ε
注：这两个都不是换热系数（全部）公式，而是换热系数中辐射换热系数的公式，只是换热系数中的一部分而已。
而且我曾经计算过，换热系数跟对流换热、接触换热系数等相比，是非常非常小的，对温度计算结果的影响基本没有。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.4.2 包壳为一灰体
包壳的黑度为εt，温度为Tt时，其换热结果应比气体 与黑体包壳间的换热量小；可乘以一个修正系数（1+εt）/2 ：
1 t q gt 5.67 2 Tg 4 Tt 4 ( ) ( ) g g 100 100
假设： qgt hgt (Tg Tt )
平壁保温层外： T 9.8 0.07(TW T )
①空气作自然对流：
圆筒壁或管道保温层外：T 9.4 0.052(TW T )
②空气沿粗糙壁面作强制对流：
空气流速u<5m/s： T 6.2 4.2u 空气流速u>5m/s：
T 7.8u 0.78
Q12 A1 E0112 A2 E02 21 0 A112T14 0 A2 21T24 T2 4 T1 4 5.67Aef ( ) ( ) 100 100
式中： Aef A112 A221
有效辐射面积，又称当量冷平面面积 或辐射交换面积
A112 A2 21
2.1.2 角系数的性质
⒊完整性（可加性）：
若表面K=K1+K2+K3，则：
1K 1K 1K 1K
1 2 3
但：
K1 K 1 K 1 K 1
1 2 3
2.1.3 几种简单情况下的角系数
⒈两无限接近平面： 11 22 0
q12 ( E01 E02 ) /( 1 1 1) 1 2
2.3.3 几种简单情况下灰表面间辐射 换热量的计算
⒉一物包一物：
Q12 q12 . A q1 . A1
q1
1 ( E01 E rf 1 ) 1
Eef 1 1 E01 1 (Eef 211 Eef 212 )
⒈归一性： 如果由n个表面组成一个封闭体系，则其中 任意表面i对其它表面的角系数之和为1 即： 或：
i1 i 2 ....... in 1
ij 1
2.1.2 角系数的性质
⒉互换性：
对任意两表面i，j（面积分别为Ai，Aj）,均有：
Aiij A j ji
证明：表面1的总辐射能力为：A1E01 表面1发射的被表面2吸收的能量为：Q12 A1 E0112 同理：表面2发射的被表面1吸收的能量为：Q21 A2 E0221 故两表面间交换的热量为： Q12 A1 E0112 A2 E0221 显然，如果两黑表面温度相等（热平衡），T1=T2，则 E01=E02，Q12=0，有：
2.3 有效辐射、灰体间的辐射换热
2.3.1 基本概念
2.3.2 Eefi的计算 2.3.3 几种简单情况下灰表面间辐射换
热量的计算
2.3.1 基本概念
自身辐射：
Ei i E0i
Eti
ρiEti Eef
ቤተ መጻሕፍቲ ባይዱ
投入辐射：
反射辐射： 有效辐射：
Eefi Ei i Eti i E0i i Eti
1 12 A1
A1
cos1 cos 2 A2 r 2 dA1dA2
2.1.1 角系数的定义
讨论：①ф12是能量分率，无单位；
②ф12表示表面1对表面2的角系数，1表 面是辐射面，2表面是接受面； ③角系数为几何性质，与表面的大小，相 对位置及形状有关，与表面的T及ε无关
2.1.2 角系数的性质
由辐射散失的热量： 或：
其中：
QR R AW (TW T )
R
4 W o (TW T 4)
TW T
2.5 设备热损失的计算
总热损失： Q QR QC ( R R ) AW (TW T ) T AW (TW T )
其中： T ( R R ) 对流－辐射联合传热系数
31 ( A1 A3 A2 ) / 2 A3
2.1.3 几种简单情况下的角系数
⒋两无限延伸表面（拉线法）：
CD DG - CG 2CD CD CF - DF' F CD,CF 2CD CG DF' F - DG - CG 1, 2 2CD
CD, DG
2.2 黑体间的辐射换热
得到与对流传热系数相当的辐射系数：
hgt 1 t 5.67 2 Tg 4 Tt 4 g ( ) g ( ) 100 100 Tg Tt
W/(m2· K)
2.5 设备热损失的计算
由对流散失的热量：
QC C AW (TW T )
4 QR W o (TW T 4)
净辐射： qi E efi Eti i E 0i i Eti Eti i ( E 0i Eti )
E efi ( E efi i E 0i ) / i
i ( E 0i E rfi ) i
2.3.2 Eefi的计算
对包含n个表面的封闭系统，对任意i表面：
Eefi i E0i i Eti
表面i的投入辐射总计为：
Ai Eti A1 Eef 11i A2 Eef 22i ...... An Eefnni
i表面的有效辐射为：
Eefi i E0i i Eefjij
j 1 n
注：对于黑体，由于不存在反射的问题，Eefi=E0i
Eef 2 2 E02 2 (Eef 121 Eef 222 )
而：ф11=0，ф12=1，联立求解：
A1 ( E01 E02 ) Q12 1 A1 1 ( 1) 1 A2 2
2.4 气体与外壳间的辐射换热
2.4.1 包壳为黑体
2.4.2 包壳为一灰体
第2节 辐射换热计算
2.1 角系数
2.2 黑体间的辐射换热
2.3 有效辐射、灰体间的辐射换热
2.4 气体与外壳间的辐射换热 2.5 设备热损失的计算
2.1 角系数
2.1.1 角系数的定义
2.1.2 角系数的性质
2.1.3 几种简单情况下的角系数
2.1.1 角系数的定义
定义：黑表面A1在空间所有的方向上发 射的总能量，直接到达另一黑表 面A2的分率，叫做表面1对表面2 的角系数，用符号ф12表示
2.4.1 包壳为黑体
包壳温度为Tt时，则气体对包壳的辐射速率应等于气体 的自身辐射εgE0g减去气体吸收的投入辐射αgE0g，即：
q gt g E 0 g g E 0t Tg 4 Tt 4 5.67 g ( ) g ( ) 100 100
其中：εg，αg－分别为气体的黑度和吸收率， 当Tg≠Tt时，εg≠αg
⒉一物包一物： 12 1 11 0
A1 12 A1 21 A2 21 A2
12 21 1
2.1.3 几种简单情况下的角系数
⒊形成密闭系统的三凸面：
12 ( A1 A2 A3 ) / 2 A1
23 ( A2 A3 A1 ) / 2 A2
2.3.3 几种简单情况下灰表面间辐射 换热量的计算
⒈两个无限接近平面：
1 q12 ( E01 Eef 1 ) 1
Eef 1 E1 1 Eef 2 1 E01 1 Eef 2
Eef 2 E2 2 Eef 1 2 E02 2 Eef 1
由于ф12=ф21=1，灰体：ε1=α1=1-ρ1，ε2=α2=1-ρ2 联立求解：