2012中考数学预测专题十七 探究型问题
- 格式:doc
- 大小:82.50 KB
- 文档页数:2

1. (2012浙江衢州12分)如图,把两个全等的Rt △AOB 和Rt △COD 分别置于平面直角坐标系中,使直角边OB 、OD 在x 轴上.已知点A (1,2),过A 、C 两点的直线分别交x 轴、y 轴于点E 、F .抛物线y =ax 2+bx +c 经过O 、A 、C 三点. (1)求该抛物线的函数解析式;(2)点P 为线段OC 上一个动点,过点P 作y 轴的平行线交抛物线于点M ,交x 轴于点N ,问是否存在这样的点P ,使得四边形ABPM 为等腰梯形?若存在,求出此时点P 的坐标;若不存在,请说明理由.(3)若△AOB 沿AC 方向平移(点A 始终在线段AC 上,且不与点C 重合),△AOB 在平移过程中与△COD 重叠部分面积记为S .试探究S 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.2. (2012浙江义乌12分)如图1,已知直线y =kx 与抛物线2422y=x +x 273交于点A (3,6). (1)求直线y =kx 的解析式和线段OA 的长度; (2)点P 为抛物线第一象限内的动点,过点P 作直线PM ,交x 轴于点M (点M 、O 不重合),交直线OA 于点Q ,再过点Q 作直线PM 的垂线,交y 轴于点N .试探究:线段QM 与线段QN 的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由;(3)如图2,若点B 为抛物线上对称轴右侧的点,点E 在线段OA 上(与点O 、A 不重合),点D (m ,0)是x 轴正半轴上的动点,且满足∠BAE =∠BED =∠AOD .继续探究:m 在什么范围时,符合条件的E 点的个数分别是1个、2个?3.(2012江苏苏州10分)如图,已知抛物线()211by=x b+1x+444-(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 的左侧),与y 轴的正半轴交于点C .⑴点B 的坐标为 ▲ ,点C 的坐标为 ▲ (用含b 的代数式表示);⑵请你探索在第一象限内是否存在点P ,使得四边形PCOB 的面积等于2b ,且△PBC 是以点P 为直角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;⑶请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.4.(2012福建龙岩)在平面直角坐标系xoy 中, 一块含60°角的三角板作如图摆放,斜边 AB 在x 轴上,直角顶点C 在y 轴正半轴上,已知点A (-1,0).(1)请直接写出点B 、C 的坐标:B ( , )、C ( , );并求经过A 、B 、C 三点的抛物线解析式; (2)现有与上述三角板完全一样的三角板DEF (其中∠EDF =90°,∠DEF =60°),把顶点E 放在线段AB 上(点E 是不与A 、B 两点重合的动点),并使ED 所在直线经过点C . 此时,EF 所在直线与(1)中的抛物线交于第一象限的点M .①设AE =x ,当x 为何值时,△OCE ∽△OBC ; ②在①的条件下探究:抛物线的对称轴上是否存在点P 使△PEM 是等腰三角形,若存在,请求点P 的坐标;若不存在,请说明理由.xyPOC BA5. (2012湖北荆门)如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=13,A(3,0),D(﹣1,0),E(0,3).(1)求抛物线的解析式及顶点B的坐标;(2)求证:CB是△ABE外接圆的切线;(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.6.(2012湖南永州)如图所示,已知二次函数y=ax2+bx﹣1(a≠0)的图象过点A(2,0)和B(4,3),l为过点(0,﹣2)且与x轴平行的直线,P(m,n)是该二次函数图象上的任意一点,过P作PH⊥l,H为垂足.(1)求二次函数y=ax2+bx﹣1(a≠0)的解析式;(2)请直接写出使y<0的对应的x的取值范围;(3)对应当m=0,m=2和m=4时,分别计算|PO|2和|PH|2的值.由此观察其规律,并猜想一个结论,证明对于任意实数m,此结论成立;(4)试问是否存在实数m可使△POH为正三角形?若存在,求出m的值;若不存在,请说明理由.7. (2012四川广安)如图,在平面直角坐标系xOy 中,AB ⊥x 轴于点B ,AB =3,tan ∠AOB =34,将△OAB 绕着原点O 逆时针旋转90°,得到△OA 1B 1;再将△OA 1B 1绕着线段OB 1的中点旋转180°,得到△OA 2B 1,抛物线y =ax 2+bx +c (a ≠0)经过点B 、B 1、A 2. (1)求抛物线的解析式.(2)在第三象限内,抛物线上的点P 在什么位置时,△PBB 1的面积最大?求出这时点P 的坐标.(3)在第三象限内,抛物线上是否存在点Q ,使点Q 到线段BB 1的距离为22?若存在,求出点Q 的坐标;若不存在,请说明理由.8. (2012四川德阳)在平面直角坐标xOy 中,(如图)正方形OABC 的边长为4,边OA 在x 轴的正半轴上,边OC 在y 轴的正半轴上,点D 是OC 的中点,BE ⊥DB 交x 轴于点E .⑴求经过点D 、B 、E 的抛物线的解析式;⑵将∠DBE 绕点B 旋转一定的角度后,边BE 交线段OA 于点F ,边BD 交y 轴于点G ,交⑴中的抛物线于M (不与点B 重合),如果点M 的横坐标为512,那么结论OF =21DG 能成立吗?请说明理由. ⑶过⑵中的点F 的直线交射线CB 于点P ,交⑴中的抛物线在第一象限的部分于点Q ,且使△PFE 为等腰三角形,求Q 点的坐标.9. (2012青海西宁)如图,在平面直角坐标系中,矩形OABC 的边OA 在y 轴的正半轴上,O 在x 轴的正半轴上,已知A (0,4)、C (5,0).作∠AOC 的平分线交AB 于点D ,连接CD ,过点D 作DE ⊥CD 交OA 于点E . (1)求点D 的坐标; (2)求证:△ADE ≌△BCD ;(3)抛物线y = 4 5x 2- 245x +4经过点A 、C ,连接AC .探索:若点P 是x 轴下方抛物线上一动点,过点P 作平行于y 轴的直线交AC 于点M .是否存在点P ,使线段MP 的长度有最大值?若存在,求出点P 的坐标;若不存在,请说明理由.10. (2012四川绵阳)如图1,在直角坐标系中,O 是坐标原点,点A 在y 轴正半轴上,二次函数y =ax 2+16x +c 的图象F 交x 轴于B 、C 两点,交y 轴于M 点,其中B (-3,0),M (0,-1)。

2012年中考数学二轮复习考点解密 规律探索性问题第一部分 讲解部分一.专题诠释规律探索型题是根据已知条件或题干所提供的若干特例,通过观察、类比、归纳,发现题目所蕴含的数字或图形的本质规律与特征的一类探索性问题。
这类问题在素材的选取、文字的表述、题型的设计等方面都比较新颖新。
其目的是考查学生收集、分析数据,处理信息的能力。
所以规律探索型问题备受命题专家的青睐,逐渐成为中考数学的热门考题。
二.解题策略和解法精讲规律探索型问题是指在一定条件下,探索发现有关数学对象所具有的规律性或不变性的问题,它往往给出了一组变化了的数、式子、图形或条件,要求学生通过阅读、观察、分析、猜想来探索规律.它体现了“特殊到一般”的数学思想方法,考察了学生的分析、解决问题能力,观察、联想、归纳能力,以及探究能力和创新能力.题型可涉及填空、选择或解答.。
三.考点精讲考点一:数与式变化规律通常根据给定一列数字、代数式、等式或者不等式,然后写出其中蕴含的一般规律,一般解法是先写出数式的基本结构,然后通过比较各式子中相同的部分和不同的部分,找出各部分的特征,改写成要求的规律的形式。
例1. 有一组数:13,25579,,101726L ,请观察它们的构成规律,用你发现的规律写出第n (n 为正整数)个数为 .分析:观察式子发现分子变化是奇数,分母是数的平方加1.根据规律求解即可.解答:解:21211211⨯-=+; 23221521⨯-=+; 252311031⨯-=+;272411741⨯-=+; 219251265+⨯-=;…; ∴第n (n 为正整数)个数为2211n n -+. 点评:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.此题的规律为:分子变化是奇数,分母是数的平方加1.例2(2010广东汕头)阅读下列材料:1×2 =31(1×2×3-0×1×2), 2×3 = 31(2×3×4-1×2×3), 3×4 = 31(3×4×5-2×3×4), 由以上三个等式相加,可得1×2+2×3+3×4=31×3×4×5 = 20. 读完以上材料,请你计算下列各题:(1) 1×2+2×3+3×4+···+10×11(写出过程);(2) 1×2+2×3+3×4+···+n ×(n +1) = ______________;(3) 1×2×3+2×3×4+3×4×5+···+7×8×9 = ______________.分析:仔细阅读提供的材料,可以发现求连续两个正整数积的和可以转化为裂项相消法进行简化计算,从而得到公式)1(433221+⨯++⨯+⨯+⨯n n Λ [])1()1()2)(1()321432()210321(31+--++++⨯⨯-⨯⨯+⨯⨯-⨯⨯⨯=n n n n n n Λ )2)(1(31++=n n n ;照此方法,同样有公式: )2()1(543432321+⨯+⨯++⨯⨯+⨯⨯+⨯⨯n n n Λ[])2()1()1()3()2()1()43215432()32104321(41+⨯+⨯⨯--+⨯+⨯+⨯++⨯⨯⨯-⨯⨯⨯+⨯⨯⨯-⨯⨯⨯=n n n n n n n n Λ)3)(2)(1(41+++=n n n n . 解:(1)∵1×2 =31(1×2×3-0×1×2), 2×3 = 31(2×3×4-1×2×3), 3×4 = 31(3×4×5-2×3×4),…10×11 =31(10×11×12-9×10×11), ∴1×2+2×3+3×4+···+10×11=31×10×11×12=440. (2))2)(1(31++n n n .(3)1260.点评:本题通过材料来探索有规律的数列求和公式,并应用此公式进行相关计算.本题系初、高中知识衔接的过渡题,对考查学生的探究学习、创新能力及综合运用知识的能力都有较高的要求.如果学生不掌握这些数列求和的公式,直接硬做,既耽误了考试时间,又容易出错.而这些数列的求和公式的探索,需要认真阅读材料,寻找材料中提供的解题方法与技巧,从而较为轻松地解决问题.例3(2010山东日照,19,8分)我们知道不等式的两边加(或减)同一个数(或式子)不等号的方向不变.不等式组是否也具有类似的性质?完成下列填空:一般地,如果⎩⎨⎧>>dc b a , 那么a +c b +d .(用“>”或“<”填空) 你能应用不等式的性质证明上述关系式吗?分析:可以用不等式的基本性质和不等式的传递性进行证明。

数学探究性题目七例1.时钟上的数学我们每个同学家里都有大大小小的钟,绝大部分钟都有时针、分针、秒针,时时刻刻都可以听到它们不停的“滴答、滴答”走动的声音,当然他们的走动有快有慢,秒针最快,时针最慢,不知你有没有注意到它们之间的一些数学关系?为了使问题简单起见,我们假设所讨论的时钟只有时针和分针。
问题:在一天之内时针和分针重合多少次?每次发生在什么时候?什么时候两针互相垂直?什么时候两针在一条直线上?如果时针和分针交换它还能表示某一时刻的时间么?希望大家在解决以上问题之后讨论一下是否还有其他有趣的问题。
2.揭穿转摊的骗术在车站,码头附近有时会看到一些碰运气、赌输赢的地摊,这些地摊大多引诱来往过路旅客,用骗术骗取他们的钱财。
转摊就是其中之一。
摊主在一个固定的圆盘上划出若干扇形区域,并顺次标上号码1,2,3,4,5,6,。
,在每一奇数扇区上放上值钱的物品,如名酒,中华香烟等,而在每一个偶数区域上放着廉价的物品,如糖块,小食品等。
圆盘中心安装一根可以转动的轴,轴的顶端有一根悬臂,臂端吊一根线,线头上系一根针。
你如果付给摊主一元钱,就可以随便转动一次,当悬臂停止转动时,针就停在某一区域,按照摊主制订的规则,这一格上的数是几,就从下一格起,按顺时针方向数出几,最后数到哪一格,那一格中的物品就归你,例如:当针指向“6”时,就要从“7”数起,顺时针方向数出“6”,最后应该数到“12”这一格。
参加这种赌博的人认为,圆盘中奇数、偶数格占一半,输赢得机会各占一半,于是就去碰碰运气,然而,不管转多少次,最后总是数到偶数区域中,你只能用自己的很多钱换来几粒糖果等廉价物品。
为什么大家的“运气”都这样不好,你能用数学知识解开这个迷吗?类似的还有1.音乐教室里有7排座位,每排7把椅子,每把椅子上坐一名学生,教师每月都要将座位调换一次,张明同学提出建议:每次交换时,每一名同学都必须与她相邻(前、后、左、右)的某一个同学交换位置,以示公平。

开放探究型问题一、选择题1、(2012年中考数学新编及改编题试卷)图(1)、图(2)、图(3)分别表示甲、乙、丙三人由A 地到B 地的路线图。
已知; 甲的路线为:A →C →B 。
乙的路线为:A →D →E →F →B ,其中E 为AB 的中点。
丙的路线为:A →G →H →K →B ,其中H 在AB 上,且AH>HB 。
若符号「→」表示「直线前进」,则根据图(1)、图(2)、图(3)的数据, 则三人行进路线长度的大小关系为( )(A) 甲=乙=丙 (B) 甲<乙<丙 (C) 乙<丙<甲 (D )丙<乙<甲 二、填空题1. (2012年江苏南通三模)一元二次方程有一根为1,此方程可以是 ▲ (写出一个即可). 答案:x 2-x=0等.2. (2012年江苏南通三模)小明、小亮各有一段长为40cm 的铁丝,将将铁丝首尾相连围成一个长方形.(1)请问他俩围成长方形一定全等吗?(2)如果围成的长方形一定全等,则长方形的长和宽分别是多少?如果围成的长方形不一定全等,请再添加一个条件,使得他俩围成的长方形全等,并求出长方形的长和宽(写出解题过程). 答案:24.(1)不一定 (2)略3、(盐城地区2011~2012学年度适应性训练)如图,已知抛物线y =x 2+bx +c 经过点(0,-3),请你确定一个b 的值,使该抛物线与x 轴的一个交点在(1,0)和(3,0)之间.你所确定的b 的值是 ▲ (写出一个值即可).CDG50︒F60︒70︒50︒ 60︒70︒ 50︒ 60︒70︒ 50︒60︒70︒ 50︒ 60︒70︒ K图(1)图(2)图(3)-331O yx答案如-1,0(不惟一,在-2<b <2内取值均可)三、解答题1、(2012年香坊区一模) (本题l0分)已知:在∆ABC 中,AB=AC ,点P 是BC 上一点,PC=2PB,连接AP ,作∠APD=∠B 交AB 于点D 。

数学中考中的几何探索题(教师版)1.(2012江苏盐城,25,10分)如图①所示,已知A、B为直线 上两点,点C为直线 上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥ 于点D1,过点E作EE1⊥ 于点E1.(1)如图②,当点E恰好在直线 的上方时(此时E1与E重合),试说明DD1=AB(2)在图①中,当D、E两点都在直线 的上方时,试探求三条线段DD1、EE1、AB之间的数量关系,并说明理由.(3)如图③,当点E在直线 的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系(不需证明).【解析】本题考查了正方形和全等三角形的判定和性质.利用两三角形全等后的对应边相等与对应角相等,是解决本题的关键(1)图②是特殊位置,直接证明三角形全等解决;(2)先猜想三条线段DD1、EE1、AB之间的数量关系,然后根据图②启示,构造两对全等三角形证明.(3)类比归纳、猜想出结论.【答案】(1)∵四边形CADF和四边形CBEG都是正方形,且DD1⊥ ,∴∠DAC=∠ABC=∠DD1A=900,又∵∠ADD1+∠DAD1=900,而∠DAD1+∠ABC=900,∴∠ADD1=∠ABC,在Rt△DD1A和在Rt△BEE1中,∵∠ABC=∠DD1A,∠ADD1=∠BAC,AD=AC,∴△DD1A≌△BEE1,∴DD1=AB.(2)AB=DD1+EE1.理由如下:过C作CM⊥AB于M,易得:△DD1A≌△ACM,∴DD1=AM,同理:△BCM≌△EBE1,∴EE1=BM,∴AB=AM+BM= DD1+EE1.(3)AB=DD1-EE1.【点评】本题是对平面几何推理证明的考查,证明两条线段相等或两角相等,常用的方法第25题图EMFDCBA就是先证得三角形全等,利用全等形的性质,推出结论,考查了同学们从特殊到一般的推理过程.2. (2012•重庆)已知:如图,在菱形ABCD 中,F 为边BC 的中点,DF 与对角线AC 交于点M ,过M 作ME ⊥CD 于点E ,∠1=∠2.(1)若CE=1,求BC 的长;(2)求证:AM=DF+ME .考点:菱形的性质;全等三角形的判定与性质.专题:综合题.分析:(1)根据菱形的对边平行可得AB ∥CD ,再根据两直线平行,内错角相等可得∠1=∠ACD ,所以∠ACD=∠2,根据等角对等边的性质可得CM=DM ,再根据等腰三角形三线合一的性质可得CE=DE ,然后求出CD 的长度,即为菱形的边长BC 的长度;(2)先利用“边角边”证明△CEM 和△CFM 全等,根据全等三角形对应边相等可得ME=MF ,延长AB 交DF 于点G ,然后证明∠1=∠G ,根据等角对等边的性质可得AM=GM ,再利用“角角边”证明△CDF 和△BGF 全等,根据全等三角形对应边相等可得GF=DF ,最后结合图形GM=GF+MF 即可得证.解答:(1)解:∵四边形ABCD 是菱形,∴AB ∥CD , ∴∠1=∠ACD , ∵∠1=∠2,∴∠ACD=∠2,∴MC=MD , ∵ME ⊥CD , ∴CD=2CE , ∵CE=1, ∴CD=2, ∴BC=CD=2;(2)证明:如图,∵F为边BC的中点,∴BF=CF=1 2 BC,∴CF=CE,在菱形ABCD中,AC平分∠BCD,∴∠ACB=∠ACD,在△CEM和△CFM中,∵ CE=CF ∠ACB=∠ACD CM=CM ,∴△CEM≌△CFM(SAS),∴ME=MF,延长AB交DF于点G,∵AB∥CD,∴∠G=∠2,∵∠1=∠2,∴∠1=∠G,∴AM=MG,在△CDF和△BGF中,∵∠G=∠2 ∠BFG=∠CFD(对顶角相等) BF=CF ,∴△CDF≌△BGF(AAS),∴GF=DF,由图形可知,GM=GF+MF,∴AM=DF+ME.点评:本题考查了菱形的性质,全等三角形3.( 2012年浙江省宁波市,12,3)勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中,就有“若勾三,股四,则弦五”记载,如图1是由边长相等的小正形和直角三角形构成的可以用其面积关系验证勾股定理。


2012年全国中考数学试题分类解析汇编专题58:开放探究型问题一、选择题二、填空题1. (2012陕西省3分)在同一平面直角坐标系中,若一个反比例函数的图象与一次函数y=2x+6-的图象无公共点,则这个反比例函数的表达式是▲ (只写出符合条件的一个即可).【答案】5yx=(答案不唯一)。
【考点】开放型问题,反比例函数与一次函数的交点问题,一元二次方程根与系数的关系。
【分析】设反比例函数的解析式为:kyx=,联立y=2x+6-和kyx=,得k2x+6x-=,即22x6x+k0-=∵一次函数y=2x+6-与反比例函数kyx=图象无公共点,∴△<0,即268k0< --(),解得k>9 2。
∴只要选择一个大于92的k值即可。
如k=5,这个反比例函数的表达式是5yx=(答案不唯一)。
2. (2012广东湛江4分)请写出一个二元一次方程组▲ ,使它的解是x=2y=1⎧⎨-⎩.【答案】x+y=1x+2y=0⎧⎨⎩(答案不唯一)。
【考点】二元一次方程的解。
【分析】根据二元一次方程解的定义,围绕x=2y=1⎧⎨-⎩列一组等式,例如:由x+y=2+(-1)=1得方程x+y=1;由x-y=2-(-1)=3得方程x-y=3;由x+2y=2+2(-1)=0得方程x+2y=0;由2x+y=4+(-1)=3得方程2x+y=3;等等,任取两个组成方程组即可,如x+y=1x+2y=0⎧⎨⎩(答案不唯一)。
3. (2012广东梅州3分)春蕾数学兴趣小组用一块正方形木板在阳光做投影实验,这块正方形木板在地面上形成的投影是可能是▲ (写出符合题意的两个图形即可)【答案】正方形、菱形(答案不唯一)。
【考点】平行投影。
【分析】根据平行投影的特点:在同一时刻,平行物体的投影仍旧平行。
所以,在同一时刻,这块正方形木板在地面上形成的投影是平行四边形或特殊的平行四边形,例如,正方形、菱形(答案不唯一)。
4. (2012浙江衢州4分)试写出图象位于第二、四象限的一个反比例函数的解析式▲ .【答案】1y=x-(答案不唯一)。
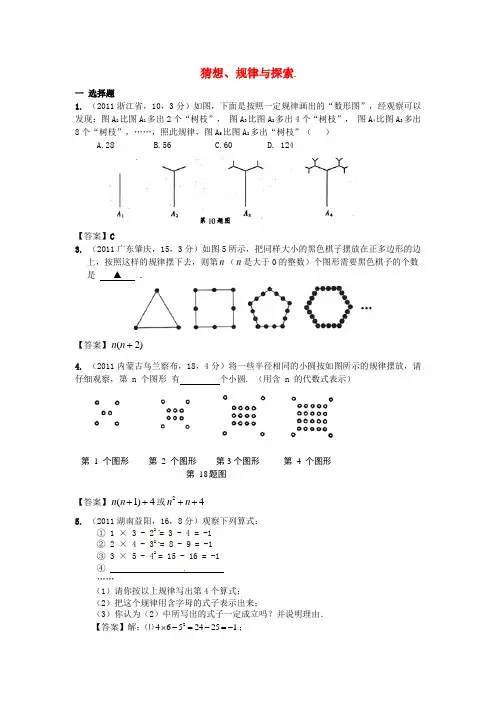
猜想、规律与探索一 选择题1. (2011浙江省,10,3分)如图,下面是按照一定规律画出的“数形图”,经观察可以发现:图A 2比图A 1多出2个“树枝”, 图A 3比图A 2多出4个“树枝”, 图A 4比图A 3多出8个“树枝”,……,照此规律,图A 6比图A 2多出“树枝”( )A.28B.56C.60D. 124【答案】C3. (2011广东肇庆,15,3分)如图5所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n (n 是大于0的整数)个图形需要黑色棋子的个数是▲ .【答案】)2(+n n4. (2011内蒙古乌兰察布,18,4分)将一些半径相同的小圆按如图所示的规律摆放,请仔细观察,第 n 个图形 有 个小圆. (用含 n 的代数式表示)【答案】(1)4n n ++或24n n ++5. (2011湖南益阳,16,8分)观察下列算式:① 1 × 3 - 22= 3 - 4 = -1② 2 × 4 - 32= 8 - 9 = -1③ 3 × 5 - 42= 15 - 16 = -1 ④ ……(1)请你按以上规律写出第4个算式; (2)把这个规律用含字母的式子表示出来;(3)你认为(2)中所写出的式子一定成立吗?并说明理由. 【答案】解:⑴246524251⨯-=-=-;第1个图形第 2 个图形 第3个图形第 4 个图形第 18题图⑵答案不唯一.如()()2211n n n +-+=-;⑶()()221n n n +-+ ()22221n n n n =+-++ 22221n n n n =+--- 1=-.6.(2011广东汕头,20,9分)如下数表是由从1 开始的连续自然数组成,观察规律并完成各题的解答.(1)表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数; (2)用含n 的代数式表示:第n 行的第一个数是 ,最后一个数是 ,第n 行共有 个数;(3)求第n 行各数之和. 【解】(1)64,8,15;(2)2(1)1n -+,2n ,21n -;(3)第2行各数之和等于3×3;第3行各数之和等于5×7;第4行各数之和等于7×7-13;类似的,第n 行各数之和等于2(21)(1)n n n --+=322331n n n -+-.二 填空题1. (2011四川绵阳18,4)观察上面的图形,它们是按一定规律排列的,依照此规律,第_____个图形共有120 个。

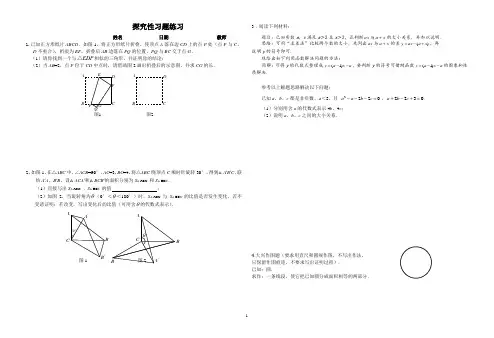
θAA 'CBB '30︒B 'A 'CB A探究性习题练习姓名 日期 教师1.已知正方形纸片ABCD .如图1,将正方形纸片折叠,使顶点A 落在边CD 上的点P 处(点P 与C 、D 不重合),折痕为EF ,折叠后AB 边落在PQ 的位置,PQ 与BC 交于点G . (1)请你找到一个与EDP △相似的三角形,并证明你的结论;(2)当AB =2,点P 位于CD 中点时,请借助图2画出折叠后的示意图,并求CG 的长.2、如图1,在△ABC 中,∠ACB =90°,AC =3,BC =4,将△ABC 绕顶点C 顺时针旋转30°,得到△A ′B ′C .联结A ′A 、B ′B ,设△ACA ′和△BCB ′的面积分别为S △ACA ′ 和S △BC B′. (1)直接写出S △ACA ′ ︰S △BC B′ 的值 ;(2)如图2,当旋转角为θ(0°<θ<180°)时,S △ACA ′ 与S △BC B′ 的比值是否发生变化,若不变请证明;若改变,写出变化后的比值(可用含θ的代数式表示).图1 图23.阅读下列材料:题目:已知实数a ,x 满足a >2且x >2,试判断ax 与a x +的大小关系,并加以说明. 思路:可用“求差法”比较两个数的大小,先列出ax 与a x +的差()y ax a x =-+,再 说明y 的符号即可.现给出如下利用函数解决问题的方法:简解:可将y 的代数式整理成(1)y a x a =--,要判断y 的符号可借助函数(1)y a x a =--的图象和性质解决.参考以上解题思路解决以下问题:已知a ,b ,c 都是非负数,a <5,且 2220a a b c ---=,2230a b c +-+=. (1)分别用含a 的代数式表示4b ,4c ; (2)说明a ,b ,c 之间的大小关系.4.大兴作图题(要求用直尺和圆规作图,不写出作法, 只保留作图痕迹,不要求写出证明过程). 已知:圆.P G QF E D C B A A B C D 图2图1求作:一条线段,使它把已知圆分成面积相等的两部分.5.小明喜欢研究问题,他将一把三角板的直角顶点放在平面直角坐标系的原点O 处,两条直角边与抛物线2(0)y ax a =<交于A 、B 两点.(1)如图1,当2OA OB ==时,则a = ;(2)对同一条抛物线,当小明将三角板绕点O 旋转到如图2所示的位置时,过点B 作BC x ⊥轴于点C ,测得1OC =,求出此时点A 的坐标;(3)对于同一条抛物线,当小明将三角板绕点O 旋转任意角度时,他惊奇地发现,若三角板的两条直角边与抛物线有交点,则线段A B 总经过一个定点,请直接写出该定点的坐标.图16、已知△ABC 的面积为a ,O 、D 分别是边AC 、BC 的中点.(1)画图:在图1中将点D 绕点O 旋转180︒得到点E , 连接AE 、CE .填空:四边形ADCE 的面积为;(2)在(1)的条件下,若F 1是AB 的中点,F 2是AF 1的中点, F3是AF 2的中点,…,Fn 是AFn -1的中点 (n为大于1的整数), 则△F 2CE的面积为; △F n CE 的面积为 .解: (1)画图:图1填空:四边形ADCE 的面积为 . 备用图(2)△F 2CE 的面积为 ; △F n CE 的面积为 .7. 如图1,若将△AOB 绕点O 逆时针旋转180°得到△COD ,则△AOB ≌△COD .此时,我们称△AOB 与△COD 为“8字全等型”.借助“8字全等型”我们可以解决一些图形的分割与拼接问题.例如:图2中,△ABC 是锐角三角形且AC >AB ,点E 为AC 中点,F 为BC 上一点且BF ≠FC (F 不与B 、C 重合),沿EF 将其剪开,得到的两块图形恰能拼成一个梯形.请分别按下列要求用直线将图2中的△ABC 重新进行分割,画出分割线及拼接后的图形. (1)在图3中将△ABC 沿分割线剪开,使得到的两块图形恰能拼成一个平行四边形;(2在图4中将△ABC 沿分割线剪开,使得到的三块图形恰能拼成一个矩形,且其中的两块为直角三角形;(3在图5中将△ABC 沿分割线剪开,使得到的三块图形恰能拼成一个矩形,且其中的一块为锐角三角形.xyBAO DO CBADO CBA探究性习题练习答案1.解:(1)与EDP △相似的三角形是PCG △(或△FQG ). ……… 1分证明:∵四边形ABCD 是正方形,∴∠A=∠B=∠C=∠D=90°. ……………………………… 2分 由折叠知 ∠EPQ=∠A=90°. ∴∠1+∠3=90°,∠1+∠2=90°.∴∠2=∠3. ……………………………………………………… 3分 ∴PCG △∽EDP △.(2)正确画出示意图. ………………………………………… 4分 ∵ 四边形ABCD 是正方形,AB =2, ∴ AB =BC =CD =DA =2. 设 AE =x ,则ED =2-x ,EP = x . ∵ P 是CD 的中点, ∴ DP =PC =1.在Rt △EDP 中,∠D =90°,根据勾股定理,得x 2=(2-x )2+1.解得 x =45.∴ ED =43. ………………………………………… 5分∵ PCG △∽EDP △,∴ ED DPPC CG =. ∴ 3141CG=.∴ CG=34. ………………………………………………………………………… 6分2.解:(1)S △ACA ′ ︰S △BC B′ = 9︰16 ; …………………………………………2分(2)S △ACA ′ 与S △BC B′ 的比值不变;证明:∵△ABC 绕点C 顺时针旋转角θ得到△A 'B 'C∴∠AC A '=∠BCB '=θ, …………………………………………3分AC=A 'C ,BC =B ' C , ∴CB CA BC AC ''=, ……………………………………………………4分 ∴△AC A '∽△BCB ', ……………………………………………………5分∴S △ACA ′ ︰S △BC B′ =(A C ︰BC )2 = 9︰16. …………… 3.解:(1)∵ 2220a a b c ---=,2230a b c +-+=,∴ 222,22 3.b c a a c b a ⎧+=-⎨-=+⎩消去b 并整理,得 243c a =+.……………1分消去c 并整理,得2423b a a =--. ………2分(2)∵ 22423(3)(1)(1)4b a a a a a =--=-+=--,将4b 看成a 的函数,由函数24(1)4b a =--的性质结合它的图象(如图7所示),以及a ,b 均为非负数得a ≥3. 又 ∵ a <5,∴ 3≤a <5.……………………………………………………………………3分 ∵ 224()63(3)12b a a a a -=--=--,将4()b a -看成a 的函数,由函数24()(3)12b a a -=--的性质结合它的图象(如图8所示)可知,当3≤a <5时,4()0b a -<. ∴ b <a . ……………………………………………4分∵ 24()43(1)(3)c a a a a a -=-+=--,a ≥3, ∴ 4()c a -≥0.∴ c ≥a .∴ b <a ≤c . ………………………………………5分阅卷说明:“b <a ,b <c ,a ≤c ”三者中,先得出其中任何一个结论即可 4PGQ FED CBA321图1AB CD EFQ GP 图2图7图8AB 为所求直线. ……………………5分 5.解:(1)22-=a .------1分 (2)由(1)可知抛物线的解析式为222x y -=. ∵OC =1, ∴y B =22-, ∴B (1,22-).------2分过点A 作AD ⊥x 轴于点D , 又BC ⊥x 轴于点C , ∴∠ADO =∠BCO =90°. ∴∠1+∠2 =90°. ∵AO ⊥OB ,∴∠1+∠3 =90°.∴∠2=∠3. ∴△DAO ∽△COB .∴OC AD BC OD =. ------3分设点A 坐标为(222,x x -),则OD =-x ,AD =222x . ∴122222xx =- , 解得x =-2, ∴y A =22-,故点A 的坐标为(-2, 22-).------4分(3)定点坐标是(0,2-).------5分 6.(1)画图: 图略(1分); 填空: a (1分) …………………………………2分 (2)a 85(1分), a n n 1212++ (2分) …7. (1)………………………………………………1分(2)………………………………………………3分(3)xy321C BADO13321ABC。

2012中考数学模拟试题及答案十七注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分120分.第Ⅰ卷1至2页,第Ⅱ卷3至8页.考试时间120分钟. 2.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用2B 铅笔涂写在答题卡上,并同时将考点、姓名、准考证号、座号填写在试卷规定的地方. 3.选择题选出答案后,用2B 铅笔把答题卡上对应题目的正确答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,答案写在试卷上无效. 4.数学考试不允许使用计算器,考试结束后,应将本试卷和答题卡一并交回.第Ⅰ卷(选择题 共45分)一、选择题(本大题共15个小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.﹣2012的相反数是( )A. 2012B.﹣2012C.20121 D. 20121-2.如图,已知∠1 = 70º,如果CD ∥BE ,那么∠B 的度数为( )A .70ºB .100ºC .110ºD .120º3.某汽车参展商为了参加第八届中国国际汽车博览会,印制了105000张宣传彩页.105000这个数字用科学记数法表示为( )A .10.5×104B .1.05×105C .1.05×106D .0.105×106 4.估计20的算术平方根的大小在( ) A.2与3之间B.3与4之间C.4与5之间D.5与6之间5.下列计算正确的是( )A.623a a a =⋅B.1055a a a =+C.2236)3(a a =-D.723)(a a a =⋅第2题图B CED A 16.若三角形的两边长分别为2和6,则第三边的长可能是( )A .3B .4C .5D .87.如图,ABC ∆中, 90=∠C ,3=AC , 30=∠B ,点P 是BC 边上的动点,则AP长不可能...是( ) A. 3.5 B. 4.2 C. 5.8 D. 78.若△ABC ∽△DEF , △ABC 与△DEF 的相似比为1∶2,则 △ABC 与△DEF 的周长比为( ) A .1∶4B .1∶2C .2∶1D .1∶29.化简41(-4x +8)-3(4-5x )的结果为( )A.-16x -10B.-16x -4C. 56x -40D. 14x -1010.不等式组211420x x ->⎧⎨-⎩,≤的解在数轴上表示为( )11.如图,△ABC 中,AB =AC =6,BC =8,AE 平分∠BAC 交BC 于点E ,点D 为AB 的中点,连接DE ,则△BDE 的周长是( ) A.75+ B. 10C.425+D. 1212.某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱比A型包装箱多装15件文具,单独使用B型包装箱比单独使用A型包装箱可少用12个. 设B型包装箱每个可以装x件文具,根据题意列方程为()A.1080x=1080x+15-12 B.1080x=1080x+15+12C.1080x=1080x-15+12 D.1080x=1080x-15-1213.现定义运算“★”,对于任意实数a、b,都有a★b=23a a b-+,如:4★5=54342+⨯-,若x★2=6,则实数x的值是()A.4-或1-B.4或1-C.4或2-D.4-或214.如图,菱形ABCD中,对角线AC、BD相交于点O,M、N分别是边AB、AD的中点,连接OM、ON、MN,则下列叙述正确的是()A.△AOM和△AON都是等边三角形B.四边形MBON和四边形MODN都是菱形C.四边形MBCO和四边形NDCO都是等腰梯形D.四边形AMON与四边形ABCD是位似图形15.如图,用围棋子按下面的规律摆图形,则摆第n 个图形需要围棋子的枚数为( ) A .5n B .5n -1 C .6n -1 D .2n 2+1第Ⅱ卷(非选择题 共75分)注意事项:1.第Ⅱ卷共6页.用蓝、黑色钢笔或圆珠笔直接答在考试卷上. 2.答卷前将密封线内的项目填写清楚.二、填空题(本大题共6个小题,每小题3分,共18分.把答案填在题中的横线上.)16.实数a ,b 在数轴上对应点的位置如图所示,则||a ||b (填“>”“<”或“=”). 17.分解因式:39a a -= __________18.不等式325x +≥的解集是 .19.将两个形状相同的三角板放置在一张矩形纸片上,按图示画线得到四边形ABCD ,则四边形ABCD 的形状是 .20. 如图,△ABD 与△AEC 都是等边三角形,AB ≠AC .下列结论中,正确的是 .①BE =CD ;②∠BOD =60º;③△BOD ∽△COE .得 分评卷人ab0 (第16题)21.如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为.三、解答题(本大题共7个小题,共57分.解答应写出文字说明、证明过程或演算步骤.)22.(本小题满分7分)完成下列各题:(1)化简:21422---xxx(2)计算:121(31)362-⎛⎫+--⎪⎝⎭.23.(本小题满分7分)完成下列各题:(1)如图,四边形ABCD中,AB∥CD,∠B=∠D,得分评卷人得分评卷人[来源:]3,6==ABBC,求四边形ABCD的周长.(2)已知:如图,在△ABC中,D为边BC上的一点,AD平分∠EDC,且∠E=∠B,DE=DC。
2012年中考数学二轮复习考点解密探索性问题Ⅰ、综合问题精讲:探索性问题是指命题中缺少一定的条件或无明确的结论,需要经过推断,补充并加以证明的题型.探索性问题一般有三种类型:(1)条件探索型问题;(2)结论探索型问题;(3)探索存在型问题.条件探索型问题是指所给问题中结论明确,需要完备条件的题目;结论探索型问题是指题目中结论不确定,不唯一,或题目结论需要类比,引申推广,或题目给出特例,要通过归纳总结出一般结论;探索存在型问题是指在一定的前提下,需探索发现某种数学关系是否存在的题目.探索型问题具有较强的综合性,因而解决此类问题用到了所学过的整个初中数学知识.经常用到的知识是:一元一次方程、平面直角坐标系、一次函数与二次函数解析式的求法(图象及其性质)、直角三角形的性质、四边形(特殊)的性质、相似三角形、解直角三角形等.其中用几何图形的某些特殊性质:勾股定理、相似三角形对应线段成比例等来构造方程是解决问题的主要手段和途径.因此复习中既要重视基础知识的复习,又要加强变式训练和数学思想方法的研究,切实提高分析问题、解决问题的能力.Ⅱ、典型例题剖析【例1】如图2-6-1,已知抛物线的顶点为A(O,1),矩形CDEF的顶点C、F在抛物线上,D、E在x轴上,CF交y轴于点B(0,2),且其面积为8.(1)求此抛物线的解析式;(2)如图2-6-2,若P点为抛物线上不同于A的一点,连结PB并延长交抛物线于点Q,过点P、Q分别作x轴的垂线,垂足分别为S、R.①求证:PB=PS;②判断△SBR的形状;③试探索在线段SR上是否存在点M,使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似,若存在,请找出M点的位置;若不存在,请说明理由.⑴解:方法一:∵B点坐标为(0,2),∴OB=2,∵矩形CDEF面积为8,∴CF=4.∴C 点坐标为(一2,2).F 点坐标为(2,2)。
设抛物线的解析式为2y ax bx c =++. 其过三点A(0,1),C(-2.2),F(2,2)。
一、选择题:1 2 3 4 5 6 CABBBA二、填空题:7. ()22x y - 8. m 2 m 3≠>且 9. y 22x =-- 10. 25° 11. 8-2π 12. ()3,3- 13.32214. 6- 15. (5,2),(35,2),(35,2)-+ 三、解答题:16. 13-. 17.提示:先证四边形APCQ 是平行四边形,再在平行四边形的基础上,证明有两邻边相等.18.(1)a =80,b =10%;(2)圆心角度数为108°;(3)5600人. 19. (1)223y x x =--(2)5EF =.20.提示:求出AC ≈27.3海里,大于25海里,故无触礁危险. 21.(1)略;(2)2;提示:过F 点分别作AB ,AC 的垂线(3)n . 22.(1)新建1个地上停车位0.1万元,新建1个地下停车位0.4万元. (2)所有方案为 :新建地上停车位30个,新建地下停车位20个; 新建地上停车位31个,新建地下停车位19个; 新建地上停车位32个,新建地下停车位18个; 新建地上停车位33个,新建地下停车位17个; 所以 共四种建造方案.(3)选择的是:新建地上停车位32个,新建地下停车位18个. 23.(1)证明略;(2)242699y x x =-+;(3)27549OF =.一、选择题:1 2 3 4 5 6 ACDBDD二、填空题:7.2 8. 2(1)x x -+ 9. 1x ≠ 10.9 11. 20x x ≤->或12.6 13.60 14.74 15.(3,2)或(-3,-2)三、解答题:16.33. 17.(1)证明略;(2)在,理由略.18. (1)20,8,0.40,0.16;(2)57.6;(3)390人. 19.20.4m.20. (1)23,2k m =-=;(2)∠ACO =30°,74. 21. (1)甲50天,乙75天(2)甲单独完成需工程费用125000元. 22. (1) 223y x x =--+,C (-1,4);(2)证明略. 23. (1)AP =EF ,AP ⊥EF ;(2)成立,证明略;(3)成立.一、选择题:1 2 3 4 5 6 ACDBDC二、填空题:7. 2(4)x y -+ 8.乙 9.56° 10.4 11.100° 12.2 13.48 14. 20122 15.8cm三、解答题:16. 12-17. (1)22a ;(2)22a . 18.(1)4月份销售总额是75万元,图略;(2)12.8万元;(3)不同意,理由:4月份为:75×17%=12.75万元,5月份为12.8万元,故5月份比4月份增加了. 19.3.5cm 20. (1)112y x =,28y x=,3210y x =-+;(2)44x x <-<<或1. 21. (1)甲500株,乙300株;(2)320株;(3)甲320株乙180株时费用最低,最低费用为22080元. 22. (1)52;(2)2;(3)BD CE ≥1,能小于43,当573-<DC ≤1时,BD CE <43. 23. (1)A 11(0,)4,OC =1;(2)①4y x =-+,②19(13,)4P +, 215(133,)4P +-,39(13,)4P -, 415(133,)4P --.一、选择题:1 2 3 4 5 6 CAABBB二、填空题:7. 31+ 8. 3 9. 0.25 10. 22 11.2812. 23 13.14k <- 14. 200cm² 15. 36三、解答题:16.3212- 17.(1)略;(2)sin E =35. 18. 1(1)(1,3);C -- 2(2)(3,1);C 33(3)(2,2),(2,1).A B --图略.19. (1)一次函数的表达式为22y x =-,反比例函数的表达式为12y x=(2)存在点P ,使AM ⊥MP ,此时P (11,0) 20.高压电线杆CD 的高度为39.0m 21.(1)略;(2)要使水的的调运量最小,调运方案为:从A 地调往甲地1万吨水,调往乙地13万吨水;从B 地调往甲地14万吨水.水的最小调水量为1280万吨•千米. 22. 图②中AF +BF =2CE 仍成立,图③中结论不成立,AF -BF =2CE .证明略. 23.(1)1b =;(2)-4 ;(3)△M 1FN 1是直角三角形,证明略;(4)存在一条定直线m ,使m 与以MN 为直径的圆相切,解析式为1y =-.一、选择题:1 2 3 4 5 6 BDDBBC二、填空题:7. 0或6 8. (3,-4) 9. 231 10. 67.5° 11. > 12.1313. 22+ 14. 5.5 15. ()32n三、解答题:16. 1 17.(1)6y x=(2)103x x -<或<< 18.(1)证明略;(2)真,假19. (1)略 (2)中位数为80,众数为45 (3)空气质量是优良的天数为252天. 20.(1)DE =56m (2)塔吊的高CH 的长68.0m21.(1)①③④⑤ (2)弓形ACB 的面积为264(163)cm 3-π22. (1)证明略 (2)△ACM ∽△DPM ,理由略.(3)证明略. 23.(1)223y x x =-++ ,D (1,4);(2)当P (12,12-)时,PQ 最长,最长为174()()12(3)1,0,2,1P P一、选择题:1 2 3 4 5 6 ADDCCC二、填空题:7. 2 8. 20a a ≥≠且 9. 2 10. 4a < 11. 50°12. 1313.50° 14. 1 15. 2三、解答题:16. 1317. 518.(1)92.7%(2)612.7 (3)41.7 (4)2010年全市每10万人口中具有大学文化程度人数比2000年增加2777人.19. (1)楼梯AD 的长为62m (2)BD 的长为(3632-)m 20.(1)13y x =-+,B (1,2)(2)当0<x <1或x >2时,21y y >, 当1<x <2时,21y y <,当x =1或x =2时,21y y =. 21.(1)50元;(2)70元. 22. (1)203t =(2)线段PH 的长不发生改变,PH =20cm 23.(1)1,2,(1,4)a b C =-=--(2)存在点D 使得△ACD 是以AC 为斜边的直角三角形,此时点D 的坐标为(0,3)或(0,1) (3)1120(,)39P 或2755(,)416P -一、选择题:1 2 3 4 5 6 ABCBAC二、填空题:7. 3a + 8. 22x y ( 答案不唯一 ) 9. 70° 10. 32 11. 6或10或12 12. 24 13. 105 14. 24 15.499三、解答题:16. 13x -≤<,图略.17.证明略18.(1)图略 (2)4 (3)两车最后一次相遇时,距离A 地的路程为100km ,货车从A 地出发了8小时19. (1)2或6 (2)0或8 (3)提示:验证x =0或8时,以点P 、A 、D 、E 为顶点的四边形恰好为菱形20.(1)同意,理由略(2)∠α的大小为22.5° 21.(1)小正方形的边长为10米或35米(2)矩形广场四角的小正方形的边长为22.5米时,所铺矩形广场地面的总费最小,最少费用为199500米22. (1)略 (2)存在此位置使OE ∥CF ,此时()()121,31,3,或E E - 23.(1)243y x x =-+(2)443x y +=±(3)1234332,,(2,6)2,,(2,6)22P P P P ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭一、选择题:1 2 3 4 5 6 CDCABC二、填空题:7.140° 8.9.5 9.3 10.> 11.440 12.110° 13.2 14.-3 15.10100π三、解答题:16. (1)31- (2)243x -<<17. (1)略 (2)25、5、5 (3)直角 10 (4)1218. (1)100 (2)112 图略 (3)4号 理由略19. (1)第一种:中型图书角18个小型图书角12个,第二种:中型图书角19个小型图书角11个,.第三种:中型图书角20个小型图书角10个 (2)第一种方案费用最低,最低费用为22320元20.(1)AB =AE ,理由略 (2)3.6km 21.(1)2<x <3 (2)2.6或2.4 (3)1.522. (1)证明略 (2)①29,②证明略 23. (1)223y x x =+- (2)存在,1317117(,)22G --+,2(1,4)G -- (3)102一、选择题:1 2 3 4 5 6 ADBBDD二、填空题:7. 123,12x x =-=- 8. 3x = 9. 3222x x x ++ 10. 012且x x ≥≠11. 13 12.75°或15° 13. 1414. 3 15. 23三、解答题: 16. 117.证明略18.(1)a =6,b =0.1 (2) 24cm (3) 160165x ≤<(4)30% 19. (1)B (-5,-4),4833y x =+ (2)四边形CBED 是菱形20.(1)相等,理由略(2)A B 之间的距离为2000.00m21.(1)1209y x =;220500220;50019811000时,>时,x y x x y x <≤==+ (2)当0<x <1000时,选择甲经销商购买合算; 当x =1000时,选择甲、乙经销商一样合算; 当x >1000时,选择乙经销商购买合算.22.(1)BG =AE (2)结论依然成立,证明略 (3)13 23.(1) 243y x x =++(2)设顶点横坐标为m ,1145114544m ---+≤≤或m =4 (3)P (0,-3)一、选择题:1 2 3 4 5 6 DCBDCA二、填空题:7. 4 8. 2x < 9. 71.5010⨯ 10. 10 11.8336+π 12. -1 13. 13 14. 1 15. 16 三、解答题:16.(1)8 (2)1≤x <4 17.证明略 18.(1)图略 (2)250,750,725 (3) 该住宅区今年每户家庭平均每月的用水量是14米³19. (1)1250m (2)略20.(1)△P 1OA 1的面积变小,理由略(2)反比例函数的解析式为3y x=、()222,0A 21.(1)13010y x =-+ 200300x ≤≤ (2)第一年亏损,最少亏损400万元(3)第二年公司重新确定产品售价,也不能使两年共盈利达1790万元,理由略 22.(1) 2114y x =-+ (2)OE =GE(3)提示:易证OH =HJ ,四边形OHJK 是菱形 23.(1) 25(2) 射线QK 能把四边形CDEF 分成面积相等的两部分,此时578t s =(3)1218515412,t s t s == (4)125340343,t s t s ==一、选择题:1 2 3 4 5 6 ABDADD二、填空题:7. 61.610-⨯ 8. ()21x y - 9. 12x y =⎧⎨=⎩ 10. 53x =11. 4 12. 8 13. 20 14.70°或20° 15. 91三、解答题:16. 4 17.(1)∠B =25°(2)AD =618.(1)极差为2.2度 平均数为4.4度 (2)680度19. (1)甲组平均每天掘进4.8m ,乙组平均每天掘进4.2m (2)10 20.(1)DE =1.6m (2)AD :BE =5:3 21.(1)函数的零点为6±(2)证明略(3)112y x =-- 22.(1)①证明略 ②成立 (2)∠ACB =∠AFC +∠DAC (3) ∠AFC=2∠ACB-∠DAC 23.(1) (3,1)(2) ∠ABQ 为定值,等于90°(3)()()323在轴负半轴时,,0;在轴正半轴时,,0P x P P x P -一、选择题:1 2 3 4 5 6 CDBADC二、填空题:7.3 8. 11x -<≤ 9.-3 10. 23()x x y - 11.70° 12.矩形 13.4 14.2 15.300三、解答题:16.2+2417.(1)证明略;(2)等腰三角形,理由略.18.(1)80;(2)26.4,27,27;(3)396. 19. 1543cm - 20.33.9m21. (1) 215000,(0100)=106000,(100250)3500,(250)x x y x x x x x ≤≤⎧⎪-+<≤⎨⎪>⎩24000y x = (2)40022.(1)证明略 (2)相等,理由略 (3)111C FB A C B ACB V V V ,,23. (1)①证明略 ②相等,理由略 (2)存在 13+17-1-17E (,)22,23-17-1+17E (,)22,3E (2,3)一、选择题:1 2 3 4 5 6 ABDACA二、填空题:7.-6 8.-1.25 9. 1y x =+ 答案不唯一 10. 75° 11. ()1,3- 12.1118 13. 13 14. 1415. 23- 三、解答题:16. 53- 17.略18.(1)略 (2)180 (3)120 (4)抽到冰箱的概率51219. (1)PD =2 (2)PD =458- 20. 停车库限高2.4米21.(1)该小区到2011年底家庭轿车将达到125辆(2)方案一:建造室内车位20个,建造露天车位50个; 方案二:建造室内车位21个,建造露天车位45个. 22.(1)略 (2) ○1结论成立 ○2 结论不成立 (3)证明略 23.(1) 21462y x x =-+(2)证明略(3)存在,()12410,2(0,)2或P P --一、选择题:1 2 3 4 5 6 ABDBBC二、填空题: 7. 94 8. 20 9. 1210.6cm 或8cm 11. 112. 7.00 13. 4 14. 422m 15. 98三、解答题: 16. 2 17.(1)证明;(2)FG =3cm.18.(1) 0.20,24,60a b c ===(2)79.5~89.5(3)圆心角为126度(4)1350 19. (1)E (0,-2) (2)一次函数解析式为122y x =-,反比例函数解析式为6y x= (3)6x >20.(1)距离为2km (2)能搭乘这趟长途客车21. (1)年平均增长率为20% (2)当购买的材料累计在2万元到3万元时,在乙商店购买获得更大优惠;当购买材料累计为3万元时,在甲乙两商店获得优惠相同;当购买的材料累计超过3万元时,在甲商店购买获得更大优惠.22.(1) 2 (2)12 (3)nn23.(1) 2142y x x =-++ (2) T (1,1)(3)226,(02)343,(23)4t t t S t t t ⎧-+<≤⎪=⎨-++<≤⎪⎩ ,S 的最大值为253一、选择题:1 2 3 4 5 6 DBCBBC二、填空题:7. 7 8. 1 9. 38,2⎛⎫ ⎪⎝⎭10. 11 11. 48°12.13 13. 112-或 14. 4 15. 8 三、解答题:16. 原式=…..= 2x ,代入x =32得值=3 17.(1)略 (2)tan ∠EBC=2218.(1) 60,0.15a b ==(2)C (3)成绩优秀的人数约为6264名 19. (1)4k = (2)5y x =-+20.(1)AD 的长为75cm (2)车座点E 到车架档AB 的距离为63cm21. (1)平均每天要生产120套单人课桌椅 (2)生产桌子的员工人数为60人,生产椅子的员工人数为24人.22.(1) 相等(2)1EG EF n = (3)1EG EF mn= 23.(1) 21119424y x x =-++(2)102(3) ①24x ≤≤②()228724438814434,<t t x S t x ⎧≤≤-+-⎪⎪=⎨⎪≤-⎪⎩ S的最大值为472012年中考数学预测试卷(十六)答案一、选择题:1 2 3 4 5 6 ADBBDB二、填空题:7. ()21a b + 8. m 9. 43x y =⎧⎨=-⎩10. 0.3 11. 270° 12.5 13. ○1○3 14. 2180y x -= 15. 80-160π 三、解答题:16.(1) 原式=4+1-4=1 (2)原式= 8+9a 17.(1)证明略;(2)外国语中学植树279棵,实验中学植树555棵.18.(1)36(2)60, 14 (3)唐老师应安排27课时复习“数与代数”内容19. (1)反比例函数的解析式为 12y x =-,一次函数的解析式为223y x =-+(2)AOC S △=620.古塔BD 的高度为27.3m21. (1)tanC = 23(2)阴影部分的面积为39 94π- 22.(1)证明略;AF =5(2)43t 的值为 (3),a b 的数量关系式为12a b +=23.(1) 2333322y x x =--+(2) HN +NM +MK 和的最小值为8一、选择题:1 2 3 4 5 6 CADBBD二、填空题:7. 115.010-⨯ 8. 2442x x y y ==⎧⎧⎨⎨==⎩⎩或 9.4 10.80° 11.722cm 12.118° 13.5.20 14.30a15. 32+(1)三、解答题:16. +2217.(1)证明略 (2)23a18.(1)甲50分 乙80分 丙70分 (2)乙被录取 (3)丙 19. (1)第二个经过 (2)B (1,0)或B (3,0)(3)当m =0时,x ≤0时,y 随x 的增大而减小;当m =2时,x ≤1时,y 随x 的增大而减小 20.11m21.(1)(60-x ) (151582x +) (400060000)x + (2)512x ≤≤ 22. (1)13(4,)4(2)t =2是S 最大为10 23.(1)255263y x x =-- (2)①2S=5-84,t t + 01t ≤≤ ②存在 126-55(,)一、选择题:1 2 3 4 5 6 A CDDDA二、填空题:7.甲 8. -2<<1x 9.m +n10. 1230,2,2x x x ===- 11.110° 12.213. 15cm 14. -112n 15. 34三、解答题:16. 5+2517.(1)①15° ②2+3 (2)(23)423y x =-+++ 18.(1)a =20,b =15 (2)1.68 (3)符合实际,理由略 19. (1)=+1y x (2)-3<<0>2x x 或 (3)5 20.7.3m21.(1)乙 (2)甲,15台22. (1)证明略 (2)成立,证明略 (3)b a23. (1)2=+2y x x (2)1D (1,3),2D (-3,3),3D (-1,-1) (3)存在,1P (3,15),2P (13,79)。
讲义例1数学课上,李老师出示了如下框中的题目.(1)特殊情况,探索结论当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:AE DB(填“>”,“<”或“=”).(2)特例启发,解答题目解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).理由如下:如图2,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)(3)拓展结论,设计新题在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).例2如图1,在等边△ABC中,点D是边AC的中点,点P是线段DC上的动点(点P与点C不重合),连结BP.将△ABP绕点P按顺时针方向旋转α角(0°<α<180°),得到△A1B1P,连结AA1,射线AA1分别交射线PB、射线B1B于点E、F.(1) 如图1,当0°<α<60°时,在α角变化过程中,△BE F 与△AEP 始终存在 ▲ 关系(填“相似”或“全等”),并说明理由; (设∠ABP =β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF 与△AEP 全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;(3)如图3,当α=60°时,点E 、F 与点B 重合. 已知AB =4,设DP =x ,△A1BB 1的面积为S ,求S 关于x 的函数关系式.例3在正方形ABCD 的边AB 上任取一点E ,作EF ⊥AB 交BD 于点F ,取FD 的中点G ,连接EG 、CG ,如图(1),易证 EG=CG 且EG ⊥CG . (1)将△BEF 绕点B 逆时针旋转90°,如图(2),则线段EG 和CG 有怎样的数量关系和位置关系?请直接写出你的猜想.(2)将△BEF 绕点B 逆时针旋转180°,如图(3),则线段EG 和CG 又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.例4己知:正方形ABCD .(1)如图1,点E 、点F 分别在边AB 和AD 上,且AE=AF .此时,线段BE 、DF 的数量关系和位置关系分别是什么?请直接写出结论.图1图2图3111(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当a=90°时,连接BE、DF,猜想沟AE与AD满足什么数量关系时,直线DF垂直平分BE.请直接写出结论.(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论.例5如图1,在△ABC中,∠ABC=90°,AB=BC,BD为斜边AC上的中线,将△ABD绕点D顺时针旋转α(0°<α<180°),得到△EFD,点A的对应点为点E,点B的对应点为点F,连接BE、CF.(1)判断BE与CF的位置、数量关系,并说明理由;(2)若连接BF、CE,请直接写出在旋转过程中四边形BEFC能形成哪些特殊四边形;(3)如图2,将△ABC中AB=BC改成AB≠BC时,其他条件不变,直接写出α为多少度时(1)中的两个结论同时成立.例6在△ABC中,∠A=90°,点D在线段BC上,∠EDB=1∠C,BE⊥DE,垂足为E,2DE与AB相交于点F.(1)当AB =AC 时,(如图13),① ∠EBF =_______°; ② 探究线段BE 与FD 的数量关系,并加以证明; (2)当AB =kAC 时(如图14),求BEFD的值(用含k 的式子表示).例7已知,△ABC 为等边三角形,点D 为直线BC 上一动点(点D 不与B 、C 重合).以AD 为边作菱形ADEF ,使∠DAF=60°,连接CF . ⑴如图1,当点D 在边BC 上时,求证:∠ADB =∠AFC ;②请直接判断结论∠AFC =∠ACB +∠DAC 是否成立; ⑵如图2,当点D 在边BC 的延长线上时,其他条件不变,结论∠AFC =∠ACB +∠DAC 是否成立?请写出∠AFC 、∠ACB 、∠DAC 之间存在的数量关系,并写出证明过程; ⑶如图3,当点D 在边CB 的延长线上时,且点A 、F 分别在直线BC 的异侧,其他条件不变,请补全图形,并直接写出∠AFC 、∠ACB 、∠DAC 之间存在的等量关系.例8在Rt △ABC 中,AB =BC =5,∠ABC =90º.一块等腰直角三角板的直角顶点放在斜边AC 的中点O 处,将三角板绕点O 旋转,三角板的两直角边分别交AB 、BC或其延第24题图图1图2 图31图13图14ABCD EFF E DCBA长线于点E 、F ,图①、②是旋转三角板所得图形的两种情况.(1)三角板绕点O 旋转,△COF 能否成为等腰直角三角形?若能,指出所有情况(即给出△COF 是等腰直角三角形时BF 的长);若不能,请说明理由. (2)三角板绕点O 旋转,线段OE 和OF 之间有什么数量关系?用图①或图②加以证明. (3)若将三角板的直角顶点放在斜边上的点P 处(如图③),当AP ∶AC =1∶4时,PE 和PF 有怎样的数量关系?证明你发现的结论.例9已知正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC 于F ,连接DF ,G 为DF 中点,连接EG ,CG .(1)求证:EG =CG ;(2)将图①中△BEF 绕B 点逆时针旋转45º,如图②所示,取DF 中点G ,连接EG ,CG .问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF 绕B 点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)AAA BB B OOPCF C E FEC EF图①图②图③D第24题图①D E第24题图②D第24题图③。
专题十七探究型问题
1.在平面直角坐标系中,点A(n,1-n)一定不在( )
A.第一象限B.第二象限C.第三象限D.第四象限
2.在平面直角坐标系中,O是坐标原点,已知A(2,2),在x轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P的个数是( )
A.4 B.3 C.2 D.1
3.已知二次函数y=x2+p x+q,若2p+q=3,则这个函数的图象必定经过点( ) A.(-2,-1)B.(-2,7)C.(2,-1)D.(2,7)
4.如图①是一瓷砖的图案,用这种瓷砖铺设地面,图②铺成了一个2×2的近似正方形,其中完整菱形共有5个;铺成3×3的近似正方形图案③,其中完整菱形有13个;铺成4×4的近似正方形图案④,其中完整的菱形有25个;如此下去,可铺成一个n×n的近似正方形图案,当得到完整的菱形共有181个时,n的值为( )
A.7 B.8 C.9 D.10
5.如图,在△ABC中,AC=BC>AB,P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB、△PBC、△PAC均是等腰三角形,则满足上述条件的所有点P的个数为( )
A.3 B.4 C.6 D.7
6.如图,物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B……的顺序循环运动,则第2012步到达点_______处.
7.在四边形ABCD中,顺次连接四边中点E、F、G、H,构成一个新的四边形,请你对四边形ABCD添加一个条件,使四边形EFGH成为一个长方形.这个条件是_______.
8.已知点P(x,y)位于第二象限.并且y≤x+4,x、y为整数,符合上述条件的点P有_______个,试写出一个点的坐标为_______.
9.平移抛物线y=x2+2x-8.能使它经过原点吗?若能,写出平移后抛物线的一个解析式:______________.10.如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.问是否存在点P,使得QP=QO.若存在,则满足上述条件的点有几个?并求出相应的∠OCP的大小;若不存在,请简要说明理由.
11.如图,把正方形ABCD绕点A按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H.试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.
12.已知一元二次方程x 2-4x +k =0有两个不相等的实数根.
(1)求k 的取值范围;
(2)如果k 是符合条件的最大整数,那么是否存在这样的实数m ,使一元二次方程x 2-4x +k =0与x 2+m x -1=0有一个相同的根.
13.如图是一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A 与点C 重合,再展开,折痕EF 交
AD 边于点E ,交BC 边于点F ,分别连接AF 和CE .
(1)求证:四边形AFCE 是菱形;
(2)若AE =10 cm ,△ABF 的面积为24 cm 2,求△ABF 的周长;
(3)在线段AC 上是否存在一点P ,使得2AE 2=AC ·AP ?若存在,请说明点P 的位置,并予以证明;若不存在,请说明理由.
14.如图,直线y =12x +1与y 轴交于A ,与x 轴交于D ,抛物线y =12
x 2+bx +c 与直线交于A 、E 两点,与x 轴交于B 、C 两点,且点B 的坐标为(1,0).
(1)求抛物线的解析式;
(2)动点P 在x 轴上移动,当△PAE 是直角三角形时,求点P 的坐标;
(3)在抛物线的对称轴上找一点M ,使AM MC 的值最大,求出点M 的坐标.
参考答案
1.C 2.A 3.D 4.D 5.C 6.A 7.答案不唯一,如四边形ABCD 是菱形 8.6 (-1,3)、(-1,2)、(-1,1)、(-2,1)、(-2,2)、(-3,1)六个中任意写出一个即可 9.答案不唯一,如y =x 2+2x 10.存在点P 有3个:当点P 在线段AO 上时,∠OCP =40°;当点P 在OB 的延长线上时,∠OCP =20°;当点P 在OA 的延长线上时,∠OCP =100° 11.HG =HB 12.(1)k<4
(2)0或-83 13.(1)略
(2)24 cm (3)存在,过点E 作AD 的垂线交AC 于点P ,则点P 即为所求.
14.(1)y =
12x 2-32x +1 (2)(12,0)或(1,0)或(3,0)或(112
,0)(3)M (32,-12)。