基于机器人避障问题的数学模型

机器人避障问题的最短路径分析摘要本论文研究了机器人避障最短路径和最短时间路径的问题。

主要讨论了在一个区域中存在12个障碍物，由出发点到达目标点以及由出发点经过若干目标点最终到达出发点的两种情况。

采用传统的避障方法——切线图法。

建立了线圆结构，这样任何路径，我们都可以将路径划分为若干个这种线圆结构来求解。

对于途中经过节点再到达目标点的状况，我们采用在转弯点和节点都采用最小转弯半径，以节点为切点的形式。

然后建立了最优化模型，利用MATLAB软件对方案进行求解。

问题一：把路径分解成若干个线圆结构来求解，然后把可能的最短路径采用穷举法列举出来，最终得出最短路径：AO→最短路径为：471.0O→最短路径为：869.5BO→最短路径为：1093.3C对于O→→→我们将A、B、C看作切点，同样采用线圆结构CBAO→计算。

O→→→→最短路径为：2827.1AOCB问题二：考虑避障路径和转弯速度，我们建立时间与路径之间的模型，用MATLAB软件求出最优解。

当转弯半径为11.5的时候，可以得出最短时间为：T=94.3关键词最优化模型避障路径线圆结构切线图法一、问题重述本文是求一个机器人在800×800的平面场景图中避开障碍物，建立从原点O(0, 0)点处出发达到终点的最短路径和最短时间路径的模型。

即求：1、O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径。

2、O →A 的最短时间路径。

机器人在行走时的要求是：1、它只能在该平面场景范围内活动2、图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物（障碍物的分布如图1）3、障碍物外指定一点为机器人要到达的目标点（要求目标点与障碍物的距离至少超过10个单位）。

4、规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

冗余机械臂避障matlab机械臂是一种能够模拟人类手臂运动的机器人，它可以完成各种复杂的工作任务。

在实际应用中，机械臂需要具备避障能力，以保证其在复杂环境中的安全运行。

冗余机械臂是一种具有多余自由度的机械臂，它可以通过调整自身姿态来避开障碍物，从而实现避障功能。

本文将介绍如何使用matlab实现冗余机械臂的避障控制。

我们需要建立机械臂的运动学模型。

运动学模型是描述机械臂运动规律的数学模型，它可以通过机械臂的关节角度计算出机械臂的末端位置和姿态。

在matlab中，我们可以使用Robotics System Toolbox工具箱来建立机械臂的运动学模型。

具体步骤如下：1. 定义机械臂的DH参数，包括关节长度、关节角度、关节偏移和连杆旋转角度。

2. 使用robotics.RigidBodyTree函数创建机械臂的刚体树模型。

3. 使用robotics.RigidBody函数创建机械臂的刚体模型，并将其添加到刚体树中。

4. 使用robotics.Joint函数创建机械臂的关节模型，并将其添加到刚体树中。

5. 使用robotics.RigidBodyJoint函数将关节模型连接到刚体模型上。

6. 使用robotics.RigidBodyTree函数计算机械臂的运动学模型。

建立好机械臂的运动学模型后，我们需要设计避障控制算法。

在冗余机械臂中，我们可以通过调整机械臂的姿态来避开障碍物。

具体步骤如下：1. 使用机械臂的运动学模型计算机械臂的末端位置和姿态。

2. 使用传感器获取障碍物的位置和大小。

3. 根据障碍物的位置和大小，计算机械臂需要调整的姿态。

4. 使用机械臂的运动学模型计算机械臂的关节角度。

5. 控制机械臂运动到目标姿态。

在matlab中，我们可以使用Robotics System Toolbox工具箱中的函数来实现避障控制算法。

具体步骤如下：1. 使用robotics.OccupancyGrid函数创建占据栅格地图。

机器人避障冲突检查模型机器人避障冲突检查模型[摘要]：分析和研究了机器人的避障最短路径问题。

通过冲突检查模型得到机器人在限定区域中行走的可能路径，对其优化得到最优路径。

[关键词]：最短路径冲突检查线圆结构解析几何最优化模型1引言机器人在800×800场景图的原点O（0，0）处，有12个不同形状的障碍物，机器人不能碰撞，障碍物的描述如图（左）所示。

机器人规定路径由直线段和圆弧组成，直线最大速度和转弯最大速度为v0=5单位/每秒、，其中ρ是半径。

建立避障最短路径的数学模型为：计算O→A、O→B、O→C的最短路径。

2模型假设假设机器人用抽象点来说明；假设障碍物拐角处的半径为10单位的圆弧；假设行走以最大速度行驶且不出现故障；假设速度突变时没有缓冲。

3模型准备3.1、模型准备一：冲突检查模型冲突即路径距离障碍物的最短距离。

模型如下：Step1：检查所有线段是否满足要求，否返回false；Step2：检查弧线是否满足要求，否返回false；Step3：若step1和step2满足，返回true。

该路径即有效路径。

3.1.1线段检查（1）线段与多边形检查：Step1：查看线段两端点到多边形各边的距离是否满足要求，否返回false；Step2：查看多边形各顶点到线段的距离是否满足要求，否返回false；Step3：若step1和step2满足，返回true。

（2）线段与圆检查：Step1：从圆心向线段做垂线，垂足落于线段，看垂线与半径差是否满足要求，否返回false，落于线段外，计算近足点到圆心距离与半径差是否满足要求，否返回false；满足返回true。

3.1.2弧线检查（1）弧线和多边形检查：Step1：查看弧线端点和多边形各顶端点是否满足要求，否返回false；Step2：从多边形各点向圆心做线段，若该线段和弧线没交点，忽略，否则若该线段长度-弧半径不满足要求，返回false；Step3：从弧心向多边形各边做垂线，若垂线和弧线相交且落在边上，查看垂线段长度-弧半径是否满足要求，否返回false，否则忽略。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）：我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：参赛队员(打印并签名) ：1.2.3.指导教师或指导教师组负责人(打印并签名)：日期：年月日编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：赛区评阅记录（可供赛区评阅时使用）：评阅人评分备注全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：机器人避障问题摘要针对题中机器人避障最短路径问题，文章使用简化后建立的最短路径的数学模型来解决此类问题。

对于问题1，我们matlab中自带函数graphshortestpath函数求解最短路径的数学模型。

其主要思想是：首先先证明出两点之间的最短路径是由两条线段和以中间点为圆心的圆的一段圆弧组成，然后证明圆弧的半径为定值10。

然后对模型简化使模型化为标准的最短路径模型，最后用graphshortestpath函数对模型求解。

针对问题2，我们建立了优化模型。

在问题1的基础上，我们对两种行走方案进行分析，根据转弯弧的半径变化对速度的影响我们锁定到一条路径，然后利用lingo对优化模型进行求解。

关键词：graphshortestpath函数、最短路径、避障问题1、问题重述已知：在下图中原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

龙源期刊网
机器人避障问题模型研究
作者：侯学慧
来源：《数字通信》2013年第06期
摘要：研究机器人避障最短路径问题，主要研究1个区域存在12个障碍物，从点O出发避开障碍物分别到达目的地点A，B，C的最短路径。

限定区域内的最短路径由2部分组成的：一部分是平面上的自然最短路径（即直线段），另一部分是限定区域的部分边界（圆弧部分），这2部分是相切且互相连接的。

可以认为最短路径一定是由线段和圆弧构成，因此建立线圆结构。

对于从出发点到目的地的路径采取2种方案：第1种方案，在拐点和节点都采用最小转弯半径的形式；第2种方案，适当扩大拐点处的转弯半径，使得机器人能够沿直线通过途中的目标点。

然后建立了最优化模型对比，最后对2种方案分别进行求解。

因为区域面积很大而限定圆半径至少为10，通过近似比较估算得出较优的最短路线方案。

结论：无论路径多么
复杂，都可以将路径划分为若干个线圆结构来求解，利用数学几何运算、直线关系以及Mathematics工具，来分析在问题中出现的3种具体的线圆结构情形，从而得到最短路径。

关键词：
线圆结构；最短路径；最优化模型；解析几何
中图分类号：TP242.6文献标识码：A文章编号：10053824（2013）06001707。

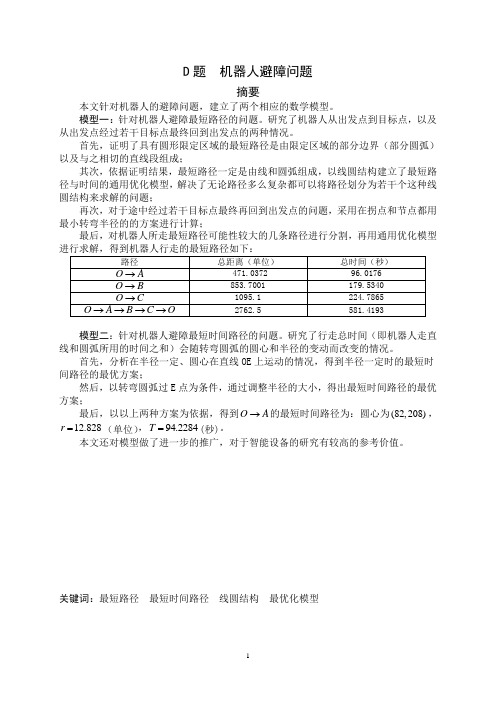
D题机器人避障问题摘要本文针对机器人的避障问题，建立了两个相应的数学模型。

模型一：针对机器人避障最短路径的问题。

研究了机器人从出发点到目标点，以及从出发点经过若干目标点最终回到出发点的两种情况。

首先，证明了具有圆形限定区域的最短路径是由限定区域的部分边界（部分圆弧）以及与之相切的直线段组成；其次，依据证明结果，最短路径一定是由线和圆弧组成，以线圆结构建立了最短路径与时间的通用优化模型，解决了无论路径多么复杂都可以将路径划分为若干个这种线圆结构来求解的问题；再次，对于途中经过若干目标点最终再回到出发点的问题，采用在拐点和节点都用最小转弯半径的的方案进行计算；最后，对机器人所走最短路径可能性较大的几条路径进行分割，再用通用优化模型进行求解，得到机器人行走的最短路径如下：路径总距离（单位）总时间（秒）→ 471.0372 96.0176O A→853.7001 179.5340O B→1095.1 224.7865O C→→→→2762.5 581.4193 O A B C O模型二：针对机器人避障最短时间路径的问题。

研究了行走总时间（即机器人走直线和圆弧所用的时间之和）会随转弯圆弧的圆心和半径的变动而改变的情况。

首先，分析在半径一定、圆心在直线OE上运动的情况，得到半径一定时的最短时间路径的最优方案；然后，以转弯圆弧过E点为条件，通过调整半径的大小，得出最短时间路径的最优方案；最后，以以上两种方案为依据，得到O A→的最短时间路径为：圆心为(82,208)，T=(秒)。

12.828r=（单位），94.2284本文还对模型做了进一步的推广，对于智能设备的研究有较高的参考价值。

关键词：最短路径最短时间路径线圆结构最优化模型1问题重述1.1 背景资料（1）图1（见附录B ）在原点O(0,0)处有一个机器人，它只能在一个800×800的平面场景范围内活动。

而图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，其障碍物的数学描述如表（见附录A ）。

机器人避障问题摘要本文研究了在已知区域障碍物分布的情况下，机器人从起点到目标点避障最短路径或最短时间路径的问题，路径必须是由圆弧和与之相切的直线段组成的线圆结构。

一开始先对模型预处理，将所有障碍物外扩10个单位长度，划定危险区域，得到障碍扩展图。

针对问题一，经过分析论证，无论起点到目标点间危险区域有多少，最短路径都应该是紧绕危险点的切线圆路径，且可根据需依次绕过的危险点情况划分为N条子路径（见图5.1.2）求解，圆弧段取允许最小转弯半径。

模型求解分两步走：一、将实际障碍图转化为加权可视图，利用Dijstra算法搜索出在可视图下的最短路径，主要是找到必须绕过的若干危险点。

二、根据障碍扩展图将可视图中的路径修正为实际情况下的切线圆路径，求出最终结果。

在求解过程中运用MATLAB数学软件给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心连接两条切线，使机器人总的行走时间最短。

而圆弧可以有圆心坐标和半径唯一确定。

由此构建机器人行走总时间的目标函数，将机器人不与障碍物碰撞作为约束条件，将该问题转变为一个非线性规划问题，借助matlab求得最优解为:T=94.3314s。

关键词：路径规划最优化模型切线圆路径 Dijstra算法非线性规划matlab求解一、问题重述图1是一个800×800的平面场景图，在原点O(0,0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为50=v 个单位/秒。

路径规划算法在机器人避障中的应用研究机器人避障是机器人领域中的核心问题之一，而路径规划算法作为机器人避障的一种关键技术手段，其应用已经得到广泛关注和研究。

本文探讨路径规划算法在机器人避障中的应用研究。

一、机器人避障简述机器人避障是机器人行走中的一项重要任务。

在执行任务过程中，机器人可能会遇到各种障碍物，如墙壁、家具、人等。

为了保证机器人的安全和任务的成功完成，机器人必须避免障碍物并找到合适的路径。

因此，如何规划机器人的路径成为研究机器人避障问题的核心。

二、路径规划算法简述路径规划算法是一种计算机程序，它可根据机器人当前位置、目标位置和环境情况，计算出机器人行走的最优路径。

路径规划算法应用广泛，可用于无人机、无人驾驶车、机器人等领域。

常见的路径规划算法包括遗传算法、蚁群算法、模拟退火算法、动态规划算法、A*算法等。

这些算法各有特点，具体适用于不同的机器人或环境。

三、路径规划算法在机器人避障中的应用研究三点式机器人是常见的机器人类型之一。

三点式机器人由三个轮子组成，每个轮子都可以独立地旋转。

这种机器人在狭小的空间中行走时，会遇到各种障碍物。

路径规划算法可用于该机器人的避障。

研究表明，A*算法可用于三点式机器人的路径规划和避障。

A*算法是贪心算法的一种，它的特点是能够快速找到最优路径并能够处理多个障碍物。

A*算法基于启发式评估函数（H），以最小化总代价（F）。

A*算法的具体实现步骤为：首先，将起点加入OPEN集。

然后，根据启发式评估函数，选出OPEN集中最优的点，将其加入CLOSED集。

接着，将与当前点相邻的点加入OPEN集。

最后，重复上述步骤，直到终点被加入CLOSED集。

在使用A*算法进行路径规划时，需要注意以下几个问题。

首先，需要选择合适的启发式评估函数。

启发式评估函数应该满足可行性和一致性。

其次，需要合理设置OPEN集和CLOSED集的参数。

最后，需要根据实际场景选择适当的路径决策方案。

四、结论路径规划算法是机器人避障中的一种关键技术手段。

麦克纳姆轮运动学模型麦克纳姆轮运动学模型是一种用于描述麦克纳姆轮机器人运动规律的数学模型。

麦克纳姆轮机器人是一种特殊的机器人，它使用三个或四个麦克纳姆轮进行运动。

这种轮子设计使得机器人能够在水平面上做任意方向的移动，具有极高的机动性和灵活性。

麦克纳姆轮运动学模型的基本原理是通过控制轮子的旋转速度和方向，来控制机器人的移动方向和速度。

在麦克纳姆轮机器人中，每个麦克纳姆轮都可以独立地转动，并且轮子之间的布局形成一个正方形或一个平行四边形。

根据轮子的转动速度和方向的变化，机器人可以向前、向后、向左、向右或斜向移动。

在麦克纳姆轮运动学模型中，使用了一些重要的参数来描述机器人的运动规律。

其中，线速度是机器人在水平面上的移动速度，角速度是机器人绕垂直轴旋转的速度。

通过控制轮子的转动速度和方向，可以精确地控制机器人的线速度和角速度。

麦克纳姆轮运动学模型中的另一个重要参数是机器人的运动方向。

机器人的运动方向可以用一个角度来表示，这个角度被称为偏航角。

偏航角的变化会影响机器人的运动方向，通过调整偏航角，可以使机器人向不同的方向移动。

麦克纳姆轮运动学模型还可以用来计算机器人的位姿，即机器人在水平面上的位置和朝向。

位姿可以用坐标系来表示，通常使用笛卡尔坐标系或极坐标系。

通过计算机器人的位姿，可以确定机器人的位置和朝向，从而精确地控制机器人的运动。

在实际应用中，麦克纳姆轮运动学模型被广泛应用于机器人的运动控制和路径规划。

通过合理地控制轮子的转动速度和方向，可以使机器人实现复杂的运动任务，如直线行走、曲线行走、圆周运动等。

同时，麦克纳姆轮运动学模型也为机器人的自主导航和避障提供了重要的理论基础。

麦克纳姆轮运动学模型是一种用于描述麦克纳姆轮机器人运动规律的数学模型。

通过控制轮子的转动速度和方向，可以精确地控制机器人的移动方向和速度。

麦克纳姆轮运动学模型在机器人的运动控制、路径规划和自主导航等方面具有重要的应用价值。

teb避障算法
TEB避障算法是一种基于时间轴的动态窗口方法来规划机器人的运动路径。

它的全称是Time-Elastic-Band避障算法，是一种基于模型预测控制（MPC）的路径规划方法。

TEB算法的核心思想是将机器人的运动路径建模为一条带状区域，在这个带状区域中，机器人可以自由移动而不会与障碍物相撞。

TEB算法通过调整带状区域的宽度和位置来实现路径规划。

在TEB算法中，机器人的运动被建模为一个无人驾驶车辆模型，该模型包括位置、速度和加速度等状态变量。

算法通过计算机模型来预测机器人的运动轨迹，然后将预测轨迹与已知的障碍物信息进行比较，以确保机器人的路径不会与障碍物相交。

通过不断地调整带状区域的宽度和位置，算法可以生成一条安全的、无碰撞的机器人运动路径。

TEB算法具有很高的实时性和适应性，能够在复杂的环境中进行高效的路径规划。

它被广泛应用于无人驾驶车辆、机器人和自主运动设备等领域，成为了一种重要的路径规划方法。