朗肯土压力范例

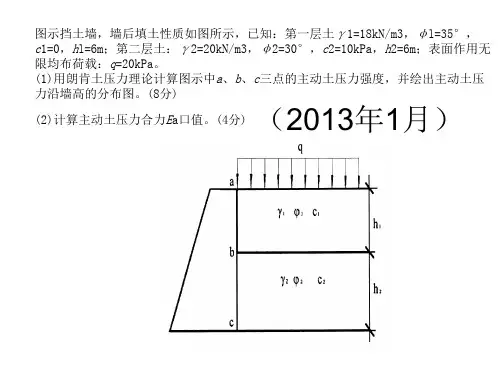
典型范例【例7-1】如图所示一高5m的挡土墙，墙后填土由两层组成，填土表面有20kPa的均布荷载，计算作用在墙上的总的主动土压力和作用点的位置。

【解题思路】本题是典型的利用朗肯土压力理论计算土压力的实际应用，在填土表面有均布荷载作用，并且墙背后填土分层，在计算土压力时，应根据每一层的土压力系数分别进行计算。

由于上下两层都是粘土层，注意要判断是否存在负侧压力区，若存在负侧压力区，在计算土压力强度中应该不予考虑。

总的土压力合力是土压力强度分布图形的面积，相应作用点在强度分布图形的形心处。

【解答】（1）主动土压力系数计算第一层填土主动土压力系数为第二层填土主动土压力系数为（2）粘性土层中负侧压力区的判断对于粘性土，需判别填土中是否存在拉应力区。

计算第一层填土中的临界深度说明在第一层中存在负侧压力区，深度为地表范围内0.50m。

第二层填土中的临界深度说明在第二层土中不存在负侧压力区。

（3）墙后各点主动土压力强度计算B点的主动土压力为F点交界面以上的主动土压力为F点交界面以下的主动土压力为A点的主动土压力为（4）主动土压力合力计算第一层总的主动土压力为第二层总的主动土压力为整个墙上总的主动土压力为（5）合力作用点计算土压力合力作用点在分布图形的形心处。

合力Ea的作用点在A点以上的距离【例7-2】某折线型挡土墙如图所示，墙背为砂性填土，填土的内摩擦角ϕ＝400，重度γ＝19kN/m3，与墙背的外摩擦角δ＝ϕ/2＝200，墙顶填土面倾角β＝29°45’（1∶1.75），上段墙背倾角α1＝18°26’（3∶1）。

下段墙背倾角为α2＝－14°02’（1∶0.25）。

试用延长墙背法计算该挡土墙背的土压力分布及其合力。

【解题思路】本题是库仑土压力理论在实际工程中具体应用的典型算例，墙背后填土不水平，墙背不光滑同时墙背倾斜而且分成两段，这种挡土墙的实用计算方法如下：将折线型挡土墙AB（上）段视为一俯斜型挡土墙，计算墙背土压力Ea1，延长BC（下）段墙背与填土面相交，得交点D，并以虚线相连，将DC视为仰斜型挡土墙墙背计算土压力Ea2（但不计虚线部分土压力），计算折线型挡土墙墙背土压力合力Ea（为Ea1和Ea2的矢量和）及其作用方向与水平面的夹角（Ea 的作用点为Ea1和Ea2作用线的交点，可通过几何关系求得）【解答】（1） AB墙段上的土压力计算AB（上）段墙背土压力分布可由库仑土压力理论求得主动土压力系数土压力分布情况A点：B点：合力大小：合力作用方向与水平面的夹角为：（2） BC墙段上的土压力计算BC（下）段墙背，计算时将其延长至与填土面相交，其交点可由填土面直线方程及BC段墙背直线方程求得，若设A点为坐标原点，则B点坐标为（0.667，－2）。

朗肯土压力计算公式朗肯土压力计算公式是土力学中一个非常重要的概念，对于咱们搞工程和研究地质的人来说，那可真是太关键啦！咱先来说说朗肯土压力计算的基本原理。

它主要是基于土的极限平衡状态来推导的。

想象一下，土地就像是一个有脾气的大家伙，当它受到外界的压力或者拉力时，就会产生不同的反应。

而朗肯土压力计算公式就是要搞清楚这个大家伙在啥时候会“发脾气”，发多大的脾气。

朗肯土压力计算公式分为主动土压力和被动土压力两种情况。

主动土压力呢，就是土自己主动往外推，想要“松口气”；被动土压力则是土被外界强行挤压，不得不“憋着气”。

我给您举个例子哈。

之前我参与过一个小型的建筑项目，在设计挡土墙的时候，就得用到朗肯土压力计算公式。

那时候，我们先对工地的土质进行了详细的勘察，了解了土的类型、密度、内摩擦角这些关键参数。

然后，把这些数据一股脑儿地放进朗肯土压力计算公式里，算出主动土压力和被动土压力的值。

这可不像做算术题那么简单，每一个数据都得小心谨慎，稍微有点差错，那后果可不堪设想。

在计算的过程中，我和同事们那是紧张又兴奋。

紧张的是万一算错了，工程质量可就没法保证；兴奋的是，如果算对了，就能设计出既安全又经济的挡土墙。

记得有一次，我们为了一个数据的准确性，反复测量了好几遍，还专门请教了经验丰富的专家。

回到朗肯土压力计算公式本身，主动土压力的计算公式是 Ea = 1/2γH²Ka ，这里面的γ是土的重度，H 是挡土墙的高度，Ka 是主动土压力系数。

而被动土压力的计算公式是Ep = 1/2 γH²Kp ，Kp 就是被动土压力系数。

要准确地运用这些公式，就得先搞清楚土的物理性质。

比如说土的重度，这可不是随便估摸的，得通过实验或者实际测量来确定。

还有内摩擦角，它反映了土颗粒之间的摩擦力大小，对土压力的计算影响可大了。

在实际工程中，朗肯土压力计算公式的应用非常广泛。

不仅仅是挡土墙的设计，像基坑支护、边坡稳定分析等等，都离不开它。

5.3朗肯土压力理论朗肯土压力理论是根据半空间的应力状态和土的极限平衡条件而得出的土压力计算方法。

图5-5(a)表示一表面为水平面的半空间，即土体向下和沿水平方向都伸展至无穷，在离地表z 处取一单位微体M ，当整个土体都处于静止状态时，各点都处于弹性平衡状态。

设土的重度为γ，显然M 单元水平截面上的法向应力等于该处土的自重应力，即：而竖直截面上的法向应力为：由于土体内每一竖直面都是对称面，因此竖直截面和水平截面上的剪应力都等于零，因而相应截面上的法向应力z σ和x σ都是主应力，此时的应力状态用莫尔圆表示为如图5-5(b)所示的圆Ⅰ，由于该点处于弹性平衡状态，故莫尔圆没有和抗剪强度包线相切。

图5-5半空间的极限平衡状态设想由于某种原因将使整个土体在水平方向均匀地伸展或压缩，使土体由弹性平衡状态转为塑性平衡状态。

如果土体在水平方向伸展，则M 单元在水平截面上的法向应力z σ不变而竖直截面上的法向应力却逐渐减少，直至满足极限平衡条件为止(称为主动朗肯状态)，此时z σ达最低限值a σ，因此，a σ是小主应力，而z σ圆平方向压缩，那末x σ不断增加而z σ)时x σ达最大限值p σ，这时，p σ为⎪⎭⎫ ⎝⎛-︒245ϕ由土的强度理论可知，当土体中某点处于极限平衡状态时，大主应力1σ和小主应力3σ之间应满足以下关系式：粘性土：245tan(2)245(tan 231ϕϕσσ+︒++︒=c 或245tan(2245(tan 213ϕϕσσ-︒--︒=c 无粘性土：)245(tan 231ϕσσ+︒=或245(tan 213ϕσσ-︒= 对于如图5-6所示的挡土墙，设墙背光滑（为了满足剪应力为零的边界应力条件）、直立、填土面水平。

当挡土墙偏离土体时，由于墙后土体中离地表为任意深度z 处的竖向应力z z γσ不变，亦即大主应力不变，而水平应力x σ却逐渐减少直至产生主动朗肯状态，此时，z σ是小主应力a σ，也就是主动土压力强度，由极限平衡条件得： 无粘性土：)245(tan 2ϕγσ-︒=z a （5-3） 或 a a zk γσ= （5-4） 粘性土：)245tan(2)245(tan 2ϕϕγσ-︒--︒=c z a （5-5） 或a a a K c zK 2-=γσ （5-6）上列各式中a K —主动土压力系数，)245(tan 2ϕ-︒=a K ；γ —墙后填土的重度，kN/m3，地下水位以下用有效重度；c —填土的粘聚力，kPa ； ϕ —填土的内摩擦角，度；z —所计算的点离填土面的深度，m 。

朗肯被动土压力计算公式朗肯被动土压力计算公式，这可是土力学里一个挺重要的知识点呢！咱先来说说啥是朗肯被动土压力。

想象一下，有一堵墙，墙后面的土使劲儿挤压着这堵墙，那这股挤压力就是土压力啦。

而朗肯被动土压力，就是在特定条件下计算这股挤压力的一个公式。

朗肯被动土压力计算公式是：Ep = 1/2γH^2Kp 。

这里面，γ是土的重度，H 是墙的高度，Kp 是朗肯被动土压力系数。

给您举个例子吧，我之前在一个建筑工地上，遇到过这么个事儿。

那时候正在挖一个大坑，准备建地下室。

周围得用挡土墙来挡着土，不然土就哗啦哗啦全塌下来了。

工程师们就在那算这个朗肯被动土压力，看看这挡土墙得建多厚多结实才能顶住土的压力。

我凑过去看他们的计算过程，只见他们先测量了土的重度，然后量了坑的深度，也就是挡土墙的高度。

接着就开始算那个朗肯被动土压力系数，这个系数的计算可复杂了，得考虑土的内摩擦角啥的。

他们拿着计算器噼里啪啦一通按，算出结果后，就开始讨论这挡土墙得用啥材料，多厚的钢筋，多高强度的混凝土。

我在旁边听着，虽然不太懂那些专业术语，但也能感觉到这个计算的重要性。

要是算错了，这挡土墙不结实，万一土塌了，那可就是大事故啦！回到这个朗肯被动土压力计算公式，要准确运用它，就得搞清楚每个参数的含义和测量方法。

土的重度，得通过实验或者经验数据来确定。

墙的高度，那得量得准准的。

而朗肯被动土压力系数，就得根据土的性质来计算。

在实际工程中，这个公式的应用可广泛了。

比如说，修大坝的时候，得算一算水和土对大坝侧面的压力，这时候朗肯被动土压力计算公式就能派上用场。

还有在地下停车场的建设中，要保证周围的土不会把墙挤垮，也得靠它来帮忙计算。

总之，朗肯被动土压力计算公式虽然看起来有点复杂，但在土力学和土木工程领域里，那可是非常重要的工具。

掌握好了它，就能让我们的建筑更安全、更牢固！希望我这大白话能让您对朗肯被动土压力计算公式有个初步的了解，要是您以后在相关领域工作或者学习，可一定要把它学透哦！。

第三节 朗肯土压力理论（1857年提出）一、基本原理朗肯研究自重应力作用下，半无限土体内各点的应力从弹性平衡状态发展为极限平很状态的条件，提出计算挡土墙土压力的理论。

（一）假设条件1．挡土墙背垂直、光滑； 2．墙后填土表面水平并无限延伸；3．挡墙背面光滑即不考虑墙与土之间的摩擦力。

（二）分析方法1．当土体静止不动时，深度z 处土单元体的应力为rz z =σ，rz k x 0=σ；2．当代表土墙墙背的竖直光滑面mn 面向外平移时，右侧土体的水平应力h σ逐渐减小，而z σ保持不变。

当mm 位移至''n m 时，应力园与土体的抗剪强度包线相交——土体达到主动极限平衡状态。

此时，作用在墙上的土压力x σ达到最小值，即为主动土压力，a p ； 3．当代表土墙墙背的竖直光滑面mn 面在外力作用下向填土方向移动，挤压土时，x σ将逐渐增大，直至剪应力增加到土的抗剪强度时，应力园又与强度包线相切，达到被动极限平衡状态。

此时作用在''''n m 面上的土压力达到最大值，即为被动土压力，p p 。

二、朗肯主动土压力当墙后填土达主动极限平衡状态时，作用于任意z 处土单元上的1σσ==rz z ，3σσ==a x p ，即x z σσ>。

1、无粘性土将rz r ==σσ1，a p =3σ代入无粘性土极限平衡条件：a rzK tg =-=)245(213ϕσσο式中：)245(2ϕ-=οtg K a ——朗肯主动土压力系数。

a p 的作用方向垂直于墙背，沿墙高呈三角形分布，当墙高为h （z=h ），则作用于单位墙高度上的总土压力Ka rh E a 22=，a E 垂直于墙背，作用点在距墙底3h处。

2、粘性土将a z p rz ===31,σσσ，代入粘性土极限平衡条件：)245(2)245(213ϕϕσσ-•--=οοtg c tg 得Kaa a crzK tg c tg p 2)245(2)245(21-=-•--=ϕϕσοο说明：粘性土得主动土压力由两部分组成，第一项：a rzK 为土重产生的，是正值，随深度呈三角形分布；第二项为粘结力c 引起的土压力a K c 2，是负值，起减少土压力的作用，其值是常量。

2.1 土压力理论土压力是指挡土墙后的填土因自重或外荷载作用对墙背产生的侧向压力。

土压力的计算是个比较复杂的问题。

它随挡土墙可能位移的方向分为主动土压力、被动土压力和静止土压力。

土压力的大小还与墙后填土的性质、墙背倾斜方向等因素有关。

2.1.1 库伦土压力[22]1773年著名的法国学者库伦(C.A.Coulomb)提出了一种计算土压力的理论。

这种理论是根据墙后所形成的滑动楔体静力平衡条件建立起来的，这种理论具有计算简单，适用范围广泛，且计算结果接近实际等优点，至今仍然被广泛使用于工程实践之中。

其基本假定如下:(l)墙后填土为理想散粒体(无粘聚力);(2)墙后填土产生主动土压力或被动土压力时，填土形成滑动楔体，且滑动面为通过墙踵的平面;(3)滑动楔体为刚体，不考虑滑动楔体内部的应力和变形条件 1、主动土压力公式：212a a E H K γ=22cos ()sin()sin(cos cos()1-cos()cos()a K ϕαϕδϕβαδααδαβ-=⎡⎤+⋅-⋅+⋅⎢⎥+⋅-⎣⎦式中：α—为墙背与铅直线夹角，逆时针为正值； K a —库仑主动土压力系数； β—填土表面与水平面所成坡角；δ—墙后填土与墙背的摩擦角，由试验或规范确定。

2、被动土压力公式212p p E H K γ=22cos ()sin()sin(cos cos()1-cos()cos()p K ϕαϕδϕβαδααδαβ+=⎡⎤+⋅+⋅-⋅⎢⎥-⋅-⎣⎦式中：K p —为库仑被动土压力系数。

2.1.2 朗肯土压力[23]朗肯土压力是英国学者朗肯在1857 年提出的一种经典的土压力理论，这种土压力理论是根据半空间体的应力状态和土的极限平衡理论得出的土压力计算理论之一。

这种土压力理论的计算方法比较简单，计算结果比较接近实际，至今仍然被广泛用于工程实践之中。

其基本假定如下:1).墙本身是刚性的，不考虑墙身的变形； 2).墙后填土面水平且填土延伸到无限远处； 3).墙背直立、光滑。