华英2010年招生考试数学卷(附答案)

2010年普通高等学校招生全国统一考试文科数学(必修+选修> 解读版参考公式：如果事件互斥，那么球的表面积公式如果事件相互独立，那么其中R表示球的半径球的体积公式如果事件A在一次实验中发生的概率是，那么次独立重复实验中事件恰好发生次的概率其中R表示球的半径一、选择题(1>(A> (B>- (C> (D>1.C【命题意图】本小题主要考查诱导公式、特殊三角函数值等三角函数知识【解读】(2>设全集，集合，，则A.B.C. D.2.C 【命题意图】本小题主要考查集合的概念、集合运算等集合有关知识【解读】，，则=(3>若变量满足约束条件则的最大值为(A>4 (B>3 (C>2 (D>13.B 【命题意图】本小题主要考查线性规划知识、作图、识图能力及计算能力.【解读】画出可行域<如右图），，由图可知,当直线经过点A(1,-1>时，z最大，且最大值为.<4）已知各项均为正数的等比数列{}，=5，=10，则(A>(B> 7 (C> 6 (D>A4.A【命题意图】本小题主要考查等比数列的性质、指数幂的运算、根式与指数式的互化等知识，着重考查了转化与化归的数学思想.mmVxZudVti【解读】由等比数列的性质知，10,所以,所以(5>的展开式的系数是(A>-6 (B>-3 (C>0 (D>35.A. 【命题意图】本小题主要考查了考生对二项式定理的掌握情况，尤其是展开式的通项公式的灵活应用，以及能否区分展开式中项的系数与其二项式系数，同时也考查了考生的一些基本运算能力.mmVxZudVti【解读】的系数是 -12+6=-6(6>直三棱柱中，若，，则异面直线与所成的角等于(A>30° (B>45°(C>60° (D>90°6.C【命题意图】本小题主要考查直三棱柱的性质、异面直线所成的角、异面直线所成的角的求法.【解读】延长CA到D，使得，则为平行四边形，就是异面直线与所成的角，又三角形为等边三角形，(7>已知函数.若且，，则的取值范围是(A> (B>(C> (D>7.C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域，考生在做本小题时极易忽视a的取值范围，而利用均值不等式求得a+b=,从而错选D,这也是命题者的用苦良心之处.mmVxZudVti【解读1】因为 f(a>=f(b>,所以|lga|=|lgb|,所以a=b(舍去>，或，所以a+b=又0<a<b,所以0<a<1<b，令由“对勾”函数的性质知函数在(0,1>上为减函数，所以f(a>>f(1>=1+1=2,即a+b的取值范围是(2,+∞>.mmVxZudVti【解读2】由0<a<b,且f(a>=f(b>得：，利用线性规划得：，化为求的取值范围问题，，过点时z最小为2,∴(C> mmVxZudVti<8）已知、为双曲线C:的左、右焦点，点P在C上，∠=，则A BC DA 1B 1C 1D 1O(A>2 (B>4 (C> 6 (D> 88.B 【命题意图】本小题主要考查双曲线定义、几何性质、余弦定理，考查转化的数学思想，通过本题可以有效地考查考生的综合运用能力及运算能力.mmVxZudVti 【解读1】.由余弦定理得cos ∠P =4【解读2】由焦点三角形面积公式得：4<9）正方体-中，与平面所成角的余弦值为 <A ）<B ）<C ） <D ）9.D 【命题意图】本小题主要考查正方体的性质、直线与平面所成的角、点到平面的距离的求法，利用等体积转化求出D 到平面AC 的距离是解决本题的关键所在,这也是转化思想的具体体现.mmVxZudVti 【解读1】因为BB1//DD1,所以B 与平面AC 所成角和DD1与平面AC 所成角相等,设DO⊥平面AC，由等体积法得,即.设DD1=a,mmVxZudVti则,.所以,记DD1与平面AC所成角为,则,所以.【解读2】设上下底面的中心分别为；与平面AC所成角就是B与平面AC所成角，<10）设则<A）<B） (C> (D>10.C 【命题意图】本小题以指数、对数为载体，主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.mmVxZudVti【解读1】 a=2=, b=In2=,而,所以a<b,c==,而,所以c<a,综上c<a<b.【解读2】a=2=,b=ln2=, ，； c=，∴c<a<b<11）已知圆的半径为1，PA、PB为该圆的两条切线，A、B为两切点，那么的最小值为(A> (B> (C> (D>11.D【命题意图】本小题主要考查向量的数量积运算与圆的切线长定理，着重考查最值的求法——判别式法,同时也考查了考生综合运用数学知识解题的能力及运算能力.mmVxZudVti 【解读1】如图所示：设PA=PB=,∠APO=,则∠APB=，PO=，，===，令，则，即，由是实数，所以，，解得或.故.此时.【解读2】设，换元：，【解读3】建系：园的方程为，设，<12）已知在半径为2的球面上有A、B、C、D四点，若AB=CD=2,则四面体ABCD的体积的最大值为mmVxZudVti(A> (B> (C> (D>12.B【命题意图】本小题主要考查几何体的体积的计算、球的性质、异面直线的距离,通过球这个载体考查考生的空间想象能力及推理运算能力.mmVxZudVti【解读】过CD作平面PCD，使AB⊥平面PCD,交AB与P,设点P到CD的距离为,则有,当直径通过AB与CD的中点时,,故.mmVxZudVti第Ⅱ卷注意事项：1．答题前，考生先在答题卡上用直径0.5毫M黑色墨水签字笔将自己的姓名、准考证号填写清楚，然后贴好条形码。

2010年河南省初中学业水平暨高级中等学校招生考试试卷一、选择题（每小题3分，共18分）1．21-的相反数是【 】 （A ）21 （B ）21- （C ）2 （D ）2-2．我省200年全年生产总值比2008年增长10.7%，达到约19367亿元．19367亿元用科学记数法表示为【 】（A ）11109367.1⨯元 （B ）12109367.1⨯元 （C ）13109367.1⨯元 （D ）14109367.1⨯元3．在某次体育测试中，九年级三班6位同学的立定跳远成绩（单位：m ）分别为：1.71，1.85，1.85，1.96，2.10，2.31．则这组数据的众数和极差分别是【 】（A ）1.85和0.21 （B ）2.11和0.46（C ）1.85和0.60 （D ）2.31和0.604．如图，△ABC 中，点DE 分别是ABAC 的中点，则下列结论：①BC =2DE ；②△ADE ∽△ABC ；③ACABAE AD =．其中正确的有【 】 （A ）3个 （B ）2个（C ）1个 （D ）0个5．方程032=-x 的根是【 】（A ）3=x （B ）3,321-==x x（C ）3=x （D ）3,321-==x x6．如图，将△ABC 绕点C （0，-1）旋转180°得到△ABC ，设点A 的坐标为),(b a 则点A 的坐标为【 】（A ）),(b a -- （B ）)1.(---b a （C ）)1,(+--b a （D ）)2,(---b a二、填空题（每小题3分，共27分）7．计算2)2(1-+-=__________________．8．若将三个数11,7,3-表示在EDCBA（第4题）（第6题）（第8题）数轴上，其中能被如图所示的墨迹覆盖的数是__________________．9．写出一个y 随x 增大而增大的一次函数的解析式：__________________．10．将一副直角三角板如图放置，使含30°角的三角板的段直角边和含45°角的三角板的一条直角边重合，则∠1的度数为______________．11．如图，AB 切⊙O 于点A ，BO 交⊙O 于点C ，点D 是⌒CmA 上异于点C 、A 的一点，若∠ABO =32°，则∠ADC 的度数是______________．12．现有点数为2，3，4，5的四张扑克牌，背面朝上洗匀，然后从中任意抽取两张，这两张牌上的数字之和为偶数的概率为______________． 13．如图是由大小相同的小正方体组成的简单几何体的主视图和左视图那么组成这个几何体的小正方体的个数最多为______________．14．如图矩形ABCD 中，AD =1，AD =，以AD 的长为半径的⊙A 交BC 于点E ，则图中阴影部分的面积为______________________．15．如图，Rt △ABC 中，∠C =90°，∠ABC =30°，AB =6．点D 在AB 边上，点E 是BC 边上一点（不与点B 、C 重合），且DA =DE ，则AD 的取值范围是___________________．三、解答题（本大题共8个大题，满分75分）16．（8分）已知.2,42,212+=-=-=x x C x B x A 将它们组合成C B A ÷-)(或C B A ÷-的形式，请你从中任选一种进行计算，先化简，再求值其中3=x ．17．（9分）如图，四边形ABCD 是平行四边形，△AB’C 和△ABC 关于AC 所在的直线对称，AD 和B’C 相交于点O ，连接BB’． （1）请直接写出图中所有的等腰三角形（不添加字母）； （2）求证：△AB’O ≌△CDO ．18．（9分）“校园手机”现象越来越受到社会的关注．“五一”期间，小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法，统计整理并制作了如下的统计图：（1）求这次调查的家长人数，并补全图①； （2）求图②中表示家长“赞成”的圆心角的度数；（3）从这次接受调查的学生中，随机抽查一个，恰好是“无所谓”态度的学生的概率是多少？OmDC BA（第11题）（第14题）（第13题）主视图 左视图CDAE（第15题）（第10题）19．（9分）如图，在梯形ABCD 中，AD //BC ，E 是BC 的中点，AD =5，BC =12，CD =24，∠C =45°，点P 是BC 边上一动点，设PB 的长为x ．（1）当x 的值为____________时，以点P 、A 、D 、E 为顶点的四边形为直角梯形；（2）当x 的值为____________时，以点P 、A 、D 、E 为顶点的四边形为平行四边形；；（3）点P 在BC 边上运动的过程中，以P 、A 、D 、E 为顶点的四边形能否构成菱形？试说明理由．P EA BCD20．（9分）为鼓励学生参加体育锻炼，学校计划拿出不超过1600元的资金再购买一批篮球和排球．已知篮球和排球的单价比为3:2．单价和为80元．（1）篮球和排球的单价分别是多少元？（2）若要求购买的篮球和排球的总数量是36个，且购买的篮球数量多于25个，有哪几种购买方案？21．（10分） （1）操作发现如图，矩形ABCD 中，E 是AD 的中点，将△AB E 沿BE 折叠后得到△GBE ，且点G 在举行ABCD 内部．小明将BG 延长交DC 于点F ，认为GF =DF ，你同意吗？说明理由．（2）问题解决保持（1）中的条件不变，若DC =2DF ，求ABAD的值； （3）类比探求保持（1）中条件不变，若DC =nDF ，求ABAD的值．2010年河南省初中学业水平暨高级中等学校招生考试试卷一、选择题（每小题3分，共18分） 1、A 2、B 3、C 4、A 5、D 6、D 二、填空题（每小题3分，共27分）AB7、5 8、7 9、答案不唯一，只要符合题意即可。

2010年考研数学(三)试卷答案速查一、选择题（1）C （2）A （3）B （4）C （5）A （6）D （7）C （8）A 二、填空题（9）1− （10）2π4（11）31(1)3e p p − （12）3（13）3 （14）22σμ+ 三、解答题（15）1e −． （16）1415． （17）max u =，min u =−． （18）（Ⅰ）[]110ln ln(1)d ln d nn t t t t t t +<⎰⎰ (1,2,)n =.（Ⅱ）lim 0n n u →∞=．（19）略．（20）（Ⅰ）1λ=−，2a =−.（Ⅱ）通解为32110210k ⎛⎫ ⎪⎛⎫ ⎪⎪⎪=+− ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭x ，k 为任意常数．（21）1a =−，0⎪=⎪⎪⎪⎪⎭Q ．（22）1πA =.222(,)()()x xy y Y X X f x y f y x f x −+−==，y −∞<<+∞．（23）（Ⅰ）(,)X Y 的概率分布为（Ⅱ）4cov(,)45X Y =−． 2010年全国硕士研究生入学统一考试数学（三）参考答案一、选择题：1～8小题,每小题4分,共32分．下列每题给出的四个选项中,只有一个选项是符合题目要求的．请将所选项前的字母填在答题纸．．．指定位置上． （1）【答案】C ．【解答】原式00111e lim e e lim 11xx x x x a a a x x x →→−⎛⎫=−+=+=−+= ⎪⎝⎭所以2a =．故选C ．（2）【答案】A ．【解答】由已知条件可得12y y λμ−是齐次方程()0y p x y '+=的解，带入可得，1122(())(())0y p x y y p x y λμ''+−+=，即()()0q x λμ−=，0λμ−=．又12y y λμ+是方程()()y p x y q x '+=的解，所以有，1122(())(())()y p x y y p x y q x λμ''+++=，可得()()()q x q x λμ+=，1λμ+=．所以12λμ==．故选A ． （3）【答案】B ．【解答】因为0()g x a =是()g x 的极值，且()g x 可导，所以0()0g x '=．记()()y f g x =，有 ()()()y f g x g x '''=⋅，()[]()2()()()()y f g x g x f g x g x ''''''''=⋅+⋅． 从而00()()0x x y f a g x ='''=⋅=，即0x 是()()f g x 的驻点．又[]02000()()()()()()x x y f a g x f a g x f a g x ='''''''''''=⋅+⋅=⋅，由极值的第二充分条件，当00()()0x x y f a g x ='''''=⋅<时，y 在0x 取极大值，因为0()0g x ''<，所以()0f a '>．故选B ． （4）【答案】C ． 【解答】因为10()limlim ()ln x x g x x f x x→+∞→+∞==+∞，10()elim lim ()xx x h x g x x →+∞→+∞==+∞，所以，当x 充分大时， ()()()f x g x h x <<．故选C ． （5）【答案】A ．【解答】因为向量组Ⅰ可由向量组Ⅱ线性表示，所以1212(,,,)(,,,)r s r r αααβββ，若向量组Ⅰ线性无关，则12(,,,)r r r =ααα，从而1212(,,,)(,,,)r s r r r s =αααβββ，即r s ．故选A ．（6）【答案】D ．【解答】设λ为A 的特征值，因为2+=A A O ，所以20λλ+=，1λ=−或0．因为A 为实对称矩阵，故A 可相似对角化，即A 相似于对角阵Λ，()()3r r ==A Λ，因此1110−⎛⎫⎪− ⎪= ⎪− ⎪⎝⎭Λ．故选D ． （7）【答案】C ．【解答】{}{}{}()()11111111101e e 22P X P X P X F F −−==−<=−−=−−=−． 故选C ． （8）【答案】A ．【解答】221()x f x −=，21,13,()40,x f x ⎧ −⎪=⎨⎪ ⎩其它.利用概率密度的性质，3312100131()d ()d ()d ()d d 2424a a f x x af x x bf x x f x xb x b +∞+∞−∞−∞−∞==+=+=+⎰⎰⎰⎰⎰，所以234a b +=．故选A ．二、填空题：9～14小题,每小题4分,共24分．请将答案写在答题纸．．．指定位置上． （9）【答案】1−． 【解答】220e d sin d x yxt t x t t +−=⎰⎰， ①两边对x 求导得2()220e(1)sin d sin xx y y t t x x −+'+=+⎰． ②把0x =代入①式，得0y =，把0x =，0y =代入②式，得1y '=−，即d 1d x yx==−．（10）【答案】2π4．【解答】222e ee1ππd πd πarctan(ln )(1ln )4V y x x x x x +∞+∞+∞====+⎰⎰． （11）【答案】31(1)3ep p −．【解答】由收益弹性3d 1d p R p R p =+，整理得2d 1d R p p R p ⎛⎫=+ ⎪⎝⎭，解得313e p R Cp =． 代入()11R =，得13e C −=，所以31(1)3()ep R p p −=．（12）【答案】3．【解答】232,62y x ax b y x a '''=++=+. 令0y ''=，得13ax =−=−，所以3a =． 又曲线过点(1,0)−，代入曲线方程，得3b =． （13）【答案】3． 【解答】因为1111111()E −−−−−−−+=+=+=+A BAE B ABB AA B A A B B ，所以11111()3−−−−−+=+=⋅+⋅=A B A A B B A A B B ． （14）【答案】22σμ+．【解答】2222221111()()()()n n i i i i ET E X E X E X DX EX n n σμ======+=+∑∑．三、解答题：15～23小题,共94分．解答应写出文字说明、证明过程或演算步骤．请将答案写在答题纸．．．指定位置上． （15）（本题满分10分） 解： 11111ln(1)ln(1)lim ln ln ln lim (1)lim eex x x x x xxxxx x x →+∞−−→+∞→+∞−==，其中，1ln 0lim lim ee 1x x xx x x →+∞→+∞===，1112111ln ln(1)1ln 1lim lim lim1ln (1)xxx x x x xx xx x x x xx x x→+∞→+∞→+∞−−−−==−1ln 1ln 1ln limlim1,1ln (e1)x x x xx xx x x x→+∞→+∞−−===−⋅−所以原式1e −=．解：积分区域如图，33223()d d (33)d d DDI x y x y x x y xy y x y =+=+++⎰⎰⎰⎰，根据对称性，13232(3)d d 2(3)d d DD I x xy x y x xy x y =+=+⎰⎰⎰⎰， 其中{}21(,)01,21D x y y y x y =+是D 的上半部分，从而 2111324202091142d 3)d 2(2)d 4415y I yx xy x y y y +=+=−++=⎰⎰⎰．（17）（本题满分10分）解：构造拉格朗日函数222(,,,)2(10)L x y z xy yz x y z λλ=++++−，由 22220,220,220,100.xyzL y x L x z y L y z L x y z λλλλ'=+=⎧⎪'=++=⎪⎨'=+=⎪⎪'=++−=⎩解得可能的最值点有5,2),(1,5,2),(5,2),(1,5,2),(22,0,2),(22,0,2)−−−−−−−−，因为5,2)(1,5,2)55u u =−−−=，(1,5,2)(5,2)55u u −=−−=−，(22,0,2)(22,0,2)0u u −=−=，所以max 55u =，min 55u =−．（18）（本题满分10分）解：（Ⅰ）当01t <时， 令()ln(1)f t t t =−+，有(0)0,'()0f f t =>，所以()0f t >且单调递增，故有0ln(1)t t <+<，所以[]ln ln(1)ln nnt t t t +<.由积分的比较性质，[]11ln ln(1)d ln d nn t t t t t t +<⎰⎰，(1,2,)n = .（Ⅱ）由（Ⅰ）可知10ln d nn u tt t <<⎰，而1111200011ln d ln d ln d()1(1)nnn t t t t t t t t n n +=−=−=++⎰⎰⎰， 所以，210(1)n u n <<+，又21lim 0(1)n n →∞=+，由夹逼定理，lim 0n n u →∞=．解：（Ⅰ）由积分中值定理，2()d 2()f x x f η=⎰，(0,2)η∈，因为22(0)()d f f x x =⎰，所以(0)()f f η=，(0,2)η∈．（Ⅱ）因为(2)(3)(0)2f f f +=，所以由介值定理，存在[2,3]c ∈，使得()(0)f c f =．从而有 (0)()()f f f c η==．现对()f x 分别在区间[0,]η和[,]c η上应用罗尔定理，得12()()0f f ξξ''==，其中12[0,],[,]c ξηξη∈∈．又()f x 二阶可导，再对()f x 在区间12[,]ξξ上应用罗尔定理，得()0f ξ''=，其中12(,)(0,3)ξξξ∈⊂．（20）（本题满分11分） 解：（Ⅰ）对增广矩阵进行初等行变换，得211111()010101011110011a a λλλλλλλ⎛⎫⎛⎫⎪⎪=−→− ⎪ ⎪ ⎪ ⎪−−+⎝⎭⎝⎭A b .当1λ=时，()1,(,)2r r ==A A b ，方程组无解；当1λ=−时，()(,)23r r ==<A A b ，方程组有无穷多解，满足=Ax b 存在两个不同的解的条件，所以1λ=−，2a =−．（Ⅱ）当1λ=−，2a =−时，增广矩阵经初等变换得3101211111()0201010200000000⎛⎫− ⎪−⎛⎫ ⎪⎪ ⎪→−→− ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭A b ，其导出组的通解为1101k ⎛⎫ ⎪= ⎪ ⎪⎝⎭x ,方程组=Ax b 的一个特解为32120⎛⎫ ⎪ ⎪ ⎪=− ⎪ ⎪ ⎪ ⎪⎝⎭η，故通解为32110210k ⎛⎫ ⎪⎛⎫ ⎪⎪⎪=+− ⎪ ⎪⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭x ，k 为任意常数．解：因为Q 的列是A的特征向量，所以设T 1=α是A 的对应于特征值1λ的特征向量，由111λ=A αα，即10141113224011a a λ−⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪−= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭，解得12,1a λ==−．由14131(4)(2)(5)041λλλλλλλ−−=−=+−−=−E A 得，A 的特征值为1232,5,4λλλ===−．对25λ=，由(5)−=E A x 0，解得A 的对应于25λ=的特征向量为T2(1,1,1)=−α． 对34λ=−，由(4)−−=E A x 0，解得A 的对应于34λ=−的特征向量为T3(1,0,1)=−α．因为A 为实对称矩阵，不同特征值的特征向量相互正交，只需单位化：T T 2323231,1),1,0,1)==−==−ααββαα，则123(,,)0⎪==⎪⎪⎪⎪⎭Q αββ，使T 254⎛⎫ ⎪== ⎪ ⎪−⎝⎭Q AQ Λ．（22）（本题满分11分） 解： 由概率密度的性质，222222()1(,)d d ed de e d d x xy y x y xf x y x y A x y A x y +∞+∞+∞+∞+∞+∞−+−−−−−∞−∞−∞−∞−∞−∞===⎰⎰⎰⎰⎰⎰22()ed ed()πx y x Ax y x A +∞+∞−−−−∞−∞=−=⎰⎰，所以1πA =． X 的边缘概率密度为222()1()(,)d e e d()πx y x x X f x f x y y y x +∞+∞−−−−−∞−∞==−=⎰⎰，x −∞<<+∞当x −∞<<+∞时，条件概率密度222(,)()()x xy yY XXf x yf y xf x−+−==，y−∞<<+∞．（23）（本题满分11分）解：（Ⅰ）X的所有可能取值为0,1，Y的所有可能取值为0,1,2．{}232610,05CP X YC====，{}11232620,15C CP X YC====，{}10,215P X Y===，{}11132611,05C CP X YC====，{}21,115P X Y===，{}1,20P X Y===．从而(,)X Y的概率分布为（Ⅱ）cov(,)()X Y E XY EX EY=−⋅，21101333EX=⨯+⨯=，2812012515153EY=⨯+⨯+⨯=，22()111515E XY=⨯⨯=，4cov(,)45X Y=−．。

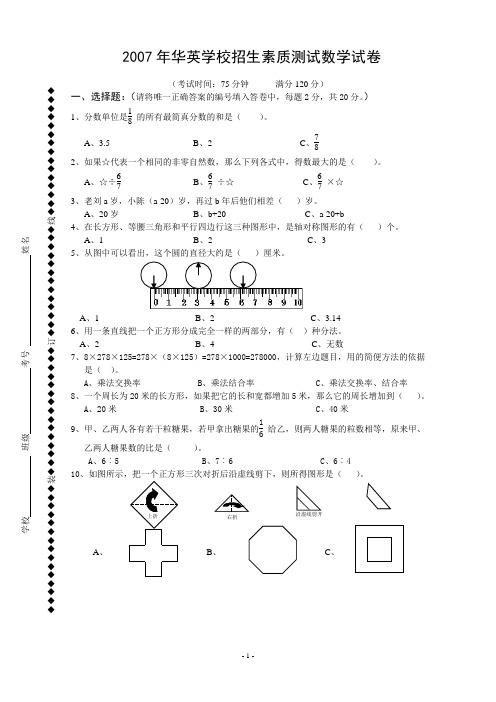
学校班级考号姓名__________________________◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆2007年华英学校招生素质测试数学试卷 （考试时间：75分钟 满分120分） 一、选择题：（请将唯一正确答案的编号填入答卷中，每题2分，共20分。

） 1、分数单位是18 的所有最简真分数的和是（ ）。

A 、3.5 B 、2 C 、78 2、如果☆代表一个相同的非零自然数，那么下列各式中，得数最大的是（ ）。

A 、☆÷67 B 、67 ÷☆ C 、67 ×☆ 3、老刘a 岁，小陈（a-20）岁，再过b 年后他们相差（ ）岁。

A 、20岁 B 、b+20 C 、a-20+b 4、在长方形、等腰三角形和平行四边行这三种图形中，是轴对称图形的有（ ）个。

A 、1 B 、2 C 、3 5、从图中可以看出，这个圆的直径大约是（ ）厘米。

A 、1B 、2C 、3.14 6、用一条直线把一个正方形分成完全一样的两部分，有（ ）种分法。

A 、2 B 、4 C 、无数 7、8×278×125=278×（8×125）=278×1000=278000，计算左边题目，用的简便方法的依据是（ ）。

A 、乘法交换率 B 、乘法结合率 C 、乘法交换率、结合率 8、一个周长为20米的长方形，如果把它的长和宽都增加5米，那么它的周长增加到（ ）。

A 、20米 B 、30米 C 、40米 9、甲、乙两人各有若干粒糖果，若甲拿出糖果的16 给乙，则两人糖果的粒数相等，原来甲、乙两人糖果数的比是（ ）。

A 、6︰5 B 、7︰6 C 、6︰4 10、如图所示，把一个正方形三次对折后沿虚线剪下，则所得图形是（ ）。

A 、B 、C 、右折二、填空题（每空2分，共24分）1、既是合数又是偶数的最小自然数是（ ）。

2014年广东省佛山市华英学校小升初数学试卷姓名一．选择题（本大题包含6小题，每小题3分，共18分）1．如图，属于钝角三角形ABC的高的是（）A．1 B．2 C．32．在不透明的袋子里装入同样数量的红球和黄球，球除颜色外完全相同，现在要使摸到红球的可能性比摸到黄球的可能性大，错误的做法是（）A．减少红球数量B．减少黄球数量C．增加红球数量3．一个正方形的边长为m厘米，如果它的边长增加4厘米，所得到的正方形面积比原来正方形面积增加了（）平方厘米．A．m2+16 B．8m+16 C．8m+324．将1立方米的大正方体锯成体积是1立方厘米的小正方体，然后将它们一个个叠成一竖列，估计它的高度约有（）A．30层楼高B．300层楼高C．3000层楼高5．有两块面积相等的白铁皮和黑铁皮，白铁皮用去平方米，黑铁皮用去，剩下的白铁皮比黑铁皮面积大，那么原来两块铁皮的面积（）A．都小于1平方米B．都等于1平方米C．都大于1平方米6．小明和小芳各走一段路，小明走的路程比小芳多，小芳用的时间比小明多，小明和小芳的速度比是（）A．8：5 B．27：20 C．16：15二、判断题：对的打“√”，错的打“×”。

（每小题2分，共10分）7．如果a＞0，那么一定小于a．（）8．把一个长方体框架拉成一个平行四边形，那么这个平行四边形的面积必定小于原来长方体的面积．（）9．钟面上分针转动的速度是时针的60倍．（）10．某小区居民每户的人数与用水量如下表，人数每增加1人，水量也相应的增加1吨，则人数与用水量成正比例．（）11．一个三角形，如果两个内角的和是钝角，则它一定是锐角三角形．（）三、填空题（每小题4分，共28分）12．如图用4张卡片摆出不同数那么所有能摆出的数中，0不读出来的最小4位数是．13．把4米长的绳子拉直后剪三刀，使每段长度相等，那么每段是米．14．某超市运来一批货物，其中土豆有2000千克，冬瓜有1620千克，芹菜700千克，番茄若干，用扇形统计图表示如图所示，则番茄有千克．15．如图小明为一副宽为60cm的照片镶上5cm 的边框后，发现照片面积占整个画框面积的80%，则原照片的长为cm．16．将长方形平均分成三个小长方形，再将每个小长方形分别平均分成2份，3份，4份，则图中阴影部分的面积是长方形面积的填分数．17．如图，半径为20cm的圆的外面和里面各有一个正方形，则外面的正方形比里面正方形的面积大cm2．18．如图，两根铁棒直立于桶底水平的木桶中，在桶中加水之后，一根漏出水面的长度是它的，另一根露出水面的长度是它的，已知两根铁棒的长度之和为38cm，那么两根铁棒露出水面之和为cm．四、计算题（第19题每空2分，20-21题每小题4分，共20分）19．直接写答案＿：= ；×9÷×9=；1.75×+0.76÷=；2520﹣36×42÷27=．20．计算1.8﹣1÷（0.75﹣）×； 5.4×0.6+3.6÷﹣1.2．21．解方程：x﹣=25%x+3．五、解决问题（每题8分，共24分）22．小丽用自制的橡皮筋来称量物体质量．她把测量的数据制作成的统计图和统计表．（皮筋最多可称量2kg质量）物体质量与皮筋伸长长度的统计表（1）根据统计图补充表格．（2）填空，我们可以发现与所称物体的质量成（选填“正比”或“反比”）（3）小丽用此皮筋称一袋苹果，皮筋长43厘米，求这袋苹果的质量．23．学校体育馆有一种长方形海绵垫，具体尺寸如图甲所示，在不使用时将两个垫子叠放在一起，并用一个罩子将其包裹（放地面部分不用包）．要设计一个面积最小的遮罩，两个垫子应如何叠放？请在图乙中的地面上画出两个垫子的叠放示意图，标注具体尺寸，并计算遮罩的最小面积．（不计算损耗）24．东西、南北两条路交叉成直角，甲在十字路口的南边距路口1500米处，乙刚好在十字路口中心．乙先由西向东出发，5分钟后甲以同样的速度开始由南向北走，又经过5分钟，甲尚未到达路口，此时两人离路口中心的距离相等．之后甲按原来速度的两倍加速前行，乙则保持原速继续前行，问再过几分钟后，两人离路口的距离又相等？（请在下图中按1：100000的比例尺画出甲乙两人的原始位置以及第二次到路口中心距离相等的位置）2014年广东省佛山市华英学校小升初数学试卷参考答案一．选择题（本大题包含6小题，每小题3分，共18分）1．C ； 2．A ； 3．B ； 4．B ； 5．C ； 6．B ；二、判断题：对的打“√”，错的打“×”。

2010年全国硕士研究生入学统一考试数学一试题一、选择题(1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸．．．指定位置上.) (1) 极限2lim ()()xx x x a x b →∞⎡⎤=⎢⎥-+⎣⎦( ) (A) 1. (B) e . (C) a be -. (D) b ae-.(2) 设函数(,)z z x y =,由方程,0y z F x x ⎛⎫=⎪⎝⎭确定,其中F 为可微函数,且20F '≠,则z zxy x y∂∂+=∂∂( ) (A) x . (B) z . (C) x -. (D) z -.(3) 设,m n 是正整数,则反常积分⎰的收敛性 ( )(A) 仅与m 的取值有关. (B)仅与n 的取值有关. (C) 与,m n 取值都有关. (D) 与,m n 取值都无关. (4) ()()2211limn nn i j nn i n j →∞===++∑∑ ( ) (A)()()120111xdx dy x y ++⎰⎰. (B) ()()100111x dx dy x y ++⎰⎰. (C)()()11111dx dy x y ++⎰⎰. (D) ()()1120111dx dy x y ++⎰⎰. (5) 设A 为m n ⨯矩阵,B 为n m ⨯矩阵,E 为m 阶单位矩阵,若AB E =,则 ( )(A) 秩()r A m =,秩()r B m =. (B) 秩()r A m =,秩()r B n =. (C) 秩()r A n =,秩()r B m =. (D) 秩()r A n =,秩()r B n =. (6) 设A 为4阶实对称矩阵,且2A A O +=,若A 的秩为3,则A 相似于 ( )(A) 1110⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭. (B) 1110⎛⎫ ⎪⎪ ⎪- ⎪⎝⎭.(C) 1110⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (D) 1110-⎛⎫ ⎪- ⎪ ⎪- ⎪⎝⎭. (7) 设随机变量X 的分布函数0,1(),0121,1x x F x x e x -<⎧⎪⎪=≤<⎨⎪-≥⎪⎩,则{}1P X == ( ) (A) 0. (B)12. (C) 112e --. (D) 11e --. (8) 设1()f x 为标准正态分布的概率密度,2()f x 为[]1,3-上均匀分布的概率密度,若12(),0()(),0af x x f x bf x x ≤⎧=⎨>⎩,(0,0)a b >>为概率密度,则,a b 应满足 ( ) (A) 234a b +=. (B) 324a b +=. (C) 1a b +=. (D) 2a b +=.二、填空题(9 14小题,每小题4分,共24分.请将答案写在答题纸．．．指定位置上.) (9) 设()20,ln 1,t tx e y u du -⎧=⎪⎨=+⎪⎩⎰ 求220t d y dx == .(10)2π=⎰.(11) 已知曲线L 的方程为[]{}11,1y x x =- ∈-,起点是()1.0-,终点是()1,0,则曲线积分2Lxydx x dy +=⎰.(12) 设(){}22,,1x y z xy z Ω=+≤≤,则Ω的形心的竖坐标z = .(13) 设()()()1231,2,1,0,1,1,0,2,2,1,1,TTTa ααα=-==,若由123,,ααα生成的向量空间的维数是2,则a = .(14) 设随机变量X 的概率分布为{}!C P X k k ==,0,1,2,k = ,则()2E X = .三、解答题(15～23小题,共94分.请将解答写在答题纸．．．指定位置上.解答应写出文字说明、证明过程或演算步骤.)求微分方程322x y y y xe '''-+=的通解． (16)(本题满分10分)求函数()()2221x t f x xt e dt -=-⎰的单调区间与极值.(17)(本题满分10分)(I)比较()1ln ln 1n t t dt +⎡⎤⎣⎦⎰与10ln nt t dt ⎰()1,2,n = 的大小,说明理由；(II)记()1ln ln 1nn u t t dt =+⎡⎤⎣⎦⎰()1,2,n = ,求极限lim n n u →∞. (18)(本题满分10分)求幂级数()121121n n n x n -∞=--∑的收敛域及和函数.(19)(本题满分10分)设P 为椭球面222:1S x y z yz ++-=上的动点,若S 在点P 处的切平面与xOy 面垂直,求点P 的轨迹C ,并计算曲面积分2x y zI ∑-=,其中∑是椭球面S 位于曲线C 上方的部分.(20)(本题满分11分)设110111a A b λλλ ⎛⎫⎛⎫ ⎪ ⎪= - 0= ⎪ ⎪ ⎪ ⎪1 1 ⎝⎭⎝⎭，,已知线性方程组Ax b =存在两个不同的解.( I ) 求λ,a ；( II ) 求方程组Ax b =的通解. (21)(本题满分11 分)已知二次型123(,,)T f x x x x Ax =在正交变换x Qy =下的标准形为2212y y +,且Q 的第三列为T. ( I ) 求矩阵A ；( II ) 证明A E +为正定矩阵,其中E 为3阶单位矩阵. (22)(本题满分11分)设二维随机变量(,)X Y 的概率密度为2222(,)x xy y f x y Ae -+-=,x -∞<<+∞,y -∞<<+∞,求常数A 及条件概率密度|(|)Y X f y x ．设总体X其中参数()0,1θ∈未知,以i N 表示来自总体X 的简单随机样本(样本容量为n )中等于i 的个数(1,2,3i =).试求常数123,,a a a ,使31iii T a N ==∑为θ的无偏估计量,并求T 的方差.2010年全国硕士研究生入学统一考试数学一试题参考答案一、选择题(1)【答案】 (C).【解析】本题属于未定式求极限,极限为1∞型,故可以用“e 的抬起法”求解．()()2lim xx x x a x b →∞⎡⎤⎢⎥-+⎣⎦()()2ln lim x x x a x b x e ⋅-+→∞=()()2lim ln x x x x a x b e →∞⋅-+=, 其中又因为()()2222()()lim ln lim ln 1()()()()lim()()()lim()()x x x x x x x a x b x x x a x b x a x b x x x a x b x a x b a b x abxx a x b a b→∞→∞→∞→∞--+⋅=+-+-+⎡⎤--+⎣⎦=-+-+=-+=-⎡⎤⎣⎦故原式极限为a be-,所以应该选择(C).(2)【答案】 (B).【解析】12221212222x z y z y zF F F F F yF zF zx x x x x F F xF F x⎛⎫⎛⎫''''-+-⋅+⋅ ⎪ ⎪'''+∂⎝⎭⎝⎭=-=-==∂''''⋅, 112211y z F F F z x y F F F x'⋅''∂=-=-=-∂'''⋅, 1212222yF zF yF F z z z x y z x y F F F ''''+⋅∂∂+=-==∂∂'''． (3) 【答案】 (D).【解析】0x =与1x =都是瑕点.应分成dx dx =+⎰,用比较判别法的极限形式,对于,由于121012[ln (1)]lim 11mnx n mx xx+→--=.显然,当1201n m<-<,则该反常积分收敛. 当120n m -≤,1210[ln (1)]lim mx nx x+→-存在,此时实际上不是反常积分,故收敛.故不论,m n 是什么正整数,总收敛.对于,取01δ<<,不论,m n 是什么正整数,1211211[ln (1)]lim lim ln (1)(1)01(1)mnmx x x xx x x δδ--→→-=--=-,所以收敛,故选(D).(4)【答案】 (D). 【解析】()()222211111()nnnn i j i j n nn i n j n i n j =====++++∑∑∑∑22111()()n n j i n n j n i ===++∑∑ 12220211111lim lim ,11()nn n n j j n dy j n jn y n→∞→∞====+++∑∑⎰ 1011111lim lim ,11()nn n n i i n dx i n i n x n→∞→∞====+++∑∑⎰()()2222111111lim lim()()n nn nn n i j j i n n j n i n i n j →∞→∞=====++++∑∑∑∑ 221(lim )nn j n n j→∞==+∑1(lim )nn i nn i →∞=+∑ 1120011()()11dx dy x y =++⎰⎰()()11200111dx dy x y =++⎰⎰. (5)【答案】 (A).【解析】由于AB E =,故()()r AB r E m ==.又由于()(),()()r AB r A r AB r B ≤≤,故(),()m r A m r B ≤≤ ①由于A 为m n ⨯矩阵,B 为n m ⨯矩阵,故(),()r A m r B m ≤≤ ②由①、②可得(),()r A m r B m ==,故选A. (6)【答案】 (D).【解析】设λ为A 的特征值,由于2A A O +=,所以20λλ+=,即(1)0λλ+=,这样A 的特征值只能为-1或0. 由于A 为实对称矩阵,故A 可相似对角化,即A Λ ,()()3r A r =Λ=,因此,1110-⎛⎫ ⎪- ⎪Λ= ⎪- ⎪⎝⎭,即1110A -⎛⎫ ⎪- ⎪Λ= ⎪- ⎪⎝⎭. (7) 【答案】 (C).【解析】离散型随机变量的分布函数是跳跃的阶梯形分段函数,连续型随机变量的分布函数是连续函数.观察本题中()F x 的形式,得到随机变量X 既不是离散型随机变量,也不是连续型随机变量,所以求随机变量在一点处的概率,只能利用分布函数的定义.根据分布函数的定义,函数在某一点的概率可以写成两个区间内概率的差,即{}{}{}()()1111111110122P X P X P X F F e e --==≤-<=--=--=-,故本题选(C).(8)【答案】 (A).【解析】根据题意知,()221x f x -=(x -∞<<+∞),()21,1340,x f x ⎧ -≤≤⎪=⎨⎪ ⎩其它利用概率密度的性质:()1f x dx +∞-∞=⎰,故()()()()03121001312424a a f x dx af x dx bf x dx f x dxb dx b +∞+∞+∞-∞-∞-∞=+=+=+=⎰⎰⎰⎰⎰所以整理得到234a b +=,故本题应选(A).二、填空题 (9) 【答案】0.【解析】因为 ()()22ln 1ln 1ttt dy t e dx e-+==-+-, ()()()()22222ln 12ln 11tt t td te d y dt t e t e e dx dt dx t -+⎡⎤=⋅=-⋅-+⋅-⎢⎥+⎣⎦,所以220t d y dx ==. (10)【答案】 4π-.t =,2x t =,2dx tdt =,利用分部积分法, 原式220cos 22cos 2sin t t tdt t tdt t d t πππ=⋅==⎰⎰⎰20002sin 2sin 4cos t t t tdt td t πππ⎡⎤=-=⎢⎥⎣⎦⎰⎰0004cos cos 4cos 4sin 4t t tdt t ππππππ⎡⎤=-=-=-⎢⎥⎣⎦⎰.(11) 【答案】0.【解析】12222LL L xydx x dy xydx x dy xydx x dy +=+++⎰⎰⎰()()()0122111x x dx x dx x x dx x dx -=+++-+-⎰⎰()()0122122xx dx x x dx -=++-⎰⎰1322310223223x x x x -⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭211203223⎛⎫⎛⎫=--++-= ⎪ ⎪⎝⎭⎝⎭(12) 【答案】23. 【解析】 ()2221221211000211212021r rrz d rdr zdxdydz d rdr zdz dxdydz d rdr dz d r rdrππππθθθθΩΩ⎛⎫⎪⋅ ⎪⎝⎭==-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰4211222r d r dr πθπ⎛⎫-⎪⎝⎭=⎰⎰126204122r r d πθ⎛⎫- ⎪⎝⎭=⎰20112266322d πθπππ⋅===⎰. (13)【答案】6a =.【解析】因为由123,,ααα生成的向量空间维数为2,所以123(,,)2r ααα=. 对123(,,)ααα进行初等行变换：123112112112211013013(,,)1010130060202000a a a ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--⎪ ⎪ ⎪=→→⎪ ⎪ ⎪-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以6a =.(14) 【答案】2.【解析】利用离散型随机变量概率分布的性质,知{}001!k k CP X k Ce k ∞∞======∑∑,整理得到1C e -=,即 {}111!!k e P X k e k k --===.故X 服从参数为1的泊松分布,则()()1,1E X D X ==,根据方差的计算公式有()()()222112E X D X E X =+=+=⎡⎤⎣⎦. 三、解答题(15)【解析】对应齐次方程的特征方程为2320λλ-+=,解得特征根121,2λλ==,所以对应齐次方程的通解为212x x c y C e C e =+．设原方程的一个特解为*()x y x ax b e =+,则()()*22x y axax bx b e '=+++,()()*2422x y axax bx a b e ''=++++,代入原方程,解得1,2a b =-=-,故特解为*(2)xy x x e =--． 故方程的通解为*212(2)x x x c y y y C e C e x x e =+=+-+． (16)【解析】因为22222222111()()x x x t t t f x x t e dt xe dt te dt ---=-=-⎰⎰⎰,所以2224423311()2222x x t x x t f x x e dt x ex ex e dt----'=+-=⎰⎰,令()0f x '=,则0,1x x ==±.又22421()24x t x f x e dt x e --''=+⎰,则21(0)20t f e dt -''=<⎰,所以2211111(0)(0)(1)22t t f t e dt e e ---=-=-=-⎰是极大值.而1(1)40f e -''±=>,所以(1)0f ±=为极小值.又因为当1x ≥时,()0f x '>；01x ≤<时,()0f x '<；10x -≤<时,()0f x '>；1x <-时,()0f x '<,所以()f x 的单调递减区间为(,1)(0,1)-∞- ,()f x 的单调递增区间为(1,0)(1,)-+∞ .(17)【解析】 (I)当01x <<时0ln(1)x x <+<,故[]ln(1)nnt t +<,所以[]ln ln(1)ln nn t t t t +<,则[]11ln ln(1)ln nn t t dt t t dt +<⎰⎰()1,2,n = .(II)()111101ln ln ln 1n n n t t dt t t dt td t n +=-⋅=-+⎰⎰⎰ ()211n =+,故由 ()1210ln 1n n u t t dt n <<=+⎰,根据夹逼定理得()210lim lim01n n n u n →∞→∞≤≤=+,所以lim 0n n u →∞=.(18)【解析】(I) (1)1222(1)1122(1)(1)2(1)121lim lim (1)(1)2121n n n n n n n n n nx x n n xx n n +-++--→∞→∞--⋅+-+=--⋅--222(21)21lim lim 2121n n n x n x x n n →∞→∞--==⋅=++, 所以,当21x <,即11x -<<时,原级数绝对收敛.当21x >时,原级数发散,因此幂级数的收敛半径1R =.当1x =±时,11211(1)(1)2121n n n n n x n n --∞∞==--⋅=--∑∑,由莱布尼兹判别法知,此级数收敛,故原级数的收敛域为[]1,1-.(II) 设1122111(1)(1)()2121n n nn n n S x x x x n n --∞∞-==⎛⎫--=⋅=⋅⋅ ⎪--⎝⎭∑∑,其中令12111(1)()21n n n S x x n -∞-=-=⋅-∑()1,1x ∈-,所以有 12221111()(1)()n n n n n S x xx ∞∞---=='=-⋅=-∑∑ ()1,1x ∈-,从而有 12211()1()1S x x x '==--+ ()1,1x ∈-, 故 11201()(0)arctan 1xS x dx S x x =+=+⎰,()1,1x ∈-.1()S x 在1,1x =-上是连续的,所以()S x 在收敛域[]1,1-上是连续的.所以()arctan S x x x =⋅,[]1,1x ∈-.(19)【解析】 ( I )令()222,,1F x y z x y z yz =++--,故动点(),,P x y z 的切平面的法向量为()2,2,2x y z zy --,由切平面垂直xOy ,故所求曲线C 的方程为222120x y z yz z y ⎧++-=⎨-=⎩. ( II ) 由⎩⎨⎧=-=-++,02,1222y z yz z y x 消去z ,可得曲线C 在xOy 平面上的投影曲线所围成的xOy 上的区域223:{(,)|1}4D x y x y +≤,由()()x x yz z y x '='-++1222,由dxdy zy yzz y dxdy y z x z dS 24412222--++=⎪⎪⎭⎫⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂+=,故(2DDDx y zI x dxdy xdxdy ∑-==+=+⎰⎰⎰⎰⎰⎰12Dπ==⋅=. (20)【解析】因为方程组有两个不同的解,所以可以判断方程组增广矩阵的秩小于3,进而可以通过秩的关系求解方程组中未知参数,有以下两种方法.方法1：( I )已知Ax b =有2个不同的解,故()()3r A r A =<,对增广矩阵进行初等行变换,得111110101010111111a A a λλλλλλ⎛⎫⎛⎫⎪⎪=-→- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭22111111010101010110011a a λλλλλλλλλ⎛⎫⎛⎫⎪⎪→-→- ⎪ ⎪ ⎪ ⎪-----+⎝⎭⎝⎭当1λ=时,11111111000100010000000A a ⎛⎫⎛⎫⎪ ⎪→→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,此时,()()r A r A ≠,故Ax b =无解(舍去)．当1λ=-时,111102010002A a -⎛⎫ ⎪→- ⎪ ⎪+⎝⎭,由于()()3r A r A =<,所以2a =-,故1λ=- ,2a =-. 方法2：已知Ax b =有2个不同的解,故()()3r A r A =<,因此0A =,即211010(1)(1)011A λλλλλ=-=-+=,知1λ=或-1.当1λ=时,()1()2r A r A =≠=,此时,Ax b =无解,因此1λ=-.由()()r A r A =,得2a =-.( II ) 对增广矩阵做初等行变换31012111211121020102010102111100000000A ⎛⎫- ⎪----⎛⎫⎛⎫ ⎪⎪ ⎪⎪=-→-→-⎪ ⎪ ⎪ ⎪ ⎪- ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭可知原方程组等价为1323212x x x ⎧-=⎪⎪⎨⎪=-⎪⎩,写成向量的形式,即123332110210x x x x ⎛⎫⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪=+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪ ⎪⎝⎭.因此Ax b =的通解为32110210x k ⎛⎫⎪⎛⎫ ⎪ ⎪ ⎪=+- ⎪ ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭,其中k 为任意常数.(21)【解析】 ( I )由于二次型在正交变换x Qy =下的标准形为2212y y +,所以A 的特征值为1231,0λλλ===.由于Q 的第3列为,0,22T ⎛ ⎝⎭,所以A 对应于30λ=的特征向量为22T⎛ ⎝⎭,记为3α. 由于A 是实对称矩阵,所以对应于不同特征值的特征向量是相互正交的,设属于121λλ==的特征向量为()123,,Tx x x α=,则30T αα=,130x =. 求得该方程组的基础解系为()()120,1,0,1,0,1TTαα==-,因此12,αα为属于特征值1λ=的两个线性无关的特征向量.由于12,αα是相互正交的,所以只需单位化：())1212120,1,0,1,0,1T Tααββαα====-. 取()1230,,10002Q ββα⎛⎪⎪==⎝⎭,则110T Q AQ ⎛⎫ ⎪=Λ= ⎪ ⎪⎝⎭,且1T Q Q -=, 故 1102201011022TA Q Q ⎛⎫- ⎪ ⎪=Λ= ⎪ ⎪- ⎪⎝⎭. ( II )A E +也是实对称矩阵,A 的特征值为1,1,0,所以A E +的特征值为2,2,1,由于A E +的特征值全大于零,故A E +是正定矩阵.(22)【解析】当给出二维正态随机变量的的概率密度(),f x y 后,要求条件概率密度|(|)Y X f y x ,可以根据条件概率公式|(,)(|)()Y X X f x y f y x f x =来进行计算.本题中还有待定参数,A 要根据概率密度的性质求解,具体方法如下.()()22222222()(),xxy y y x x xy x X f x f x y dy A e dy A e dy Ae e dy +∞+∞+∞+∞-+--------∞-∞-∞-∞====⎰⎰⎰⎰2,x x -=-∞<<+∞.根据概率密度性质有()21x X f x dx e dx A π+∞+∞--∞-∞===⎰,即1A π-=,故()2x X f x -=,x -∞<<+∞.当x -∞<<+∞时,有条件概率密度()()()22222222(),,,x xy y x xy y x y Y X X f x y f y x x y f x -+--+---==-∞<<+∞-∞<<+∞.(23)【解析】()()()22123~,1,~,,~,N B n N B n N B n θθθθ--()()()()31122331i i i E T E a N a E N a E N a E N =⎛⎫==++ ⎪⎝⎭∑()()221231a n a n a n θθθθ=-+-+()()212132na n a a n a a θθ=+-+-.因为T 是θ的无偏估计量,所以()E T θ=,即得()()12132010na n a a n a a =⎧⎪-=⎨⎪-=⎩,整理得到10a =,21,a n = 31a n=.所以统计量()()12323111110T N N N N N n N n n n n=⨯+⨯+⨯=⨯+=⨯-.注意到1(,1)N B n θ- ,故()()()11211D T D n N D N n n⎡⎤=⨯-=⨯⎢⎥⎣⎦()11n θθ=-.。

2011年初一招生素质测评数学试卷（满分100分，考试时间45分钟）一、选择题（每题只有一个正确的答案，每小题3分，共24分）1、甲乙两地实际距离是320千米，在一幅地图上量得的距离是4厘米，这幅地图的比例尺是（ ）。

A 、1：80B 、1：8000C 、1：8000000 2、在下面的式子里，（ ）是方程。

A 、5X+4B 、3X-5＜7C 、X=0 3、正方形的周长和它的边长（ ）。

A 、成正比例B 、成反比例C 、不成比例 4、真分数除以真分数，所得的商一定（ ）。

A 、大于被除数B 、小于被除数C 、大于15、10名学生的平均成绩是X ，如果另外5名学生每人得84分，那么整个组的平均成绩是（ ）。

A 、X+842B 、10X+42015C 、10X+84156、有一个两位数，它的十位数字是a ，个位数字是b ，则这个两位数的大小是（ ）。

A 、a+bB 、10（a+b ）C 、10 a+b7、某商场卖出两个进价不同的手机，都卖了1200元，其中一个盈利50%，另一个亏本20%，在这次买卖中，这家商场（ ）。

A 、不赔不赚B 、赔100元C 、赚100元8、5个选手P 、Q 、R 、S 、T 举行一场赛跑，P 胜Q ，P 胜R ，Q 胜S ，并且T 在P 之后，Q 之前跑完全程，谁不可能得第三名（ ）。

A 、P 与QB 、P 与RC 、P 与S二、填空题（每题3分，共21分）9、4.09吨＝（ ）吨（ ）千克 3时20分＝（ ）时 10、以“万”为单位，准确数5万与近似数5万比较最多相差_____________。

11、a=2×3×m ，b=3×5×m （m 是自然数且m ≠0），如果a 和b 的最大公约数是21，则m 是___________，a 和b 的最小公倍数是______________。

12、把5米长的钢筋，锯成每段一样长的小段，共锯6次，每段占全长的______，每段长______米，如果锯成两段需2分钟，锯成6段共需______分钟。