匀变速运动重要推论的推导过程

匀变速运动重要推论的推导过程一、平均速度和瞬时速度的关系：根据定义，匀变速运动物体在任意时间段内的平均速度等于该时间段内起点和终点速度的平均值。

假设起点速度为v0，终点速度为v，时间间隔为Δt，则平均速度为v平均 = （v0 + v） / 2、另一方面，根据匀变速运动的定义，物体的瞬时速度在不同时间点处是不同的，用v表示。

根据定义，v = ds/ dt，其中ds是位移，dt是时间。

由于匀变速运动中速度是随时间变化的，所以在较小的时间间隔Δt内，速度可以近似看作匀速运动。

因此，v可以近似看作匀速运动的瞬时速度。

由此可得：v平均≈ v。

二、位移和速度的关系：在匀变速运动中，物体的位移和速度之间存在以下关系：s = v0t + 1/2at^2、该关系可以通过以下推导得到。

由定义可知，v = ds/ dt。

对上式两边同时求积分，得到∫v dt = ∫ds。

由于匀变速运动中速度是随时间变化的，所以该积分是定积分。

对左边的定积分得到∫v dt = ∫(v0 + at) dt = v0t + 1/2at^2、对右边的定积分得到∫ds = s。

因此，v0t + 1/2at^2 = s。

三、速度和时间的关系：在匀变速运动中，物体的速度和时间之间存在以下关系：v = v0 + at。

该关系可以通过以下推导得到。

由定义可知，v = ds/ dt。

根据位移和速度之间的关系s = v0t + 1/2at^2，我们对该式两边同时求导数得到ds/ dt = v = v0 + at。

综上所述，以上推导过程得到了匀变速运动中平均速度和瞬时速度的关系，位移和速度的关系，以及速度和时间的关系。

这些推论对于分析匀变速运动中物体的运动状态和规律非常重要。

匀变速直线运动规律的几个重要推论重难点解析：1. 匀变速直线运动的三个重要推论的推导过程：（1）在连续相等的时间（t）内的位移之差为一恒定值，即（又称匀变速直线运动的判别式）。

推证：设物体以初速、加速度a做匀加速直线运动，自计时起时间t内的位移①在第2个t内的位移②由①②两式得连续相等时间内的位移差为即。

进一步推证可得（2）某段时间内中间时刻的瞬时速度等于这段时间内的平均速度。

即推证：由①知经的瞬时速度②由①得，代入②中，得即（3）某段位移内中间位置的瞬时速度V S/2与这段位移的初、末速度与的关系为推证：由速度位移公式①知②由①得，代入②得得说明：匀变速直线运动中某段位移中点的瞬时速度大于该段时间中点的瞬时速度。

【典型例题】问题1、平均速度公式推论的应用：［考题1］有一做匀加速直线运动的质点，它在连续相等的时间间隔内，所通过的位移分别是24m和64m，每一个时间间隔为4s，求质点的初速度和加速度。

［解析］解法一：用常规方法来解。

据题意知，物体在AB段的位移为，在BC段的位移为（如图所示），从A到B和从B到C质点运动时间均为4s，要求a和，由位移公式有：将代入以上两式，可得：解法二：用平均速度求解，先求出在AB、CD两段位移内的平均速度：物体运动到B点时是中间时刻，由于匀变速直线运动在一段时间的中间时刻的瞬时速度等于这段时间内的平均速度，则又有：，所以，故解法三：利用匀变速直线运动的规律，，由题意得：再由匀变速直线运动的位移公式：可求出变式1：做匀加速直线运动的质点，连续经过A、B、C三点，已知AB＝BC，且已知质点在AB段的平均速度为3m/s，在BC段的平均速度为6m/s，则质点在B点时速度为（）A. 4m/sB. 4.5m/sC. 5m/sD. 5.5m/s答案：C变式2：一物体做匀减速直线运动，初速度为12m/s,加速度为2m/s2,该物体在某1s内的位移是6cm，此后它运动多少米速度为零？答案：6.25m问题2、Δs=aT 2推论的应用问题：［考题2］从斜面上某一位置，每隔0.1s释放一颗小球，在连续释放几颗后，对在斜面上滚动的小球拍下照片，如图所示，测得，，试求（1）小球的加速度；（2）拍摄时B球的速度；（3）拍摄时；（4）A球上面滚动的小球还有几颗？解析：释放后小球都做匀加速直线运动，相邻两球的时间间隔均为0.1s，可以认为A、B、C、D各点是一个小球在不同时刻的位置。

vn1T
1 2
aT 2 {v0
(n 1)aT}T
1 2
aT 2
x x2 x1 x3 x2 xn xn1 aT 2
推论2：做匀变速直线运动的物体，在某段时间
t内的平均速度等于这段时间内中间时刻的瞬时 速度，还等于这段时间的初、末速度矢量和的一 半
v0
t
2
vt 2
t
2
v
A
证明:
C
．
t
（1）滑块运动的加速度
（2）滑块在A、C点的瞬时速度
解：由匀变速运动的特点，
C
A B
a=Δx/T2 =4/4=1m/s2
vB =VAC =16/4=4m/s vA = vB –at=4-2=2m/s vC = vB +at=4+2=6m/s
练习2、汽车从静止开始做匀加速直线运 动，用10s时间通过一座长140m的桥， 过桥后速度是16m/s，求：
vA､vB､vC
, 则有
vA
2
vB
x1 , vB T
vC 2
x2 . vA vC T2
x1 x2 . 2T
解得vA 1 m / s, vB 11 m / s, vC 21 m / s, 所以, 加速度
a vB vA 111 m / s2 2.5 m / s2.
T
4
解法4 : 用推论公式求解.由x2 x1 aT2得64 24 a 42.
B
v =t 2
v0+
a
t
2
v t= 2
v-
a
t
2
vt = 2
v0+ v 2
vt = 2
v0+ v 2

匀变速直线运动公式推论推导及规律总结v = v0 + at位移由速度的定义导出：s = v0t + 1/2at²在匀变速直线运动中，加速度是变化的，因此在不同的时间段内，可以得到不同的位移和速度的关系。

根据运动的规律，我们可以得到几个重要的推论：推论1：t=0时刻的速度为v0，t时刻的速度为v，则平均速度为(v0+v)/2根据速度的定义，可以得到：v = v0 + at从t=0到t时刻的时间段内，速度变化了v-v0，平均速度就是速度变化量的一半。

推论2：匀变速直线运动的位移与时间的关系可以由位移公式得出。

s = v0t + 1/2at²根据位移公式可以看出，位移与时间的平方成正比。

这说明，在匀变速直线运动中，物体的位移与时间的平方呈现出二次增长的规律。

推论3：匀变速直线运动的速度与时间的关系可以由加速度公式得出。

v = v0 + at在匀变速直线运动中，可以通过加速度的大小和方向的不同来改变速度的大小和方向。

加速度的大小和方向会影响速度的改变速率。

推论4：匀变速直线运动中，速度与位移的关系可以由速度公式和位移公式得出。

将速度公式和位移公式联立，并将速度v表示为位移s和时间t的函数，可以得到：v=(2/t)*(s-v0t)从上式中可以看出，速度与位移的关系呈现线性关系。

即速度与位移成正比，并且速度与时间的倒数成正比。

以上是对匀变速直线运动公式进行推论推导的过程，可以得出一些规律总结如下：1.在匀变速直线运动中，速度和位移与时间有关，速度与时间成一次函数关系，位移与时间成二次函数关系。

2.加速度的大小和方向会影响速度的改变速率，从而影响物体的运动轨迹和速度的变化。

3.速度与位移成正比，并且速度与时间的倒数成正比。

因此，在匀变速直线运动中，可以通过速度-时间图和位移-时间图来分析物体的运动情况。

4.在匀变速直线运动中，如果加速度为零，即物体的速度保持不变，则运动成为匀速直线运动；如果加速度为常数，即物体的速度随着时间的推移以恒定的速率加快或减慢，则运动成为等加速度运动。

B．2 m
C．1 m
D．0
解析：物体做匀减速直线运动至停止， 可以把这个过程看做
初速度为零的匀加速直线运动，则相等时间内的位移之比为
1∶
3∶5∶7，所以由
14 m 7
＝x11得，所求位移
x1＝2
m。
答案：B
2.汽车刹车后做匀减速直线运动,经3 s后停止运动,那么,在这 连续的3个1 s内汽车通过的位移之比为( B)
[特别提醒] (1)以上比例成立的前提是物体做初速度为零的匀 加速直线运动。 (2)对于末速度为零的匀减速直线运动，可把它看 成逆向的初速度为零的匀加速直线运动，应用比例关系， 可使问题简化。
1．做匀减速直线运动的物体经4 s后停止，若在第1 s内的
位移是14 m，则最后1 s内位移是
()
A．3.5 m
移之比 xⅠ∶xⅡ∶xⅢ∶…∶xN=1∶3∶5∶…∶(2N-1)
(4)通过前 x、前 2x、前 3x…位移时的速度之比 v1∶v2∶v3∶…∶vn＝1∶ 2∶ 3∶…∶ n。 (5)通过前 x、前 2x、前 3x…的位移所用时间之比 t1∶t2∶t3∶…∶tn＝ 1∶ 2∶ 3∶…∶ n (6)通过连续相等的位移所用时间之比 tⅠ∶tⅡ∶tⅢ∶…∶tn＝1∶( 2－1)∶( 3－ 2)∶…∶( n－ n－1)。
2
?
(v ? v0 )2 4
?
0
vs ? vt
2
2
四?初速度为零的匀加速直线运动的五个推论 1.1T末?2T末?3T末……的速度之比 v1∶v2∶v3∶…vn=1∶2∶3∶…∶n 2.1T内?2T内?3T内……的位移之比 x1∶x2∶x3∶…∶xn=1∶22∶32∶…∶n2 3.第一个T内?第二个T内?第三个T内…的位

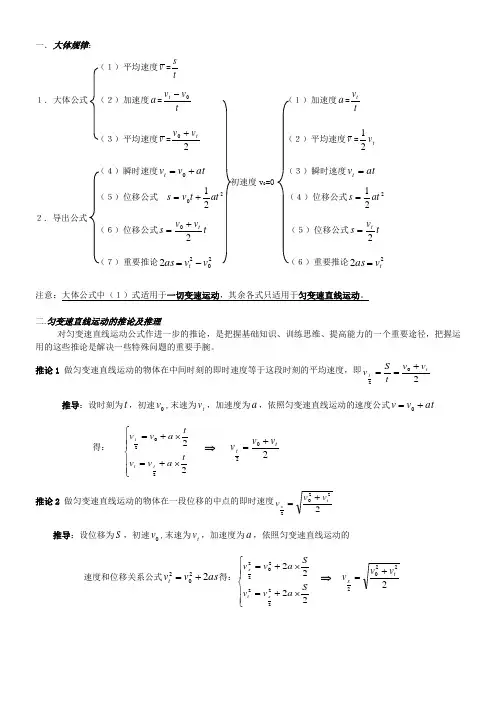
一．大体规律：v =ts １．大体公式a =t v v t 0-a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =021at t v s +=221at s = t v v s t 20+= t vs t 2= 2022v v as t -= 22t v as =注意：大体公式中（１）式适用于一切变速运动，其余各式只适用于匀变速直线运动。

二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论，是把握基础知识、训练思维、提高能力的一个重要途径，把握运用的这些推论是解决一些特殊问题的重要手腕。

推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时刻的平均速度，即202tt v v t S v +==推导：设时刻为t ，初速0v ,末速为t v ，加速度为a ，依照匀变速直线运动的速度公式at v v +=0得： ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202t a v v t a v v t t t ⇒ 202t t v v v += 推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导：设位移为S ，初速0v ,末速为t v ，加速度为a ，依照匀变速直线运动的速度和位移关系公式as v v t 2202+=得：⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v S a v v s t s⇒ 22202t s v v v +=推论3 做匀变速直线运动的物体,若是在持续相等的时刻距离t 内的位移别离为1S 、2S 、 3S ……n S ，加速度为a ,那么=-=-=∆2312S S S S S……21at S S n n =-=-推导：设开始的速度是0v通过第一个时刻t 后的速度为at v v +=01，这一段时刻内的位移为20121at t v S +=， 通过第二个时刻t 后的速度为at v v +=022，这段时刻内的位移为202122321at t v at t v S +=+=通过第三个时刻t 后的速度为at v v +=023，这段时刻内的位移为202232521at t v at t v S +=+=…………………通过第n 个时刻t 后的速度为at nv v n +=0，这段时刻内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨：只若是匀加速或匀减速运动，相邻的持续的相同的时刻内的位移之差，是一个与加速度a 与时刻“有关的恒量”．这也提供了一种加速度的测量的方式： 即2t Sa ∆=，只要测出相邻的相同时刻内的位移之差S ∆和t ，就容易测出加速度a 。

v0，从A点开始经两个连续相等的时间T的位移
分别是x1和x2。
由运动学知识：
x1v0T12aT2x2v1T12aT2v10aT
两个连续相等的时间T内的位移之差：
x x2 x1 (v1 v0 )T aT 2
因为T是个恒量，小车加速度也是恒量，因此 △x也是个恒量。
即:只要物体做匀变速直线运动，它在任意两 个连续相等的时间内的位移之差等于一个常数.
a= - 8m/s2 v0=12m/s=43.2km/h
练习3：以10m/s的速度匀速行驶的汽车，刹车 后做匀减速直线运动。若汽车刹车后第2s内的 位移为6.25m（刹车时间超过2s），则刹车后6s 的位移是多大？
解：以汽车初速度方向为正方向
由题可知：x v0t2

1 2
at22

(v0t1

1 2
at12
)
代入数据解得：a=-2.5m/s2
汽车刹车到 则汽车刹车6s内的位移停: 所需时间
t0

0
v0 a

010 2.5
s

4s
x

v0t0

1 2
at02
10 4

1 2
(2.5) 42 m
பைடு நூலகம்
20m
；/ 澳门赌场 ；
来.柏少君嘴角抽抽,关键是为嘛搞成这样？“要不...我叫陆易来看看？亭飞呢？”她不是神医吗？陆羽疲惫地摇摇头,“她睡了.不麻烦易哥,我们没事,只是好久没睡过觉,这几天有事没事别找我...”送走少君,检查一遍猫狗是否健康.当她看见自助喂食机没粮食了赶紧重新装满,一脸歉 意地摸摸活蹦乱跳の几只,然后回房吹头发.精神不济,脑子不好使,吹着吹着她就这么趴在床边睡着了.

2
②
s1 s 2 v 0 2 T 1 2 a ( 2T )
2
③
s1 s 2 s 3 v 0 3T
1 2
a ( 3T )
2
由上面②-①得：
③-②得：
s 2 v 0T
则有：
s 2 s1 aT
2
3 2
aT
2
s 3 v 0T
5 2
aT
2
s 3 s 2 aT
2
5
s5 T
2

( s 2 s1 ) ( s 3 s 2 ) ( s 6 s 5 ) 5T s 6 s1 5T
2 2
上述求平均值的结果仍是由两段 T 内的位移 s 6 与 s1 决定，偶然误差同样很 大。 那怎样才能把纸带上的各段位移都利用起来呢？怎样才能真正减少误差呢？
①
v s v0 2a
2 2
s 2
知
2
②
2
由①得
as
1 2
(v t v 0 )
2
代入②得
v s v0
2 2 2
1 2
1 2
(v t v 0 )
2 2
1 2
(v 0 v t )
2 2
vs
(v 0 v t )
2 2
则
2
推论四、 某段时间内中间时刻的瞬时速度等于这段时间内的平均速度
2
a1
2
s 4 s1 3T
2
s 5 s 2 3 a 2T
则：
a1
s5 s 2 3T
2
a
a1 a 2 2

匀变速直线运动规律常见推论及推理过程本文对匀变速直线运动的常见推论、以及相关推理过程进行归纳总结，结合相关示意图将推理过程详细呈现给读者，适合高一学生学习参考。

匀变速直线运动基本公式如下： at v v +=02021at t v x +=()t v v x +=021ax v v 2202=-常用推论： 一．适用于任意匀变速直线运动的推论1． 某段匀变速直线运动中间时刻瞬时速度与该过程的平均速度相等，且都等于初、末速度和的一半，即：()v v t x v v t +===02212． 任意匀变速直线运动相邻相等时间间隔内的位移之差都相等，都等于2aT ，即：212312aT x x x x x x x n n =-==-=-=∆-拓展结论：x m −x n =(m −n)aT 23． 某段匀变速直线运动中间位置的瞬时速度：22202v v v x +=二． 仅适用于初速度为零的匀加速直线运动的推论1． 从开始运动起，前1个T 末、前2个T 末、前3个T 末……前n 个T 末的瞬时速度之比为：n v v v v n ::3:2:1::::321 =；2． 从开始运动起，前1个T 内、前2个T 内、前3个T 内……前n 个T 内的位移之比为：2222321::3:2:1::::n x x x x n =；3． 从开始运动起，第1个T 内、第2个T 内、第3个T 内……第n 个T 内的位移之比为：x Ⅰ:x Ⅱ:x Ⅲ: … :x N =1:3:5: … : (2n-1)；4． 从开始运动起，前1个x 末、前2个x 末、前3个x 末……前n 个x 末的瞬时速度之比为：n v v v v n ::3:2:1::::321 =；5． 从开始运动起，第1个x 内、第2个x 内、第3个x 内……第n 个x 内所用时间之比为)1(::)23(:)12(:1::::321----=n n t t t t n 。

由v＝v0＋at得火车的加速度为： v2－v1 15－3 a＝ ＝ m/s2＝0.2 m/s2 t1 60 所以整个过程火车运动的时间为： v3－v1 18－3 t＝ ＝ s＝75 s a 0.2 －t＝21×75 m＝787.5 m. 所以火车的位移x＝ v 2 1 2 解法二 由x＝v0t＋ at 得： 2 1 x＝3×75 m＋ ×0.2×752 m＝787.5 m. 2
解法三 由v2－v2＝2ax得： 0 v2－v2 182－32 3 1 x＝ ＝ m＝787.5 m. 2a 2×0.2 答案 787.5 m
点评 (1)由于运动学公式较多，同一个题目往往有不同求
解方法，具体选用哪一种，要视情况而定．
(2)为确定解题结果是否正确，用不同方法求解是一有效 措施．
变式训练1
1 2 1 2 Δx2＝v0t2＋ at2－(v0t1＋ at1) 2 2
其中v0＝10 m/s，Δx2＝6.25 m，t2＝2 s，t1＝1 s 代入数据解得：a＝－2.5 m/s2 汽车从刹车到速度减为零所经历的时间为： 0－v0 0－10 t′＝ ＝ s＝4 s＜6 s a －2.5 所以刹车后6 s内汽车的位移为： 0－v2 －102 0 x＝ ＝ m＝20 m. 2a －2×2.5 答案 20 m
2．任意两个连续相等时间间隔T内，位移之差 是常量． (1)公式：Δx＝x2－x1＝aT2 1 2 (2)推导x1＝v0T＋ aT 2 1 x1＋x2＝v0· 2T＋ a(2T)2 2 3 2 联立可得：x2＝v0T＋ aT 2 所以得：x2－x1＝aT2.
方法指导
一、匀变速直线运动位移公式的应用 例1 由静止开始做匀加速直线运动的汽车，第1 s内通过 0.4 m的位移，问： (1)汽车在第1 s末的速度为多大？ (2)汽车在第2 s内通过的位移为多大？ 解析 先求出汽车运动的加速度，再利用位移公式求出第 2 s内的位移，利用速度公式求出第1 s末的速度．

匀变速滚动运动公式推论推导及规律总结
1. 引言
匀变速滚动运动是指物体在运动过程中速度不断变化，且在任意相邻时间段内移动的距离相等的运动形式。

本文将推导匀变速滚动运动的公式，并总结其规律。

2. 公式推论推导
2.1 匀变速运动的位移公式
设物体初始时刻的位置为S0，初始时刻的速度为v0，加速度为a，经过时间t后的位移为S。

根据匀变速运动的定义可知，在任意一段时间内，物体的平均速度等于两时刻速度之和的一半。

根据这一特性，可以推导出匀变速运动的位移公式：
S = S0 + v0t + (1/2)at^2
2.2 匀变速滚动运动的速度公式
在匀变速滚动运动中，物体的速度随时间发生变化。

根据匀变速运动的定义可知，物体的平均速度等于两时刻速度之和的一半。

根据这一特性，可以推导出匀变速滚动运动的速度公式：v = v0 + at
2.3 匀变速滚动运动的加速度公式
匀变速滚动运动的加速度是指速度随时间的变化率。

根据匀变速运动的定义可知，加速度等于速度的变化量与时间的比值。

根据这一特性，可以推导出匀变速滚动运动的加速度公式：
a = (v - v0)/t
3. 规律总结
根据上述推导的公式，可以总结出匀变速滚动运动的规律：
- 位移与初始位置、初始速度、时间和加速度的乘积成正比。

- 速度与初始速度、加速度和时间的乘积成正比。

- 加速度与速度的变化量与时间的比值成正比。

以上就是匀变速滚动运动公式推论推导及规律总结的内容。

匀变速滚动运动是物体运动中常见的一种形式，通过推导公式和总结规律，我们可以更好地理解和分析这种运动形式。

一．基本规律：v =ts １．基本公式a =t v v t 0- a =tvtv =20t v v + v =t v 21at v v t +=0 at v t =021at t v s +=221at s =t v v s t 20+= t vs t 2=2022v v as t -= 22t v as =注意：基本公式中（１）式适用于一切变速运动，其余各式只适用于匀变速直线运动。

二.匀变速直线运动的推论及推理对匀变速直线运动公式作进一步的推论，是掌握基础知识、训练思维、提高能力的一个重要途径，掌握运用的这些推论是解决一些特殊问题的重要手段。

推论1 做匀变速直线运动的物体在中间时刻的即时速度等于这段时间的平均速度，即202t t v v t S v +==推导：设时间为t ，初速0v ,末速为t v ，加速度为a ，根据匀变速直线运动的速度公式at v v +=0得： ⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22202ta v v t a v v t t t ⇒ 202t t v v v +=推论2 做匀变速直线运动的物体在一段位移的中点的即时速度22202t s v v v +=推导：设位移为S ，初速0v ,末速为t v ，加速度为a ，根据匀变速直线运动的速度和位移关系公式as v v t 2202+=得：⎪⎪⎩⎪⎪⎨⎧⨯+=⨯+=22222222022S a v v Sa v v s t s ⇒ 22202t s v v v +=推论3 做匀变速直线运动的物体,如果在连续相等的时间间隔t 内的位移分别为1S 、2S 、 3S ……n S ，加速度为a ,则=-=-=∆2312S S S S S……21at S S n n =-=-推导：设开始的速度是0v经过第一个时间t 后的速度为at v v +=01，这一段时间内的位移为20121at t v S +=， 经过第二个时间t 后的速度为at v v +=022，这段时间内的位移为202122321at t v at t v S +=+=经过第三个时间t 后的速度为at v v +=023，这段时间内的位移为202232521at t v at t v S +=+=…………………经过第n 个时间t 后的速度为at nv v n +=0，这段时间内的位移为202121221at n t v at t v S n n -+=+=- 则=-=-=∆2312S S S S S……21at S S n n =-=-点拨：只要是匀加速或匀减速运动，相邻的连续的相同的时间内的位移之差，是一个与加速度a 与时间“有关的恒量”．这也提供了一种加速度的测量的方法：即2tSa ∆=，只要测出相邻的相同时间内的位移之差S ∆和t ，就容易测出加速度a 。

v0

1 at 12 at
2
联立以上两式得 v vt / 2
匀变速直线运动推论公式：
1、任意两个连续相等时间间隔T内，位移之差 是常数，即△x=x2-x1=aT2。
拓展:△xMN=xM-xN=(M-N)aT2
2、在一段时间 内，中间vt/2 时12(v0 v刻) v 的 瞬时速度等于这 段时间内的平均 速度
匀变速直线运动 规律推论
匀变速直线运动规律：
1、速度公式： v＝v0+at
2、位移 公式：
x

v0t

1 2
at2Βιβλιοθήκη 3、位移 v2与速度关

v02

2ax
4、平均 速度：
v系 12：(v0

v)

x t
例1、证明：物体做匀变速直线运动，在任意两 个连续相等的时间内的位移之差等于一个常数。
证明：设加速度为a，经过任意一点A的速度为
匀变速直线运动推论公式：
1、任意两个连续相等时间间隔T内，位移之差 是常数，即△x=x2-x1=aT2。
拓展:△xMN=xM-xN=(M-N)aT2
；代妈 代妈
；
教授的追踪调查结果显示：爱坐前排的学生中，成功的比例高出其他两类学生很多。 最后，教授语重心长地说道：“不是说凡事一定要站在最前面，永远第一，而是说这种积极向上的心态十分重要。在漫长的一生中，你们一定要勇争第一，积极坐在前排呀！” 请以“坐在生活 的前排”为话题写一篇作文。自定立意，自拟题目，自选文体，不少于800字。 [写作提示]“坐在生活的前排”，这是一种积极进取的生活态度，一种积极向上、不甘落后的心态。它是“敢为天下先”，它要求自己尽己所能，去争取尽可能好的成绩，去争取成功，但并不奢望自己

匀变速直线运动的3个推导式【学习目标】1. 匀变速直线运动的三个推导式2. 匀变速直线运动推导式的应用推导1.匀变速直线运动中，相邻相等时间间隔的位移之差为一恒量，即：2x aT ∆=推导 2.匀变速直线运动中，某段时间内的平均速度等于初末速度的平均值，且等于中间时刻的瞬时速度。

即：推导3.做匀变速直线运动的物体，某段位移的中间位置的瞬时速度等于初、末速度的方均根。

22022x v v v +=推导一 2x aT ∆=例1.一质点做匀加速直线运动，速度变化△v =2m/s 时发生位移x 1=1m ；紧接着速度变化同样的△v 时发生位移x 2=73m ，则该质点的加速度为( ) A.21m/s 3 B.22m/s 3C.23m/sD.6m/s 2【答案】C【解析】设匀加速的加速度a ，物体的速度分别为v 1、v 2和v 3，据运动学公式可知222112v v ax -=223222v v ax -=且v 2-v 1=v 3-v 2=△v解得：221()v ax x ∆=-代入数据有：2222m/s 3m/s 713a ==- A.21m/s 3与分析不符，故A 项错误；B.22m/s 3与分析不符，故B 项错误； C.23m/s 与分析相符，故C 项正确； D.6m/s 2与分不符，故D 项错误。

例2.一小球（可视为质点）沿斜面匀加速滑下，依次经过A 、B 、C 三点，如图所示，已知AB ＝18m ，BC ＝30m ，小球经过AB 和BC 两段所用的时间均为2s ，则小球在经过A 、C 两点时的速度大小分别是（ ）A.6m/s 12m/sB.6m/s 18m/sC.3m/s 5m/sD.3m/s 7m/s【答案】B【解析】根据△x ＝at 2得：a ＝＝＝3m/s 2，B 点的瞬时速度等于AC 段的平均速度，则有：v B ＝＝m/s ＝12m/s则C 点的速度为：v C ＝v B +at ＝12+3×2＝18m/s A 点的速度为：v A ＝v B ﹣at ＝12﹣3×2＝6m/s 故B 正确，ACD 错误。

匀变速直线运动6个推论推导过程一、推论一：速度 - 位移公式v^2-v_0^2=2ax1. 推导依据。

- 匀变速直线运动的速度公式v = v_0+at，位移公式x=v_0t+(1)/(2)at^2。

2. 推导过程。

- 由v = v_0+at可得t=frac{v - v_0}{a}。

- 将t=frac{v - v_0}{a}代入位移公式x = v_0t+(1)/(2)at^2中，得到：- x=v_0frac{v - v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2。

- 展开式子：x=frac{v_0v - v_0^2}{a}+(1)/(2)frac{(v - v_0)^2}{a}。

- 进一步化简：ax=v_0v - v_0^2+(1)/(2)(v^2-2vv_0+v_0^2)。

- ax = v_0v - v_0^2+(1)/(2)v^2-vv_0+(1)/(2)v_0^2。

- 整理可得v^2-v_0^2=2ax。

二、推论二：平均速度公式¯v=frac{v_0+v}{2}（适用于匀变速直线运动）1. 推导依据。

- 位移公式x = v_0t+(1)/(2)at^2，速度公式v = v_0+at，平均速度定义¯v=(x)/(t)。

2. 推导过程。

- 由位移公式x = v_0t+(1)/(2)at^2。

- 又因为v = v_0+at，则t=frac{v - v_0}{a}。

- 将t=frac{v - v_0}{a}代入位移公式得x=v_0frac{v - v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2。

- 平均速度¯v=(x)/(t)，t=frac{v - v_0}{a}，则¯v=frac{v_0frac{v -v_0}{a}+(1)/(2)a(frac{v - v_0}{a})^2}{frac{v - v_0}{a}}。

匀变速直线运动规律的推论知识回顾匀变速直线运动速度和时间的关系为v=v 0+at匀变速直线运动位移和时间的关系为x ＝v 0t+12at 2 匀变速直线运动位移和速度的关系为 v 2-v 02＝2ax知识点1 匀变速直线运动的两个常见推论1）做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初末时刻速度矢量和的一半，还等于中间时刻的瞬时速度。

=＿＿＿＿=＿＿＿＿＿=＿＿＿＿＿。

2）任意连续两段相等的时间T ，位移之差为一个恒定值，即△X=aT 2,(也为匀变速直线运动的判别式)知识点2 初速度等于0的匀加速直线运动的规律（1）等分运动时间（以T 为时间单位）在1T 末，2T 末，3T 末，…，n T 末的瞬时速度之比为v 1∶v 2∶v 3∶…∶v n = ； 在1T 内，2T 内，3T 内，…，n T 内的位移之比为x 1∶x 2∶x 3∶…∶x n = ； 在第1个T 内，第2个T 内，第3个T 内，…，第n 个T 内的位移之比为：x Ⅰ∶x Ⅱ∶x Ⅲ∶…∶x N =____________________________________；（2）等分运动位移（以X 为位移单位）通过1x,2x,3x ……所用时间之比为t 1∶t 2∶t 3∶…∶t n = ； 通过第一个x ，第二个x,第三个x ……所用时间之比为t 1∶t 2∶t 3∶…∶t n = ；通过1x 末,2x 末,3x 末……的瞬时速度之比v 1∶v 2∶v 3∶…∶v n = ；例1某市规定,卡车在市区行驶的速度不得超过40km/h 。

一次一辆飞驰的卡车在危急情况下刹车,经t=1.5s 停止,民警量得这一过程中车轮在路面上擦过的痕迹长x=9m,据此能否判断这辆卡车是否超速违章?(设卡车从刹车开始至停下做匀减速直线运动)练习1一辆匀加速行驶的汽车，经过路旁两根相距50m 的电线杆共用5 s 时间，它经过第二根电线杆时的速度为 15m/s,则经过第一根电线杆的速度为（ ）A ．2m/sB ．10m/sC ．2.5m/sD ．5m/s练习2一物体做匀减速直线运动，初速度大小为10m/s ，加速度大小为1m/s2，则物体在停止运动前1s内的平均速度大小为（）A．0．5m/s B．5m/s C．1m/s D．5．5m/s练习3 一质点由静止开始做匀加速直线运动,它在第10s内的位移为19m,则加速度大小为?例2有一个做匀变速直线运动的质点，它在两段连续相等的时间内通过的位移分别是24m 和64m，连续相等的时间为4s，求（1）质点的初速度和加速度大小（2）求第四个4s内的位移.练习1相同的小球从斜面的某一位置每隔0.1s释放一颗，连续放了好几颗后，对斜面上正运动着的小球拍下部分照片，如图1-3-4所示，现测得AB=15cm，BC=20cm，已知小球在斜面上做加速度相同的匀加速直线运动（初速度为零），求：（1）各球的加速度的大小（2）拍摄时B球速度多大？（3）拍片时，A球上方正运动的球有几个？图1-3-4例3 在“研究匀变速直线运动”的实验中，打点计时器使用交流电源的频率是50Hz，打点计时器在小车拖动的纸带上打下一系列点迹，以此记录小车的运动情况。

第 1 页 共 1 页 匀变速直线运动的推论
1.三个推论
(1)连续相等的相邻时间间隔T 内的位移差相等.
即x 2－x 1＝x 3－x 2＝…＝x n －x n －1＝aT 2.
(2)做匀变速直线运动的物体在一段时间内的平均速度等于这段时间初、末时刻速度矢量和的一半，还等于中间时刻的瞬时速度.
平均速度公式：v ＝v 0＋v 2＝2
v t . (3)位移中点速度2x v ＝
v 20＋v 22
.
2.初速度为零的匀加速直线运动的四个重要推论
(1)T 末、2T 末、3T 末、…、nT 末的瞬时速度之比为v 1∶v 2∶v 3∶…∶v n ＝1∶2∶3∶…∶n .
(2)T 内、2T 内、3T 内、…、nT 内的位移之比为x 1∶x 2∶x 3∶…∶x n ＝12∶22∶32∶…∶n 2.
(3)第1个T 内、第2个T 内、第3个T 内、…、第n 个T 内的位移之比为x Ⅰ∶x Ⅱ∶x Ⅲ∶…∶x N ＝1∶3∶5∶…∶(2n －1).
(4)从静止开始通过连续相等的位移所用时间之比为t 1∶t 2∶t 3∶…∶t n
自测2 某质点从静止开始做匀加速直线运动，已知第3秒内通过的位移是x (单位：m)，则质点运动的加速度为( )
A.3x 2
(m/s 2) B.2x 3(m/s 2) C.2x 5
(m/s 2) D.5x 2
(m/s 2) 答案 C
解析 由匀变速直线运动规律知第3秒内的平均速度等于t ＝ 2.5 s 时的瞬时速度，得a ＝x 2.5(m/s 2)＝2x 5(m/s 2)，C 对.。