小数点移动的计算方法

小数的移动规律知识点小数的移动规律是数学中一个重要的概念，对于小数的加减乘除运算以及科学计数法的使用都有重要的意义。

本文将介绍小数的移动规律及其应用。

一、小数的移动规律小数的移动规律是指在小数中加上或减去一个数时，小数点的位置也相应地向右或向左移动相同的位数。

例如，2.3加上0.7时，可以将0.7的小数点向右移动一位，变为7，然后将其与2.3相加得到3，在最后的结果中再将小数点向左移动一位，得到3.0。

同样地，在小数中乘以或除以一个数时，小数点的位置也相应地向右或向左移动相同的位数。

例如，2.3乘以10时，可以将2.3的小数点向右移动一位，变为23，得到结果23.0。

再例如，1.5除以0.1时，可以将1.5的小数点向左移动一位，变为0.15，得到结果15.0。

二、小数的加减乘除运算使用小数的移动规律可以方便地进行小数的加减乘除运算。

例如，将2.3加上0.7时，可以将0.7的小数点向右移动一位，变为7，然后将其与2.3相加得到3，在最后的结果中再将小数点向左移动一位，得到3.0。

同样地，将2.3减去0.7时，也可以将0.7的小数点向右移动一位，变为7，然后将其与2.3相减得到1.6，在最后的结果中再将小数点向左移动一位，得到1.6。

在小数的乘除运算中，也可以使用小数的移动规律。

例如，将2.3乘以10时，可以将2.3的小数点向右移动一位，变为23，得到结果23.0。

同样地，将1.5除以0.1时，可以将1.5的小数点向左移动一位，变为0.15，得到结果15.0。

三、科学计数法的使用科学计数法是一种表示非常大或非常小的数的方法。

它由一个实数与10的幂的乘积表示，其中实数的绝对值必须大于等于1且小于10，指数为一个整数。

例如，1.23×10^3就是用科学计数法表示的1230。

在科学计数法中，使用小数的移动规律可以方便地进行数的乘除运算。

例如，将1.23×10^3乘以2.5×10^2时，可以将1.23与2.5相乘得到3.075，指数为3+2=5，因此结果为3.075×10^5。

小数移位的技巧
小数移位是一种常见的数学技巧，用于改变小数的位置，使其更容易进行计算或比较。

这个技巧可以应用于各种数学问题和实际应用中。

下面将介绍一些常见的小数移位技巧及其拓展应用。

1. 小数点向左移位：当小数点向左移动一位时，数值变为原来的十分之一。

这个技巧常用于除法运算中，可以简化计算过程。

例如，计算0.25除以10，可以将小数点向左移动一位，变为0.025。

这样就可以更容易地进行除法运算。

2. 小数点向右移位：当小数点向右移动一位时，数值变为原来的十倍。

这个技巧常用于乘法运算中，可以快速计算出结果。

例如，计算0.3乘以100，可以将小数点向右移动两位，变为30。

这样就可以直接得出结果。

3. 移位运算的应用：小数移位技巧不仅在基本数学运算中有应用，还可以拓展到其他领域。

例如，在编程中，移位运算可以用于快速计算小数的乘除法。

通过将小数转化为整数，进行移位运算，然后再转回小数，可以提高运算效率。

4. 小数的规范表示：小数移位技巧也可以用于规范小数的表示方式。

例如，当小数的小数点前面没有数字时，可以通过向左移位，将小数点移到第一个非零数字的位置，或者移到整数部分的末尾，以使表示更规范。

这在科学计数法中常见，例如将0.000025表示为2.5 x 10^-5。

小数移位技巧是数学中一个简单而实用的技巧，可以帮助我们更有效地进行数值运算和表示。

通过掌握这些技巧，我们可以更加灵活地处理小数，并简化数学问题的求解过程。

无论是在日常生活中还是在学习和工作中，小数移位技巧都是一个非常有用的工具。

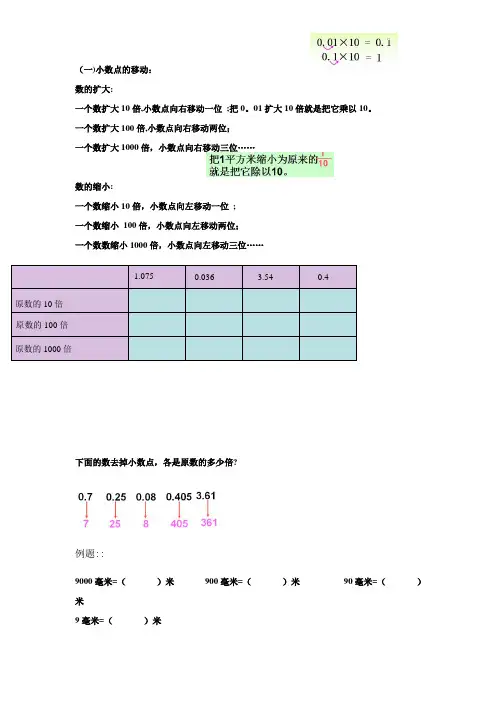
（一)小数点的移动：数的扩大:一个数扩大10倍,小数点向右移动一位 ;把0。

01扩大10倍就是把它乘以10。

一个数扩大100倍,小数点向右移动两位；一个数扩大1000倍，小数点向右移动三位……数的缩小:一个数缩小10倍，小数点向左移动一位 ;一个数缩小 100倍，小数点向左移动两位；一个数数缩小1000倍，小数点向左移动三位…… 例题： 在下表的空格里填上正确的数:下面的数去掉小数点，各是原数的多少倍?例题::9000毫米=（ ）米 900毫米=（ ）米 90毫米=（）米9毫米=（ ）米 原数的10倍 原数的100倍 原数的1000倍 1.075 0.036 3.54 0.40.001米=( )毫米0。

01米=（)毫米0。

1米=（）毫米1米=（）毫米1、判断题。

（1）0.001×1000＝10 （）（2）15.6÷100＝1.56 （）(3)0。

207的小数点向右最多移三位，所以0.207最多只能扩大1000倍. （)2、单选题。

（1)把40。

28去掉小数点变成整数,原数就（）A、缩小100倍B、扩大100倍C、缩小2倍D、扩大2倍（2）把0.02的小数点向左移动一位后再向右移动三位得（）A、2B、0。

2C、20D、200（3）把一个小数的小数点先向右移动五位,再向左移动三位,那么移动后的小数比原小数( ）A、扩大3倍B、扩大100倍C、缩小1000倍3、在横线上填上适当的数或文字。

(1）把0。

43扩大_________倍是430。

把0。

1_ 倍是0。

01。

把10。

45扩大100倍是_________，小数点向左移动三位是_________。

（2）0.54扩大100倍是_________，再缩小1000倍是_________。

（3）有甲、乙、丙三个数，若把甲数的小数点向右移动三位，乙数的小数点向左移动四位，得到的两个数正好与丙数相等，若丙数是7。

04，则甲数是_________，乙数是_________。

小数点的移动简介小数点的移动是数学中的一种操作，指的是将一个数的小数点向左或向右移动一定的位数。

小数点的移动在数值计算、科学研究和工程设计等领域中经常应用到。

本文将介绍小数点的移动的原理、方法和应用案例。

原理小数点的移动是通过改变数字符号位来实现的。

当小数点向左移动时，数字符号位的指数增加，当小数点向右移动时，数字符号位的指数减小。

根据数字符号位的指数变化，小数点的位移可以用科学记数法来表示，例如，移动2位就是乘以10的2次方，移动-3位就是除以10的3次方。

方法小数点的移动可以通过以下两种方法实现：方法一：乘法或除法可以将需要移动的数与10的幂次方相乘或相除来实现小数点的移动。

例如，将数值5.6向右移动3位，可以将其除以10的3次方，即5.6 / 1000 = 0.0056。

方法二：科学记数法可以将需要移动的数表示为科学记数法的形式，并通过改变指数来实现小数点的移动。

例如，将数值8.9向左移动2位，可以将其表示为8.9 × 10的2次方，即8.9 × 100 = 890。

应用案例小数点的移动在各个领域中得到广泛应用，在以下几个方面有着重要的作用：1. 科学研究在科学研究中，需要对非常大或非常小的数进行计算和比较。

小数点的移动可以方便地将数值调整到合适的范围，以便进行精确的计算和分析。

例如，天文学家使用小数点的移动来处理宇宙中的距离和质量等数据。

2. 工程设计在工程设计中，小数点的移动可以用于测量数据的单位转换和计算结果的精度控制。

例如，建筑设计师使用小数点的移动来处理长度、体积和重量等数据，以便进行准确的设计和施工。

3. 经济和金融在经济和金融领域，小数点的移动可以方便地处理货币计算、利率计算和投资分析等问题。

例如，金融分析师使用小数点的移动来计算股票收益率和债券价格等指标。

4. 计算机科学在计算机科学中，小数点的移动被广泛应用于浮点数的表示和计算。

小数点的移动可以通过改变指数位来调整浮点数的范围和精度，以适应不同的计算需求。

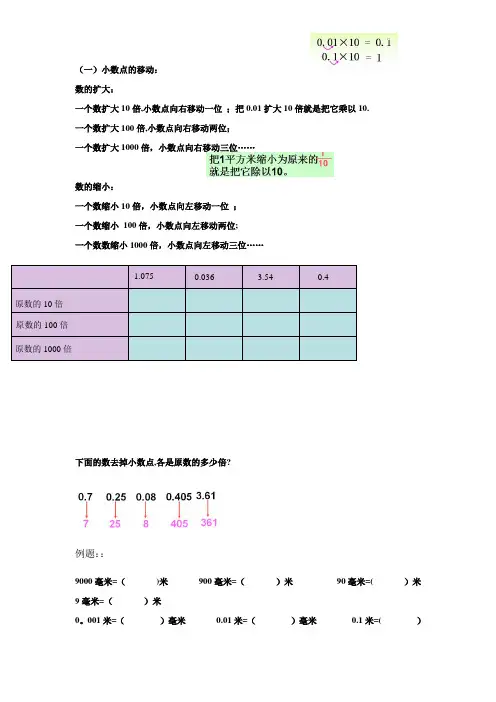
（一）小数点的移动：数的扩大：一个数扩大10倍,小数点向右移动一位 ；把0.01扩大10倍就是把它乘以10.一个数扩大100倍,小数点向右移动两位；一个数扩大1000倍，小数点向右移动三位……数的缩小：一个数缩小10倍，小数点向左移动一位 ；一个数缩小 100倍，小数点向左移动两位;一个数数缩小1000倍，小数点向左移动三位…… 例题： 在下表的空格里填上正确的数：下面的数去掉小数点,各是原数的多少倍?例题：：9000毫米=（ )米 900毫米=（ ）米 90毫米=(）米 9毫米=（ ）米0。

001米=（ ）毫米 0.01米=（ ）毫米 0.1米=(）原数的10倍 原数的100倍 原数的1000倍 1.075 0.036 3.54 0.4毫米1米=（)毫米1、判断题。

（1）0.001×1000＝10 （)(2）15。

6÷100＝1.56 （)(3)0.207的小数点向右最多移三位，所以0.207最多只能扩大1000倍. ( ）2、单选题。

(1）把40。

28去掉小数点变成整数，原数就( ）A、缩小100倍B、扩大100倍C、缩小2倍D、扩大2倍（2）把0.02的小数点向左移动一位后再向右移动三位得（）A、2B、0.2C、20D、200(3）把一个小数的小数点先向右移动五位,再向左移动三位,那么移动后的小数比原小数（）A、扩大3倍B、扩大100倍C、缩小1000倍3、在横线上填上适当的数或文字。

(1）把0.43扩大_________倍是430。

把0.1_ 倍是0.01。

把10.45扩大100倍是_________,小数点向左移动三位是_________。

（2)0。

54扩大100倍是_________，再缩小1000倍是_________。

（3）有甲、乙、丙三个数，若把甲数的小数点向右移动三位，乙数的小数点向左移动四位,得到的两个数正好与丙数相等，若丙数是7。

04，则甲数是_________，乙数是_________。

c语言小数点移位全文共四篇示例，供读者参考第一篇示例：C语言是一种广泛应用的计算机编程语言，其功能强大且灵活性高，在软件开发领域有着广泛的应用。

在C语言中，有关小数点移位的操作是一项常见且重要的功能。

小数点移位是指将一个数的小数点向左或向右移动若干位，从而改变数值的大小和精度。

在这篇文章中，我们将详细介绍C语言中的小数点移位操作，包括移位的原理、移位的方法和应用示例等内容。

一、小数点移位的原理在C语言中，小数点移位是通过对浮点数进行位运算来实现的。

浮点数是由两个部分组成的：尾数和指数。

尾数表示数值的大小，指数表示小数点的位置。

通过改变指数的值，就可以实现小数点的移位。

当指数增大时，小数点向右移动，数值变大；当指数减小时，小数点向左移动，数值变小。

在C语言中，可以通过移位操作符和位运算来实现小数点的移位。

常用的移位操作符包括<<和>>，分别表示左移和右移。

具体方法如下：1. 左移操作符：<<左移操作符<<可以将一个数的二进制表示向左移动若干位。

左移n位相当于将数值乘以2的n次方。

假设有一个浮点数x，要将其小数点向左移动n位，则可以使用以下代码：```cx = x * pow(2, n);```以下是一个简单的示例，演示如何在C语言中实现小数点的移位操作：```c#include <stdio.h>#include <math.h>x = x * pow(2, n); // 将小数点向左移动两位printf("移位后的值为：%f\n", x);return 0;}```运行以上代码，输出结果为：```移位后的值为：12.56```通过上述示例可以看出，将小数点向左移动两位后，数值变为12.56。

小数点移位是C语言中一项常见的操作，通过改变小数的指数值，可以实现小数点的移动，从而改变数值的大小和精度。

在实际开发中，小数点移位常用于数据处理和算法优化等方面，能够提高程序的性能和效率。

五年级上册小数单元的换算一、小数点位置移动1.移动小数点的意义：移动小数点实际上就是根据10的倍数关系移动小数点的位置。

2.移动小数点的方法：（1）小数点向右移动：将原数乘10的n次方，其中n为小数点向右移动的位数。

（2）小数点向左移动：将原数除以10的n次方，其中n为小数点向左移动的位数。

二、小数大小比较1.比较方法：先比较整数部分，再比较小数部分，从高位到低位依次进行比较。

2.比较规则：（1）整数部分相同，小数部分不同，则小数大的反而小。

（2）整数部分和十分位相同，百分位不同，则百分位大的反而大。

（3）整数部分、十分位和百分位都相同，千分位不同，则千分位大的反而大。

三、小数与整数互化1.小数化整数：将小数点向左移动，直至小数点移动到整数部分为止。

2.整数化小数：将整数乘以期数（如10, 100, 1000等）。

四、小数与分数互化1.小数化分数：将小数乘以分子和分母的最大公约数，再化简分数。

2.分数化小数：用分子除以分母，得到的小数即为所求。

五、小数加减法1.计算方法：相同数位对齐，从低位加起，满十进一。

2.注意点：在进行加减法运算时，要遵循运算顺序，先算乘除后算加减。

六、小数乘法1.计算方法：先按整数乘法法则计算，再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

2.注意点：在进行乘法运算时，要遵循运算顺序，先算乘除后算加减。

七、小数除法1.计算方法：先将除数变为整数（除数的小数点向右移动几位，被除数的小数点也向右移动相同的位数），再按照整数除法法则进行计算。

2.注意点：在进行除法运算时，要遵循运算顺序，先算乘除后算加减。

八、小数混合运算1.混合运算的顺序与整数的混合运算顺序相同。

2.在进行混合运算时，要注意优先级问题：括号>乘除>加减。

3.对于带有小数的混合运算，要特别注意运算顺序和精度问题。

九、小数的应用1.小数的应用广泛，例如在生活中我们经常会用到小数来进行度量、计算等操作。