六年级数学计算阴影部分的面积(一)

六年级求阴影面积练习题阴影面积是数学中一个常见的概念，通常以几何图形的形式出现。

在六年级中，学生需要掌握求解阴影面积的基本方法。

本篇文章将为大家提供一些六年级上阴影面积练习题，并给出相应的解答与解题步骤。

练习题一：下图是一个矩形，阴影部分是一个三角形，求阴影部分的面积。

```__________________| | || | ||__________|_______|```解答与解题步骤：1. 观察图形，我们可以发现矩形与阴影部分之间存在一条直线；2. 这条直线正好是矩形的对角线，所以阴影部分是矩形的一半；3. 根据矩形的面积公式 S = 长 ×宽，可以得出阴影部分的面积为(长 ×宽) ÷ 2。

练习题二：下图是一个圆形与一个矩形的组合图形，求阴影部分的面积。

```20cm___________| | 30cm20cm| 阴影 ||___________|```解答与解题步骤：1. 我们可以将阴影部分分成两个部分：矩形和扇形；2. 首先，求矩形的面积。

根据矩形的面积公式 S = 长 ×宽，可以得出矩形的面积为 20cm × 30cm；3. 其次，求扇形的面积。

扇形的面积公式为S = πr² × (θ/360°)，其中 r 为半径，θ 为扇形的角度。

在这个题目中，半径为 20cm，角度为90°；4. 将矩形的面积与扇形的面积相加，即可得到阴影部分的面积。

练习题三：下图是一个梯形，求阴影部分的面积。

```12cm___________| | 24cm6cm | 阴影 ||___________|```解答与解题步骤：1. 观察图形，我们可以发现阴影部分是梯形中较小的一个三角形；2. 求解阴影部分的面积，可以先求梯形的面积，再减去较大三角形的面积；3. 首先，求梯形的面积。

梯形的面积公式为 S = (上底 + 下底) ×高÷ 2。

求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：?圆面积减去等腰直角三角形的面积，?×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个?圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米?（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5 例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，所以阴影面积为：π÷4-12.5=7.125平方厘米?(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

六年级数学求阴影面积与周长例1.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例2.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例3.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

(单位:厘米)解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积。

1、几何图形计算公式1)正方形：周长＝边长×4C=4a面积=边长×边长S=a×a2)正方体：表面积=棱长×棱长×6S表=a×a×6体积=棱长×棱长×棱长V=a×a×a3)长方形：周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4)长方体：表面积=(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)体积=长×宽×高V=abh5)三角形：面积=底×高÷2s=ah÷26)平行四边形：面积=底×高s=ah7)梯形：面积=(上底+下底)×高÷2s=(a+b)×h÷28)圆形：周长=直径×Π=2×Π×半径C=Πd=2Πr面积=半径×半径×Π9)圆柱体：侧面积=底面周长×高表面积=侧面积+底面积×2体积=底面积×高10)圆锥体：体积=底面积×高÷32、面积求解类型.面积求解类型从整体图形中减去局部；割补法：将不规则图形通过割补，转化成规则图形。

重难点：观察图形的特点，根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

练习题例1.求阴影部分的面积。

(单位:厘米)例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)例3.求图中阴影部分的例4.求阴影部分的面面积。

(单位:厘米)积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

(单位:厘米)例8.求阴影部分的面积。

六年级容斥原理求阴影部分面积容斥原理是数学中一种常用的计数方法，可以用于解决一些重叠问题。

在六年级数学课程中，容斥原理也被引入，用来求解一些具体问题。

本文将着重介绍如何利用容斥原理来求解阴影部分的面积问题。

问题描述我们考虑一个简化的问题：一个正方形A和一个圆形B被放置在坐标系中，如图所示。

我们需要求解阴影部分的面积。

________| 正方形A ||________|___| || B ||___|已知正方形A的边长为2，圆形B的半径为1。

我们需要计算出阴影部分的面积。

解决思路利用容斥原理容斥原理可以帮助我们解决一些重叠问题。

在这个问题中，我们可以利用容斥原理来求解阴影部分的面积。

容斥原理的基本思想是，我们可以通过求解各个部分的面积，再进行一些相应的加减运算，来得到最后的结果。

分解问题首先，我们可以将问题分解为两个简单的部分：正方形A的面积和圆形B的面积。

然后，我们再分别求解这两部分的面积。

求解正方形A的面积正方形A的边长为2，那么它的面积就是2乘以2，即4平方单位。

求解圆形B的面积圆形的面积公式为：面积= π * 半径的平方。

圆形B的半径为1，那么它的面积就是π * 1的平方，即π平方单位。

求解阴影部分的面积接下来，我们需要求解阴影部分的面积。

根据容斥原理，我们可以通过以下公式求解：阴影部分的面积 = 正方形A的面积 - 圆形B的面积将之前计算得到的数值代入公式，我们可以得到：阴影部分的面积 = 4 - π平方单位这就是阴影部分的面积的具体数值。

结论根据我们之前的计算，阴影部分的面积为4 - π平方单位。

以上就是利用容斥原理来求解阴影部分面积的具体步骤。

通过将问题分解为一些简单的部分、计算各个部分的面积，并利用容斥原理进行加减运算，我们可以得到最后的结果。

在这个例子中，我们通过容斥原理求解了一个简单的阴影面积问题，但容斥原理在更复杂的问题中也同样有着广泛的应用。

希望本文对你理解容斥原理的求解过程有所帮助！。

求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法： 圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为 r ，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例 3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积， 16-π()=16-4π=3.44平方厘米例 5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见， 我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形， π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分） π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5 所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

人教版小学六年级上册数学计算阴影部分的面积在一个长为6m、宽为3m的长方形中，画了一个最大的半圆。

现在需要计算图中阴影部分的面积和周长。

为了计算阴影部分的面积和周长，需要先确定半圆的半径。

由于半圆是最大的，因此它的直径应该等于长方形的宽。

所以半径为1.5m。

阴影部分可以分为两个部分：长方形和半圆的组合部分和半圆外的部分。

首先计算长方形和半圆的组合部分的面积和周长。

长方形的面积为18m²，周长为18m。

半圆的面积为7.07m²，周长为4.71m。

组合部分的面积为25.07m²，周长为22.71m。

然后计算半圆外的部分的面积和周长。

半圆外的部分是一个矩形，长为6m，宽为1.5m。

面积为9m²，周长为15m。

最后将组合部分和矩形的面积相减，得到阴影部分的面积为16.07m²。

周长为37.71m。

在一个正方形中剪下一个面积为314厘米²的1/4圆，现在需要计算阴影部分的面积。

首先需要确定正方形的边长。

由于1/4圆的面积为314厘米²，因此整个圆的面积为1256厘米²。

圆的面积公式为S=πr²，所以圆的半径为20厘米。

正方形的面积为1256-314=942厘米²。

正方形的边长为√942≈30.68厘米。

阴影部分是正方形和1/4圆外的部分。

1/4圆的面积为314/4=78.5厘米²。

正方形和1/4圆组合部分的面积为942-78.5=863.5厘米²。

因此阴影部分的面积为863.5厘米²。

已知圆的周长为18.84dm，需要计算阴影部分的面积。

由于圆的周长公式为C=2πr，因此圆的半径为3dm。

阴影部分是圆内的部分，因此需要先计算圆的面积。

圆的面积公式为S=πr²，因此圆的面积为28.27dm²。

阴影部分是圆的外部分，因此需要用长方形的面积减去圆的面积。

长方形的面积为S=18.84/4×3=1.41dm²。

包含与排除和旋转对称课前预习铅球比赛场地有人参加过铅球比赛么？有谁知道铅球的比赛场地是什么样子的？如何才能画一个标准的铅球比赛场地呢？铅球的比赛场地是一个扇形的比赛场地，上面有环形的尺度，下面介绍一种铅球比赛场地的画法。

在学校运动会、小型比赛及体育教学中，铅球场地往往都被安排在远离径赛场地的“偏僻角落里”。

其一，是为了安全；其二，是为了保护塑胶场地；其三，是铅球比赛需要土质场地或草皮。

铅球场地的传统画法是：先用测绳测量，再用标枪沿测绳划出痕迹，后用白灰浇出白线。

而往往“偏僻角落里”的场地质地较差，高洼不平，杂草丛生，即使勉强画上白线，也模糊不清、参差不齐、宽窄不一。

况且在比赛过程中，人为踩踏，器械砸击、风吹雨淋，使角度线、远度线和延长线变得更加模糊，裁判员需经常描画，给裁判工作带来诸多不便。

本人在实际教学、裁判工作中摸索出一种用白布条（或白塑料编织材料）代替白灰绘制比赛场地的方法。

第一：材料与制作用白布裁剪、缝制成宽5厘米、厚3—4层的白布条，长度可根据比赛的组别，及实际情况而定，可剪短，可接长。

第二：具体画法把白布条沿用测绳已测量好的角度线、远度线和延长线拉直且相吻合，用长铁钉钉地固定两端，再沿白布条的两边缘每隔1—2米用铁钉交错钉牢，用醒目的颜色在白布条上注明远度数字。

第三：延用此法可延用于其他田赛项目的比赛场地、以及径赛项目的起点、终点和弯直道交接线的绘制。

第四：备用比赛完毕后，将铁钉拔出，白布条捆扎、收藏好以备下次再用。

瞧，用这法绘制比赛场地，既经济实用，避免重复测画场地，又能及时、公正、准确地测定学生和运动员的练习和比赛成绩。

您不妨一试。

知识框架圆的知识：1. 当一条线段绕着它的一个端点O 在平面上旋转一周时，它的另一端点所画成的封闭曲线叫做圆，点O 叫做这个圆的圆心.2. 连结一个圆的圆心和圆周上任一点的线段叫做圆的半径.3. 连结圆上任意两点的线段叫做圆的弦.过圆心的弦叫做圆的直径.4. 圆的周长与直径的比叫做圆周率.圆周上任意两点间的部分叫做弧.5. 圆周长=直径×π.=半径×2π 圆面积=π×半径2.扇形的知识：1. 扇形是圆的一部分，它是由圆心角的两条半径和圆心角所对的弧组成的图形.顶点在圆心的角叫做圆心角. 2. 我们经常说的12圆、14圆、16圆等等其实都是扇形，而这个几分之几表示的其实是这个扇形的圆心角占这个圆周角的几分之几．那么一般的求法是什么呢？关键是360n． 3. 扇形中的弧长= 180r n π.扇形的周长= 180r n π+2r.扇形的面积=3602r n π =.弓形的知识：弦与它所对的弧所组成的图形叫做弓形。

例1.求阴影部分的面积。

（单位:厘米）
解：这是最基本的方法：圆面积减去等腰直角三角形的面积，
-2 X 1=1.14平方厘米）
7 平方厘米，求阴影部分的面积。

（单位:厘米）
例 2. 正方形面积是
解：这也是一种最基本的方法用正方形的面积减去 圆的面积。

设圆的半径为 r
因为正方形的面积为 7 平方厘米
=7
,
7-
=7-
X 7=1.50呼方厘米
例3.求图中阴影部分的面积。

（单位:厘米）
解：最基本的方法之
圆组成一个圆，用正方形的
面积减去圆的面积，
所以阴影部分的面积:
2X2- n= 0.86平方厘米。

例4.求阴影部分的面积。

（单位:厘米）解：
同上，正方形面积减去圆面积，
16- n()=16-4n=3.44平方厘米例5.求阴影部分的面积。

（单位:厘米）。

【小学数学】六年级数学预习专题：求阴影部分面积（含答案）1) 正方形：周长＝边长×4 C=4a 面积=边长×边长 S=a×a2) 正方体：表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长 V=a×a×a3) 长方形：周长=(长+宽)×2 C=2(a+b) 面积=长×宽 S=ab4) 长方体：表面积=(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh) 体积=长×宽×高 V=abh5) 三角形：面积=底×高÷2 s=ah÷26) 平行四边形：面积=底×高 s=ah7) 梯形：面积=(上底+下底)×高÷2 s=(a+b)×h÷28) 圆形：周长=直径×Π=2×Π×半径C=Πd=2Πr面积=半径×半径×Π9) 圆柱体：侧面积=底面周长×高表面积=侧面积+底面积×2 体积=底面积×高10) 圆锥体：体积=底面积×高÷32、面积求解类型从整体图形中减去局部;割补法：将不规则图形通过割补;转化成规则图形。

重难点：观察图形的特点;根据图形特点选择合适的方法求解图形的面积。

能灵活运用所学过的基本的平面图形的面积求阴影部分的面积。

练习题例1.求阴影部分的面积。

(单位:厘米) 例2.正方形面积是7平方厘米;求阴影部分的面积。

(单位:厘米)例3.求图中阴影部分的面积。

(单位:厘米)例4.求阴影部分的面积。

(单位:厘米)例5.求阴影部分的面积。

(单位:厘米)例6.如图：已知小圆半径为2厘米;大圆半径是小圆的3倍;问：空白部分甲比乙的面积多多少厘米？例7.求阴影部分的面积。

求阴影部分面积例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为 r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来例8.求阴影部分的面积。

(单位:厘米) 解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米求,无需割、补、增、减变形)例9.求阴影部分的面积。

六年级上册数学教案《求阴影部分的面积》人教版一. 教材分析《求阴影部分的面积》是人教版六年级上册数学教材中的一课，主要让学生掌握求阴影部分面积的方法，培养学生的几何思维和解决问题的能力。

本节课是在学生已经掌握了平面几何图形的面积计算方法的基础上进行的，通过求阴影部分的面积，让学生进一步理解和掌握几何图形的面积计算方法。

二. 学情分析六年级的学生已经具备了一定的几何图形知识，对平面几何图形的面积计算有一定的了解。

但是，对于一些复杂图形的面积计算，学生可能还存在一定的困难。

因此，在教学过程中，教师需要引导学生通过观察、思考、操作等方法，逐步掌握求阴影部分面积的方法。

三. 教学目标1.让学生掌握求阴影部分面积的方法。

2.培养学生的几何思维和解决问题的能力。

3.激发学生学习数学的兴趣，提高学生的自主学习能力。

四. 教学重难点1.重点：让学生掌握求阴影部分面积的方法。

2.难点：对于一些复杂图形的面积计算，如何引导学生通过观察、思考、操作等方法，逐步掌握求阴影部分面积的方法。

五. 教学方法1.情境教学法：通过生活情境，引导学生理解求阴影部分面积的意义。

2.启发式教学法：引导学生通过观察、思考、操作等方法，自主探索求阴影部分面积的方法。

3.小组合作学习：引导学生分组讨论，培养学生的合作能力和解决问题的能力。

六. 教学准备1.教学课件：制作课件，展示相关几何图形和阴影部分的图片。

2.学具：准备一些几何图形和阴影部分的模型，供学生操作。

3.练习题：准备一些有关求阴影部分面积的练习题，供学生巩固所学知识。

七. 教学过程导入（5分钟）教师通过展示一些生活中的图片，如房子、车子等，引导学生观察这些图片中的阴影部分，让学生初步了解阴影部分的意义。

然后提出问题：“如果我们知道了一个几何图形的面积，如何求出它阴影部分的面积呢？”引发学生的思考。

呈现（10分钟）教师通过课件展示一些简单的几何图形，如正方形、圆形、三角形等，以及它们的阴影部分。

计算阴影部分的面积需要了解阴影是如何形成的以及数学中用到的相关知识。

在计算阴影面积时可以采用以下步骤：1.确定阴影的形状：阴影可以有多种形状，例如矩形、三角形、圆形等。

在计算阴影面积之前，首先要确定阴影的形状，以便选择合适的计算公式。

2.确定阴影的尺寸：测量阴影的尺寸是计算阴影面积的前提。

尺寸可以通过用尺子或者其他测量工具进行测量得到。

确保测量的准确性对于计算阴影面积非常重要。

3.选择合适的计算公式：根据阴影的形状选择合适的计算公式。

以下是常见的几种阴影形状及其对应的计算公式：a.矩形阴影的面积计算：阴影的面积等于其长度乘以宽度，即A=l*w。

b.三角形阴影的面积计算：阴影的面积等于底边乘以高度再除以2，即A=(b*h)/2c.圆形阴影的面积计算：阴影的面积等于圆的面积减去半圆的面积，即A=π*r^2-π*r^2/2=π*r^2/24.进行计算：根据选择的计算公式，将测量得到的尺寸代入计算公式中进行计算。

确保计算的准确性，并注意单位的一致性。

下面通过几个例子具体说明如何计算阴影部分的面积：例一：计算矩形阴影的面积假设一个矩形的长度为10cm，宽度为5cm，我们要计算其阴影的面积。

解：根据矩形阴影的面积计算公式A = l * w，代入已知的尺寸，得到A= 10cm * 5cm = 50cm²。

所以矩形阴影的面积为50cm²。

例二：计算三角形阴影的面积假设一个三角形的底边长度为6cm，高度为8cm，我们要计算其阴影的面积。

解：根据三角形阴影的面积计算公式 A = (b * h) / 2，代入已知的尺寸，得到A = (6cm * 8cm) / 2 = 24cm²。

所以三角形阴影的面积为24cm²。

例三：计算圆形阴影的面积假设一个圆的半径为5cm，我们要计算其阴影的面积。

解：根据圆形阴影的面积计算公式 A = π * r^2 / 2，代入已知的尺寸，得到A = π * 5cm^2 / 2 ≈ 7.85cm²。

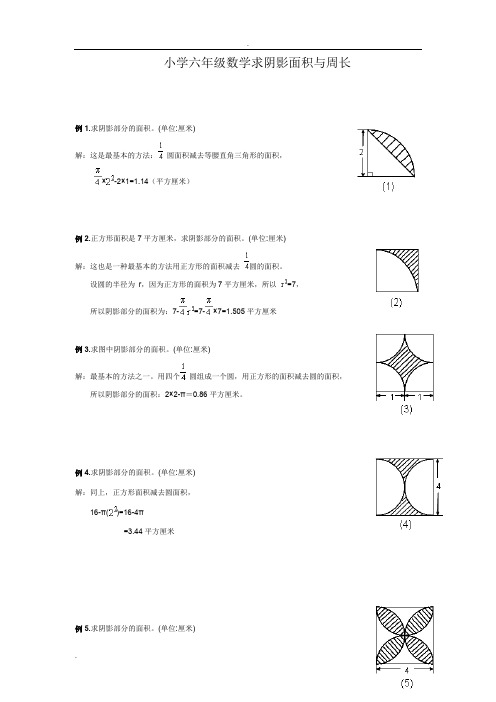
小学六年级数学求阴影面积与周长例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

六年级数学阴影部分面积解题技巧
六年级数学中，一个重要的知识点就是求解阴影部分的面积。

掌握这一技巧对于解决数学问题至关重要，因为很多问题都需要求出面积。

以下是一些六年级数学阴影部分面积的解题技巧：
1. 明确几何图形的类型
首先，我们需要明确所求几何图形的类型。

例如，圆形、三角形、矩形、梯形等。

不同类型的几何图形有不同的面积计算公式。

因此，我们需要先确定所求图形的类型，以便选择正确的面积计算公式。

2. 计算几何图形的周长
在计算面积之前，我们需要先计算几何图形的周长。

因为有些几何图形的面积可以通过周长和半径或边长来计算。

例如，圆形的面积可以通过周长和π来计算。

因此，我们需要先计算出所求图形的周长。

3. 套用面积计算公式
根据所求几何图形的类型，我们可以套用相应的面积计算公式。

例如，圆形的面积可以通过周长和π来计算。

因此，我们需要根据所求图形的类型，选择正确的面积计算公式。

4. 检验答案
最后，我们需要检验所得答案的正确性。

我们可以重新审视所求几何图形的类型和面积计算公式，检查所得答案是否符合题意。

如果所得答案不符合题意，我们需要重新计算或检查之前的计算步骤。

总之，掌握这些六年级数学阴影部分面积的解题技巧对于解决数学问题非常重要。

小学六年级数学求阴影面积与周长例1.求阴影部分的面积。

(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。

(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。

设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。

(单位:厘米)解：最基本的方法之一。

用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。

例4.求阴影部分的面积。

(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。

(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。

例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）例7.求阴影部分的面积。

(单位:厘米)解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。

(单位:厘米)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。

小学人教版六年级数学下册求几何图形阴影部分的面积1.如图，大圆半径为5厘米，小圆半径为3厘米,求阴影部分的面积,2.如图，已知两同心圆（圆心相同，半径不相等的两个圆），大圆半径为3厘米，小圆半径为1厘米，求阴影部分的面积3.如图，大圆半径为6cm，小圆半径为4cm，求阴影部分的面积4.已知如图大圆的半径为4cm，小圆的半径为3cm，求两个圆阴影部分的面积的差5.求图中阴影部分的面积(单位:厘米)6.求阴影部分的面积(单位:厘米)7.求阴影部分的面积(单位:厘米)8.如图,已知小圆半径为2厘米，大圆半径是小圆的3倍，问空白部分甲比乙的面积多多少厘米？9.求阴影部分的面积(单位:厘米)10.求阴影部分的面积(单位:厘米)11.已知直角三角形面积是12平方厘米，求阴影部分的面积12.求阴影部分的面积(单位:厘米)13.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长14.正方形边长为2厘米，求阴影部分的面积15.图中四个圆的半径都是1厘米，求阴影部分的面积16.如图，正方形边长为8厘米，求阴影部分的面积17.图中的4个圆的圆心是正方形的4个顶点，，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少？18.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。

如果圆周π率取3.1416，那么花瓣图形的的面积是多少平方厘米？19.如图，四个扇形的半径相等，求阴影部分的面积(单位:厘米)20.如图，等腰直角三角形ABC和四分之一圆DEB，AB=5厘米，BE=2厘米，求图中阴影部分的面积21.如图，正方形ABCD的对角线AC=2厘米，扇形ACB是以AC为直径的半圆，扇形DAC是以D为圆心，AD为半径的圆的一部分，求阴影部分的面积22.求阴影部分的面积(单位:厘米)23.图中直角三角形ABC的直角三角形的直角边AB=4厘米，BC=6厘米，扇形BCD所在圆是以B为圆心，半径为BC的圆，∠CBD=500,问阴影部分甲比乙面积小多少？24.如图，三角形ABC是直角三角形，阴影部分甲比阴影部分乙面积大28平方厘米，AB=40厘米,求BC的长度25.如图是一个正方形和半圆所组成的图形，P为半圆周的中点，Q为正方形一边上的中点，求阴影部分的面积26.如图，大正方形的边长为6厘米，小正方形的边长为4厘米。