基于β面截断重要抽样法可靠性灵敏度估计及其方差分析

1. 什么是生物统计学生物统计学的主要内容和作用是什么生物统计学是用数理统计的原理和方法来分析和解释生物界各种现象和试验调查资料，是研究生命过程中以样本来推断总体的一门学科。

生物统计学主要包括试验设计和统计分析两大部分的内容。

其基本作用表现在以下4个方面：1.提供整理和描述数据资料的科学方法，确定某些性状和特性的数量特征。

2.判断试验结果的可靠性。

3.提供由样本推断总体的方法。

4.提供试验设计的一些重要原则。

2. 随即误差与系统误差有何区别随机误差也称为抽样误差或偶然误差，它是由于试验中许多无法控制的偶然因素所造成的试验结果与真实结果之间的误差，是不可避免的，随机误差可以通过试验设计和精心管理设法减小，而不能完全消除。

系统误差也称为片面误差，是由于试验处理以外的其他条件明显不一致所产生的带有倾向性或定向性的偏差。

系统误差主要由一些相对固定的因素引起，在某种程度上是可控制的。

3. 准确性与精确性有何区别准确性指在调查和实验中某一实验指标或性状的观测值和真实值接近程度。

精确性指调查和实验中同一实验指标或性状的重复观察值彼此接近的程度。

准确性是说明测定值和真实值之间符合程度的大小；精确性是反映多次测定值的变异程度。

4. 平均数与标准差在统计分析中有何用处他们各有哪些特性平均数的用处：①平均数指出了一组数据的中心位置，标志着资料所代表性状的数量水平和质量水平；②作为样本或资料的代表数据与其他资料进行比较。

平均数的特征：①离均差之和为零；②离均差平方和为最小。

标准差的用处：①标准差的大小，受实验后调查资料中的多个观测值的影响，如果观测值之间的差异大，离均差就越大；②在计算标准差是如果对观察值加上一个或减去一个a，标准差不变；如果给各观测值乘以或除以一个常数a，所得的标准差就扩大或缩小a倍；③在正态分布中，X+-S内的观测值个数占总个数的%，X-+2s内的观测值个数占总个数的%，x-+3s 内的观测值个数占总个数的%。

卫⽣统计学第三章总体均数的区间估计和假设检验第⼀节均数的抽样误差与标准误⼀、标准误的意义及计算标准误是反映均数抽样误差⼤⼩的指标；同类性质的资料，标准误越⼩，表⽰样本均数与总体均数越接近，也就是抽样误差越⼩，说明样本均数推论总体均数的可靠性越⼤；反之，标准误越⼤，说明抽样误差越⼤，表⽰样本均数推论总体均数的可靠性越⼩。

数理统计已证明：标准误的⼤⼩与总体标准差成正⽐，⽽与样本含量的平⽅根成反⽐，即，当总体中各变量值都相等时，即σ=0，则抽取的各样本均数与总体均数必然相同，即抽样误差为零；⽽当总体中变量值间的变异度越⼤时，即σ越⼤，则抽取的各样本均数间离散度也越⼤，即抽样误差也越⼤；同时，当样本含量n越⼤时，则样本均数与总体均数越接近，抽样误差越⼩；反之，抽样误差越⼤。

因此可以适当增加样本例数来缩⼩抽样误差。

实际⼯作中总体标准差σ往往是不知道的，⽽只知道样本标准差S，所以只能⽤S代替，求得标准误的估计值，即⼆、标准误的应⽤▲表⽰抽样误差的⼤⼩，从⽽说明样本均数的可靠性。

（在医学⽂献上常⽤样本均数加减标准误的形式表⽰资料的均数及可靠程度）进⾏总体均数的区间估计进⾏均数的t检验第⼆节t分布⼀、t分布的概念如果从⼀个正态总体中，抽取样本含量为n的许多样本，分别计算其和，然后求出每⼀个t值，这样可有许多t值。

这些t值有⼤有⼩，有正有负，其频数分布是⼀种连续性分布，这就是统计上著名的t分布。

⼆、t分布曲线的特征▲特征：①t分布曲线是单峰分布，以0为中⼼，左右两侧对称，曲线的中间⽐标准正态曲线（u分布曲线）低，两侧翘得⽐标准曲线略⾼。

②当样本含量越⼩（严格地说是⾃由度v=n-1越⼩），t分布与u分布差别越⼤；当v逐渐增⼤时，t分布逐渐逼近u分布，当v=∞时，t分布就完全成为u分布。

所以t分布曲线的形状随v的变动⽽变化。

在⾃由度为v的t分布曲线下双侧尾部合计⾯积或单侧尾部⾯积为指定值α时，常把横轴上相应的t界值记为tα,v。

特征抽取中的特征重要性评估与特征选择方法在机器学习和数据挖掘领域，特征抽取是一个关键的步骤，它涉及从原始数据中提取出最具代表性的特征，以便用于模型训练和预测。

然而，由于原始数据的维度通常很高，特征抽取中的特征重要性评估和特征选择方法变得非常重要。

特征重要性评估是指对每个特征的重要性进行度量和评估的过程。

它可以帮助我们理解每个特征对于模型的贡献程度，从而帮助我们进行特征选择。

常用的特征重要性评估方法包括信息增益、方差分析、相关系数等。

信息增益是一种常用的特征重要性评估方法，它基于信息论的概念。

信息增益衡量了一个特征对于分类任务的贡献程度，即使用该特征进行分类时，所获得的信息增益。

信息增益越高，表示该特征对于分类任务的贡献越大。

方差分析则是一种用于连续型特征的重要性评估方法，它基于方差的概念。

方差分析衡量了一个特征对于样本之间的差异程度的贡献，即特征的方差越大，表示该特征对于样本的差异程度越大，从而对于分类任务的贡献越大。

相关系数是一种用于衡量特征与目标变量之间相关程度的方法，它可以帮助我们理解每个特征与目标变量之间的线性关系程度，从而判断特征的重要性。

特征选择是指从原始特征集合中选择出最具代表性的特征子集的过程。

特征选择的目的是降低数据维度，减少特征空间的复杂度，从而提高模型的训练效率和预测性能。

常用的特征选择方法包括过滤法、包装法和嵌入法。

过滤法是一种简单而有效的特征选择方法，它基于特征与目标变量之间的相关性进行选择。

过滤法通过计算每个特征与目标变量之间的相关系数或信息增益，然后根据设定的阈值进行特征选择。

过滤法的优点是计算简单，计算效率高，但它忽略了特征之间的相互关系，可能会选择出冗余特征。

包装法是一种更为精确的特征选择方法，它基于模型的性能评估进行选择。

包装法通过训练一个模型，并使用特征子集进行交叉验证，然后根据模型的性能评估选择最佳的特征子集。

包装法的优点是可以考虑特征之间的相互关系，但它的计算复杂度较高，需要进行多次模型训练和交叉验证。

Tobit模型估计方法与应用一、本文概述本文旨在全面探讨Tobit模型估计方法及其应用。

Tobit模型，也称为截取回归模型或受限因变量模型，是一种广泛应用于经济学、社会学、生物医学等领域的统计模型。

该模型主要处理因变量在某一范围内被截取或受限的情况，例如，当因变量只能取正值或只能在某一特定区间内变动时。

本文首先将对Tobit模型的基本理论进行阐述，包括模型的设定、参数的估计方法以及模型的检验等方面。

随后，文章将详细介绍Tobit模型在各个领域中的应用案例，包括工资水平、耐用消费品需求、医疗支出等方面的研究。

通过这些案例，我们将展示Tobit模型在处理受限因变量问题时的独特优势和应用价值。

文章还将对Tobit模型的发展趋势和前景进行展望，以期为相关领域的研究提供有益的参考和启示。

二、Tobit模型的基本原理Tobit模型，也称为受限因变量模型或截取回归模型，是一种广泛应用于经济学、社会学、生物医学等领域的统计模型。

该模型主要处理因变量受到某种限制或截取的情况，例如因变量只能取正值、只能在某个区间内取值等。

Tobit模型的基本原理基于最大似然估计法，通过构建似然函数来估计模型的参数。

截取机制：在Tobit模型中，因变量的取值受到某种截取机制的限制。

这种截取机制可以是左截取、右截取或双侧截取。

左截取意味着因变量只能取大于某个阈值的值，右截取则意味着因变量只能取小于某个阈值的值，而双侧截取则限制了因变量的取值范围在两个阈值之间。

潜在变量：在Tobit模型中，通常假设存在一个潜在变量（latent variable），它是没有受到截取限制的因变量。

潜在变量与观察到的因变量之间的关系由截取机制决定。

潜在变量通常假设服从某种分布，如正态分布。

最大似然估计：在给定截取机制和潜在变量分布的假设下，可以通过构建似然函数来估计Tobit模型的参数。

似然函数反映了观察到的数据与模型参数之间的匹配程度。

通过最大化似然函数，可以得到模型参数的估计值。

基于抽样的敏感性分析方法在 LBLOCA 质能释放 PIRT评级中的应用扈本学;王喆;王伟伟;王国栋;王章立;唐国锋;张今朝;杨萍;刘鑫【摘要】基于随机抽样的非参量敏感性统计分析方法是一种有效的敏感性分析方法，通过计算热工水力分析程序多个抽样输入参数与输出参数之间的相关系数来评价各输入参数对输出参数影响的重要程度。

通过耦合DAKOTA和WCOBRA／TRAC程序，开发了基于抽样的适用于非能动核电厂大破口失水事故质能释放的敏感性分析方法，该方法可全面定量评估各敏感性参数对计算结果的影响。

计算结果表明：堆芯初始功率、燃耗、衰变热、安注箱初始水温、初始水体积、安注箱管道阻力系数、堆芯补水箱初始水温、喷放系数及破口阻力系数对破口质能释放具有显著影响。

该分析结果可为大破口失水事故质能释放分析现象识别和重要度排序表评级提供定量依据。

%T he sampling based statistical sensitivity analysis is an effective sensitivity analysis method ,and the importance of input parameters of a thermal hydraulic analysis code could be evaluated by calculating the correlation coefficients of input parameters and output parameters .A sampling based sensitivity analysis method for LBLOCA mass and energy release of the large passive plant was developed ,by coupling DAKOTA and WCOBRA/TRAC codes .The calculated results show that the initial core power ,fuel burnup ,decay heat ,initial accumulator water temperature ,initial accumulator water volume ,accumulator pipe friction coefficient ,initial core makeup tank water tempera‐ture ,discharge coefficient and break resistance coefficient affect mass and energy release greatly .The results can provide quantitative support for evaluation ofLBLOCA mass and energy release analysis phenomena identification and ranking table .【期刊名称】《原子能科学技术》【年(卷),期】2016(050)002【总页数】5页(P290-294)【关键词】大破口失水事故;质能释放;敏感性分析;现象识别和重要度排序表;统计法;偏相关系数【作者】扈本学;王喆;王伟伟;王国栋;王章立;唐国锋;张今朝;杨萍;刘鑫【作者单位】上海核工程研究设计院，上海 200233;上海核工程研究设计院，上海 200233;上海核工程研究设计院，上海 200233;上海核工程研究设计院，上海200233;上海核工程研究设计院，上海 200233;上海核工程研究设计院，上海200233;上海核工程研究设计院，上海 200233;上海核工程研究设计院，上海200233;上海核工程研究设计院，上海 200233【正文语种】中文【中图分类】TL364对核电厂安全分析程序的开发而言，虽然核电厂中所有的热工水力现象均精确模拟是不现实的，但要求准确模拟在事故下所有的重要热工水力现象。

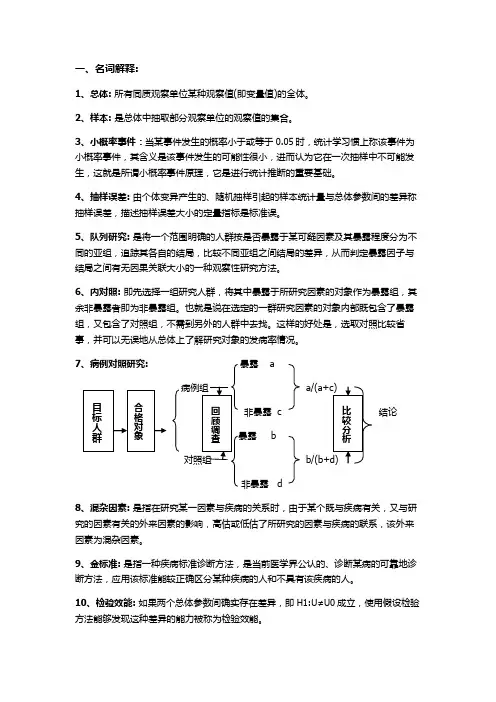
一、名词解释:1、总体: 所有同质观察单位某种观察值(即变量值)的全体。

2、样本:是总体中抽取部分观察单位的观察值的集合。

3、小概率事件：当某事件发生的概率小于或等于0.05时，统计学习惯上称该事件为小概率事件，其含义是该事件发生的可能性很小，进而认为它在一次抽样中不可能发生，这就是所谓小概率事件原理，它是进行统计推断的重要基础。

4、抽样误差: 由个体变异产生的、随机抽样引起的样本统计量与总体参数间的差异称抽样误差，描述抽样误差大小的定量指标是标准误。

5、队列研究: 是将一个范围明确的人群按是否暴露于某可疑因素及其暴露程度分为不同的亚组，追踪其各自的结局，比较不同亚组之间结局的差异，从而判定暴露因子与结局之间有无因果关联大小的一种观察性研究方法。

6、内对照:即先选择一组研究人群，将其中暴露于所研究因素的对象作为暴露组，其余非暴露者即为非暴露组。

也就是说在选定的一群研究因素的对象内部既包含了暴露组，又包含了对照组，不需到另外的人群中去找。

这样的好处是，选取对照比较省事，并可以无误地从总体上了解研究对象的发病率情况。

7、病例对照研究:暴露 aa/(a+c)非暴露 c 结论bb/(b+d)非暴露 d8、混杂因素:是指在研究某一因素与疾病的关系时，由于某个既与疾病有关，又与研究的因素有关的外来因素的影响，高估或低估了所研究的因素与疾病的联系，该外来因素为混杂因素。

9、金标准: 是指一种疾病标准诊断方法，是当前医学界公认的、诊断某病的可靠地诊断方法，应用该标准能较正确区分某种疾病的人和不具有该疾病的人。

10、检验效能: 如果两个总体参数间确实存在差异，即H1:U≠U0成立，使用假设检验方法能够发现这种差异的能力被称为检验效能。

二、填空题1、t检验的应用条件: 小样本、正态分布、方差相等。

2、变量变换的目的:使资料转换为正态分布、使资料达到方差齐性、使曲线直线化。

3、根据误差产生的来源，在医学科研设计时必须遵守四个基本原则: 对照原则、重复原则、随机化原则、盲法设计原则。

质量专业技术人员职业资格考试质量专业技术人员职业资格的适用对象为在企业、事业单位和团体中从事质量专业工作及相关工作的人员（在质量技术监督检验机构从事专职检验工作的人员除外）。

质量专业技术人员职业资格考试分初级和中级两个级别.取得初级资格,作为质量专业岗位职业资格的上岗证,可根据《工程技术人员职务条例》有关规定,聘任为工程技术员或助理质量工程师职务;取得中级资格，作为某些重要产品生产企业关键质量岗位职业资格的，可根据《工程技术人员职务条例》有关规定，聘任为质量工程师职务。

质量专业实行职业资格考试制度后,不再进行工程系列相应专业技术职务任职资格的评审工作。

质量专业中级资格考试设质量专业综合知识、质量专业理论与实务两个科目，考试的主要知识点介绍如下：科目一：质量专业综合知识第一章质量管理概论第一节质量的基本知识第二节质量管理的基本知识第三节方针目标管理第四节质量经济性分析第五节质量信息管理第六节质量教育培训第七节质量与标准化第八节卓越绩效评价准则第九节产品质量法和职业道德规范第二章供应商质量控制与顾客关系管理第一节供应商选择与质量控制第二节供应商契约与供应商动态管理第三节顾客满意第四节顾客关系管理第三章质量管理体系第一节质量管理体系的基本知识第二节质量管理体系的基本要求第三节质量管理体系的建立与实施第四节质量管理体系审核第四章质量检验第一节质量检验概述第二节质量检验机构第三节质量检验计划第四节质量特性分析和不合格品控制第五章计量基础第一节基本概念第二节计量单位第三节测量仪器第四节测量结果第五节测量误差和测量不确定度第六节测量控制体系科目二:质量专业理论与实务第一章概率统计基础知识第一节概率基础知识第二节随机变量及其分布第三节统计基础知识第四节参数估计第五节假设检验第二章常用统计技术第一节方差分析第二节回归分析第三节试验设计第三章抽样检验第一节抽样检验的基本概念第二节计数标准型抽样检验第三节计数调整型抽样检验及２８2８．1的使用第四节孤立批计数抽样检验及2８2８。

截断正态分布情况下失效概率计算的截断重要抽样法
池巧君;吕震宙;宋述芳
【期刊名称】《计算力学学报》
【年(卷),期】2010(27)6
【摘要】截断重要抽样法是在传统的重要抽样方法的基础上,引入截断抽样函数来计算结构的失效概率,本文运用此方法来解决工程中普遍存在的截断分布问题.首先将截断分布情况下的可靠性模型转化为非截断分布情况下的多模式并联系统的可靠性模型,然后采用截断重要抽样法求解,推导了截断分布可靠性估计值的方差分析公式.文中给出的算例结果表明:截断重要抽样法适用于截断分布的可靠性分析,且在相同的计算精度下,截断重要抽样法比传统的重要抽样法效率要高.
【总页数】6页(P1079-1084)
【作者】池巧君;吕震宙;宋述芳
【作者单位】西北工业大学,航空学院,西安,710072;西北工业大学,航空学院,西安,710072;西北工业大学,航空学院,西安,710072
【正文语种】中文
【中图分类】O213.2;TB114.3
【相关文献】
1.失效概率计算的截断重要抽样法 [J], 袁修开;吕震宙;宋述芳
2.基于β面截断重要抽样法可靠性灵敏度估计及其方差分析 [J], 张峰;吕震宙;崔利杰
3.截断相关正态变量情况下可靠性模型及其求解的自适应超球抽样法 [J], 王维虎;吕震宙;吕媛波
4.基于β面的截断重要抽样法 [J], 张峰;吕震宙;赵新攀
5.截断正态分布情况下结构可靠性分析的方向抽样和方向重要抽样估计及其方差分析 [J], 池巧君;吕震宙;宋述芳
因版权原因，仅展示原文概要，查看原文内容请购买。

antithetic variate method全文共四篇示例，供读者参考第一篇示例：对于概率和统计学领域的专业人士来说，可能并不陌生antithetic variate method这个概念。

这种方法是一种常见的模拟技术，常用于减少模拟过程的方差，提高模拟的效率。

在本文中，我们将深入探讨antithetic variate method的原理、应用以及优缺点。

让我们先来了解一下antithetic variate method是什么。

在概率和统计学中，我们经常需要估计一些特定的数学量，比如期望值或者方差。

通常情况下，我们可以通过蒙特卡洛模拟的方法来进行估计，即通过随机抽样的方式生成一组数据，然后根据这组数据来估计我们所关心的数学量。

在实际应用中，我们往往会遇到一个问题，就是生成的数据方差较大，导致估计结果不够准确。

这时，antithetic variate method就派上了用场。

该方法的基本思想是通过引入对称的反变量来减小模拟过程的方差。

具体来说，对于一个随机变量X，我们可以生成一个与X对称的反变量-Y，使得X与Y之间呈现一种反相关的关系。

这样一来，我们可以在蒙特卡洛模拟中同时使用X和Y来生成数据，从而减小生成数据的方差，提高模拟的效率。

举个简单的例子来说明这个方法。

假设我们要估计一个随机变量X 的期望值，我们可以通过蒙特卡洛模拟生成n组服从均值为μ、方差为σ^2的正态分布数据，然后将这些数据分成两组，分别记为X和Y。

接着，我们可以得到如下的估计式：E[(X+Y)/2] ≈ (1/n) * Σ(Xi+Yi)/2，其中Xi和Yi分别表示第i组数据的X和Y的观测值。

可以看出，通过引入反变量Y，我们可以得到一个更加准确的估计结果。

除了用于估计随机变量的期望值之外，antithetic variate method还可以用于估计其他数学量，比如方差、累积分布函数等。

在实际应用中，该方法被广泛应用于金融、工程、物理等领域。