高二上学期期末考试说明

2021-2022学年甘肃省兰州市第一中学高二上学期期末考试数学（文）试题一、单选题1．抛物线28y x =的焦点坐标为 A ．(0,2) B ．(2,0) C ．1(,0)32D ．1(0,)32答案：D解：抛物线28y x =可化为218x y =，∴抛物线28y x =的焦点在y 轴上，∵128=p ，∴11 232p =，∴抛物线的焦点坐标为10,32⎛⎫⎪⎝⎭，故选D ． 2．双曲线221416y x -=的渐近线方程为（ ）A ．12y x =± B ．2y x =± C ．14y x =±D ．4y x =±答案：A令双曲线方程得右边为0，可得双曲线的渐近线方程.解：解：令双曲线方程得右边为0，可得220416y x -=，可得12y x =±，即：双曲线221416y x -=的渐近线方程为12y x =±，故选：A.点评：本题主要考查双曲线的渐近线方程，注意牢记双曲线渐近线的求法. 3．若方程2212x y m m+=-表示椭圆，则实数m 的取值范围为（ ） A ．()0,1 B ．()1,2 C ．()0,2 D ．()()0,11,2答案：D由题知0202m m m m >⎧⎪->⎨⎪≠-⎩，解不等式组即可得答案.解：解：因为方程2212x y m m+=-表示椭圆 所以0202m m m m >⎧⎪->⎨⎪≠-⎩，解得021m m m >⎧⎪<⎨⎪≠⎩，所以实数m 的取值范围为()()0,11,2故选：D4．命题“00x ∃>，00sin x x <”的否定是（ ） A ．00x ∃≤，00sin x x < B ．00x ∃≥，00sin x x > C ．0x ∀>，sin x x ≥ D ．0x ∀>，sin x x >答案：C特称命题否定为全称命题即可解：命题“00x ∃>，00sin x x <”的否定是“0x ∀>，sin x x ≥”， 故选：C5．如果质点A 按照规律23s t =运动，则在3t =时的瞬时速度为 A ．6 B ．18C ．54D ．81答案：B对23s t =求导，再把3t =代入,从而可得3t =时的瞬时速度. 解：质点A 按照规律23s t =运动，'6s t ∴=，∴根据导数的物理意义可得，在3t =时的瞬时速度为6318⨯=，故选B.点评：本题主要考查导数的物理意义，意在考查利用所学知识解决实际问题的能力，属于简单题.6．设函数y ＝f (x )＝x 2－1，当自变量x 由1变为 1.1时，函数的平均变化率为（ ） A ．2.1 B ．1.1 C ．2 D ．0答案：A由平均变化率的定义计算．解：22(1.1)(1)(1.11)(11) 2.11.110.1y f f x ∆----===∆- 故选：A ．7．已知0a >，0b >，则“4a b +=1a =，4b =”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分又不必要条件答案：B根据基本不等式确定等式成立的条件，然后由充分必要条件的定义判断．解：0a >，0b >时，4a b +≥=4a b =.因为4a b =时，不一定有1a =，4b = 故选：B.8．椭圆与双曲线2213y x -=有相同的焦点1F ，2F ，离心率互为倒数，P 为椭圆上任意一点，则角12F PF ∠的最大值为（ ） A ．5π6B ．2π3 C ．π2D ．π3答案：D设椭圆方程为22221x y a b+=，根据条件列方程求出,a b ，即可求出椭圆方程，当点P 为椭圆短轴端点时角12F PF ∠最大，利用余弦定理可求得该角. 解：设椭圆方程为22221x y a b+=，则222213211c c a a b c ⎧=+⎪⎪⋅=⎨⎪=+⎪⎩，解得2216,12a b ==， 则椭圆方程为2211612x y +=， 当点P 为椭圆短轴端点时角12F PF ∠最大，此时()22212221616161cos 22162a a c F PF a +-+-∠===⨯， 因为()120,F PF π∠∈，12π3F PF ∴∠= 故选：D.9．已知点P 是抛物线22y x =-上的一个动点，则点P 到点()0,2M 的距离与点P 到该抛物线准线的距离之和的最小值为（ ） AB ．3 CD ．92答案：A求出抛物线的焦点F 的坐标，分析可知点P 到点()0,2M 的距离与点P 到准线12x =的距离之和等于点P 到点()0,2M 的距离与点P 到点F 的距离之和，利用当点P 为线段MF 与抛物线的交点时，即M 、P 、F 三点共线时取PM PF +取最小值可得结果.解：抛物线22y x =-的焦点为1,02F ⎛⎫- ⎪⎝⎭，准线方程为12x =，如下图所示，由抛物线的定义知，点P 到准线12x =的距离PD 等于点P 到焦点F 的距离PF ，因此点P 到点()0,2M 的距离与点P 到准线12x =的距离之和等于点P 到点()0,2M 的距离与点P 到点F 的距离之和，其最小值为点()0,2M 到点1,02F ⎛⎫- ⎪⎝⎭的距离（当点P 为线段MF 与抛物线的交点时，即M 、P 、F 三点共线时）11744+ 故选：A.10．已知点1F ，2F 为椭圆22142x y+=的左右焦点，过点1F 与x 轴垂直的直线与椭圆交于A ，B 两点，则三角形2ABF 的内切圆的半径为（ ）A ．2B ．1C 2D 2答案：C根据题意得2ABF 的周长为48a =，2AB =，进而等面积法求解即可. 解：解：根据题意得2,2a b c ===()12,0F ， 因为过点1F 与x 轴垂直的直线与椭圆交于A ，B 两点 所以()()2,1,2,1A B ---，2AB = 根据椭圆定义得2ABF 的周长为48a =， 不妨设三角形2ABF 的内切圆的半径为r ，所以根据等面积法得21211422ABF S a r AB F F =⨯⋅=△，代入数据得22r故选：C11．已知椭圆C ：22221x y a b +=()0a b >>的右焦点为(),0F c ，右顶点为A ，以OA 为直径的圆交直线cy x b=于点B （不同于原点O ），设OBF 的面积为S ．若S AB AF =⋅，则椭圆C 的离心率为（ ） A ．12 B ．13C ．34D ．35答案：D由题可得Rt OAB 的三边长，再结合三角形面积公式及向量数量积公式可得,,a b c 的关系式，即求.解：依题意，得OB AB ⊥， ∴点A 到直线c y x b =的距离22||AB c b c==+， 在Rt OAB 中，∵OA a =，AB c =， ∴OB b =， ∵S AB AF =⋅，∴1sin ()cos 2bc BOA c a c BAO ∠=-∠，其中sin cos BOA BAO ∠=∠， ∴()2b a c =-，∴()224b a c =-，即225830c ac a -+=， 得2583e e -+=(53)(1)0e e --=，∴35e =或1e =（舍）∴离心率为35.故选：D.12．下列结论正确的个数为（ ）①已知1F ，2F 分别为椭圆22:143x y C +=的左、右焦点，点P 为椭圆C 上的动点，则12PF F △的重心G 的轨迹方程为()2293104x y y +=≠②若动点(),P x y2，则点P 的轨迹为双曲线；③动点P 到直线40x +=的距离减去它到()2,0M 的距离之差是2，则点P 的轨迹是抛物线；④点2F 为椭圆2212516x y +=的右焦点，点P 为椭圆上任意一点，点()1,3M ，则2PF PM+的最小值为5；⑤斜率为2的直线与椭圆()222210x y a b a b+=>>交于A ，B 两点，点M 为AB 的中点，直线OM 的斜率为14-（O 为坐标原点）A ．1B ．2C ．3D ．4答案：D设()G x y ,，由重心坐标公式可得(3,3)P x y ，代入椭圆方程化简即可判断①，根据两点间的距离公式及双曲线的定义可判断②，由抛物线的定义判断③，根据椭圆的定义转化为动点到两定点间距离差的最大值，数形结合求解即可判断④，由点差法建立,a b 关系，求出离心率判断⑤.解：设椭圆的动点坐标00(,)P x y ，12PF F △的重心()G x y ,，则003003x c c x y y +-⎧=⎪⎪⎨++⎪=⎪⎩， 所以03x x =，030y y =≠，代入椭圆方程可得()2293104x y y +=≠，故①正确； 动点(),P xy24<，即动点到定点(2,0)-与(2,0)的距离之差为定值且小于两定点间的距离，所以动点轨迹为双曲线一支，故②错误； 动点P 到直线40x +=的距离减去它到()2,0M 的距离之差是2，即动点P 到直线20x +=的距离与P 到()2,0M 的距离相等，所以点P 的轨迹是抛物线，故③正确； 由M 在椭圆内，如图，22211||||10(||||)10||10(13)(30)1055PM PF PF PM F M ∴+=--≥-=++-=-=当且仅当1,,P F M 共线时，2||||PM PF +取得最小值，即最小值为5成立，故④正确；设1122,,()()A x y B x y ，，可得22221122222211,，x y x y a b a b+=+=两式相减可得1212121222()()()()x x x x y y y y a b -+-+=-，由题意可得12122y y x x --=，且1212(,)22x x y y M ++，121214y y x x +=-+，所以22112(),42b a -=⨯-=-则22121122c b e a a ==--=故⑤正确. 所以正确的结论有4个， 故选：D 二、填空题13．下列各结论中，正确的是______．①“p q ∧为真”是“p q ∨为真”的充分不必要条件； ②“p q ∧为假”是“p q ∨为假”的充分不必要条件； ③“p q ∨为真”是“p ⌝为假”的必要不充分条件； ④“p ⌝为真”是“p q ∧为假”的必要不充分条件． 答案：①③利用充分条件和必要条件结合复合命题的真假判断方法分析判断即可解：对于①，当p q ∧为真时，,p q 都为真，所以p q ∨为真，当p q ∨为真时，,p q 至少有一个为真，则p q ∧不一定为真，所以“p q ∧为真”是“p q ∨为真”的充分不必要条件，所以①正确，对于②，当p q ∧为假时，,p q 中至少有一个为假，则p q ∨不一定为假，当p q ∨为假时，,p q 都为假，则p q ∧一定为假，所以“p q ∧为假”是“p q ∨为假”的必要不充分条件，所以②错误，对于③，当p q ∨为真时，,p q 至少有一个为真，所以p ⌝不一定为假，而当p ⌝为假时，p 为真，所以p q ∨一定为真，所以“p q ∨为真”是“p ⌝为假”的必要不充分条件，所以③正确，对于④，当p ⌝为真时，p 为假，则p q ∧为假，当p q ∧为假时，,p q 中至少有一个为假，所以p 不一定为假，则p ⌝不一定为真，所以“p ⌝为真”是“p q ∧为假”的充分不必要条件， 所以④错误， 故答案为：①③14．与双曲线221916x y -=有共同的渐近线,且经过点()3,23-的双曲线方程是______. 答案：224194x y -=解：设22916x y λ-=,将()3,23-代入求得14λ=. 双曲线方程是224 1.94x y -= 15．在平面直角坐标系xoy 中，点M 是椭圆()222210x y a b a b+=>>上的点，以M 为圆心的圆与x 轴相切于椭圆的焦点F ，圆M 与y 轴相交于P 、Q 两点．若MPQ 为锐角三角形，则该椭圆离心率的取值范围是____________． 答案：6251,22⎛⎫-- ⎪ ⎪⎝⎭【解析】解：试题分析：∵△PQM 是锐角三角形， ∴∴2222cos cos 4MD c QMD ac a c b QMaπ∠==>=<- 22222,ac a c ac a c >-<- ∴22210,10e e e e +->+-< 解得6251e e --><∴该椭圆离心率的取值范围是6251--⎝⎭ 故答案为6251--⎝⎭16．已知抛物线C ：2y 2px(p 0)=>的焦点为F ，过F 且倾斜角为60的直线l 与抛物线C在第一、四象限分别交于A 、B 两点，与它的准线交于点P ，则AB PB=_____．答案：2：1设出A 、B 坐标，利用焦半径公式求出|AB |，结合x 1x 2＝24p ，求出A 、B 的坐标，然后求其比值．解：设A （x 1，y 1），B （x 2，y 2），则y 12＝2px 1，y 22＝2px 2， |AB |＝x 1+x 2+p ＝2028sin 603p p =，即有x 1+x 2＝53p ， 由直线l 倾斜角为60°，则直线l 的方程为：y ﹣0x ﹣2p ）， 联立抛物线方程，消去y 并整理，12x 2﹣20px +3p 2＝0， 则x 1x 2＝24p ，可得x 1＝32p ，x 2＝16p ，则|AP |＝4p ， ∴AB PB=2.故答案为:2:1.点评：本题考查直线的倾斜角，抛物线的简单性质，考查学生分析问题解决问题的能力，属于中档题．本题主要考查直线与圆锥曲线位置关系，所使用方法为韦达定理法：因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用． 三、解答题17．已知集合{}22A x a x a =-≤≤+，{}14B x x =<<． (1)当3a =时，求A B ；(2)“x A ∈”是“x B ∈”的充分不必要条件，求实数a 的取值范围． 答案：(1){}15A B x x ⋃=-≤≤ (2){}1a a <（1）由3a =，得到{}15A x x =-≤≤，再利用并集的运算求解； （2）根据 “x A ∈”是“x B ∈”的充分不必要条件，得到AB ，然后分A =∅，A ≠∅讨论求解. (1)解：当3a =时，{}15A x x =-≤≤． 因为{}14B x x =<<， 所以{}15A B x x ⋃=-≤≤． (2)因为“x A ∈”是“x B ∈”的充分不必要条件， 所以AB ．当A =∅时，符合题意，此时有22a a +<-，解得：0a <．当A ≠∅时，要使AB ，只需22,24,21,a a a a +≥-⎧⎪+<⎨⎪->⎩解得：01a ≤<，综上：1a <．所以实数a 的取值范围{}1a a <． 18．已知命题p ：方程表示焦点在x 轴上的双曲线．命题:q 曲线2(23)1y x m x =+-+与x 轴交于不同的两点，若p q ∧为假命题，p q ∨为真命题，求实数m 的取值范围． 答案：522m <≤或12m <. 分别求出命题p 、q 为真命题时m 的范围，根据复合命题真值表可得命题p ，q 命题一真一假，分p 真q 假和p 假q 真求出m 的范围，再求并集． 解：解：方程22122x y m m -=-表示焦点在x 轴上的双曲线， ∴20220m m m >⎧⇒>⎨->⎩若p 为真时：2m >，曲线2(23)1y x m x =+-+与x 轴交于不同的两点， 则△25(23)402m m =-->⇒>或12m <， 若q 真得：52m >或12m <， 由复合命题真值表得：若p q ∧为假命题，p q ∨为真命题，p ，q 命题一真一假若p 真q 假：522m <； 若p 假q 真：12m <∴实数m 的取值范围为：522m<或12m <． 19．设1F ,2F 分别是椭圆E ：22221(0)x y a b a b+=>>的左、右焦点，过点1F 的直线交椭圆E 于,A B 两点，113AF BF =（1）若24,AB ABF =∆的周长为16，求2AF ； （2）若23cos 5AF B ∠=，求椭圆E 的离心率.答案：（1）5；（2）2. 【解析】解：试题分析：（1）由题意113,4AF F B AB ==可以求得113,1AF F B ==，而2ABF ∆的周长为16，再由椭圆定义可得12416,28a AF AF a =+==.故212835AF a AF =-=-=.（2）设出1F B k =，则0k >且13,4AF k AB k ==.根据椭圆定义以及余弦定理可以表示出,a k 的关系()(3)0a k a k +-=，从而3a k =，2123,5AF k AF BF k ===，则22222||||BF F A AB =+，故12F A F A ⊥，12AF F ∆为等腰直角三角形.从而2c a =，所以椭圆E 的离心率2c e a ==. （1）由113,4AF F B AB ==，得113,1AF F B ==.因为2ABF ∆的周长为16，所以由椭圆定义可得12416,28a AF AF a =+==.故212835AF a AF =-=-=.（2）设1F B k =，则0k >且13,4AF k AB k ==.由椭圆定义可得2223,2AF a k BF a k =-=-.在2ABF ∆中，由余弦定理可得22222222||||2cos AB AF BF AF BF AF B =+-⋅∠，即2226(4)(23)(2)(23)(2)5k a k a k a k a k =-+---⋅-，化简可得()(3)0a k a k +-=，而0a k +>，故3a k =.于是有2123,5AF k AF BF k ===.因此22222||||BF F A AB =+，可得12F A F A ⊥，故12AF F ∆为等腰直角三角形.从而c =，所以椭圆E 的离心率c e a ==. 【解析】1.椭圆的定义；2.椭圆的离心率求解.20．已知椭圆C :22221(0)x y a b a b+=>>的离心率为12，椭圆的左、右焦点分别是12F F 、，点M 为椭圆上的一个动点，12MF F △（Ⅰ）求椭圆C 的方程：（Ⅱ）P 为椭圆上一点，1PF 与y 轴相交于Q ，且112F P FQ =，若1PF 与椭圆相交于另一点R ， 求2PRF △的面积 .答案：（1）22143x y +=（2）157 【解析】解：试题分析：（Ⅰ）由已知条件：12c e a ==，122c b bc ⋅⋅==椭圆C 的方程；（Ⅱ） 由112F P FQ =，知Q 为1F P 的中点，设()0,Q y ，则()1,2P y ，由此利用韦达定理、弦长公式能求出2PRF ∆的面积. 试题解析：解：（I )由已知条件：12c e a ==，122c b bc ⋅⋅=∴2,1a b c === ∴椭圆C 的方程为22143x y += . (Ⅱ)由112F P FQ =，知Q 为1F P 的中点，所以设()0,Q y ，则()1,2P y , 又P 满足椭圆的方程，代入求得34y =. ∴直线1PF 方程为()314y x =+ . 由()22314{143y x x y =++= 得 276130x x +-= . 设()11,P x y ，()22,R x y ，则 1212613,77x x x x +=-=- .∴1212627,728y y y y +==- ，∴212115227PRF S c y y c ∆=⋅⋅-==. 说明：各题如有其它解法可参照给分.点睛：本题考查椭圆方程的求法，考查三角形面积的求法，是基础题，解题时要认真审题，注意椭圆性质、韦达定理、弦长公式的合理运用；当直线与圆锥曲线相交时，将三角形的面积转化为求弦长问题，即联立直线的方程与圆锥曲线的方程构成方程组，结合韦达定理12y y -=.21．已知双曲线()22122:10,0x y C a b a b -=>>与双曲线222:142x y C -=有相同的渐近线，且点(P 在1C 上. （1）求1C 的标准方程；（2）过点()1,1M 的直线l 与双曲线1C 交于,A B 两点，且M 恰好是线段AB 的中点，求直线l 的方程.答案：（1）2212x y -=；（2）210x y -+=.（1）设()221:042x y C λλ-=≠，将(P 代入可得λ，进而可得1C 的标准方程； （2）设直线():11l y k x =-+，将其与1C 联立得到关于x 的方程，根据根与系数的关系和中点坐标公式可解得k ，进而可得直线l 的方程.解：（1）因为1C 与2C 的渐近线相同，可设()221:042x y C λλ-=≠将(P 代入得831422λ=-=，所以1C 的标准方程为2212x y -=. （2）直线l 的斜率显然存在，设直线():11l y k x =-+， 联立方程组()221211x y y k x ⎧-=⎪⎨⎪=-+⎩，消去y 可得()()()22212412120k x k k x k -+----=，由221208(22)0k k k ⎧->⎨∆=-+->⎩得11k <<且2≠±k . 设()1122(),,,A x y B x y ，则()1224121k k x x k -+=-因为M 是线段AB 的中点，所以()122211221k k x xk -+==-，解得12k =，满足题意.所以直线l 的方程为()1112y x =-+，即210x y -+=.22．已知F 为抛物线C ：x 2=2py (p >0)的焦点，点M 在抛物线C 上，O 为坐标原点，△OFM 的外接圆与抛物线C 的准线相切，且该圆面积为94π. （1）求抛物线C 的方程；（2）设A (2，1)，B 是抛物线C 上异于A 的一点，直线AB 与直线y =x -2交于点P ，过点P 作x 轴的垂线交抛物线C 于点N ，证明：直线BN 恒过一定点，并求出该定点的坐标.答案：（1）x 2=4y ；（2）证明见解析，定点(2，2).(1)由题意知圆心必在4p y =，由相切即可知34pr =，结合已知圆的面积即可求出p =2，进而可求出抛物线的方程.(2) 设211(,)4x B x ，写出直线AB 的方程与y =x -2联立，求出P 的横坐标，即可知N 的横坐标，进而可求出N 的坐标，由直线的点斜式可写出直线BN 的方程，从而可求出所过定点.解：解：（1）设△OFM 外接圆的半径为r ，由题知圆心必在4py =， 且圆心到准线的距离3424p p p r +==，所以239()44p π⋅=π，解得p =2， 所以抛物线C 的方程为：x 2=4y .（2）设211(,)4xB x ，由题意知，12x ≠，则直线AB 的方程：211141(2)2x y x x --=--，化简得：121(2)4x y x +-=-，与y =x -2联立得121(2)42x y x y x +⎧-=-⎪⎨⎪=-⎩， 解得11282p x x x -=-，把112(4)2p x x x -=-代入x 2=4y 得：2114()2N x y x -=-， 即211112(4)4(,())22x x N x x ----，则直线BN 的方程：221121111114()42()2(4)42x x x x y x x x x x ----=----， 约分得：11211142()2()44x x x x y x x -+--=-，化简得111141()()422x x x y x x x --+--， 因为与x 1无关，所以当x =2，y =2时恒成立，所以直线BN 恒过定点(2，2).点评：关键点睛:本题第二问的关键是联立直线和直线求出P 的横坐标，写出N 的坐标后，写出直线BN 的方程.。

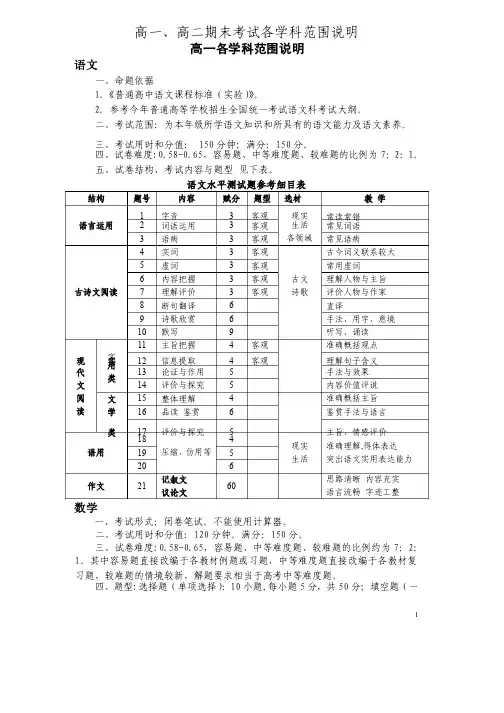
高一、高二期末考试各学科范围说明高一各学科范围说明语文一、命题依据1．《普通高中语文课程标准（实验）》。

2．参考今年普通高等学校招生全国统一考试语文科考试大纲。

二、考试范围：为本年级所学语文知识和所具有的语文能力及语文素养。

三、考试用时和分值： 150分钟；满分：150分。

四、试卷难度:0.58-0.65，容易题、中等难度题、较难题的比例为7：2：1。

五、试卷结构、考试内容与题型见下表。

语文水平测试题参考细目表结构题号内容赋分题型选材教学语言运用1 字音3 客观现实生活各领域常读常错2 词语运用3 客观常见词语3 语病3 客观常见语病古诗文阅读4 实词3 客观古文诗歌古今词义联系较大5 虚词3 客观常用虚词6 内容把握3 客观理解人物与主旨7 理解评价3 客观评价人物与作家8 断句翻译6 直译9 诗歌欣赏6 手法、用字、意境10 默写9 听写、诵读现代文阅读实用类11 主旨把握4 客观准确概括观点12 信息提取4 客观理解句子含义13 论证与作用5 手法与效果14 评价与探究5 内容价值评说文学类15 整体理解4 准确概括主旨16 品读鉴赏6 鉴赏手法与语言17 评价与探究5 主旨、情感评价语用18 压缩、仿用等4 现实生活准确理解,得体表达突出语文实用表达能力19 5 20 6 作文21 记叙文议论文60 思路清晰内容充实语言流畅字迹工整数学一、考试形式：闭卷笔试。

不能使用计算器。

二、考试用时和分值：120分钟。

满分：150分。

三、试卷难度:0.58-0.65，容易题、中等难度题、较难题的比例约为7：2：1。

其中容易题直接改编于各教材例题或习题，中等难度题直接改编于各教材复习题，较难题的情境较新，解题要求相当于高考中等难度题。

四、题型:选择题（单项选择）：10小题,每小题5分，共50分；填空题（一1 空或多空）:4小题,每小题5分,共20分；解答题（一问或多问）:6小题,共80分。

五、内容范围：必修1-4，以必修3、4为主（与必修3、4内容有关的试题分值约占70%）。

A．没有大脑皮层的调控，排尿反射可以进行但排尿不完全
B．若损伤①③，则不能产生尿意，不能完成排尿反射
C．若损伤②③，则能产生尿意，不能完成排尿反射
D．若损伤③④，则能产生尿意，不能完成排尿反射
19．下列有关免疫学的说法，正确的是（ ）
A．在过敏反应中，抗生素作为抗原引起浆细胞活化并分泌抗体
B．青霉素引起的病理性免疫反应，具有特异性和记忆性
27．为指导遗传咨询，医生通过产前诊断技术从孕妇体内取得胎儿细胞进行检查分析，以此判断胎儿是否患遗传病。下列叙述正确的是（ ）
A．对胎儿细胞的染色体进行分析，可诊断胎儿是否患红绿色盲
B．通过基因检测，可诊断胎儿是否患猫叫综合征
C．对胎儿细胞的染色体进行数量分析，可判断胎儿是否患唐氏综合征
D．借助光学显微镜检查胎儿细胞，可判断胎儿是否患有青少年型糖尿病
C．白化病是基因通过控制酶的合成来控制代谢过程，进而控制生物体性状的实例
D．翻译过程需要mRNA、tRNA、rRNA、氨基酸、核糖体、能量等
5．下列是某同学关于真核生物基因的叙述，其中全错的一项是（ ）
①携带遗传信息 ②能转运氨基酸 ③能与核糖体结合 ④能转录产生RNA
⑤每相邻三个碱基组成一个反密码子 ⑥可能发生碱基对的增添、缺失、替换
B．RNA病毒都携带有逆转录酶
C．在遗传信息的流动过程中，所有生物均存在图中①②③ 过程
D．原核生物拟核基因的②和③在时间和空间上是未分开的
4．关于基因表达和中心法则 叙述，错误的是（ ）
A．转录是以DNA的一条链为模板、四种脱氧核苷酸为原料合成RNA
B．衰老细胞内染色质收缩，造成细胞核基因难以复制和表达
C．实验中两组实验小鼠形成相互对照，且实验前两组小鼠的生理状态应相同

B．装置①总电极反应式为2Cu2＋＋2H2O 2Cu＋O2↑＋4H＋，反应中产生氢离子，c(H＋)增大，溶液pH减小，装置②发生Zn＋H2SO4=ZnSO4＋H2↑，反应中消耗氢离子，c(H＋)降低，pH增大，故B正确；
C．①的阴极反应Cu2++2e—=Cu，导线中通过0.2 mol电子时，阴极产生铜的质量m=nM=0.2mol×64g/mol=12.8g，装置②为原电池，两个电极上没有固体析出，则电极上析出固体质量①＞②，故C错误
A.a点所示溶液中c(Na+)＞c(A-)＞c(H+)＞c(HA)
B.a、b两点所示溶液中水的电离程度相同
C.b点所示溶液中c(A-)＞c(HA)
D.pH=7时，c(Na+)=c(A-)+c(HA)
【答案】C
【解析】
【详解】A．a点时消耗0.1mol/L一元酸HA10mL，酸碱恰好中和生成盐，溶液pH=8.7，溶液显碱性，则该盐为强碱弱酸盐，说明HA为弱酸，NaA溶液水解呈碱性，应为c(HA)＞c(H+)，故A错误；
B. K连N，称外接电流的阴极保护法
C. K连M，X为Zn 时，铁不易被腐蚀
D. K连M，铁上电极反应为2H++2e→H2↑
【答案】D
【解析】
A. K连N，X极发生氧化反应，铁电极上发生还原反应，保护铁不被氧化，A正确；B. K连N，称外接电流的阴极保护法，B正确；C. K连M，X为Zn时，锌失电子，铁不易被腐蚀，C正确；D. K连M，铁电极上产要发生吸氧腐蚀，电极反应为：O2+4e-+2H2O—4OH-，D错误。答案选D。
3.下列各物质加入水中，能促进水的电离的是( )
A. NaClB. NaOHC. Na2CO3D. NaHSO4

2021级高二上学期期末线上考试语文试卷分值：150分考试时间：150分钟答题说明（必读）：1、选择题答案用2B铅笔涂写到答题卷相应的题号上，注意不要错位。

2、主观题答到答题卷规定区域内，超出答题区域不得分。

3、不要答错题号位置，答错位置不得分。

一、现代文阅读（35分）（一）现代文阅读Ⅰ（本题共5小题，17分）阅读下面的文字，完成1～5小题。

材料一：随着公共生活空间日益拓展，人们的交往与合作愈加丰富多样，集体行动以及由此产生的集体责任逐渐成为学界关注的焦点。

在集体行动中，个人以公共理性参与集体行动，在公共生活中与他人的行为选择发生重叠、缠绕和相互作用，进而双方根据在交互结构中形成的集体理性作出选择。

这种个人理性和集体理性之间的交互关系就是集体行动背后的交互理性结构。

它让个人在作出选择的时候获得了超越个体的集体思维方式，也为个人生存的社会性提供了道德基础。

理解集体行动，要避免个体主义的视角，要认识到简单物理还原论的不足。

仅仅从行动的物理基础出发，只是在物理层面描述和重现了行为的发生，并没有提供对于集体行动完整的真正的理解。

例如，一个乐团的交响乐合奏这个集体行为不仅仅是“单管演奏者在第三节开头吹出了一个低音”，加上“首席钢琴师弹出F大调音阶”，加上“大提琴手接连拉出三个跳音”，即便这个客观物理的描述可以不断叠加，最后穷尽整场演奏会的所有细节，却依然无法让我们真正理解乐团合奏这个集体行动。

这种方法论犯了本末倒置的错误。

恰恰是“乐团要合奏交响乐”这个集体行动的理由解释了每个演奏人员的个体行为，而不是每个演奏人员的个体行为解释了集体行动。

理解集体行动，要重视它的双重实现条件。

一方面，集体行动的实现有赖于个体对集体行动的认同和理解；另一方面，集体行动的维系有赖于外在制度和秩序。

长期、稳定、有效的合作不能只依赖于个体动机的简单重合。

只有在个体动机之上设立制度和秩序，稳固集体行为的实现方式，才能保证集体行动有效进行。

D
【详解】A．0.1mol·L-1HX溶液的pH=4，说明该溶液中c(H+)=10−4mol/L＜c(HX)，则HX部分电离，能说明一元酸HX是弱酸，A错误；
B．0.1mol·L-1NaX溶液pH＞7，溶液显碱性，说明NaX是强碱弱酸盐，能说明一元酸HX是弱酸，B错误；
C．0.1mol·L-1HX溶液比0.1mol·L-1硝酸导电能力弱，说明HX的酸性弱于硝酸，能说明一元酸HX是弱酸，C错误；
A
【详解】反应①N2(g)+O2(g)=2NO(g)△H1=+180.5 kJ·mol-1
反应②2H2(g)+O2(g) = 2H2O(l)△H2= -571.6 kJ·mol-1
反应②-反应①得：2H2(g)+2NO(g)=2H2O(l)+N2(g)△H=△H2-△H1=(-571.6 kJ·mol-1)-( +180.5 kJ·mol-1)=-752.1kJ·mol-1；22.4L(标准状况下)NO的物质的量为1mol，则该温度下H2催化还原22.4L(标准状况下)NO放出752.1 kJ÷2=376.05kJ的能量，A符合题意；
N2(g)+O2(g)=2NO(g)△H=+ 180.5 kJ·mol-1
2H2(g)+O2(g) = 2H2O(l)△H= -571.6 kJ·mol-1
则该温度下H2催化还原22.4L(标准状况下)NO达到消除环境污染目的的能量变化为
A.放出376. 05 kJB.放出752.1 kJ
C.吸收376.05 kJD.吸收752.1kJ
选A。
10.下列实验装置，不H溶液 反应热
B.用乙装置验证纯水具有微弱 导电性
C.用丙装置制取少量Fe(OH)2沉淀

A.2v(CO)消耗=3v(H2O)生成
B.断裂3NA个H-H键的同时，生成30 g的1-丙醇
C.若反应在绝热密闭容器中进行，容器中的压强已不再变化
D.若反应在恒容密闭容器中进行，混合气体的密度已不再改变
C
【分析】
【详解】A．2v(CO)消耗=3v(H2O)生成表示的都是反应正向进行，不能据此判断反应是否达到平衡状态，A不符合题意；
D．熔融碳酸钠含有自由移动的离子能够导电，是电解质，故D选；
故选D。
【点睛】明确概念是解题关键，电解质是在水溶液里或熔融状态下能导电的化合物，包括酸、碱、盐、活泼金属氧化物和水；非电解质是在水溶液里和熔融状态下都不能导电的化合物，包括一些非金属氧化物、氨气、大多数有机物（如蔗糖、酒精等）；物质导电的条件：含有自由移动的离子或自由电子；单质和混合物既不是电解质也不是非电解质。
答案选C。
11.下列说法不正确的是
A.加热0.01 mol·L-1NaOH溶液，溶液的pH逐渐减小
B.相同温度下，pH相等的醋酸和硫酸中所含的n(OH-)也一定相同
C.常温下，分别中和等体积、等浓度的KOH溶液和氨水，所需HCl的物质的量相同D.300 mL0.2 mol·L-1NH4Cl溶液和200 mL0.3 mol·L-1NH4Cl溶液中的n( )不同
4.下列物质的水溶液因水解而呈酸性的是
A.KHSO4B.NaHSO3C.H2SO4D.NH4Cl
D
【分析】
【详解】A．KHSO4不水解，电离出氢离子而显酸性，A错误；
B．NaHSO3溶于水后，亚硫酸氢根离子的电离程度大于其水解程度，溶液显酸性，B错误；
C．H2SO4是二元强酸，电离出氢离子显酸性，C错误；
D．NH4Cl溶于水铵根水解，溶液显酸性，D正确，

2022-2023学年（上）期末考试 高2024届化学试题（答案在最后）考试说明：1.考试时间90分钟 2.试题总分100分 3.试卷页数8页可能用到的相对原子质量：H-1 C-12 O-16 Ar-40 Ca-40 Cu-64第Ⅰ卷（选择题 共42分）选择题（每题只有一个选项符合题意，每题3分，共42分） 1.水是一种重要的资源，关于水的下列说法正确的是（ ） A.化学反应中生成1mol 2H O 所释放的能量称为中和热 B.水的离子积可表示为14110W K -=⨯C.山泉水并非纯净物，加热者沸时易产生3CaCO 和4CaSO 等水垢D.利用光伏电站电解2H O 制备2H 和2O 的反应属于放热反应 2.设A N 为阿伏加德罗常数的值，下列说法正确的是（ ） A.40g 处于基态的氩气中含有的p 轨道电子总数为12A N B.0.1mol /L 的3CH COOH 溶液中H +数目一定小于0.1A N C.电解精炼含锌的粗铜，阳极质量减少64g ，转移电子总数为2A N D.100mL 0.1mol /L 的227K Cr O 溶液中，227Cr O -数目为0.01A N 3.下列各元素性质的叙述中，正确的是（ ） A.N 、O 、F 的电负性依次减小B.Na 、Mg 、Al 的第一电离能依次增大C.符号为199X -和2311X +的基态微粒的轨道表示式相同 D.基态Cu 原子的电子排布式为：22626921s 2s 2p 3s 3p 3d 4s 4.在给定的四种溶液中，以下各种离子能大量共存的是（ ） A.无色透明溶液中：K +、4NH +、Cl -、3CO -B.滴加石蕊试液显红色的溶液：2Cu+、Na +、223S O -、Cl -C.pH 值为1的溶液：3Fe +、SCN -、Cl -、24SO -D.无色透明溶液中：K +、3HCO -、3NO -、3Al + 5.下列有关电解质溶液的说法正确的是（ ） A.向0.11mol L -⋅3CH COOH H 溶液中加入水，溶液中()()()33H CH COO CH COOH c c c +-⋅增大B.0.11mol L -⋅的2Na S 溶液中，()()()()2c OHc H c HS c H S -+-=++C.向盐酸中加入MgO 固体当溶液呈中性时，()()2ClMg c c -+=D.向AgCl 、AgBr 的混合饱和溶液中加入少量AgNO3固体，溶液中()()Cl Br c c --不变6.根据下列实验操作和现象得出的结论正确的是（ ）[4CuCl 镀锌后的铁更易发生析氢腐蚀(12Ka H CO 7.下图为用直流电源电解稀24Na SO 水溶液的装置。

【详解】A．根据图2可知，240℃之前甲烷的物质的量百分数随温度升高明显增大，说明240℃之前随温度升高，催化剂对∗OH+∗C+∗H→H2O+CH4(未配平)的选择性较大，A错误；
B．200℃时甲烷的物质的量百分数约为70%，说明此时的主反应为CO2+4H2 CH4+2H2O，B错误；
C．从图中可知，当温度较低时，甲烷的物质的量百分数并不是特别高，说明低温状态下，发生副反应的程度较大，因此CO2和H2的浓度越大，转化为CH4的速率不一定越快，这还与反应温度有关，C错误；
D．从图2可以看出，当温度高于260℃时，二氧化碳的转化率继续增大，而甲烷的物质的量百分数几乎没有变化，说明继续升温甲烷产率几乎不变，D正确；
故答案选D。
14.Y、Sc( ， )单原子催化剂可用于常温常压下的电化学催化氢气还原氮气的反应。反应历程与相对能量模拟计算结果如图所示(*表示稀土单原子催化剂)。下列说法错误的是
体系颜色变深
C
向 溶液中滴2滴 溶液；再滴2滴 溶液
先生成白色沉淀，后生成黄色沉淀
D
取 溶液于试管中并加入几滴酚酞溶液，加热
溶液红色变深
溶液中存在水解平衡
A.AB.BC.CD.D
【答案】D
【解析】
【详解】A．用pH试纸分别测定相同浓度的 和 溶液的pH，pH： ，只能说明亚硫酸的酸性强于碳酸，不能得出硫酸的酸性大于碳酸，故A错误；
高二化学
可能用到的相对原子质量：
一、选择题：本题共10小题，每小题2分，共20分。每小题只有一个选项符合题意。
1.化学与生产、生活息息相关。下列说法错误的是
A.热的纯碱溶液可用于清洗厨房油污
B. 可以用于天然水的消毒、净化

2023-2024学年度(上)沈阳市五校协作体期末考试高二年级英语试卷考试时间：120分钟分数：150分试卷说明：试卷共四部分：第一部分：听力（共两节，满分30分）第二部分：阅读理解（共两节，满分50分）第三部分语言运用：（共两节，满分30分）第四部分写作：（共两节，满分40分）第一部分：听力（共两节，满分30分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节（共5小题；每小题1．5分，满分7．5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1．How many people on the bus escaped unhurt in the accident?A．6.B．5.C．4.2．What are the speakers mainly talking about?A．A book.B．A movie.C．A song.3．What did the speakers do last week?A．They had a celebration dinner.B．They went to see a newborn baby.C．They sent a mail to their neighbors.4．Where does the conversation take place?A．In a supermarket.B．In a restaurant.C．In a farm.5．What are the speakers talking about?A．How to preserve strawberries.B．Where to buy strawberriesC．How to wash strawberries.第二节（共15小题；每小题 1.5分，满分22.5分）听下面对话或独白。

【详解】
如图所示，由已知可得， 为等腰三角形，且 ，翻折后可得 、 ，平面 平面 ，
对于选项A，平面 平面 ，平面 平面 ，且 ，所以 平面 ，而 平面 ，故 ，该选项正确；
对于选项B， 、 且 ，故 平面 ，所以 与平面BCD的法向量平行，该选项正确；
对于选项C，由选项A可知， ，假设 成立，则 平面 ，此时 ，该结论与 矛盾，故该选项错误；
故选：A.
6.在直三棱柱 中， ， ， ，则异面直线 与 所成角的余弦值为（）
A. B. C. D.
【答案】D
【解析】
【分析】以 为坐标原点，向量 ， ， 方向分别为 、 、 轴建立空间直角坐标系，利用空间向量夹角公式进行求解即可.
【详解】以 为坐标原点，向量 ， ， 方向分别为 、 、 轴建立空间直角坐标系，
故选：BCD
【点睛】对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.
第Ⅱ卷
三、填空题：本题共4小题，每小题5分，共20分．
13.已知双曲线 ，则圆 的圆心C到双曲线渐近线的距离为______．
【答案】2
【解析】
【分析】求出圆心和双曲线的渐近线方程，即得解.
【详解】直线 的斜率不大于0，则直线l斜率可能等于零，此时直线倾斜角为0°，不为钝角，故“直线 的斜率不大于0”不是“直线 的倾斜角为钝角”充分条件；
直线 的倾斜角为钝角时，直线的斜率为负，满足直线 的斜率不大于0，即“直线 的倾斜角为钝角”是“直线 的斜率不大于0”的充分条件，“直线 的斜率不大于0”是“直线 的倾斜角为钝角”的必要条件；
故 故答案为：
16.已知抛物线C： 的焦点为F，过M（4，0）的直线 交C于A、B两点，设 ， 的面积分别为 、 ，则 的最小值为______．

高二语文 xx．1第Ⅰ卷满分50分一、阅读下面《龄官划蔷痴及局外》选段，完成1~4题。

（每小题3分，共12分）且说那宝玉见王夫人醒来，自己没趣，忙进大观园来。

只见赤日当空，树（yīn）合地，①。

刚到了蔷薇花架，只听有人哽噎．．之声。

宝玉心中疑惑，便站住细听，【甲】架下那边有人。

如今五月之际，那蔷薇正是花叶【乙】之际，宝玉便悄悄的隔着篱笆洞儿一看，只见一个女孩子蹲在花下，手里拿着根绾头．．，一面悄悄的流泪，宝玉心中想道：“难道这也是个痴．．的簪子．．在地下抠土丫头，又像颦儿来葬花不成？”因又自叹道：“若真也葬花，可谓‘东施效颦’，不但不为新特，且更可厌了。

”想毕，便要叫那女子，说：“你不用跟着那林姑娘学了。

”话未出口，幸而再看时，这女孩子面生，不是个侍儿，倒像是那十二个学戏的女孩子之内的，却（biàn）不出他是生旦净丑的那一个角色来。

宝玉忙把舌头一伸，将口掩住，自己想道：“幸而不曾造次。

上两次皆因造次了，颦儿也生气，宝儿也多心，如今再得罪了他们，越发没意思了。

”一面想，一面又恨认不得这个是谁。

再留神细看，只见这女孩子眉（cù）春山，眼颦秋水，面薄腰纤．．，袅袅（tínɡ tínɡ），大有林黛玉之态。

宝玉早又不忍弃他而去，只管痴看。

只见他虽然用金簪划地，并不是掘土埋花，竟是向土上画字。

宝玉用眼随着簪子的起落，一直一画一点一勾的看了去，数一数，十八笔。

自己又在手心里用指头按着他方才下笔的规矩．．写了，猜是个什么字。

写成一想，原来就是个蔷薇花的“蔷”字。

宝玉想道：“必定是他也要作诗填词。

这会子见了这花，因有所感，或者偶成了两句，一时兴至恐忘，在地下画着【丙】，也未可知。

且看他底下再写什么。

”一面想，一面又看，只见那女孩子还在那里画呢，画来画去，还是个“蔷”字。

再看，还是个“蔷”字。

里面的原是早已痴了，画完一个又画一个，已经画了有几千个“蔷”。

外面的不觉也看痴了，两个眼睛珠儿只管随着簪子动，心里却想：“这女孩子一定有什么话说不出来的大心事，才这样个形景。

梅河口市第五中学2022～2023学年度上学期期末考试高二历史试题说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至4页，第Ⅱ卷5页，共5页。

满分100分，考试时间75分钟。

第Ⅰ卷（选择题，共72分）注意事项：1．答卷前，考生务必将自己的姓名、考号填写在答题卡上并将条形码粘贴在粘贴处。

2．回答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、单项选择题(本大题共24小题，每小题3分，共72分)1．春秋战国时期，农民耕作“百亩之田”可以养活五到九个人，比之前养活的人口多。

这使得“五口”到“九口”之家的小农，成为农业生产的主力。

“百亩之田”和农业生产主力的变化根本上取决于（）A．法家思想的普遍化发展B．农民生产积极性的提高C．铁犁牛耕的使用和推广D．诸侯争霸战争的影响2．恩格斯在《英国工人阶级状况》中写道：“工人家庭不分男女老幼地挤在一起，在这些家庭中有四分之三只有一个房间。

”《泰晤士报》群众来信中写道：“我们生活在肮脏的地方。

我们没有私人厕所，没有垃圾箱，没有排水沟……”这反映当时（）A．英国城市化进程不断推进B．工业革命造成了贫富分化C．工业建设不受政府重视D．城市基础设施建设滞后3．2022年美联储在6月、7月以及9月连续3次加息75个基点，利率由1.75%达到了3.25%,加剧跨境资本流动，导致美元快速回流美国；欧元、英镑、日元等经济体货币贬值压力加大，部分新兴经济体深陷债务危机，甚至将重蹈上世纪滞胀的覆辙。

这主要反映了（）A．当今世界金融体系的不合理性存在B．世界经济发展的不平衡性加剧C．新兴经济体经济基础薄弱D．世界经济危机周而复始4．自明朝中期起，白银逐渐成为国家财政和民间交易的基本支付手段，物价也多以银两计算。

高二第一学期期末试卷生物学一、选择题1.研究者使用含32P磷酸盐的营养液培养动物细胞，一段时间后细胞内的物质或结构不会．．出现放射性的是（）A.核糖 B.DNA C.细胞膜 D.线粒体基质【答案】A【分析】动物细胞吸收的磷酸盐用于合成含有P的物质或结构，因此用含32P的磷酸盐的营养液培养动物细胞，一段时间后，含有P的物质或结构都可能出现放射性。

【详解】A、核糖属于糖类，元素组成为C、H、O，不含有P元素，因此不可能含有放射性，A符合题意；B、DNA的元素组成是C、H、O、N、P，含有P元素，因此可能会出现放射性，B不符合题意；C、细胞膜的组成成分主要有蛋白质和磷脂，磷脂中含有P，因此可能会出现放射性，C不符合题意；D、线粒体基质中含有DNA、RNA、ATP、ADP等含有P元素的化合物，因此线粒体基质中可能会出现放射性，D 不符合题意。

故选A。

2.下列物质与其功能对应有误．．的是（）A.DNA聚合酶：催化DNA复制过程B.糖原：植物细胞的能源物质C.抗利尿激素：促进水的重吸收D.生长素：细胞间传递信息的分子【答案】B【分析】糖类分为单糖、二糖和多糖，其中多糖包括淀粉、纤维素和糖原，淀粉是植物细胞的储能物质，糖原是动物细胞的储能物质，纤维素是植物细胞壁的组成成分。

【详解】A、DNA复制的过程中需要DNA聚合酶的催化，A正确；B、糖原是动物细胞的能源物质，B错误；C、抗利尿激素能够促进肾小管和集合管对水的重吸收，C正确；D、生长素是植物细胞间传递信息的分子，是促进植物生长的重要内源激素，生长素是一种信息分子，起到调节的作用，D正确。

故选B。

3.下列有关于线粒体和叶绿体的叙述，错误的是（）A.叶绿体合成葡萄糖，线粒体分解葡萄糖B.叶绿体类囊体膜上蛋白质含量高于外膜C.二者都能进行DNA复制和蛋白质合成D.二者都能在膜上进行ATP合成【答案】A【详解】试题分析：阅读题干可知，该题的知识点是线粒体、叶绿体的形态、结构和功能的比较．线粒体：广泛分布于真核细胞中椭球形或球形．化学组成：DNA、RNA、磷脂、蛋白质，结构：双层膜结构，内膜向内突出形成嵴．在内膜（嵴）和基质中，分布着许多与有氧呼吸作用有关的酶类．功能：有氧呼吸的主要场所，“动力工厂”．叶绿体：仅存在于绿色植物细胞中棒状、粒状，化学组成：DNA、RNA、磷脂、蛋白叶绿体质、色素等．结构：双层膜结构，基质内分布着许多由片层结构组成的基粒．在基质、基粒的片层结构的薄膜上分布着许多与光合作用有关的酶类．在基粒片层薄膜上还分布有叶绿素等色素．功能：光合作用的场所，“养料加工厂”和“能量转换器”．解：A、叶绿体合成葡萄糖，细胞质基质分解葡萄糖，A错误；B、与外膜相比，叶绿体类囊体膜功能更复杂，内膜上的蛋白质的种类和数量更多，B正确；C、线粒体、叶绿体中均含DNA，故二者都能进行DNA复制和蛋白质合成，C正确；D、线粒体中进行有氧呼吸的第三阶段线粒体内膜，能合成ATP，叶绿体的光反应阶段能合成ATP，因此二者能在膜上进行ATP合成，D正确．故选A．考点：线粒体、叶绿体的结构和功能．4.协同转运是一种常见的跨膜运输方式，例如葡萄糖利用储存在Na+浓度梯度中的能量进入细胞（如图所示）。

高二期末考试总结与反思8篇篇1随着高二期末考试的结束，我们不禁要思考这次考试给我们带来了哪些启示和反思。

在这篇总结中，我们将从考试整体情况、各学科表现、学习态度与方法、身体与心理健康等方面进行全面分析，以期找出不足，为未来的学习打下坚实的基础。

一、考试整体情况这次高二期末考试，我们班级的整体成绩呈现出稳步上升的趋势。

在全校范围内的排名也有所提升，这充分体现了同学们在学习上的进步和努力。

然而，我们也发现了一些需要改进的地方，如在某些学科上还有提升空间，需要在未来的学习中加以重视。

二、各学科表现在各学科表现方面，我们发现在一些传统优势学科上，同学们的成绩依然保持稳定，这得益于平时的扎实学习和老师的悉心指导。

而在一些薄弱学科上，同学们的成绩还有待提高，需要加强对这些学科的学习和复习。

此外，我们还发现了一些同学在某一学科上存在严重偏科现象，需要在未来的学习中加以纠正。

三、学习态度与方法在学习态度与方法方面，我们发现在学习态度上，大多数同学都能够保持积极向上的态度，认真对待每一次考试和作业。

然而，也有一些同学在学习上存在懈怠和马虎的现象，需要引起重视。

在学习方法上，我们发现一些同学采用了科学有效的方法，如制定合理的学习计划、做好课堂笔记、及时复习等，这些方法对于提高学习成绩非常有帮助。

而一些同学则存在学习方法不当、效率低下的问题，需要在未来的学习中加以改进。

四、身体与心理健康在身体与心理健康方面，我们发现在学习压力下，一些同学出现了身体不适和情绪波动的问题。

这些问题不仅影响了同学们的学习效率和质量，还可能对身心健康造成长期影响。

因此，我们需要关注同学们的身体和心理健康状况，及时给予关心和支持。

五、未来展望面对未来，我们希望同学们能够继续保持积极的学习态度和科学的学习方法，不断提高自己的学习成绩和综合素质。

同时，我们也希望同学们能够重视身体和心理健康，合理安排学习和休息时间，保持良好的心态和状态。

在未来的学习和生活中，我们相信同学们一定能够取得更加优异的成绩和更加美好的未来。

哈三中2021—2022学年度上学期高二学年期末考试数学试卷考试说明：（1）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，满分150分．考试时间为120分钟；（2）第I 卷，第II 卷试题答案均答在答题卡上，交卷时只交答题卡．第I 卷（选择题,共60分）一、选择题（共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的）1.经过()()3,0,6,3A B -两点的直线的倾斜角为A ．4πB ．34πC ．2πD ．3π2.在等差数列{}n a 中，若4567890a a a a a ++++=，则39a a +=A ．18B ．30C ．36D ．723.若直线1:230l ax y a +++=，()2:150l x a y +--=平行，则实数a 的值为A ．1-B ．2C ．1或2-D ．1-或24.方程2890x x -+=的两根的等比中项是A ．4-B ．3-和3C ．4-和4D ．35.若椭圆的两个焦点21,F F 与它短轴的一个端点B 是一个等腰直角三角形的三个顶点，则椭圆的离心率为A ．22B C ．12D ．36.以下结论正确的是A ．事件A 与事件B 的和事件的概率一定大于事件A 的概率B ．事件A 与事件B 是对立事件，则它们一定是互斥的C ．事件A 与事件B 互斥，则有()()1P A P B =-D ．事件A 与事件B 满足()()1P A P B +=，则A ，B 是对立事件7.已知R a ∈，||3a ≥是直线:20l x y -=与圆22:52a C x y ⎛⎫+-= ⎪⎝⎭相离的A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件8.2021年某省实施新的“3+1+2”高考改革方案，“3”即为语文、数学、英语3科必选，“1”即为从物理和历史中任选一科，“2”即为从化学、生物、地理、政治中任选2科，则该省某考生选择全理科(物理、化学、生物)的概率是A ．16B ．18C ．110D ．1129.一种卫星接收天线如图（1）所示，其曲面与轴截面的交线为抛物线.在轴截面内的卫星波束呈近似平行状态射入形为抛物线的接收天线，经反射聚集到焦点F 处，如图（2）所示，已知接收天线的口径AB 为4.8m ，深度为1m .若P 为接收天线上一点，则点P 与焦点F 的最短距离为A ．0.72mB ．1.44mC ．2.44mD ．2.88m10.等差数列{}n a 的前n 项和为n S ，前n 项积为n T ，已知24a =-，31a =-，则A ．n S 有最小值，n T 有最小值B ．n S 有最大值，n T 有最大值C ．n S 有最小值，n T 有最大值D ．n S 有最大值，n T 有最小值11.2021年11月，满洲里市再次出现由新型冠状病毒引发的疫情.哈尔滨市派出5个医疗小组前往满洲里市区内三所医院开展抗疫工作，因疫情需要，每所医院至少需要安排一个医疗组，其中甲、乙两个医疗小组必须安排在同一所医院，丙、丁两个小组不能安排在同一所医院，则不同的安排方案的总数为A ．36B ．24C ．30D ．1812.在等腰梯形ABCD 中，//AB CD ，且2,1,2AB AD CD x ===，其中()0,1x ∈，以,A B为焦点且过点D 的椭圆的的离心率为1e ，以,C D 为焦点且过点A 的双曲线离心率为2e ，21e e +的取值范围A ．(B ．)+∞C ．(D ．(第Ⅱ卷（非选择题,共90分）二、填空题(本大题共4小题，每小题5分，共20分．将答案填在答题卡相应的位置上)13.与双曲线221916x y -=有共同的渐近线，且过点(-的双曲线的方程为__________________．14.等比数列{}n a 中，258,64a a ==，则{}n a 的前7项和7S =_______________．15.()5(12)13x x -+的展开式中2x 项的系数为__________________．16.意大利数学家列昂纳多·斐波那契是第一个研究了印度和阿拉伯数学理论的欧洲人，斐波那契数列又称黄金分割数列，因列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”．斐波那契数列用递推的方式可如下定义：用n a 表示斐波那契数列的第n 项，则数列{}n a 满足：11a =，21a =，()*123,n n n a a a n n N --=+≥∈，记121ni n i a a a a ==+++∑ ，则下列结论①32a =②()2233n n n a a a n -+=+≥③202120231i i aa ==∑④20212202120221i i aa a ==⋅∑其中正确的命题序号是．三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17.已知数列{}n a 是一个等差数列，且2511,45a S ==．（1）求{}n a 的通项n a ；（2）求{}n a 的前n 项和n S 的最大值．18.已知y x m =+与抛物线x y 42=交于,A B 两点．（1）若28=AB ，求实数m 的值；（2）O 为坐标原点，若OA OB ⊥，求实数m 的值．19.某超市举办有奖促销活动，顾客购买一定金额的商品后即可抽奖，每次抽奖都是从装有1个红球，3个白球的甲箱和装有2个红球、2个白球的乙箱中，各随机摸出1个球，若都是红球，则可获得现金100元；若只有1个红球，则可获得现金50元；若没有红球，则不获奖.球的大小重量完全相同，每次抽奖后都将球放回且搅拌均匀．（1）若某顾客有1次抽奖机会，求该顾客获得现金100元或50元的概率；（2）若某顾客有2次抽奖机会，求该顾客在2次抽奖中一共获得现金100元的概率．20.在平面直角坐标系xOy 中，已知一个圆的圆心C 在直线20x y +=上，与直线2y x =-相切于点()2,0．（1）求C 的方程；（2）若经过点()5,1的直线l 与圆C 相交于,M N 两点，且MN =求直线l 的方程．21.已知数列{}n a 中，31=a ，且满足11323++⨯+=n n n a a .（1）证明：数列⎭⎬⎫⎩⎨⎧n n a 3为等差数列，并求出数列{}n a 的通项公式;（2）若不等式3842+->n n a n λ，对+∈∀N n 恒成立，求λ的范围.22.如图，已知椭圆()01:2222>>=+b a b y a x M 的离心率为21，以该椭圆上的任意一点和椭圆的左、右焦点21,F F 为顶点的三角形的周长为6.双曲线N 的顶点是椭圆M 的焦点，离心率为2.设P 为双曲线N 椭圆M 的交点分别为B A ,和D C ,.（1）求椭圆M 和双曲线N 的标准方程；（2）设直线1PF 、2PF 的斜率分别为1k 、2k ，求证：21k k ⋅为定值；（3）是否存在常数λ，使得·AB CD AB CD λ+=若存在，求出λ的值；若不存在，请说明理由.。

杭州学军中学2022学年第一学期期末考试高二数学试卷命题人：郑日锋审题人：林智恒一、单选题：（本大题共8小题，每小题6分，共48分）1.抛物线22x y =的准线方程为（）A.12x =-B.=1x -C.12y =-D.1y =-2.若直线y x b =+与圆221x y +=有公共点，则实数b 的取值范围是（）A.[]1,1- B.[]0,1 C.⎡⎣ D.⎡⎣3.已知空间两不同直线m ，n ，两不同平面α，β，下列命题正确的是（）A .若m α∥且n α∥，则m n∥B.若m β⊥且m n ∥，则n β∥C.若m α⊥且m β∥，则αβ⊥D.若m 不垂直于α，且n ⊂αm 不垂直于n4.直线l 的方程为：(2)(31)1a y a x -=--，若直线l 不经过第二象限，则实数a 的取值范围为（）A.2a > B.23a -≤≤ C.2a ≥ D.4a ≥5.若a ，b 是异面直线，下列四个命题中正确的是（）A.过不在a ，b 上任一点P ，必可作直线与a ，b 都平行B.过不在a ，b 上任一点P ，必可作直线与a ，b 都相交C.过不在a ，b 上任一点P ，必可作直线与a ，b 都垂直D.过不在a ，b 上任一点P ，必可作平面与a ，b 都平行.6.已知圆221x y +=与抛物线()220y px p =>交于A ，B 两点，与抛物线的准线交于C ，D 两点，若四边形ABCD 是矩形，则p 等于（）A.B.5C.522D.7.已知菱形 ABCD 边长为1，60BAD ︒∠=，对角线AC 与BD 交于点O ，将菱形ABCD 沿对角线BD 折成平面角为θ的二面角，若60,120θ︒︒⎡⎤∈⎣⎦，则折后点O 到直线AC 距离的最值为（）A.最小值为34，最大值为32 B.最小值为34，最大值为34C.最小值为14，最大值为34D.最小值为34，最大值为328.已知椭圆2222:1(0)x y a b a b Γ+=>>内有一定点(1,1)P ，过点P 的两条直线1l ，2l 分别与椭圆Γ交于A 、C 和B 、D 两点，且满足AP PC λ= ，BP PD λ= ，若λ变化时，直线CD 的斜率总为14-，则椭圆Γ的离心率为A.32B.12C.22D.5二、多选题（每小题6分，全部选对得6分，部分选对得3分，选错得0分，共24分）9.如图，长方体1111ABCD A B C D -被平面BCFE 截成两个几何体，其中E ，F 分别在11AB 和11DC 上，且11EF B C ∥，则以下结论正确的是（）A.EF BC∥ B.AD ∥平面BCFE C.几何体11AA EB DD FC -为棱台D.几何体11BB E CC F -为棱柱10.已知曲线C ：221mx ny +=，下列结论正确的是（）A.若0m n >>，则C 是椭圆，其焦点在x 轴上B.若0m n >>，则C 是双曲线，其焦点在x 轴上C.若0m =，0n >，则C 是两条直线D.若m n =，则C 是圆11.若OA ，OB ，OC是三个不共面的单位向量，且两两夹角均为θ，则（）A.θ的取值范围是()0,πB.{},,OA AB BC能构成空间的一个基底C.“3OP OA OB OC =--”是“P ，A ，B ，C 四点共面”的必要不充分条件D.()OA OB OC BC ++⋅= 12.如图，过双曲线222:1(0)y C x b b-=>右支上一点P 作双曲线的切线l 分别交两渐近线于A 、B 两点，交x轴于点D ，12,F F 分别为双曲线的左、右焦点，O 为坐标原点，则下列结论正确的是（）A.min ||AB =B.OAP OBP S S =△△C.AOB S b=△D.若存在点P ，使121cos 4F PF ∠=，且122F D DF = ，则双曲线C 的离心率2e =三、填空题（本大题共4小题，每小题5分，共20分）13.以A (1,3)，B (－5,1)为端点的线段的垂直平分线的方程是__________14.若圆锥的侧面面积为2π，底面面积为π，则该圆锥的母线长为______.15.已知P 是抛物线2y x =上的动点，记点P 到直线l ：40x y -+=的距离为d ，则d 的最小值为______．16.已知球O 是正三棱锥（底面为正三角形，顶点在底面的射影为底面中心）A-BCD 的外接球，BC=3，AB =点E 在线段BD 上，且BD=3BE，过点E 作圆O 的截面，则所得截面圆面积的取值范围是__.四、解答题（本大题共5小题，共58分.解答应写出文字说明、证明过程或演算步骤）17.等差数列{}n a 的前n 项和为n S ，已知52a =-，324S =-，求（1）数列{}n a 通项公式；（2）{}n a 的前n 项和n S 的最小值.18.已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形.2AB BC ==，E ，F 分别为AC 和1CC 的中点，11BF A B ⊥.（1）求四棱锥11E BB C F -的体积；（2）是否存在点D 在直线11A B 上，使得异面直线BF ，DE 的距离为1?若存在，求出此时线段DE 的长；若不存在，请说明理由.19.1F ，2F 分别为椭圆C ：()222210x y a b a b+=>>的左、右焦点，B 为短轴的一个端点，E 是椭圆C 上的一点，满足12OE OF OE =+，且12EF F 的周长为)22.（1）求椭圆C 的方程；（2）三个顶点均在椭圆上的三角形称为椭圆的内接三.角形，BMN 是以B 为直角顶点的椭圆内接等腰直角三角形，求BMN 的面积.20.如图，在四棱锥P ABCD -中，1,90,1,2AD BC ADC PAB BC CD AD E ∠∠=====∥为边AD 的中点，异面直线PA 与CD 所成的角为90 .（1）在直线PA 上找一点M ，使得直线//MC 平面PBE ，并求AMAP的值；（2）若直线CD 到平面PBE 的距离为5，求平面PBE 与平面PBC 夹角的正弦值.21.已知点()2,0A ，104,33B ⎛⎫-- ⎪⎝⎭在双曲线E ：()222210,0x y a b a b -=>>上．（1）求双曲线E 的方程；（2）直线l 与双曲线E 交于M ，N 两个不同的点（异于A ，B ），过M 作x 轴的垂线分别交直线AB ，直线AN 于点P ，Q ，当M P PQ =时，证明：直线l 过定点．杭州学军中学2022学年第一学期期末考试高二数学试卷命题人：郑日锋审题人：林智恒一、单选题：（本大题共8小题，每小题6分，共48分.在每个小题给出的四个选项中，只有一项是符合题目要求的）1.抛物线22x y =的准线方程为（）A.12x =- B.=1x - C.12y =-D.1y =-【答案】C 【解析】【分析】直接根据抛物线的方程求出准线方程；【详解】因为抛物线22x y =，所以其准线方程为12y =-.故选：C.2.若直线y x b =+与圆221x y +=有公共点，则实数b 的取值范围是（）A.[]1,1- B.[]0,1 C.⎡⎣ D.⎡⎣【答案】D 【解析】分析】利用点到直线距离公式，列出不等式，求解作答.【详解】依题意，圆心(0,0)O 到直线y x b =+的距离1d =≤，解之得b ≤≤所以实数b 的取值范围是⎡⎣.故选：D 3.已知空间两不同直线m ，n ，两不同平面α，β，下列命题正确的是（）A.若m α∥且n α∥，则m n ∥ B.若mβ⊥且m n ∥，则n β∥C.若m α⊥且m β∥，则αβ⊥ D.若m 不垂直于α，且n ⊂α，则m 不垂直于n【答案】C 【解析】【分析】根据空间中点线面的位置关系结合选项即可逐一求解.【详解】对于A,若m α∥且n α∥，则m n ∥或者,m n 异面，或者,m n 相交，故A 错误，对于B,若mβ⊥且m n ∥，则n β⊥，故B 错误，对于C ，若m α⊥且m β∥，则αβ⊥，故C 正确，对于D ，若m 不垂直于α，且n ⊂α，则m 有可能与n 垂直,例如在正方体1111ABCD A B C D -中，1AC 不垂直平面ABCD ,BD ⊂平面ABCD ,但是1A C BD ⊥,理由如下：1AA ⊥平面ABCD ，BD ⊂平面ABCD ,所以1,AA BD ⊥又BD CA ⊥，11,,CA AC C CA AC ⋂=⊂平面1A AC ,所以BD ⊥平面1A AC ,1AC ⊂平面1A AC ,故1A C BD ⊥，故D 错误，故选：C4.直线l 的方程为：(2)(31)1a y a x -=--，若直线l 不经过第二象限，则实数a 的取值范围为（）A.2a > B.23a -≤≤ C.2a ≥ D.4a ≥【答案】C 【解析】【分析】根据直线斜率与截距讨论不经过第二象限时所满足的条件，解得结果.【详解】若直线l 斜率不存在，即12,5al x ==：不经过第二象限，若直线l 斜率存在，即3112,22a a l y x a a -≠=---：，所以31022102a a a a -⎧≥⎪⎪-⇒>⎨⎪-≤⎪-⎩，综上实数a 的取值范围为2a ≥，选C.【点睛】本题考查直线方程，考查空基本分析与求解能力，属于中档题．5.若a ，b 是异面直线，下列四个命题中正确的是（）A.过不在a ，b 上任一点P ，必可作直线与a ，b 都平行B.过不在a ，b 上任一点P ，必可作直线与a ，b 都相交C.过不在a ，b 上任一点P ，必可作直线与a ，b 都垂直D.过不在a ，b 上任一点P ，必可作平面与a ，b 都平行.【答案】C 【解析】【分析】根据异面直线的定义，结合线线平行、线面平行、线面垂直的性性质逐一判断即可.【详解】A ；设过P 的直线为l ，如果//,//l a l b ，显然可得//a b ，这与a ，b 是异面直线相矛盾，因此本选项不正确；B ：在a 任取一点M ，在b 上任取一点N ，直线MN 上的点才可作一条直线与a 、b 都相交．其它的点不行，因此本选项不正确；C ：过P 点作//,//c a d b ，显然,c d确定一个平面β，显然存在一条直线n ，n β⊥，过P 点一定存在直线与n 平行，因此本选项正确；D ：经过空间任意一点不一定可作一个平面与两条已知异面直线都平行，有时会出现其中一条直线在所做的平面上，因此本选项不正确；故选：C6.已知圆221x y +=与抛物线()220y px p =>交于A ，B 两点，与抛物线的准线交于C ，D 两点，若四边形ABCD 是矩形，则p 等于（）A.B.5C.2D.5【答案】D 【解析】【分析】由题，结合抛物线与圆的对称性得弦AB 为抛物线()220y px p =>的通径，进而有2212p p ⎛⎫+= ⎪⎝⎭，解方程即可得答案.【详解】解：因为四边形ABCD 是矩形，所以由抛物线与圆的对称性知：弦AB 为抛物线()220y px p =>的通径，因为圆的半径为1，抛物线的通径为2p ，所以有：2212p p ⎛⎫+= ⎪⎝⎭，解得255p =故选：D7.已知菱形 ABCD 边长为1，60BAD︒∠=，对角线AC 与BD 交于点O ，将菱形ABCD 沿对角线BD 折成平面角为θ的二面角，若60,120θ︒︒⎡⎤∈⎣⎦，则折后点O 到直线AC 距离的最值为（）A.最小值为34，最大值为32 B.最小值为34，最大值为34C.最小值为14，最大值为34D.最小值为34，最大值为32【答案】B 【解析】【分析】首先由二面角的定义可知AOC θ∠=，60,120θ︒︒⎡⎤∈⎣⎦，再在AOC 中解决点到直线的距离的最值.【详解】,AO BD CO BD ⊥⊥，AOC θ∴∠=，60,120θ︒︒⎡⎤∈⎣⎦菱形 ABCD 边长为1，60BAD ︒∠=，32AO CO ∴==，点O 到AC 的距离31cos 22d AOC =⋅∠当60AOC θ∠== 时，d取得最大值333224⨯=,当120AOC θ∠== ，d取得最小值313224⨯=,故选：B8.已知椭圆2222:1(0)x y a b a b Γ+=>>内有一定点(1,1)P ，过点P 的两条直线1l ，2l 分别与椭圆Γ交于A 、C 和B 、D 两点，且满足AP PC λ= ，BP PD λ= ，若λ变化时，直线CD 的斜率总为14-，则椭圆Γ的离心率为A.32B.12C.22D.55【答案】A 【解析】【分析】设出,,,A B C D 四点的坐标，将,A B 两点坐标代入椭圆方程并化简，同理将,C D 两点坐标代入椭圆方程并化简，根据14AB CDk k ==-化简上述两个式子，由此求得22b a的值，进而求得椭圆离心率.【详解】设()()()()11324423,,,,,,,,A x yB x yC x yD x y 因为()1,1P ，且AP PC=uu u r uu u rλ，所以131311x x y y λλλλ+=+⎧⎨+=+⎩，同理242411x x y y λλλλ+=+⎧⎨+=+⎩.将,A B两点坐标代入椭圆方程并化简得()()()()22121212120b x x x x a y y y y +-++-=，即()()2212120AB b x x a y y k +++=，同理()()2234340CD b x x a y y k +++=，由于AP PC=uu u r uu u rλ，BP PD=uu r uu u r λ，所以14AB CDk k ==-，即()()()()221212223434104104b x x a y y b x x a y y ⎧⎛⎫+++⋅-= ⎪⎪⎪⎝⎭⎨⎛⎫⎪+++⋅-= ⎪⎪⎝⎭⎩，即()()()()221212223434104104b x x a y y b x x a y y λλ⎧⎛⎫+++⋅-= ⎪⎪⎪⎝⎭⎨⎛⎫⎪+++⋅-= ⎪⎪⎝⎭⎩，两式相加得()()221324132404a b x x x x y y y y λλλλ+++-+++=，即()()22222204a b λλ+-+=，所以2214b a =，所以2e ===，故选A.【点睛】本小题主要考查直线和椭圆的位置关系，考查定比分点坐标公式，考查点在曲线上的运用，考查化归与转化的数学思想方法，考查运算求解能力，考查椭圆离心率的求法，难度较大，属于难题.二、多选题（每小题6分，全部选对得6分，部分选对得3分，选错得0分，共24分）9.如图，长方体1111ABCD A B C D -被平面BCFE 截成两个几何体，其中E ，F 分别在11A B 和11D C 上，且11EF B C ∥，则以下结论正确的是（）A.EF BC∥ B.AD ∥平面BCFEC.几何体11AA EB DD FC -为棱台 D.几何体11BB ECC F-为棱柱【答案】ABD 【解析】【分析】A 由长方体的性质及线线平行的推论判断；B 根据线面平行的判定判断；C 、D 根据棱台、棱柱的定义判断正误.【详解】由11//B C BC 及11//EF B C ，得//EF BC ，则A 正确；由//AD BC，BC ⊂平面BCFE ，AD ⊄平面BCFE ，得//AD 平面BCFE ，则B 正确；以两个平行的平面1AA EB 和1DD FC 为底面，其余四面都是四边形，且每相邻两个四边形的公共边都平行，符合棱柱的定义，则C 错误（由于11,,,AA DD CF BE延长后不交于一点，则几何体11AA EB DD FC -不为棱台）；以两个平行的平面1BB E 和1CC F 为底面，其余三面都是四边形，且每相邻两个四边形的公共边都平行，符合棱柱的定义，则D 正确，故选：ABD10.已知曲线C ：221mx ny +=，下列结论正确的是（）A.若0m n >>，则C 是椭圆，其焦点在x 轴上B.若0m n >>，则C 是双曲线，其焦点在x 轴上C.若0m=，0n >，则C 是两条直线D.若m n =，则C 是圆【答案】BC 【解析】【分析】根据椭圆方程、双曲线方程、直线方程、圆的方程特征进行逐一判断即可.【详解】对于A ：当0m n >>时，22221111x y mx ny m n+=⇒+=，由11000m n m n mn mn n m>>⇒>>⇒>>，所以C 是椭圆，其焦点在y 轴上，因此本选项不正确；对于B ：当0m n >>时，22221111x y mx ny m n+=⇒+=，由1100m n mn mn mn n m>>⇒<⇒<<，所以C 是双曲线，其焦点在x 轴上，因此本选项正确；对于C ：当0m=，0n >时，22211mx ny ny y n+=⇒=⇒=±，所以C 是两条直线，因此本选项正确；对于D ：若0m n ==，显然221mx ny +=不成立，所以C 没有轨迹，因此本选项不正确；故选：BC 11.若OA，OB，OC是三个不共面的单位向量，且两两夹角均为θ，则（）A.θ的取值范围是()0,π B.{},,OA AB BC能构成空间的一个基底C.“3OP OA OB OC =--”是“P ，A ，B ，C 四点共面”的必要不充分条件D.()OA OB OC BC ++⋅= 【答案】BD 解析】【分析】利用向量的夹角的定义判断A ；利用空间向量的基底的性质判断B ；利用共面向量定理判断C ；利用向量数量积公式判断D.【详解】解：因为OA ，OB ，OC是三个不共面的单位向量，且两两夹角均为θ，对于A ，由向量所成角的定义得θ∈2π0,3⎛⎫⎪⎝⎭，故错误；对于B ，因为,,OA AB BC u u u r u u u r u u u r不共面，所以{},,OA AB BC能构成空间的一个基底，故正确；对于C ，因为3OPOA OB OC =--，3-1-1=1，所以P ，A ，B ，C 四点共面；当P ，A ，B ，C 四点共面时，不一定有3OP OA OB OC =--成立，所以“3OP OA OB OC =--”是“P ，A ，B ，C 四点共面”的充分不必要条件，故错误；对于D ，()()()OA OB OC BC OA OB OC OC OB ++⋅=++⋅-u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r =22OA OC OA OB OB OC OB OC OB OC ⋅-⋅+⋅-+-⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r =2211cos 11cos 110OA OC OA OB OB OC θθ⋅-⋅-+=⨯⨯-⨯⨯-+=u u u r u u u r u u u r u u u r u u u r u u u r ，故正确.故选：BD.12.如图，过双曲线222:1(0)y C x b b-=>右支上一点P 作双曲线的切线l 分别交两渐近线于A 、B 两点，交x 轴于点D ，12,F F 分别为双曲线的左、右焦点，O 为坐标原点，则下列结论正确的是（）A.min ||AB = B.OAP OBP S S =△△C .AOB S b=△D.若存在点P ，使121cos 4FPF ∠=，且122F D DF = ，则双曲线C 的离心率2e =【答案】BCD 【解析】【分析】联立切线方程与渐近线方程，求出,A B的坐标，即可得AB =0x 的取值范围即可得min ||2AB b =，从而可判断A ，由中点坐标公式可判断P 是,A B 的中点，由此可判断BC ，由余弦定理结合122F D DF =可判断D.【详解】先求双曲线2221y x b-=上一点00(,)P x y 的切线方程：不妨先探究双曲线在第一象限的部分（其他象限由对称性同理可得）.由2221y x b -=，得y =，所以2y '=，则在00(,)P x y的切线斜率2200b x y y '==，所以在点00(,)P x y 处的切线方程为：20000()b x y y x x y -=-又有220021y x b-=，化简即可得切线方程为：0021y y x x b -=.不失一般性，设00(,)P x y 是双曲线在第一象限的一点，11(,)A x y 是切线与渐近线在第一象限的交点，22(,)B x y 是切线与渐近线在第四象限的交点,双曲线的渐近线方程是y bx ±=，联立：0021y y x x by bx ⎧-=⎪⎨⎪=⎩，解得：20000(,)b b A bx y bx y --，联立：0021y y x x by bx ⎧-=⎪⎨⎪=-⎩，解得：20000(,)b b B bx y bx y -++，则AB ==又因为01x ≥，所以AB≥2b =，即min ||2AB b =，A 错误；由220000000000,22b b b b bx y bx y bx y bx y x y -++-+-+==，可知00(,)P x y 是,A B 的中点，所以OAP OBP S S =△△，B 正确；易知点D 的坐标为01(,0)x ，则221200000111()22AOB ADO BDOb b S S S OD y y b x bx y bx y =+=⨯⨯-=⨯⨯=-+ ，当点00(,)P x y 在顶点(1,0)时，仍然满足AOB S b =△，C 正确；因为1201(,0),(,0),(,0)F c F c D x -，所以101(,0)F D c x =+ ，21(,0)DF c x =- ，因为122F D DF = ，则0012()c c x x +=-，解得03c x =，即03x c=，代入220021y x b -=，得222029b y b c=-，所以222222212223999()6b b PF c b c b c c c c=++-=+++-2222299(1)6(1)16c c c c c -=+++--=，222222222223999()6b b PF c b c b c c c c=-+-=+-+-2222299(1)6(1)4c c c c c-=+-+--=，所以2222212121212164451cos 224244PF PF F F c c F PFPF PF +-+--∠====⨯⨯⨯⨯，所以24c =，2c =，所以离心率2ce a==，D 正确.【点睛】关键点点睛：利用导数几何意义求得在双曲线上一点00(,)P x y 的切线方程，并联立渐近线方程，求得,A B 的坐标，判断出P 是AB 中点.三、填空题（本大题共4小题，每小题5分，共20分）13.以A (1,3)，B (－5,1)为端点的线段的垂直平分线的方程是__________【答案】340x y ++=.【解析】【详解】试题分析：解：因为A （1，3），B （-5，1），所以AB 的中点坐标（-2，2），直线AB 的斜率为：3-11=153+，所以AB 的中垂线的斜率为：-3，所以以A （1，3），B （-5，1）为端点的线段的垂直平分线方程是y-2=-3（x+2），即3x+y+4=0．故答案为3x+y+4=0．考点：直线方程点评：本题考查直线的一般式方程与直线的垂直关系，直线方程的求法，考查计算能力．14.若圆锥的侧面面积为2π，底面面积为π，则该圆锥的母线长为______.【答案】2【解析】【分析】根据圆面积公式算出底面半径r ＝1，再由圆锥侧面积公式建立关于母线l 的方程，解之即可得到该圆锥的母线长．【详解】解：∵圆锥的底面积为π，∴圆锥的底面半径为r ，满足2r ππ=，解得1r =又∵圆锥的侧面积为2π，∴设圆锥的母线长为l ，可得2rl ππ=，12l ππ⨯⨯=，解之得2l =故答案为：2【点睛】本题给出圆锥的底面圆面积和侧面积，求它的母线长，着重考查了圆的面积公式和圆锥侧面积公式等知识，属于基础题．15.已知P 是抛物线2y x =上的动点，记点P 到直线l ：40x y -+=的距离为d，则d的最小值为______．【答案】1528【解析】【分析】作直线l ：40x y -+=的平行线且与抛物线相切，再求两平行线间的距离即可．【详解】设直线直线l ：40x y -+=的平行线为y x b =+且与抛物线2y x =相切，联立2y x b y x =+⎧⎨=⎩，整理得20y y b -+=，则140b ∆=-=，得14b =，则d的最小值为8d ==．故答案为：1528．16.已知球O 是正三棱锥（底面为正三角形，顶点在底面的射影为底面中心）A-BCD的外接球，BC=3，AB =E 在线段BD 上，且BD=3BE，过点E 作圆O 的截面，则所得截面圆面积的取值范围是__.【答案】[2,4]ππ【分析】设△BDC 的中心为O 1，球O 的半径为R ，连接1OO ,O 1D ，OD ，O 1E ，OE ，可得R 2＝3+（3﹣R ）2，解得R ＝2，过点E 作圆O 的截面，当截面与OE 垂直时，截面的面积最小，当截面过球心时，截面面积最大，即可求解．【详解】如图：设△BDC 的中心为O 1，球O 的半径为R ，连接1OO ,O 1D ，OD ，O 1E ，OE ，则0123sin 603O D=⨯=，AO 1 3.==在Rt △OO 1D 中，R 2＝3+（3﹣R ）2，解得R ＝2，∵BD ＝3BE ，∴DE ＝2在△DEO 1中，O 1E 0.==∴OE ==过点E 作圆O 的截面，当截面与OE 垂直时，截面的面积最小，=，最小面积为2π．当截面过球心时，截面面积最大，最大面积为4π．故答案为[2π，4π]【点睛】本题考查了球与三棱锥的组合体，考查了空间想象能力，转化思想，解题关键是要确定何时取最值，属于中档题．四、解答题（本大题共5小题，共58分.解答应写出文字说明、证明过程或演算步骤）17.等差数列{}n a 的前n 项和为n S ，已知52a =-，324S =-，求（1）数列{}n a 通项公式；（2）{}n a 的前n 项和n S 的最小值.【答案】（1）212na n =-（2）-30【解析】【分析】（1）根据数列的基本公式求出通项公式，（2）根据（1）表达出n S ，利用二次函数性质求出n S 的最小值.【小问1详解】由已知得11423324a d a d +=-⎧⎨+=-⎩，解得1102a d =-⎧⎨=⎩，所以()11212n a a n d n =+-=-.【小问2详解】()22111112111224nn n Sna d n n n -⎛⎫=+=-=--⎪⎝⎭.当5n=或6时，n S 有最小值-30.18.已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形.2AB BC ==，E ，F 分别为AC 和1CC 的中点，11BF A B ⊥.（1）求四棱锥11E BB C F-的体积；（2）是否存在点D 在直线11A B 上，使得异面直线BF ，DE 的距离为1?若存在，求出此时线段DE 的长；若不存在，请说明理由.【答案】（1）1（2）存在，DE =2【解析】【分析】（1）找到四棱锥的高，利用四棱锥体积公式求出体积；（2）根据题目中的条件建立空间直角坐标系，表达出与BF ，ED均垂直的向量，进而利用异面直线BF ，DE 的距离为1建立等式求出a .【小问1详解】∵侧面11AA B B 为正方形，∴111A B BB ⊥，又11BFA B ⊥，且1BB BF B ⋂=，1,BB BF ⊂面11BB C C ，∴11A B ⊥平面11BB C C ，又11//AB A B ，∴AB ⊥平面11BB C C ，取BC 中点G ，则//EG AB ，∴EG ⊥平面11BB C C .∴()()1111111111122113232E BB C FVC F BB B C EG -=⨯+⋅⋅=⨯⋅+⋅⋅=.【小问2详解】以B 为原点，分别以BA ，BC ，1BB所在直线建立空间直角坐标系，如图，则()0,0,0B ，()1,1,0E ，()0,2,1F ，设(),0,2D a ，则()0,2,1BF = ，()1,1,2ED a =-- ，()1,1,0BE =.设与BF ，ED均垂直的向量为(),,n x y z = ，则·0·0BF n ED n ⎧=⎪⎨=⎪⎩，即20(1)20y z a x y z +=⎧⎨--+=⎩，取()()5,1,21n a a =--- ，∴异面直线BF ，DE 的距离1BE n d n ⋅=== ，解得1a =或72.∴ED ==或2.故存在点D 在直线11A B 上，使得异面直线BF ，DE的距离为1，且此时ED =或2.19.1F ，2F 分别为椭圆C ：()222210x ya b a b+=>>的左、右焦点，B 为短轴的一个端点，E 是椭圆C 上的一点，满足12OE OF OE =+ ，且12EF F 的周长为)22+.（1）求椭圆C 的方程；（2）三个顶点均在椭圆上的三角形称为椭圆的内接三.角形，BMN 是以B 为直角顶点的椭圆内接等腰直角三角形，求BMN 的面积.【答案】（1）2214x y +=（2）6425或3215【解析】【分析】（1）利用题目条件建立a c 、的方程组，进而求出椭圆C 的方程；（2）联立直线与椭圆表示出M N 、的横坐标,进而表示出BM BN 、，利用等角三角形求出k 的值，从而求出BMN 的面积.【小问1详解】设()0,B b ，由112OE OF OB =+ ，得1,2E c b ⎛⎫- ⎪⎝⎭.∵点E 在椭圆C 上，∴22114c a +=，即2c a =.①∵12EF F的周长为)22+，∴)2222a c +=，即2a c +=.②联立①②解得2a=，c =1b =.∴椭圆C 的方程为2214x y +=.【小问2详解】不妨设M ，N 分别在y 轴左、右侧，设BM ：()10y kx k =+>，则BN：11y x k=-+.由221,44,y kx x y =+⎧⎨+=⎩消去y 得()221480k x kx ++=.∴点M 的横坐标2814M k x k =-+.以1k-代k 得点N 的横坐标284N k x k =+∴2814M kBM k ==+，284N BN k ==+.∵BM BN=2288144k k k =++.即324410k k k -+-=.解得11k =，232k +=，332k =.BMN 的面积()()2222321124k S BN k +==+.当1k=时，6425S =；当32k±=时，3215S=.20.如图，在四棱锥P ABCD-中，1,90,1,2AD BC ADC PAB BC CD E∠∠=====∥ 为边AD 的中点，异面直线PA与CD 所成的角为90 .（1）在直线PA 上找一点M，使得直线//MC 平面PBE ，并求AM AP的值；（2）若直线CD 到平面PBE 的距离为255，求平面PBE 与平面PBC 夹角的正弦值.【答案】（1）2（2）65【解析】【分析】（1）建立空间直角坐标系，利用向量垂直充要条件列出等式，解之即可求得AMAP的值；（2）先由直线CD 到平面PBE 25求得PA 的长度，再利用平面PBE 与平面PBC 法向量的夹角公式去求平面PBE 与平面PBC 夹角的正弦值.【小问1详解】在四棱锥P ABCD -中，90PAB ∠=o ，异面直线PA 与CD 所成的角为90 .即,PAAB PA CD ⊥⊥,又AB CD 、为两相交直线，则PA ⊥平面ABCD取PD 中点F ，连接EF ，又AE DE =，则//PA EF ，则EF ⊥平面ABCD又四边形ABCD 中，1,90,12AD BC ADC BC CD AD ∠==== ∥，AE DE =则BEAD ⊥，则三直线BE AD EF 、、两两互相垂直以E 为原点，分别以ED 、EB 、EF 所在直线为x 、y 、z轴建立空间直角坐标系如图：设(0)PA h h =>，则(0,0,0)E ，(1,0,0)A -，(0,1,0)B ，(1,1,0)C ，(1,0,0)D ，(1,0,)P h -，(1,1,)PB h =- ,(1,0,)PE h =-设平面PBE 的一个法向量为111(,,)n x y z =，则00PE n PB n ⎧⋅=⎨⋅=⎩，即1111100x hz x y hz -=⎧⎨+-=⎩，令11z =，则110x h y ==，，则(,0,1)n h =设(1,0,)M t -，则(2,1,)MCt =-由直线//MC 平面PBE，可得MCn ⊥，即0MC n ⋅=则200h t +-=，解之得2t h =，则2AM h =，又PA h =，则22AM hAP h==【小问2详解】由直线CD 到平面PBE的距离为5，得点C 到平面PBE的距离为5，又(1,0,0)CB=- ，(,0,1)nh =为平面PBE 的一个法向量则CB n n⋅==，解之得2h =，则(1,0,2)P -，(2,0,1)n =，(1,1,2)PB =- 设平面PBC 的一个法向量为222(,,)m x y z = ，又(1,0,0)CB =-则00CB m PB m ⎧⋅=⎨⋅=⎩，即2222020x x y z -=⎧⎨+-=⎩，令21z =，则2202x y ==，，则(0,2,1)m = 设平面PBE 与平面PBC 夹角为θ则1cos cos 5m nm n m nθ⋅===⋅，又π02θ≤≤，则26sin 5θ==21.已知点()2,0A ，104,33B ⎛⎫--⎪⎝⎭在双曲线E ：()222210,0x y a b a b -=>>上．（1）求双曲线E 的方程；（2）直线l 与双曲线E 交于M ，N 两个不同的点（异于A ，B ），过M 作x 轴的垂线分别交直线AB ，直线AN 于点P ，Q ，当M P PQ =时，证明：直线l 过定点．【答案】（1）2214x y -=（2）证明见解析【解析】【分析】（1）将点坐标代入双曲线方程，即可求解,a b 的值，进而得双曲线方程；（2）设直线方程，联立直线与双曲线方程，得到韦达定理，根据向量关系，转化为坐标关系，即可得,m k 的关系，进而可得直线过定点.【小问1详解】由题知，222224111014133a a b ⎧=⎪⎪⎨⎛⎫⎛⎫⎪---= ⎪ ⎪⎪⎝⎭⎝⎭⎩，得21b =，所以双曲线E 的方程为2214x y -=．【小问2详解】由题意知，当l ⊥x 轴时，Q 与N 重合，由M P PQ =可知：P 是MQ 的中点，显然不符合题意，故l 的斜率存在，设l 的方程为y kx m =+，联立2214y kx m x y =+⎧⎪⎨-=⎪⎩，消去y 得()222148440k x kmx m ----=，则()()()222222641611416140k m m k m k ∆=++-=+->，即2214m k +>，且2140k -≠，设()11,M x y ，()22,N x y ，122814kmx x k +=-，21224414m x x k +=--，AB 方程为()124y x =-，令1x x =，得112,4x P x -⎛⎫ ⎪⎝⎭，AN 方程为()2222y y x x =--，令1x x =得11222,2x Q x y x ⎛⎫- ⎪-⎝⎭，由M P PQ = ，得111222222x x y y x --=+⋅-，即12121222y y x x +=--，即()()()()()12211212122242kx m x kx m x x x x x +-++=-++⎡⎤⎣⎦，即()()()121214422480k x x k m x x m -+--+++=，将122814kmx x k +=-，21224414m x x k +=--代入得即22416161680m km k k m ++--=，所以()()2220m k m k ++-=，得22m k =-或2m k =-，当22m k =-，此时由0∆>，得58k <，符合题意；当2m k =-，此时直线l 经过点A ，与题意不符，舍去所以l 的方程为22y kx k =+-，即()22y k x =-+，所以l 过定点()2,2．。