第11章机械波作业答案
- 格式:ppt
- 大小:907.50 KB
- 文档页数:22

一. 选择题[ C ]1. 一沿x 轴负方向传播的平面简谐波在t = 2 s 时的波形曲线如图所示,则原点O 的振动方程为<A> )21(cos 50.0ππ+=t y , <SI>.<B> )2121(cos 50.0ππ-=t y , <SI>.<C> )2121(cos 50.0ππ+=t y , <SI>.<D> )2141(cos 50.0ππ+=t y ,<SI>.提示:设O 点的振动方程为O 0()cos()y t A t ωϕ=+.由图知,当t=2s 时,O 点的振动状态为:[ B ]2. 图中画出一向右传播的简谐波在t 时刻的波形图,BC 为波密介质的反射面,波由P 点反射,则反射波在t 时刻的波形图为提示:由题中所给波形图可知,入射波在P 点的振动方向向下;而BC 为波密介质反射面,故在P 点反射波存在"半波损失〞,即反射波与入射波反相,所以,反射波在P 点的振动方向向上,又P 点为波节,因而得答案B.[ A ]3. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是[ B ]4.一平面简谐波在弹性媒质中传播时,某一时刻媒质中某质元在负的最大位移处,则它的能量是<A> 动能为零,势能最大. <B> 动能为零,势能为零. <C>动能最大,势能最大. <D> 动能最大,势能为零.提示:动能=势能,在负的最大位移处时,速度=0,所以动能为零,势能也为零.[ B ]5. 在驻波中,两个相邻波节间各质点的振动<A> 振幅相同,相位相同. <B> 振幅不同,相位相同.<C>振幅相同,相位不同. <D> 振幅不同,相位不同.提示:根据驻波的特点判断.[ C ]6. 在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4,则两列波的振幅之比是<A> A 1 / A 2 = 16.<B> A 1 / A 2 = 4.<C> A 1 / A 2 = 2.<D> A 1 / A 2 = 1 /4.二. 填空题1. 一平面简谐机械波在媒质中传播时,若一媒质质元在t 时刻的总机械能是10 J,则在)(T t +2. 一列强度为I 的平面简谐波通过一面积为S 的平面,波速u 与该平面的法线0n 的夹角为θ,则通过该平面的能流是cos IS θ.提示:θIScos IS ==⊥流过该平面的能流3. 如图所示,波源S 1和S 2发出的波在P 点相遇,P 点距波源S 1和S 2的距离分别为 3λ 和10 λ / 3 ,λ 为两列波在介质中的波长,若P 点的合振幅总是极大值,则两波在P 点的振动频率相同,波源S 1 的相位比S 2 的相位领先43π.4.设沿弦线传播的一入射波的表达式为]2cos[1λωxt A y π-=,波在x = L 处〔B 点〕发生反射,反射点为自由端〔如图〕.设波在传播和反射过程中振幅不变,则反射波的表达式是y 2 = 24cos xL A t ππωλλ⎛⎫=+-⎪⎝⎭. 提示:因为反射点为自由端,所以反射波没有半波损失,反射波与入射波在B 点引起的振动同相.PS S5. 一静止的报警器,其频率为1000 Hz,有一汽车以79.2 km 的时速驶向和背离报警器时,坐在汽车里的人听到报警声的频率分别是1065Hz 和935Hz 〔设空气中声速为340 m/s 〕.6. 一球面波在各向同性均匀介质中传播,已知波源的功率为100W,若介质不吸收能量,则距波源10 m 处的波的平均能流密度为7.96×10-2 W/m 2.提示:根据平均能流密度I 和功率P 的关系,得7. 一弦上的驻波表达式为t x y 1500cos 15cos 100.22-⨯= <SI>.形成该驻波的两个反向传播的行波的波速为100 m/s .场强度为)312cos(300π+π=t E x ν<SI>,则O 点处磁场强度为0.796cos(2ππ/3) (A/m)y H t ν=-+.在图上表示出电场强度,磁场强度和传播速度之间的相互关系.提示:根据电磁波的性质,E H S ⨯=,三者的关系如图所示.E H 和同相,H ∴三. 计算题1.图示一平面余弦波在t = 0 时刻与t = 2 s 时刻的波形图.已知波速为u ,求 <1> 坐标原点处介质质点的振动方程;<2> 该波的波动表达式.解:<1> 比较t = 0 时刻波形图与t = 2 s 时刻波形图,可知此波向左传播〔向x 轴负向传播〕.设坐标原点O 处质点的振动方程为()00,cos()y t A t ωϕ=+.在t = 0时刻,O 处质点的振动状态为:0(0,0)cos 0y A ϕ==,00v sin 0A ωϕ=->, 故02ϕ=-π又t = 2 s,O 处质点位移为/cos(2)2A A ω=-π,且振动速度>0,所以224ω-=-ππ, 得 8ω=π∴振动方程为()0,cos()82y t A t =-ππ<SI><2> 由图中可见,波速为u = 20 /2 m/s = 10 m/s,向x 轴负向传播;又有()0,cos()82y t A t =-ππ ∴波动表达式为(),cos 8102x y x t A t ⎡⎤⎛⎫=+- ⎪⎢⎥⎝⎭⎣⎦ππ 〔SI 〕2. 一平面简谐波沿Ox 轴的负方向传播,波长为λ ,P 处质点的振动规律如图所示. <1> 求P 处质点的振动方程; <2> 求此波的波动表达式;<3> 若图中λ21=d ,求坐标原点O 处质点的振动方程.解:<1> 设P 处质点振动方程为0()cos()P y t A t ωϕ=+,由振动曲线可知,在t = 0时刻,0cos A A ϕ-=,∴0ϕπ=; t=1s 时,0cos()A ωπ=+,且振动速度>0,∴32πωπ+=,2πω=; ∴cos()2P y A t π=+π <SI><2> 设波速为u,则24u Tλωλλπ===,且波沿Ox 轴的负方向传播, ∴波动表达式为2(,)cos cos ()22x d y x t A t A t x d u λ⎡π-⎤ππ⎛⎫⎡⎤=++π=+-+π ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦<SI> <3> λ21=d 时,将x=0代入波动表达式,即得O 处质点的振动方程3. 如图所示,两相干波源在x 轴上的位置为S 1和S 2,其间距离为d = 30 m,S 1位于坐标原点O .设波只沿x 轴正负方向传播,单独传播时强度保持不变.x 1 = 9 m 和x 2 = 12 m 处的两点是相邻的两个因干涉而静止的点.求两波的波长和两波源间最小相位差.解:设S 1和S 2的振动初相位分别为10ϕ和20ϕ,在x 1点两波因干涉而静止,所以在x 1点两波引起的振动相位差为π的奇数倍,即()()12010112πd x x ϕϕϕλ∆=----⎡⎤⎣⎦π+=)12(K ① 同理,在x 2点两波引起的振动相位差()()22010222πd x x ϕϕϕλ∆=----⎡⎤⎣⎦π+=)32(K ② ②-①得:214()2x x λ-=ππ, ∴6)(212=-=x x λm ;由①得:120102(21)2(25)d x K K ϕϕλ--=++=+πππ;当K = -2、-3时相位差最小:2010ϕϕ-=±π4. 一平面简谐波在介质中以速度u = 20 m/s 自左向右传播.已知在传播路径上的某点A 的振动方程为)4cos(3.0π-π=t y <SI>.另一点D 在A 点右方9米处.<1> 若取x 轴方向向左,并以A 为坐标原点,试写出波的表达式,并求出D 点的振动方程.<2> 若取x 轴方向向右,以A 点左方5米处的O 点为x 轴原点,再写出波的表达式与D 点的振动方程.解:该波波速u = 20 m/s,(1) 若取x 轴方向向左,并以A 为坐标原点,则由已知条件知:)4cos(3.0),0(ππ-=t t y 〔m 〕所以,波的表达式为⎥⎦⎤⎢⎣⎡-+=-+=πππ)20(4cos 3.0))(4cos(3.0),(x t u x t t x y π〔m 〕 D 点的坐标为x D = -9 m 代入上式有)544cos(3.0)5144cos(3.0)209(4cos 3.0),(ππππππ-=-=⎥⎦⎤⎢⎣⎡--+=t t t t x y D 〔m 〕(2) 若取x 轴方向向右,以A 点左方5米处的O 点为x 轴原点,则由已知条件知:)4cos(3.0),5(ππ-=t t y 〔m 〕所以,波的表达式为)54cos(3.0)5(4cos 3.0),(x t u x t t x y πππ-=⎥⎦⎤⎢⎣⎡---=π〔m 〕 D 点的坐标为x D = 14 m 代入上式, 有)544cos(3.0)5/144cos(3.0ππ-=-=t t y D ππ<m>此式与<1> 结果相同.5. 由振动频率为 400 Hz 的音叉在两端固定拉紧的弦线上建立驻波.这个驻波共有三个波腹,其振幅为0.30 cm .波在弦上的速度为320 m/s .<1> 求此弦线的长度.<2> 若以弦线中点为坐标原点,试写出弦线上驻波的表达式.解:<1> 23λ⨯=Lλν = u∴20.14003202323=⨯==νu L m 〔2〕设驻波的表达式为)cos()cos(103),('3ϕωϕ++⨯=-t kx t x y πππνλπ25320400222=⨯===u k 〔m -1〕πππνω80040022=⨯== 〔rad/s 〕弦的中点x=0是波腹, 故πϕϕϕor kx x 0,1cos )cos(''0'=∴==+=所以)800cos(25cos 100.3),(3ϕπ+⨯±=-t x t x y π <m>式中的ϕ由初始条件决定.[选做题]1.如图,一角频率为ω,振幅为A 的平面简谐波沿x 轴正方向传播,设在t = 0时该波在原点O 处引起的振动使媒质元由平衡位置向y 轴的负方向运动.M 是垂直于x 轴的波密媒质反射面.已知OO '= 7 λ /4,PO '= λ /4〔λ为该波波长〕;设反射波不衰减,求: <1> 入射波与反射波的表达式;;<2> P 点的振动方程.解:<1> 设O 处振动方程为00cos()y A t ωϕ=+当t = 0时,y 0 = 0,v 0 < 0,∴012ϕπ=∴)21cos(0π+=t A y ω入射波朝x 轴正向传播,故入射波表达式为)22cos(2)(cos ),πλωπω+-=⎥⎦⎤⎢⎣⎡+-=x t A ux t A t x y π(入在O ′处入射波引起的振动方程为由于M 是波密媒质反射面,所以O ′处反射波振动有一个相位的突变π.∴)cos(t 47π+π-=t A y ωλ),(反t A ωcos = 所以反射波表达式为<2> 合成波为),(),(),(t x y t x y t x y 反入+=]22cos[π+π-=x t A λω]22cos[π+π++x t A λω 将P 点坐标λλλ234147=-=x 代入上述方程,得P 点的振动方程为)2cos(2π+-=t A y P ω。



高二物理单元测验题 第11章 《机械振动》班级 学号 姓名 成绩(总分100分 完成时间40分钟)一、不定项选择题(每题5分,共50分。
选不全得3分,错选不得分) 1、弹簧振子做简谐运动时,以下说法正确的是( ) A .振子通过平衡位置时,回复力一定为零 B .振子做减速运动时,加速度却在增大C .振子向平衡位置运动时,加速度方向与速度方向相反D .振子远离平衡位置运动时,加速度方向与速度方向相反 2、单摆的振动周期在发生下述哪些情况中增大( )A .摆球质量增大B .摆长减小C .单摆由赤道移到北极D .单摆由海平面移到高山顶上3、一洗衣机在正常工作时非常平稳,当切断电源后发现先是振动越来越剧烈,然后振动逐渐减弱,对这一现象下列说法正确的是( )A .正常工作时,洗衣机波轮的运转频率大于洗衣机的固有频率B .正常工作时,洗衣机波轮的运转频率比洗衣机的固有频率小C .当洗衣机振动最剧烈时,波轮的运动频率恰好等于洗衣机的固有频率D .当洗衣机振动最剧烈时,固有频率最大4、如图1所示的实线和虚线分别表示同一个单摆在A 、B两个大小相同的星球表面上的振动图象。
其中实线是A 星球上的,虚线是B 星球上的,那么两个星球的平均密度之比B A ρρ: 为( )A . 1 : 1B . 1 : 2C . 61 : 1D . 1 :4 5、一个单摆在山脚下经t 0的时间内振动了N 次,将此单摆移至山顶后发现在t 0的时间内振动了N -1次,若山脚距地心的距离为R 0,则此山的高度为( ) A . R 0 / N B . R 0 /(N -1)C . R 0 /(N +1)D . (N -1)R 0 /(N +1)6、劲度系数为k的轻质弹簧,下端挂质量为m的小球,小球静止时离地面高为h,用力向下拉球,使之与地面接触,而后从静止放开小球(弹簧未超过弹性限度)则( ) A 球在运动过程中,距地面的最大高度为2h B 球在上升过程中弹性势能不断减少 C 球距地面高度为h 时,速度最大 D 球的最大加速度为 kh /m7、如图2所示,一弹簧振子A 沿光滑水平面做简谐运动,在振幅相同的条件下,第一次当振子A 通过平衡位置时,将一块橡皮泥B 轻粘在A 上共同振动,第二次当振子A 刚好位移最大时将同一块橡皮泥B 轻粘在A 上共同振动,前后两次B 粘在A 上之后的振动-2图2过程中,具有不同的物理量是( )A .振动的周期B .振幅C .最大速度D .振动的频率8、一弹簧振子做简谐振动,从振子经过某一位置开始计时,下列说法正确的是( ) A 若Δt =T /2,则在t 时刻和(t +Δt )时刻弹簧的长度一定相等B 当振子的速度再次与零时刻的速度相同时,经过的时间为一个周期C 当振子经过的路程为振幅的4倍时,经过的时间为一个周期D 当振子再次经过此位置时,经过的时间是一个周期9、一个质点做简谐运动的图象如图3所示,下述正确的是( )A 质点振动频率为4赫兹B 在10 s 内质点经过的路程是20 cmC 在5 s 末,速度为零,加速度最大D t = 1.5 s 和t = 4.5 s 两时刻质点的速度相同,加速度相同10、卡车在水平道路上行驶,货物随车厢底板上下振动而不脱离底板,设货物的振动为简谐运动,以向上的位移为正,其振动图象如图4所示。

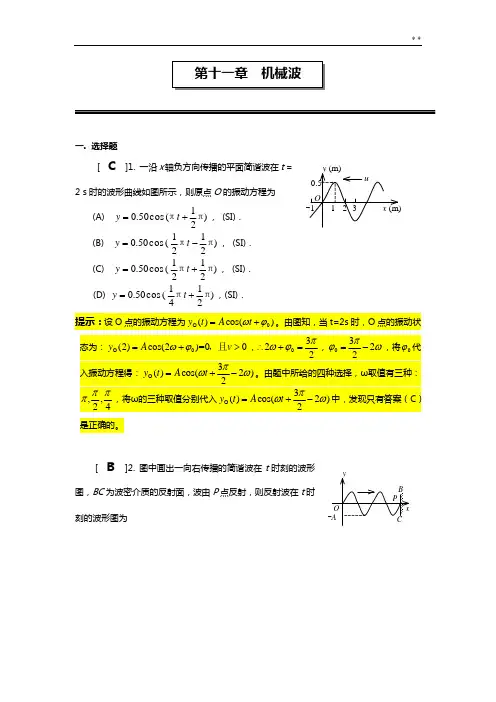
一. 选择题[ C ]1. 一沿x 轴负方向传播的平面简谐波在t = 2 s 时的波形曲线如图所示,则原点O 的振动方程为(A) )21(cos 50.0ππ+=t y , (SI).(B) )2121(cos 50.0ππ-=t y , (SI).(C) )2121(cos 50.0ππ+=t y , (SI).(D) )2141(cos 50.0ππ+=t y ,(SI).提示:设O 点的振动方程为O 0()cos()y t A t ωϕ=+。
由图知,当t=2s 时,O 点的振动状是正确的。
[ B ]2. 图中画出一向右传播的简谐波在t 时刻的波形图,BC 为波密介质的反射面,波由P 点反射,则反射波在t 时刻的波形图为提示:由题中所给波形图可知,入射波在P 点的振动方向向下;而BC 为波密介质反射面,故在P 点反射波存在“半波损失”,即反射波与入射波反相,所以,反射波在P 点的振动方向向上,又P 点为波节,因而得答案B 。
[ A ]3. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是ωSAϖO ′ωSA ϖO ′ωϖO ′ωSAϖO ′(A)(B)(C)(D)S[ B ]4. 一平面简谐波在弹性媒质中传播时,某一时刻媒质中某质元在负的最大位移处,则它的能量是(A) 动能为零,势能最大.(B) 动能为零,势能为零.(C) 动能最大,势能最大.(D) 动能最大,势能为零.提示:动能=势能,在负的最大位移处时,速度=0,所以动能为零,势能也为零。
[ B ]5. 在驻波中,两个相邻波节间各质点的振动(A) 振幅相同,相位相同.(B) 振幅不同,相位相同.(C) 振幅相同,相位不同.(D) 振幅不同,相位不同.提示:根据驻波的特点判断。
[ C ]6. 在同一媒质中两列相干的平面简谐波的强度之比是I1 / I2 = 4,则两列波的振幅之比是(A) A1 / A2 = 16.(B) A1 / A2 = 4.(C) A1 / A2 = 2.(D) A1 / A2 = 1 /4.二.填空题1. 一平面简谐机械波在媒质中传播时,若一媒质质元在t时刻的总机械能是10 J,则(t+在2. 一列强度为I 的平面简谐波通过一面积为S 的平面,波速u ϖ与该平面的法线0n v的夹角为θ,则通过该平面的能流是cos IS θ。

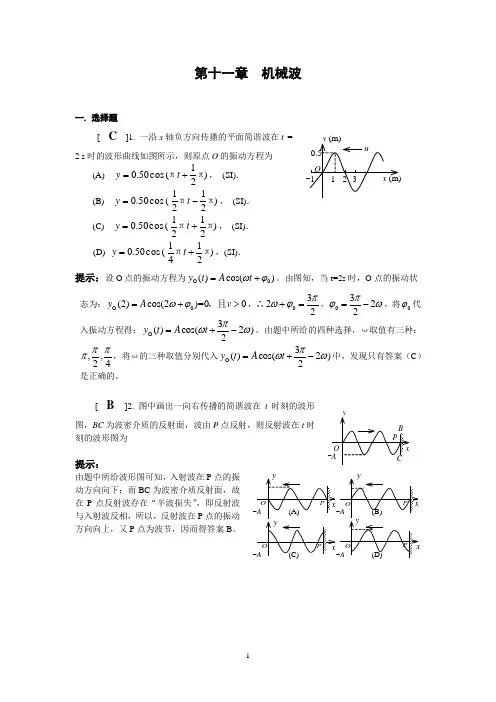
第十一章 机械波一. 选择题[ C ]1. 一沿x 轴负方向传播的平面简谐波在t = 2 s 时的波形曲线如图所示,则原点O 的振动方程为 (A) )21(cos 50.0ππ+=t y , (SI). (B) )2121(cos 50.0ππ-=t y , (SI).(C) )2121(cos 50.0ππ+=t y , (SI).(D) )2141(cos 50.0ππ+=t y ,(SI).提示:设O 点的振动方程为O 0()cos()y t A t ωϕ=+。
由图知,当t=2s 时,O 点的振动状态为:O 0(2)cos(2)=0 0y A v ωϕ=+>,且,∴0322πωϕ+=,0322πϕω=-,将0ϕ代入振动方程得:O 3()cos(2)2y t A t πωω=+-。
由题中所给的四种选择,ω取值有三种:,,24πππ,将ω的三种取值分别代入O 3()cos(2)2y t A t πωω=+-中,发现只有答案(C )是正确的。
[ B ]2. 图中画出一向右传播的简谐波在t 时刻的波形图,BC 为波密介质的反射面,波由P 点反射,则反射波在t 时刻的波形图为提示:由题中所给波形图可知,入射波在P 点的振动方向向下;而BC 为波密介质反射面,故在P 点反射波存在“半波损失”,即反射波与入射波反相,所以,反射波在P 点的振动方向向上,又P 点为波节,因而得答案B 。
[ A ]3. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是提示:由图可知,P 点的振动在t=0[ B ]4. 一平面简谐波在弹性媒质中传播时,某一时刻媒质中某质元在负的最大位移处,则它的能量是(A) 动能为零,势能最大. (B) 动能为零,势能为零. (C) 动能最大,势能最大. (D) 动能最大,势能为零.提示:动能=势能,在负的最大位移处时,速度=0,所以动能为零,势能也为零。
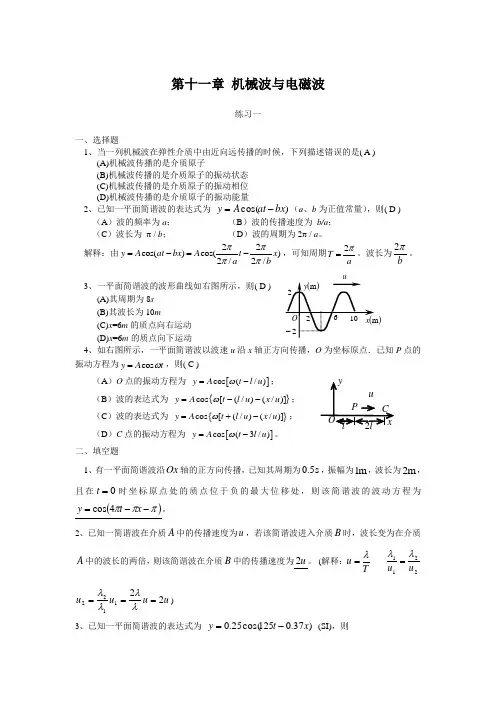
第十一章 机械波与电磁波练习一一、选择题1、当一列机械波在弹性介质中由近向远传播的时候,下列描述错误的是( A ) (A)机械波传播的是介质原子(B)机械波传播的是介质原子的振动状态 (C)机械波传播的是介质原子的振动相位 (D)机械波传播的是介质原子的振动能量2、已知一平面简谐波的表达式为 )cos(bx at A y -=(a 、b 为正值常量),则( D ) (A )波的频率为a ; (B )波的传播速度为 b/a ; (C )波长为 π / b ; (D )波的周期为2π / a 。
解释:由22cos()cos()2/2/y A at bx A t x a b ππππ=-=-,可知周期2T a π=。
波长为bπ2。
3、一平面简谐波的波形曲线如右图所示,则( D )(A)其周期为8s (B)其波长为10m(C)x =6m 的质点向右运动(D)x =6m 的质点向下运动4、如右图所示,一平面简谐波以波速u 沿x 轴正方向传播,O 为坐标原点.已知P 点的振动方程为cos y A t ω=,则( C )(A )O 点的振动方程为 []cos (/)y A t l u ω=-; (B )波的表达式为 {}cos [(/)(/)]y A t l u x u ω=--; (C )波的表达式为 {}cos [(/)(/)]y A t l u x u ω=+-; (D )C 点的振动方程为 []cos (3/)y A t l u ω=-。
二、填空题1、有一平面简谐波沿Ox 轴的正方向传播,已知其周期为s 5.0,振幅为m 1,波长为m 2,且在0=t 时坐标原点处的质点位于负的最大位移处,则该简谐波的波动方程为()πππ--=x t y 4cos 。
2、已知一简谐波在介质A 中的传播速度为u ,若该简谐波进入介质B 时,波长变为在介质A 中的波长的两倍,则该简谐波在介质B 中的传播速度为2u 。
![第十一章+波动答案[1]..](https://uimg.taocdn.com/c246b14369eae009581bec4a.webp)
一. 选择题[D] 1.(基础训练2)一平面简谐波,沿x 轴负方向传播.角频率为ω ,波速为u .设 t = T /4 时刻的波形如图14-11所示,则该波的表达式为:(A) )(cos xu t A y -=ω.(B)]21)/(cos[π+-=u x t A y ω.(C) )]/(cos[u x t A y +=ω.(D)])/(cos[π++=u x t A y ω. 【提示】}])4[(cos{ϕω++-=uxT t A y 。
ϕ为0=x 处初相。
[C] 2.(基础训练4) 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是 (A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. 【提示】波的能量特点。
[B] 3.(基础训练5)在驻波中,两个相邻波节间各质点的振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同.(C) 振幅相同,相位不同. (D) 振幅不同,相位不同. 【提示】驻波特点。
[C] 4.(基础训练8)如图14-15所示两相干波源S 1和S 2相距λ /4,(λ 为波长),S 1的相位比S 2的相位超前π21,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的相位差是:(A) 0. (B) π21. (C) π. (D) π23. 【提示】21212()r r πϕϕϕπλ-∆=--=-[D] 5.(自测提高6)如图14-25所示,S 1和S 2为两相干波源,它们的振动方向均垂直于图面,发出波长为λ 的简谐波,P 点是两列波相遇区域中的一点,已知 λ21=P S ,λ2.22=P S ,两列波在P 点发生相消干涉.若S 1的振动方程为 )212cos(1π+π=t A y ,则S 2的振动方程为图14-25(A) )212cos(2π-π=t A y . (B) )2cos(2π-π=t A y . (C) )212cos(2π+π=t A y . (D) )1.02cos(22π-π=t A y【提示】21212()r r πϕϕϕλ∆=---22(2.2 2.0)(21)2k ππϕλλπλ=---=+[C] 6.(自测提高7)在弦线上有一简谐波,其表达式是 ]3)2002.0(2cos[100.221π+-π⨯=-x t y (SI) 为了在此弦线上形成驻波,并且在x = 0处为一波节,此弦线上还应有一简谐波,其表达式为:(A) ]3)2002.0(2cos[100.222π++π⨯=-x t y (SI). (B) ]32)2002.0(2cos[100.222π++π⨯=-x t y (SI).(C) ]34)2002.0(2cos[100.222π++π⨯=-x t y (SI).(D) ]3)2002.0(2cos[100.222π-+π⨯=-x t y (SI).【提示】两沿反方向传播的波在0x =处振动合成为零。

第十一章机械波一、是非题1.机械波的强度与振幅的平方、频率的平方成正比,与媒质的密度无关··················()2.机械波的强度与媒质的密度成正比,与振幅无关。
··································()3.声强30dB的声音听起来一定比20dB的声音响。
···································()4.声波在空气中只能以横波的形式传播············································()5.波动方程表示在沿波的传播方向上各个不同质点在不同时刻的位移··················()6.机械波的强度既与振幅和频率有关,还与媒质的密度和波速有关·····················()7.机械波传播过程中,任意时刻,体元中动能与势能相等。
一. 选择题[ C ]1. 图中画出一平面简谐波在t = 2 s 时刻的波形图,则平衡位置在P 点的质点的振动方程是 (A) ]31)2(cos[01.0π+-π=t y P (SI).(B) ]31)2(cos[01.0π++π=t y P (SI).(C)]31)2(2cos[01.0π+-π=t y P (SI).(D)]31)2(2cos[01.0π--π=t y P (SI).由t=2s 波形,及波向X 轴负向传播,波动方程}])2[(cos{ϕω+-+-=ux x t A y ,ϕ为P 点初相。
以0x x =代入。
[ D ]2. 一平面简谐波,沿x 轴负方向传播.角频率为ω ,波速为u .设 t = T /4 时刻的波形如图所示,则该波的表达式为:(A) )(cos xu t A y -=ω. (B) ]21)/(cos[π+-=u x t A y ω. (C) )]/(cos[u x t A y +=ω. (D) ])/(cos[π++=u x t A y ω. 同1。
})4[(cos{ϕω++-=uxT t A y 。
ϕ为0=x 处初相。
[ A ]3. 一平面简谐波沿x 轴正方向传播,t = 0 时刻的波形图如图所示,则P 处质点的振动在t = 0时刻的旋转矢量图是由波形图知P 点振动正通过平衡位向正向运动。
[ C ]4. 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是 (A) 动能为零,势能最大. (B) 动能为零,势能为零.(C) 动能最大,势能最大. (D) 动能最大,势能为零. 波的能量特点y (m)ωS A ϖO ′ωS A ϖO ′ωϖO ′ωSA ϖO ′(A)(B)(C)(D) S[ B ]5. 在驻波中,两个相邻波节间各质点的振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同.(C) 振幅相同,相位不同. (D) 振幅不同,相位不同. 驻波特点[ C ]6. 在同一媒质中两列相干的平面简谐波的强度之比是I 1 / I 2 = 4,则两列波的振幅之比是(A) A 1 / A 2 = 16. (B) A 1 / A 2 = 4. (C) A 1 / A 2 = 2. (D) A 1 / A 2 = 1 /4. 波的强度与振幅平方成正比。
篇一:选修(xuǎnxiū)3-4 第十二章机械波教案篇二:3-4机械振动及机械波复习题和答案(dá àn)(二)最新机械波复习(fùxí)一、机械波的传播(chuánbō)1.一列简谐横波沿x轴负方向(fāngxiàng)传播,图1是t=1s时的波形图,图2是波中某振动质元位移随时间变化的振动图线(两图用同一时间起点),则图2可能是图1中哪个质元的振动图线?A.x=0处的质元 B.x=1m处的质元C.x=2m处的质元 D.x=3m处的质元2.一列沿着x正方向传播的横波,振幅为A,波长为λ,某时刻的波形如图所示。
该时刻某一质点的坐标为(5λ,0),经过T/4的时间,该质点的坐标为 435A.(λ,0)B. (λ,-A) 2453C. (λ,A) D. (λ,A) 244.如图所示,一根张紧的水平弹性长绳上的 a、b两点,相距14.0 m ,b 点在 a点的右方.当一列简谐横波沿此绳向右传播时,若 a点的位移达到正极大时,b点的位移恰为零,且向下运动.经过1.00 s 后,a点的位移为零,且向下运动,而 b点的位移恰达到负极大.则这简谐横波的波速可能等于A.14 m/sB.10 m/sC.6 m/sD.4.67 m/s5.简谐横波在某时刻的波形图线如图所示,由此图可知A.若质点 a向下运动,则波是从左向右传播的B.若质点b向上运动,则波是从左向右传播的C. 若波从右向左传播,则质点 c向下运动D.若波从右向左传播,则质点d向上运动6.如图所示,O是波源,a、b、c、d是波传播方向上各质点的平衡位置,且Oa=ab=bc=cd=3 m,开始各质点均静止在平衡位置,t=0时波源O开始向上做简谐运动,振幅是0.1 m,波沿Ox 方向传播,波长是8 m,当O 点振动了一段时间后,经过的路程是0.5 m ,各质点运动的方向是A.a 质点向上 B.b质点向上 C.c质点向下 D.d质点向下7.如图在x y平面内有一沿x轴正方向传播的简谐横波,波速为1 m/s,振幅为4 cm,频率为2.5 Hz.在t=0时刻,P点位于其平衡位置上方最大位移处,则距P为0.2 m的Q点A.在0.1 s时的位移是4 cm B.在0.1 s时的速度最大C.在0.1 s时的速度向下 D.在0到0.1 s时间内的路程是4 cm8.一列简谐横波,在t=0时刻的波形如图8-13所示,自右向左传播,已知在t1=0.7 s时,P点出现(chūxiàn)第二次波峰(0.7 s内P点出现两次波峰),Q点的坐标是(-7,0),则以下(yǐxià)判断中正确的是A.质点A和质点B在t=0时刻的位移是相等B.在t=0时刻,质点C向上(xiàngshàng)运动C..在t2=0.9 s 末Q点第一次出现(chūxiàn)波峰D.在t3=1.26 s 末Q点第一次出现波峰二、波的特性(tèxìng)1.类比是一种有效的学习方法,通过归类和比较,有助于掌握新知识,提高学习效率。
课时分层作业(十一)波的形成◎题组一机械波的形成和传播1.科学探测表明,月球表面无大气层,在月球上,两名宇航员面对面讲话也无法听到,这是因为()A.月球太冷,声音传播太慢B.月球上没有空气,声音无法传播C.宇航员不适应月球,声音太轻D.月球上太嘈杂,声音听不清楚[答案]B2.下列关于机械波的说法正确的是()A.机械波是机械振动在介质中传播形成的B.把小石头扔到平静的湖水里,水面上便会激起水波,水波将促使水面上的漂浮物向远方运动C.某空间找不到机械波,则在这一空间一定没有波源D.横波与纵波,其质点的振动方向不同,因此,横波和纵波不可能沿同方向传播A[机械波是机械振动在介质中传播形成的,A项正确;若只有波源而无介质,不能产生机械波,所以C项错误;丢石块不可以使漂浮物远去,漂浮物只在原平衡位置做上下振动,不随波迁移,故B项错误;横波和纵波的质点振动方向不同,但可沿同一方向传播,例如地震波包含横波和纵波,且两种波的传播方向可能相同,所以D项错误。
]3.在敲响大钟时,有的同学发现,停止对大钟的撞击后,大钟仍“余音未绝”,分析其原因是()A.大钟的回声B.大钟在继续振动,空气中继续形成声波C.人的听觉发生“暂留”D.大钟停止振动,但空气仍在振动B[停止对大钟的撞击后,大钟的振动不会立即停止,振动的能量不会凭空消失,大钟做阻尼振动一段时间,因此还会在空气中形成声波,所以选项A、C、D错误,B正确。
]◎题组二横波与纵波4.关于横波和纵波,下列说法不正确的是()A.质点的振动方向和波的传播方向垂直的波叫作横波B.质点的振动方向跟波的传播方向在同一直线上的波叫作纵波C.横波有波峰和波谷,纵波有密部和疏部D.声波是横波D[本题考查纵波和横波的概念。
由定义知,A、B、C正确;声波是纵波,故D错误。
]5.下列关于横波、纵波的说法不正确的是()A.凸凹相间的波叫横波,凸起的最高处叫波峰,凹下的最低处叫波谷B.质点振动方向和波的传播方向在同一直线上的波叫纵波C.横波和纵波传播的都只是振动这种运动形式D.沿横向传播的波叫横波,沿纵向传播的波叫纵波D[质点的振动方向与波的传播方向垂直的波为横波,质点的振动方向与波的传播方向在同一直线上的波为纵波;横波具有波峰和波谷,两种波传播的都是运动形式,A、B、C正确,D错误。