两位数乘两位数的巧算方法
- 格式:docx
- 大小:21.45 KB
- 文档页数:1

两位数乘两位数的巧算方法步骤一:将两位数分解首先,把两位数乘法的两个数分解为个位数和十位数的和。
例如,对于一个两位数xy (其中x为十位数,y为个位数),可以将其分解为10x+ y。
这样我们就将两位数拆分为了两个一位数的和。
步骤二:相乘然后,将分解后的两个一位数相乘,得到两部分的乘积。
即(10x + y) × (10a + b) = 100ax + 10bx + 10ay + by。
步骤三:简化计算接下来,我们可以将乘法计算进行简化。
首先,我们可以将上面的式子重组成 100ax + 10ay + 10bx + by,然后根据加法的交换律和结合律,将其重写为 100ax + 10(ay + bx) + by。
这样,我们就可以通过两个两位数的乘法和一个两位数的乘法来得到相同的结果。
步骤四:相加最后,将得到的各部分乘积相加,即 100ax + 10(ay + bx) + by,得到最终的乘积结果。
这一步可以通过头脑中的计算或者通过列竖式相加来完成。
下面通过一个具体的例子来说明这种巧算方法:例子一:计算45×231.将45分解为4×10+5,23分解为2×10+32.相乘后得到(4×10+5)×(2×10+3)=100×4+10×(4×3+5×2)+5×33.进一步简化得到100×4+10×(12+10)+5×34.相加得到400+10×22+15=400+220+15=635通过这种巧算方法,我们只需要进行一次两位数的乘法和两次一位数的乘法,就得到了最终的乘积结果。
相比于传统的列竖式相乘方法,这种巧算方法更加简洁高效,并且容易记忆和计算。
无论是计算两位数乘两位数的乘法还是更复杂的多位数乘法,这种巧算方法都可以帮助我们更快速地得到结果。
需要注意的是,巧算方法只适用于乘法,不适用于除法、加法和减法。

两位数乘两位数的口算技巧分解口算技巧1:加减法中的分解——避开进退位在加减法计算中,笔算方法是先将数位对齐(末位对齐),再从末位(即个位)开始,逐位相加减——加法满十进一,减法不够减的,从高一位借一来减。
口算方法的难度在于,在脑中要记住进一或借一(在高位加减一),要解决这个难题,可以将数字进行分解,直接看成所要加减的不用进退位的数。
如:48+76 可以看成40+70,8+6,得到110+14=12439+126 可以看成30+120,9+6,得到150+15=165256+378 可以看成200+300,50+70,6+8得到500+120+14=63454-33 可以看成50-30,4-3,得到20+1=2163-38 中个位不够减,可以将63直接看成50和13,相当于口算50-30,13-8,得到20+5=25324-176 中后两位都不够减,可以将324看成200和124,相当于算200-100,124-76,而124又看成110和14,最终相当于算200-100,110-70,14-6,得到100+40+8=148练习1:89+24= 76+87= 158+274=84-28= 135-86= 423-289=口算技巧2:加减法中的凑整——加减转换在加减法计算中,整十数、整百数比较好算,不用进退位的数也很好算,因此,将非整十、整百的数看成整十、整百的数就是一个很重要的技巧,可以将加减进行转换(主要是把不方便的减法转化为容易做的加法),也可以避开进退位。
如:267+735,可以看成270-3,740-5,相当于算270+740,3+5,得到1010-8=1002。
如果熟悉“凑一百”的数的话,也可以直接把267看成265+2,相当于算265+735,2,得到1000+2=1002135+287,可以把287看成300-13,相当于算135+300-13,得到435-11=422,当然也可想成把135分成122和13,13和287凑300,相当于算122+300=422546-389,要连续退位很不方便,可以将389看成400-11,相当于算546-400+11=146+11=1571235-874,个位直减,1230-870要退位,将870看成1000-130,相当于算1230-1000+130,得到360+1=361练习2:说出下列100减去下列各数的差35、67、89、46、51、72、93、29 规律是:个位凑十,其它凑九27+85=139+289=366+578=83-38=523-378=1024-768=口算技巧3:两位数乘一位数乘法的口算——拆数、凑整一位数乘法口算可以运用九九乘法口诀,而两位数乘一位数乘法的口算就比较麻烦,可以将两位数拆成十位和个位的数,分别乘以一位数,再相加。



两位数乘两位数巧算技巧“十位同1”的两位数乘法口诀:1与个位积排两边;个位的和放中间,满十进位。
12X13=1(2+3)(2X3)=15614X12=1(4+2)(4X2)=16817X15=1(7+5)(7X5)=25518X14=1(8+4)(8X4)=252“首相同”的两位数乘法口诀:同位乘积排两边,个位和乘十位的积排中间,满十进位。
18x13=(1X1)〔1X(8+3)〕(8X3)=23484x89=(8X8)〔8X(4+9)〕(4X9)=747635x32=(3X3)〔3X(5+2)〕(5X2)=112056x58=(5X5)〔5X(6+8)〕(6X8)=3248首同末合十的两位数的乘法口诀:十位加1的和乘十位的积排左边,个位积排右边(不够两位时十位补0)。
36X34=(3X4)(6X4)=122453X57=(5X6)(3X7)=302142X48=(4X5)(2X8)=201971X79=(7X8)(1X9)=5609末同首合十”的两位数的乘法口诀:十位积加个位的和排在左边,个位积排在右边(不够两位时十位补0)。
16X96=(1X9+6)(6X6)=153627X87=(2X8+7)(7X7)=234978X38=(7X3+8)(8X8)=296463X43=(6X4+3)(3X3)=2709个位同1的两位数的乘法­­口诀:十位积与1排两边;十位和排中间,满十进位。
­31X21=(3X2)(3+2)1=651­­41X51=(4X5)(4+5)1=2091­­41X81=(4X8)(4+8)1=3321­­91X21=(9X2)(9+2)1=1911­......末相同的两位数乘法口诀:同位乘积排两边;十位和乘个位的积排中间,满十进位。

两位数巧算技巧总结1、首位是1的两位数相乘[口诀]头是一,尾加尾,尾乘尾(超过十要进位)例:(1)13×12尾加尾:3+2=5 尾乘尾:3×2=613×12=156(2)14×17尾加尾:4+7=11 (1进位,与头1相加为2)尾乘尾:4×7=28(2进位,与前1相加为3)14×17=2382、末位是1的两位数相乘[口诀]头乘头,头加头,尾为1(超过十要进位)例:21×41头乘头:2×4=8头加头:2+4=6尾为1 21×41=8613、首同尾合十[口诀]头×(头+1),尾乘尾占两位例:(1)23×272×(2+1)=63×7=2123×27=621(2)84×868×(8+1)=724×6=2484×86=7224 4、尾同首合十[口诀]头×头+尾,尾乘尾占两位例:(1)32×723×7+2=232×2=432×72=2304(2)87×278×2+7=237×7=4987×27=2349 5、两位数与11相乘[口诀]首尾都不动,相加放中间例:(1)11×727+2=911×72=792(2)87×118+7=1587×11=957[口诀]减1添补数例:(1) 53×9953−1=52100−53=4753×99=5247(2) 97×9997−1=96100−97=397×99=9603 7、首位是9的两位数相乘[步骤]1.第一个数减第二个数的补数,作前两位2.两个数的补数相乘,作后两位。
例:(1) 97×9597−5=927×5=1597×95=9215(2) 97×9997−1=963×1=397×99=96038、末位是9的两位数相乘[口诀]头数各加1,相乘再乘10;减去相加数,最后再放1例:(1) 39×59(3+1)×(5+1)×10=240(3+1)×(5+1)=10240−10=23039×59=2301(2) 79×498×5×10=4008+5=13400−13=38779×49=38719、互补数乘以叠数[口诀] 头加1再乘头;尾乘尾占两位例:(1) 37×22(3+1)×2=8(3+1)×(5+1)=10240−10=23039×59=2301(2) 91×77(9+1)×7=701×7=791×77=7007[口诀] 加半加零例:(1) 34×1534+17=5134×15=510(2) 23×1523+11.5=34.523×15=34511、两位数乘以25[步骤]1. 熟记:25×4=100 25×3=75 25×2=502.如果这个两位数是4的倍数,那么是4的几倍,结果就是几百。



两位数乘法巧算口诀和练习两位数乘法巧算1. 首位是1的两位数相乘(十几乘十几)特点: (使用此口诀必须满足的条件)两个因数都是十几口诀:(一个因数 + 另外一个因数的尾数) x 10 + 尾 x 尾也可以用口诀2:(跟下面一种情况可以统一起来)头 x 头 x 100 + (尾 + 尾) x 10 + 尾 x 尾注意:1. 头乘头作百位。
2. 非1的那一位相加作十位。
3. 尾 x 尾在末尾。
例题:13 x 15= (13 + 5) x 10 + 3 x 5= 180 + 15= 195方法的另外一种讲解:从个位起:1. 两尾数相乘,作个位。
注意进位。
2. 两尾数相加,作十位。
注意进位。
3. 两首数相乘,作百位。
如:18×19= 342:8×9=72,则进7,2作个位; 8+9+7=24,则进2,4作十位;1×1+2=3 作百位。
12×13=1563. 11 x 184. 14 x 145. 19 x 177. 15 x 178. 19 x 189. 18 x 1710. 16 x 172. 末位是1的两位数相乘(几十一乘几十一)特点: 两个因数的个位都是1.口诀:头 x 头 x 100 + (头 + 头) x 10 + 尾 x 尾注意:1. 头乘头作百位。
2. 非1的那一位相加作十位。
3. 尾 x 尾在末尾。
例题:21 x 41= 2 x 4 x 100 + (2 + 4) x 10 + 1 x 1= 800 + 60 + 1= 861方法的另外一种讲解:从个位起:1. 两尾数相乘,作个位。
肯定是12. 两首位相加,作十位。
注意进位。
3. 两首数相乘,作百位和千位。
如:41×71=2911 31×21=6513. 41 x 814. 71 x 515. 91 x 316. 81 x 317. 61 x 418. 71 x 3110. 91 x 813. 头同尾合十(尾相加等于10)特点:1. 十位相同2. 个位相加等于10口诀:(头 + 1) x 头 x 100 + 尾 x 尾口诀2:(可以跟下面一个统一起来)(头 x 头 + 头<相同数>) x 100 + 尾 x 尾注:前面的数是:头 x 头 + 相同数例题:53 x 57= (5 + 1) x 5 x 100 + 3 x 7= 3000 + 21= 3021方法的另外一种讲解:从高位起:1. 首数乘首数加1,作前两位或前一位。

两位数乘两位数的简便方法在进行数学运算中,乘法是一种常见且重要的运算方法。
而在乘法中,两位数乘两位数是一个相对复杂的计算过程,需要耗费较多时间和精力。
然而,有一些简便的方法可以帮助我们在计算两位数乘两位数时更加高效和准确。
本文将为您介绍几种简便的方法和具体技巧,帮助您更好地掌握两位数乘两位数的计算。
一、竖式计算法竖式计算法是一种常用且直观的计算两位数乘两位数的方法。
具体步骤如下:1. 将两个两位数写在纸上,上方的数称为被乘数,下方的数称为乘数。
2. 从乘数的个位数开始,依次与被乘数的各位数相乘,将结果写在下方。
3. 每一位相乘得到的结果需要对齐写在一列,并进行进位操作。
4. 最后将每一列的结果相加,并注意进位操作。
例如,计算42乘23的运算过程如下:```42x 23_____84 <- 十位数上的计算结果+ 840 <- 个位数上的计算结果______966 <- 最终结果```竖式计算法需要逐位相乘,并且注意进位操作。
虽然运算过程相对冗长,但是它是一种直观和易于理解的计算方法,适合在纸上进行。
二、拆分法拆分法是一种常用的简便计算两位数乘两位数的方法。
通过拆分两位数,将乘法运算转化为多个小的乘法运算,从而简化计算。
具体步骤如下:1. 将两位数拆分成个位数和十位数的和,例如:42可以拆分为40和2。
2. 将被乘数和乘数分别与拆分后的个位数和十位数相乘。
3. 将乘法运算结果相加得到最终结果。
例如,计算42乘23的运算过程如下:```42乘23 = 40乘20 + 40乘3 + 2乘20 + 2乘3= (40乘20) +(40乘3) +(2乘20) +(2乘3)= 800 + 120 + 40 + 6= 966```通过拆分后的小的乘法运算,我们可以更快地求得最终结果。
同时,拆分法也可以应用于更多位数的乘法运算中,通过不断拆分和相加,逐步求得最终结果。
三、交叉相乘法交叉相乘法是一种快速计算两位数乘两位数的方法。
人教版数学三年级下册-打印版
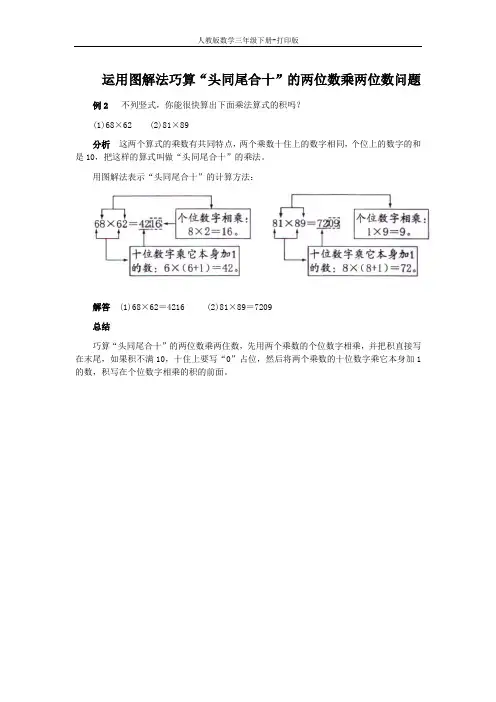
运用图解法巧算“头同尾合十”的两位数乘两位数问题例2不列竖式,你能很快算出下面乘法算式的积吗?
(1)68×62 (2)81×89
分析这两个算式的乘数有共同特点,两个乘数十住上的数字相同,个位上的数字的和是10,把这样的算式叫做“头同尾合十”的乘法。
用图解法表示“头同尾合十”的计算方法:
解答 (1)68×62=4216 (2)81×89=7209
总结
巧算“头同尾合十”的两位数乘两住数,先用两个乘数的个位数字相乘,并把积直接写在末尾,如果积不满10,十住上要写“0”占位,然后将两个乘数的十位数字乘它本身加1的数,积写在个位数字相乘的积的前面。
两位数乘法的巧算技巧
1. 嘿,你知道吗?十几乘十几有个超简单的巧算方法哦!比如 13 乘以14,那就把 13 加上 4 等于 17,然后后面直接填上 3 乘以 4 的积 12,结
果就是 182 啦,是不是很神奇呀?
2. 哇哦,个位数相同的两位数相乘也有巧妙的办法呢!就像 34 乘以 74,
用十位数相乘加上个位数的结果 3 乘以 7 加 4 等于 25,再把个位数相乘 4 乘以 4 等于 16 放后面,就是 2516 呀,你说妙不妙?
3. 嘿呀,头同尾合十的两位数相乘绝对让你大开眼界!例如 72 乘以 78,
先把十位数 7 加上 1 乘以 7 等于 56,然后 2 乘以 8 等于 16 放后面,这不就得出 5616 了嘛,好厉害的吧!
4. 嘿嘿,十位数相同的两位数相乘还有另一种巧算哦!就像 63 乘以 67,
先计算 6 乘以 6+6 等于 42,再用 3 乘以 7 等于 21,组合起来就是 4221 啦,是不是很有趣呀?
5. 哇,还有这种巧算呀!当两位数乘以 11 的时候,就像 45 乘以 11,把
45 拆开,4 和 5 中间加上 4 加 5 的和 9,结果就是 495 了呢,这也太简单了吧?
6. 哈哈,你瞧,一个接近整十的数乘另一个数也有办法哦!比如 29 乘以 4,就把 29 当成 30 减 1,先用 30 乘以 4 得 120,再减去 4,就是 116 啦,
是不是很机智呀?
7. 哎呀呀,还有一种巧算呢!像 43 乘以 99,先把 43 减去 1 等于 42,后面加上 43 和 1 之差的补数 57,不就是 4257 嘛,你觉得神不神?
8. 哇塞,十几乘任意数也能巧算呀!。
两位数乘两位数的巧算方法乘法是学生学习中较为重要的。
熟练掌握乘法,可以帮助学生更好地把握数学的基本原理,掌握乘法的各种方法也能加快解决数学问题的步伐。
本文首先介绍如何合理地运用按两位数乘两位数的巧算方法,其次给出一些实例,最后介绍如何更好地掌握乘法。
按照两位数乘两位数的巧算方法,可以把两个两位数的乘积分解为四个一位数的乘积,再把四个一位数的乘积分步进行计算,就可以得到最终的结果。
两位数乘两位数的巧算方法如下:首先,把乘积分解为四个一位数的乘积。
将乘数的十位数和个位数分别乘以被乘数的十位数和个位数,得到四个一位数的乘积,分别为第一步,第二步,第三步和第四步。
第一步,以乘数的十位数和被乘数的十位数相乘,将结果记下来。
第二步,以乘数的十位数和被乘数的个位数相乘,将结果记下来。
第三步,以乘数的个位数和被乘数的十位数相乘,将结果记下来。
第四步,以乘数的个位数和被乘数的个位数相乘,将结果记下来。
接下来,将四个一位数的乘积分别按次序相加,即可得到乘积的最终结果。
下面以计算27×39为例,来看看按两位数乘两位数的巧算方法。
首先,把乘积27×39分解为四个一位数的乘积:第一步,2×3,得到6;第二步,2×9,得到18;第三步,7×3,得到21;第四步,7×9,得到63。
接下来,把四个一位数的乘积相加,即6+18+21+63,最终得到结果108,也就是27×39的乘积,即1053。
可以看出,按照两位数乘两位数的巧算方法,可以快速计算出两个两位数的乘积,而且操作起来也比较简单,易于掌握和应用。
当然,要想熟练掌握乘法,就要在日常的学习中多加练习,通过多加练习,不仅能够掌握相关的知识点,而且能够加深对乘法的理解,从而达到熟能生巧的程度。
除了常规的练习以外,也可以使用常见数学软件,将其中的难题、练习题尽量利用不同的计算法则解决,以此来加深认知,提高计算乘法的能力。
两位数乘两位数的计算技巧为了提高学生的计算能力和对数的敏感程度以及对计算的热情。
1.同头尾合十(也叫首同尾互补)25×25 34×36 42×48 53×57求积方法:十位上的数乘上比它大一的数作积的首位,个位上两数的积写在积的后面。
例如: 25×25=625 [2×(2+1)=6 5×5=25]你自己也来试一试吧42×48 53×57 22×28 39×312.同尾首合十(也叫尾同首互补)34×74 25×85 47×67 18×98求积方法:十位上的数乘十位上的数再加上个位上的数字作积的首位,个位上两数的积写在积的后面。
例如: 34×74=2516 [3×7+4)=25 4×4=16]你自己也来试一试吧25×85 47×67 18×98 24×843.去一添补(两位数×99)34×99 27×99 35×99 48×99求积方法:第一个乘数去掉1作积的前两位,第一个乘数的补数作积的后两位数例如: 34×99=3366第一个乘数34去掉1得33作积的前两位, 34的补数66(因为34+66=100)作积的后两位数。
你自己也来试一试吧34×99 27×99 35×99 48×99两位数乘两位数的基本计算技能口算、笔算、估算和简算是乘法的四项基本技能。
1.口算两位数乘整十数和整十数乘整十数,都可以先用0前面的数相乘,然后在积的末尾添上相应个数的0。
例如:22×40先算出22×4=88,然后在88的后面添上1个0得880。
2.笔算两位数乘两位数,先分别用一个乘数的个位数和十位数分别去乘另一个乘数,然后把两次乘得的积加起来。
两位数乘两位数的计算技巧
为了提高学生的计算能力和对数的敏感程度以及对计算的热情。
1.同头尾合十(也叫首同尾互补)
25×25 34×36 42×48 53×57 求积方法:十位上的数乘上比它大一的数作积的首位,个位上两
数的积写在积的后面。
例如: 25×25=625 [2×(2+1)=6 5×5=25]
你自己也来试一试吧
42×48 53×57 22×28 39×31
2.同尾首合十(也叫尾同首互补)
34×74 25×85 47×67 18×98 求积方法:十位上的数乘十位上的数再加上个位上的数字作积的首位,个位上两数的积写在积的后面。
例如: 34×74=2516 [3×7+4)=25 4×4=16]
你自己也来试一试吧
25×85 47×67 18×98 24×84 3.去一添补(两位数×99)
34×99 27×99 35×99 48×99 求积方法:第一个乘数去掉1作积的前两位,第一个乘数的补数作积的后两位数
例如:34×99=3366第一个乘数34去掉1得33作积的前两位, 34的补数66(因为34+66=100)作积的后两位数。
你自己也来试一试吧
34×99 27×99 35×99 48×99
两位数乘两位数的基本计算技能口算、笔算、估算和简算是乘法的四项基本技能。
1.口算
两位数乘整十数和整十数乘整十数,都可以先用0前面的数相乘,然后在积的末尾添上相应个数的0。
例如:22×40先算出22×4=88,然后在88的后面添上1个0得880。
2.笔算
两位数乘两位数,先分别用一个乘数的个位数和十位数分别去乘另一个乘数,然后把两次乘得的积加起来。
3.估算
当不需要算出乘法的精确结果时,可以采用估算。
接近整十的数相乘,可以把它们看作整十数相乘.如32×69的估算方法有三种 1)把两个乘数都看作和它们相近的较小的整十数来乘,即30×60。
(2)把两个乘数都看作和它们相近得较大整十数来乘,即40×70。
(3)把两个数都看作和它们最为接近的整十数来乘,即30×70。
这三种估算方法都可以,只是(1)(2)种误差大些,(3)种与准确结果比较接近。
4.简算
熟记一些特殊数据相乘的积,学会发现和运用规律进行简算。
如:25×12=25×4×3=100×3=300。