2010年部分省市中考数学试题分类汇编-图形的相似与位似(含答案)

2010年部分省市中考数学试题分类汇编操作探究(2010年安徽省B 卷)10．在二行三列的方格棋盘上沿骰子的某条棱翻动骰子（相对面上分别标有1点和6点，2点和5点，3点和4点），在每一种翻动方式中，骰子不能后退．开始时骰子如图（1）那样摆放，朝上的点数是2；最后翻动到如图（2）所示的位置，此时骰子朝上的点数不可能．．．是下列数中的（ ）A ．5【关键词】图形的变换 【答案】D ．23（2010年浙江省东阳县）如图，在一块正方形ABCD 木板上要贴三种不同的墙纸，正方形EFCG 部分贴A 型墙纸，△ABE 部分贴B 型墙纸，其余部分贴C 型墙纸。

A 型、B 型、C 型三种墙纸的单价分别为每平方60元、80元、40元。

探究1：如果木板边长为2米，FC ＝1米，则一块木板用墙纸的费用需 元； 探究2：如果木板边长为1米，求一块木板需用墙纸的最省费用； 探究3：设木板的边长为a （a 为整数），当正方形 EFCG 的边长为多少时？墙纸费用最省；如要用这 样的多块木板贴一堵墙（7×3平方米）进行装饰， 要求每块木板A 型的墙纸不超过1平方米，且尽量 不浪费材料，则需要这样的木板 块。

【关键词】操作探究 【答案】（1）220 （2）y=20x 2—20x+60 当x=21时，y 小=55元。

（3）y=20x 2—20ax+60a 2当x=21a 时，21块23．（2010年山东省青岛市）问题再现现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见．在八年级课题学习“平面图形的镶嵌”中，对于单种多边形的镶嵌，主要研究了三角形、四边形、正六边形的镶嵌问题．今天我们把正多边形．．．．的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．如右图中，用正方形镶嵌平面，可以发现在一个顶点O 周围围绕着4个正方形的内角. 试想：如果用正六边形来镶嵌平面，在一个顶点周围应该围绕着 个 正六边形的内角．问题提出如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？ 问题解决猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？分析：我们可以将此问题转化为数学问题来解决．从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点．具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角．验证1：在镶嵌平面时，设围绕某一点有x 个正方形和y 个正八边形的内角可以拼成一个周角．根据题意，可得方程：()82180903608x y -⨯+= ，整理得：238x y +=，我们可以找到惟一一组适合方程的正整数解为12x y =⎧⎨=⎩ ．结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．验证2：结论2： ． 上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其它可能的组合方案．问题拓广O请你仿照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程．猜想3：.验证3：结论3：.【关键词】【答案】解：3个；················ 1分验证2：在镶嵌平面时，设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角．根据题意，可得方程：60120360a b+=．整理得：26a b+=，可以找到两组适合方程的正整数解为22ab=⎧⎨=⎩和41ab=⎧⎨=⎩．························· 3分结论2：镶嵌平面时，在一个顶点周围围绕着2个正三角形和2个正六边形的内角或者围绕着4个正三角形和1个正六边形的内角可以拼成一个周角，所以同时用正三角形和正六边形两种正多边形组合可以进行平面镶嵌．5分猜想3：是否可以同时用正三角形、正方形和正六边形三种正多边形组合进行平面镶嵌？······························ 6分验证3：在镶嵌平面时，设围绕某一点有m个正三角形、n个正方形和c个正六边形的内角可以拼成一个周角. 根据题意，可得方程：6090120360m n c++=，整理得：23412m n c++=，可以找到惟一一组适合方程的正整数解为121mnc=⎧⎪=⎨⎪=⎩. ······························ 8分结论3：镶嵌平面时，在一个顶点周围围绕着1个正三角形、2个正方形和1个正六边形的内角可以拼成一个周角，所以同时用正三角形、正方形和正六边形三种正多边形组合可以进行平面镶嵌. （说明：本题答案不惟一，符合要求即可.）1.（2010年福建省晋江市）如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；...，根据以上操作，若要得到2011个小正方形，则需要操作的次数是( ) .A. 669B. 670C.671D. 672【关键词】正方形、实验操作、规律探索答案：B；22．(2010年北京崇文区) 正方形A B C D 的边长为a ，等腰直角三角形F A E 的斜边A E b = （a b 2<），且边A D 和A E 在同一直线上 ．小明发现：当b a =时，如图①，在B A 上选取中点G ，连结F G 和C G ,裁掉F A G ∆和C H D ∆的位置构成正方形F G C H ． （1）类比小明的剪拼方法，请你就图②和图③两种情形分别画出剪拼成一个新正方形的示意图．（2）要使（1）中所剪拼的新图形是正方形，须满足=AEBG ．【关键词】正方形的剪拼、 【答案】（1）（2）21．(2010年浙江省绍兴市)分别按下列要求解答：（1）在图1中,将△ABC 先向左平移5个单位,再作关于直线AB 的轴对称图形,经两次变换后得到△A 1B 1 C 1.画出△A 1B 1C 1； （2）在图2中,△ABC 经变换得到△A 2B 2C 2.描述变换过程.1211 10 9 8 76 5 4 32 AC2B 2 12 11 10 9 8 7 6 5 4 3 2 C【答案】(1) 如图．(2) 将△ABC先关于点A作中心对称图形,再向左平移2个单位,得到△A2B2C2．（变换过程不唯一）2.（2010年宁德市）如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个直角三角形，展开后得到一个等腰三角形.则展开后三角形的周长是（）.A．2＋10B．2＋210C．12 D．18【答案】B27．（2010江苏泰州，27，12分）如图，二次函数cxy+-=221的图象经过点D⎪⎭⎫⎝⎛-29,3，与x轴交于A、B两点．⑴求c的值；⑵如图①，设点C为该二次函数的图象在x轴上方的一点，直线AC将四边形ABCD的面积二等分，试证明线段BD被直线AC平分，并求此时直线AC的函数解析式；⑶设点P、Q为该二次函数的图象在x轴上方的两个动点，试猜想：是否存在这样的点P、Q，使△AQP≌△ABP？如果存在，请举例验证你的猜想；如果不存在，请说明理由．（图②供选用）第18题图1 第18题图2第18题图②4【答案】⑴ ∵抛物线经过点D (29,3-)∴29)3(212=+-⨯-c∴c=6.⑵过点D 、B 点分别作AC 的垂线，垂足分别为E 、F ，设AC 与BD 交点为M ， ∵AC 将四边形ABCD 的面积二等分，即：S △ABC =S △ADC ∴DE =BF 又∵∠DME =∠BMF ， ∠DEM =∠BFE ∴△DEM ≌△BFM∴DM =BM 即AC 平分BD ∵c =6. ∵抛物线为6212+-=x y∴A （0,32-）、B （0,32）∵M 是BD 的中点 ∴M （49,23） 设AC 的解析式为y =kx +b ，经过A 、M 点∴⎪⎩⎪⎨⎧=+=+-4923032b k b k 解得⎪⎪⎩⎪⎪⎨⎧==591033b k ∴直线AC 的解析式为591033+=x y.⑶存在．设抛物线顶点为N (0，6)，在Rt △AQN 中，易得AN=，于是以A 点为圆心，AB =为半径作圆与抛物线在x 上方一定有交点Q ，连接AQ ，再作∠QAB 平分线AP 交抛物线于P ，连接BP 、PQ ，此时由“边角边”易得△AQP ≌△ABP ．【关键词】二次函数、一次函数、解直角三角形及其知识的综合运。

2010年部分省市中考数学试题分类汇编综合型问题20、（2010年浙江省东阳县）如图，BD 为⊙O 的直径，点A 是弧BC 的中点，AD 交BC 于E 点，AE=2，ED=4.（1）求证: ABE ∆～ABD ∆；(2) 求tan ADB ∠的值； （3）延长BC 至F ，连接FD ，使BDF ∆的面积等于 求EDF ∠的度数.【关键词】圆、相似三角形、三角形函数问题【答案】（１）∵点A 是弧BC 的中点 ∴∠ＡＢＣ＝∠ＡＤＢ 又∵∠ＢＡＥ＝∠ＢＡＥ ∴△ＡＢＥ∽△ＡＢＤ（２）∵△ＡＢＥ∽△ＡＢＤ ∴ＡＢ２＝２×６＝１２ ∴ＡＢ＝２3在Ｒｔ△ＡＤＢ中，ｔａｎ∠ＡＤＢ＝33632=（３）连接ＣＤ，可得ＢＦ＝８，ＢＥ＝４，则ＥＦ＝４，△ＤＥＦ是正三角形， ∠ＥＤＦ＝６０°20．（2010年山东省青岛市）某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．（1）求该校八年级学生参加社会实践活动的人数；（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．请你计算本次社会实践活动所需车辆的租金． 【关键词】不等式与方程问题 【答案】解：（1）设单独租用35座客车需x 辆，由题意得：3555(1)45x x =--,解得：5x =.∴35355175x =⨯=（人）.答：该校八年级参加社会实践活动的人数为175人． ········· 3分 （2）设租35座客车y 辆，则租55座客车（4y -）辆，由题意得：3555(4)175320400(4)1500y y y y +-⎧⎨+-⎩≥≤， ······· 6分解这个不等式组，得111244y ≤≤．∵y 取正整数， ∴y = 2.∴4－y = 4－2 = 2.∴320×2＋400×2 = 1440（元）.所以本次社会实践活动所需车辆的租金为1440元． (2010年安徽省B 卷)23.（本小题满分１２分）如图， Rt ABC △内接于O ⊙，AC BC BAC =∠，的平分线AD 与O ⊙交于点D ，与BC 交于点E ，延长BD ，与AC 的延长线交于点F ，连接CD G ，是CD 的中点，连结OG ．（1）判断OG 与CD 的位置关系，写出你的结论并证明； （2）求证：AE BF =； （3）若3(2OG DE = ，求O ⊙的面积．【关键词】圆 等腰三角形 三角形全等 三角形相似 勾股定理【答案】（1）猜想：OG CD ⊥． 证明：如图，连结OC 、OD ． ∵OC OD =，G 是CD 的中点，∴由等腰三角形的性质，有OG CD ⊥．（2）证明：∵AB 是⊙O 的直径，∴∠ACB ＝90°． 而∠CAE ＝∠CBF （同弧所对的圆周角相等）． 在Rt △ACE 和Rt △BCF 中， ∵∠ACE =∠BCF ＝90°，AC =BC ，∠CAE =∠CBF ， ∴Rt △ACE ≌Rt △BCF （ASA ） ∴ AE BF =．（3）解：如图，过点O 作BD 的垂线，垂足为H ．则H 为BD 的中点．∴OH ＝12AD ，即AD =2OH ． 又∠CAD ＝∠BAD ⇒CD =BD ，∴OH =OG ． 在Rt △BDE 和Rt △ADB 中， ∵∠DBE ＝∠DAC ＝∠BAD ， ∴Rt △BDE ∽Rt △ADB∴BD DE AD DB=，即2BD AD DE =·AA∴226(2BD AD DE OG DE ===·· 又BD FD =，∴2BF BD =．∴22424(2BF BD == … ① 设AC x =，则BC x =，．∵AD 是∠BAC 的平分线， ∴FAD BAD ∠=∠．在Rt △ABD 和Rt △AFD 中， ∵∠ADB =∠ADF ＝90°，AD =AD ，∠F AD ＝∠BAD ， ∴Rt △ABD ≌Rt △AFD （ASA ）． ∴AF =AB，BD =FD ． ∴CF =AF -AC1)x x -= 在Rt △BCF 中，由勾股定理，得2222221)]2(2BF BC CF x x x =+=+= …②由①、②，得22(224(2x =． ∴212x =．解得x =-．∴AB ===∴⊙O∴π6πO S =⋅2⊙＝(2010年安徽省B 卷)24.（本小题满分12分）已知：抛物线()20y ax bx c a =++≠的对称轴为1x =-与x 轴交于A B ，两点，与y 轴交于点C ，其中()30A -，、()02C -，．（1）求这条抛物线的函数表达式．（2）已知在对称轴上存在一点P ，使得PBC △的周长最小．请求出点P 的坐标．（3）若点D 是线段OC 上的一个动点（不与点O 、点C 重合）．过点D 作DE PC ∥交x 轴于点E ．连接PD 、PE ．设CD 的长为m ，PDE △的面积为S ．求S 与m 之间的函数关系式．试说明S 是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．【关键词】二次函数解析式 对称点 相似三角形 三角形面积【答案】（1）由题意得129302b a a bc c ⎧=⎪⎪⎪-+=⎨⎪⎪=-⎪⎩解得23432a b c ⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩∴此抛物线的解析式为224233y x x =+- （2）连结AC 、BC .因为BC 的长度一定，所以PBC △周长最小，就是使PC PB +最小.B 点关于对称轴的对称点是A 点，AC 与对称轴1x =-的交点即为所求的点P .设直线AC 的表达式为y kx b =+则302k b b -+=⎧⎨=-⎩，解得232k b ⎧=-⎪⎨⎪=-⎩∴此直线的表达式为223y x =--．把1x =-代入得43y =-∴P 点的坐标为413⎛⎫--⎪⎝⎭， （3）S 存在最大值 理由：∵DE PC ∥，即DE AC ∥． ∴OED OAC △∽△．∴OD OE OC OA =，即223m OE-=． ∴332OE m =-，连结OPOAC OED AEP PCD S S S S S =---△△△△=()1131341323212222232m m m m ⎛⎫⨯⨯-⨯-⨯--⨯⨯-⨯⨯ ⎪⎝⎭ =()22333314244m m m -+=--+ ∵304-<∴当1m =时，34S =最大（2010年福建省晋江市）已知：如图，把矩形OCBA 放置于直角坐标系中，3=OC ，2=BC ，取AB 的中点M ，连结MC ，把MBC ∆沿x 轴的负方向平移OC 的长度后得到DAO ∆.(1)试直接写出点D 的坐标；(2)已知点B 与点D 在经过原点的抛物线上，点P 在第一象限内的该抛物线上移动，过点P 作x PQ ⊥轴于点Q ，连结OP .①若以O 、P 、Q 为顶点的三角形与DAO ∆相似，试求出点P 的坐标；②试问在抛物线的对称轴上是否存在一点T ，使得TB TO -的值最大.【关键词】二次函数、相似三角形、最值问题答案：解：(1)依题意得：⎪⎭⎫ ⎝⎛-2,23D ；(2) ① ∵3=OC ，2=BC ， ∴()2,3B .∵抛物线经过原点，∴设抛物线的解析式为bx ax y +=2()0≠a又抛物线经过点()2,3B 与点⎪⎭⎫⎝⎛-2,23D∴⎪⎩⎪⎨⎧=-=+22349,239b a b a 解得：⎪⎪⎩⎪⎪⎨⎧-==32,94b a ∴抛物线的解析式为x x y 32942-=. ∵点P 在抛物线上， ∴设点⎪⎭⎫ ⎝⎛-x x x P 3294,2. 1)若PQO ∆∽DAO ∆，则AO QO DA PQ =， 22332942x xx =-，解得：01=x (舍去)或16512=x ，∴点⎪⎭⎫⎝⎛64153,1651P . 2)若OQP ∆∽DAO ∆，则AO PQ DA OQ =， 23294232xx x -=，解得：01=x (舍去)或292=x ，∴点⎪⎭⎫⎝⎛6,29P . ②存在点T ，使得TO TB -的值最大. 抛物线x x y 32942-=的对称轴为直线43=x ，设抛物线与x 轴的另一个交点为E ，则点⎪⎭⎫⎝⎛0,23E . ∵点O 、点E 关于直线43=x 对称， ∴TE TO =要使得TB TO -的值最大，即是使得TB TE -的值最大，根据三角形两边之差小于第三边可知，当T 、E 、B 三点在同一直线上时，TB TE -的值最大.设过B 、E 两点的直线解析式为b kx y +=()0≠k ，∴⎪⎩⎪⎨⎧=+=+023,23b k b k 解得：⎪⎩⎪⎨⎧-==2,34b k∴直线BE 的解析式为234-=x y . 当43=x 时，124334-=-⨯=y . ∴存在一点⎪⎭⎫⎝⎛-1,43T 使得TO TB -最大.2. （2010年福建省晋江市）如图，在等边ABC ∆中，线段AM 为BC 边上的中线. 动点D 在直线．．AM 上时，以CD 为一边且在CD 的下方作等边CDE ∆，连结BE .(1) 填空：______ACB ∠=度；(2) 当点D 在线段．．AM 上(点D 不运动到点A )时，试求出BEAD的值； (3)若8=AB ，以点C 为圆心，以5为半径作⊙C 与直线BE 相交于点P 、Q 两点，在点D 运动的过程中(点D 与点A 重合除外)，试求PQ 的长.(2)∵ABC ∆与DEC ∆都是等边三角形∴BC AC =，CE CD =，︒=∠=∠60DCE ACB ∴BCE DCB DCB ACD ∠+∠=∠+∠ ∴BCE ACD ∠=∠CAB 备用图(1) AB C备用图(2)∴ACD ∆≌BCE ∆()SAS∴BE AD =，∴1=BEAD. (3)①当点D 在线段AM 上（不与点A 重合）时，由(2)可知ACD ∆≌BCE ∆，则︒=∠=∠30CAD CBE ，作BE CH ⊥于点H ，则HQ PQ 2=，连结CQ ，则5=CQ .在CBH Rt ∆中，︒=∠30CBH ，8==AB BC ，则421830sin =⨯=︒⋅=BC CH . 在CHQ Rt ∆中，由勾股定理得：3452222=-=-=CH CQ HQ ，则②当点D 在线段AM 的延长线上时，∵ABC ∆与DEC ∆都是等边三角形 ∴BC AC =，CE CD =，︒=∠=∠60DCE ACB ∴DCB ACB =∠+∠∴BCE ACD ∠=∠ ∴ACD ∆≌BCE ∆(∴=∠=∠CAD CBE ③当点D 在线段MA ∵ABC ∆与DEC ∆∴BC AC =，CD =∴=∠+∠ACE ACD ∴BCE ACD ∠=∠ ∴ACD ∆≌BCE ∆(∴CAD CBE ∠=∠∵︒=∠30CAM∴︒=∠=∠150CAD CBE ∴︒=∠30CBQ . 同理可得：6=PQ . 综上，PQ 的长是6.1.（2010年浙江省东阳市）如图，P 为正方形ABCD 的对称中心，A （0，3），B （1，0），直线OP 交AB 于N ，DC 于M ，点H 从原点O 出发沿x 轴的正半轴方向以1个单位每秒速度运动，同时，点R 从O 出发沿OM 方向以2个单位每秒速度运动，运动时间为t 。

2010年部分省市中考数学试题分类汇编 (1平行四边形、矩形、菱形与正方形1. (2010重庆市潼南县如图24,四边形ABCD 是边长为2的正方形,点G 是BC 延长线上一点,连结AG ,点E 、F 分别在AG 上,连接BE 、DF ,∠1=∠2 , ∠3=∠4. (1证明:△AB E ≌△DAF ;(2若∠AGB =30°,求EF 的长. 解:(1∵四边形ABCD 是正方形∴AB=AD在△ABE 和△DAF 中⎪⎩⎪⎨⎧∠=∠=∠=∠3412DA AB ∴△ABE ≌△DAF -----------------------4分(2∵四边形ABCD 是正方形∴∠1+∠4=900∵∠3=∠4∴∠1+∠3=900∴∠AFD=900----------------------------6分在正方形ABCD 中, AD ∥BC∴∠1=∠AGB=300在Rt △ADF 中,∠AFD=900AD=2∴AF=3 DF =1----------------------------------------8分由(1得△ABE ≌△ADF∴AE=DF=1∴EF=AF-AE=13- -----------------------------------------10分2. (2010年青岛已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF .(1求证:BE = DF ;(2连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM .判断四边形AEMF是什么特殊四边形?并证明你的结论.【答案】证明:(1∵四边形ABCD 是正方形,∴AB =AD ,∠B = ∠D = 90°.∵AE = AF ,∴Rt Rt ABE ADF △≌△.∴BE =DF .(2四边形AEMF 是菱形.∵四边形ABCD 是正方形,∴∠BCA = ∠DCA = 45°,BC = DC .∵BE =DF ,题图24A D B E F O CM第21题图∴BC -BE = DC -DF . 即CE CF =. ∴OE OF =. ∵OM = OA ,∴四边形AEMF 是平行四边形. ∵AE = AF ,∴平行四边形AEMF 是菱形.3.(2010福建龙岩中考20.(10分如图,平行四边形ABCD 中,E 、F 是对角线BD 上的点,且BE =DF . (1请你写出图中所有的全等三角形(2试在上述各对全等三角形中找出一对加以证明.4.(2010年益阳市如图7,在菱形ABCD 中,∠A =60°,AB =4,O 为对角线BD 的中点,过O 点作OE ⊥AB ,垂足为E . (1 求∠ABD 的度数; (2求线段BE 的长.【关键词】菱形性质、等边三角形、【答案】解:⑴在菱形ABCD 中,AD AB =,︒=∠60A∴ABD ∆为等边三角形∴︒=∠60ABD⑵由(1可知4==AB BD又∵O 为BD 的中点∴2=OB 又∵AB OE ⊥,及︒=∠60ABD ∴︒=∠30BOE ∴1=BE5.(2010年山东省青岛市已知:如图,在正方形ABCD 中,点E 、F 分别在BC 和CD 上,AE = AF .(1求证:BE = DF ;(2连接AC 交EF 于点O ,延长OC 至点M ,使OM = OA ,连接EM 、FM .判断四边形AEMF 是什么特殊四边形?并证明你的结论.7图【关键词】菱形的判定【答案】证明:(1∵四边形ABCD 是正方形,∴AB =AD ,∠B = ∠D = 90°. ∵AE = AF ,∴Rt Rt ABE ADF △≌△. ∴BE =DF .(2四边形AEMF 是菱形.∵四边形ABCD 是正方形,∴∠BCA = ∠DCA = 45°,BC = DC . ∵BE =DF ,∴BC -BE = DC -DF . 即CE CF =. ∴OE OF =. ∵OM = OA ,∴四边形AEMF 是平行四边形. ∵AE = AF ,∴平行四边形AEMF 是菱形.6. (2010年浙江省绍兴市 (1 如图1,在正方形ABCD 中,点E ,F 分别在边BC ,CD 上,AE ,BF 交于点O ,∠AOF =90°. 求证:BE =CF .(2 如图2,在正方形ABCD 中,点E ,H ,F ,G 分别在边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH =90°, EF =4.求GH 的长.(3 已知点E ,H ,F ,G 分别在矩形ABCD 的边AB ,BC ,CD ,DA 上,EF ,GH 交于点O ,∠FOH =90°,EF =4. 直接写出下列两题的答案:①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长; ②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长(用n的代数式表示.【答案】(1 证明:如图1,∵四边形ABCD 为正方形,∴ AB =BC ,∠ABC =∠BCD =90°, ∴∠EAB +∠AEB =90°. ∵∠EOB =∠AOF =90°, ∴∠FBC +∠AEB =90°,∴∠EAB =∠FBC ,∴△ABE ≌△BCF , ∴ BE =CF .(2 解:如图2,过点A 作AM //GH 交BC 于M ,第23题图1第23题图3 第23题图 4 第23题图1第23题图2O ′N AD BEFOC第21题图过点B 作BN //EF 交CD 于N ,AM 与BN 交于点O /, 则四边形AMHG 和四边形BNFE 均为平行四边形, ∴ EF=BN ,GH=AM ,∵∠FOH =90°, AM //GH ,EF//BN , ∴∠NO /A =90°, 故由(1得, △ABM≌△BCN , ∴ AM =BN , ∴ GH =EF =4. (3 ① 8.② 4n .7.(2010年宁德市(本题满分13分如图,四边形ABCD 是正方形,△ABE 是等边三角形,M 为对角线BD (不含B 点上任意一点,将BM 绕点B 逆时针旋转60°得到BN ,连接EN 、AM 、CM. ⑴求证:△AMB ≌△ENB ;⑵①当M 点在何处时,AM +CM 的值最小;②当M 点在何处时,AM +BM +CM 的值最小,并说明理由; ⑶当AM +BM +CM 的最小值为13【答案】解:⑴∵△ABE 是等边三角形, ∴BA =BE ,∠ABE =60°. ∵∠MBN=60°,∴∠MBN -∠ABN =∠ABE -∠ABN. 即∠BMA =∠NBE. 又∵MB =NB ,∴△AMB ≌△ENB (SAS .⑵①当M 点落在BD 的中点时,AM +CM 的值最小. ②如图,连接CE ,当M 点位于BD 与CE 的交点处时, AM +BM +CM 的值最小. ………………9分理由如下:连接MN.由⑴知,△AMB ≌△ENB , ∴AM =EN.∵∠MBN =60°,MB =NB , ∴△BMN 是等边三角形. ∴BM =MN.∴AM +BM +CM =EN +MN +CM.根据“两点之间线段最短”,得EN +MN +CM =EC 最短∴当M 点位于BD 与CE 的交点处时,AM +BM +CM 的值最小,即等于EC 的长.⑶过E 点作EF ⊥BC 交CB 的延长线于F , ∴∠EBF =90°-60°=30°.A DB C F A DB CABC DFED CB AO E设正方形的边长为x ,则BF =23x ,EF =2x . 在Rt △EFC 中,∵EF 2+FC 2=EC 2, ∴(2x 2+(23x +x 2=(213+.解得,x =2(舍去负值. ∴正方形的边长为2.8.(2010年四川省眉山市如图,O 为矩形ABCD 对角线的交点,DE ∥AC ,CE ∥BD .(1试判断四边形OCED 的形状,并说明理由;(2若AB =6,BC =8,求四边形OCED 的面积.【关键词】平行四边形的判定、菱形的性质与判定和面积、矩形的性质【答案】解:(1四边形OCED 是菱形.∵DE ∥AC ,CE ∥BD ,∴四边形OCED 是平行四边形, 又在矩形ABCD 中,OC =OD , ∴四边形OCED 是菱形.(2连结OE .由菱形OCED 得:CD ⊥OE , ∴OE ∥BC 又 CE ∥BD∴四边形BCEO 是平行四边形∴OE =BC =8 ∴S 四边形OCED =11862422OE CD ⋅=⨯⨯=9.(2010年浙江省东阳市(6分如图,已知BE ⊥AD ,CF ⊥AD ,且BE =CF . (1 请你判断AD 是△ABC 的中线还是角平分线?请证明你的结论.(2连接BF 、CE ,若四边形BFCE 是菱形,则△ABC 中应添加一个条件▲ 【关键词】三角形的全等【答案】(1AD 是△ABC 的中线.................................1分理由如下:∵BE⊥AD,CF⊥AD,∴∠BED=∠CFD=90°.........1分又∵BE=CF,∠BDE=∠CFD ∴△BDE≌△CFD(AAS.......2分(2AB=AC或∠ABC=∠ACB或AD⊥BC或AD平分∠BAC.......2分10. (2010年安徽中考如图,AD ∥FE ,点B 、C 在AD 上,∠1=∠2,BF =BC⑴求证:四边形BCEF 是菱形⑵若AB =BC =CD ,求证:△ACF ≌△BDE 。

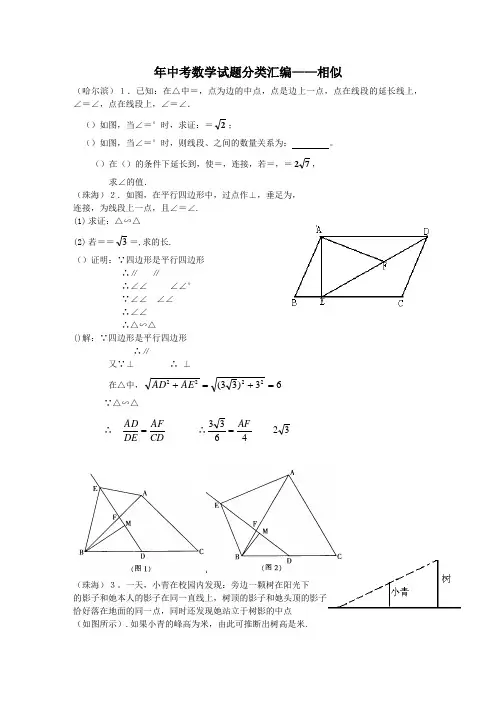
年中考数学试题分类汇编——相似（哈尔滨）１．已知：在△中＝，点为边的中点，点是边上一点，点在线段的延长线上，∠＝∠，点在线段上，∠＝∠．（）如图，当∠＝°时，求证：＝2；（）如图，当∠＝°时，则线段、之间的数量关系为： 。

（）在（）的条件下延长到，使＝，连接，若＝，＝72， 求∠的值．（珠海）２．如图，在平行四边形中，过点作⊥，垂足为， 连接，为线段上一点，且∠＝∠. (1) 求证：△∽△(2) 若＝＝3＝,求的长. （）证明：∵四边形是平行四边形 ∴∥ ∥∴∠∠ ∠∠° ∵∠∠ ∠∠ ∴∠∠ ∴△∽△()解：∵四边形是平行四边形 ∴∥又∵⊥ ∴ ⊥ 在△中，63)33(2222=+=+AE AD∵△∽△ ∴ CDAFDE AD =∴4633AF = 32（珠海）３。

一天，小青在校园内发现：旁边一颗树在阳光下的影子和她本人的影子在同一直线上，树顶的影子和她头顶的影子 恰好落在地面的同一点，同时还发现她站立于树影的中点（如图所示）.如果小青的峰高为米，由此可推断出树高是米.（桂林）．如图，已知△与△的相似比为：，则△ 与△的面积比为（ ）．． ： ． ：． ： ． ：（年兰州）. 如图，上体育课，甲、乙两名同学分别站在、的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距米.甲身高米，乙身高米，则甲的影长是 米. 答案（宁波市）．如图，在平面直角坐标系中，是坐标原点，□的顶点的坐标为（－，），点的坐标为（，），点在轴的正半轴上，点为线段的中点，过点的直线与轴交于点，与射线交于点． （）求∠的度数；（）当点的坐标为（－，），求点的坐标；（）连结，以所在直线为对称轴，△经轴对称变换后得到△′，记直线′与射线的交点为．① 如图，当点在点的左侧时，求证：△≌△； ② △若的面积为，请你直接写出点的坐标. （年金华）(本题分)AD E B C如图，把含有°角的三角板置入平面直角坐标系中，，两点坐标分别为（，）和(，.(长度单位秒)﹒一直尺的上边缘从轴的位置开始以 (长度单位秒)的速度向上平行移动（即移动过程中保持∥轴），且分别与，交于，两点﹒设动点与动直线同时出发，运动时间为秒，当点沿折线运动一周时，直线和动点同时停止运动． 请解答下列问题：（）过，两点的直线解析式是 ▲ ；（）当﹦时，点的坐标为 ▲ ；当 ﹦ ▲ ，点与点重合； （）① 作点关于直线的对称点′. 在运动过程中，若形成的四边形′为 菱形，则的值是多少？② 当﹦时，是否存在着点，使得△请说明理由．解：（）333+-=x y ；………分 （）（,3（）①当点P 在线段AO 上时，过F 作FG ⊥x 轴，G 为垂足（如图） ∵FG OE =,FP EP =,∠=EOP ∠=FGP ° ∴△EOP ≌△FGP ，∴PG OP =﹒又∵t FG OE 33==,∠=A °,∴t FG AG 3160tan 0== (图)而t AP =，∴t OP -=3,t AG AP PG 32=-=由t t 323=-得 59=t ；………………………………………………………………分当点在线段OB 上时，形成的是三角形，不存在菱形；当点在线段BA 上时， 过作PH ⊥EF ，PM ⊥OB ，H 、M∵t OE 33=,∴t BE 3333-=,∴3360tan 0t BE EF -== ∴6921tEF EH MP -===， 又∵)6(2-=t BP 在△BMP 中，MP BP =⋅060cos 即6921)6(2tt -=⋅-，解得745=t ．…………………………………………………分 ②存在﹒理由如下：∵2=t ，∴332=OE ,2=AP ，1=OP 将△BEP 绕点E 顺时针方向旋转°，得到 △EC B '（如图）∵OB ⊥EF ，∴点B '在直线EF 上， 点坐标为（332，332－）过F 作FQ ∥C B '，交EC 于点,则△FEQ ∽△EC B '由3=='=QE CE FE E B FE BE ，可得的坐标为（－32，33）………………………分 根据对称性可得，关于直线的对称点Q '（－32，3）也符合条件．……分．（年长沙）如图，在平面直角坐标系中，矩形的两边分别在轴和轴上，OA =， ，现的速度匀速运动，在线段上沿方向以每秒 的速度匀速运动．设运动时间为秒． （）用的式子表示△的面积；（）求证：四边形的面积是一个定值，并求出这个定值；（）当△与△和△相似时，抛物线214y x bx c =++经过、两点，过线段上一动点作y 轴的平行线交抛物线于，当线段的长取最大值时，求直线把四边形分成两部分的面积之比．(图)解：()∴－∴△＝21(8)22t t -=-+（＜＜）…………………分 () ∵四边形＝矩形－△－△＝1188)22⨯⨯-⨯⨯………… 分 …………分（）当△与△和△相似时, △必须是一个直角三角形，依题意只能是∠＝°又∵与不平行∴∠不可能等于∠，∠不可能等于∠∴根据相似三角形的对应关系只能是△∽△∽△………………分 8=解得：＝经检验：＝是方程的解且符合题意（从边长关系和速度） 此时（，）∵（214y x bx c =++经过、两点， ∴抛物线是2184y x =-+，直线是：8y =- …………………分 设（8-）、(，2184m -+)∵在上运动∴m ≤≤∵21184y x =-+与28y-交于、两点且抛物线的顶点是 ∴当m ≤≤时，12y y > ………………………………分∴12MN y y =-＝21(24m --+∴当m = 第题图∴设与交于点则M、H ∴△＝132⨯⨯∴△ ：五边形＝＝∴当取最大值时两部分面积之比是：． …………………分（年湖南郴州市）.如图，已知平行四边形ABCD ，E 是AB 延长线上一点，连结DE 交BC 于点F ，在不添加任何辅助线的情况下，请补充一个条件，使CDF BEF △≌△，这个条件是 ．（只要填一个）答案DC EB =或CF BF =或DF EF = 或为的中点或为的中点或AB BE =或为的中点(湖北省荆门市)．(本题满分分)如图，圆的直径为，在圆上位于直径的异侧有定点和动点，已知∶＝∶，点在半圆弧上运动(不与、重合)，过作的垂线交的延长线于点 ()求证：·＝·；()当点运动到弧中点时，求的长；()当点运动到什么位置时，△的面积最大？并求这个最大面积．答案．解：()∵为直径，∴∠＝°．又∵⊥，∴∠＝°． 而∠＝∠，∴△∽△．∴AC BCCP CD=．∴·＝·；………………………………………………………………………分第题图第题FEC BB'C'()当点运动到弧中点时，过点作⊥于点． ∵是中点，∴∠＝°．又∠＝∠，∴∠＝∠＝43．∴＝tan BE CPB ∠＝3)4．由()得＝43()当点在上运动时，△＝12·．由()可知，＝43． ∴△＝23．故最大时，△取得最大值； 而为直径时最大，∴△的最大值＝23×＝503．………………………………分（年眉山）．如图，△ ' ' 是由△绕点顺时针旋转得到的，连结 ' 交斜边于点， ' 的延长线交' 于点．（）证明：△∽△；（）设∠α，∠ ' β，试探索α、β满足什么关系时，△与△是全等三角形，并说明理由．答案：．（）证明：∵△ ' ' 是由△绕点顺时针旋转得到的， ∴ '， '，∠∠ ' ' ………………（分） ∴∠ '∠ '∴∠ '∠ ' ……………………………………（分） 又∠∠∴△∽△ ……………………………………（分）（）解：当2βα=时，△≌△． …………………（分） 在△'中，∵ '， ∴180'180'9022CAC ACC βα︒-∠︒-∠===︒- ………（分）在△中，第题图FEC BAB'C' ∠'∠°，即9090BCE α︒-+∠=︒， ∴∠α． ∵∠α，∴∠∠ ……………………（分） ∴由（）知：△∽△，∴△≌△．………………………（分）．(重庆潼南县)△与△的相似比为：，则△与△的周长比为．：、（年杭州市）如图， ， ，又∥，点，，在同一条直线上.() 求证：△∽△；() 如果 ， 22，设 ，求的长.答案：() ∵ ∥，点，，在同一条直线上， ∴ ∠ ∠, 又∵3==AEBDAC AB , ∴ △∽△. () ∵ ， 2 ， ∴ ， ∴∠ °, 由（）得 ∠ ∠ °, ∵31 , 31232, ， ∴在△中， ( ) (31 ) (322) 9108 ,∴ 32 .（陕西省）、如图在△中是边上一点，连接，要使△与△相似，应添加的条件是 ∠∠ ∠∠AD ACAC AB=（年天津市）（）如图，等边三角形ABC 中，D 、E 分别为AB 、BC 边上的点，AD BE =，AE 与CD 交于点F ，AG CD ⊥于点G ， 则AGAF的值为．（山西．在 △中，∠＝º，若将各边长度都扩大为原来的倍，则∠的正弦值（） ．扩大倍 ．缩小倍 ．扩大倍 ．不变（宁夏．关于对位似图形的表述，下列命题正确的是 ②③ ．（只填序号）2． 相似图形一定是位似图形，位似图形一定是相似图形； 3． 位似图形一定有位似中心；4． 如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个点，那么，这两个图形是位似图形；5． 位似图形上任意两点与位似中心的距离之比等于位似比． （宁夏．(分)已知：正方形中，、分别是边、上的点，且，与交于点． （）求证：△≌△；（）找出图中与△相似的所有三角形（不添加任何辅助线）．．()证明：在正方形中： , 且∠∠090 ∵∴ 即： 在△与△中⎪⎩⎪⎨⎧=∠=∠=已证）已证）已证）(((DE AF ADE BAF DA AB ∴△≌△（）分（）与△相似的三角形有：△; △; △分（山西．在直角梯形中，∥，∠＝º，＝，＝，＝．分别以、边所在直线为轴、轴建立如图（第题） MFE D CBAM FE D C BA第（）题所示的平面直角坐标系．（）求点的坐标；（）已知、分别为线段、上的点，＝，＝，直线交轴于点．求直线的解析式；（）点是（）中直线上的一个动点，在轴上方的平面内是否存在另一个点．使以、、、为顶点的四边形是菱形？若存在，请求出点的坐标；若不存在，请说明理由．．（四川宜宾）如图，在△中，∠°，∠°，⊥于点.则△与△的周长之比为（ ） ．︰ ．︰ ．︰ ．︰答案：（年安徽）.如图，已知△∽△111C B A ，相似比为k （1>k ），且△的三边长分别为a 、b 、c （c b a >>），△111C B A 的三边长分别为1a 、1b 、1c 。

2010年部分省市中考数学试题分类汇编阅读理解型15．（2010年浙江省东阳县）阅读材料，寻找共同存在的规律：有一个运算程序a ⊕b = n ， 可以使：（a+c ）⊕b= n+c ，a ⊕（b+c ）=n －2c ， 如果1⊕1=2，那么2010⊕2010 = ． 【关键词】阅读理解 【答案】-200722．（2010年山东省青岛市）某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y （件）与销售单价x （元）之间的关系可近似的看作一次函数：10500y x =-+．（1）设李明每月获得利润为w （元），当销售单价定为多少元时，每月可获得最大利润？（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？ （成本＝进价×销售量） 【关键词】函数的应用 【答案】解：（1）由题意，得：w = (x －20)·y=(x －20)·(10500x -+) 21070010000x x =-+-352b x a=-=.答：当销售单价定为35元时，每月可获得最大利润． ········ 3分 （2）由题意，得：210700100002000x x -+-= 解这个方程得：x 1 = 30，x 2 = 40．答：李明想要每月获得2000元的利润，销售单价应定为30元或40元. ···· 6分（3）法一：∵10a =-<0，∴抛物线开口向下. ∴当30≤x ≤40时，w ≥2000． ∵x ≤32， ∴当30≤x ≤32时，w ≥2000． 设成本为P （元），由题意，得： 20(10500)P x =-+ 20010000x =-+ ∵200k =-<0，∴P 随x 的增大而减小.∴当x = 32时，P 最小＝3600.答：想要每月获得的利润不低于2000元，每月的成本最少为3600元．1．（2010年浙江省东阳市）阅读材料，寻找共同存在的规律：有一个运算程序a ⊕b = n ，法二：∵10a =-<0， ∴抛物线开口向下. ∴当30≤x ≤40时，w ≥2000． ∵x ≤32，∴30≤x ≤32时，w ≥2000． ∵10500y x =-+，100k =-<， ∴y 随x 的增大而减小. ∴当x = 32时，y 最小＝180. ∵当进价一定时，销售量越小，成本越小，∴201803600⨯=（元）.可以使：（a+c ）⊕b= n+c ，a ⊕（b+c ）=n －2c ， 如果1⊕1=2，那么2010⊕2010 = ▲ ． 关键词：阅读理解 答案：-20071、（2010年宁波市）《几何原本》的诞生，标志着几何学已成为一个有着严密理论系统和科学方法的学科，它奠定了现代数学的基础，它是下列哪位数学家的著作（ ） A 、欧几里得 B 、杨辉 C 、费马 D 、刘徽【关键词】数学阅读知识 【答案】A(2010年浙江省绍兴市)在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形, 叫做此一次函数的坐标三角形.例如，图中的一次函数的图象与x ,y 轴分别交于点A ,B ,则△OAB 为此函数的坐标三角形.（1）求函数y ＝43-x ＋3的坐标三角形的三条边长； （2）若函数y ＝43-x ＋b （b 为常数）的坐标三角形周长为16求此三角形面积.【答案】解：(1) ∵ 直线y ＝43-x ＋3与x 轴的交点坐标为（4,0），与y 轴交点坐标为（0,3）， ∴函数y ＝43-x ＋3的坐标三角形的三条边长分别为3,4,5. (2) 直线y ＝43-x ＋b 与x 轴的交点坐标为（b 34,0），与y 轴交点坐标为（0,b ），当b >0时,163534=++b b b ，得b =4，此时,坐标三角形面积为332；当b <0时，163534=---b b b ，得b =－4，此时,坐标三角形面积为332.综上,当函数y ＝43-x ＋b 的坐标三角形周长为16时,面积为332．2010年益阳市） 我们把对称中心重合，四边分别平行的两个正方形之间的部分叫“方形环”，易知方形环四周的宽度相等．．．．. 一条直线l 与方形环的边线有四个交点M 、'M 、'N 、N ．小明在探究线段'MM 与N N ' 的数量关系时，从点'M 、'N 向对边作垂线段E M '、F N '，利用三角形全等、相似及锐角三角函数等相关知识解决了问题．请你参考小明的思路解答下列问题： ⑴当直线l 与方形环的对边相交时（如图18-），直线l 分别交AD 、D A ''、C B ''、BC 于M 、'M 、'N 、N ，小明发现'MM 与N N '相等，请你帮他说明理由； ⑵当直线l 与方形环的邻边相交时（如图28-），l 分别交AD 、D A ''、C D ''、DC于M 、'M 、'N 、N ，l 与DC 的夹角为α，你认为'MM 与N N '还相等吗？若 相等，说明理由；若不相等，求出NN MM ''的值（用含α的三角函数表示）.第21题图【关键词】正方形性质、相似三角形、三角函数值 【答案】⑴解: 在方形环中，∵AD BC F N AD E M ,',⊥⊥'∥BC ∴NF N M EM FN N EM M F N E M ',90','∠='∠=∠='∠='︒ ∴△E MM '≌△F NN '∴N N M M '='⑵解法一：∵α='∠='∠︒='∠='∠M M E N FN M ME N NF ,90 ∴N NF '∆∽EM M '∆ ∴NF EM N N M M '='' ∵F N E M '='∴αtan ''='=NF F N N N MM （或ααcos sin ） ①当︒=45α时，tan α=1,则N N M M '=' ②当︒≠45α时，N N M M '≠'则 αtan =''N N M M （或ααcos sin ）解法二：在方形环中，︒=∠90D又∵CD F N AD E M ⊥⊥'', ∴E M '∥E M F N DC '=', ∴α=∠='∠NF N E M M ' 在F N N Rt '∆与E M M Rt '∆中， MM EM N N F N ''='=ααcos ,'sin N N M M E M M M N N F N ''=''⋅'=='cos sin tan ααα 即 αtan =''N N M M （或ααcos sin ）B18-图28-图①当︒=45α时，N N M M '=' ②当︒≠45α时，N N M M '≠'则 αtan =''N N M M （或ααcos sin ）。

2010中考数学分类汇编 一、选择题1．（2010山东烟台）手工制作课上，小红利用一些花布的边角料，剪裁后装饰手工画，下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边，其中，每个图案花边的宽度都相等，那么，每个图案中花边的内外边缘所围成的几何图形不相似的是 【答案】D2．（2010山东烟台）如图，△ ABC 中，点D 在线段BC 上，且△ ABC ∽△ DBA ，则下列结论一定正确的是A 、AB 2=BC ·BD B 、AB 2=AC ·BD C 、AB ·AD=BD ·BC D 、AB ·AD=AD ·CD 【答案】A3．（2010台湾） 图(一)表示D 、E 、F 、G 四点在△ABC 三边上的位置，其中DG 与EF 交于H 点。

若?ABC =?EFC =70?，?ACB =60?，?DGB =40?，则下列哪 一组三角形相似？(A) △BDG ，△CEF (B) △ABC ，△CEF(C) △ABC ，△BDG (D) △FGH ，△ABC 。

【答案】B4．（2010浙江嘉兴）如图，已知AD 为△ABC 的角平分线，AB DE //交AC 于E ，如果32=EC AE ，那么=ACAB（ ▲ ） （A ）31（B ）32 （C ）52（D ）53AB C E（第7题）A BCD E H图(一)【答案】B5．（2010 福建德化）下列各组线段（单位：㎝）中，成比例线段的是（）A、1、2、3、4B、1、2、2、4C、3、5、9、13D、1、2、2、3【答案】B6．（2010江苏泰州）一个铝质三角形框架三条边长分别为24cm、30cm、36cm，要做一个与它相似的铝质三角形框架，现有长为27cm、45cm的两根铝材，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为另外两边．截法有（）种 B. 1种 C. 2种 D. 3种【答案】B7．（2010年上海）下列命题中，是真命题的为（）A.锐角三角形都相似B.直角三角形都相似C.等腰三角形都相似D.等边三角形都相似【答案】D8．（2010山东潍坊）如图所示，一般书本的纸张是原纸张多次对开得到的，矩形ABCD沿EF对开后，再把矩形EFCD沿MN对开，依次类推，若各种开本的矩形都相似，那么AB AD等于（）．A．0．618 BCD．2【答案】B9．（2010北京）如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD∶AB=3∶4，AE=6，则AC等于( )A．3 B．4 C．6 D． 8【答案】D10．（2010年上海）下列命题中，是真命题的为（）A.锐角三角形都相似B.直角三角形都相似C.等腰三角形都相似D.等边三角形都相似【答案】D11．（2010云南楚雄）下列说法不正确的是（）A．在选举中，人们通常最关心的数据是众数．B．掷一枚骰子，3点朝上是不确定事件．C．数据3，5，4，1，－2的中位数是3．D．有两边对应成比例且有一个角对应相等的两个三角形相似．【答案】D12．（2010河南）如图，在△ABC中，点D、E分别是AB、AC的中点，则下列结论：①BC=2DE；②△ADE∽△ABC；③AD ABAE AC.其中正确的有(A)3个 (B)2个(C)1个（D）0个【答案】A13．（2010 四川绵阳）如图，梯形ABCD的对角线AC、BD相交于O，G是BD的中点．若AD = 3，BC = 9，则GO: BG =（）．A．1 : 2 B．1 : 3C．2 : 3 D．11 : 20【答案】A14．（2010广西桂林）如图，已知△ADE与△ABC的相似比为1：2，则△ADE 与△ABC的面积比为（）．A．1：2 B．1：4C．2：1 D．4：1【答案】B15．（2010辽宁沈阳）如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的边长为A．9 B．12 C．15 D．18【答案】A16．（2010福建省南平）下列说法中，错误的是( )A．等边三角形都相似B．等腰直角三角形都相似C．矩形都相似D．正方形都相似【答案】C17．（2010吉林）如图，在△ABC中，∠C=900，D是AC上一点，DE⊥AB于点E，若AC=8，BC=6，DE=3，则AD的长为（）A ．3B ．4C ．5D ．6【答案】C18．（2010内蒙赤峰）如图，有一矩形纸片ABCD ，AB=6，AD=8，将纸片折叠，使AB 落在AD 边上，折痕为AE ，再将△AEB 以BE 为折痕向右折叠，AE 与DC 交于点F ，则CDFC 的值是 （ ） 【答案】C19．（2010广西百色）下列命题中，是假命题的是（ ）A.全等三角形的对应边相等B.两角和一边分别对应相等的两个三角形全等C.对应角相等的两个三角形全等D.相似三角形的面积比等于相似比的平方 【答案】C20．（2010广西百色）如图，△ABC 中，D 、E 分别为AC 、BC 边上的点，AB ∥DE ，CF 为AB 边上的中线，若AD =5，CD =3，DE =4，则BF 的长为（ ）A. 332B. 316C. 310D. 381．∽△DEF ， △ABC 与△DEF 的相似比为1∶2，则△ABC 与△【答案】1∶22．（2010 嵊州市）如图，射线AM ，BN 都垂直于线段AB ，点E 为AM 上一点，过点A 作BE 的垂线AC 分别交BE ，BN 于点F,C ，过点C 作AM 的垂线CD ，垂足为D ，若CD ＝CF ，则=ADAE。

∴DE= 3t 8 3 - 3t = 8 3 2 3t
∴等边△DEF 的 DE 边上的高为：12 3t ∴当点 F 在 BO 边上时：12 3t = t ，∴ t =3 ……………………5 分
……………………4 分
① 当 0≤ t <3 时，重叠部分为等腰梯形，可求梯形上底为： 8 3 2 3t - 2 3 t …7 分 3
t S= (8
2
32
= t (16 3 14 3t)
2
3
3t 8
图b
（2）在图 b 中，将直线 AB 绕点 B 逆时针方向旋转一定角度交直线 CD 于点 Q， 如图 c，则∠BPD﹑∠B﹑∠D﹑∠BQD 之间有何数量关系？（不需证明）；
（3）根据（2）的结论求图 d 中∠A+∠B+∠C+∠D+∠E+∠F 的度数．
图c
解：（1）不成立，结论是∠BPD=∠B+∠D. 延长 BP 交 CD 于点 E, ∵AB∥CD. ∴∠B=∠BED. 又∠BPD=∠BED+∠D， ∴∠BPD=∠B+∠D.
（2）结论： ∠BPD=∠BQD+∠B+∠D.
（3）由（2）的结论得：∠AGB=∠A+∠B+∠E. 又∵∠AGB=∠CGF. ∠CGF+∠C+∠D+∠F=360° ∴∠A+∠B+∠C+∠D∠E+∠F=360°.
（桂林 2010）26．（本题满分 12 分）如图，过 A（8，0）、B（0， 8 3 ）两点的直线与直
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电通，力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置，机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2，荷试而下卷且高总可中体保资配障料置各试时类卷，管调需路控要习试在题验最到；大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资，常料要工试加况卷强下安看与全22过，22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资；中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整，高核或中对者资定对料值某试，些卷审异弯核常扁与高度校中固对资定图料盒纸试位，卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置，地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中，案资要，料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气，设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术，技槽以来术、及避管系免架统不等启必多动要项方高方案中式；资，对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资，件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调，并试合且技理进术利行，用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活：。。在对对分于于线调差盒试动处过保，程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试，题技应，术采作是用为指金调发属试电隔人机板员一进，变行需压隔要器开在组处事在理前发；掌生同握内一图部线纸故槽资障内料时，、，强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试，卷卷线试切缆验除敷报从设告而完与采毕相用，关高要技中进术资行资料检料试查，卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

2010年中考数 学 试 卷*考试时间120分钟 试卷满分150分一、选择题（本大题共7小题，每小题4分，共28分）每题所给的四个选项中只有一项是符合题目要求的，请将所选项的代号字母填在答卷的相应位置处． 1） A． BC．-D2．反比例函数23m y x--=的图象位于（ ）A ．第一、三象限B ．第二、四象限C ．第二、三象限D ．第一、二象限3．从2、3、4、5这四个数中，任取两个数()p q p q ≠和，构成函数2y px y x q =-=+和，并使这两个函数图象的交点在直线2x =的右侧，则这样的有序数对()p q ，共有（ ） A ．12对 B ．6对 C ．5对 D ．3对4．把多项式2288x x -+分解因式，结果正确的是（ ） A ．()224x -B ．()224x -C ．()222x -D ．()222x +5．某等腰三角形的两条边长分别为3cm 和6cm ，则它的周长为（ ） A ．9cm B ．12cm C ．15cm D ．12cm 或15cm6．一次函数y kx b =+（k b ，是常数，0k ≠）的图象如图所示，则不等式0kx b +>的解集是A ．2x >-；B ．0x >；C ．2x <-；D ．0x <7．若0a >且2x a =，3y a =，则x ya -的值为（ ）A ．1-B ．1C ．23D ．32二、填空题（本大题共6小题，每小题4分，共24分）把答案直接填在答卷的相应位置处．xb +8．将点(12)，向左平移1个单位，再向下平移2个单位后得到对应点的坐标是 ．9．幼儿园把新购进的一批玩具分给小朋友．若每人3件，那么还剩余59件；若每人5件，那么最后一个小朋友分到玩具，但不足4件，这批玩具共有 件．10．李师傅随机抽查了本单位今年四月份里6天的日用水量（单位：吨）结果如下：7，8，8，7，6，6，根据这些数据，估计四月份本单位用水总量为 吨．11．我们知道利用相似三角形可以计算不能直接测量的物体的高度，阳阳的身高是1.6m ，他在阳光下的影长是 1.2m ，在同一时刻测得某棵树的影长为 3.6m ，则这棵树的高度约为 m ． 12．如图所示的半圆中，AD 是直径，且3AD =，2AC =，则sin B 的值是 ．13．某个圆锥的侧面展开图形是一个半径为6cm ，圆心角为︒120的扇形，则这个圆锥的底面半径为______________cm ．三、解答题（本大题Ⅰ—Ⅴ题，共10小题，共98分）解答时应在答卷的相应位置处写出文字说明、证明过程或演算过程． Ⅰ．（本题满分12分，第14题6分，第15题6分）14．计算：230116(2)(πtan60)3-⎛⎫--÷-+-- ⎪⎝⎭．15．先化简，再求值：221111121x x x x x +-÷+--+，其中1x =． Ⅱ．（本题满分28分，第16题7分，第17题10分，第18题11分）C BD A16．如图，线段AB 与⊙O 相切于点C ，连结OA ，OB ，OB 交⊙O 于点D ，已知6OA OB ==，AB =（1）求⊙O 的半径； （2）求图中阴影部分的面积．17．响应“家电下乡”的惠农政策，某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台，其中甲种电冰箱的台数是乙种电冰箱台数的2倍，购买三种电冰箱的总金额不超．．过．132 000元．已知甲、乙、丙三种电冰箱的出厂价格分别为：1 200元/台、1 600元/台、2 000元/台．(1)至少购进乙种电冰箱多少台？(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数，则有哪些购买方案？18．甲、乙两名运动员进行长跑训练，两人距终点的路程y （米）与跑步时间x （分）之间C OABD的函数图象如图所示，根据图象所提供的信息解答问题：(1) 他们在进行 米的长跑训练，在0＜x ＜15的时段内，速度较快的人是 ；(2) 求甲距终点的路程y （米）和跑步时间 x （分）之间的函数关系式； (3) 当x =15时，两人相距多少米？在15＜x ＜20的时段内，求两人速度之差．Ⅲ．（本题满分36分，第19题12分，第20题12分，第21题12分）19．把一副扑克牌中的3张黑桃牌（它们的正面牌面数字分别是3、4、5）洗匀后正面朝下放在桌面上．（1）如果从中随机抽取一张牌，那么牌面数字是4的概率是多少？（2）小王和小李玩摸牌游戏，游戏规则如下：先由小王随机抽出一张牌，记下牌面数字后放回，洗匀后正面朝下，再由小李随机抽出一张牌，记下牌面数字．当2张牌面数字相同时，小王赢；当2张牌面数字不相同时，小李赢．现请你利用树状图或列表法分析游戏规则对双方是否公平？并说明理由．20．如图，河流两岸a b ，互相平行，C D ，是河岸a 上间隔50m 的两个电线杆．某人在河分)岸b 上的A 处测得30DAB ∠= ，然后沿河岸走了100m 到达B 处，测得60CBF ∠=，求河流的宽度CF 的值（结果精确到个位）．21．三个生产日光灯管的厂家在广告中宣称，他们生产的日光灯管在正常情况下，灯管的使用寿命为12个月．工商部门为了检查他们宣传的真实性，从三个厂家各抽取11只日光灯管进行检测，灯管的使用寿命（单位：月）如下：试问：（1）这三个厂家的广告，分别利用了统计中的哪一个特征数（平均数、中位数、众数）进行宣传？（2）如果三种产品的售价一样，作为顾客的你选购哪个厂家的产品？请说明理由．Ⅳ（本题满分8分）BED CFab A22．如图， 已知等边三角形ABC 中，点D ，E ，F 分别为边AB ，AC ，BC 的中点，M 为直线BC 上一动点，△DMN 为等边三角形（点M 的位置改变时， △DMN 也随之整体移动） ． （1）如图①，当点M 在点B 左侧时，请你判断EN 与MF 有怎样的数量关系？点F 是否在直线NE 上？都请直接．．．．写出结论，不必证明或说明理由； （2）如图②，当点M 在BC 上时，其它条件不变，（1）的结论中EN 与MF 的数量关系是否仍然成立?若成立，请利用图②证明；若不成立，请说明理由；（3）若点M 在点C 右侧时，请你在图③中画出相应的图形，并判断（1）的结论中EN 与MF 的数量关系是否仍然成立?若成立?请直接写出结论，不必证明或说明理由．Ⅴ（本题满分14分）图① 图② 图③A·BCD EF··N MFEDCB ANMF EDCBA·23．如图，在平面直角坐标系中，以点(11)C ，为圆心，2为半径作圆，交x 轴于A B ，两点，开口向下的抛物线经过点A B ，，且其顶点P 在C 上．（1）求ACB 的大小；（2）写出A B ，两点的坐标； （3）试确定此抛物线的解析式；（4）在该抛物线上是否存在一点D ，使线段OP 与CD 互相平分？若存在，求出点D 的坐标；若不存在，请说明理由．2010年中考数学试题参考答案及评分标准二、填空题（本大题共6小题，每小题4分，共24分） 8．(00)，；9．152；10．210；11．4.8；12．23；13．4 三、解答题（本大题Ⅰ—Ⅴ题，共10小题，共98分） Ⅰ．（本题满分12分，第14题6分，第15题6分） 14．解：原式＝9－16÷（－8）＋1－23×23……………………2分 ＝9＋2＋1－3.……………………………………4分 ＝9 ………………………………6分15．解：原式211(1)1(1)(1)1x x x x x -=-++-+······································································ 2分 2211(1)(1)1(1)(1)x x x x x x -+--=-=+++ ······························································· 4分 22(1)x =+ ········································································································ 5分当1x =时，原式23== ··································································· 6分 Ⅱ．（本题满分28分，第16题7分，第17题10分，第18题11分）16．（1）连结OC ，则 OC AB ⊥． …………………………………………………1分∵OA OB =，∴1122AC BC AB ===⨯ ………………………………………2分在Rt AOC △中，3OC ===．∴ ⊙O 的半径为3． …………………………………………………………3分 （2）∵ OC =12OB , ∴ ∠B =30o , ∠COD =60o ． ……………………………………5分 ∴扇形OCD 的面积为OCD S 扇形=260π3360⨯⨯=32π． …………………………………5分阴影部分的面积为：Rt Δ=OBC OCD S S S -阴影扇形=12OC CB ⋅－3π2－3π2．…………………………7分 17．解：（1）设购买乙种电冰箱x 台，则购买甲种电冰箱2x 台，丙种电冰箱(803)x -台，根据题意，列不等式： ································································ 1分120021600(803)2000132000x x x ⨯++-⨯≤． ···························································· 3分解这个不等式，得14x ≥． ·································································································· 4分 ∴至少购进乙种电冰箱14台． ····························································································· 5分 （2）根据题意，得2803x x -≤． ····················································································· 6分 解这个不等式，得16x ≤． ·································································································· 7分 由（1）知14x ≥． 1416x ∴≤≤． 又x 为正整数， 141516x ∴=，，． ···················································································································· 8分 所以，有三种购买方案：方案一：甲种电冰箱为28台，乙种电冰箱为14台，丙种电冰箱为38台； 方案二：甲种电冰箱为30台，乙种电冰箱为15台，丙种电冰箱为35台； 方案三：甲种电冰箱为32台，乙种电冰箱为16台，丙种电冰箱为32台． ··················· 10分 18．解：（1）5000…………………………………2分甲 ………………………………4分（2）设所求直线的解析式为：y =kx +b (0≤x ≤20)， ………5分由图象可知：b =5000，当x =20时，y =0， ∴0=20k +5000，解得k = -250. …7分即y = -250x +5000 (0≤x ≤20) ……………7分（3）当x =15时，y = -250x +5000= -250×15+5000=5000-3750=1250. ………8分 两人相距：(5000 -1250)-(5000-2000)=750（米）………………9分 两人速度之差:750÷(20-15)=150（米/分）……………11分Ⅲ．（本题满分36分，第19题12分，第20题12分，第21题12分） 19解：（1）P （抽到牌面数字是4）13=； ········································································ 2分（2）游戏规则对双方不公平． ················································································· 5分 理由如下：由上述树状图或表格知：所有可能出现的结果共有9种． P （抽到牌面数字相同）=3193=， P （抽到牌面数字不相同）=6293=．∵1233<，∴此游戏不公平，小李赢的可能性大． ············································ 12分 （说明：答题时只需用树状图或列表法进行分析即可）20．解：过点C 作CE AD ∥，交AB 于E CD AE ∥，CE AD ∥ ····································································································· 2分∴四边形AECD 是平行四边形 ······························································································ 4分 50AE CD ∴==m ，50EB AB AE =-=m ，30CEB DAB ∠=∠= ···························· 6分又60CBF ∠=，故30ECB ∠=，50CB EB ∴==m ···················································· 8分∴在Rt CFB △中，sin 50sin 6043CF CB CBF =∠=≈m ········································ 11分 答：河流的宽度CF 的值为43m ． ······················································································ 12分21．答：（1）甲厂的广告利用了统计中的平均数． ····························································· 2分乙厂的广告利用了统计中的众数． ············································································ 4分 丙厂的广告利用了统计中的中位数． ············································································ 7分分…………………………8分11F B C （2） 选用甲厂的产品． 因为它的平均数较真实地反映灯管的使用寿命 ······················· 10分 或选用丙厂的产品．因为丙厂有一半以上的灯管使用寿命超过12个月 ··························· 10分Ⅳ．（本题满分8分）22．（1）判断：EN 与MF 相等 （或EN=MF ），点F 在直线NE 上， ········ 2分（2）成立． ······························ 3分 证明：法一：连结DE ，DF ．∵△ABC 是等边三角形， ∴AB =AC =BC ．又∵D ，E ，F 是三边的中点，∴DE ，DF ，EF 为三角形的中位线．∴DE =DF =EF ，∠FDE =60°．又∠MDF +∠FDN =60°， ∠NDE +∠FDN =60°，∴∠MDF =∠NDE ．在△DMF 和△DNE 中，DF =DE ，DM =DN ， ∠MDF =∠NDE ，∴△DMF ≌△DNE ． 8∴MF =NE ． ·························· 6分法二：延长EN ，则EN 过点F ．∵△ABC 是等边三角形， ∴AB =AC =BC ．又∵D ，E ，F 是三边的中点， ∴EF =DF =BF ．∵∠BDM +∠MDF =60°， ∠FDN +∠MDF =60°，∴∠BDM =∠FDN ．又∵DM =DN ， ∠ABM =∠DFN =60°，∴△DBM ≌△DFN ．∴BM =FN ．∵BF =EF ， ∴MF =EN ． ·························· 6分（3）画出图形（连出线段NE ）， 6MF 与EN 相等的结论仍然成立（或MF =NE 成立）． ·············· 8分Ⅴ．（本题满分14分）23．解：（1）作CHN C A B F M D E NC A B F MD E12 1CH = ，半径2CB = ·························································· 1分60BCH ∠= ，120ACB ∴∠= ········································· 3分（2）1CH = ，半径2CB =HB ∴=(1A ，················································ 5分(1B ··············································································· 6分 （3）由圆与抛物线的对称性可知抛物线的顶点P 的坐标为(13)， ······································· 7分 设抛物线解析式2(1)3y a x =-+ ·························································································· 8分把点(1B 代入上式，解得1a =- ·············································································· 9分 222y x x ∴=-++ ·············································································································· 10分 （4）假设存在点D 使线段OP 与CD 互相平分，则四边形OCPD 是平行四边形 ·········· 11分 PC OD ∴∥且PC OD =．PC y ∥轴，∴点D 在y 轴上． ····················································································· 12分又2PC = ，2OD ∴=，即(02)D ，． 又(02)D ，满足222y x x =-++， ∴点D 在抛物线上 ··············································································································· 13分 所以存在(02)D ，使线段OP 与CD 互相平分． ·································································· 14分。

（第3题）2010年部分省市中考数学试题分类汇编点、线、面、角1．(2010年福建晋江) 附加题：若︒=∠35A ， 则A ∠的余角等于 度. 答案：552010年广东省广州市）将图1所示的直角梯形绕直线l 旋转一周，得到的立体图开是（ ）lA ．B ．C ．D ． 图1 【关键词】面动成体 【答案】C2．（2010年浙江台州市）如图，△ABC 中，∠C =90°，AC =3，点P 是边BC 上的动点， 则AP 长不可能．．．是(▲) A ．2.5 B ．3 C ．4 D ．5 【关键词】点到直线的距离 【答案】A3．（2010年益阳市）如图3，已知△ABC ，求作一点P ，使P 到∠A 的两边的距离相等，且P A ＝PB ．下列Ａ．P 为∠A 、∠B 两角平分线的交点Ｂ．P 为∠A 的角平分线与AB 的垂直平分线的交点 Ｃ．P 为AC 、AB 两边上的高的交点 Ｄ．P 为AC 、AB 两边的垂直平分线的交点【关键词】角平分线、垂直平分线、三角形的高 【答案】B4.（2010年台湾省）如图(十二)，直线CP 是AB 的中垂线且交AB 于P ，其中AP =2CP 。

甲、乙两人想在AB 上取两点D 、E ，使得AD =DC =CE =EB ，其作法如下：(甲) 作∠ACP 、∠BCP 之角平分线，分别交AB 于D 、E ， 则D 、E 即为所求(乙) 作AC 、BC 之中垂线，分别交AB 于D 、E ，则D 、 E 即为所求对于甲、乙两人的作法，下列判断何者正确？ABCP 图(十二)AB3图(A) 两人都正确 (B) 两人都错误 (C) 甲正确，乙错误 (D) 甲错误，乙正确。

【关键词】垂线 【答案】D5、（2010年宁波）《几何原本》的诞生，标志着几何学已成为一个有着严密理论系统和科学方法的学科，它奠定了现代数学的基础，它是下列哪位数学家的著作（ ） A 、欧几里得 B 、杨辉 C 、费马 D 、刘徽 答案：A4. (金华)下图所示几何体的主视图是（ ▲ ） A . B . C . D .正面。

20XX 年部分省市中考数学试题分类汇编图形的相似与位似1. （20XX 年福建省德化县）如图，小“鱼”与大“鱼”是位似图形，如果小“鱼”(a, b)，那么大“鱼”上对( )E 、( 2a , b) D 、(2b, 2a)【关键词】位似中心是原点的坐标之间的关系（若相似比为 则坐标之比同侧为 k 异侧为-k ） 【答案】C2.（ 2010江苏泰州，）一个铝质三角形框架三条边长分别为24cm 、30cm 、36cm ,要做一个与它相似的铝质三角形框架，现有长为27cm 、45cm 的两根铝材，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为另外两边.截法有（ ）A.0种B. 1 种C. 2 种D. 3 种 【答案】B【关键词】相似三角形的判定3. （20XX 年宁德市）如图，在 口 ABCD 中，AE = EB AF = 2,贝U FC 等于 ______ .【答案4】5.（2010福建泉州市惠安县）两个相似三角形的面积比是 9:16，则这两个三角形的相似比是（ ）A.9:16B. 3:4C.9: 4D.3:16【关键词】相似三角形的性质 【答案】B6. （20XX 年兰州市）如图，上体育课，甲、乙两名同学分别站在C 、D 的位置时，乙的影子恰好在甲的影子里边, 的影长是 米.【关键词】图形的相似上一个"顶点”的4. （20XX 年台湾省）图（一）表示D 、E 、F 、G 四点在△ABC 三边上的位置，其中 交于H 点。

若 ABC= 一组三角形相似？（A ） △ BDG , △ CEF （C ） △ ABC , △ BDG 【关键词】相似 【答案】BEFC=70 , (B) △ ABC , △ CEF (D) △ FGH , △ ABC 。

DG 与 EFB【答案】6已知甲，乙同学相距1米.甲身高1.8米，乙身高1.5米，则甲7. （2010辽宁省丹东市）如图，△ ABC与厶ABC是位似图形，且位似比是1: 2，若AB=2cm,则A B cm并在图中画出位似中心O.【关键词】位似【答案】.4 （填空2分，画图1分）& （20XX年安徽省芜湖市）如图，光源P在横杆AB的正上方，AB在灯光下的影子为CD , AB// CD, AB = 2m, CD = 6m，点P至U CD的距离是2.7m，贝U AB与CD间的距离是 _________ m ./ \tZ ----------------------- D筒13世圏【关键词】投影相似三角形【答案】1.89. （2010重庆市）已知△ ABC与厶DEF相似且对应中线的比为2:3，则△ ABC与厶DEF的周长比为_______________ .解析：由相似三角形的对应线段比等于相似比知，△ABC与厶DEF的周长比为2:3答案：2: 3.10. （2010山东德州）如图，小明在A时测得某树的影长为2m, B时又测得该树的影长为8m,若两次日照的光线互相垂直，则树的高度为________ m.第14题图【关键词】三角形相似【答案】411. （2010重庆潼南县）12. △ ABC与厶DEF的相似比为3: 4,则厶ABC与厶DEF的周长第11题图比为____________ .答案：3: 412. （2010重庆市潼南县）△ ABC 与厶DEF 的相似比为 3: 4，则△ ABC 与厶DEF 的周长比答案：3:4.13.. （2010浙江衢州）如图，方格纸中每个小正方形的边长为 〔，△ ABC 和厶DEF的顶点都在方格纸的格点上.（1） 判断△ ABC 和厶DEF 是否相似，并说明理由；（2） P 1 , P 2, P 3, P 4, P 5, D , F 是厶DEF 边上的7个格点，请在这 7个格点中选取 3 个点作为三角形的顶点，使构成的三角形与△ABC 相似（要求写出2个符合条件的三角形，并在图中连结相应线段，不必说明理由 ）•14. （2010江西）图1所示的遮阳伞，伞炳垂直于水平地面，起示意图如图2•当伞收紧时，点P 与点A 重合；当三慢慢撑开时，动点 P 由A 向B 移动；当点P 到达点B 时，伞张 得最开。

2010年部分省市中考数学试题分类汇编 有理数一 选择题1．(2010重庆市) 3的倒数是（）A ．13B ．— 13C ．3D ．—3解析：由一个不为0的数a 倒数是a 1知： 3的倒数是— 13 .答案：B.2. (2010重庆市潼南县)2的倒数是（ ）A ．21 B ．-2 C . -21D . 2 答案：A3.（2010年四川省眉山市）5-的倒数是A ．5B ．15C ．5-D ．15- 【关键词】有理数的倒数的概念和性质 【答案】D4.（2010年福建省晋江市）51-的相反数是( ). A. 51 B. 51- C. 5 D.5-【关键词】倒数的概念与性质 【答案】D5.（2010年浙江省东阳市）73是 （ ） A ．无理数B ．有理数C ．整数D ．负数【关键词】有理数的概念 【答案】B6.（2010年浙江省东阳市）73是 （ ） A ．无理数B ．有理数C ．整数D ．负数【关键词】有理数的概念 【答案】B7.（2010年四川省眉山市）5-的倒数是A ．5B ．15 C ．5- D ．15- 【关键词】有理数的倒数的概念和性质 【答案】D8.（2010年福建省晋江市）51-的相反数是( ). A.51 B. 51- C. 5 D.5- 【关键词】倒数的概念与性质 【答案】D9．(2010重庆市) 3的倒数是（）A ．13B ．— 13C ．3D ．—3解析：由一个不为0的数a 倒数是a 1知： 3的倒数是— 13 .答案：B.10.（2010江苏宿迁）3)2(-等于（ ）A ．－6B ．6C ．－8D ．8 【关键词】有理数的乘方【答案】C11.（2010江苏宿迁）有理数a 、b 在数轴上的位置如图所示，则b a +的值A ．大于0B ．小于0C ．小于aD ．大于b 【关键词】数轴 【答案】A12.（2010江苏宿迁）下列运算中，正确的是（ ）A ．325=-m mB ．222)(n m n m +=+C ．n m nm =22 D ．222)(mn n m =⋅【关键词】有理数的运算【答案】D13.（2010年毕节地区）若23(2)0m n -++=，则2m n +的值为（ ） A ．4- B ．1- C ．0 D ．4 【关键词】绝对值、代数式的值、两个非负数的和 【答案】B14.（2010年重庆市潼南县）2的倒数是（ ）A ．21 B ．-2 C . -21D . 2 【关键词】有理数运算、倒数 【答案】A(第3题)15. （2010年浙江省东阳市）73是 ( ) A ．无理数 B ．有理数C ．整数D ．负数【关键词】有理数 【答案】B16. （2010年浙江省东阳市）某电视台报道，截止到2010年5月5日，慈善总会已接受支援玉树地震灾区的捐款15510000元．将15510000用科学记数法表示为 ( )A.8101551.0⨯ B. 4101551⨯ C.710551.1⨯ D.61051.15⨯【关键词】科学记数法 【答案】C17.（2010年安徽中考） 在2,1,0,1-这四个数中，既不是正数也不是负数的是（ ） A ）1- B ）0 C ）1 D ）2 【关键词】有理数 【答案】B18. （2010年安徽中考） 2010年一季度，全国城镇新增就业人数为289万人，用科学记数法表示289万正确的是…………………………（ ）A ）2.89×107.B ）2.89×106 .C ）2.89×105.D ）2.89×104. 【关键词】科学记数法 【答案】B19. （2010年宁波市）－3的相反数是（ ） A 、3 B 、31 C 、－3 D 、31- 【关键词】相反数【答案】A 20、（2010年宁波市）据《中国经济周刊》报道，上海世博会第四轮环保活动投资总金额高达820亿元，其中820亿用科学记数法表示为（ ） A 、111082.0⨯ B 、10102.8⨯ C 、9102.8⨯ D 、81082⨯ 【关键词】科学记数法 【答案】B21.（2010·重庆市潼南县）2的倒数是（ ）A ．21 B ．-2 C. -21D. 2 【关键词】倒数的概念 【答案】A22.(2010年山东聊城)据市旅游局统计，今年“五·一”小长假期间，我市旅游市场走势良好，假期旅游总收入达到8.55亿元，用科学记数法可以表示为A ．8.55×106B ．8.55×107C ．8.55×108D ．8.55×109 【关键词】科学记数法 【答案】C23.（2010·重庆市潼南县）2的倒数是（ ）A ．21 B ．-2 C. -21D. 2 【关键词】倒数的概念 【答案】A24.（2010年辽宁省丹东市）在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中，首次使用了我国科研人员自主研制的强度为84.610⨯帕的钢材，那么84.610⨯的原数为（ ）A ．4 600 000B ．46 000 000C ．460 000 000D ．4 600 000 000 【关键词】科学计数法 【答案】C 25（2010辽宁省丹东市）1在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中，首次使用了我国科研人员自主研制的强度为84.610⨯帕的钢材，那么84.610⨯的原数为（ ）A ．4 600 000B ．46 000 000C ．460 000 000D ．4 600 000 000 【关键词】科学记数法 【答案】C 25.(2010年山东聊城)据市旅游局统计，今年“五·一”小长假期间，我市旅游市场走势良好，假期旅游总收入达到8.55亿元，用科学记数法可以表示为A ．8.55×106B ．8.55×107C ．8.55×108D ．8.55×109 【关键词】科学记数法 【答案】C 1、（2010年宁波）－3的相反数是（ ） A 、3 B 、31 C 、－3 D 、31- 答案：A27、（2010年宁波）据《中国经济周刊》报道，上海世博会第四轮环保活动投资总金额高达820亿元，其中820亿用科学记数法表示为（ ） A 、111082.0⨯ B 、10102.8⨯ C 、9102.8⨯ D 、81082⨯ 答案：B28．（2009年山东省济南市）某市2009年元旦的最高气温为2℃，最低气温为－8℃，那么这天的最高气温比最低气温高 （ ） A ．-10℃ B ．-6℃ C ．6℃ D ．10℃ 【关键词】有理数 【答案】D29.（2010年台湾省）下列何者是0.000815的科学记号？(A) 8.15⨯10-3 (B) 8.15⨯10-4 (C) 815⨯10-3 (D) 815⨯10-6 。

2010中考数学试题分类汇编--相似（2010哈尔滨）1 .已知：在△ ABC中AB = AC,点D为BC边的中点，点F是AB边上一点，点E在线段DF 的延长线上，/ BAE =Z BDF，点M在线段DF上，/ ABE = Z DBM .（1）如图1，当/ ABC = 45° 时，求证：AE = 2 MD ;（2）如图2，当/ ABC = 60°时，则线段AE、MD之间的数量关系为： _____________________ 。

（3）在（2）的条件下延长BM到P,使MP= BM，连接CP，若AB = 7, AE = 2 7 ,求tan/ ACP的值.（2010珠海）2 .如图，在平行四边形ABCD中,过点A作AE丄BC垂足为E,连接DE, F为线段DE上一点，且/ AFE=/ B.(1) 求证：△ ADF^A DEC(2) 若AB= 4,AD = 3 .3,AE = 3,求AF 的长.(1) 证明：•••四边形ABCD是平行四边形••• AD// BC AB // CD•••/ ADF=/ CED / B+/ C=180°•// AFE+/ AFD=180 / AFE=/ B•••/ AFD=/ C• △ADF^A DEC⑵解：•••四边形ABCD是平行四边形• AD// BC CD=AB=4又••• AE丄BC • AE 丄AD在Rt △ ADE中, DE=.、AD2 AE2二,(3 .. 3)2 32 =6•/△ADF^A DECAD AF.3、.3 _ AF—rtr—z. v aDE CD64C旁边一颗树在阳光下”十青（2010珠海）3。

一天，小青在校园内发现：的影子和她本人的影子在同一直线上，树顶的影子和她头顶的影子恰好落在地面的同一点，同时还发现她站立于树影的中点（如图所示）•如果小青的峰高为1.65米，由此可推断出树高是____________ 米.3.3（2010年兰州）19.如图，上体育课，甲、乙两名同学分别站在 C D的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距1米.甲身高1.8米，乙身高1.5米，则甲的影长是____________ 米.答案6（2010宁波市）26.如图1,在平面直角坐标系中，0是坐标原点，口ABCD的顶点A的坐标为（一2, 0）, 点D的坐标为（0, 2羽），点B在x轴的正半轴上，点E为线段AD的中点，过点E的直线I与x轴交于点F，与射线DC交于点G.（1）求/ DCB的度数；（2）当点F的坐标为（一4, 0）,求点的坐标；（3）连结0E,以0E所在直线为对称轴，△ OEF经轴对称变换后得到△ OEF '，记直线EF '与射线DC 的交点为H.①如图2,当点G在点H的左侧时，求证：△ DEG DHE ;②△若EHG的面积为3 ,3,请你直接写出点F的坐标24. （2010年金华）（本题12分）与厶ABC的面积比为(BA . 1: 2B.1:C. 2: 1D. 4:（桂林2010）6.如图，已知△（罠"【件厠图）如图，把含有30。

2010年部分省市中考数学试题分类汇编分式与分式方程11．（2010年山东省青岛市）某市为治理污水，需要铺设一段全长为300 m 的污水排放管道．铺设120 m 后，为了尽量减少施工对城市交通所造成的影响，后来每天的工效比原计划增加20%，结果共用30天完成这一任务．求原计划每天铺设管道的长度．如果设原计划每天铺设m x 管道，那么根据题意，可得方程 ． 【关键词】分式方程【答案】()()12030012030120%120180301.2x xxx-+=++=或7．（2010年益阳市） 货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x 千米/小时,依题意列方程正确的是Ａ．203525-=x x Ｂ．x x 352025=- Ｃ．203525+=x x Ｄ．xx 352025=+【关键词】分式方程 【答案】C（2010年广东省广州市）已知关于x 的一元二次方程)0(012≠=++a bx ax有两个相等的实数根，求4)2(222-+-b a ab的值。

【关键词】分式化简，一元二次方程根的判别式 【答案】解：∵)0(012≠=++a bx ax有两个相等的实数根，∴⊿＝240b ac -=，即240b a -=． ∵2222222222244444)2(aab ba a abb a a abb a ab=+-=-++-=-+-∵0a ≠，∴4222==ab aab21．(2010重庆市)先化简，再求值：（x 2＋4x －4）÷ x 2－4x 2＋2x，其中x ＝－1解：原式=4244222-+⋅+-x x x xx x =)2)(2()2()2(2-++⋅-x x x x xx =2-x当x ＝－1时，原式=2-x =-1.6．（2010江苏泰州，6，3分）下列命题：①正多边形都是轴对称图形；②通过对足球迷健康状况的调查可以了解我国公民的健康状况；③方程1312112-=+--x x x 的解是0=x ；④如果一个角的两边与另一个角的两边分别平行，那么这两个角相等．其中真命题的个数有（ ）A.1个B.2个C.3个D.4个 【答案】B 【关键词】轴对称与中心对称 随机抽样 分式方程的解法 简单的推理21．(2010重庆市)先化简，再求值：（x 2＋4x －4）÷ x 2－4x 2＋2x，其中x ＝－1解：原式=4244222-+⋅+-x x x xx x =)2)(2()2()2(2-++⋅-x x x x xx =2-x当x ＝－1时，原式=2-x =-1.3.（2010年福建省晋江市）先化简，再求值：x x x x x x11132-⋅⎪⎭⎫ ⎝⎛+--，其中22-=x【关键词】分式运算、化简求值【答案】解一：原式=()()()()()()x x x x x x x x x x 111111132-⋅⎥⎦⎤⎢⎣⎡+---+-+ =()()xxx x xxx x11133222-⋅+-+-+=()()xxx x xx1114222-⋅+-+=()()()()()xx x x x x x 111122-+⋅+-+=()22+x 当22-=x 时，原式=()2222+-=22解二：原式=xx x x xx x x 1111322-⋅+--⋅-= ()()()()xx x x xxx x x x 1111113+-⋅+-+-⋅-= ()()113--+x x = 133+-+x x =42+x 当22-=x 时，原式=224+）=224.（2010年辽宁省丹东市）进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话:【关键词】分式方程的实际应用【答案】解：设原来每天加固x 米，根据题意，得926004800600=-+xx ．去分母，得 1200+4200=18x （或18x =5400） 解得 300x =． 检验：当300x =时，20x ≠（或分母不等于0）． ∴300x =是原方程的解． 答：该地驻军原来每天加固300米．通过这段对话,请你求出该地驻军原来每天加固的米数.。

2010年部分省市中考数学试题分类汇编 开放型问题23. （2010年安徽中考）如图，已知△ABC ∽△111C B A ，相似比为k （1>k ），且△ABC 的三边长分别为a 、b 、c （c b a >>），△111C B A 的三边长分别为1a 、1b 、1c 。

⑴若1a c =，求证：kc a =；⑵若1a c =，试给出符合条件的一对△ABC 和△111C B A ，使得a 、b 、c 和1a 、1b 、1c 进都是正整数，并加以说明；⑶若1a b =，1b c =，是否存在△ABC 和△111C B A 使得2=k ？请说明理由。

c 1b 1a 1C 1B 1A 1c b aA【关键词】三角形相似 【答案】（1） 证明：∵△ABC ∽△111C B A ，且相似比为k （1>k ），∴1ak a =∴1a ka = 又∵1a c =，所以kc a =（2）取a=8,b=6,c=4，同时取1114,3,2a b c === 此时1112a b ca b c ===∴1111ABC A B C c a ∆∆= 且 （1） 不存在这样的△ABC 和△111C B A ，理由如下：若k=2，则1112,2,2a a b b c c === 又∵1a b =，1b c =， ∴112244a a b b c ==== ∴b=2c∴b+c=2c+c<4c=a ，而b+c>a故不存在这样的△ABC 和△111C B A 使得2=k 。

2010年宁德市）（本题满分8分）如图，已知AD 是△ABC 的角平分线，在不添加任何辅助线的前提下，要使△AE D ≌△AFD ，需添加一个条件是：_______________，并给予证明. 【答案】解法一：添加条件：AE ＝AF ，证明：在△AED 与△AFD 中，∵AE ＝AF ，∠EAD ＝∠FAD ，AD ＝AD ， ∴△AED ≌△AFD （SAS ）. 解法二：添加条件：∠EDA ＝∠FDA ，证明：在△AED 与△AFD 中，∵∠EAD ＝∠FAD ，AD ＝AD ，∠EDA ＝∠FDA ， ∴△AED ≌△AFD （ASA ）.（2010江苏泰州，28，12分）在平面直角坐标系中，直线y kx b =+（k 为常数且k ≠0）分别交x 轴、y 轴于点A 、B ，⊙O⑴如图甲，若点A 在x 轴正半轴上，点B 在y 轴正半轴上，且OA=OB ． ①求k 的值；②若b =4，点P 为直线y kx b =+上的动点，过点P 作⊙O 的切线PC 、PD ，切点分别为C 、D ，当PC ⊥PD 时，求点P 的坐标． ⑵若12k =-，直线y kx b =+将圆周分成两段弧长之比为1∶2，求b 的值．（图乙供选用）【答案】⑴①根据题意得：B 的坐标为（0，b ），∴OA =OB =b ，∴A 的坐标为（b ，0），代入y ＝kx ＋b 得k ＝－1.B D CAEF②过P 作x 轴的垂线，垂足为F ，连结OD . ∵PC 、PD 是⊙O 的两条切线，∠CPD =90°， ∴∠OPD =∠OPC =12∠CPD =45°， ∵∠PDO=90°，，∠POD =∠OPD ＝45°，∴OD ＝PD OP ∵P 在直线y ＝－x ＋4上，设P （m ，－m ＋4），则OF =m ，PF =－m ＋4， ∵∠PFO =90°， OF 2＋PF 2＝PO 2，∴ m 2＋ (－m ＋4)22， 解得m=1或3，∴P 的坐标为（1，3）或（3，1）⑵分两种情形，y ＝－12x ＋54，或y ＝－12x －54。

2010相似分类1.（2010某某）如图，D ，E 分别是△ABC 的边AC 和BC 的中点，已知DE =2，则AB =( D )A ．1B ．2C ．3D ．42.（2010某某）在△ABC 中，D 、E 分别是边AB 、AC 的中点，若BC ＝5，则DE 的长是（A ） A ．．5C ．10D ．153.（2010某某）在△ABC 中，D 、E 分别是AB 、AC 的中点，若DE =2cm ，则BC 的长是（ C ） A ．2cm B ．3cm C ．4cm D ．5cm4.（2010某某）如图，在Rt △ABC 中，∠ACB=90°，∠A=30°，CD ⊥AB 于点D .则△BCD 与△ABC 的周长之比为（ A ）A ．1︰2B ．1︰3C ．1︰4D ．1︰55.(2010义乌)如图，将三角形纸片ABC 沿DE 折叠，使点A 落在BC 边上的点F 处，且DE ∥BC ，下列结论中，一定正确的个数是( C )①BDF ∆是等腰三角形 ②BC DE 21=③四边形ADFE 是菱形④2BDF FEC A ∠+∠=∠ A ．1B ．2C ．3D ．46.(2010某某）如图,EF 是△ABC 的中位线，将△AEF 沿中线AD 方向平移到△A 1E 1F 1的位置，使E 1F 1与BC 边重合，已知△AEF 的面积为7，则图中阴影部分的面积为（B ） A. 7 B. 14 C. 21 D. 287.（2010某某）如图，在△ABC 中，CD 是∠ACB 的平分线，∠A =80°，∠ACB=60°，那么∠BDC=（ D ） A ．80° B ．90° C ．100° D ．110°8.(2010红河)下列命题错误的是 （ B ）A. 四边形内角和等于外角和B. 相似多边形的面积比等于相似比C. 点P （1,2）关于原点对称的点的坐标为（-1，-2）D. 三角形的中位线平行于第三边，且等于第三边的一半 9.（2010某某）下列命题中，是真命题的为（ D ） A .锐角三角形都相似 B .直角三角形都相似 C .等腰三角形都相似 D .等边三角形都相似10.(2010某某)如图，已知△ADE 与△ABC 的相似比为1：2，则△ADE 与△ABC 的面积比为（ B ）．A ．1：2B ．1：4C ．2：1D ．4：111. (2010黄冈)如图，过边长为1的等边△ABC 的边AB 上一点P ，作PE ⊥AC 于E ，Q 为 BC 延长线上一点，当PA ＝CQ 时，连PQ 交AC 边于D ，则DE 的长为（ B ）A ．13 B ．12 C ．23D ．不能确定12．(2010 达州 )如图，在一块形状为直角梯形的草坪中，修建了一条由A →M →N →C 的AD EB C小路（M 、N 分别是AB 、CD 中点）.极少数同学为了走“捷径”，沿线段AC 行走，破坏了草坪，实际上他们仅少走了( B )A. 7米B. 6米C. 5米D. 4米13.ABCD 沿EF 对开后，再把矩形EFCD 沿MN 对开，依此类推.若各种开本的矩形都相似，那么ABAD等于（ B ） A ．0.618 B.22C.2D.21.(2010某某)如图，在△ABC 中，AB ＝AC ＝13，BC ＝10，D 是AB 的中点，过点D 作DE ⊥AC 于点E ，则DE 的长是______________．60132.(2010某某)如图在△ABC 中D 是AB 边上一点，连接CD ，要使△ADC 与△ABC 相似，应添加的条件是 ∠ACD=∠B ∠ADC=∠AOBAD ACAC AB3.(2010某某)在△ABC 中，AB=AC=12cm ，BC=6cm ，D 为BC 的中点，动点P 从B 点出发，以每秒1cm 的速度沿B →A →C 的方向运动．设运动时间为t 秒，过D 、P 两点的直线将△ABC 的周长分成两个部分，使其中一部分是另一部分的2倍，那么t 的值为.7秒或17秒 4.（2010某某）如图，在△ABC 中，点D 、E 、F 分别是AB 、BC 、CA 的中点，若△ABC 的周长为10cm ，则△DEF 的周长是cm ．55.(2010某某)如图，在平行四边形ABCD 中，CD=10，F 是AB 边上一点，DF 交AC 于点E ， 且的面积的面积则CDE AEF EC AE ∆∆=,52=，BF=.6,2546.(2010某某)如图，小明在A 时测得某树的影长为2m ，B 时又测得该树的影长为8m ，若两次 日照的光线互相垂直，则树的高度为_____m.47.（2010某某）如图，△ABC 中，点D 在边AB 上，满足∠ACD =∠ABC ，若AC = 2，AD= 1，则DB = __3________.8.(2010某某)关于对位似图形的表述，下列命题正确的是．（只填序号）②③① 相似图形一定是位似图形，位似图形一定是相似图形； ② 位似图形一定有位似中心；DA BCA 时B 时③ 如果两个图形是相似图形，且每组对应点的连线所在的直线都经过同一个 点，那么，这两个图形是位似图形；④ 位似图形上任意两点与位似中心的距离之比等于位似比．9.(2010某某)如图，上体育课，甲、乙两名同学分别站在C 、D 的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距1米，乙身高10.(2010滨州)如图，A 、B 两点被池塘隔开，在AB 外取一点c ，连结AC 、BC ，在AC 上取点M ，使AM=3MC ，作MN ∥AB 交BC 于N ，量得MN=38m ，则AB 的长为____________．152m11.(2010某某)如图，梯形ABCD 中，AD ∥BC ，EF 是梯形的中位线，对角线AC 交EF于G ，若BC=10cm ，EF=8cm ，则GF 的长等于cm ．312.(2010某某)如图，在△ABC 中，AB ＝AC ＝8，AD 是底边上的高，E 为AC 中点， 则DE ＝． 4GF E D CBAAE13.(2010某某) 如图，ABC △与A B C '''△是位似图形，且位似比是1:2，若AB =2cm ，则A B ''=cm ，并在图中画出位似中心O ．414．(2010 达州 )如图，△ABC 中，CD ⊥AB ，垂足为D.下列条件中，能证明△ABC 是直角三角形的有（多选、错选不得分）. ①②④①∠A+∠B=90°②222AB AC BC =+ ③AC CD AB BD=④2CD AD BD =⋅ 15．（2010某某）如图，一根直立于水平地面的木杆AB 在灯光下形成影子，当木杆绕点A 按逆时针方向旋转直至到达地面时，影子的长度发生变化.设AB 垂直于地面时的影子为AC （假定AC>AB ），影长的最大值为m.最小值为n,那么下列结论：①m>AC;②m ＝AC;③n ＝AB;④影子的长度先增大后减小. 其中，正确结论的序号是. ①③④（多填或错填的得0分，少填的酌情给分）16.（2010某某）如图，在□ ABCD 中，点E 在边BC 上，BE ：EC =1：2，连接AE 交BD 于点F ，则△BFE 的面积与△DF A 的面积之 比为1：9′A BC AB C′ ′′A BC AB C′ ′ODA16.（2010某某）在同一时刻，身高的小强在阳光下的影长为，一棵大树的影长为米，则这棵树的高度为米 17.（2010某某）如果两个相似三角形的一组对应边分别为3cm 和5cm ，且较小三角形的周长为15cm ，则较大三角形的周长为__________cm ．251.(2010滨州)如图，在△ABC 和△ADE 中，∠BAD=∠CAE ，∠ABC=∠ADE 。

中考试题专题之——相似形一、选择题1．如图所示，给出下列条件：①B ACD ∠=∠；②ADC ACB ∠=∠；③AC ABCD BC=；④2AC AD AB = ．其中单独能够判定ABC ACD △∽△的个数为（ C ）A ．1B ．2C ．3D ．42.如图，已知AB CD EF ∥∥，那么下列结论正确的是（A ） A ．AD BCDF CE= B ．BC DFCE AD= C ．CD BCEF BE= D ．CD ADEF AF=3.已知△ABC∽△DEF，且AB ：DE=1：2，则△ABC 的面积与△DEF 的面积之比为（ B ） (A)1：2 (B)1：4 (C)2：1 (D)4：14. 如图，已知等边三角形ABC 的边长为2，DE 是它的中位线，则下面四个结论：（1）DE=1，（2）△CDE ∽△CAB ，（3）△CDE 的面积与△CAB 的面积之比为1：4.其中正确的有：( D ) A ．0个 B ．1个 C ．2个D ．3个5.如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值（ B ）A 只有1个 B 可以有2个 C 有2个以上但有限D ．有无数个6. 小明在一次军事夏令营活动中，进行打靶训练，在用枪瞄准目标点B 时，要使眼睛O 、准星A 、目标B 在同一条直线上，如图4所示，在射击时，小明有轻微的抖动，致使准星A 偏离到A ′，若OA=0.2米，OB=40米，AA ′=0.0015米，则小明射击到的点B ′偏离目标点B 的长度BB ′为 ( B ）A ．3米B ．0.3米C ．0.03米 D ．0.2米7.如图，在ABC △中，C ∠9060B D =∠=°，°，是AC 上一点，DE AB ⊥于E ，且21CD DE ==，，则BC 的长为（B ）A ．2 B ．433C ．23D ．43 8.在ABC △和DEF △中，22AB DE AC DF A D ==∠=∠，，，如果ABC △的周长是16，面积是12，那么DEF △的周长、面积依次为（ A ）A ．8，3B ．8，6C ．4，3D ４，69.如图， ABC △中，CD AB ⊥于D ，一定能确定ABC △为直角三角形的条件的个数是（ C ）①1A ∠=∠，②CD DBAD CD=，③290B ∠+∠=°，④345BC AC AB =∶∶∶∶，⑤ CD AC BD AC ∙=∙A ．1 B ．2 C ．3 D ．410. 在△ABC 中，AB =12，AC =10，BC =9，AD 是BC 边上的高.将△ABC 按如图所示的方式折叠，使点A 与点D 重合，折痕为EF ，则△DEF 的周长为( D ) A ．9.5 B ．10.5 C ．11 D ．15.511.如图，△ABC 中，A ，B 两个顶点在x 轴的上方，点C 的坐标是(-1，0)．以点C 为位似中心，在x 轴的下方作△ABC 的位似图形，并把△ABC 的边长放大到原来的2倍，记所得的像是△A ′B ′C ．设点B 的对应点B ′的横坐标是a ，则点B 的横坐标是( D)A ．12a -B ．1(1)2a -+C ．1(1)2a -- D ．1(3)2a -+12.如图，在长为8 cm 、宽为4 cm 的矩形中，截去一个矩形，使得留下的矩形（图中阴影部分）与原矩形相似，则留下矩形的面积是（ C ）A. 2 cm 2 B. 4 cm 2 C. 8 cm 2 D. 16 cm213. 若一个图形的面积为2，那么将它与成中心对称的图形放大为原来的两倍后的图形面积为（ A ）A. 8 B. 6 C. 4 D. 2 14.如图，正方形ABCD 中，E 为AB 的中点，AF ⊥DE 于点O ， 则DOAO等于（D ） A ．352 B ．31 C ．32 D ．21 15.如图，在正三角形ABC 中，D ，E ，F 分别是BC ，AC ，AB 上的点，DE AC ⊥，EF AB ⊥，FD BC ⊥，则DEF △的面积与ABC △的面积之比等于（ A ）A ．1∶3B ．2∶3C ．3∶2D ．3∶316．如图，AB 是O ⊙的直径，AD 是O ⊙的切线，点C 在O ⊙上，BC OD ∥，23AB OD ==，,则BC 的长为（ A ） A ．23B ．32 C 32 D ．2217．如图，在Rt ABC △中，90ACB ∠=°，3BC =，4AC =，AB 的垂直平分线DE 交BC 的延长线于点E ，则CE 的长为（ B ）A ．32 B ．76C ．D ．2 18. 如图，AB 是O ⊙的直径，点C 在圆上，CD AB DE BC ⊥，∥，则图中与ABC △相似的三角形的个数有（ ）A ．4个B ．3个C ．2个D ．1个CBDO AE二、填空题1.锐角△ABC 中，BC ＝6,,12=∆ABC S 两动点M 、N 分别在边AB 、AC 上滑动，且MN ∥BC ，以MN 为边向下作正方形MPQN ，设其边长为x ，正方形MPQN 与△ABC 公共部分的面积为y （y ＞0）,当x ＝ 3 ，公共部分面积y 最大，y 最大值 ＝ 6 ,2.在平面直角坐标系中，ABC △顶点A 的坐标为(23)，，若以原点O 为位似中心，画ABC△的位似图形A B C '''△，使ABC △与A B C '''△的相似比等于12，则点A '的坐标为（4，6） ． 3.如图，OAB △的顶点B 的坐标为（4，0），把OAB △沿x 轴向右平移得到CDE △，如果1,CB =那么OE 的长为 7 ．4.如图，ABC △与AEF △中，AB AE BC EF B E AB ==∠=∠，，，交EF 于D ．给出下列结论：①AFC C ∠=∠；②D F C F =；③A D E F D B △∽△；④BFD CAF ∠=∠．其中正确的结论是 ①，③，④ （填写所有正确结论的序号）．5.如图，点M 是△ABC 内一点，过点M 分别作直线平行于△ABC 的各边，所形成的三个小三角形△1、△2、△3（图中阴影部分）的面积分别是4，9和49．则△ABC 的面积是 144 ．6.Rt ABC △中，90ACB ∠=°，直线EF BD ∥，交AB 于点E ，交AC 于点G ，交AD 于点F ，若13AEG EBCG S S =△四边形，则CF AD= 12 ． 7. 已知A B C A B '''△∽△且1:2ABC A B C S S '''=△△:，则:A B A B ''= 1:2 ．8.在□ABCD 中，E 在DC 上，若:1:2DE EC =，则:BF BE = 5:3 ．三、解答题1.如图，在矩形A B C D 中，点E F 、分别在边A D D C 、上，A B E D E F △∽△，692AB AE DE ===，，，求EF 的长．解：∵四边形ABCD 是矩形，AB=6∴∠A=∠D=90°，DC=AB=6又∵AE=9 ∴在Rt △ABE 中，由勾股定理得：BE=117692222=+=+AB AE∵ABE DEF △∽△，∴EF BE DE AB =，即EF 11726=∴EF=31172．（2009年长春）如图，在ABCD中，32BAD ∠=°，分别以BC CD 、为边向外作BCE △和DCF △，使B E B C D F D C E B C C D F ==∠=∠，，．延长AB 交边EC 于点H ，点H在E C 、两点之间，连结AE AF 、．（1）求证：ABE FDA △≌△． （2）当A E A F ⊥时，求EBH ∠的度数．（1）证明：在平行四边形ABCD 中，AB=DC. 又∵DF=DC ，∴AB=DF. 同理EB=AD.在平行四边形ABCD 中，∠ABC=∠ADC. 又∵∠EBC=∠CDF ，∴∠ABE=∠ADF ，∴△ABE ≌△FDA.（2）解：∵△ABE ≌△FDA ， ∴∠AEB=∠DAF.∵∠EBH=∠AEB+∠EAB,∴∠EBH=∠DAF+∠EAB.∵AE ⊥AF ，∴∠EAF=90°.∵∠BAD=32°，∴∠DAF+∠EAB=90°-32°=58°，∴∠EBH=58°. 3.如图，M 为线段AB 的中点，AE 与BD 交于点C ，∠DME ＝∠A ＝∠B ＝α，且DM 交AC 于F ，ME 交BC 于G ．（1）写出图中三对相似三角形，并证明其中的一对；（2）连结FG ，如果α＝45°，AB ＝42，AF ＝3，求FG 的长．1）证：△AMF ∽△BGM ，△DMG ∽△DBM ，△EMF ∽△EAM （写出两对即可） 以下证明△AMF ∽△BGM ．∵∠AFM ＝∠DME ＋∠E ＝∠A ＋∠E ＝∠BMG ，∠A ＝∠B ∴△AMF ∽△BGM ．（2）解：当α＝45°时，可得AC ⊥BC 且AC ＝BC ∵M 为AB 的中点，∴AM ＝BM ＝22分又∵AMF ∽△BGM ，∴AF BMAM BG=∴2222833AM BM BG AF ⨯=== 又42cos454AC BC === ，∴84433CG =-=，431CF =-=∴2222451()33FG CF CG =+=+=4.如图，△ABC 内接于⊙O ，AD 是△ABC 的边BC 上的高，AE 是⊙O 的直径，连接BE ，△ABE与△ADC 相似吗？请证明你的结论．△ABE 与△ADC 相似．理由如下：在△ABE 与△ADC 中∵AE 是⊙O 的直径， ∴∠ABE =90o ，∵AD 是△ABC 的边BC 上的高， ∴∠ADC =90o ， ∴∠ABE =∠ADC ．又∵同弧所对的圆周角相等， ∴∠BEA =∠DCA ．∴△ABE ～△ADC ．5.如图，已知抛物线与x 交于A(－1，0)、E(3，0)两点，与y 轴交于点B(0，3)。