修正的时间序列回归法(精)

线性回归模型的经典假定及检验、修正一、线性回归模型的基本假定1、一元线性回归模型一元线性回归模型是最简单的计量经济学模型，在模型中只有一个解释变量，其一般形式是Y =β0+β1X 1+μ其中，Y 为被解释变量，X 为解释变量，β0与β1为待估参数，μ为随机干扰项。

回归分析的主要目的是要通过样本回归函数（模型）尽可能准确地估计总体回归函数（模型）。

为保证函数估计量具有良好的性质，通常对模型提出若干基本假设。

假设1：回归模型是正确设定的。

模型的正确设定主要包括两个方面的内容：（1）模型选择了正确的变量，即未遗漏重要变量，也不含无关变量；（2）模型选择了正确的函数形式，即当被解释变量与解释变量间呈现某种函数形式时，我们所设定的总体回归方程恰为该函数形式。

假设2：解释变量X 是确定性变量，而不是随机变量，在重复抽样中取固定值。

这里假定解释变量为非随机的，可以简化对参数估计性质的讨论。

假设3：解释变量X 在所抽取的样本中具有变异性，而且随着样本容量的无限增加，解释变量X 的样本方差趋于一个非零的有限常数，即∑(X i −X ̅)2n i=1n→Q,n →∞ 在以因果关系为基础的回归分析中，往往就是通过解释变量X 的变化来解释被解释变量Y 的变化的，因此，解释变量X 要有足够的变异性。

对其样本方差的极限为非零有限常数的假设，旨在排除时间序列数据出现持续上升或下降的变量作为解释变量，因为这类数据不仅使大样本统计推断变得无效，而且往往产生伪回归问题。

假设4：随机误差项μ具有给定X 条件下的零均值、同方差以及无序列相关性，即E(μi|X i)=0Var(μi|X i)=σ2Cov(μi,μj|X i,X j)=0, i≠j随机误差项μ的条件零均值假设意味着μ的期望不依赖于X的变化而变化，且总为常数零。

该假设表明μ与X不存在任何形式的相关性，因此该假设成立时也往往称X为外生性解释变量随机误差项μ的条件同方差假设意味着μ的方差不依赖于X的变化而变化，且总为常数σ2。

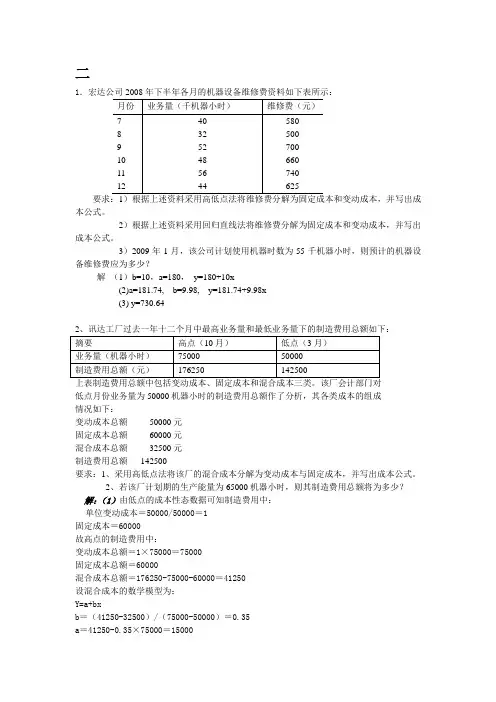
二1本公式。

2）根据上述资料采用回归直线法将维修费分解为固定成本和变动成本，并写出成本公式。

3）2009年1月，该公司计划使用机器时数为55千机器小时，则预计的机器设备维修费应为多少？解（1）b=10，a=180，y=180+10x(2)a=181.74, b=9.98, y=181.74+9.98x(3) y=730.64上表制造费用总额中包括变动成本、固定成本和混合成本三类。

该厂会计部门对低点月份业务量为50000机器小时的制造费用总额作了分析，其各类成本的组成情况如下：变动成本总额50000元固定成本总额60000元混合成本总额32500元制造费用总额142500要求：1、采用高低点法将该厂的混合成本分解为变动成本与固定成本，并写出成本公式。

2、若该厂计划期的生产能量为65000机器小时，则其制造费用总额将为多少？解：（1）由低点的成本性态数据可知制造费用中：单位变动成本＝50000/50000＝1固定成本＝60000故高点的制造费用中：变动成本总额＝1×75000＝75000固定成本总额＝60000混合成本总额＝176250-75000-60000＝41250设混合成本的数学模型为：Y=a+bxb＝（41250-32500）/（75000-50000）＝0.35a＝41250-0.35×75000＝15000混合成本的数学模型为：Y＝15000+0.35x（2）当计划期的生产能量为65000机器小时时，变动成本总额＝1×65000＝65000固定成本总额＝60000混合成本总额＝15000+0.35×65000＝37750所以制造费用＝65000+60000+37750＝162750三4．假定某企业只产销一种产品，其有关资料如下：生产量2 000件，销售量1 800件，期初存货0件，边际贡献率60％，原材料6 000元，计件工资4 000元，其他变动性制造费用每件0.4元，固定性制造费用总额2 000元，变动性销售与管理费用每件0.2元，固定性销售与管理费用总额为300元。

判断题1.财务会计主要以整个企业为核算对象，而管理会计既涉及整体又涉及局部。

（）答案：正确2.单位变动成本随业务量的增加而减少。

（）答案：错误3.销售预测中的趋势分析法和相关因数分析法属于定量分析法。

（）答案：错误4.变动成本法与完全成本法的主要区别表现在产品成本的构成、存货计价、盈亏计算等三个方面的不同。

（）答案：错误5.企业处于保本状态时，安全边际率０，保本作业率等于１。

（）答案：正确6.在产品生产决策中，可以产品的单位贡献毛益的大小作为择优的标准。

（）答案：正确7.企业为了扭亏为盈，凡是亏损产品都应停产。

（）答案：错误8.只要固定成本不等于０，经营杠杆系数恒大于１。

（）答案：正确9.在滚动预算中预算期是连续不断的，始终保持一定期限。

（）答案：正确10.成本中心之间相互提供产品或劳务，可以按实际成本作为内部转移价格。

（）答案：错误1.成本性态分析中高低点法的优点是计算精度高，缺点是过于计算过程过于复杂。

（）答案：错误2.导致两种方法分期营业利润出现狭义差额的根本原因，就在于它们对固定性制造费用的处理采取了不同的方式。

（）答案：错误3.在其他条件不变情况下，固定成本越高，保本量越大。

（）答案：正确4.成本预测是其他各项预测的前提。

（）5.在管理会计的调价决策中，如果调高价格后预计销量超过利润无差别点的销售量，那么就应当进行调价。

（）答案：错误6.在建设期等于零时，则长期投资项目的投资职能采取一次性投入方式。

（）答案：错误7.预计资产负债表和预计利润表构成了整个的财务预算。

（）答案：错误8.在标准成本控制系统中，计算价格差异的用量基础是实际产量下的实际耗用量。

（）答案：错误9.确定最优生产批量时，考虑的相关成本有调整准备成本、储存成本和生产中的变动成本。

（）答案：错误10.著名的管理学家西蒙首次提出“战略管理会计”一词的年限是1981年。

（）答案：正确1.为保证管理会计信息质量对决策有用，通常要求将有关的未来信息估计误差控制在决策者可以接受的一定可信区间内，这体现了可信性原则的可理解性要求。

(完整版)5习题与答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)5习题与答案）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)5习题与答案的全部内容。

（完整版)5习题与答案编辑整理：张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是我们任然希望（完整版）5习题与答案这篇文档能够给您的工作和学习带来便利.同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉，前进的动力.本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为 <(完整版)5习题与答案〉这篇文档的全部内容。

第五章练习题一、单项选择题1。

企业根据现有的经济条件和掌握的历史资料以及客观事物的内在联系，对生产经营活动的未来发展趋势和状况进行的预计和测算的过程，就是管理会计的（）。

A。

经营决策 B。

经营预测 C.生产决策 D.生产预测2。

下列各项中，属于因果预测分析法的是（）。

A.趋势平均法B.移动平均法C.指标建立法D.平滑指数法3。

下列各项中，不属于定量分析法的是（）.A.判断分析法B.算术平均法C.回归分析法 D。

平滑指数法4。

通过函询方式,在互不通气的前提下向若干经济专家分别征求意见的方法是（）.A。

专家函询法 B.专家小组法 C。

专家个人意见集合法 D。

特尔菲法5。

下列各种销售预测方法中，属于没有考虑远近期销售业务量对未来销售状况会产生不同影响的方法是（）。

A.移动平均法B.算术平均法C.加权平均法 D。

时间序列的协整检验与误差修正模型讲义时间序列的协整检验与误差修正模型是在经济学和金融学中广泛使用的方法，用于分析两个或多个变量之间的长期稳定关系。

本讲义将介绍协整检验的基本概念和步骤，并讨论误差修正模型的理论背景和实际应用。

一、协整检验1. 概念与原理协整是指两个或多个变量之间存在长期稳定的关系，即它们的线性组合是平稳的。

协整关系可以用来解释一个变量对另一个变量的影响，并提供长期均衡关系的信息。

协整检验的基本原理是利用单位根检验方法，测试变量是否存在单位根（非平稳性）。

如果变量存在单位根，则它们是非平稳的；如果变量不存在单位根，则它们是平稳的。

如果变量之间存在协整关系，它们的线性组合将是平稳的。

2. 协整检验的步骤协整检验的一般步骤如下：- 收集数据并绘制时间序列图，观察变量之间的趋势和关系；- 进行单位根检验，常用的方法包括ADF检验、Phillips-Perron检验等；- 如果变量存在单位根，则进行差分，直到变量变为平稳的；- 应用最小二乘法等方法，估计协整关系方程；- 进行残差平稳性检验，确保协整关系的合理性；- 如果协整关系存在，可以进行模型的进一步分析与应用。

二、误差修正模型（Error Correction Model, ECM）1. 概念与原理误差修正模型是一种动态模型，用于解释协整关系的调整速度和误差纠正机制。

在误差修正模型中，除了协整关系的线性组合外，还引入了误差修正项，用于捕捉变量之间的短期非平衡关系。

误差修正项反映了系统离开长期均衡后的调整速度，通过估计误差修正项的系数，可以判断系统是否有趋向于均衡的能力。

当误差修正项的系数为负数且显著时，表示系统具有自我修复的能力；当系数为零时，表示系统处于长期均衡状态；当系数为正数时，表示系统趋向于进一步偏离均衡。

2. ECM模型的应用误差修正模型可以用于解释和预测时间序列数据的长期和短期动态变化。

它在经济学和金融学中有广泛的应用，如货币供给与通货膨胀、利率与消费支出、汇率与经济增长等领域。

时间序列的协整检验与误差修正模型时间序列的协整检验与误差修正模型是经济学中常用的方法，用于分析两个或多个变量之间的长期关系。

协整检验是在时间序列数据中，判断变量之间是否存在长期平衡关系的一种方法。

误差修正模型是在协整关系已经验证的基础上，建立起变量之间的因果关系，对短期的偏离进行修正的模型。

协整检验的原理是基于单位根检验的思想，判断时间序列是否为平稳序列。

平稳序列是指序列的均值和方差不随时间发生变化。

如果两个变量都是非平稳序列，但它们的线性组合是平稳序列，那么可以认为这两个变量是协整的。

常用的协整检验方法有Engle-Granger方法和Johansen方法。

Engle-Granger方法是一种直观简单的协整检验方法。

它的步骤如下：首先，分别对两个变量进行单位根检验，确认它们是否为非平稳序列。

然后，对两个变量进行线性回归，得到残差序列。

接下来，对残差序列进行单位根检验，确认它是否为平稳序列。

最后，如果残差序列是平稳序列，则可以判断两个变量之间存在协整关系。

协整检验完成后，接下来可以建立误差修正模型。

误差修正模型是基于协整关系的基础上建立起来的，以短期的偏离修正为核心。

它的核心假设是，在长期平衡关系的约束下，两个变量之间的短期偏离可以通过一个修正项来消除。

误差修正模型的基本形式是多元线性回归模型，其中包含自变量、因变量以及一个误差修正项。

误差修正模型的估计和推断可以使用最小二乘法或最大似然法等统计方法进行。

通过对误差修正模型的估计和推断，可以对变量之间的因果关系进行分析。

同时，误差修正模型还可以用于预测和决策分析。

综上所述，时间序列的协整检验与误差修正模型是分析变量之间长期关系的重要工具。

协整检验可以判断变量是否具有长期平衡关系，而误差修正模型则可以分析变量之间的短期调整过程。

这些方法在经济学、金融学、管理学等领域都有广泛的应用。

时间序列的协整检验与误差修正模型是经济学中常用的方法，用于分析两个或多个变量之间的长期关系。