广工数媒计算机图形学之5基本图形生成算法-多边形扫描转换及区域填充
- 格式:ppt
- 大小:397.01 KB
- 文档页数:20


多边形的扫描转换算法概述多边形的扫描转换算法是计算机图形学中用于将多边形转换为像素的常用算法。
它通过扫描线的方式来确定多边形与像素的相交关系,并将多边形的内部区域填充为指定的颜色。
本文将详细介绍多边形的扫描转换算法的原理、步骤和应用。
原理多边形的扫描转换算法基于扫描线的概念,将多边形的边界线与一条水平线或垂直线进行比较,从而确定多边形的内部和外部区域。
算法的关键在于边界线的处理和内部区域的填充。
步骤多边形的扫描转换算法一般包括以下步骤:1.初始化扫描线的位置和内部区域的填充颜色。
2.遍历多边形的边界线,将其与扫描线比较,确定内部和外部区域。
3.根据内部区域的状态,进行填充颜色。
4.更新扫描线的位置,继续扫描下一条线段,直至完成对所有边界线的处理。
算法详解初始化扫描线在开始进行多边形的扫描转换之前,需要初始化扫描线的位置和内部区域的填充颜色。
一般情况下,扫描线的位置可以从多边形的最低点开始,逐渐向上扫描。
内部区域的填充颜色可以根据具体需求进行选择。
边界线处理多边形的边界线可以由多个线段组成,需要按照一定的顺序进行处理。
一种常用的处理方式是按照边界线的上端点的纵坐标从小到大排序,然后依次处理每条线段。
对于每条线段,通过比较线段的上端点和下端点的纵坐标与扫描线的位置,可以确定线段与扫描线的相交关系。
根据线段的斜率可以进一步确定线段与扫描线的交点。
内部区域填充确定了线段与扫描线的相交关系后,就可以确定内部和外部区域。
一般情况下,内部区域被定义为线段上方的区域,而外部区域被定义为线段下方的区域。
根据内部区域的状态,可以进行填充颜色。
如果内部区域是连续的,则可以使用扫描线的颜色进行填充。
如果内部区域有间隙,则需要采用其他填充算法,如边界填充算法或种子填充算法。
更新扫描线处理完当前线段后,需要更新扫描线的位置,继续扫描下一条线段。
一般情况下,扫描线的位置会逐渐向上移动,直至到达多边形的最高点。
应用多边形的扫描转换算法在计算机图形学中有广泛的应用。

计算机图形学——多边形的扫描转换(基本光栅图形算法)⼀、多边形扫描转换在光栅图形中,区域是由【相连的】像素组成的集合,这些像素具有【相同的】属性值或者它们位于某边界线的内部1、光栅图形的⼀个基本问题是把多边形的顶点表⽰转换为点阵表⽰。
这种转换成为多边形的扫描转换。
2、多边形的扫描转换与区域填充问题是怎样在离散的像素集上表⽰⼀个连续的⼆维图形。
3、多边形有两种重要的表⽰⽅法:(1)顶点表⽰:⽤多边形的定点序列来表⽰多边形优点:直观、⼏何意义强、占内存少、易于进⾏⼏何变换缺点:没有明确指出那些象素在多边形内,故不能直接⽤于上⾊(2)点阵表⽰:是⽤位于多边形内的象素集合来刻画多边形缺点:丢失了许多⼏何信息(eg:边界、顶点等)但是【点阵表⽰是光栅显⽰系统显⽰时所需的表现形式。
】多边形的扫描转换就是把多边形的顶点表⽰转换为点阵表⽰,即从多边形的给定边界出发,求出位于其内部的各个像素,并将帧缓冲器内的各个对应元素设置相应的灰度或颜⾊。
实际上就是多边形内的区域的着⾊过程。
4、多边形分类⼆、X扫描线算法X扫描线算法填充多边形的基本思想是按扫描线顺序,计算扫描线与多边形的相交区间,再⽤要求的颜⾊显⽰这些区间的象素,即完成填充⼯作。
区间的端点可以通过计算扫描线与多边形边界线的交点获得。
如扫描线y=3与多边形的边界相交于4点(2,3)、(4,3)、(7,3)、(9,3)这四个点定义了扫描线从x=2到x=4,从x=7到x=9两个落在多边形内的区间,该区间内像素应取填充⾊。
算法的核⼼是按x递增顺序排列交点的x坐标序列。
由此可得到扫描线算法步骤如下:算法步骤:1.确定多边形所占有的最⼤扫描线数,得到多边形定点的最⼩最⼤值(y min和y max);2.从y min到ymax每次⽤⼀条扫描线进⾏填充;3.对⼀条扫描线填充的过程分为四个步骤:a)求交点;b)把所有交点按递增顺序排序;c)交点配对(第⼀个和第⼆个,第三个和第四个);d)区间填⾊。

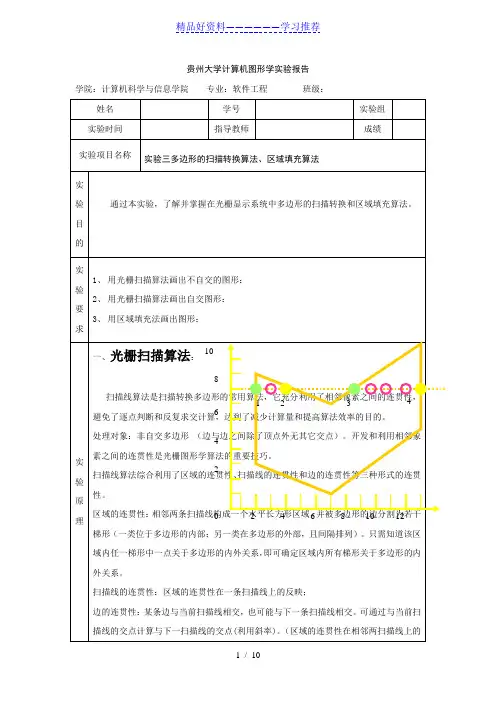
贵州大学计算机图形学实验报告学院:计算机科学与信息学院专业:软件工程班级:反映)根据扫描线的连贯性可知:一条扫描线与多边形的交点中,入点和出点之间所有点都是多边形的内部点。
所以,对所有的扫描线填充入点到出点之间的点就可填充多边形。
如何具体实现(如何找到入点、出点)?根据区域的连贯性,分为3个步骤:(1)求出扫描线与多边形所有边的交点;(2)把这些交点按x坐标值以升序排列;(3)对排序后的交点进行奇偶配对,对每一对交点间的区域进行填充。
步骤(3)如上图:对y=8的扫描线,对交点序列按x坐标升序排序得到的交点序列是(2,4,9,13),然后对交点2与4之间、9与13之间的所有象素点进行填充。
求交点、排序、配对、填色利用链表:与当前扫描线相交的边称为活性边(Active Edge),把它们按与扫描线交点x坐标递增的顺序存入一个链表中,称为活性边表AEL (AEL, Active Edge List)。
它记录了多边形边沿扫描线的交点序列。
AEL中每个对象需要存放的信息:ymax:边所交的最高扫描线;x:当前扫描线与边的交点;Δx:从当前扫描线到下一条扫描线之间的x增量next:指向下一对象的指针。
伪码:建立ET,置y为ET中非空桶的最小序号;置AEL表为空,且把y桶中ET表的边加入AEL表中;while AEL表中非空do begin对AEL表中的x、Δx按升序排列;按照AEL表中交点前后次序,在每对奇偶交点间的x段予以填充;计算下一条扫描线:y=y+1;if 扫描线y=ymax then 从AEL表中删除这些边;对在AEL表中的其他边,计算与下一条扫描线的交点:x=x +Δx 按照扫描线y值把ET表中相应桶中的边加入AEL表中;endend of algorithm二、区域填充算法:区域可采用两种表示形式:内点表示枚举区域内部的所有像素;内部的所有像素着同一个颜色;边界像素着不同的颜色。
边界表示:枚举出边界上所有的像素;边界上的所有像素着同一颜色;内部像素着不同的颜色。



计算机科学与技术学院2013-2014学年第一学期《计算机图形学》实验报告班级:学号:姓名:教师:成绩:实验项目(2、多边形的扫描转换与区域填充)一、实验目的与要求(1)了解多边形扫描转换的各种算法,掌握多边形的扫描转换与区域填充算法。
(2)进一步掌握在VC集成环境中实现图形算法的方法与过程。
二、实验内容设计菜单程序,利用消息处理函数,完成以下要求:(1)给出凸多边形的若干顶点(3 ~ 5个),实现多边形的“x扫描算法”。
(2)实现种子填充,泛填充算法(四邻法)。
(3)设计程序,实现判断一个点是否在多边形区域内部。
三、重要算法分析(一)边界表示的四连通区域种子填充算法此方法的基本思想是,从多边形内部任一像素出发,按照“左上右下”的顺序判断相邻像素,若不是边界像素且没有被填充过,则对其填充,并且重复上述过程,直到所有像素填充完毕。
(1)从种子点出发,向左判断多边形内部颜色,如果不是填充颜色并且不是边界颜色,则填充,直到遇到边界为止。
(2)从种子点出发,向右判断多边形内部颜色,如果不是填充颜色并且不是边界颜色,则填充,直到遇到边界为止。
(3)将种子点的坐标y值上移一个像素,重复步骤(1)、(2)直到遇到上面边界为止。
(4)将种子点的坐标y值下移一个像素,重复步骤(1)、(2)直到遇到上面边界为止。
(二)判断一个点是否在多边形内部解决方案是将测试点的y坐标与多边形的每一个点进行比较,我们会得到一个测试点所在的行与多边形边的交点的列表。
如果测试点的两边点的个数都是奇数个则该测试点在多边形内,否则在多边形外。
如图1所示,判断点(红点)y值左边与多边形有5个交点,右边与多边形有3个交点,则该点在多边形内部。
图1如图2所示,判断点(红点)y值左边与多边形有2个交点,右边与多边形有2个交点,则该点在多边形外部。
图2但是有一种特殊情况须特别处理一下,当与多边形顶点相交时,需要将改点计算为两个交点,如图3所示:图3四、程序运行截图1.种子四连通域填充法,如图4所示。

计算机图形学多边形填充算法计算机图形学中的多边形填充算法是指将给定的多边形区域进行颜色填充,以使其完全填充的过程。
在图形学中,多边形是由一系列连续的线段组成的封闭图形。
填充算法可用于渲染图形、绘制图像等应用场景。
多边形填充算法的目标是根据设计要求和用户输入,给定一个多边形的边界,将多边形的内部区域进行颜色填充。
填充算法的实现涉及到图像的扫描线和区域判定,以确定填充的区域和颜色。
在本文中,我们将介绍常见的多边形填充算法,包括扫描线填充算法、边界填充算法等,并讨论它们的优缺点和适用场景。
扫描线填充算法扫描线填充算法是一种常见且简单的多边形填充算法。
该算法将多边形划分为一条条水平扫描线,并通过判断扫描线与多边形边界的交点,确定填充区域。
具体步骤如下:1.找到多边形边界的最上端和最下端。
2.从最上端开始,逐行进行扫描。
3.在每一行,通过求解扫描线与多边形边界的交点,确定填充区域。
4.对于每个填充区域,根据设计要求进行颜色填充。
扫描线填充算法的优点是简单易懂、实现较为容易。
然而,该算法存在一些缺点。
首先,对于具有复杂形状的多边形,扫描线填充算法可能会产生很多不必要的计算,导致效率降低。
其次,该算法需要处理多边形边界相交的情况,可能出现像素重复填充的问题,需要进行额外的处理。
边界填充算法边界填充算法是另一种常见的多边形填充算法。
与扫描线填充算法不同的是,边界填充算法是从多边形的边界出发,向内部填充颜色。
该算法的基本思想是对多边形的每条边进行填充,最终得到多边形的填充区域。
具体步骤如下:1.遍历多边形的每条边,保存每条边的起点和终点。
2.对于每个边,根据设计要求进行颜色填充。
3.对于多边形内部的区域,根据边界的颜色填充。
边界填充算法的优点是适用于复杂形状的多边形,无需处理边界相交的问题。
然而,该算法的实现相对复杂,需要处理边界的细化以及边缘像素重复填充的问题。
适用场景不同的多边形填充算法在不同场景下有不同的适用性。

多边形的扫描转换与区域填充在计算机图形学中,多边形有两种重要的表示方法:顶点表示和点阵表示。
顶点表示是用多边形的顶点序列来表示多边形。
这种表示直观、几何意义强、占内存少,易于进行几何变换,但由于它没有明确指出哪些象素在多边形内,故不能直接用于面着色;点阵表示是用位于多边形内的象素集合来刻画多边形。
这种表示丢失了许多几何信息,但便于帧缓冲器表示图形,是面着色所需要的图形表示形式。
光栅图形的一个基本问题是把多边形的顶点表示转换为点阵表示,这种转换称为多边形的扫描转换。
区域填充则是指先将在点阵表示的多边形区域内的一点(称为种子点)赋予指定的颜色和灰度,然后将这种颜色和灰度扩展到整个区域内的过程。
多边形的扫描转换多边形扫描转换算法对多边形的形状没有限制,但多边形的边界必须时封闭的,且不自交。
我们可以将多边形分为三种:凸多边形、凹多边形、含内环的多边形。
所谓凸多边形是指任意两顶点间的连线均在多边形内;凹多边形是指任意两顶点间的连线有不在多边形内的部分;而含内环的多边形则是指多边形内再套有多边形,多边形内的多边形也叫内环,内环之间不能相交。
多边形的扫描转换与区域填充扫描线算法:扫描线算法是按扫描线顺序,计算扫描线与多边形的相交区间,再用要求的颜色显示这些区间的象素,完成转换工作。
区间的端点可以通过计算扫描线与多边形边界线的交点获得。
对于一条扫描线,多边形的扫描转换过程可以分为四个步骤:(1)求交:计算扫描线与多边形各边的交点;(2)排序:把所有交点按x值递增顺序排序;(3)配对:第一个与第二个,第三个与第四个等等;每对交点代表扫描线与多边形的一个相交区间,(4)着色:把相交区间内的象素置成多边形颜色,把相交区间外的象素置成背景色。
图2.3.2 一个多边形与若干扫描线为了提高效率,在处理一条扫描线时,仅对与它相交的多边形的边进行求交运算。
我们把与当前扫描线相交的边称为活性边,并把它们按与扫描线交点x坐标递增的顺序存放在一个链表中,称此链表为活性边表(AET)。
