对数专题(相关资料及练习)

对数及其运算基础知识及例题1、定义：对数是指用一个数b（b>0且不等于1）作为底数，将一个正数a表示成幂b的指数的形式，即a=b^x（x为实数），则x称为以b为底a的对数，记作logb a。

2、性质：①logb 1=0（b>0且不等于1）②logb b=1（b>0且不等于1）③logb (mn)=logb m+logb n（m>0，n>0，b>0且不等于1）④logb (m/n)=logb m-logb n（m>0，n>0，b>0且不等于1）⑤logb m^k=klogb m（m>0，b>0且不等于1，k为任意实数）3、对数的运算性质：①logb (mn)=logb m+logb n②logb (m/n)=logb m-logb n③logb m^k=klogb m④logb (a^k)=klogb a⑤logb a=logc a/logc b（b>0，且不等于1，c>0，且不等于1）4、换底公式：XXX b（b>0，且不等于1，c>0，且不等于1）5、对数的其他运算性质：①logb a=logb c，则a=c②logb a=logc a/logc b=logd a/logd b6、常用对数和自然对数：常用对数：以10为底数的对数，记作XXX。

自然对数：以自然常数e（e≈2.）为底数的对数，记作ln。

典型例题】类型一、对数的概念例1.求下列各式中x的取值范围：1）log2(x-5)≥0；（2）log(x-1)-log(x+2)0.改写为：1）x≥5；2）x>1且x<2；3）x>1且x1且x>1.类型二、指数式与对数式互化及其应用例2.将下列指数式与对数式互化：1)log2 16=4；(2)log1/27=-3；(3)log3 1/2= -1/log2 3；(4)53=125；(5)2^-1=1/2；(6)(1/3)^x=9.改写为：1)2^4=16；2)1/27=3^-3；3)3^-1/2=2/log2 3；4)5^3=125；5)2^-1=1/2；6)x=log(1/3)9/log(1/3)2.类型三、利用对数恒等式化简求值1+log5 77=log5 500.类型四、积、商、幂的对数例4.用loga x,loga y,loga z表示下列各式：1)loga (xy/z)=loga x+loga y-loga z；2)loga (xy)=loga x+loga y；3)loga (x^2/y^3z)=2loga x-3loga y-loga z；4)loga (x^2y^3/z)=2loga x+3loga y-loga z。

对数与对数运算练习题在数学中，对数是解决指数问题的一种重要工具。

对数运算是指对数之间的各种运算，包括加法、减法、乘法和除法等。

本文将提供一些对数与对数运算的练习题，以帮助读者更好地理解和掌握这一概念。

练习题一：基础对数运算1. 计算 log₄ 16。

2. 计算 log₂ 8 + log₄ 2。

3. 计算 log₃ 9 - log₅ 125。

4. 计算 log₁₀ 100 - log₁₀ 10。

练习题二：对数的性质运用1. 若logₓ y = 3，计算logₓ √y 的值。

2. 若logₓ y = a，logₓ z = b，求logₓ (yz) 的值。

3. 若logₐ b = x，logₓ b = y，求logₐ x 的值。

4. 若 log₂ a = m，log₂ b = n，求logₐ (ab) 的值。

练习题三：对数方程的求解1. 解方程logₓ (x - 2) = 1。

2. 解方程 log₂ (3x + 1) = log₂ (2x - 4)。

3. 解方程 log₄ (x² - 5x + 4) = 2。

练习题四：对数运算的应用1. 在化学实验中，若酸的浓度 c 可以表示为 pH = -log₁₀ c，若某酸的浓度为 10⁻⁴ mol/L，求其 pH 值。

2. 若一座大楼的高度 H 可以表示为 H = log₂ (t + 5) + 10，其中 t 为某物体从大楼顶部自由下落所需时间（单位：秒），求当 t = 2 时，大楼的高度 H。

以上是对数与对数运算的练习题，通过解题的过程，我们可以更好地理解对数的概念及其运算规律。

希望这些练习题能够帮助读者提高对数的应用能力，并在数学学习中取得更好的成绩。

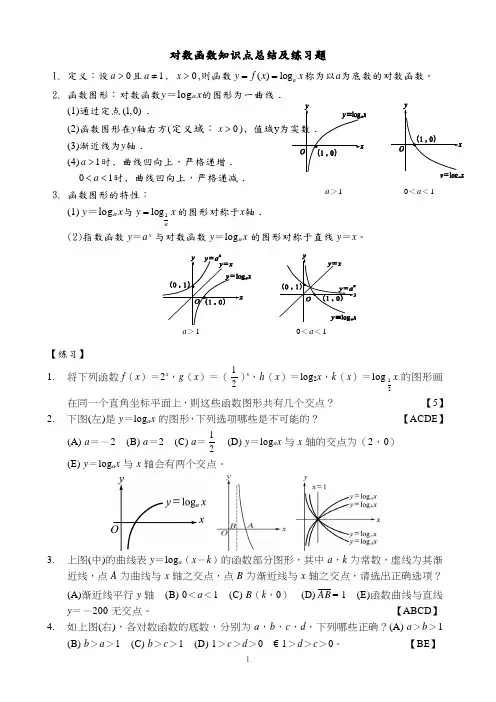
１对数函数知识点总结及练习题1. 定义：设0a >且1a ≠﹐0x >,则函数()log a y f x x ==称为以a 为底数的对数函数。

2. 函数图形：对数函数y ＝log a x 的图形为一曲线﹒(1)通过定点(1,0)﹒(2)函数图形在y 轴右方(定义域：0x >)﹐值域y 为实数﹒(3)渐近线为y 轴﹒(4)1a >时﹐曲线凹向上，严格递增﹒01a <<时﹐曲线凹向上，严格递减﹒3. 函数图形的特性：(1) y ＝log a x 与1log a y x =的图形对称于x 轴﹒(2)指数函数 y ＝a x 与对数函数 y ＝log a x 的图形对称于直线 y ＝x 。

【练习】 1. 将下列函数 f （x ）＝2x ，g （x ）＝（21）x ，h （x ）＝log 2x ，k （x ）＝log 21x 的图形画在同一个直角坐标平面上，则这些函数图形共有几个交点？ 【5】2. 下图(左)是 y ＝log a x 的图形，下列选项哪些是不可能的？ 【ACDE 】(A) a ＝－2 (B) a ＝2 (C) a ＝21 (D) y ＝log a x 与 x 轴的交点为（2，0） (E) y ＝log a x 与 x 轴会有两个交点。

3. 上图(中)的曲线表 y ＝log a （x －k ）的函数部分图形，其中 a ，k 为常数，虚线为其渐近线，点 A 为曲线与 x 轴之交点，点 B 为渐近线与 x 轴之交点，请选出正确选项？(A)渐近线平行 y 轴 (B) 0＜a ＜1 (C) B （k ，0） (D)AB = 1 (E)函数曲线与直线 y ＝－200 无交点。

【ABCD 】4. 如上图(右)，各对数函数的底数，分别为 a ，b ，c ，d ，下列哪些正确？(A) a ＞b ＞1(B) b ＞a ＞1 (C) b ＞c ＞1 (D) 1＞c ＞d ＞0 € 1＞d ＞c ＞0。

4．3对数4．3.1对数的概念1．对数(1)指数式与对数式的互化及有关概念：(2)底数a的范围是a>0，且a≠1．2．常用对数与自然对数3．对数的基本性质(1)负数和零没有对数．(2)log a1＝0(a>0，且a≠1)．(3)log a a＝1(a>0，且a≠1)．1．log b N＝a(b>0，b≠1，N>0)对应的指数式是() A．a b＝N B．b a＝N C．a N＝b D．b N＝aB解析：因为log b N＝a，所以b a＝N.2．若a2＝M(a>0，且a≠1)，则有()A．log2M＝a B．log a M＝2 C．log22＝M D．log2a＝M B解析：∵a2＝M，∴log a M＝2.3．若log3x＝3，则x＝()A．1 B．3C．9 D．27D 解析：∵log 3x ＝3，∴x ＝33＝27. 4．ln 1＝________，lg 10＝________．0 1 解析：∵log a 1＝0，∴ln 1＝0.又log a a ＝1，∴lg 10＝1. 5．已知log x 16＝2，则x ＝________．4 解析：因为log x 16＝2，所以x 2＝16，所以x ＝±4.又x >0，且x ≠1，所以x ＝4.【例1】(1)对数式log (x －2)(x ＋2)中实数x 的取值范围是________． (2)已知4a ＝2，lg x ＝a ，则x ＝________.(1)(2，3)∪(3，＋∞) (2)10 解析：(1)由题意可得⎩⎪⎨⎪⎧x ＋2>0，x －2>0，x －2≠1，解得x >2，且x ≠3，所以实数x 的取值范围是(2，3)∪(3，＋∞)．(2)因为4a ＝2，所以a ＝12.又lg x ＝a ，所以x ＝10a ＝10.指数式与对数式互化的方法(1)将指数式化为对数式，只需要将幂作为真数，指数当成对数值，底数不变，写出对数式．(2)将对数式化为指数式，只需将真数作为幂，对数作为指数，底数不变，写出指数式．将下列指数式与对数式互化： (1)log 216＝4；(2)log 1327＝－3；(3)log 3x ＝6；(4)43＝64； (5)3－2＝19；(6)⎝⎛⎭⎫14－2＝16.解：(1)24＝16.(2)⎝⎛⎭⎫13－3＝27. (3)(3)6＝x . (4)log 464＝3. (5)log 319＝－2.(6)log 1416＝－2.【例2】求下列各式中的x 的值． (1)log x 27＝32；(2)log 2x ＝－23；(3)x ＝log 2719；(4)x ＝log 1216.解：(1)由log x 27＝32，可得x 32＝27，∴x ＝2723＝(33)23＝32＝9.(2)由log 2x ＝－23，可得x ＝2－23，∴x ＝⎝⎛⎭⎫1223＝314＝322.(3)由x ＝log 2719，可得27x ＝19，∴33x ＝3－2，∴x ＝－23.(4)由x ＝log 1216，可得⎝⎛⎭⎫12x＝16， ∴2－x ＝24，∴x ＝－4.利用指数式与对数式的互化求变量值的策略(1)若已知的式子为指数式，则直接利用指数运算求值． (2)若已知的式子为对数式，则先把对数式化为指数式，再求值．1．已知log 2m ＝2.016，log 2n ＝1.016，则nm 等于( )A ．2 B.12 C ．10 D.110B 解析：因为log 2m ＝2.016，log 2n ＝1.016， 所以m ＝22.016，n ＝21.016，所以n m ＝21.01622.016＝12.2．已知log a 2＝m ，log a 3＝n ，则a 2m －n ＝________． 43解析：因为log a 2＝m ，log a 3＝n ， 所以a m ＝2，a n ＝3， 所以a 2m －n ＝a 2m a n ＝223＝43.探究题1 求下列各式中x 的值． (1)log 5(log 3x )＝0； (2)log 3(lg x )＝1； (3)ln[log 2(lg x )]＝0.解：(1)设t ＝log 3x ，则log 5t ＝0，∴t ＝1， 即log 3x ＝1，∴x ＝3.(2)∵log 3(lg x )＝1，∴lg x ＝3，∴x ＝103＝1 000. (3)∵ln[log 2(lg x )]＝0，∴log 2(lg x )＝1， ∴lg x ＝2，∴x ＝102＝100.探究题2 若log 2[log 3(log 4x )]＝log 3[log 4(log 2y )]＝0，求x ＋y 的值． 解：∵log 2(log 3(log 4x ))＝0，∴log 3(log 4x )＝1，∴log 4x ＝3.∴x ＝43＝64. 同理求得y ＝16.∴x ＋y ＝80.1．利用对数的性质求解的两类问题(1)求多重对数式的值应由内到外，如求log a (log b c )的值，先求log b c 的值，再求log a (log b c )的值．(2)已知多重对数式的值，求变量值，应从外到内，逐步脱去“log ”后再求解． 2．性质a log a N ＝N 与log a a b ＝b 的作用(1)a log a N ＝N 能把任意一个正实数转化为以a 为底的指数形式． (2)log a a b ＝b 能把以a 为底的指数转化为一个实数．1．计算下列各式的值． (1)2512log 54＝________．(2)31＋log32＝________．(1)4 (2)6 解析：(1)2512log 54＝(52)12log 54＝5 log 54＝4.(2)31＋log32＝3×3 log 32＝3×2＝6.2．求下列各式中的x . (1)ln 2x －ln x ＝0； (2)log 7[log 3(log 2x )]＝0.解：(1)因为ln 2x －ln x ＝0，所以ln x (ln x －1)＝0， 所以ln x ＝1或ln x ＝0， 所以x ＝e 或x ＝1.(2)由题意，log 3(log 2x )＝1，故log 2x ＝3， 所以x ＝23＝8.对数的概念练习 (30分钟 60分)1.(5分)在log3(m －1)中，实数m 的取值范围是( ) A ．R B ．(0，＋∞)C．(－∞，1) D．(1，＋∞)D解析：由m－1>0得m>1，故选D.2．(5分)下列指数式与对数式互化不正确的一组是()A．100＝1与lg 1＝0B．27－13＝13与log2713＝－13C．log39＝2与912＝3D．log55＝1与51＝5C解析：C不正确，由log39＝2可得32＝9.3．(5分)log(2＋1)(3－22)等于()A．－2 B．－4C．2 D．4A解析：3－22＝2－22＋1＝(2)2－22＋12＝(2－1)2＝12＋12＝(2＋1)－2.设log(2＋1)(3－22)＝t，则(2＋1)t＝3－22＝(2＋1)－2，∴t＝－2.4．(5分)若3x＝2，则x等于()A．log23B．log32C．32 D．23B解析：3x＝2⇔x＝log32.5．(5分)方程2log3x＝14的解是()A．x＝19 B．x＝33C．x＝3 D．x＝9A解析：∵2 log3x＝2－2，∴log3x＝－2，∴x＝3－2＝19.6．(5分)下列四个等式：①lg(lg 10)＝0；②lg(ln e)＝0；③若lg x＝10，则x＝10；④若ln x＝e，则x＝e2.其中正确的是()A．①③B．②④C．①②D．③④C解析：①lg(lg 10)＝lg 1＝0；②lg(ln e)＝lg 1＝0；③若lg x＝10，则x＝1010；④若ln x ＝e，则x＝ee.7.(5分)设a＝log310，b＝log37，则3a－b＝________．107解析：∵a＝log310，b＝log37，∴3a＝10，3b＝7，∴3a－b＝3a3b＝107.8.(5分)已知f(log2x)＝x，则f12＝________．2解析：令log2x＝12，则x＝212＝2，即f12＝f(log22)＝2.9.(5分)已知x＝log23，则23x－2－3x2x－2－x＝________．919解析：由x＝log23，得2x＝3，∴2－x＝12x＝13，23x＝(2x)3＝33＝27，2－3x＝123x＝127，∴23x－2－3x2x－2－x＝27－1273－13＝272－13×27－9＝72872＝919.10.(5分)求值．(1)912log34；(2)51＋log52.解：(1)912log34＝(32) 12log34＝3 log34＝4.(2)51＋log52＝5×5 log52＝5×2＝10.11.(10分)若log12x＝m，log14y＝m＋2，求x2y的值．解：∵log12x＝m，∴12m＝x，x2＝122m.∵log14y＝m＋2，∴14m＋2＝y，即y＝122m＋4，∴x2y＝122m122m＋4＝122m－（2m＋4）＝12－4＝16.。

高中数学《对数》精选练习（含详细解析）一、选择题1.已知lo b=c,则有( )A.a2b=cB.a2c=bC.b c=2aD.c2a=b2.下列指数式与对数式互化不正确的一组是( )A.e0=1与ln1=0B.log8=-与=C.log39=2与=3D.log88=1与81=83.已知x2+y2-4x-2y+5=0,则log x(y x)的值为( )A.xB.yC.1D.04.使log(3a-1)(4-a)有意义的a的取值是( )A.<a<4B.<a<4且a≠C.a<4D.a>5.已知f(3x)=log2,则f(1)的值为( )A.1B.2C.-1D.6如果f(e x)=x,则f(e)= ( )A.1B.eC.2eD.e2二、填空题7若log2[lg(lnx)]=0,则x= .8有以下四个结论:①lg(lg10)=0;②lg(lne)=0;③若e=lnx,则x=e2;④ln(lg1)=0.其中正确的是( )A.①②B.①②③C.①②④D.②③④9计算+= .10若x>0,x2=,则= .11化简:lo(+)= .三、解答题12设log a2=m,log a3=n,求a3m+2n的值.13设M={0,1},N={lga,2a,a,11-a},是否存在a的值,使M∩N={1}?参考答案与解析1【解析】选B.根据指数与对数的关系的转化,有(a2)c=b,即a2c=b.2【解析】选C.由指数与对数的互化关系:a x=N⇔x=log a N可知A,B,D都正确,C中log39=2⇔32=9,所以C项错误.3【解析】选 D.由于x2+y2-4x-2y+5=0可得(x-2)2+(y-1)2=0,则x=2,y=1.故log x(y x)=log2(12)=0.4【解析】选B.由对数的定义可知解得<a<4且a≠.5【解析】选D.由f(3x)=log2,得f(x)=log2,f(1)=log2=.6【解析】选A.令e x=t,则x=lnt,所以f(t)=lnt.故f(e)=lne=1.7【解析】因为log2[lg(lnx)]=0.所以lg(lnx)=20=1,所以10=lnx,所以e10=x.答案:e108【解析】选A.可根据对数、常用对数和自然对数的概念以及对数式与指数式的转化,对各结论进行判断.由于1的对数等于0,底数的对数等于1,所以可判断①②均正确;③中应得到x=e e,故③错误;④中由于lg1=0,而0没有对数,所以此式不成立.综上可知,正确的结论是①②.9【解析】+=23×+=8×3+=25.答案:2510【解析】由x>0,x2=,可知x=,所以==.答案:11【解析】设lo(+)=x,则(-)x=+,又因为+=,所以x=-1.答案:-112【解题指南】将log a2=m,log a3=n表示成指数式,然后结合幂的运算性质进行运算.【解析】因为log a2=m,log a3=n,所以a m=2,a n=3,所以a3m+2n=(a m)3×(a n)2=23×32=8×9=72.13【解析】不存在a的值,使M∩N={1}成立.若lga=1,则a=10,此时11-a=1,从而11-a=lga=1,与集合元素的互异性矛盾; 若2a=1,则a=0,此时lga无意义;若a=1,此时lga=0,从而M∩N={0,1},与条件不符;若11-a=1,则a=10,从而lga=1,与集合元素的互异性矛盾.。

4.3.2 对数的运算1．对数运算性质如果a >0，且a ≠1，M >0，N >0，那么 (1)log a (MN )＝log a M ＋log a N ； (2)log a MN ＝log a M －log a N ；(3)log a M n ＝n log a M (n ∈R)． 2．换底公式若a >0，且a ≠1，b >0，c >0，且c ≠1， 则有log a b ＝log c blog c a．1．计算log 84＋log 82等于( ) A ．log 86 B ．8 C ．6D ．1D 解析：log 84＋log 82＝log 88＝1. 2．计算log 510－log 52等于( ) A ．log 58 B ．lg 5 C ．1D ．2 C 解析：log 510－log 52＝log 55＝1. 3．计算2log 510＋log 50.25＝( ) A ．0 B ．1 C ．2D ．4 C 解析：2log 510＋log 50.25＝log 5100＋log 50.25＝log 525＝2. 4．计算log 23·log 32＝________． 1 解析：log 23·log 32＝lg 3lg 2×lg 2lg 3＝1. 5．计算log 225·log 322·log 59＝________． 6 解析：原式＝lg 25lg 2·lg 22lg 3·lg 9lg 5＝2lg 5lg 2·32lg 2lg 3·2lg 3lg 5＝6.【例1】(1)若lg 2＝a ，lg 3＝b ，则lg 45lg 12＝( ) A.a ＋2b 2a ＋b B.1－a ＋2b 2a ＋bC.1－b ＋2a 2a ＋bD.1－a ＋2b a ＋2b(2)计算：lg 52＋2lg 2－⎝⎛⎭⎫12－1＝________．(1)B (2)－1 解析：(1)lg 45lg 12＝lg 5＋lg 9lg 3＋lg 4＝1－lg 2＋2lg 3lg 3＋2lg 2＝1－a ＋2b2a ＋b .(2)lg 52＋2lg 2－⎝⎛⎭⎫12－1＝lg 5－lg 2＋2lg 2－2＝(lg 5＋lg 2)－2＝1－2＝－1.【例2】计算：(1)log 345－log 35； (2)log 2(23×45)；(3)lg 27＋lg 8－lg 1 000lg 1.2；(4)log 29·log 38.解：(1)log 345－log 35＝log 3455＝log 39＝log 332＝2.(2)log 2(23×45)＝log 2(23×210)＝log 2(213) ＝13log 22＝13. (3)原式＝lg （27×8）－lg 1032lg 1210＝lg （332×23÷1032）lg 1210＝lg⎝⎛⎭⎫3×41032lg 1210＝32lg1210lg 1210＝32.(4)log 29·log 38＝log 232·log 323 ＝2log 23·3log 32＝6log 23·1log 23＝6.利用对数运算性质化简与求值的原则和方法(1)基本原则：①正用或逆用公式，对真数进行处理；②选哪种策略化简，取决于问题的实际情况，一般本着便于化简的原则进行． (2)两种常用的方法：①“收”，将同底的两对数的和(差)收成积(商)的对数； ②“拆”，将积(商)的对数拆成同底的两对数的和(差)．提醒：对于对数的运算性质要熟练掌握，并能够灵活运用，在求值过程中，要注意公式的正用和逆用．计算下列各式的值： (1)12lg 3249－43lg 8＋lg 245； (2)lg 52＋23lg 8＋lg 5·lg 20＋(lg 2)2；(3)lg 2＋lg 3－lg 10lg 1.8.解：(1)原式＝12(5lg 2－2lg 7)－43×32lg 2＋12(2lg 7＋lg 5)＝52lg 2－lg 7－2lg 2＋lg 7＋12lg 5＝12lg 2＋12lg 5＝12(lg 2＋lg 5) ＝12lg 10＝12. (2)原式＝2lg 5＋2lg 2＋lg 5(2lg 2＋lg 5)＋(lg 2)2 ＝2lg 10＋(lg 5＋lg 2)2＝2＋(lg 10)2＝2＋1＝3. (3)原式＝12（lg 2＋lg 9－lg 10）lg 1.8＝lg 18102lg 1.8＝lg 1.82lg 1.8＝12.【例3】已知log 189＝a ，18b ＝5，求log 3645. 解：因为18b ＝5，所以log 185＝b . (方法一)log 3645＝log 1845log 1836＝log 18（9×5）log 181829＝log 189＋log 1852log 1818－log 189＝a ＋b2－a.(方法二)因为lg 9lg 18＝log 189＝a ， 所以lg 9＝a lg 18，同理得lg 5＝b lg 18， 所以log 3645＝lg 45lg 36＝lg （9×5）lg 1829＝lg 9＋lg 52lg 18－lg 9＝a lg 18＋b lg 182lg 18－a lg 18＝a ＋b2－a.应用换底公式应注意的两个方面(1)化成同底的对数时，要注意换底公式的正用、逆用以及变形应用． (2)题目中有指数式和对数式时，要注意将指数式与对数式统一成一种形式．1．已知2x ＝3y ＝a ，且1x ＋1y ＝2，则a 的值为( )A ．36B ．6C ．2 6 D. 6D 解析：因为2x ＝3y ＝a ， 所以x ＝log 2a ，y ＝log 3a ，所以1x ＋1y ＝1log 2a ＋1log 3a ＝log a 2＋log a 3＝log a 6＝2，所以a 2＝6，解得a ＝±6.又a ＞0，所以a ＝ 6. 2．求值：(1)log 23·log 35·log 516； (2)(log 32＋log 92)(log 43＋log 83)．解：(1)原式＝lg 3lg 2·lg 5lg 3·lg 16lg 5＝lg 16lg 2＝4lg 2lg 2＝4.(2)原式＝⎝⎛⎭⎫lg 2lg 3＋lg 2lg 9⎝⎛⎭⎫lg 3lg 4＋lg 3lg 8 ＝⎝⎛⎭⎫lg 2lg 3＋lg 22lg 3⎝⎛⎭⎫lg 32lg 2＋lg 33lg 2 ＝3lg 22lg 3·5lg 36lg 2＝54.探究题1 若log 23＝a ，log 25＝b ，则用a ，b 表示log 415＝________． a ＋b 2 解析：log 415＝log 215log 24＝log 23＋log 252＝a ＋b2.探究题2 已知3a ＝5b ＝c ，且1a ＋1b ＝2，求c 的值．解：∵3a ＝5b ＝c ， ∴a ＝log 3c ，b ＝log 5c ， ∴1a ＝log c 3，1b＝log c 5， ∴1a ＋1b ＝logc 3＋log c 5＝log c 15＝2. 得c 2＝15， 即c ＝15.解决对数的运算问题，主要依据是对数的运算性质．常用方法有： (1)将真数化为“底数”；(2)将同底数的对数的和、差、倍合并； (3)利用常用对数中的lg 2＋lg 5＝1.已知x ，y ，z 为正数，3x ＝4y ＝6z ，且2x ＝py . (1)求p 的值； (2)证明：1z －1x ＝12y.解析：设3x ＝4y ＝6z ＝k (显然k ＞0，且k ≠1)，则x ＝log 3k ，y ＝log 4k ，z ＝log 6k .(1)由2x ＝py ，得2log 3k ＝p log 4k ＝p ·log 3klog 34，因为log 3k ≠0，所以p ＝2log 34＝4log 32. (2)证明：1z －1x ＝1log 6k －1log 3k＝log k 6－log k 3＝log k 2＝12log k 4＝12y .对数的运算练习(30分钟60分)1.(5分)计算：log153－log62＋log155－log63＝()A．－2B．0C．1 D．2B解析：原式＝log15(3×5)－log6(2×3)＝1－1＝0.2．(5分)设10a＝2，lg 3＝b，则log26＝()A.baB.a＋baC．ab D．a＋bB解析：∵10a＝2，∴lg 2＝a，∴log26＝lg 6lg 2＝lg 2＋lg 3lg 2＝a＋ba.3．(5分)设a，b，c均为不等于1的正实数，则下列等式中恒成立的是() A．logab•logcb＝logcaB．logab•logca＝logcbC．loga(bc)＝logab•logacD．loga(b＋c)＝logab＋logacB解析：由logab•logcb＝lg blg a•lg blg c≠logca，故A错；由logab•logca＝lg blg a•lg alg c ＝lg blg c＝logcb；loga(bc)＝logab＋logac，故C，D错．故选B.4．(5分)如果lg x＝lg a＋3lg b－5lg c，那么()A．x＝ab3c5 B．x＝3ab5cC．x＝a＋3b－5c D．x＝a＋b3－c3A解析：lg a＋3lg b－5lg c＝lg a＋lg b3－lg c5＝lgab3c5，由lg x＝lgab3c5，可得x＝ab3c5. 5．(5分)log2 4等于()A.12B.14C．2 D．4D解析：log2 4＝log2 (2)4＝4.6．(5分)已知lg 2＝a，lg 3＝b，则用a，b表示lg 15为()A．b－a＋1B．b(a－1)C．b－a－1D．b(1－a)A解析：lg 15＝lg(3×5)＝lg 3＋lg 5＝lg 3＋lg 102＝lg 3＋1－lg 2＝b－a＋1.7.(5分)方程lg x＋lg(x＋3)＝1的解是x＝________．2解析：原方程可化为lg(x2＋3x)＝1，∴x>0，x＋3>0，x2＋3x－10＝0，解得x＝2.8.(5分)若3x＝4y＝36，则2x＋1y＝________．1解析：3x＝4y＝36，两边取以6为底的对数，得xlog63＝ylog64＝2，∴2x＝log63，2y＝log64，即1y＝log62，故2x＋1y＝log63＋log62＝1.9.(5分)已知log23＝a，log37＝b，则log1456＝________(用a，b表示)．3＋ab1＋ab解析：由log23＝a，log37＝b，得log27＝ab，则log1456＝log256log214＝log28＋log27log22＋log27＝3＋log271＋log27＝3＋ab1＋ab. 10.(15分)计算．(1)log535－2log573＋log57－log51.8；(2)log2748＋log212－12log242－1.解：(1)原式＝log5(5×7)－2(log57－log53)＋log57－log595＝log55＋log57－2log57＋2log53＋log57－2log53＋log55＝2.(2)原式＝log2748＋log212－log242－log22＝log27×1248×42×2＝log2122＝log22－23＝－32.。

专题：对数运算题型一：对数概念的理解：例1：求下列各式中得x 取值范围（1）)10(2log -x （2）)2()1(log +-x x变式练习：求下列各式中得x 值（1）812log = （2）=421log （3）若4log 16-=x，求x 值题型二：对数式与指数式的转化例2：对数式与指数式的转化（1）62554= （2）3log 82= （3）16)41(2=- 变式练习：对数式与指数式的转化（1）2log 01.01.0= （2）32)32(1-=+-题型三：化简与求值例3：求下列各式的值（1）32log 318- （2）)32(2)32(2log log -++变式练习：（1）40lg 50lg 8lg 5lg 2lg --+= （2）若,3010.02lg =求5lg（3）设3643==y x ，求yx 12+的值 题型四：换底公式的应用 例4：（1）求32log 9log 278∙的值 （2）求证z z y x y x log log log =⋅变式练习：（1）计算5log 4log 85⋅（2）已知b a ==4log ,3log 55，求：12log 25 (用a,b 表示)应用练习：1．若log x (2＋1)=－1, 则x = 。

2．已知f (e x )=x ，则f (5)等于 。

3．对数式)5(log )2(a a -- 中实数a 的取值范围是 。

4．若10≤x ≤100, 则｜3－lg x ｜－4)x lg(x lg 42+-= 。

5．已知集合A={y|y=log 2 x,x>1},B={y|y=(21)x ,x>1},则A ⋂B 等于 。

6．已知函数f (x )=⎪⎩⎪⎨⎧<+≥)4()1()4()21(x x f x x , 则f (log 23)=_________7．已知 log 18 9=a ,18b =5：用a , b 表示 log 36 45。

对数与对数函数1.对数（1）对数的定义：如果a b =N （a ＞0，a ≠1），那么b 叫做以a 为底N 的对数，记作log a N =b . （2）指数式与对数式的关系：a b =N log a N =b （a ＞0，a ≠1，N ＞0）.两个式子表示的a 、b 、N 三个数之间的关系是一样的，并且可以互化. （3）对数运算性质: ①log a （MN ）=log a M +log a N . ②log a NM =log a M －log a N .③log a M n =n log a M .（M ＞0，N ＞0，a ＞0，a ≠1） ④对数换底公式：log b N =bNa a log log （a ＞0，a ≠1，b ＞0，b ≠1，N ＞0）.2.对数函数（1）对数函数的定义函数y =log a x （a ＞0，a ≠1）叫做对数函数，其中x 是自变量，函数的定义域是（0，+∞）.注意：真数式子没根号那就只要求真数式大于零,如果有根号,要求真数大于零还要保证根号里的式子大于零，底数则要大于0且不为1对数函数的底数为什么要大于0且不为1呢？在一个普通对数式里 a<0,或=1 的时候是会有相应b 的值的。

但是，根据对数定义: log a a=1；如果a=1或=0那么log a a 就可以等于一切实数（比如log 1 1也可以等于2，3，4，5，等等）第二，根据定义运算公式：log a M^n = nlog a M 如果a<0,那么这个等式两边就不会成立 （比如，log (-2) 4^(-2) 就不等于(-2)*log (-2) 4；一个等于1/16，另一个等于-1/16） （2）对数函数的图象x y> Oxy<a <y = l o g x a 111()) x 轴对称.（3）对数函数的性质: ①定义域：（0，+∞）. ②值域：R .③过点（1，0），即当x =1时，y =0.④当a ＞1时，在（0，+∞）上是增函数；当0＜a ＜1时，在（0，+∞）上是减函数.基础例题1.函数f （x ）=|log 2x |的图象是11xy y y y OA BC D解析：f （x ）=⎩⎨⎧<<-≥.10,log ,1,log 22x x x x答案：A2.若f －1（x ）为函数f （x ）=lg （x +1）的反函数，则f －1（x ）的值域为___________________.解析：f －1（x ）的值域为f （x ）=lg （x +1）的定义域.由f （x ）=lg （x +1）的定义域为（－1，+∞），∴f －1（x ）的值域为（－1，+∞）. 答案：（－1，+∞）3.已知f （x ）的定义域为［0，1］，则函数y =f ［log 21（3－x ）］的定义域是__________.解析：由0≤log 21（3－x ）≤1⇒log 211≤log 21（3－x ）≤log 2121⇒21≤3－x ≤1⇒2≤x ≤25. 答案：［2，25］4.若log x 7y =z ，则x 、y 、z 之间满足A.y 7=x zB.y =x 7zC.y =7x zD.y =z x解析：由log x 7y =z ⇒x z =7y ⇒x 7z=y ，即y =x 7z . 答案：B5.已知1＜m ＜n ，令a =（log n m ）2，b =log n m 2，c =log n （log n m ），则A.a ＜b ＜cB.a ＜c ＜bC.b ＜a ＜cD.c ＜a ＜b解析：∵1＜m ＜n ，∴0＜log n m ＜1. ∴log n （log n m ）＜0. 答案：D6.若函数f （x ）=log a x （0＜a ＜1）在区间［a ，2a ］上的最大值是最小值的3倍，则a 等于 A.42B.22C.41D.21解析：∵0＜a ＜1，∴f （x ）=log a x 是减函数.∴log a a =3·log a 2a . ∴log a 2a =31.∴1+log a 2=31.∴log a 2=－32.∴a =42. 答案：A7.函数y ＝log 2｜ax －1｜（a ≠0）的对称轴方程是x ＝－2，那么a 等于A.21B.－21C.2D.－2解析：y =log 2|ax －1|=log 2|a （x －a1）|，对称轴为x =a1，由a1=－2 得a =－21. 答案：B注意：此题还可用特殊值法解决，如利用f （0）=f （－4）， 可得0=log 2|－4a －1|.∴|4a +1|=1.∴4a +1=1或4a +1=－1. ∵a ≠0，∴a =－21.8.函数f （x ）=log 2|x |，g （x ）=－x 2+2，则f （x ）·g （x ）的图象只可能是xyxyx yxyABC D解析：∵f （x ）与g （x ）都是偶函数，∴f （x ）·g （x ）也是偶函数，由此可排除A 、D.又由x →+∞时，f （x ）·g （x ）→－∞，可排除B. 答案：C9.设f －1（x ）是f （x ）=log 2（x +1）的反函数，若［1+ f －1（a ）］［1+ f －1（b ）］=8，则f （a +b ）的值为 A.1B.2C.3D.log 23解析：∵f －1（x ）=2x －1，∴［1+ f －1（a ）］［1+ f －1（b ）］=2a ·2b =2a +b .由已知2a +b =8，∴a +b =3. 答案：C10.方程lg x +lg （x +3）=1的解x =___________________. 解析：由lg x +lg （x +3）=1，得x （x +3）=10，x 2+3x －10=0. ∴x =－5或x =2.∵x ＞0，∴x =2. 答案：2典型例题【例1】 已知函数f （x ）=⎪⎩⎪⎨⎧<+≥,4),1(,4,)21(x x f x x则f （2+log 23）的值为 A.31B.61C.121D.241剖析：∵3＜2+log 23＜4，3+log 23＞4， ∴f （2+log 23）=f （3+log 23）=（21）3+log 23=241. 答案：D【例2】 求函数y ＝log 2｜x ｜的定义域，并画出它的图象，指出它的单调区间. 解：∵｜x ｜＞0，∴函数的定义域是｛x ｜x ∈R 且x ≠0｝.显然y ＝log 2｜x ｜是偶函数，它的图象关于y 轴对称.又知当x ＞0时，y ＝log 2｜x ｜⇔y ＝log 2x .故可画出y ＝log 2｜x ｜的图象如下图.由图象易见，其递减区间是（－∞，0），递增区间是（0，＋∞）.1-1O xy注意：研究函数的性质时，利用图象会更直观.【例3】 已知f （x ）=log 31［3－（x －1）2］，求f （x ）的值域及单调区间.解：∵真数3－（x －1）2≤3，∴log 31［3－（x －1）2］≥log 313=－1，即f （x ）的值域是［－1，+∞）.又3－（x－1）2＞0，得1－3＜x ＜1+3，∴x ∈（1－3，1］时，3－（x －1）2单调递增，从而f （x ）单调递减；x ∈［1，1+3）时，f （x ）单调递增.注意：讨论复合函数的单调性要注意定义域.【例4】已知y =log a （3－ax ）在［0，2］上是x 的减函数，求a 的取值范围. 解：∵a ＞0且a ≠1，∴t =3－ax 为减函数.依题意a ＞1，又t =3－ax 在［0，2］上应有t ＞0，∴3－2a ＞0.∴a ＜23.故1＜a ＜23.【例5】设函数f （x ）=lg （1－x ），g （x ）=lg （1+x ），在f （x ）和 g （x ）的公共定义域内比较|f （x ）|与|g （x ）|的大小. 解：f （x ）、g （x ）的公共定义域为（－1，1）. |f （x ）|－|g （x ）|=|lg （1－x ）|－|lg （1+x ）|.（1）当0＜x ＜1时，|lg （1－x ）|－|lg （1+x ）|=－lg （1－x 2）＞0； （2）当x =0时，|lg （1－x ）|－|lg （1+x ）|=0；（3）当－1＜x ＜0时，|lg （1－x ）|－|lg （1+x ）|=lg （1－x 2）＜0. 综上所述，当0＜x ＜1时，|f （x ）|＞|g （x ）|；当x =0时，|f （x ）|=|g （x ）|；当－1＜x ＜0时，|f （x ）|＜|g （x ）|. 【例6】 求函数y =2lg （x －2）－lg （x －3）的最小值.解：定义域为x ＞3，原函数为y ＝lg 3)2(2--x x .又∵3)2(2--x x ＝3442-+-x x x ＝31)3(2)3(2-+-+-x x x ＝（x －3）＋31-x ＋2≥4，∴当x ＝4时，y min ＝lg4.【例7】 （2003年北京宣武第二次模拟考试）在f 1（x ）=x 21，f 2（x ）=x 2，f 3（x ）=2x ，f 4（x ）=log 21x 四个函数中，x 1＞x 2＞1时，能使21［f （x 1）+f （x 2）］＜f （221x x +）成立的函数是A.f 1（x ）=x 21B.f 2（x ）=x 2C.f 3（x ）=2xD.f 4（x ）=log 21x解析：由图形可直观得到：只有f 1（x ）=x 21为“上凸”的函数. 答案：A探究创新1.若f （x ）=x 2－x +b ，且f （log 2a ）=b ，log 2［f （a ）］=2（a ≠1）. （1）求f （log 2x ）的最小值及对应的x 值；（2）x 取何值时，f （log 2x ）＞f （1）且log 2［f （x ）］＜f （1）？ 解：（1）∵f （x ）=x 2－x +b ，∴f （log 2a ）=log 22a －log 2a +b . 由已知有log 22a －log 2a +b =b ，∴（log 2a －1）log 2a =0. ∵a ≠1，∴log 2a =1.∴a =2.又log 2［f （a ）］=2，∴f （a ）=4. ∴a 2－a +b =4，b =4－a 2+a =2.故f （x ）=x 2－x +2， 从而f （log 2x ）=log 22x －log 2x +2=（log 2x －21）2+47.∴当log 2x =21即x =2时，f （log 2x ）有最小值47. （2）由题意⎪⎩⎪⎨⎧<+->+-2)2(log 22log log 22222x x x x ⇒⎩⎨⎧<<-<<>⇒21102x x x 或0＜x ＜1. 2.已知函数f （x ）=3x +k （k 为常数），A （－2k ，2）是函数y = f －1（x ）图象上的点.（1）求实数k 的值及函数f －1（x ）的解析式；（2）将y = f －1（x ）的图象按向量a =（3，0）平移，得到函数 y =g （x ）的图象，若2 f －1（x +m －3）－g （x ）≥1恒成立，试求实数m 的取值范围.解：（1）∵A （－2k ，2）是函数y = f －1（x ）图象上的点， ∴B （2，－2k ）是函数y =f （x ）上的点.∴－2k =32+k .∴k =－3. ∴f （x ）=3x －3.∴y = f －1（x ）=log 3（x +3）（x ＞－3）. （2）将y = f －1（x ）的图象按向量a =（3，0）平移，得到函数 y =g （x ）=log 3x （x ＞0），要使2 f －1（x +m －3）－g （x ）≥1恒成立，即使2log 3（x +m ）－log 3x ≥1恒成立，所以有x +xm +2m ≥3在x ＞0时恒成立，只要（x +xm +2m ）min ≥3.又x +xm ≥2m （当且仅当x =xm ，即x =m 时等号成立），∴（x +xm +2m ）min =4m ，即4m ≥3.∴m ≥169.小结1.对数的底数和真数应满足的条件是求解对数问题时必须予以特别重视的.2.比较几个数的大小是对数函数性质应用的常见题型.在具体比较时，可以首先将它们与零比较，分出正负；正数通常都再与1比较分出大于1还是小于1，然后在各类中间两两相比较.3.在给定条件下，求字母的取值范围是常见题型，要重视不等式知识及函数单调性在这类问题上的应用.。

对数函数专题——含参对数函数完整版题型汇总一、定义与性质1. 对数函数的定义对数函数是指定义域在正数集合上的函数，它的函数值是指数函数的反函数。

通常用符号 $\log$ 表示对数函数。

2. 对数函数的性质- 对数函数的图像是一条倾斜的曲线，与指数函数的图像关于直线 $y = x$ 对称。

- 对数函数具有单调递增性质，即随着自变量的增加，函数值也会增加。

- 对数函数的定义域是正数集合，值域是实数集合。

二、常见题型1. 对数运算题型例题：计算 $\log_3 27$。

解析：由于 $3^3 = 27$，所以 $\log_3 27 = 3$。

2. 对数方程题型例题：求解方程 $2^x = 8$。

解析：将 $8$ 表示成 $2$ 的幂次形式得到 $8 = 2^3$，所以$2^x = 2^3$，即 $x = 3$。

3. 对数不等式题型例题：求解不等式 $\log_2 \left( \frac{x}{3} \right) \geq 2$。

解析：根据对数定义，$\log_2 \left( \frac{x}{3} \right) \geq2$ 可转化为 $\frac{x}{3} \geq 2^2$，即 $\frac{x}{3} \geq 4$。

解得$x \geq 12$。

三、注意事项1. 在计算对数函数的值时，要注意指数与对数的关系，充分运用指数函数和对数函数的定义和性质。

2. 在解对数方程和不等式时，要注意将题目中的式子转化为指数形式，再进行相应的运算。

以上是对数函数专题中含参对数函数完整版题型汇总的简要内容。

对数函数作为数学中常见的函数之一，在应用中具有广泛的用途。

掌握对数函数的基本定义、性质和解题方法，有助于提高数学问题的解决能力。

对数的运算练习题一、对数的定义与性质对数是指数运算的逆运算。

如果 a^x = b，那么我们可以说 x 是以 a为底，以 b 为真数的对数，记作logₐb。

对数有一些重要的性质，我们在进行对数的运算练习题之前，需要先了解这些性质。

1. 对数的定义性质：对任意的正实数 a、b 和 c，以及任意的实数 x 和 y，满足以下等式：(1) a^logₐb = b(2) logₐ(a^x) = x2. 对数的运算性质：对于任意的正实数 a、b 和 c，满足以下等式：(1) logₐ(bc) = logₐb + logₐc(2) logₐ(b/c) = logₐb - logₐc(3) logₐ(b^c) = c logₐb二、对数运算练习题现在我们开始进行一些对数的运算练习题，以巩固我们对对数的理解和运用。

1. 计算以下各式中的对数：(1) log₂4 = ?(2) log₃9 = ?(3) log₅25 = ?(4) log₁₀100 = ?2. 计算以下各式中的底数：(1) 2^log₂7 = ?(2) 3^log₃(1/9) = ?(3) 4^log₄256 = ?3. 计算以下各式中的指数：(1) log₅125 = ?(2) log₇(1/49) = ?(3) log₀.₁₀1 = ?4. 进行对数的运算：(1) log₂8 + log₃27 = ?(2) log₄16 - log₂4 = ?(3) log₂3 + log₃2 = ?(4) log₅(1/25) + log₂(1/8) = ?5. 解方程：(1) log₄x = 2，求 x 的值。

(2) log₅(x + 1) = log₅3，求 x 的值。

(3) logₓ8 = 1/3，求 x 的值。

三、对数运算练习题的解答1. 解答：(1) log₂4 = 2，因为 2^2 = 4。

(2) log₃9 = 2，因为 3^2 = 9。

(3) log₅25 = 2，因为 5^2 = 25。

对数函数及其性质1．对数函数的概念(1)定义：一般地，我们把函数y ＝log a x (a ＞0，且a ≠1)叫做对数函数，其中x 是自变量，函数的定义域是(0，＋∞)．(2)对数函数的特征：特征⎩⎪⎨⎪⎧log a x 的系数：1log a x 的底数：常数，且是不等于1的正实数log a x 的真数：仅是自变量x判断一个函数是否为对数函数，只需看此函数是否具备了对数函数的特征．比如函数y ＝log 7x 是对数函数，而函数y ＝－3log 4x 和y ＝log x 2均不是对数函数，其原因是不符合对数函数解析式的特点．【例1－1】函数f (x )＝(a 2－a ＋1)log (a ＋1)x 是对数函数，则实数a ＝__________． 解析：由a 2－a ＋1＝1，解得a ＝0,1．又a ＋1＞0，且a ＋1≠1，∴a ＝1．答案：1 【例1－2】下列函数中是对数函数的为__________．(1)y ＝log (a ＞0，且a ≠1)；(2)y ＝log 2x ＋2；(3)y ＝8log 2(x ＋1)；(4)y ＝log x 6(x ＞0，且x ≠1)； (5)y ＝log 6x ． 解析：2．对数函数y ＝log a x (a ＞0，且a ≠1)的图象与性质(1)图象与性质谈重点对对数函数图象与性质的理解对数函数的图象恒在y轴右侧，其单调性取决于底数．a＞1时，函数单调递增；0＜a＜1时，函数单调递减．理解和掌握对数函数的图象和性质的关键是会画对数函数的图象，在掌握图象的基础上性质就容易理解了．我们要注意数形结合思想的应用．(2)指数函数与对数函数的性质比较(3)底数a对对数函数的图象的影响①底数a与1的大小关系决定了对数函数图象的“升降”：当a＞1时，对数函数的图象“上升”；当0＜a＜1时，对数函数的图象“下降”．②底数的大小决定了图象相对位置的高低：不论是a＞1还是0＜a＜1，在第一象限内，自左向右，图象对应的对数函数的底数逐渐变大．【例2】如图所示的曲线是对数函数y ＝log a x 的图象．已知a ，43，35，110中取值，则相应曲线C 1，C 2，C 3，C 4的a 值依次为( )A 43，35，110B ，43，110，35C ．43，35，110 D ．43110，35解析：由底数对对数函数图象的影响这一性质可知，C 4的底数＜C 3的底数＜C 2的底数＜C 1的底数．故相应于曲线C 1，C 2，C 3，C 443，35，110．答案：A点技巧 根据图象判断对数函数的底数大小的方法 (1)方法一：利用底数对对数函数图象影响的规律：在x 轴上方“底大图右”，在x 轴下方“底大图左”；(2)方法二：作直线y ＝1，它与各曲线的交点的横坐标就是各对数的底数，由此判断各底数的大小．3．反函数(1)对数函数的反函数指数函数y ＝a x(a ＞0，且a ≠1)与对数函数y ＝log a x (a ＞0，且a ≠1)互为反函数． (2)互为反函数的两个函数之间的关系①原函数的定义域、值域是其反函数的值域、定义域； ②互为反函数的两个函数的图象关于直线y ＝x 对称． (3)求已知函数的反函数，一般步骤如下： ①由y ＝f (x )解出x ，即用y 表示出x ； ②把x 替换为y ，y 替换为x ；③根据y ＝f (x )的值域，写出其反函数的定义域．【例3－1】若函数y ＝f (x )是函数y ＝a x(a ＞0，且a ≠1)的反函数，且f (2)＝1，则f (x )＝( )A ．log 2xB ．12x C ．12log x D ．2x －2解析：因为函数y ＝a x(a ＞0，且a ≠1)的反函数是f (x )＝log a x ， 又f (2)＝1，即log a 2＝1，所以a ＝2．故f (x )＝log 2x ． 答案：A 【例3－2】函数f (x )＝3x(0＜x ≤2)的反函数的定义域为( )A ．(0，＋∞)B ．(1,9]C ．(0,1)D ．[9，＋∞) 解析：∵ 0＜x ≤2，∴1＜3x ≤9，即函数f (x )的值域为(1,9]．故函数f(x)的反函数的定义域为(1,9]．答案：B【例3－3】若函数y＝f(x)的反函数图象过点(1,5)，则函数y＝f(x)的图象必过点( ) A．(5,1) B．(1,5) C．(1,1) D．(5,5)解析：由于原函数与反函数的图象关于直线y＝x对称，而点(1,5)关于直线y＝x的对称点为(5,1)，所以函数y＝f(x)的图象必经过点(5,1)．答案：A4．利用待定系数法求对数函数的解析式及函数值对数函数的解析式y＝log a x(a＞0，且a≠1)中仅含有一个常数a，则只需要一个条件即可确定对数函数的解析式，这样的条件往往是已知f(m)＝n或图象过点(m，n)等等．通常利用待定系数法求解，设出对数函数的解析式f(x)＝log a x(a＞0，且a≠1)，利用已知条件列方程求出常数a的值．利用待定系数法求对数函数的解析式时，常常遇到解方程，比如log a m＝n，这时先把对数式log a m＝n化为指数式的形式a n＝m，把m化为以n为指数的指数幂形式m＝k n(k＞0，且k≠1)，则解得a＝k＞0．还可以直接写出1na m=，再利用指数幂的运算性质化简1nm．例如：解方程log a4＝－2，则a－2＝4，由于2142-⎛⎫= ⎪⎝⎭，所以12a=±．又a＞0，所以12a=．当然，也可以直接写出124a-=，再利用指数幂的运算性质，得11212214(2)22a---====．【例4－1】已知f(e x)＝x，则f(5)＝( )A．e5B．5e C．ln 5 D．log5e解析：(方法一)令t＝e x，则x＝ln t，所以f(t)＝ln t，即f(x)＝ln x．所以f(5)＝ln 5．(方法二)令e x＝5，则x＝ln 5，所以f(5)＝ln 5．答案：C【例4－2】已知对数函数f(x)的图象经过点1,29⎛⎫⎪⎝⎭，试求f(3)的值．分析：设出函数f(x)的解析式，利用待定系数法即可求出．解：设f(x)＝log a x(a＞0，且a≠1)，∵对数函数f(x)的图象经过点1,29⎛⎫⎪⎝⎭，∴11log299af⎛⎫==⎪⎝⎭．∴a2＝19．∴a＝11222111933⎡⎤⎛⎫⎛⎫==⎢⎥⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦．∴f(x)＝13log x．∴f(3)＝111331log 3log3-⎛⎫= ⎪⎝⎭＝－1．【例4－3】已知对数函数f(x)的反函数的图象过点(2,9)，且f(b)＝12，试求b的值．解：设f(x)＝log a x(a＞0，且a≠1)，则它的反函数为y＝a x(a＞0，且a≠1)，由条件知a2＝9＝32，从而a＝3．于是f(x)＝log3x，则f(b)＝log3b＝12，解得b＝123=5．对数型函数的定义域的求解(1)对数函数的定义域为(0，＋∞)．(2)在求对数型函数的定义域时，要考虑到真数大于0，底数大于0，且不等于1．若底数和真数中都含有变量，或式子中含有分式、根式等，在解答问题时需要保证各个方面都有意义．一般地，判断类似于y ＝log a f (x )的定义域时，应首先保证f (x )＞0．(3)求函数的定义域应满足以下原则： ①分式中分母不等于零；②偶次根式中被开方数大于或等于零； ③指数为零的幂的底数不等于零； ④对数的底数大于零且不等于1；⑤对数的真数大于零，如果在一个函数中数条并存，求交集． 【例5】求下列函数的定义域．(1)y ＝log 5(1－x )；(2)y ＝log (2x －1)(5x －4)；(3)y=．分析：利用对数函数y ＝log a x (a ＞0，且a ≠1)的定义求解． 解：(1)要使函数有意义，则1－x ＞0，解得x ＜1， 所以函数y ＝log 5(1－x )的定义域是{x |x ＜1}．(2)要使函数有意义，则54>0,21>0,211,x x x -⎧⎪-⎨⎪-≠⎩解得x ＞45且x ≠1，所以函数y ＝log (2x －1)(5x －4)的定义域是4,15⎛⎫⎪⎝⎭(1，＋∞)．(3)要使函数有意义，则0.5430,log (43)0,x x ->⎧⎨-≥⎩解得34＜x ≤1，所以函数y=的定义域是3<14x x ⎧⎫≤⎨⎬⎩⎭．6．对数型函数的值域的求解(1)充分利用函数的单调性和图象是求函数值域的常用方法．(2)对于形如y ＝log a f (x )(a ＞0，且a ≠1)的复合函数，其值域的求解步骤如下： ①分解成y ＝log a u ，u ＝f (x )这两个函数； ②求f (x )的定义域； ③求u 的取值范围；④利用y ＝log a u 的单调性求解．(3)对于函数y ＝f (log a x )(a ＞0，且a ≠1)，可利用换元法，设log a x ＝t ，则函数f (t )(t ∈R )的值域就是函数f (log a x )(a ＞0，且a ≠1)的值域．注意：(1)若对数函数的底数是含字母的代数式(或单独一个字母)，要考查其单调性，就必须对底数进行分类讨论．(2)求对数函数的值域时，一定要注意定义域对它的影响．当对数函数中含有参数时，有时需讨论参数的取值范围．【例6－1】求下列函数的值域：(1)y ＝log 2(x 2＋4)；(2)y ＝212log (32)x x ＋－．解：(1)∵x 2＋4≥4，∴log 2(x 2＋4)≥log 24＝2．∴函数y ＝log 2(x 2＋4)的值域为[2，＋∞)． (2)设u ＝3＋2x －x 2，则u ＝－(x －1)2＋4≤4．∵u ＞0，∴0＜u ≤4． 又y ＝12log u 在(0，＋∞)上为减函数，∴12log u ≥－2．∴函数y ＝212log (32)x x ＋－的值域为[－2，＋∞)．【例6－2】已知f (x )＝2＋log 3x ，x ∈[1,3]，求y ＝[f (x )]2＋f (x 2)的最大值及相应的x 的值．分析：先确定y ＝[f (x )]2＋f (x 2)的定义域，然后转化成关于log 3x 的一个一元二次函数，利用一元二次函数求最值．解：∵f (x )＝2＋log 3x ，x ∈[1,3]，∴y ＝[f (x )]2＋f (x 2)＝(log 3x )2＋6log 3x ＋6且定义域为[1,3]．令t ＝log 3x (x ∈[1,3])．∵t ＝log 3x 在区间[1,3]上是增函数，∴0≤t ≤1．从而要求y ＝[f (x )]2＋f (x 2)在区间[1,3]上的最大值，只需求y ＝t 2＋6t ＋6在区间[0,1]上的最大值即可．∵y ＝t 2＋6t ＋6在[－3，＋∞)上是增函数，∴当t ＝1，即x ＝3时，y max ＝1＋6＋6＝13．综上可知，当x ＝3时，y ＝[f (x )]2＋f (x 2)的最大值为13．7．对数函数的图象变换及定点问题(1)与对数函数有关的函数图象过定点问题对数函数y ＝log a x (a ＞0，且a ≠1)过定点(1,0)，即对任意的a ＞0，且a ≠1都有log a 1＝0．这是解决与对数函数有关的函数图象问题的关键．对于函数y ＝b ＋k log a f (x )(k ，b 均为常数，且k ≠0)，令f (x )＝1，解方程得x ＝m ，则该函数恒过定点(m ，b )．方程f (x )＝0的解的个数等于该函数图象恒过定点的个数．(2)对数函数的图象变换的问题①函数y ＝log a x (a ＞0，且a ≠1)――----------------→向左(b >0)或向右(b <0)平移|b |个单位长度函数y ＝log a (x ＋b )(a ＞0，且a ≠1)②函数y ＝log a x (a ＞0，且a ≠1)――---------------→向上(b >0)或向下(b <0)平移|b |个单位长度函数y ＝log a x ＋b (a ＞0，且a ≠1)③函数y ＝log a x (a ＞0，且a ≠1)―----------------―→当x >0时，两函数图象相同当x <0时，将x >0时的图象关于y 轴对称函数y ＝log a |x |(a ＞0，且a≠1)④函数y ＝log a x (a ＞0，且a ≠1)――----------------------------------------→保留x 轴上方的图象同时将x 轴下方的图象作关于x 轴的对称变换函数y ＝|log a x |(a＞0，且a ≠1)【例7－1】若函数y ＝log a (x ＋b )＋c (a ＞0，且a ≠1)的图象恒过定点(3,2)，则实数b ，c 的值分别为__________．解析：∵函数的图象恒过定点(3,2)，∴将(3,2)代入y ＝log a (x ＋b )＋c (a ＞0，且a ≠1)，得2＝log a (3＋b )＋c ．又∵当a ＞0，且a ≠1时，log a 1＝0恒成立，∴c ＝2．∴log a (3＋b )＝0．∴b ＝－2． 答案：－2,2【例7－2】作出函数y ＝|log 2(x ＋1)|＋2的图象． 解：(第一步)作函数y ＝log 2x 的图象，如图①；(第二步)将函数y ＝log 2x 的图象沿x 轴向左平移1个单位长度，得函数y ＝log 2(x ＋1)的图象，如图②；(第三步)将函数y ＝log 2(x ＋1)在x 轴下方的图象作关于x 轴的对称变换，得函数y ＝|log 2(x ＋1)|的图象，如图③；(第四步)将函数y ＝|log 2(x ＋1)|的图象，沿y 轴方向向上平移2个单位长度，便得到所求函数的图象，如图④．8．利用对数函数的单调性比较大小两个对数式的大小比较有以下几种情况： (1)底数相同，真数不同．比较同底数(是具体的数值)的对数大小，构造对数函数，利用对数函数的单调性比较大小． 要注意：明确所给的两个值是哪个对数函数的两个函数值；明确对数函数的底数与1的大小关系；最后根据对数函数的单调性判断大小．(2)底数不同，真数相同．若对数式的底数不同而真数相同时，可以利用顺时针方向底数增大画出函数的图象，再进行比较，也可以先用换底公式化为同底后，再进行比较．(3)底数不同，真数也不同．对数式的底数不同且指数也不同时，常借助中间量0,1进行比较．(4)对于多个对数式的大小比较，应先根据每个数的结构特征，以及它们与“0”和“1”的大小情况，进行分组，再比较各组内的数值的大小即可．注意：对于含有参数的两个对数值的大小比较，要注意对底数是否大于1进行分类讨论．【例8－1】比较下列各组中两个值的大小．(1)log31.9，log32；(2)log23，log0.32；(3)log aπ，log a3.141．分析：(1)构造函数y＝log3x，利用其单调性比较；(2)分别比较与0的大小；(3)分类讨论底数的取值范围．解：(1)因为函数y＝log3x在(0，＋∞)上是增函数，所以f(1.9)＜f(2)．所以log31.9＜log32．(2)因为log23＞log21＝0，log0.32＜log0.31＝0，所以log23＞log0.32．(3)当a＞1时，函数y＝log a x在定义域上是增函数，则有log aπ＞log a3.141；当0＜a＜1时，函数y＝log a x在定义域上是减函数，则有log aπ＜log a3.141．综上所得，当a＞1时，log aπ＞log a3.141；当0＜a＜1时，log aπ＜log a3.141．【例8－2】若a2＞b＞a＞1，试比较log a ab，log bba，log b a，log a b的大小．分析：利用对数函数的单调性或图象进行判断．解：∵b＞a＞1，∴0＜ab＜1．∴log a ab＜0，log a b＞log a a＝1，log b1＜log b a＜log b b，即0＜log b a＜1．由于1＜ba＜b，∴0＜log bba＜1．由log b a－log bba＝2logbab，∵a2＞b＞1，∴2ab＞1．∴2logbab＞0，即log b a＞log bba．∴log a b＞log b a＞log b ba＞log aab．9．利用对数函数的单调性解对数不等式(1)根据对数函数的单调性，当a＞0，且a≠1时，有①log a f(x)＝log a g(x)⇔f(x)＝g(x)(f(x)＞0，g(x)＞0)；②当a＞1时，log a f(x)＞log a g(x)⇔f(x)＞g(x)(f(x)＞0，g(x)＞0)；③当0＜a＜1时，log a f(x)＞log a g(x)⇔f(x)＜g(x)(f(x)＞0，g(x)＞0)．(2)常见的对数不等式有三种类型：①形如log a f(x)＞log a g(x)的不等式，借助函数y＝log a x的单调性求解，如果a的取值不确定，需分a＞1与0＜a＜1两种情况讨论．②形如log a f(x)＞b的不等式，应将b化为以a为对数的对数式的形式，再借助函数y＝log a x的单调性求解．③形如log a f (x )＞log b g (x )的不等式，基本方法是将不等式两边化为同底的两个对数值，利用对数函数的单调性来脱去对数符号，同时应保证真数大于零，取交集作为不等式的解集． ④形如f (log a x )＞0的不等式，可用换元法(令t ＝log a x )，先解f (t )＞0，得到t 的取值范围．然后再解x 的范围．【例9－1】解下列不等式：(1)1177log log (4)x x >-；(2)log x (2x ＋1)＞log x (3－x )．解：(1)由已知，得>0,4>0,<4,x x x x ⎧⎪-⎨⎪-⎩解得0＜x ＜2．所以原不等式的解集是{x |0＜x ＜2}．(2)当x ＞1时，有21>3,21>0,3>0,x x x x +-⎧⎪+⎨⎪-⎩解得1＜x ＜3；当0＜x ＜1时，有21<3,21>0,3>0,x x x x +-⎧⎪+⎨⎪-⎩解得0＜x ＜23．所以原不等式的解集是20<<1<<33xx x ⎧⎫⎨⎬⎩⎭或．【例9－2】若22log 3a ⎛⎫ ⎪⎝⎭＜1，求a 的取值范围．解：∵22log 3a ⎛⎫ ⎪⎝⎭＜1，∴－1＜2log 3a ＜1，即12log log log 3a a a a a <<．(1)∵当a ＞1时，y ＝log a x 为增函数，∴123a a <<．∴a ＞32，结合a ＞1，可知a ＞32．(2)∵当0＜a ＜1时，y ＝log a x 为减函数，∴12>>3a a ． ∴a ＜23，结合0＜a ＜1，知0＜a ＜23．∴a 的取值范围是230<<>32a a a ⎧⎫⎨⎬⎩⎭，或．10．对数型函数单调性的讨论(1)解决与对数函数有关的函数的单调性问题的关键：一是看底数是否大于1，当底数未明确给出时，则应对底数a 是否大于1进行讨论；二是运用复合法来判断其单调性；三是注意其定义域．(2)关于形如y ＝log a f (x )一类函数的单调性，有以下结论：函数y ＝log a f (x )的单调性与函数u ＝f (x )(f (x )＞0)的单调性，当a ＞1时相同，当0＜a ＜1时相反．例如：求函数y ＝log 2(3－2x )的单调区间．分析：首先确定函数的定义域，函数y ＝log 2(3－2x )是由对数函数y ＝log 2u 和一次函数u ＝3－2x 复合而成，求其单调区间或值域时，应从函数u ＝3－2x 的单调性、值域入手，并结合函数y ＝log 2u 的单调性考虑．解：由3－2x ＞0，解得函数y ＝log 2(3－2x )的定义域是⎝⎛⎭⎫－∞，32．设u ＝3－2x ，x ∈⎝⎛⎭⎫－∞，32，∵u ＝3－2x 在⎝⎛⎭⎫－∞，32上是减函数，且y ＝log 2u 在(0，＋∞)上单调递增，∴函数y ＝log 2(3－2x )在⎝⎛⎭⎫－∞，32上是减函数．∴函数y ＝log 2(3－2x )的单调减区间是⎝⎛⎭⎫－∞，32．【例10－1】求函数y ＝log a (a －a x)的单调区间．解：(1)若a ＞1，则函数y ＝log a t 递增，且函数t ＝a －a x递减．又∵a －a x ＞0，即a x ＜a ，∴x ＜1．∴函数y ＝log a (a －a x)在(－∞，1)上递减． (2)若0＜a ＜1，则函数y ＝log a t 递减，且函数t ＝a －a x递增．又∵a －a x ＞0，即a x ＜a ，∴x ＞1．∴函数y ＝log a (a －a x)在(1，＋∞)上递减． 综上所述，函数y ＝log a (a －a x)在其定义域上递减．析规律 判断函数y ＝log a f (x )的单调性的方法 函数y ＝log a f (x )可看成是y ＝log a u 与u＝f (x )两个简单函数复合而成的，由复合函数单调性“同增异减”的规律即可判断．需特别注意的是，在求复合函数的单调性时，首先要考虑函数的定义域，即“定义域优先”．【例10－2】已知f (x )＝12log (x 2－ax －a )在1,2⎛⎫-∞-⎪⎝⎭上是增函数，求a 的取值范围． 解：1,2⎛⎫-∞-⎪⎝⎭是函数f (x )的递增区间，说明1,2⎛⎫-∞- ⎪⎝⎭是函数u ＝x 2－ax －a 的递减区间，由于是对数函数，还需保证真数大于0．令u (x )＝x 2－ax －a ，∵f (x )＝12log ()u x 在1,2⎛⎫-∞- ⎪⎝⎭上是增函数，∴u (x )在1,2⎛⎫-∞-⎪⎝⎭上是减函数，且u (x )＞0在1,2⎛⎫-∞- ⎪⎝⎭上恒成立． ∴1,2210,2au ⎧≥-⎪⎪⎨⎛⎫⎪-≥ ⎪⎪⎝⎭⎩即1,10.42a a a ≥-⎧⎪⎨+-≥⎪⎩ ∴－1≤a ≤12．∴满足条件的a 的取值范围是112a a ⎧⎫-≤≤⎨⎬⎩⎭．11．对数型函数的奇偶性问题判断与对数函数有关的函数奇偶性的步骤是：(1)求函数的定义域，当定义域关于原点不对称时，则此函数既不是奇函数也不是偶函数，当定义域关于原点对称时，判断f (－x )与f (x )或－f (x )是否相等；(2)当f (－x )＝f (x )时，此函数是偶函数；当f (－x )＝－f (x )时，此函数是奇函数；(3)当f (－x )＝f (x )且f (－x )＝－f (x )时，此函数既是奇函数又是偶函数；(4)当f (－x )≠f (x )且f (－x )≠－f (x )时，此函数既不是奇函数也不是偶函数．例如，判断函数f (x )＝log )a x (x ∈R ，a ＞0，且a ≠1)的奇偶性．解：∵f (－x )＋f (x )＝log )a x ＋log )a x )＝log a (x 2＋1－x 2)＝log a 1＝0，∴f (－x )＝－f (x )．∴f (x )为奇函数．【例11】已知函数f (x )＝1log 1ax x +-(a ＞0，且a ≠1)． (1)求函数f (x )的定义域；(2)判断函数f (x )的奇偶性；(3)求使f (x )＞0的x 的取值范围．分析：对于第(2)问，依据函数奇偶性的定义证明即可．对于第(3)问，利用函数的单调性去掉对数符号，解出不等式．解：(1)由11x x+-＞0，得－1＜x ＜1，故函数f (x )的定义域为(－1,1)． (2)∵f (－x )＝1log 1a x x -+＝1log 1a x x+--＝－f (x )， 又由(1)知函数f (x )的定义域关于原点对称，∴函数f (x )是奇函数． (3)当a ＞1时，由1log 1a x x +-＞0＝log a 1，得11x x+-＞1，解得0＜x ＜1； 当0＜a ＜1时，由1log 1ax x +-＞0＝log a 1，得0＜11x x +-＜1，解得－1＜x ＜0． 故当a ＞1时，x 的取值范围是{x |0＜x ＜1}；当0＜a ＜1时，x 的取值范围是{x |－1＜x ＜0}．12．对数型函数模型的实际应用地震震级的变化规律、溶液pH 的变化规律、航天问题等，可以用对数函数模型来研究．此类题目，通常给出函数解析式模型，但是解析式中含有其他字母参数．其解决步骤是：(1)审题：弄清题意，分清条件和结论，抓住关键的词和量，理顺数量关系；(2)建模：将文字语言转化成数学语言，利用数学知识，求出函数解析式模型中参数的值；(3)求模：求解函数模型，得到数学结论；(4)还原：将用数学方法得到的结论还原为实际问题的结论．由此看，直接给定参数待定的函数模型时，利用待定系数法的思想，代入已知的数据得到相关的方程而求得待定系数．一般求出函数模型后，还利用模型来研究一些其他问题．代入法、方程思想、对数运算性质，是解答此类问题的方法精髓．【例12】我国用长征二号F型运载火箭成功发射了“神舟”七号载人飞船，实现了中国历史上第一次的太空漫步，令中国成为世界上第三个有能力把人送上太空并进行太空漫步的国家(其中，翟志刚完全出舱，刘伯明的头部和手部部分出舱)．在不考虑空气阻力的条件下，假设火箭的最大速度y(单位：km/s)关于燃料重量x(单位：吨)的函数关系式为y＝k ln(m＋x)－k)＋4ln 2(k≠0)，其中m是箭体、搭载的飞行器、航天员的重量和．当燃料重量为－1)m吨时，火箭的最大速度是4 km/s．(1)求y＝f(x)；(2)已知长征二号F型运载火箭的起飞重量是479.8吨(箭体、搭载的飞行器、航天员、燃料)，火箭的最大速度为8 km/s，求装载的燃料重量(e＝2.7，精确到0.1)．解：(1)由题意得当x＝1)m时，y＝4，则4＝k ln[m＋－1)m]－k)＋4ln 2，解得k＝8．所以y＝8ln(m＋x)－)＋4ln 2，即y＝8ln m x m+．(2)由于m＋x＝479.8，则m＝479.8－x，令479.888ln479.8x=-，解得x≈302.1．故火箭装载的燃料重量约为302.1吨．。

一、对数的基本概念1. 下列各数中，哪些是正数、负数、零？log₂3log₃9log₄16log₅25log₆362. 判断下列各对数是否成立：log₂4 = 2log₃27 = 3log₄16 = 4log₅25 = 5log₆36 = 63. 求下列各对数的底数：logₐ16 = 4logₐ25 = 2logₐ36 = 2logₐ49 = 2logₐ64 = 34. 求下列各对数的真数：log₂8 = alog₃27 = blog₄16 = clog₆36 = e5. 求下列各对数的对数底数： logₐ16 = 4logₐ25 = 2logₐ36 = 2logₐ49 = 2logₐ64 = 3二、对数的运算1. 求下列各对数的值：log₂(8 ÷ 4)log₃(27 ÷ 9)log₄(16 ÷ 4)log₅(25 ÷ 5)log₆(36 ÷ 6)2. 求下列各对数的值：log₂(8 × 4)log₃(27 × 9)log₄(16 × 4)log₅(25 × 5)log₆(36 × 6)3. 求下列各对数的值：log₂(8 + 4)log₃(27 + 9)log₅(25 + 5)log₆(36 + 6)4. 求下列各对数的值：log₂(8 4)log₃(27 9)log₄(16 4)log₅(25 5)log₆(36 6)5. 求下列各对数的值：log₂(8 ÷ 4) + log₂4log₃(27 ÷ 9) + log₃3log₄(16 ÷ 4) + log₄4log₅(25 ÷ 5) + log₅5log₆(36 ÷ 6) + log₆6三、对数的应用1. 某商品原价为100元，现在打八折，求打折后的价格。

2. 某人存款10000元，年利率为5%，求2年后存款的利息。

对数与对数函数二、知识要点梳理知识点一、对数及其运算我们在学习过程遇到2x=4的问题时，可凭经验得到x=2的解，而一旦出现2x=3时，我们就无法用已学过的知识来解决，从而引入出一种新的运算——对数运算.(一)对数概念:1. 如果，那么数b叫做以a为底N的对数，记作:log a N=b.其中a叫做对数的底数，N叫做真数.2. 对数恒等式：3. 对数具有下列性质：(1)0和负数没有对数，即；(2)1的对数为0，即；(3)底的对数等于1，即.(二)常用对数与自然对数通常将以10为底的对数叫做常用对数，.以e为底的对数叫做自然对数，.(三)对数式与指数式的关系由定义可知:对数就是指数变换而来的，因此对数式与指数式联系密切，且可以互相转化.它们的关系可由下图表示.由此可见a，b，N三个字母在不同的式子中名称可能发生变化.(四)积、商、幂的对数已知(1)；推广：(2)；(3).(五)换底公式同底对数才能运算，底数不同时可考虑进行换底，在a＞0，a≠1，M＞0的前提下有:(1)令log a M=b，则有a b=M，(a b)n=M n，即，即，即:.(2) ，令log a M=b，则有a b=M，则有即，即，即当然，细心一些的同学会发现(1)可由(2)推出，但在解决某些问题(1)又有它的灵活性.而且由(2)还可以得到一个重要的结论:.知识点二、对数函数1. 函数y=log a x(a＞0，a≠1)叫做对数函数.2. 在同一坐标系内，当a＞1时，随a的增大，对数函数的图像愈靠近x轴；当0＜a＜1时，对数函数的图象随a的增大而远离x轴.(见图1)(1)对数函数y=log a x(a＞0，a≠1)的定义域为(0，+∞)，值域为R(2)对数函数y=log a x(a＞0，a≠1)的图像过点(1，0)(3)当a＞1时，三、规律方法指导容易产生的错误(1)对数式log a N=b中各字母的取值范围(a＞0 且a≠1，N＞0，b∈R)容易记错.(2)关于对数的运算法则，要注意以下两点：一是利用对数的运算法则时，要注意各个字母的取值范围，即等式左右两边的对数都存在时等式才能成立.如：log2(-3)(-5)=log2(-3)+log2(-5)是不成立的，因为虽然log2(-3)(-5)是存在的，但log2(-3)与log2(-5)是不存在的.二是不能将和、差、积、商、幂的对数与对数的和、差、积、商、幂混淆起来，即下面的等式是错误的：log a(M±N)=log a M±log a N，log a(M·N)=log a M·log a N，loga.(3)解决对数函数y=log a x (a＞0且a≠1)的单调性问题时，忽视对底数a的讨论.(4)关于对数式log a N的符号问题，既受a的制约又受N的制约，两种因素交织在一起，应用时经常出错.下面介绍一种简单记忆方法，供同学们学习时参考.以1为分界点，当a，N同侧时，log a N＞0；当a，N异侧时，log a N＜0.经典例题透析类型一、指数式与对数式互化及其应用1.将下列指数式与对数式互化：(1)；(2)；(3)；(4)；(5)；(6).思路点拨：运用对数的定义进行互化.解：(1)；(2)；(3)；(4)；(5)；(6).总结升华：对数的定义是对数形式和指数形式互化的依据，而对数形式和指数形式的互化又是解决问题的重要手段.举一反三：【变式1】求下列各式中x的值：(1)(2)(3)lg100=x (4)思路点拨：将对数式化为指数式，再利用指数幂的运算性质求出x.解：(1)；(2)；(3)10x=100=102，于是x=2；(4)由.类型二、利用对数恒等式化简求值2．求值：解：.总结升华：对数恒等式中要注意格式：①它们是同底的；②指数中含有对数形式；③其值为真数.举一反三：【变式1】求的值(a，b，c∈R+，且不等于1，N>0)思路点拨：将幂指数中的乘积关系转化为幂的幂，再进行运算.解：.类型三、积、商、幂的对数3.已知lg2=a，lg3=b，用a、b表示下列各式.(1)lg9 (2)lg64 (3)lg6 (4)lg12 (5)lg5 (6) lg15解：(1)原式=lg32=2lg3=2b(2)原式=lg26=6lg2=6a(3)原式=lg2+lg3=a+b(4)原式=lg22+lg3=2a+b(5)原式=1-lg2=1-a(6)原式=lg3+lg5=lg3+1-lg2=1+b-a举一反三：【变式1】求值(1)(2)lg2·lg50+(lg5)2 (3)lg25+lg2·lg50+(lg2)2解：(1)(2)原式=lg2(1+lg5)+(lg5)2=lg2+lg2lg5+(lg5)2=lg2+lg5(lg2+lg5)=lg2+lg5=1(3)原式=2lg5+lg2(1+lg5)+(lg2)2=2lg5+lg2+lg2lg5+(lg2)2=1+lg5+lg2(lg5+lg2)=1+lg5+lg2=2.【变式2】已知3a=5b=c，，求c的值.解：由3a=c得：同理可得.【变式3】设a、b、c为正数，且满足a2+b2=c2.求证：.证明：.【变式4】已知：a2+b2=7ab，a＞0，b＞0. 求证：.证明：∵a2+b2=7ab，∴a2+2ab+b2=9ab，即(a+b)2=9ab，∴lg(a+b)2=lg(9ab)，∵a＞0，b＞0，∴2lg(a+b)=lg9+lga+lgb ∴2[lg(a+b)-lg3]=lga+lgb即.类型四、换底公式的运用4.(1)已知log x y=a，用a表示；(2)已知log a x=m，log b x=n，log c x=p，求log abc x.解：(1)原式=；(2)思路点拨：将条件和结论中的底化为同底.方法一：a m=x，b n=x，c p=x∴，∴；方法二：.举一反三：【变式1】求值：(1)；(2)；(3).解：(1)；(2)；(3)法一：法二：.总结升华：运用换底公式时，理论上换成以大于0不为1任意数为底均可，但具体到每一个题，一般以题中某个对数的底为标准，或都换成以10为底的常用对数也可.类型五、对数运算法则的应用5.求值(1) log89·log2732(2)(3)(4)(log2125+log425+log85)(log1258+log254+log52)解：(1)原式=.(2)原式=(3)原式=(4)原式=(log2125+log425+log85)(log1258+log254+log52)举一反三：【变式1】求值：解：另解：设=m (m＞0).∴，∴，∴，∴lg2=lgm，∴2=m，即.【变式2】已知：log23=a，log37=b，求：log4256=?解：∵∴，类型六、函数的定义域、值域求含有对数函数的复合函数的定义域、值域，其方法与一般函数的定义域、值域的求法类似，但要注意对数函数本身的性质（如定义域、值域及单调性）在解题中的重要作用.6. 求下列函数的定义域：(1)；(2).思路点拨：由对数函数的定义知：x2＞0，4-x＞0，解出不等式就可求出定义域.解：(1)因为x2＞0，即x≠0，所以函数；(2)因为4-x＞0，即x＜4，所以函数.举一反三：【变式1】求下列函数的定义域.(1) y=(2) y=ln(a x-k·2x)(a＞0且a≠1，k∈R).解：(1)因为，所以，所以函数的定义域为(1，)(，2).(2)因为a x-k·2x＞0，所以()x＞k.[1]当k≤0时，定义域为R；[2]当k＞0时，(i)若a＞2，则函数定义域为(k，+∞)；(ii)若0＜a＜2，且a≠1，则函数定义域为(-∞，k)；(iii)若a=2，则当0＜k＜1时，函数定义域为R；当k≥1时，此时不能构成函数，否则定义域为.【变式2】函数y=f(2x)的定义域为[-1，1]，求y=f(log2x)的定义域.思路点拨：由-1≤x≤1，可得y=f(x)的定义域为[，2]，再由≤log2x≤2得y=f(log2x)的定义域为[，4].类型七、函数图象问题7．作出下列函数的图象：(1) y=lgx，y=lg(-x)，y=-lgx；(2) y=lg|x|；(3) y=-1+lgx.解：(1)如图(1)；(2)如图(2)；(3)如图(3).类型八、对数函数的单调性及其应用利用函数的单调性可以：①比较大小；②解不等式；③判断单调性；④求单调区间；⑤求值域和最值.要求同学们：一是牢固掌握对数函数的单调性；二是理解和掌握复合函数的单调性规律；三是树立定义域优先的观念.8. 比较下列各组数中的两个值大小：(1)log23.4，log28.5(2)log0.31.8，log0.32.7(3)log a5.1，log a5.9(a＞0且a≠1)思路点拨：由数形结合的方法或利用函数的单调性来完成.(1)解法1：画出对数函数y=log2x的图象，横坐标为3.4的点在横坐标为8.5的点的下方，所以，log23.4＜log28.5；解法2：由函数y=log2x在R+上是单调增函数，且3.4＜8.5，所以log23.4＜log28.5；解法3：直接用计算器计算得：log23.4≈1.8，log28.5≈3.1，所以log23.4＜log28.5；(2)与第(1)小题类似，log0.3x在R+上是单调减函数，且1.8＜2.7，所以log0.31.8＞log0.32.7；(3)注：底数是常数，但要分类讨论a的范围，再由函数单调性判断大小.解法1：当a＞1时，y=log a x在(0，+∞)上是增函数，且5.1＜5.9，所以，log a5.1＜log a5.9当0＜a＜1时，y=log a x在(0，+∞)上是减函数，且5.1＜5.9，所以，log a5.1＞log a5.9 解法2：转化为指数函数，再由指数函数的单调性判断大小，令b1=log a5.1，则，令b2=log a5.9，则当a＞1时，y=a x在R上是增函数，且5.1＜5.9所以，b1＜b2，即当0＜a＜1时，y=a x在R上是减函数，且5.1＜5.9所以，b1＞b2，即.举一反三：【变式1】若log m3.5＞log n3.5(m，n＞0，且m≠1，n≠1)，试比较m ，n的大小.解：(1)当m＞1，n＞1时，∵3.5＞1，由对数函数性质：当底数和真数都大于1时，对同一真数，底数大的对数值小，∴n＞m＞1.(2)当m＞1，0＜n＜1时，∵log m3.5＞0，log n3.5＜0，∴0＜n＜1＜m也是符合题意的解.(3)当0＜m＜1，0＜n＜1时，∵3.5＞1，由对数函数性质，此时底数大的对数值小，故0＜m＜n＜1.综上所述，m，n的大小关系有三种：1＜m＜n或0＜n＜1＜m或0＜m＜n＜1.9. 证明函数上是增函数.思路点拨：此题目的在于让学生熟悉函数单调性证明通法，同时熟悉利用对函数单调性比较同底数对数大小的方法.证明：设，且x1＜x2则又∵y=log2x在上是增函数即f(x1)＜f(x2)∴函数f(x)=log2(x2+1)在上是增函数.举一反三：【变式1】已知f(log a x)=(a＞0且a≠1)，试判断函数f(x)的单调性.解：设t=log a x(x∈R+，t∈R).当a＞1时，t=log a x为增函数，若t1＜t2，则0＜x1＜x2，∴f(t1)-f(t2)=，∵0＜x1＜x2，a＞1，∴f(t1)＜f(t2)，∴f(t)在R上为增函数，当0＜a＜1时，同理可得f(t)在R上为增函数.∴不论a＞1或0＜a＜1，f(x)在R上总是增函数.10．求函数y=(-x2+2x+3)的值域和单调区间.解：设t=-x2+2x+3，则t=-(x-1)2+4.∵y=t为减函数，且0＜t≤4，∴y≥=-2，即函数的值域为[-2，+∞.再由：函数y=(-x2+2x+3)的定义域为-x2+2x+3＞0，即-1＜x＜3.∴t=-x2+2x+3在-1，1）上递增而在[1，3)上递减，而y=t为减函数.∴函数y=(-x2+2x+3)的减区间为(-1，1)，增区间为[1，3.类型九、函数的奇偶性11. 判断下列函数的奇偶性.(1)(2).(1)思路点拨：首先要注意定义域的考查，然后严格按照证明奇偶性基本步骤进行.解：由所以函数的定义域为：(-1，1)关于原点对称又所以函数是奇函数；总结升华：此题确定定义域即解简单分式不等式，函数解析式恒等变形需利用对数的运算性质.说明判断对数形式的复合函数的奇偶性，不能轻易直接下结论，而应注意对数式的恒等变形.(2)解：由所以函数的定义域为R关于原点对称又即f(-x)=-f(x)；所以函数.总结升华：此题定义域的确定可能稍有困难，函数解析式的变形用到了分子有理化的技巧，要求掌握. 类型十、对数函数性质的综合应用12．已知函数f(x)=lg(ax2+2x+1).(1)若函数f(x)的定义域为R，求实数a的取值范围；(2)若函数f(x)的值域为R，求实数a的取值范围.思路点拨：与求函数定义域、值域的常规问题相比，本题属非常规问题，关键在于转化成常规问题.f(x)的定义域为R，即关于x的不等式ax2+2x+1＞0的解集为R，这是不等式中的常规问题.f(x)的值域为R与ax2+2x+1恒为正值是不等价的，因为这里要求f(x)取遍一切实数，即要求u=ax2+2x+1取遍一切正数，考察此函数的图象的各种情况，如图，我们会发现，使u 能取遍一切正数的条件是.解：(1)f(x)的定义域为R，即：关于x的不等式ax2+2x+1＞0的解集为R，当a=0时，此不等式变为2x+1＞0，其解集不是R；当a≠0时，有a＞1.∴a的取值范围为a＞1.(2)f(x)的值域为R，即u=ax2+2x+1能取遍一切正数a=0或0≤a≤1，∴a的取值范围为0≤a≤1.11。

高中对数基础练习题及讲解1. 对数的定义与性质- 问题：如果 \( \log_{2}8 = 3 \)，那么 \( \log_{2}64 \) 等于多少？- 解释：由于 \( 2^3 = 8 \)，我们可以推断出 \( 2^6 = 64 \)。

因此，\( \log_{2}64 = 6 \)。

2. 对数的运算法则- 问题：计算 \( \log_{10}(100) + \log_{10}(0.01) \)。

- 解释：根据对数的乘法法则，\( \log_{10}(100 \times 0.01)= \log_{10}(1) \)。

由于任何数的对数底数为1都等于0，所以\( \log_{10}(100) + \log_{10}(0.01) = 0 \)。

3. 换底公式的应用- 问题：将 \( \log_{4}16 \) 转换为以10为底的对数。

- 解释：使用换底公式 \( \log_b a = \frac{\log_c a}{\log_c b} \)，我们有 \( \log_{4}16 = \frac{\log_{10} 16}{\log_{10} 4} \)。

由于 \( 16 = 2^4 \) 且 \( 4 = 2^2 \)，我们得到\( \log_{4}16 = \frac{4 \log_{10} 2}{2 \log_{10} 2} = 2 \)。

4. 复合对数的求解- 问题：如果 \( \log_{3}9 = a \)，求 \( \log_{9}3 \)。

- 解释：由于 \( 3^a = 9 \)，我们可以将 \( 9 \) 写成 \( 3^2 \)，因此 \( \log_{9}3 = \frac{1}{2} \)。

5. 对数方程的解法- 问题：解对数方程 \( \log_{x}y = 2 \)。

- 解释：根据对数的定义，我们知道 \( x^2 = y \)。

所以，\( y \) 必须是 \( x \) 的平方。

对数及其运算基础知识及例题1、定义：2、性质：3、对数的运算性质：4、换底公式：5、对数的其他运算性质6、常用对数和自然对数：【典型例题】类型一、对数的概念例1.求下列各式中x 的取值范围：（1）2log (5)x -；（2）(1)log (2)x x -+；（3）2(1)log (1)x x +-．类型二、指数式与对数式互化及其应用 例2.将下列指数式与对数式互化： (1)2log 164=；(2)13log 273=-；(3)3x =；(4)35125=；(5)1122-=；(6)2193-⎛⎫= ⎪⎝⎭.类型三、利用对数恒等式化简求值例3．求值： 71log 57+类型四、积、商、幂的对数例4. z y x a a a log ,log ,log 用表示下列各式2353(1)log ;(2)log ();(3)log ;(4)log a a a ax yxyxx y zz例5.已知18log 9,185ba ==，求36log 45．类型六、对数运算法则的应用 例6.求值 (1) 91log 81log 251log 32log 53264⋅⋅⋅(2) 7lg142lg lg 7lg183-+-(3))36log 43log 32(log log 42122++(4)()248125255log 125log 25log 5(log 8log 4log 2)++++对数及其运算练习题一、选择题 1、 25)(log 5a -（a ≠0）化简得结果是（ ） A 、－aB 、a 2C 、｜a ｜D 、a2、 log 7［log 3（log 2x ）］＝0，则21-x 等于（ ）A 、31B 、321 C 、221 D 、3313、 nn ++1log（n n －＋1）等于（ ） A 、1B 、－1C 、2D 、－24、 已知32a =，那么33log 82log 6-用表示是（ ）A 、2a -B 、52a -C 、23(1)a a -+ D 、 23a a -5、 2log (2)log log a a a M N M N -=+，则NM的值为（ ） A 、41B 、4C 、1D 、4或1 6、 若log m 9<log n 9<0,那么m,n 满足的条件是（ ） A 、m>n>1 B 、n>m>1 C 、0<n<m<1 D 、0<m<n<17、 若1<x<b,a=log ２b x,c=log a x,则a,b,c 的关系是（ ） A 、a<b<c B 、 a<c<b C 、c<b<a D 、c<a<b 8、在)5(log 2a b a -=-中，实数a 的范围是（ ）A 、 a >5或a <2B 、 25<<aC 、 23<<a 或35<<aD 、 34<<a9、 若log [log (log )]4320x =，则x -12等于（ ） A 、 142 B 、122 C 、 8D 、 410、334log的值是（ ）A 、 16B 、 2C 、 3D 、 411、 已知b a ==4log 3log 55，，则log 2512是（ ） A 、 a b +B 、)(21b a + C 、 ab D 、12ab 12、 已知21366log log x =-，则x 的值是（ ） A 、 3B 、 2C 、 2或-2D 、 3或213、 计算=++5lg 2lg 35lg 2lg 33（ ） A 、 1B 、 3C 、 2D 、 014、 已知23834x y ==，log ，则x y +2的值为（ ） A 、 3B 、 8C 、 4D 、 log 4815、 设a 、b 、c 都是正数，且cb a 643==，则（ ）A 、111c a b=+ B 、221c a b =+ C 、 122c a b=+ D 、212c a b=+ 二、填空题16、 若log a x ＝log b y ＝－21log c 2，a ，b ，c 均为不等于1的正数，且x ＞0，y ＞0，c ＝ab ，则xy ＝________17 、若lg2＝a ，lg3＝b ，则log 512＝________18、 3a＝2，则log 38－2log 36＝__________ 19、 若2log 2,log 3,m na a m n a+===___________________20、 lg25+lg2lg50+(lg2)2=21、 若1)12(log -=+x ，则x=________，若log28=y ，则y=___________。

对数的概念的题摘要：一、对数的概念简介1.对数的定义2.对数的基本性质3.对数的运算法则二、对数的分类与应用1.常见对数2.对数的应用领域三、对数函数及其性质1.对数函数的定义2.对数函数的性质3.对数函数的图像和值域四、对数方程和不等式的解法1.对数方程的解法2.对数不等式的解法正文：一、对数的概念简介对数的概念最早由数学家约翰·纳皮尔在1614年提出。

对数是一种将乘法转化为加法的运算，可以简化幂运算和指数运算。

对数的定义是：若a^x = N，则称x为以a为底N的对数，记作logaN。

其中，a称为底数，N称为真数。

对数的基本性质有：1.loga1 = 0；2.loga(N * M) = logaN + logaM；3.loga(N^k) = k * logaN。

对数的运算法则包括：1.乘法法则：loga(M * N) = logaM + logaN；2.除法法则：loga(M / N) = logaM - logaN；3.幂法则：loga(M^N) = N * logaM。

二、对数的分类与应用对数有多种类型，常见的有自然对数、常用对数和任意对数。

自然对数以e为底，常用对数以10为底，任意对数则是以任意正数为底。

对数广泛应用于指数函数、对数函数、反函数等领域，以及物理学、化学、生物学、经济学等领域。

三、对数函数及其性质对数函数是指以某个正数为底，以实数为自变量的函数。

对数函数的定义为：y = loga(x)。

对数函数的性质有：1.函数的定义域为(0, +∞)；2.函数的值域为R；3.函数是单调递增的。

对数函数的图像通常为一条斜率为正的直线，截距为0。

四、对数方程和不等式的解法对数方程的解法主要包括换元法、分式法、对数性质法等。

对数的概念的题
（实用版）
目录
1.对数的概念
2.对数的应用
3.对数的重要性
正文
对数是我们数学中一个非常重要的概念，它在我们的日常生活中也经常被使用到。

对数，简单来说，就是指一个数的幂次。

具体来说，如果一个数 a 的 b 次方等于 c，那么我们就可以说，c 的对数是 b，记作logb(c)。

对数有许多实际应用，例如在计算机科学中，对数被用来表示数据的大小。

比如，我们常用的 log10(x) 表示以 10 为底的对数，它描述了 x 的数量级。

又如在统计学中，对数被用来进行数据的变换，使得数据更符合模型的假设。

对数在数学中也起着重要的作用。

对数的概念是微积分的基础，它在微积分的运算中扮演了重要的角色。

此外，对数也是概率论和复分析等领域的重要工具。

总的来说，对数是一个重要的数学概念，它在我们的日常生活中和数学研究中都扮演着重要的角色。

第1页共1页。

对数与对数函数（讲义）知识点睛一、对数与对数的运算1.对数（1）如果x a N =(a >0，且a ≠1)，那么数x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做对数的底数，N 叫做真数．常用对数：10log lg N N =；自然对数：e log ln N N =．（2）当a >0，且a ≠1时，x a N =⇔log a x N =．（3）负数和零没有对数；log 10a =，log 1a a =．2.对数的运算性质（1）如果a >0，且a ≠1，M >0，N >0，那么①log ()log log a a a M N M N ⋅=+；②log log log aa a MM N N=-；③log log ()n a a M n M n =∈R ．（2）换底公式：log log log c a c bb a=(a >0，且a ≠1；c >0，且c ≠1；b >0)．（3）log (010)a b a b a a b =>≠>，；．二、对数函数及其性质1.定义：一般地，函数log (0,1)a y x a a =>≠且叫做对数函数，其中x 是自变量，函数的定义域是(0，+∞)．2.对数函数log (0,1)a y x a a =>≠且的图象和性质：0<a <1a >1图象定义域(0，+∞)值域R性质①过定点(1，0)，即x =1时，y =0②在(0，+∞)上是减函数②在(0，+∞)上是增函数3.对数函数底数变化与图象分布规律1log a y x =；②log b y x =；③log c y x =；④log d y x =，则有0<b <a <1<d <c ，即：x ∈(1，+∞)时，log log log log a b c d x x x x <<<；x ∈(0，1)时，log log log log a b c d x x x x >>>．4.反函数对数函数与指数函数互为反函数，互为反函数的两个函数的图象关于直线y x =对称．精讲精练1.把下列指数式化为对数式，对数式化为指数式．（1）32=8_______________；（2）415625-=_______________；（3）13127=3-_______________；（4）lg 0.0013=-_____________；（5）0.3log 2=a _____________；（6）ln x =_____________．2.求下列各式的值．（1）43log (927)⨯（2）1lg lg 4lg 52++（3）661log 12log 2-（4）22333399(log 2)(log )log log 422++⋅（5）2345log 3log 4log 5log 2⋅⋅⋅（6）48525(log 5log 5)(log 2log 2)++3.已知234log [log (log )]0x =，则x 的值为_________．4.已知3485log 4log 8log log 25m ⋅⋅=，那么m 的值为（）A ．9B ．18C ．12D ．275.已知4823log 3x y ==，，则x +2y 的值为（）A ．3B ．8C ．4D ．log 486.已知log 3a m =，log 2a n =，那么a 2m +3n =（）A ．17B ．72C ．108D ．317.已知lg lg 2lg(2)x y x y +=-，则xy的值为_________．8.设lg a ，lg b 是方程2x 2-4x +1=0的两个实根，则2(lg )ab的值等于（）A ．2B ．12C ．4D ．149.已知函数()lg f x x =．若()1f ab =，则22()()f a f b +=_____．10.下列函数表达式中是对数函数的是（）A ．0.01log (0)y x x =>B ．22log y x =C ．2log (2)(2)y x x =+>-D ．2ln(1)y x =+11.若点(a ，b )在lg y x =图象上，且a ≠1，则下列点也在此图象上的是（）A ．1()b a ，B ．(10a ，1-b )C ．10(1)b a+，D ．(a 2，2b )12.若函数log ()a y x b =+(a >0，a ≠1)的图象过两点(-1，0)和(0，1)，则（）A ．a =2，b =2B ．2a b ==C ．a =2，b =1D ．a b ==13.直接写出下列函数的定义域：311log (2)_______________2345log (3)_______________16_______________ln(1)x y x y y y y x y x -=-====-=+=+（）；（）；（）；（）；（）；（）．14.已知()f x 的定义域为[0，1]，则函数12[log (3)]y f x =-的定义域是_____________．15.函数212log (613)y x x =++的值域为（）A ．RB ．[8，+∞)C ．(-∞，-2]D ．[-3，+∞)16.函数log a y x =在区间[2，π]上最大值比最小值大1，则a =__________．17.下列判断不正确的是（）A ．22log 3.4log 4.3<B ．0.20.3log 0.4log 0.4<C ．67log 7log 6>D ．30.3log log 4π<18.为了得到函数3lg10x y +=的图象，只需把函数lg y x =的图象上所有的点（）A ．向左平移3个单位长度，再向上平移1个单位长度B ．向右平移3个单位长度，再向上平移1个单位长度C ．向左平移3个单位长度，再向下平移1个单位长度D ．向右平移3个单位长度，再向下平移1个单位长度19.函数21log (01)1a x y a a x +=>≠-，的图象过定点P ，则点P 的坐标为（）A ．(1，0)B ．(-2，0)C ．(2，0)D ．(-1，0)20.已知函数()log (1)a f x x =+，()log (1)a g x x =-(a >0，且a ≠1)．（1）求函数()()f x g x +的定义域；（2）判断函数()()f x g x +的奇偶性，并说明理由．21.设a ，b ∈R 且a ≠2，定义在区间(-b ，b )上的函数1()lg12axf x x+=+满足：()()0f x f x +-=．（1）求实数a 的值；（2）求b 的取值范围．22.已知关于x 的方程212log 210x a x ⋅--=有实数根，求a 的取值范围．23.已知函数2log [(21)]a y x a x a =--+的定义域为R ，求实数a 的取值范围．回顾与思考________________________________________________________________________________________________________________________________________________________________________【参考答案】1．（1）2log 83=；（2）51log 4625=-；（3）2711log 33=-；（4）3100.001-=；（5）0.32a =；（6）e x =2．（1）11；（2）1；（3）12；（4）4；（5）1；（6）543．644．A 5．A 6．B 7．48．A 9．210．A 11．D 12．A13．（1）(2)+∞，；（2）(0)+∞，；（3）2(1]3，；（4）(0；（5）(12)(23)⋃，，；（6）(10)(02]-⋃，，14．5[22，15．C16．2π或2π17．D18．C 19．B20．（1）(-1，1)；（2）偶函数，证明()()()()f x g x f x g x -+-=+21．（1）2a =-；（2）102b ≤<22．02a ≤<23．33(11)(1122，-⋃+对数与对数函数（随堂测试）1.函数22()log (2)f x x x a =-+的值域为[0，+∞)，则正实数a 等于（）A ．1B ．2C ．3D ．42.求函数2log (4)(01)a y x x a a =->≠，且的单调递减区间．【参考答案】1.B2.当01a <<时，f (x )的单调递减区间为(0，2]；当1a >时，f (x )的单调递减区间为[2，4)对数与对数函数（作业）1.求下列各式的值．（1）lg +（2）553log 10log 0.125+（3）22(lg 2)(lg 5)lg 4lg 5++⋅（4）22lg 5lg83+（5）20321log log ()52-+-（6）231lg 25lg 2lg log 9log 22+-⨯2.下列对数运算中，一定正确的是（）A ．lg()lg lg M N M N +=⋅B ．ln ln n M n M =C ．lg()lg lg M N M N⋅=+D ．lg log lg a b b a=3.已知3log 2a =，那么33log 22log 6-用a 表示是（）A ．5a -2B ．-a -2C ．3a -(1+a )2D ．3-a 2-14.设a ，b ，c 均为不等于1的正实数，则下列等式中恒成立的是（）A ．log log log a c c b b a ⋅=B ．log log log a c c b a b ⋅=C ．log ()log log a a a bc b c =⋅D ．log ()log log a a a b c b c+=+5.已知x ，y 为正实数，则下列式子中正确的是（）A ．lg lg lg lg 222x y x y +=+B ．lg()lg lg 222x y x y +=⋅C ．lg lg lg lg 222x y x y⋅=+D ．lg()lg lg 222x y x y⋅=⋅6.设方程22(lg )lg 30x x --=的两实根是a ，b ，则log log a b b a +等于（）A ．1B ．-2C ．-4D ．103-7.在(2)log (5)a y a -=-中，实数a 的取值范围是（）A ．5a >或2a <B ．23a <<或35a <<C ．25a <<D ．34a <<8.函数()ln1xf x x =+-的定义域为（）A ．(0，+∞)B ．(1，+∞)C ．(0，1)D ．(0，1)∪(1，+∞)9.已知函数12()2log f x x =的值域为[-1，1]，则函数()f x 的定义域为（）A ．22B ．[11]-，C ．1[2]2，D ．2(])2-∞⋃∞，+10.已知3log 6a =，5log 10b =，7log 14c =，则（）A ．c b a >>B ．b c a >>C ．a c b >>D ．a b c>>11.已知2log 3.45a =，4log 3.65b =，3log 0.31()5c =，则（）A ．a b c >>B ．b a c >>C ．a c b >>D ．c a b>>12.函数12log 2y x =+的单调增区间为（）A ．()-∞∞，+B ．(2)-∞-，C ．(2)-∞+，D ．(2)(2)-∞-⋃∞，，+13.若函数log (01)a y x a =<<在区间[a ，2a ]上的最大值是最小值的3倍，则a的值为（）A ．22B ．24C ．12D ．1414.函数log (2)5a y x =-+过定点（）A ．(1，0)B ．(3，1)C ．(3，5)D ．(1，5)15.当a >1时，在同一坐标系中，函数x y a -=与log a y x =的图象大致是（）A ．B ．C ．D ．16.设函数()(01)x x f x ka a a a -=->≠，在()-∞+∞，上既是奇函数又是增函数，则()log ()a g x x k =+的图象是（）A ．B ．C ．D ．17.已知函数e 1(1)()ln (1)x x f x x x ⎧-=⎨>⎩≤，则(ln 2)f 的值为_________．18.函数12log (1)()2(1)x x x f x x ⎧⎪=⎨⎪<⎩≥的值域是_________________．19.已知13log 2a =，0.62b =，4log 3c =，则a ，b ，c 的大小关系为_____________．20.给出下列命题：12log 2log a a x x =；2函数2log (1)y x =+是对数函数；3函数1ln1xy x+=-与ln(1)ln(1)y x x =+--的定义域相同；4若log log a a m n <，则m n <．其中正确的命题是_________．21.已知函数()f x 在[0)+∞，上是增函数，()(||)g x f x =-，若(lg )(1)g x g >，求x 的取值范围．22.设函数212log (0)()log ()(0)xx f x x x >⎧⎪=⎨-<⎪⎩，若()()f a f a >-，求实数a 的取值范围．23.已知函数3()2log f x x =+(1≤x ≤9)，求函数22[()]()y f x f x =+的最大值．【参考答案】24．（1）1；（2）3；（3）1；（4）2；（5）4；（6）12-25．D26．B27．B28．D29．D30．B31．B32．A33．D34．C35．B36．B37．C38．A39．C40．141．(2)-∞，42．a <c <b43．③44．11010x <<45．1a >或10a -<<46．22阅读材料反函数趣谈在指数函数2x y =中，x 为自变量，y 为因变量．如果把y 当成自变量，x 当成因变量，同学们思考一下，x 是不是y 的函数？在指数函数2x y =中，过y 轴正半轴上任意一点作x 轴的平行线，与2x y =的图象有且只有一个交点．另一方面，根据指数与对数的关系，由指数式2x y =可得到对数式2log x y =．这样，对于任意一个(0)y ∈+∞，，通过式子2log x y =，在R 中都有唯一确定的x 和它对应．此时，可以把y 作为自变量，x 作为y 的函数，这时我们就说2log x y =((0))y ∈+∞，是函数2x y =()x ∈R 的反函数．注意到，在函数2log x y =中，y 是自变量，x 是函数，但是习惯上，我们通常用x 表示自变量，y 表示函数，因此我们对调函数2log x y =中的字母，把它写成2log y x =，这样，对数函数2log y x =((0))x ∈+∞，是指数函数2x y =()x ∈R 的反函数．由前面的讨论可知，指数函数2x y =()x ∈R 与对数函数2log y x =((0))x ∈+∞，是互为反函数的．类似地，我们可以得到对数函数log (01)a y x a a =>≠，且和指数函数x y a =(01)a a >≠，且互为反函数．在上面的讨论过程中我们发现，过y 轴正半轴上任意一点作x 轴的平行线，与2x y =的图象有且只有一个交点，这就保证了对于任意一个(0)y ∈+∞，，都有唯一确定的2log x y =和它对应，进而才能得到反函数．这就启发我们，不是任意的函数都存在反函数的，只有一一对应的函数才存在反函数．一一对应的函数是指值域中的每一个元素y 只有定义域中的唯一的一个元素x 和它相对应，即定义域中的元素x 和值域中的元素y ，通过对应法则y=f (x )存在着一一对应关系．清楚了反函数存在的条件后，我们接下来讨论反函数的性质．通过画出指数函数2x y =与对数函数2log y x =的图象后，我们发现它们是关于直线y=x 对称的，也就是互为反函数的两个函数的图象是关于直线y=x 对称的．这与我们前面的分析也是一致的，原函数与反函数是定义域、值域互换，对应法则互逆．研究反函数的性质离不开函数的单调性和奇偶性，下面的结论同学们可以自己尝试证明．一个函数与它的反函数在相应区间上单调性是一致的，也就是说如果原函数在某个区间上是单调递增（减）的，那么它的反函数在相应区间上也是单调递增（减）的．关于奇偶性，如果一个奇函数存在反函数，那么它的反函数也是奇函数；一般情况下偶函数是不存在反函数的，例外情况是f (x )=C （C 为常数）．学习了反函数这种重要的工具，它可以帮助我们解决很多问题．当原函数的性质不容易研究时，我们可以考虑研究它的反函数．比如当直接求原函数的值域比较困难时，可以通过求其反函数的定义域来确定原函数的值域，来看一道具体的例题．【例】已知函数10110x xy =+，求它的值域．解析：先计算它的反函数，由10110x x y =+得到(110)10x x y +=，解得101x y y =-，反函数即为lg 1y x y =-，反函数的定义域为原函数的值域，也就是01y y >-，原函数的值域即为(01)，．练习题1.下列函数中，有反函数的是（）A ．22y x x=+B ．||y x =C ．2lg y x =D ．11y x =-2.函数21x y =-的反函数为_____________．3.已知函数1212x x y -=+，求它的值域．【参考答案】1.D2.2log (1)y x =+3.(-1，1)。