三角函数的化简求值(含答案) (1)

（山东省德州市2019届高三期末联考数学（理科）试题）8.第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础设计的，会标是四个全等的直角三角形与一个小正方形拼成的一个大正方形，如果小正方形的面积为，大正方形的面积为，直角三角形中较小的锐角为，则（）A. B. C. D.【答案】D【解析】【分析】由图形可知三角形的直角边长度差为a，面积为6，列方程组求出直角边得出sinθ，代入所求即可得出答案．【详解】由题意可知小正方形的边长为a，大正方形边长为5a，直角三角形的面积为6，设直角三角形的直角边分别为x，y且x＜y，则由对称性可得y＝x+a，∴直角三角形的面积为S xy＝6，联立方程组可得x＝3a，y＝4a，∴sinθ，tanθ＝．∴===，故选：D．【点睛】本题考查了解直角三角形，三角恒等变换，属于基础题．（山东省潍坊市2019届高三上学期期末测试数学（理科）试题）3.若，则（）A. B. C. D.【答案】C【解析】【分析】本道题化简式子,计算出,结合,即可.【详解】,得到,所以,故选C.【点睛】本道题考查了二倍角公式,难度较小.（山东省烟台市2018届高三下学期高考诊断性测试数学（文）试题）14.已知,则_______【答案】【解析】原式化为，，所以，，填。

（江西省新余市2019届高三上学期期末考试数学（理）试题）15.已知，则______．【答案】【解析】【分析】根据同角的三角函数的关系和二倍角公式即可求出．【详解】解：，，，，，故答案为：．【点睛】本题考查同角的三角函数关系式和二倍角公式的应用，属于基础题．（湖南省长沙市2019届上学期高三统一检测理科数学试题）15.在平面直角坐标系中，角的顶点在原点，始边与轴的非负半轴重合，终边过点，则__________.【答案】【解析】【分析】结合终边过点坐标，计算出，结合二倍角公式和余弦两角和公式，即可。

【详解】，所以【点睛】本道题考查了二倍角公式与余弦的两角和公式，难度中等。

第九讲: 三角函数的化简与求值一、知识要点1．两角和与差的正弦、余弦、正切公式(1)C (α－β)：cos(α－β)＝cos_αcos_β＋sin_αsin_β； (2)C (α＋β)：cos(α＋β)＝cos_αcos_β－sin_αsin_β； (3)S (α＋β)：sin(α＋β)＝sin_αcos_β＋cos_αsin_β； (4)S (α－β)：sin(α－β)＝sin_αcos_β－cos_αsin_β； (5)T (α＋β)：tan(α＋β)＝tan α＋tan β1－tan αtan β；(6)T (α－β)：tan(α－β)＝tan α－tan β1＋tan αtan β.2．二倍角的正弦、余弦、正切公式 (1)S 2α：sin 2α＝2sin_αcos_α；(2)C 2α：cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α； (3)T 2α：tan 2α＝2tan α1－tan 2α.3．有关公式的逆用、变形等(1)tan α±tan β＝tan(α±β)(1∓tan_αtan_β)； (2)cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2； (3)1＋sin 2α＝(sin α＋cos α)2,1－sin 2α＝(sin α－cos α)2， sin α±cos α＝2sin ⎝⎛⎭⎪⎫α±π4.4．函数f (α)＝a cos α＋b sin α(a ，b 为常数)，可以化为f (α)＝a 2＋b 2sin(α＋φ)或f (α)＝a 2＋b 2cos(α－φ)，其中φ可由a ，b 的值唯一确定． 二、方法点拨三角变换是运算化简过程中运用较多的变换, 也是历年高考命题的热点.提高三角变换能力, 要学会设置条件, 灵活运用三角公式, 掌握运算、化简的方法和技能.常用的数学思想方法技巧如下: 1. 角的变换: 在三角化简、求值、证明中, 表达式往往出现较多的相异角, 可根据角与角之间的和差、倍半、互补、互余的关系, 运用角的变换, 沟通条件与结论中的差异, 使问题获解.对角的变形如下:角的变换：β＝α＋β2－α－β2；α－β2＝⎝ ⎛⎭⎪⎫α＋β2－⎝ ⎛⎭⎪⎫α2＋β)2()2()(,2304560304515α-β-β+α=β-β+α=α=-=-=,)4()4()()(2α-π-α+π=β-α+β+α=α,)4(24α-π-π=α+π特别地, α+π4与α-π4为互余角, 它们之间可以互相转化, 在三角变形中使用频率高.2. 函数名称变换: 三角变形中, 常常需要变函数名称为同名函数. 如在三角函数中正余弦是基础, 通常化切、割为弦, 变异名为同名.3. 常数代换: 在三角函数运算、求值、证明中, 有时需要将常数转化为三角函数值, 例如常数“1”的代换变形有: α-α=α-α=α+α=222222cot csc tan sec cos sin 1.4. 幂的变换: 降幂是三角变换时常用方法, 对次数较高的三角函数式, 一般采用降幂处理的方法. 常用降幂公式有:1cos sin ,22cos 1cos ,22cos 1sin 2222=α+αα+=αα-=α 等, 三角变换时, 有时需要升幂, 如对无理式α+cos 1常用升幂化为有理式, 升幂公式与降幂公式是相对而言的.5. 公式变形式: 根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，其手法通常有：“常值代换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等．三角公式是变换的依据, 应熟练掌握三角公式的直接应用,逆用以及变形式的应用.如:)tan tan 1)(tan(tan tan ,sin 22sin cos β⋅αβ±α=β±ααα=α 等. 三、典型例题讲解:考点一、三角函数式的化简【例1】►化简2cos 4x －2cos 2x ＋122tan ⎝⎛⎭⎪⎫π4－x sin 2⎝ ⎛⎭⎪⎫π4＋x .三角函数式的化简要遵循“三看”原则：(1)一看“角”，通过看角之间的差别与联系，把角进行合理的拆分，从而正确使用公式；(2)二看“函数名称”，看函数名称之间的差异，从而确定使用的公式；(3)三看“结构特征”，分析结构特征，找到变形的方向． 【训练1】 化简：(sin α＋cos α－1)(sin α－cos α＋1)sin 2α.考点二、三角函数式的求值【例1】已知0＜β＜π2＜α＜π，且cos ⎝ ⎛⎭⎪⎫α－β2＝－19，sin ⎝ ⎛⎭⎪⎫α2－β＝23，求cos(α＋β)的值．训练1】 已知α，β∈⎝ ⎛⎭⎪⎫0，π2，sin α＝45，tan(α－β)＝－13，求cos β的值． 训练2】已知cos(α-6π)+sin α=354，则sin(α+67π)的值是（ ）训练3】已知tan ⎝ ⎛⎭⎪⎫x ＋π4＝2，则tan x tan 2x 的值为________训练4】已知2π＜β＜α＜43π,cos(α－β)=1312,sin(α+β)=－53,求sin2α的值_________考点三、三角函数的求角问题【例1】►已知cos α＝17，cos(α－β)＝1314，且0＜β＜α＜π2，求β.通过求角的某种三角函数值来求角，在选取函数时，遵照以下原则：①已知正切函数值，选正切函数；②已知正、余弦函数值，选正弦或余弦函数；若角的范围是⎝ ⎛⎭⎪⎫0，π2，选正、余弦皆可；若角的范围是(0，π)，选余弦较好；若角的范围为⎝ ⎛⎭⎪⎫－π2，π2，选正弦较好．【训练1】 已知α，β∈⎝ ⎛⎭⎪⎫－π2，π2，且tan α，tan β是方程x 2＋33x ＋4＝0的两个根，求α＋β的值．【训练2】已知tan(α－β)＝12，tan β＝－17，且α，β∈(0，π)，求2α－β的值．考点四、 三角函数的综合应用【例1】►设0<θ<2π，曲线x 2sin θ+y 2cos θ=1和x 2cos θ－y 2sin θ=1有4个不同的交点。

三角函数的化简求值一、单选题(共10道，每道10分)1.化简的结果是( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简2.化简的结果是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简3.下列选项中，不是化简的结果的是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简4.化简的结果的是( )A.，其中B.，其中C.，其中D.，其中答案：B解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简5.函数（）的值域为( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简6.函数（）的值域为( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简7.已知函数，若为偶函数，则的一个值为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简8.函数（）的值域为( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简9.函数（）的值域为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简10.函数（）的值域是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：形如asinx+bcosx的化简。

)＝cos_αcos_β＋sin_αsin_β； (2)C (α＋β)：cos(α＋β)＝cos_αcos_β－sin_αsin_β； (3)S (α＋β)：sin(α＋β)＝sin_αcos_β＋cos_αsin_β； (4)S (α－β)：sin(α－β)＝sin_αcos_β－cos_αsin_β；(5)T (α＋β)：tan(α＋β)＝tan α＋tan β1－tan αtan β；(6)T (α－β)：tan(α－β)＝tan α－tan β1＋tan αtan β. 2．二倍角的正弦、余弦、正切公式．二倍角的正弦、余弦、正切公式 (1)S 2α：sin 2α＝2sin_αcos_α；(2)C 2α：cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α；(3)T 2α：tan 2α＝2tan α1－tan 2α. 3．有关公式的逆用、变形等．有关公式的逆用、变形等(1)tan α±tan β＝tan(α±β)(1∓tan_αtan_β)；(2)cos 2α＝1＋cos 2α2，sin 2α＝1－cos 2α2；(3)1＋sin 2α＝(sin α＋cos α)2,1－sin 2α＝(sin α－cos α)2，sin α±cos α＝2sin èæøöα±π4. ＝α＋β2－α－β2；α－β2＝èæøöα＋β2－èæøöα2＋β.原则: 用已知表示待求用已知表示待求 （2） 化简技巧：切化弦、“1”的代换等．的代换等． 6 三个变化三个变化(1)变角：目的是沟通题设条件与结论中所涉及的角，其手法通常是“配凑”． (2)变名：变名：通过变换函数名称达到减少函数种类的目的，通过变换函数名称达到减少函数种类的目的，通过变换函数名称达到减少函数种类的目的，其手法通常有其手法通常有“切化弦”、“升幂与降幂”等．等．(3)等．等．二 典型题目1 三角函数式的化简【例1】►化简2cos 4x －2cos 2x ＋122tan èæøöπ4－x sin 2èæøöπ4＋x. 【训练1】 化简 (sin cos 1)(sin cos 1)sin 2a a a a a+--+：. 1三角三角函数式函数式的化简求值训练 一．重要公式与方法技巧：1 两角和与差的两角和与差的正弦正弦、余弦、正切公式、余弦、正切公式(1)C (α－β)：cos(α－β4．函数f (α)＝a cos α＋b sin α(a ，b 为常数)，可以化为f (α)＝a 2＋b 2sin(α＋φ)或f (α)＝a 2＋b 2c os(α－φ)，其中φ可由a ，b 的值唯一确定．的值唯一确定． 5两个技巧两个技巧（1）拆角、拼角技巧：2α＝(α＋β)＋(α－β)；α＝(α＋β)－β；β变式：根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，其手法通常有：“常值代换”、“逆用变用公式”、“通分约分”、“分解与分解与组合组合”、“配方与配方与平方平方”＜π2＜α＜π，且cos èæøöα－β2＝－19，sin èæøöα2－β＝23，求cos(α＋β)的值．的值．【训练2】 已知α，β∈èæøö0，π2，sin α＝45，tan(α－β)＝－13，求cos β的值．的值．三 三角函数的求角问题三角函数的求角问题【例3】►已知cos α＝17，cos(α－β)＝1314，且0＜β＜α＜π2，求β. 【训练3】 已知α，β∈èæøö－π2＋33x ＋4＝0的两个根，求α＋β的值．的值．四 三角函数的综合应用三角函数的综合应用【例4】►已知函数f (x )＝2cos 2x ＋sin 2x .(1)求f èæø－π62二 三角三角函数式函数式的求值的求值【例2】►已知0＜β，π2，且tan α，tan β是方程x 2öπ3的值；(2)求f (x )的最大值和最小值．和最小值．【训练4】 已知函数f (x )＝2sin(π－x )cos x . (1)求f (x )的最小正周期；的最小正周期；(2)求f (x )在区间ëéûù，π2上的最大值和最小值．上的最大值和最小值．一、给值求值一、给值求值一般是给出某些角的三角函数式的值，求另外一些角的求另外一些角的三角函数值三角函数值，解题的关键在于“变角”，如α＝(α＋β)－β，2α＝(α＋β)＋(α－β)等，把所求角用含已知角的式把所求角用含已知角的式子表示子表示，求解时要注意角的范围的讨论．角的范围的讨论．3【示例】►已知tan èæøöx ＋π4＝2，则tan ＝12，tan β，π2. (1)求sin θ和cos θ的值；的值；(2)若5cos(θ－φ)＝35cos φ，0＜φ＜π2，求cos φ的值．的值．【课后巩固】1．81cos sin =×a a ，且4p ＜a ＜2p，则a a sin cos -的值为：的值为：A 、23B 、23-C 、43D 、43-2．已知a a aa a cos 3sin 2cos sin ,2tan +--=则的值是的值是A 、－1 B 、1 C 、－3 D 、3 3．已知=-=+-=-)sin(,21sin cos ,43cos sin a b b a b a 则A 、3219B 、3219-C 、0 D 、1916-4．已知 5.已知3sin(),45x p -=则sin 2x 的值为的值为 （ ）A.1925 B.1625 C.1425 D.7256．已知1sin cos 5q q -=，则sin 2q 的值是的值是A 、45B 、45-C 、2425D 、－24257．已知54)cos(-=-b a 54)cos(=+b a ),2(p p b a Î-)2,23(p p b a Î+则cos2a =( ） xtan 2x 的值为________．二、给值求角二、给值求角“给值求角”：实质上也转化为“给值求值”，关键也是变角，把所求角用含已知角的式把所求角用含已知角的式子表示子表示，由所得的函数值结合该函数的单调由所得的函数值结合该函数的单调区间区间求得角．求得角．【示例】►已知tan(α－β)＝－17，且α，β∈(0，π)，求2α－β的值．的值． ▲三角恒等变换与▲三角恒等变换与向量向量的综合问题的综合问题 两角和与差的两角和与差的正弦正弦、余弦、正切公式作为解题工具，是每年余弦、正切公式作为解题工具，是每年高考高考的必考内容，常在选择题中以条件求值的形式考查．近几年该部分内容与向量的综合问题常出现在解答题中，并且成为高考的一个新考查方向．高考的一个新考查方向．【示例】► 已知向量a ＝(sin θ，－2)与b ＝(1，cos θ)互相互相垂直垂直，其中θ∈èæøö0q tam 和)4(q p-tam 是方程02=++q px x 的两根，则p 、q 间的关系是：间的关系是： A 、01=+-q p B 、01=++q p C 、01=-+q p D 、01=--q p4A 、257-B 、257C 、1-D 、1 8．22cos 75cos 15cos75cos15++ 的值等于（的值等于（ ） A 、62 B 、32 C 、54D 、1＋349．已知tan(α+β)＝52，tan(β－4p )＝41，那么tan(α+4p )的值是的值是A ．1813 B ．223 C ．2213 D ．18310.若,(0,)2pa b Î，3cos()22ba -=,1sin()22a b -=-，则cos()a b +的值等于 （A ）32-（B ）12- （C ）12（D ）32 11、已知tan 2a =，求2212sin cos cos sin a a a a +-12．求tan200+tan400+3tan200tan400的值. 13.已知3110,tan 4tan 3pa p a a<<+=-（Ⅰ）求tan a的值；（Ⅱ）求225sin 8sin cos 11cos 822222sin 2a a a a p a ++-æö-ç÷èø 14.已知40,sin 25pa a <<=（Ⅰ）求22sin sin 2cos cos 2a a a a++的值；（Ⅱ）求5tan()4pa -的值。

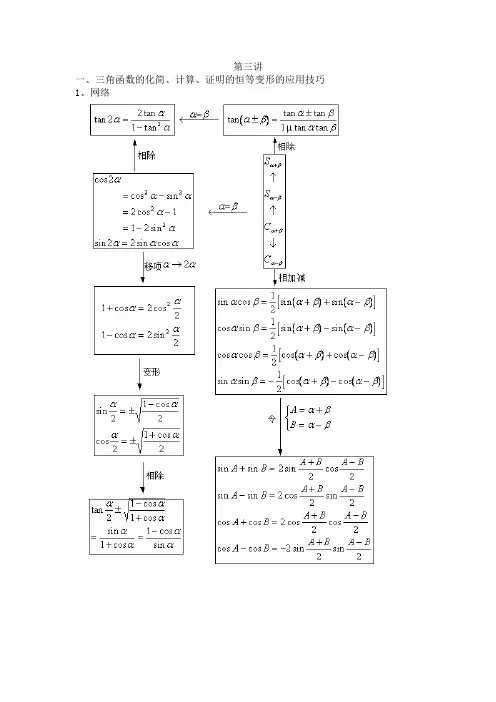
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结（1）变换函数名对于含同角的三角函数式，通常利用同角三角函数间的基本关系式及诱导公式，通过“切割化弦”，“切割互化”，“正余互化”等途径来减少或统一所需变换的式子中函数的种类，这就是变换函数名法．它实质上是“归一”思想，通过同一和化归以有利于问题的解决或发现解题途径。

【例1】已知θ同时满足和,且a、b 均不为0，求a、b的关系。

练习：已知sin（α＋β）＝，cos（α－β）＝，求的值。

2）变换角的形式对于含不同角的三角函数式，通常利用各种角之间的数值关系，将它们互相表示，改变原角的形式，从而运用有关的公式进行变形，这种方法主要是角的拆变．它应用广泛，方式灵活，如α可变为（α＋β）－β；2α可变为（α＋β）＋（α－β）；2α－β可变为（α－β）＋α；α／2可看作α／4的倍角；（45°＋α）可看成（90°＋2α）的半角等等。

【例2】求sin（θ＋75°）＋cos（θ＋45°）－cos（θ＋15°）的值。

练习已知，求的值【例3】已知sinα＝Ａsin（α＋β）（其中cosβ≠A），试证明：tan（α＋β）＝提示：sin[（α＋β）－β]＝Ａsin （α＋β）（3）以式代值利用特殊角的三角函数值以及含有1的三角公式，将原式中的1或其他特殊值用式子代换，往往有助于问题得到简便地解决。

这其中以“1”的变换为最常见且最灵活。

“1”可以看作是sin2x＋cos2x, sec2x－tan2x, csc2x －cot2x，tanxcotx, secxcosx, tan45°等，根据解题的需要，适时地将“1”作某种变形，常能获得较理想的解题方法。

【例4】化简：（4）和积互化积与和差的互化往往可以使问题得到解决，升幂和降次实际上就是和积互化的特殊情形。

这往往用到倍、半角公式。

三角函数式的求值【知识点精讲】三角函数式的求值的关键是熟练掌握公式及应用, 掌握公式的逆用和变形三角函数式的求值的类型一般可分为:(1)“给角求值”：给出非特殊角求式子的值。

仔细观察非特殊角的特点，找出和特殊角之间的关系，利用公式转化或消除非特殊角（2）“给值求值”：给出一些角得三角函数式的值，求另外一些角得三角函数式的值。

找出已知角与所求角之间的某种关系求解（3）“给值求角”：转化为给值求值，由所得函数值结合角的范围求出角。

（4）“给式求值”：给出一些较复杂的三角式的值，求其他式子的值。

将已知式或所求式进行化简，再求之三角函数式常用化简方法：切割化弦、高次化低次注意点：灵活角的变形和公式的变形重视角的范围对三角函数值的影响，对角的范围要讨论【例题选讲】一、“给角求值”例1、计算)310(tan 40sin 00-的值。

练习1:tan20°+4sin20°练习2、（1）化简;︒--︒︒︒-20sin 1160sin 20cos 20sin 212；（2）求值： .练习3：求()00001tan21tan24tan21tan24++⋅ ()()()()()000021tan11tan21tan431tan44+⋅+++练习4、不查表求sin 220°+cos 280°+3sin20°cos80°的值二、“给值求值”：例2、已知tan(45°+θ)=3,求sin2θ-2cos 2θ的值练习:)6sin(,212tan παα+=求已知 例3、已知sin(-4πx)=135，0<x<4π，求)4cos(2cos x x +π的值。

[点评]：分析:角之间的关系：2)4()4(πππ=++-x x 及)4(222x x -=-ππ ，利用余角间的三角函数的关系便可求之。

︒︒+︒+︒50tan 10tan 350tan 10tan常用凑角：)2()2()(,2304560304515α-β-β+α=β-β+α=α=-=-=, )4()4()()(2α-π-α+π=β-α+β+α=α，2()()βαβαβ=+--，)4(24α-π-π=α+π，特别地, α+π4与α-π4为互余角, 它们之间可以互相转化。

难点16 三角函数式的化简与求值三角函数式的化简和求值是高考考查的重点内容之一.通过本节的学习使考生掌握化简和求值问题的解题规律和途径，特别是要掌握化简和求值的一些常规技巧，以优化我们的解题效果，做到事半功倍.●难点磁场(★★★★★)已知2π＜β＜α＜43π,cos(α－β)=1312,sin(α+β)=－53,求sin2α的值_________.●案例探究［例1］不查表求sin 220°+cos 280°+3cos20°cos80°的值.命题意图：本题主要考查两角和、二倍角公式及降幂求值的方法，对计算能力的要求较高.属于★★★★级题目.知识依托：熟知三角公式并能灵活应用.错解分析：公式不熟，计算易出错.技巧与方法：解法一利用三角公式进行等价变形；解法二转化为函数问题，使解法更简单更精妙，需认真体会.解法一：sin 220°+cos 280°+3sin 220°cos80° =21 (1－cos40°)+21 (1+cos160°)+3sin20°cos80° =1－21cos40°+21cos160°+3sin20°cos(60°+20°) =1－21cos40°+21(cos120°cos40°－sin120°sin40°)+3sin20°(cos60°cos20°－sin60°sin20°)=1－21cos40°－41cos40°－43sin40°+43sin40°－23sin 220° =1－43cos40°－43(1－cos40°)= 41 解法二：设x =sin 220°+cos 280°+3sin20°cos80°y =cos 220°+sin 280°－3cos20°sin80°，则x +y =1+1－3sin60°=21，x －y =－cos40°+cos160°+3sin100° =－2sin100°sin60°+3sin100°=0∴x =y =41，即x =sin 220°+cos 280°+3sin20°cos80°=41. ［例2］设关于x 的函数y =2cos 2x －2a cos x －(2a +1)的最小值为f (a )，试确定满足f (a )=21的a 值，并对此时的a 值求y 的最大值. 命题意图：本题主要考查最值问题、三角函数的有界性、计算能力以及较强的逻辑思维能力.属★★★★★级题目知识依托：二次函数在给定区间上的最值问题.错解分析：考生不易考查三角函数的有界性，对区间的分类易出错.技巧与方法：利用等价转化把问题化归为二次函数问题，还要用到配方法、数形结合、分类讲座等.解：由y =2(cos x －2a)2－2242+-a a 及cos x ∈［－1，1］得：f (a )⎪⎪⎩⎪⎪⎨⎧≥-<<-----≤)2( 41)22( 122)2( 12a a a a a a ∵f (a )=21,∴1－4a =21⇒a =81∉［2,+∞) 故－22a －2a －1=21，解得：a =－1，此时， y =2(cos x +21)2+21，当cos x =1时，即x =2k π，k ∈Z ，y max =5.［例3］已知函数f (x )=2cos x sin(x +3π)－3sin 2x +sin x cos x(1)求函数f (x )的最小正周期；(2)求f (x )的最小值及取得最小值时相应的x 的值；(3)若当x ∈［12π，127π］时，f (x )的反函数为f －1(x )，求f -－1(1)的值. 命题意图：本题主要考查三角公式、周期、最值、反函数等知识，还考查计算变形能力，综合运用知识的能力，属★★★★★级题目.知识依托：熟知三角函数公式以及三角函数的性质、反函数等知识.错解分析：在求f -－1(1)的值时易走弯路.技巧与方法：等价转化，逆向思维.解：(1)f (x )=2cos x sin(x +3π)－3sin 2x +sin x cos x=2cos x (sin x cos 3π+cos x sin 3π)－3sin 2x +sin x cos x=2sin x cos x +3cos2x =2sin(2x +3π)∴f (x )的最小正周期T =π(2)当2x +3π=2k π－2π，即x =k π－125π (k ∈Z )时，f (x )取得最小值－2. (3)令2sin(2x +3π)=1，又x ∈［27,2ππ］, ∴2x +3π∈［3π,23π］,∴2x +3π=65π，则 x =4π，故f -－1(1)= 4π.●锦囊妙计本难点所涉及的问题以及解决的方法主要有：1.求值问题的基本类型：1°给角求值，2°给值求值，3°给式求值，4°求函数式的最值或值域，5°化简求值.2.技巧与方法：1°要寻求角与角关系的特殊性，化非特角为特殊角，熟练准确地应用公式. 2°注意切割化弦、异角化同角、异名化同名、角的变换等常规技巧的运用. 3°对于条件求值问题，要认真寻找条件和结论的关系，寻找解题的突破口，很难入手的问题，可利用分析法.4°求最值问题，常用配方法、换元法来解决.●歼灭难点训练一、选择题1.(★★★★★)已知方程x 2+4ax +3a +1=0(a ＞1)的两根均tan α、tan β，且α，β∈(－2,2ππ)，则tan 2βα+的值是( ) A.21 B.－2 C.34 D. 21或－2 二、填空题2.(★★★★)已知sin α=53，α∈(2π，π)，tan(π－β)= 21，则tan(α－2β)=_________.3.(★★★★★)设α∈(43,4ππ)，β∈(0，4π)，cos(α－4π)=53，sin(43π+β)=135，则sin(α+β)=_________.三、解答题4.不查表求值:.10cos 1)370tan 31(100sin 130sin 2︒+︒+︒+︒ 5.已知cos(4π+x )=53，(1217π＜x ＜47π)，求x x x tan 1sin 22sin 2-+的值. 6.(★★★★★)已知α－β=38π，且α≠k π(k ∈Z ).求)44(sin 42sin 2csc )cos(12βπαααπ-----的最大值及最大值时的条件. 7.(★★★★★)如右图，扇形OAB 的半径为1，中心角60°，四边形PQRS 是扇形的内接矩形，当其面积最大时，求点P 的位置，并求此最大面积.8.(★★★★★)已知cos α+sin β=3，sin α+cos β的取值范围是D ，x ∈D ，求函数y =10432log 21++x x 的最小值，并求取得最小值时x的值.参考答案难点磁场 解法一：∵2π＜β＜α＜43π,∴0＜α－β＜4π.π＜α+β＜43π, ∴sin(α－β)=.54)(sin 1)cos(,135)(cos 122-=+--=+=--βαβαβα。

，故选 B．
3．【2017
届广西玉林市、贵港市高中毕业班质量检测】若
cos
−
3sin
=
0
，则
tan
−
4
=
（
）
−1
1
A． 2
B．-2
C． 2
D．2
【答案】A
【解析】由 cos
− 3sin
=
0
tan
，知
=
1 3
，则
tan
− 4
=
tan −1 1+ tan
=
−
1 2
，故选 A
．
4．【山西省孝义市 2017 届高三下学期高考考前质量检测三（5 月）】已有角 的顶点与坐标原点重合，
+ cos2
sin ”；（3）化正弦、余弦为正切，即 cos
=
tan
；
tan = sin
（4）化正切为正弦、余弦，即
cos ；（ 5 ） 正 弦 、 余 弦 和 （ 差 ） 与 积 的 互 化 ， 即
(sin cos )2 =1 2sin cos ．
tan = 3
1− sin 2 =
【变式 1】【例题中的条件不改变，所求三角函数式改变】若
【解析】
16 8 ，选 D．
【方法技巧归纳】二倍角公式的正用、逆用、变形用是公式的种主要应用手段，特别是二倍角的余弦 公式，其变形公式在求值与化简中有广泛的应用，在综合使用两角和与差、二倍角公式化简求值时，要注 意以下几点：(1)熟练掌握公式的正用、逆用和变形使用；(2)擅于拆角、配角；(3)注意二倍角的相对性； (4)注意角的范围；(5)熟悉常用的方法和技巧，如切化弦、异名化同名、异角化同角等．

1分钟学会-诱导公式化简求值问题【三角函数】在数学中，诱导公式是指将某个三角函数表达式中的自变量通过某种方式转换成其他三角函数的自变量的公式。

主要应用于三角函数的公式化简和求值。

常见的诱导公式有三个，它们分别是正弦诱导公式、余弦诱导公式和正切诱导公式。

下面我们来一一介绍它们的具体内容以及应用方法。

正弦诱导公式：$$\sin(A+B)=\sin A\cos B+\cos A\sin B$$这个公式主要应用于将$\sin(A+B)$转换成其他三角函数的和的形式。

可以通过将公式右边的$\cos A$换成$\sin(A+\frac{\pi}{2})$，将公式左边的$\sin(A+B)$替换成$\sin C$，最终得到以下诱导公式：$$\sin C=2\sin\frac{C}{2}\cos\frac{C}{2}$$余弦诱导公式：$$\cos(A+B)=\cos A\cos B-\sin A\sin B$$这个公式主要应用于将$\cos(A+B)$转换成其他三角函数的和的形式。

可以通过将公式右边的$\sin A$换成$\cos(A+\frac{\pi}{2})$，将公式左边的$\cos(A+B)$替换成$\cos C$，最终得到以下诱导公式：$$\cos C=2\cos^2\frac{C}{2}-1=1-2\sin^2\frac{C}{2}$$这个公式有一个重要的应用，即将$\cos C$转换成$\sin C$。

正切诱导公式：$$\tan(A+B)=\frac{\tan A+\tan B}{1-\tan A\tan B}$$这个公式主要应用于将$\tan(A+B)$转换成其他三角函数的和的形式。

可以通过将公式右边的$\tan A$和$\tan B$分别换成$\frac{\sin A}{\cos A}$和$\frac{\sin B}{\cos B}$，并进行通分，最终得到以下诱导公式：$$\tan C=\frac{2\tan\frac{C}{2}}{1-\tan^2\frac{C}{2}}$$这个公式可以看作是正切半角公式的推广。

三角函数的化简1、三角函数式的化简：（1）常用方法：①直接应用公式进行降次、消项；②切割化弦，异名化同名，异角化同角；③ 三角公式的逆用等。

（2）化简要求：①能求出值的应求出值；②使三角函数种数尽量少；③使项数尽量少；④尽量使分母不含三角函数；⑤尽量使被开方数不含三角函数2、三角函数的求值类型有三类：（1）给角求值：一般所给出的角都是非特殊角，要观察所给角与特殊角间的关系，利用三角变换消去非特殊角，转化为求特殊角的三角函数值问题；（2）给值求值：给出某些角的三角函数式的值，求另外一些角的三角函数值，解题的关键在于“变角”，如2(),()()ααββααβαβ=+-=++-等，把所求角用含已知角的式子表示，求解时要注意角的范围的讨论；（3）给值求角：实质上转化为“给值求值”问题，由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。

3、三角等式的证明：（1）三角恒等式的证题思路是根据等式两端的特征，通过三角恒等变换，应用化繁为简、左右同一等方法，使等式两端的化“异”为“同”；（2）三角条件等式的证题思路是通过观察，发现已知条件和待证等式间的关系，采用代入法、消参法或分析法进行证明。

一、化简 【例1】求值：︒+︒︒⋅︒+︒+︒80cot 40csc 10sin 20tan 10cos 20sin 2.【变式】1、求值()︒+︒︒+︒+︒10cos 110tan 60tan 110cos 40cos 2【变式】2、求0020210sin 21)140cos 1140sin 3(⋅-。

【例2】（三兄弟）已知23523sin cos παπαα<<=-，且，求αααtan 1sin 22sin 2-+的值【变式】（05天津）已知727sin(),cos 241025παα-==，求sin α及tan()3πα+．【例3】（最值辅助角）已知函数f (x )=2a sin 2x －23a sin x cos x +a +b －1，（a 、b 为常数，a <0），它的定义域为[0,2π]，值域为[－3,1]，试求a 、b 的值。

[基础巩固]1．(多选)如果α是第二象限的角，下列各式不正确的是( )A ．tan α＝－sin αcos αB ．cos α＝－1－sin 2 αC ．sin α＝－1－cos 2 αD ．tan α＝cos αsin α解析 由商数关系可知A 、D 均不正确，当α为第二象限角时，cos α＜0，sin α＞0，故B 正确．答案 ACD2．已知sin α－cos α＝－54，则sin α·cos α等于( ) A ．74 B ．－916C ．－932D ．932 解析 因为sin α－cos α＝－54， 平方可得1－2sin αcos α＝2516， 所以2sin αcos α＝－916， 即sin αcos α＝－932. 答案 C3．已知tan θ＝2，则sin 2θ＋sin θcos θ－2cos 2θ等于( )A ．－43B ．54C ．－34D ．45解析 sin 2θ＋sin θcos θ－2cos 2θ＝sin 2θ＋sin θcos θ－2cos 2θsin 2θ＋cos 2θ＝tan 2θ＋tan θ－2tan 2θ＋1， 又tan θ＝2，故原式＝4＋2－24＋1＝45. 答案 D4．若α是第三象限角且cos α＝－33，则sin α＝________，tan α＝________.解析 ∵α是第三象限角且cos α＝－33， ∴sin α＝－1－cos 2α＝－63， ∴tan α＝sin αcos α＝ 2. 答案 －63 2 5．已知cos θ＝13，则⎝⎛⎭⎫tan θ＋1tan θ·sin θ的值为________． 解析 原式＝⎝⎛⎭⎫sin θcos θ＋cos θsin θ·sin θ ＝sin 2θ＋cos 2θcos θ·sin θ·sin θ ＝1cos θ＝3.答案 36．已知tan α＝2，求下列代数式的值：(1)4sin α－2cos α5cos α＋3sin α； (2)14sin 2α＋13sin αcos α＋12cos 2α. 解析 (1)原式＝4tan α－25＋3tan α＝611. (2)原式＝14sin 2α＋13sin αcos α＋12cos 2αsin 2α＋cos 2α＝14tan 2α＋13tan α＋12tan 2α＋1＝14×4＋13×2＋125＝1330. [能力提升]7．化简sin 2α＋cos 4α＋sin 2αcos 2α的结果是( )A ．14B ．12C ．1D ．32解析 原式＝sin 2α＋cos 2α(cos 2α＋sin 2α)＝sin 2α＋cos 2α＝1.答案 C8．已知cos α＝－35，且tan α>0，则sin αcos 2α1－sin α＝____________ . 解析 由cos α<0，tan α>0知α是第三象限角，且sin α＝－45， 故原式＝sin αcos 2α1－sin α＝sin α(1－sin 2α)1－sin α＝sin α(1＋sin α)＝⎝⎛⎭⎫－45·⎝⎛⎭⎫1－45＝－425. 答案 －4259．已知关于x 的方程4x 2－2(m ＋1)x ＋m ＝0的两个根恰好是一个直角三角形的一个锐角的正弦、余弦，则实数m 的值为________．解析 由题意知Δ＝4(m ＋1)2－16m ≥0，解得m ∈R .不妨设sin A ＝x 1，cos A ＝x 2，则x 1＋x 2＝12(m ＋1)，x 1·x 2＝14m ， 即sin A ＋cos A ＝12(m ＋1)，sin A cos A ＝14m ， 所以1＋2×14m ＝14(m ＋1)2， 解得m ＝3或m ＝－ 3.当m ＝－3时，sin A cos A ＝－34<0，不合题意，舍去，故m ＝ 3. 答案 3 10．已知sin θ，cos θ是关于x 的方程x 2－ax ＋a ＝0的两个根．求：(1)sin 3θ＋cos 3θ；(2)tan θ＋1tan θ. 解析 根据题意，方程判别式Δ≥0，即(－a )2－4a ≥0，所以a ≤0或a ≥4，且⎩⎪⎨⎪⎧sin θ＋cos θ＝a ，sin θcos θ＝a . 因为(sin θ＋cos θ)2＝1＋2sin θcos θ，即a 2－2a －1＝0，所以a ＝1－2(1＋2舍去)．所以sin θ＋cos θ＝sin θcos θ＝1－ 2.(1)sin 3θ＋cos 3θ＝(sin θ＋cos θ)(sin 2θ－sin θcos θ＋cos 2θ)＝(1－2)[1－(1－2)]＝2－2.(2)tan θ＋1tan θ＝sin θcos θ＋cos θsin θ＝sin 2θ＋cos 2θsin θcos θ＝11－2＝－2－1. [探索创新]11．设α是第三象限角，问是否存在实数m ，使得sin α，cos α是关于x 的方程8x 2＋6mx ＋2m ＋1＝0的两个根？若存在，求出实数m ；若不存在，请说明理由．解析 假设存在实数m 满足条件，由题设得，Δ＝36m 2－32(2m ＋1)≥0，①∵sin α＜0，cos α＜0，∴sin α＋cos α＝－34m ＜0，② sin αcos α＝2m ＋18＞0.③ 又sin 2α＋cos 2α＝1，∴(sin α＋cos α)2－2sin αcos α＝1.把②③代入上式得 ⎝⎛⎭⎫－34m 2－2×2m ＋18＝1， 即9m 2－8m －20＝0，解得m 1＝2，m 2＝－109. ∵m 1＝2不满足条件①，舍去；m 2＝－109不满足条件③，舍去． 故满足题意的实数m 不存在．。

三角函数中的化简求值模型【问题背景】三角函数的化简求值几乎是高考的必考内容之一，化简三角函数式是为了更清楚地显示式中所含量之间的关系，以便于某种要求的应用．一般从函数名、角、运算三方面进行差异分析，遵循化繁为简、清除差异的原则，常用的方法技巧有：切割化弦，降幂，用三角公式转化出现特殊角，异角化同角，异名化同名，高次化低次等.【解决方法】【典例1】（2024高三下·全国·专题练习）已知角α，β的顶点均为坐标原点，始边均与x 轴的非负半轴重合，终边分别过点()1,2A ，()2,1B -，则tan 2αβ+=．【答案】3-【分析】利用三角函数的定义求得tan 2α=，1tan 2β=-，可求得()tan αβ+，再利用二倍角的正切公式解得tan2αβ+，进而确定2αβ+的范围，求得tan2αβ+的值.【套用模型】第一步：因为角α，β的终边分别过点()1,2A ，()2,1B -，所以tan 2α=，1tan 2β=-，（提示：若角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边过点()(),0x y x ≠，则tan y xα=），第二步：因此()tan tan 3tan 1tan tan 4αβαβαβ++==-，又()22tan32tan 41tan 2αβαβαβ++==+-，所以tan32αβ+=-或1tan23αβ+=．第三步：因为角α的终边过点()1,2A ，因此112,242k k ππαππ⎛⎫∈++⎪⎝⎭，1k ∈Z ，因为角β的终边()2,1B -，因此2232,24k k πβπππ⎛⎫∈++ ⎪⎝⎭，2k ∈Z ，所以3,224k k αβππππ+⎛⎫∈++ ⎪⎝⎭，k ∈Z ，所以tan 32αβ+=-．【典例2】（2024·山西晋城·二模）已知tan 2tan αβ=，1sin()4αβ+=，则)in(s βα-=．【答案】112-【分析】由tan 2tan αβ=切化弦可得sin cos 2cos sin αβαβ=，结合两角和差公式分析求解.【套用模型】第一步：因为tan 2tan αβ=，即sin 2sin cos cos αβαβ=，可得sin cos 2cos sin αβαβ=，第二步：又因为()1sin sin cos cos sin 3cos sin 4αβαβαβαβ+=+==，可得1cos sin 12αβ=，第三步：所以()sin cos sin sin cos cos sin 112βααβαβαβ-=-=-=-.故答案为：112-.【典例3】（2024·全国·模拟预测）在ABC 中，tan A ，tan B 是方程2670x x -+=的两个根，则C 的值是．【答案】4π/45︒【分析】根据根与系数的关系及两角和的正切公式求得()tan A B +，再利用诱导公式求解.【套用模型】第一步：由题意，tan tan 6A B +=，tan tan 7A B ⋅=，第二步：所以tan tan 6tan ()11tan tan 17A B A B A B ++===--⋅-，第三步：在ABC 中，()()tan tan πtan 1C A B A B =-+=-+=⎡⎤⎣⎦，由0πC <<，可知π4C =.故答案为：π4（2024·全国·二模）1．已知6cos tan 7sin ααα=-，则cos2α=.（2024·云南昆明·一模）2．已知cos α=π0,2α⎛⎫∈ ⎪⎝⎭，则tan 2α=．（2024·宁夏银川·一模）3．已知3cos si 2n x x +=，则sin 2πcos 4xx =⎛⎫- ⎪⎝⎭.（2024·青海·模拟预测）4．若3π4αβ+=，tan 2α=，则tan β=．（2024·山东·二模）5．在平面直角坐标系中，角α的始边与x轴非负半轴重合，终边经过点()2，则πsin 3α⎛⎫+=⎪⎝⎭．（2024·内蒙古呼伦贝尔·二模）6．已知tan α，tan β是方程2530x x +-=的两个根，则()()22cos sin αβαβ+=-．（2024·广西·二模）7．已知2sin sin2αα=，则πtan 4α⎛⎫+=⎪⎝⎭.（2024·全国·模拟预测）8．已知点()()()cos ,sin A βαβα--与点5π5πcos ,sin 1212B ββ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭关于原点对称，则sin cos αα+=．（2024·全国·模拟预测）9．在ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，若2222024a b c +=，则2tan tan tan (tan tan )A BC A B =+.（2024·陕西安康·模拟预测）10．若()2tan 2024π3α-=，则2sin cos 2cos cos2αααα-=.（2024·山西朔州·一模）11．若πtan 26α⎛⎫-= ⎪⎝⎭，则2ππ1tan cos 362αα⎛⎫⎛⎫-+--=⎪ ⎪⎝⎭⎝⎭．（2024·全国·模拟预测）12．在平面直角坐标系中，若角π3α-的顶点为原点，始边为x 轴非负半轴，终边经过点()3,4P --，则πtan 23α⎛⎫+=⎪⎝⎭.（2024·陕西安康·模拟预测）13．已知π,,π2αβ⎛⎫∈ ⎪⎝⎭，且πsin2sin 21cos21sin αβαβ⎛⎫+ ⎪⎝⎭-=+，则tan tan21tan tan 2βαβα+=-．（2024·河北沧州·模拟预测）14．已知1cos sin 63παα⎛⎫--= ⎪⎝⎭，则πcos 23α⎛⎫+=⎪⎝⎭．（2024·上海嘉定·二模）15．已知()22sin cos f x x x =+，π0,2x ⎛⎫∈ ⎪⎝⎭，则函数()y f x =的最小值为．（2024·吉林长春·模拟预测）16．已知tan 3,2sin cos 1tan 2ααββ==，则()2tan αβ+=.（2024·全国·模拟预测）17．已知锐角三角形ABC 的内角,,A B C 的对边分别为,,a b c ，若sin 2A =则a b 的取值范围是.（2024·全国·模拟预测）18．已知,αβ为锐角，满足()1sin sin ,cos 69αβαβ+=+=-，则sin2αβ+=，()cos αβ-=．（2024·全国·模拟预测）19．已知πtan ,74x x ⎛⎫+= ⎪⎝⎭为第二象限角，则10πsin 21x ⎛⎫+=⎪⎝⎭．（2024·上海·一模）20．已知ABC 中，,,A B C 为其三个内角，且tan ,tan ,tan A B C 都是整数，则tan tan tan A B C ++=．三角函数中的化简求值模型解析：1．725##0.28【分析】切化弦，然后整理可得sin α，再利用倍角公式计算即可.【详解】6cos sin tan 7sin cos ααααα==-，得()()226co 7sin s 61n s s n i i αααα==--，解得3sin 5α=或sin 2α=-（舍）所以2237cos212sin 12525αα⎛⎫=-=-⨯= ⎪⎝⎭.故答案为：725.2．-【分析】根据同角三角函数关系式求出sin α，tan α，再利用二倍角正切公式求解.【详解】由cos απ0,2α⎛⎫∈ ⎪⎝⎭，sin 3α∴，sin tan cos ααα∴==，22tan tan 21tan 1ααα∴==---.故答案为：-3．73-【分析】由倍角公式和差角公式、平方关系求解即可.【详解】sin 2πcos 4x x =⎛⎫- ⎪⎝⎭2273133⎡⎤⎛+-⎢⎥=-=- ⎢⎥⎝⎭⎣⎦，故答案为：73-..4．3【分析】由已知条件可得3π4βα=-，根据两角和的正切公式化简即可求解.【详解】因为3π4αβ+=，所以3π4βα=-，所以3πtan tan 3π4tan tan 3π41tan tan 4αβαα⎛⎫- ⎪⎛⎫⎝⎭=-= ⎪⎛⎫⎝⎭+⋅ ⎪⎝⎭，又因为tan 2α=，3πtan 14⎛⎫=- ⎪⎝⎭，所以上式可化为：12tan 312β--==-.故答案为：35．14-##【分析】先利用角α的终边所经过的点求出sin ,cos αα，再求πsin 3α⎛⎫+ ⎪⎝⎭.【详解】因为角α的始边与x轴非负半轴重合，终边经过点()2，所以sin 7α=，cos 7α==-；πππsin sin cos cos sin 33314ααα⎛⎫+=+=- ⎪⎝⎭.故答案为：6．1637【分析】利用韦达定理可得tan tan 5αβ+=-，tan tan 3αβ=-，再利用两角和差公式和三角函数的商数关系求解即可.【详解】因为tan α，tan β是方程2530x x +-=的两个根，所以tan tan 5αβ+=-，tan tan 3αβ=-，则cos cos 0αβ≠，所以()()2222cos cos cos sin sin 1tan tan sin sin cos cos sin tan tan αβαβαβαβαβαβαβαβ+⎛⎫⎛⎫--=== ⎪ ⎪---⎝⎭⎝⎭()2161637tan tan 4tan tan αβαβ=+-．故答案为：16377．1或3-【分析】由已知可得sin 0α=或sin 2cos αα=，从而可求出πtan 4α⎛⎫+ ⎪⎝⎭的值.【详解】由2sin sin2αα=可得2sin 2sin cos ααα=，所以sin 0α=或sin 2cos αα=，即tan 0α=或tan 2α=，当tan 0α=时，πtan 1tan 141tan ααα+⎛⎫+== ⎪-⎝⎭当tan 2α=时，πtan 1tan 341tan ααα+⎛⎫+==- ⎪-⎝⎭，故答案为：1或3-.8．22【分析】根据题意，列出方程组，求得7π2π,Z 12k k αββ-=+-∈，得到7π2π,Z 12k k α=+∈，结合πsin cos 4ααα⎛⎫+=+ ⎪⎝⎭，即可求解．【详解】因为点()()()cos ,sin A βαβα--与点5π5πcos ,sin 1212B ββ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭关于原点对称，所以()()5πcos cos 125πsin sin 12βαββαβ⎧⎛⎫-=-+ ⎪⎪⎪⎝⎭⎨⎛⎫⎪-=-+ ⎪⎪⎝⎭⎩，即()()5πcos cos π125πsin sin π12αββαββ⎧⎡⎤⎛⎫-=-+⎪ ⎪⎢⎥⎝⎭⎪⎣⎦⎨⎡⎤⎛⎫⎪-=-+ ⎪⎢⎥⎪⎝⎭⎣⎦⎩，所以7π2π,Z 12k k αββ-=+-∈，解得7π2π,Z 12k k α=+∈，所以π7ππ5π2sin cos 412462ααα⎛⎫⎛⎫+=+=+== ⎪ ⎪⎝⎭⎝⎭．故答案为：22.9．2023【分析】将已知条件切化弦，然后结合两角和的正弦公式、正余弦定理，将等量关系转化为2a ，2b ，2c 间的关系，则问题可解.【详解】2tan tan 2211cos cos tan (tan tan )tan tan tan tan sin sin A BB AC A B C C B A B A ==+⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2sin sin 2sin sin 2sin sin tan (sin cos cos sin )tan sin()tan sin A B A B A B C A B A B C A B C C ===++222sin sin cos 2cos sin A B C ab CC c ==，由余弦定理有：222222cos ab C a b c c c +-=，又2222024a b c +=，所以原式22220242023c c c -==.故答案为：202310．3215-【分析】利用诱导公式求出tan α，再由二倍角公式及同角三角函数的基本关系将弦化切，最后代入计算可得.【详解】因为()2tan 2024π3α-=，所以2tan 3α=-，所以2sin cos 2cos cos 2αααα-222sin cos 2cos cos sin ααααα=--2tan 121tan αα=--221323215213-=-=-⎛⎫-- ⎪⎝⎭.故答案为：3215-11．8310-+【分析】根据同角三角函数关系求出2π1cos 65α⎛⎫-= ⎪⎝⎭，利用正切差角公式得到πtan 3α⎛⎫- ⎪⎝⎭，从而求出答案.【详解】由题意得ππsin 2cos 66αα⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭，又22ππsin cos 166αα⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，解得2π1cos 65α⎛⎫-= ⎪⎝⎭，ππtan tan 2πππtan tan 8666ππ31tan tan 666αααα⎛⎫-- ⎪⎡⎤⎛⎫⎛⎫⎝⎭-=--==- ⎪ ⎪⎢⎥⎛⎫⎝⎭⎝⎭⎣⎦+- ⎪⎝⎭2ππ111tan cos 8362283510αα⎛⎫⎛⎫-+--=-++-=-+ ⎪ ⎪⎝⎭⎝⎭故答案为：8310-+12．247-【分析】先利用三角函数的定义得到πtan 3α⎛⎫- ⎪⎝⎭，再利用倍角公式和诱导公式进行转化求得πtan 23α⎛⎫+ ⎪⎝⎭.【详解】由三角函数的定义，得π4tan 33α⎛⎫-= ⎪⎝⎭，所以πππtan 2tan 2πtan2333ααα⎡⎤⎛⎫⎛⎫⎛⎫+=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦2π82tan 243316π711tan 93αα⎛⎫- ⎪⎝⎭===-⎛⎫--- ⎪⎝⎭.故答案为：247-13．1【分析】利用二倍角公式，同角关系，两角和与差的正切公式变形求解．【详解】由πsin2sin 21cos21sin αβαβ⎛⎫+ ⎪⎝⎭-=+得1cos2cos sin 21sin αβαβ-=+，22222cos sin 2sin 222sin cos cos sin 2sin cos 2222ββαββββαα-=++,所以cossinsin 22cos cos sin 22ββαββα-=+，即π1tantantan π242tan tan()π421tan 1tan tan242βββαββ--==-++，又π,,π2αβ⎛⎫∈ ⎪⎝⎭，所以ππ42βα=-+，即5π24βα+=，所以tan tan5π2tan()tan 1241tan tan 2βαβαβα+=+==-．故答案为：1.14．79-【分析】根据题意，由余弦的和差角公式展开可得π1 cos 63α⎛⎫+= ⎪⎝⎭，再由二倍角公式，即可得到结果.【详解】因为π1cos sin 63αα⎛⎫--= ⎪⎝⎭，整理得ππ1cos cos sin sin sin 663ααα+-=，11sin 23αα-=，所以π1cos 63α⎛⎫+= ⎪⎝⎭，所以2ππ17cos 22cos 1213699αα⎛⎫⎛⎫+=+-=⨯-=- ⎪ ⎪⎝⎭⎝⎭．故答案为：79-15．【分析】令πsin cos )4t x x x =+=+，可求t 的范围，利用同角的基本关系对已知函数化简计算，结合函数的单调性即可求解.【详解】由题意知，222(sin cos )()sin cos sin cos x x f x x x x x+=+=，令πsin cos 4t x x x =+=+，由π02x <<，得ππ3π444x <+<，所以2πsin()124x <+≤，则1t <≤由sin cos t x x =+，得22(sin cos )12sin cos t x x x x =+=+，所以21sin cos 2t x x -=，则原函数可化为22244()1112ttg t t t t t ===---，又函数1,y t y t ==-在上单调递增，所以1y t t =-在上单调递增，故当t 时，1y t t =-取得最大值22，此时()g t取得最小值故答案为：16．2511##3211【分析】根据同角三角函数关系，结合已知条件求得cos sin αβ，以及()sin αβ+，()2sin αβ+，()2cos αβ+，再求结果即可.【详解】由tan 3tan 2αβ=可得：sin cos 3cos sin 2αβαβ=，又2sin cos 1αβ=，即1sin cos 2αβ=，则1cos sin 3αβ=，故()115sin sin cos cos sin 236αβαβαβ+=+=+=，()225sin 36αβ+=，则()()2211cos 1sin 36αβαβ+=-+=，故()()()22225sin 2536tan 11cos 1136αβαβαβ++===+.故答案为：2511.17．【分析】由二倍角公式可得cos 2c bA b-=，利用正弦定理边化角，结合和差公式整理可得()sin sin B A B =-，可得2A B =，根据三角形ABC 为锐角三角形求出角B 的范围，然后利用正弦定理和二倍角公式可得2cos aB b=，可得范围.【详解】因为sin2A 23sin 24A b c b -=，所以2cos 12sin 22A c b A b -=-=，由正弦定理得sin sin cos 2sin C B A B -=，即2sin cos sin sin B A C B =-，所以()2sin cos sin sin B A A B B =+-，所以sin cos cos sin sin A B A B B -=，即()sin sin B A B =-，所以B A B =-或πB A B +-=（舍去），因为三角形ABC 为锐角三角形，所以π20,2A B ⎛⎫=∈ ⎪⎝⎭，又π3,π2A B B ⎛⎫+=∈ ⎪⎝⎭，解得64ππ,B ⎛⎫∈ ⎪⎝⎭，所以cos 22B ⎛⎫∈ ⎪ ⎪⎝⎭.因为sin sin22cos sin sin a A B B b B B ===，所以a b 的取值范围为.故答案为：18．14##0.25【分析】由,2222αβαβαβαβαβ+-+-=+=-，利用两角和与差的正弦公式和余弦的二倍角公式，求出sin 2αβ+；再用余弦的二倍角公式求出()cos αβ-.【详解】因为,2222αβαβαβαβαβ+-+-=+=-，所以sin sin sin 22αβαβαβ+-⎛⎫+=++ ⎪⎝⎭sin 2sin cos 2222αβαβαβαβ+-+-⎛⎫-=⋅ ⎪⎝⎭，又sin sin αβ+=sin cos 2212αβαβ+-=，因为,αβ为锐角，所以2αβ+为锐角，又()21cos 12sin 29αβαβ++=-=-，所以sin 2αβ+=又52sin cos 2212αβαβ+-=，所以cos 2αβ-=，所以()2101cos 2cos 1212164αβαβ--=-=⨯-=．故答案为：3；14.19【分析】由π2tan 74x ⎛⎫+= ⎪⎝⎭及同角三角函数的基本关系可求得ππsin ,cos 77x x ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭，再根据10πππ2173x x ⎛⎫+=++ ⎪⎝⎭并结合两角和的正弦公式即可得解．【详解】 π2tan 74x ⎛⎫+= ⎪⎝⎭，π2πsin cos 747x x ⎛⎫⎛⎫∴+=-+ ⎪ ⎪⎝⎭⎝⎭，2222ππππsin cos cos 7777x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴+++=-+++⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦29πcos 187x ⎛⎫=+= ⎪⎝⎭，x 为第二象限角，∴πcos 7x ⎛⎫+= ⎪⎝⎭，π1sin 73x ⎛⎫∴+= ⎪⎝⎭，10πππππππsin sin sin cos cos sin 21737373x x x x ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴+=++=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦1122312632326-=⨯-=．20．6【分析】不妨令A B C ≤≤，利用正切函数的单调性，结合已知求出tan A ，再利用和角的正切公式分析求解即得.【详解】在ABC 中，不妨令A B C ≤≤，显然A 为锐角，而tan A 是整数，若πtan 2tan 3A =>=，又函数tan y x =在π(0,2上单调递增，则π3A >，此时3πABC A ++≥>与πA B C ++=矛盾，因此tan 1A =，π3π,44A B C =+=，tan tan tan()11tan tan B C B C B C++==--，整理得(tan 1)(tan 1)2B C --=，又tan ,tan B C 都是整数，且tan tan B C ≤，因此tan 2,tan 3B C ==，所以tan tan tan 6A B C ++=.故答案为：6。

三角函数专项一、化简求值 1、若02πα＜＜，02πβ-＜＜，1cos()43πα+=，cos()423πβ-=，则cos()2βα+=A．3B．3-C．9D．9-【答案】C 2、已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线2y x =上，则cos 2θ=（A ） 45- （B ）35-（C ）35（D ）45【答案】B 3、设sin 1+=43πθ（），则sin 2θ=（A ）79- （B ）19-（C ）19（D ）79【答案】A4、函数sin()cos()26y x x ππ=+-的最大值为 。

【答案】24+5、已知1sin cos 2α=+α，且0,2π⎛⎫α∈ ⎪⎝⎭，则cos 2sin 4πα⎛⎫α- ⎪⎝⎭的值为__________【答案】2-6、已知a ∈（2π，π），5tan2α=【答案】43-7、已知,2)4tan(=+πx 则xx 2tan tan 的值为__________【答案】948、若tan α=3，则2sin 2cos aα的值等于 A ．2B ．3C ．4D ．6【答案】D二、三角函数图像 9、函数2sin 2x y x =-的图象大致是【答案】C10、已知函数)(x f =A tan （ωx +ϕ）（2||,0πϕω<>），y =)(x f 的部分图像如下图，则=)24(πf ．10、函数ϕϕ,,(),sin()(w A wx A x f +=是常数，)0,0>>w A 的 部分图象如图所示，则f (0)= 【答案】2611、设函数()cos (0)f x x ωω=＞，将()y f x =的图像向右平移3π个单位长度后，所得的图像与原图像重合，则ω的最小值等于A ．13B ．3C ．6D ．9三、三角函数性质12、若函数()sin f x x ω= (ω>0)在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增，在区间,32ππ⎡⎤⎢⎥⎣⎦上单调递减，则ω= A ．3 B ．2 C ．32D ．23【答案】C13、已知函数()cos ,f x x x x R =-∈，若()1f x ≥，则x 的取值范围为A ．|,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭ B ．|22,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭C ．5{|,}66x k x k k Z ππππ+≤≤+∈D ．5{|22,}66x k x k k Z ππππ+≤≤+∈【答案】B14、设函数()s i n ()c o s (f x x x ωϕωϕ=+++(0,||)2πωϕ><的最小正周期为π，且()()f x f x -=则（A ）()y f x =在(0,)2π单调递减 （B ）()y f x =在3(,)44ππ单调递减（C ）()y f x =在(0,)2π单调递增 （D ）()y f x =在3(,)44ππ单调递增【答案】A15、已知函数()sin(2)f x x ϕ=+，其中ϕ为实数，若()()6f x f π≤对x R ∈恒成立，且()()2f f ππ>，则()f x 的单调递增区间是（A ）,()36k k k Z ππππ⎧⎫-+∈⎨⎬⎩⎭（B ）,()2k k k Z πππ⎧⎫+∈⎨⎬⎩⎭（C ）2,()63k k k Z ππππ⎧⎫++∈⎨⎬⎩⎭ （D ）,()2k k k Z πππ⎧⎫-∈⎨⎬⎩⎭【答案】C四、正余弦定理16、若△ABC 的内角A 、B 、C 所对的边a 、b 、c 满足22a b 4c +-=（），且C=60°，则ab 的值为A ．43B．8-C ． 1D ．23【答案】A17、如图，在△ABC 中，D 是边A C上的点，且,2,2AB C D AB BC BD ===，则sin C 的值为 A．3 B．6C 3D 6【答案】D18、在∆ABC 中．222sin sin sin sin sin A B C B C ≤+-．则A 的取值范围是A ．（0，6π]B ．[ 6π，π）C ．（0，3π]D ．[ 3π，π）【答案】C【解析】由题意正弦定理22222222211cos 023b c aa b c bc b c a bc A A bcπ+-≤+-⇒+-≥⇒≥⇒≥⇒<≤【答案】C19、△ABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，a sin A sin B +b cos 2A =a 2，则=a b（A ） （B ） （C （D【答案】D20、在相距2千米的A ．B 两点处测量目标C ，若0075,60C AB C BA ∠=∠=，则A ．C两点之间的距离是 千米。

三角化简求值测试题1．若sin α＝35，α∈(－π2，π2)，则cos(α＋5π4)＝________.2．已知π<θ<32π，则 12＋12 12＋12cos θ＝________.3．计算：cos10°＋3sin10°1－cos80°＝________.4．函数y ＝2cos 2x ＋sin2x 的最小值是__________________．5．函数f (x )＝(sin 2x ＋12010sin 2x )(cos 2x ＋12010cos 2x)的最小值是________． 6．若tan(α＋β)＝25，tan(β－π4)＝14，则tan(α＋π4)＝_____.7．若3sin α＋cos α＝0，则1cos 2α＋sin2α的值为________．8.2＋2cos8＋21－sin8的化简结果是________．9．若tan α＋1tan α＝103，α∈(π4，π2)，则sin(2α＋π4)的值为_________．10．若函数f (x )＝sin2x －2sin 2x ·sin2x (x ∈R )，则f (x )的最小正周期为________．11． 2cos5°－sin25°cos25°的值为________．12．向量a ＝(cos10°，sin10°)，b ＝(cos70°，sin70°)，|a －2b |＝________________.13．已知1－cos2αsin αcos α＝1，tan(β－α)＝－13，则tan(β－2α)＝________.14．设a ＝sin14°＋cos14°，b ＝sin16°＋cos16°，c ＝62，则a 、b 、c 的大小关系是________.15．已知角α∈(π4，π2)，且(4cos α－3sin α)(2cos α－3sin α)＝0.(1)求tan(α＋π4)的值；(2)求cos(π3－2α)的值．16. 已知tan α＝2.求(1)tan(α＋π4)的值；(2)sin2α＋cos 2(π－α)1＋cos2α的值．17．如图，点A ，B 是单位圆上的两点，A ，B 两点分别在第一、二象限，点C 是圆与x 轴正半轴的交点，△AOB 是正三角形，若点A 的坐标为(35，45)，记∠COA ＝α. (1)求1＋sin2α1＋cos2α的值；(2)求|BC |2的值．18．△ABC 中，A ，B ，C 所对的边分别为a ，b ，c ，tan C ＝sin A ＋sin Bcos A ＋cos B，sin(B －A )＝cos C .，，求角A 。

三角函数的恒等变换及化简求值（北京习题集）（教师版）一．选择题（共5小题）1．（2018•西城区校级模拟）若函数())cos(2)(0)f x x x θθθπ=+++<<的图象经过点(2π，0)，则( )A ．()f x 在(0,)2π上单调递减B ．()f x 在(4π，3)4π上单调递减 C ．()f x 在(0,)2π上单调递增D ．()f x 在(4π，3)4π上单调递增 2．（2018•北京模拟）在sin50︒，sin50-︒，sin40︒，sin40-︒四个数中，与sin130︒相等的是( ) A ．sin50︒B ．sin50-︒C ．sin40︒D ．sin40-︒3．（2018秋•海淀区校级月考）函数21()sin sin cos 2f x x x x =+-的最小正周期和振幅分别是(( )A ．B ．2C ．2πD ．π4．（2017秋•大兴区期末）设3a ln =，8b π=，sin8c π=，则a ，b ，c 之间的大小关系是( )A ．a b c >>B ．a c b >>C ．b c a >>D ．c b a >>5．（2018秋•海淀区期中）函数()sin()f x x ϕ=+满足()13f π=，则5()6f π的值是( )A ．0B ．12C D ．1二．填空题（共8小题）6．（2019秋•海淀区校级月考）若角α满足sin cos αα-=α= ．7．（2019•海淀区校级模拟）已知α锐角，且cos()2πα-=，则tan α= ．8．（2019秋•东城区校级月考）已知1sin cos 3αα+=，则2sin ()4πα-= ．9．（2017秋•昌平区期末）已知tan 2α=，则5cos sin sin 2cos αααα-=+ ．10．（2017秋•东城区校级期末）已知tan 2α=，则sin 3cos sin cos αααα-=+ ，2sin 2sin cos ααα+= ．11．（2018春•通州区期末）已知(0,)2πα∈，tan 2α=，则cos α= ．12．（2017秋•西城区期末）已知函数()sin tan f x x x =．给出下列结论： ①函数()f x 是偶函数； ②函数()f x 在区间(,0)2π-上是增函数；③函数()f x 的最小正周期是2π； ④函数()f x 的图象关于直线x π=对称．其中正确结论的序号是 ．（写出所有正确结论的序号）13．（2018•顺义区二模）在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，他们的终边关于x 轴对称，若1cos 4α=，则cos()αβ-= ． 三．解答题（共2小题）14．（2019•房山区一模）已知函数()f x =．（Ⅰ）求(0)f 的值； （Ⅱ）求函数()f x 的定义域；（Ⅲ）求函数()f x 在(0,)2π上的取值范围．15．（2018秋•海淀区校级期末）求值：tan150cos(210)sin(420)sin1050cos(600)︒-︒-︒︒-︒．三角函数的恒等变换及化简求值（北京习题集）（教师版）参考答案与试题解析一．选择题（共5小题）1．（2018•西城区校级模拟）若函数())cos(2)(0)f x x x θθθπ=+++<<的图象经过点(2π，0)，则( )A ．()f x 在(0,)2π上单调递减B ．()f x 在(4π，3)4π上单调递减 C ．()f x 在(0,)2π上单调递增D ．()f x 在(4π，3)4π上单调递增 【分析】利用三角恒等变换化简函数的解析式，再利用正弦函数的单调性，得出结论．【解答】解：函数())cos(2)2sin(2)6f x x x x πθθθ=+++=++(0)θπ<<的图象经过点(2π，0)，2sin()06ππθ∴++=，sin()06πθ∴+=，6k πθπ∴+=，k Z ∈，56πθ∴=，5()2sin(2)2sin 266f x x x ππ=++=-． 在(0,)2π上，2(0,)x π∈，()2sin 2f x x =-没有单调性，故排除A 、C ；在(4π，3)4π上，2(2x π∈，3)2π，()2sin 2f x x =-单调递增，故排除B ，故选：D ．【点评】本题主要考查三角恒等变换，正弦函数的单调性，属于基础题．2．（2018•北京模拟）在sin50︒，sin50-︒，sin40︒，sin40-︒四个数中，与sin130︒相等的是( ) A ．sin50︒B ．sin50-︒C ．sin40︒D ．sin40-︒【分析】利用诱导公式化简可得答案．【解答】解：由sin130sin(18050)sin50︒=︒-︒=︒．∴与sin130︒相等的是sin50︒故选：A ．【点评】题主要考察了诱导公式的应用，属于基本知识的考查． 3．（2018秋•海淀区校级月考）函数21()sin sin cos 2f x x x x =+-的最小正周期和振幅分别是(( )A ．B ．2C ．22πD ．2π【分析】利用倍角公式降幂，再由辅助角公式化积，则答案可求． 【解答】解：211cos211()sin sin cos sin 22222x f x x x x x -=+-=+-1(sin 2cos2))24x x x π=--．∴函数()f x 的最小正周期为22ππ=，振幅是2． 故选：D ．【点评】本题考查sin()y A x ωϕ=+型函数的图象和性质，是基础题． 4．（2017秋•大兴区期末）设3a ln =，8b π=，sin8c π=，则a ，b ，c 之间的大小关系是( )A ．a b c >>B ．a c b >>C ．b c a >>D ．c b a >>【分析】借用中间值和三角函数公式化简即可比较大小． 【解答】解：31a ln lne =>= 0.390.48b π<=<．由sin 2sin cos 488πππ==，即sin cos88ππ22sin cos 188ππ+=sin0.388c π==≈ a b c ∴>>．故选：A ．【点评】本题考查三角恒等变换及化简求值，是中档题．5．（2018秋•海淀区期中）函数()sin()f x x ϕ=+满足()13f π=，则5()6f π的值是( )A ．0B ．12C D ．1【分析】由已知求得ϕ，进一步得到5()6f π的值． 【解答】解：由()sin()f x x ϕ=+满足()13f π=，得sin()13πϕ+=，即232k ππϕπ+=+，k Z ∈．则26k πϕπ=+，k Z ∈．()sin()sin(2)sin()66f x x x k x ππϕπ∴=+=++=+．∴5()sin 06f ππ==． 故选：A ．【点评】本题考查三角函数的化简求值，考查由已知三角函数值求角，是基础题． 二．填空题（共8小题）6．（2019秋•海淀区校级月考）若角α满足sin cos 2αα-=，则α= 5212k ππ+或13212k ππ+，k Z ∈ ． 【分析】由已知推导出1sin()42πα-=，由此能求出α．【解答】解：sin cos αα-∴)4πα-=， 1sin()42πα∴-=，∴246k ππαπ-=+或5246k ππαπ-=+，k Z ∈， ∴5212k παπ=+或13212k παπ=+，k Z ∈． 故答案为：5212k ππ+或13212k ππ+，k Z ∈． 【点评】本题考查三角函数中角的求法，是基础题，解题时要认真审题，注意三角函数的性质的合理运用．7．（2019•海淀区校级模拟）已知α锐角，且cos()2πα-=，则tan α【分析】由已知利用诱导公式求得α，进一步得到tan α的值．【解答】解：由cos()2πα-=sin α，α是锐角，60α∴=︒，则tan α．【点评】本题考查三角函数的化简求值，考查由已知三角函数值求角，是基础题． 8．（2019秋•东城区校级月考）已知1sin cos 3αα+=，则2sin ()4πα-= 1718．【分析】利用平方化简已知条件，两角和与差的三角函数化简求解即可． 【解答】解：1sin cos 3αα+=，可得82sin cos 9αα=-，则2211817sin ())(12sin cos )(1)422918πααααα-==-=+=．故答案为：1718．【点评】本题考查两角和差的三角函数，三角函数化简求值，考查计算能力． 9．（2017秋•昌平区期末）已知tan 2α=，则5cos sin sin 2cos αααα-=+34． 【分析】利用同角三角函数的基本关系化弦为切，然后代值计算即可得答案． 【解答】解：tan 2α=，∴5cos sin 5tan 523sin 2cos tan 2224αααααα---===+++．故答案为：34． 【点评】本题考查了同角三角函数基本关系的意义，熟练掌握基本关系是解本题的关键，是基础题． 10．（2017秋•东城区校级期末）已知tan 2α=，则sin 3cos sin cos αααα-=+ 13- ，2sin 2sin cos ααα+= ．【分析】把要求值的式子化弦为切求解． 【解答】解：tan 2α=，∴sin 3cos tan 3231sin cos tan 1213αααααα---===-+++；2222222sin cos 2tan 448sin 2sin cos 1415sin tan sin cos tan ααααααααααα++++====+++．故答案为：18,35-．【点评】本题考查三角函数的化简求值，考查同角三角函数基本关系式的应用，是基础题．11．（2018春•通州区期末）已知(0,)2πα∈，tan 2α=，则cos α=． 【分析】由题意利用同角三角函数的基本关系、以及三角函数在各个象限中的符号，求得cos α的值． 【解答】解：已知(0,)2a π∈，sin 0α∴>，cos 0α>，tan sin 2cos ααα==，22sin cos 1αα+=，则cos α=【点评】本题主要考查同角三角函数的基本关系、以及三角函数在各个象限中的符号，属于基础题． 12．（2017秋•西城区期末）已知函数()sin tan f x x x =．给出下列结论： ①函数()f x 是偶函数； ②函数()f x 在区间(,0)2π-上是增函数；③函数()f x 的最小正周期是2π； ④函数()f x 的图象关于直线x π=对称．其中正确结论的序号是 ①③④ ．（写出所有正确结论的序号）【分析】利用函数奇偶性的判定判断①；举例说明②错误；利用周期函数的定义判断③；由()()f x f x ππ-=+判断④．【解答】解：对于()sin tan f x x x =，其定义域为{|2x x k ππ≠+，}k Z ∈，关于原点对称，且()sin()tan()sin tan f x x x x x -=--=，∴函数()f x 是偶函数，故①正确；当3x π=-时，3()sin()tan()3332f πππ-=--=，当6x π=-时，()sin()tan()666f πππ-=--36ππ-<-，而()()36f f ππ->-，故②错误；(2)sin(2)tan(2)sin tan f x x x x x πππ+=++=，∴函数()f x 的最小正周期是2π，故③正确；()sin()tan()sin tan f x x x x x πππ-=--=-， ()sin()tan()sin tan f x x x x x πππ+=++=-，()()f x f x ππ∴-=+，即函数()f x 的图象关于直线x π=对称，故④正确．∴正确结论的序号是①③④．故答案为：①③④．【点评】本题考查命题的真假判断与应用，考查三角函数的性质，是中档题．13．（2018•顺义区二模）在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，他们的终边关于x 轴对称，若1cos 4α=，则cos()αβ-= 78- ． 【分析】由已知求得cos β，进一步求得sin sin αβ的值，展开两角差的余弦即可求得cos()αβ-． 【解答】解：1cos 4α=，且α与角β均以Ox 为始边，他们的终边关于x 轴对称， 1cos 4β∴=， 若α为第一象限角，则β为第四象限角， 若α为第四象限角，则β为第一象限角， 15sin sin 16αβ∴=-， 11157cos()cos cos sin sin 44168αβαβαβ∴-=+=⨯-=-．故答案为：78-．【点评】本题考查三角函数的化简求值，考查两角差的余弦，是基础的计算题． 三．解答题（共2小题）14．（2019•房山区一模）已知函数()f x =．（Ⅰ）求(0)f 的值； （Ⅱ）求函数()f x 的定义域；（Ⅲ）求函数()f x 在(0,)2π上的取值范围．【分析】（Ⅰ）直接在函数解析式中取0x =求解；（Ⅱ）由分式函数的分母不为0即可求得函数定义域；（Ⅲ）把已知函数解析式变形，再由x 的范围求得相位的范围，则函数值域可求． 【解答】解：（Ⅰ）3sin 0cos011(0)12f ++===；（Ⅱ）由cos 0x ≠，得,2x k k Z ππ≠+∈．∴函数的定义域是,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭；（Ⅲ）232sin cos 2cos1()x x x f x +-+=..sin cos 2sin()6x x x π=+=+．(0,)2x π∈，即02x π<<，∴2663x πππ<+<， ∴1sin()126x π<+，得12sin()26x π<+． ∴函数()f x 在(0,)2π上的取值范围为(1，2]．【点评】本题考查三角函数的化简求值，考查三角函数中的恒等变换应用，考查sin()y A x ωϕ=+型函数的图象和性质，是中档题．15．（2018秋•海淀区校级期末）求值：tan150cos(210)sin(420)sin1050cos(600)︒-︒-︒︒-︒．【分析】由条件利用诱导公式求得tan15︒、cos210︒、sin 420︒、sin1050︒、cos(600)-︒的值，可得要求式子的值． 【解答】解：由诱导公式可得：tan150tan(18030)tan30︒=︒-︒=-︒=，cos(210)cos210cos(18030)cos30-︒=︒=︒+︒=-︒=， sin(420)sin 420sin(36060)sin 60-︒=-︒=-︒+︒=-︒=，1sin1050sin(336030)sin302︒=⨯︒-︒=-︒=-， 1cos(600)cos600cos(318060)cos602-︒=︒=⨯︒+︒=-︒=-，∴原式3()(3224111()()224-===--．【点评】本题主要考查诱导公式的应用，特殊角的三角函数值，属于基础题．。

A B C B【例4] 在中，若sin2_2 +sin2y +sin2y =cos2_2 ,tan—• tan —=-.2 2 3B 满足关系式：V3 (tan a • t^n B +a) +tan a =0,则tan B 二c- f(1+a)D- T(1~a) A. V3 (1+a) B. V3 (1 —爲)三角函数的化简1、三角函数式的化简：(1)常用方法：①直接应用公式进行降次、消项；②切割化弦，异名化同名，异角化同角；③三角公式的逆用等。

(2)化简要求：①能求出值的应求出值；②使三角函数种数尽量少；③使项数尽量少；④尽量使分母不含三角函数；⑤尽量使被开方数不含三角函数2、三角函数的求值类型有三类：(1)给角求值：一般所给出的角都是非特殊角，要观察所给角与特殊角间的关系，利用三角变换消去非特殊角，转化为求特殊角的三角函数值问题；(2)给值求值：给出某些角的三角函数式的值，求另外一些角的三角函数值，解题的关键在于“变角”，如& =(© + "丿—0,2Q =(Q +"丿+ (©-0丿等，把所求角用含己知角的式子表示，求解时要注意角的范围的讨论；(3)给值求角：实质上转化为“给值求值”问题，由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。

3、三角等式的证明：(1)三角恒等式的证题思路是根据等式两端的特征，通过三角恒等变换，应用化繁为简、左右同一等方法，使等式两端的化“异”为“同”；(2)三角条件等式的证题思路是通过观察, 发现已知条件和待证等式间的关系，采用代入法、消参法或分析法进行证明。

一、化简［例求值.2sin2(P + cosl0o + tan20。

sin 10°esc 40° + cot 80°2 cos 40° + cosl 0°(1 + tan60°tanl 0°) Jl + cosl0°【例2】（三兄弟）已知s 阮普，"罟,求畔翥卫的值【变式】（05天津）已知sin （&） =晋,COS 2*£,【例3］（最值辅助角）已知函数A^）=2asin 2T —273 asinxcosA+a+b —1,（弘b 为常数，a<0）,它的定 义域为［0,兰］,值域为［ — 3,1］,试求禺b 的值。

一、题型选讲
题型一灵活运用和与差的正弦、余弦和正切、二倍角等公式化简求值
通过两角和与差的正弦、余弦和正切以及二倍角公式或者公式的变形进行化简求值。

在应用同角三角函数的关系或两角和与差的三角函数公式求值时，需要注意解题的规范性，一要注意角的范围对三角函数值的符号的影响；二要注意“展示”三角函数的公式．否则，就会因为不规范而导致失分．
求tan()
αβ
-的值．
题型二探究角度之间的关系
在三角函数的化简求值中，往往出现已知角与所求角不同，此时要观察两个角度之间的关系，寻求角度之间的特殊性，通过二倍角、互补、互与余等公式进行转化。

应用三角公式解决问题的三个变换角度
(1)变角：目的是沟通题设条件与结论中所涉及的角，其手法通常是“配凑”.
(2)变名：通过变换函数名称达到减少函数种类的目的，其手法通常有“切化弦”、“升幂与降幂”等.
(3)变式：根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，其手法通常有：“常值代
换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等.
．
题型三、运用构造法化简与求值
2、(2018南京、盐城一模）已知锐角α，β满足(tanα－1)(tanβ－1)＝2，则α＋β的值为________．。