分数加减法混合运算简算
- 格式:docx
- 大小:10.46 KB
- 文档页数:3


分数的加减法一、同分母的分数加减法知识点:在计算同分母的分数加减法中,分母不变,直接用分子相加减.注意:在计算同分母的分数加减法中,得数如果不是最简分数,我们必须将得数约分,使它成为最简分数。
例题一5654+=510564=+=2 注意:因为510不是最简分数,所以得约分,10和5的最大公因数是5,所以分子和分母同时除以5,最后得数是2. 例题二1059105109=-=-注意:因为10不是最简分数,必须约分,因为4和10的最大公因数是2,所以分子和分母同时除以2,最后的数是52知识点回顾:如何将一个不是最简的分数化为最简?(将一个非最简分数化为最简,我们就是将这个分数进行约分,一直约到分子和分母互质为止。
所以要将一个分数进行约分,我们必须找到分子和分母的最大公因数,然后用分子和分母同时除以他们的最大公因数.)专项练习一:同分母的分数加减法的专项练习一、计算错误!- 错误! 错误!— 错误! 1 - 错误! 错误!— 错误!错误!+ 错误! 错误!+ 错误! 错误!+错误! 错误!+ 错误!二、连线19 + 错误! 2 7377+1错误!+错误! 18987+ 错误!+ 错误! 1错误! 11511141+错误!+错误! 2错误!9392+2错误!+错误! 错误! 2121+三、判断对错,并改正(1)错误!+错误!= 错误! (2)6 — 错误!- 错误!=5错误!—错误!—错误! =5错误!-错误!=517四、应用题(1)一根铁丝长错误!米,比另一根铁丝长错误!米,了;另一根铁丝长多少米?(2)3天修一条路,第一天修了全长的错误! ,第二天修了全长的错误!错误!,第三天修了全长的几分之几?二、异分母的分数加减法。
在异分母的分数加减法中,可分为三种情况。
分别是分母是互质关系、分母是倍数关系、分母是一般关系(即非互质也非倍数) 例:A 代表一个分数的分母,B 代表另一个分数的分母ABA B AB B A B A ±±=±或11,分母是倍数关系)(即分子都为的倍数)是或的倍数)是(、,分母互质)即分子都为或、1(1111)2(1(11)1(AB A B AB A B A B B A ABA B AB B A B A ±±=±±±=±)3(、A 和B 是一般关系,就找到A 和B 的最小公倍数,进行通分,再加减。

分数加减法混合运算简便计算
首先,我们需要知道的是分数是怎么回事。
分数是一个把一些整数分成若干份,把每份称为一分,用来表示不同数量的分数。
比如说,1/2表示1整数被分成2份,每份即为1/2;3/4表示3整数被分成4份,每份即为3/4
接下来,我们就可以进行分数加减法混合运算了。
首先,我们需要判断几种情况,分别是:
一、分母相同的情况:
当分数的分母都相同时,可以使用简单的加法运算,只要把分子相加即可获得结果。
比如说:
1/2+3/2=4/2=2
二、分母不同的情况:
当分数的分母不同时,首先需要将分数进行约分,即通分,将分数的分母变成相同的,这可以使用最小公倍数的方法来实现。
比如说,将1/2和3/4进行约分,可以得到:
1/2=2/43/4=3/4
两者的最小公倍数是4,将两个分数的分母变为4,即可得到:
1/2=2/43/4=6/4
将1/2和3/4进行约分后,我们就可以使用简单的加法运算,把分子相加:
2/4+6/4=8/4=2
三、分子为负数的情况:
有时候分子会出现负数的情况,解决负数的问题,我们需要将负数看做和正数一样,首先将负数的分子变为正数,然后将它们相加。

分数加减法简便计算方法
嘿,朋友们!今天咱就来讲讲分数加减法简便计算方法,这可真是个超棒的东西啊!
比如说,计算 1/3 + 1/4 ,哎呀,直接通分计算多麻烦呀!但要是咱会一些简便方法,那就轻松多啦!
想象一下,分数就像一个个小积木,我们要把它们巧妙地组合在一起。
比如同分母的分数,那不就像同一种颜色的积木嘛,可以很容易地放在一起计算呀!像 3/4 + 1/4 不就等于 1 嘛!这多简单。
还有啊,有时候可以找“好朋友”分数呢!啥意思?就好比 1/2 和 1/2 就是一对好朋友,它们加起来正好是 1 呀!你看,多有趣!
再给你们举个例子,计算 3/5 - 1/5 ,这不一眼就看出来等于 2/5 嘛!这种同分母的计算是不是特轻松?
咱再说回不同分母的情况,这就像搭一个更复杂的积木造型。
那咱得想办法把它们变成同分母呀!这时候通分就派上用场啦!为了能更快更准地算出来,费点小功夫也是值得的呀,对吧?
像 1/2 + 1/3 ,通分后变成 3/6 + 2/6 ,那不就等于 5/6 嘛!是不是恍然大悟啦?
所以啊,朋友们,分数加减法的简便计算方法真的超有用!它就像一把钥匙,能帮我们轻松打开分数计算的大门!学会了这些,咱面对分数加减就再也不会头疼啦,而是能开心地把它们搞定!相信我,去试试这些方法吧,你会发现分数计算原来可以这么有趣!这么容易!。

分数加减法混合运算简便计算分数的加减法混合运算是数学中的一项基础运算,它要求对分数的加法和减法进行合理的组合和运算。
下面我将详细介绍分数的加减法混合运算的简便计算方法。
一、分数的加法分数的加法可以通过以下步骤进行简便计算:1.确定被加数和加数的分子和分母。
2.寻找它们的最小公倍数(即分母的最小公倍数)。
3.将两个分数的分子分别乘以分子的最小公倍数除以分母,并将结果相加,得到新的分子。
4.将两个分数的分母乘以分子的最小公倍数除以分母,得到新的分母。
5.化简所得的分数,如果分子能被分母整除,就进行约分。
例如:计算3/4+2/3步骤1:分母为4和分母为3,最小公倍数为12步骤2:3×3/4×3+2×4/3×4=9/12+8/12步骤3:9+8/12=17/12步骤4:分子为17,分母为12,不能约分,所以结果为17/12二、分数的减法分数的减法与加法类似,也可以通过以下步骤进行简便计算:1.确定被减数和减数的分子和分母。
2.寻找它们的最小公倍数(即分母的最小公倍数)。
3.将两个分数的分子分别乘以分子的最小公倍数除以分母,并将结果相减,得到新的分子。
4.将两个分数的分母乘以分子的最小公倍数除以分母,得到新的分母。
5.化简所得的分数,如果分子能被分母整除,就进行约分。
例如:计算3/4-2/3步骤1:分母为4和分母为3,最小公倍数为12步骤2:3×3/4×3-2×4/3×4=9/12-8/12步骤3:9-8/12=1/12步骤4:分子为1,分母为12,不能约分,所以结果为1/12三、分数的加减法混合运算分数的加减法混合运算需要根据具体的题目要求进行相应的计算顺序和合并运算。
一般的计算顺序是从左到右按照加减法的次序进行运算。
例如:计算1/2+3/4-2/3步骤1:计算1/2+3/4分母为2和分母为4,最小公倍数为4(1×2+3×1)/2×2=5/4步骤2:计算5/4-2/3分母为4和分母为3,最小公倍数为12(5×3-2×4)/4×3=(15-8)/12=7/12所以,1/2+3/4-2/3=7/12分数的加减法混合运算的简便计算方法就是先计算每一个加法或减法运算,然后按照加法减法的次序进行计算,最后得出结果。

五年级下册分数加减混合运算题简算一、分数的加减法规则1.1 分数的加法规则分数的加法规则是指两个分数相加时,首先要找到它们的公共分母,然后将分子相加而保持公共分母不变,最后将结果化简即可。
例如:⅔ + ¼ = (2×2)/(3×2) + 1/4 = 4/6 + 3/12 = 8/12 + 3/12 = 11/121.2 分数的减法规则分数的减法规则是指两个分数相减时,也要先找到它们的公共分母,然后将分子相减而保持公共分母不变,最后将结果化简即可。
例如:⅘ - 1/3 = (3×5)/(5×3) - 5/15 = 15/15 - 5/15 = 10/15 = 2/3二、分数加减混合运算题简算例题2.1 例题一:⅗ + 1/4 - 2/3解:首先找到⅗和 1/4 的公共分母,得到 4/20 和 5/20,然后将其相加得到 9/20。
再将 9/20 和 2/3 的分数相减,得到 9/20 - 13/20 = -4/20 = -1/5。
⅗ + 1/4 - 2/3 = -1/5。
2.2 例题二:2/3 - 1/8 + 3/4解:首先找到2/3 和 1/8 的公共分母,得到16/24 和 3/24,然后将其相减得到13/24。
再将13/24 和 3/4 的分数相加,得到 13/24 +18/24 = 31/24 = 1又7/24。
2/3 - 1/8 + 3/4 = 1又7/24。
2.3 例题三:4/5 + 3/4 - 1/2解:首先找到4/5 和 3/4 的公共分母,得到 16/20 和 15/20,然后将其相加得到 31/20。
再将 31/20 和 1/2 的分数相减,得到 31/20 -20/20 = 11/20。
4/5 + 3/4 - 1/2 = 11/20。
总结:分数的加减混合运算题,首先要注意找到分数的公共分母,然后进行相应的加减操作,并最终将结果化简。

分数混合运算总结(一)分数混合运算的总结一、运算1.分数加减法:同分母分数相加减,分母不变,分子相加减,异分母分数相加减,要先通分为同分母分数再相加减。
同分母分数加减法②法则:异分母分数相加减,先通分,然后按照同分母分数加减法进行计算。
注意:计算的结果,能约分的要约成最简分数,是假分数的一般要化成带分数或整数。
步骤:一看二通三算四约五化验算:分数加减法的验算方法与整数加减法的验算相同。
例:6562362633121=+=+=+ (和的分母是两个分母的积) 8786186814381=+=+=+ (分母是其中一个分母的)2411249224924283121=+=+=+(分母是最小公倍数)2计算技巧:能约分的,先约分再算。
分数的意义: 把单位“1”平均分成若干份,表示这样的一份或者几份的数,叫做分数。
在分数里,表示把单位“1”平均分成多少份的数,叫做分母;表示这样多少份的数,叫做分子;其中的一份,叫做分数单位。
分数混合运算顺序1.含有同级运算的按从左到右的顺序计算;2.含有两级运算的先算乘除,后算加减;3.有括号的先算括号里的运算。
分数简便运算常见题型涉及定律:乘法分配律逆向定律 )(c b a c a b a ±=⨯±⨯基本方法:提取两个乘式中共有的因数,将剩余的因数用加减相连,同时添加括号,先行运算。
第四种:添加因数“1”例题:1)759575⨯- 2)9216792⨯- 3)23233117233114+⨯+⨯持一致。
第六种:带分数化加式例题:1)4161725⨯ 2)351213⨯ 3)135127⨯涉及定律:乘法分配律基本方法:将带分数转化为整数部分和分数部分相加的形式,再按照乘法分配律计算。
第七种:乘法交换律与乘法分配律相结合例题:1)7495⨯+⨯2)86611⨯+⨯3)1137137139⨯+⨯59321 5+29×31044-72×51223+(47+12)×7256.8×51+51×3.2 (32+43-21)×12 53×914-94×53913952534 ×4= 54×(89 - 56 ) 229 ×(15×2931)11 13-1113×133338-0.125)×413241241343651211÷⎪⎭⎫⎝⎛-+-19。


人教版五年级下册数学第六单元《分数加减法》知识点总结第六单元《分数的加法和减法》,是数学运算的重要基础知识之一,能否掌握分数加法、减法的计算方法是评价学生是否拥有良好的运算能力,拥有良好的数感的一项重要指标。
本单元学习的内容:同分母分数加、减法,异分母分数加减法,分数加减混合运算,整数加法的运算定律推广到分数以及用分数解决问题。
一、同分母分数加、减法1、分数加法的意义与整数加法的意义相同,就是把两个数合并成一个数的运算。
2、分数减法的意义与整数减法的意义相同,已知两个数的和与其中的一个加数,求另一个加数的运算。
3、同分母分数加减法计算的方法同分母分数相加、减,分母不变,只把分子相加或相减,能约分的要约成最简分数。
4、同分母分数连加的计算方法从左往右依次计算,也可以直接把加数的分子连加起来作分子,分母不变。
5、同分母分数连减的计算方法从左往右依次计算,也可以直接用被减数的分子连续减去减数的分子作分子,分母不变。
二、异分母分数加、减法1、异分母分数加减法的计算方法异分母分数相加、减,先通分,然后按照同分母分数加、减法的方法进行计算,能约分的要约成最简分数。
通分时,一般用几个分母的最小公倍数作公分母。
如果是用这几个分母的公倍数作公分母,不算错,但由于分母过大,无形中增加了学生的计算量,使计算难度加大。
2、特殊的异分母分数加减法的计算方法如:两个分数相加(减)时,当两个分数的分母互质,只有公因数1,且分子都是1时,计算只需将分母相乘的积作分母,分母相加(减)的结果作分子,就可算出得数。
字母表示为:(a 、b均不为0)三、分数加减混合运算1、分数加减混合运算的运算顺序和方法分数加减混合运算的运算顺序与整数加减混合运算的运算顺序相同,没有括号的,按照从左往右的顺序依次计算,有括号的先算括号里面的,再算括号外面的。
计算方法:异分母分数的加减混合运算,计算过程中如果没有括号,几个分数可以一次性通分进行计算,也可以分步通分,分步计算。
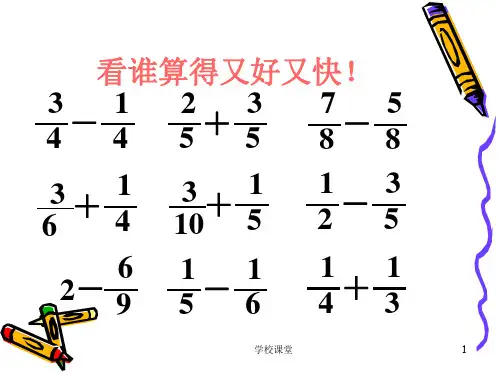

2022-2023学年五年级数学下册书山有路勤学系列之 第五单元:分数加减法混合运算和简便计算专项练习(解析版)1.计算。
(能简便的要简便计算)351()468-- 42577979-+- 2.仔细算一算,怎样简便就怎样计算。
437()51020-+ 7427911911+++ 3.计算下面各题,怎样简便就怎样算。
321836-+ 52539595-++ 4.计算下面各题,能简算的要简算。
72512312⎛⎫-- ⎪⎝⎭ 7112443-+ 5.计算下面各题,怎样简便就怎样算。
11311286⎛⎫-+ ⎪⎝⎭ 32175959+-+ 6.计算下面各题,怎样简便就怎样算。
523183⎛⎫-+ ⎪⎝⎭97265995+-+7.仔细算一算,怎么简便就怎样计算。
215737++551964⎛⎫+- ⎪⎝⎭ 8.计算下面各题,怎样简便就怎样算。
2384711117+++ 811926⎛⎫-- ⎪⎝⎭9.计算下面各题,怎样简便就怎样算。
851963⎛⎫-- ⎪⎝⎭ 11524137137++- 10.仔细算一算,怎样简便就怎样计算。
9311085++ 184********-+-11.计算下面各题,怎样简便就怎样算。
12721199-- 54212175517+-+ 12.计算下面各题,能简算的要简算。
315848-+ 1511-(411+913) 13.脱式计算,能简算的要简算。
3558118++ 112213713-+ 14.仔细计算,怎样简便就怎样算。
315848-+ 1726()11911+- 15.计算下面各题,能简算的要简算。
711-38+411 9121025⎛⎫+- ⎪⎝⎭16.计算下面各题,怎样简便就怎样算。
12+(65-23)79217913913+-+ 17.怎样计算简便就怎样计算。
229-(29+512) 15+38+45 189-23+1318.脱式计算,能简算的要简算。
111486+- 731()452-+ 1371124924-+ 3729516516+++。
分数加减法简便计算大全一、同分母分数的加法和减法1.分子相加、分母不变:当两个分数的分母相同时,加减法可以直接将分子相加或相减,分母保持不变即可。
例如:3/5+2/5=5/5=1(已经是最简分数)4/7-2/7=2/72.扩分后相加、分母相同:当两个分数的分母不同但可以通过扩分使得分母相同时,我们可以先将分数扩分,使得分母相同后再相加。
例如:1/3+1/4=4/12+3/12=7/123.通分后相加:当两个分数的分母不同而且无法通过扩分使得分母相同时,我们需要将它们通分后再相加。
通分的方法是找到它们最小公倍数作为新的分母,并将两个分数的分子按比例乘以扩大后的倍数。
例如:2/3+1/4=8/12+3/12=11/122/5-1/3=6/15-5/15=1/15二、分数的加法和减法1.整数和分数相加减:将整数看作分母为1的分数,然后用上述方法进行计算。
例如:2+1/3=6/3+1/3=7/32.带分数的加法和减法:将带分数转换为假分数,再用上述方法进行计算。
例如:11/2+22/3=3/2+8/3=9/6+16/6=25/631/4-13/8=13/4-11/8=26/8-11/8=15/8三、分数的合并与分解1.分数的合并:当有多个分数需要相加时,可以先合并同类项,再进行后续计算。
例如:1/2+1/4+1/8=4/8+2/8+1/8=7/82.分数的分解:当需要减去一个分数时,我们可以将减法转化为加法,先找到减数的相反数,再进行相加。
例如:2/3-5/12=2/3+(-5/12)=8/12+(-5/12)=3/12四、分数的简化1.分子分母同时除以最大公约数:将分子和分母都除以它们的最大公约数,将分数化简为最简分数。
8/12=(8÷4)/(12÷4)=2/3五、分数的加减混合运算1.先化为同分母:将分数、整数和带分数统一化为假分数或带分数,再按照对应的加减法进行计算。
例如:21/3-1/4+3/8=7/3-1/4+3/8=56/24-6/24+9/24=59/242.先计算乘除法:将分数和整数按照乘除法的优先级先进行计算,再进行加减法。
分数加减法简算题分数加减法简算题一、分数的加法1. 4/5 + 2/5 = _______解答:分子相加,分母保持不变,所以4/5 + 2/5 = 6/52. 2/3 + 1/6 = _______解答:分子相加,分母保持不变,所以2/3 + 1/6 = 4/6 + 1/6 = 5/63. 3/8 + 5/8 = _______解答:分子相加,分母保持不变,所以3/8 + 5/8 = 8/8 = 14. 1/2 + 3/4 = _______解答:分母不相同,需要通分。
1/2的分母乘以2,分子也乘以2,得到2/4。
所以1/2 + 3/4 = 2/4 + 3/4 = 5/45. 3/4 + 1/3 = _______解答:分母不相同,需要通分。
3/4的分母乘以3,分子也乘以3,得到9/12。
所以3/4 + 1/3 = 9/12 + 4/12 = 13/12二、分数的减法1. 4/5 - 1/5 = _______解答:分子相减,分母保持不变,所以4/5 - 1/5 = 3/52. 3/4 - 1/8 = _______解答:分子相减,分母保持不变,所以3/4 - 1/8 = 6/8 - 1/8 = 5/83. 7/8 - 3/8 = _______解答:分子相减,分母保持不变,所以7/8 - 3/8 = 4/8 = 1/24. 3/5 - 1/2 = _______解答:分母不相同,需要通分。
3/5的分母乘以2,分子也乘以2,得到6/10。
所以3/5 - 1/2 = 6/10 - 5/10 = 1/105. 5/6 - 2/3 = _______解答:分母不相同,需要通分。
5/6的分母乘以2,分子也乘以2,得到10/12。
所以5/6 - 2/3 = 10/12 - 8/12 = 2/12 = 1/6本文介绍了分数的加法和减法的简算题。
通过对分子的相加或相减,并保持分母不变,我们可以快速计算出结果。
课题分数的加减混合运算与简便计算重点难点分数的加减法运算定律、性质;几种常见的简便计算类型;教学步骤及教学内容教学步骤1、检查上次布置的课后作业及学校周末作业完成情况,并作变式练习2、师生板书例题问答,引导学生回顾本章节具体知识3、课前限时练习,讲练结合,查验学生薄弱点4、解疑答惑,引导学生积极思考5、本堂课内容知识小结6、课堂练习精析精讲7、重点知识提炼与总结8、本节课堂总结与反思教学内容运算定律、性质和其它①整数加法的交换律、结合律,以及减法的性质,在分数运算中同样适用。
能够运用这些定律和性质进行简算的,应尽可能运用。
例1、此题运用了加法交换律。
例2、此题运用了加法结合律。
例3、此题运用了减法性质。
加法结合律、交换律和减法性质要学会灵活运用。
例1、例2、()ab c a b c)在加减混合运算中,改变各部分运算顺序,结果不变:ab c a c b , a b c a c b)一个数减去两个数的和,等于用这个数依次减去括号里的两个数:ab c a b c)一个数加上两个数的差,等于先与括号里的被减数相加,再减去括号里的减数:a b c a b c712192921-1-4)--(32125 75182518251(0)1)aa 可以把这个分数拆分成111a a ,即111(1)1a a a a ;形如(0,0)a bab a b的分数可以拆分成11b,即:11a b a ba b 。
111111223344556练习:1111123344556910111112242462468246810例2:借还法 111111248163264练习:1- 12 - 14 - 18 - 116 - 132 - 164例3:平均求和 19981+19982+19983+……+19981997 练习:1354950505050科组长检查签字:教导主任检查签字:日期:年月日课后评价一、学生对于本次课的评价○特别满意○满意○一般○差二、教师评定1、学生上次作业评价:○好○较好○一般○差2、学生本次上课情况评价:○好○较好○一般○差作业布置课后作业(见下面作业布置)分数加减混合运算一、直接写出得数67+17= 1-513=67-0=89+0=95+75= 100-76= 1.25×0.8= 0.5÷0.25=二、解下列方程1.x-415=162.57-x =3113.516-x =512三、下面各题能简算的要用简便方法计算1、49+518+59+7182、87-25-353、911-57+2114、613+115+815+713四、生活中的问题。
问题一:分数加减混合运算没有括号的怎么计算?有括号的怎么计算?问题二:用不同的方法计算课本例1中的第(2)题,说一说有什么不同?运算法则1.先乘除,最后加减;2.同级运算从左到右按顺序运算;一、计算下列各题。
3/8+1/5-1/8 1/3+5/9-2/9 1-2/7-3/74/5-3/10+1/3 1-(3/4-3/8) 9/10-(1/6+1/5)1/2+(2/3-1/4) 5/8-(1/2-1/3) 7/12-3/5+1/67/20-(2/5+9/20) 2/9+(9/10-2/5) 7/8-(2/5+3/16)分数加减法简便计算习题班级: 座号 姓名一、计算。
1、直接写出得数。
59 +89 = 18 +78 = 1924 -1324= 1936 +336 = 37 +47 = 118 -18= 14 -19 = 1213 -313 = 89 +411 +19= 1-16 -16 = 34 +14 +14 = 78 -38 +38= 2、简便方法计算,写出主要计算过程。
(1)6.12+37 +2.88+47 (2)2924 -(524 -49) (3) 1811 -(711 + 38 ) (4) 79 +310 -29 +1710(5) 715 +712 +815 -712 (6)825 + 713 + 1725 + 6133、解方程。
(1) 2x -818 =1818 (2) 3x +139 = 149(3) x + 59 =1 (4) 2x -56 =56(5) x -(314 +47 )=12 (6) x -(74 - 38 )=78异分母分数加减法练习题一、口算。
=+5251 =-8385 =+3121 =-2143 =+8381 =+3195 =-10121 =+15153 =+18198 =+114117 =-3265 =-411二、填空。
(1)2个101是( ),107里面有( )个101。
分数的加减法一、同分母的分数加减法知识点:在计算同分母的分数加减法中,分母不变,直接用分子相加 减。
注意:在计算同分母的分数加减法中,得数如果不是最简分数,我们 必须将得数约分,使它成为最简分数。
例题一4 6 = 4 6 105555=2注意:因为 10不是最简分数,所以得约分,10 和 5 的最大公因数是 5,5所以分子和分母同时除以 5,最后得数是 2.例题二959 5 4 2 10 1010105注意:因为4不是最简分数,必须约分,因为4 和 10 的最大公因数10是 2,所以分子和分母同时除以2,最后的数是 25知识点回顾:如何将一个不是最简的分数化为最简?(将一个非最简分数化为最简, 我们就是将这个分数进行约分,一直约到分子和分母互质为止。
所以要将一个分数进行约分, 我们必须找 到分子和分母的最大公因数, 然后用分子和分母同时除以他们的最大 公因数。
)专项练习一:同分母的分数加减法的专项练习 一、计算7 2 7 199 15 -1512-121 -1611-7 113 3 1 1 3 3 3 3 8 +86 +614+144 +4二、连线14 +994 1 1+5 54 67+71 78 +845211+11三、判断对错,并改正4 3 7(1) 7 + 7 = 142112=5 =5=57 3777 98 83 1415711 119 2 3 11 9 9 5 1 1 922(2)6 -75-3775 37 - 7 - 7 2 3 7 - 7 1 7四、应用题73( 1)一根铁丝长 10 米,比另一根铁丝长 10 米,了;另一根铁丝长多少米?15( 2)3 天修一条路,第一天修了全长的12,第二天修了全长的12,第三天修了全长的几分之几?二、异分母的分数加减法。
在异分母的分数加减法中,可分为三种情况。
分别是分母是互质关系、分母是倍数关系、分母是一般关系(即非互质也非倍数)例: A代表一个分数的分母,B代表另一个分数的分母(1)11A B或B A即分子都为,分母互质)、A B AB AB(1B(是的倍数)A是的倍数)11A 1 B A或B1(A B(即分子都为,分母是倍数关系)、B BA A(3) 、A和B是一般关系,就找到A和B的最小公倍数,进行通分,再加减。