4800计算器使用方法

CASIO4800坐标计算程序CASIO4800缓和曲线、圆曲线和直线段上的任意中、边桩坐标计算程序1、该程序适用于计算器 CASVO fx-4800P，可计算与线路中心成任意夹角的缓和曲线、圆曲线、直线段中、边桩坐标及切线方位角。

2、A？输入转角：左转为负，右转为正3、R？输入圆曲线半径4、LS？输入缓和曲线长度5、JD？输入交点桩号6、J？输入0程序计算中桩，输入1程序计算边桩7、N？ E？输入交点X、Y坐标8、FW 待求点切线方位角9、当计算交角为60°时，则公式改为（U+60），（U-120）1 A：R：C“LS”：D“JD”2 P=C∧2/24/R-C∧4/2688/R∧33 Q=C/2-C∧3/240/R∧24 B=90C/兀/R5 T=(R+P)tan(AbsA/2)+Q◢6 W=(R+P)/cos(A/2)-R◢7 L=((AbsA)-2B)兀R/180+2C◢8 G=D-T◢9 H=G+C◢10 I=G+L/2◢11 K=G+L-C◢12 M=G+L◢13 N：E：F: J14 A＜0=>S=-1:≠=>S=1⊿15 U=F+A/2+90S16 V=W+R17 B=N+VcosU18 O=E+VsinU19 Lbl 120 {Z}21 Z≤G=>L=T+G-Z22 V=F+18023 U=F24 Goto 2⊿25 Z≤H=>L=Z-G26 V=L-L∧5/(90R∧2C∧2)27 L=30L∧2S/(兀RC)28 P=F+18029 Q=F+L30 U“FW”=F+3L◢31 Goto 4⊿32 Z≤K=>L=F+A/2+90S+180+180(Z-I)S/R/兀33 U“FW”=L+90S◢34 Goto 5⊿35 Z≤M=>L=M-Z36 V=L-L∧5/(90R∧2C∧2)37 L=30SL∧2/(兀RC)38 P=F+A39 Q=F+A+180-L40 U=F-3L+A◢41 Goto4⊿42 Z>M=>L=Z-M+T43 U=F+A44 V=U45 Goto 246 Lbl 247 X=N+LcosV◢48 Y=E+LsinV◢49 Goto 6⊿50 Lbl 351 {W}52 P“XL”=X+Wcos(U-90) ◢53 Q“YL”=Y+Wsin(U-90) ◢54 P“XR”=X+Wcos(U+90)◢55 Q“YR”=Y+Wsin (U+90) ◢56 Goto 157 Lbl 458 X=N+TcosP+VcosQ◢59 Y=E+TsinP+VsinQ◢60 Goto 661 Lbl 562 X=B+R cosL◢63 Y=O+RsinL◢64 Goto 665 Lbl 666 J=1=> Goto 3⊿67 Goto 1。

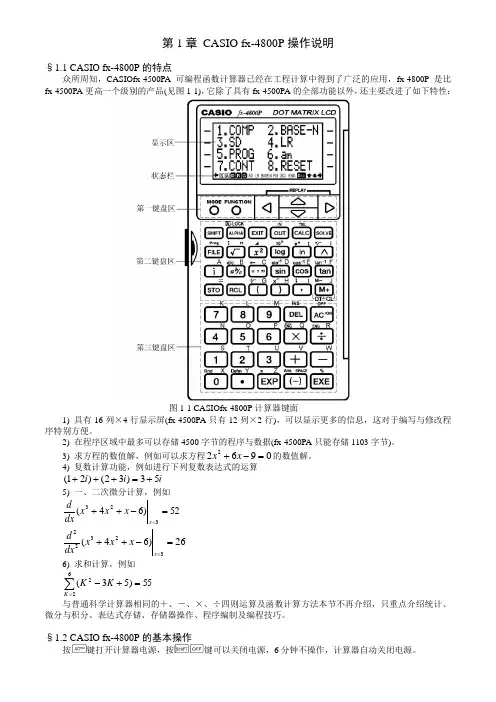
第1章 CASIO fx-4800P 操作说明§1.1 CASIO fx-4800P 的特点众所周知，CASIOfx-4500PA 可编程函数计算器已经在工程计算中得到了广泛的应用，fx-4800P 是比fx-4500PA 更高一个级别的产品(见图1-1)，它除了具有fx-4500PA 的全部功能以外，还主要改进了如下特性：1) 具有16列×4行显示屏(fx-4500PA 只有12列×2行)，可以显示更多的信息，这对于编写与修改程序特别方便。

2) 在程序区域中最多可以存储4500字节的程序与数据(fx-4500PA 只能存储1103字节)。

3) 求方程的数值解，例如可以求方程09622=-+x x 的数值解。

4) 复数计算功能，例如进行下列复数表达式的运算i i i 53)32()21(+=+++5) 一、二次微分计算，例如 52)64(323=-++=x x x x dx d 26)64(32322=-++=x x x x dx d 6) 求和计算，例如55)53(622=+-∑=K K K与普通科学计算器相同的＋、－、×、÷四则运算及函数计算方法本节不再介绍，只重点介绍统计、微分与积分、表达式存储、存储器操作、程序编制及编程技巧。

§1.2 CASIO fx-4800P 的基本操作 按键打开计算器电源，按键可以关闭电源，6分钟不操作，计算器自动关闭电源。

图1-1 CASIOfx-4800P 计算器键面(1) 键盘区简介fx-4800P的键盘分三个区排列。

1) 第一键盘区有模式键、功能键和四个光标移动/重演键。

计算器的微分、积分、表达式存储、程序编制等功能都是通过按和键调出相应的菜单选项选择来实现的，四个光标移动/重演键主要用于重复计算和编辑表达式。

2) 第二键盘区有4行6列共24个键，其键面功能主要是数学函数运算；3) 第三键盘区有4行5列共20个键，其键面功能主要是数字和＋、－、×、÷四则运算。

O —X N Y N计算L1 ZX？输入置镜点X 坐标X “ ZX ” Y “ ZY ” ZKA “ ZH ” B ZY？输入置镜点丫坐标“ XZH ” S“ YZH ” O“ EJ”：R“ R Z？输入置镜点高程(L- , R+ ) ” = 9 — Goto E / I “ LS ”K？输入仪器高度L : Lbl E : Q= 9 : J “ HX ” U ZH？输入直缓点里程Goto 6 ： Lbl 9 XZH？输入直缓点X 坐标L2 YZH？输入直缓点丫坐标G : “ — E ” 丄Lbl 1 : {N} : N “ —L” ：EJ？输入直缓点方位角W=Abs ( A-AbsN ： N= 9 — Goto 9 R(L— , R +)？输入圆曲线半径,/ E=O: F= 9 : P= 9 : R 工9 — Q=90/ 左偏为负, 右偏为正n R : Goto2 / Rec ( W, 18 9 +O : LS？输入直缓点至缓圆点长度Goto4 / Lbl 2 L？输入完整曲线长度,即两倍L3 LS 加圆曲线长I < W — E=Q ( W-I : Goto 3 / HX？输入后视点X 坐标P=QW2/I Rec( W-Wx y5/9 9 R2I 2 , HY？输入后视点丫坐标P/3+O : Goto4 / Lbl 3 —E 显示后视方位角L4 —L？输入计算里程W > L-I — Goto 1 / F=2RsinE : E = 显示视方位角P=E+O+IQ FcosP+Rec ( I － Ix y3/9 S = 显示前视距离9 R2, IQ/3+O Lbl 4 M？输入1 进入①中桩计算模L5 式, 输入9 进入②边桩计算模式 , Q=B+Ans J=Q F=S+W+FsinP 输入竖直角度进入③测距仪计算U=Ans : N > 9 — Goto 6 / Lbl 5 模式L6{D} : D= 9 — Goto 1 / D=1 — Goto 8 ① 中桩计算模式/ H=P+E — 9 9 AbsD/D : J=Q+Rec XD = 显示计算里程中桩X 坐标( Abs D , P+E-9 9 AbsD/D YD = 显示计算里程中桩Y 坐标U=F+W Lbl 6 —L？输入下一计算里程L7 ② 边桩计算模式Pol ( J-X , U-Y : W v 9 — W+36 D？输入边桩距离,左侧输正值, 9 :工—W / Q=9 —G=Ans : Goto 右侧输负值9 / “ E=” 丄V: “ S=” 丄Lbl 7 E = 显示前视方位角L8 s= 显示前视距离{CMTH} : M= 9 — Goto 5 / M =1 M？输入1 显示边桩坐标—Goto 8 / C Abs sinM : “ — D= ”—L？输入下一计算里程丄V— Ans : “ / S=” 丄Z= 9 — Goto 7 ③测距仪计算模式/ T= 9 — Goto 7 / C？输入斜距K-T+H+Z+CcosM : “ —H ” 丄Goto —D = 显示平距5 / Lb1 8 / S= 显示距离仪器？mL9 说明“ 9 ” 为零 , O 为英文字J: “XD= ” 丄U: “ YD = ” 丄Goto 1C “ X 9 = ”：D “ Y 9 = ”：E “ W 9 = ”： N=Ans : R “ R= ”： L “ L 卩。

CASIO 4800计算器程序使用说明一、程序列表：1。

PQX：主程序，计算路线的中边桩坐标。

(1)"L0"--- 输入测段的近似桩号，来调取合适的平曲线要素数据，输入0则默认上次输的平曲线要素。

输入-1可以手工输入交点桩号JL，交点X坐标JX，交点Y坐标JY，I0为前一交点与本交点的直线方位角，J0为本交点的偏角(左负右正)，R为圆曲线半径，LS为缓和曲线长度，L1为上一交点的HZ(或YZ)的桩号，L2为下一交点的ZH(或ZY)桩号。

(2)"L"---输入计算点的桩号(3)"JJ"---输入与路线前进方向的右交角（正交为90）(4)"YC"---输入与中桩的距离(左侧为负,右侧为正)注:若JJ和YC中任一个输入为0,则可返回上一级,重新输入桩号计算.若YC输入为-1,可以输入实测点的坐标X和Y来反算与中桩宽度YC,桩号差值DL和该点的近似桩号L.(5)"X,Y"数值1数值2显示计算点的坐标值X,Y(6)"A,D"ddd°mm′ss″数值4显示测站点与放样点的方位角及平距(7)"TMP"---进入自由运算状态,若计算结果为0则退出该状态.该状态会破坏变量I的内容.(8)"YC"---输入-1进入反算桩号模式,程序要求输x,y坐标,若x,y坐标其中任一输入为0则退出该状态.2.LYC程序:两个作用:一是根据实测坐标反算桩号L和与中桩宽度YC, 二是根据输入的三维坐标x,y,z和输入的设计标高SG以及"YC0","HC0","M"来进行边坡放样.(1)"L0"--- 输入测段的近似桩号，(2)"XF","YF","ZF"----输入测点的三维坐标x,y,z若ZF输为0则只反算桩号,若不为0则进行边桩放样.(3)"DL"---反算桩号时显示中间结果桩号差值DL,若DL值过大,可以重新输入测段的近似桩号来计算.(4) "L,YC"---显示桩号L和与中桩距YC(左负右正),存在变量L和O中.(5) "SG:"---输入路基边缘的设计高程(请分清左右),存在变量Z[10]中.(6) TW---显示填挖高度值(负值为挖方高度,正值为填方高度),存在变量C中.(7) "YC0"-路基横断面图上最后一个变坡点与中桩的水平宽度(左右均为正值),存在变量P中.(8)"HC0"---路基横断面图上最后一个变坡点与路基边缘设计标高的高差,挖方平台为正值,填方平台为负值,存在变量Q中.(9) "M="---路基横断面图上最后一级边坡的坡比,存在变量T中.(10) "BL"---显示在实测标高位置的路基设计宽度,存在变量U中.(11)"DB"---显示设计宽度和实测宽度的差值,存在变量J中.若DB为负值,则应往中桩位置移动(宽度减小),若DB为正值,则应往路线外侧移动(宽度增大).3、ZZ子程序---计算中桩坐标以及前进方位角的子程序。

§1.4 fx-4800P的统计计算普通计算器一般都有单变量统计计算功能，fx-4800P具有单变量和双变量统计计算功能。

(1) 单变量统计计算按键进入单变量统计模式，状态行显示；按键清除统计存储器P、Q、R、U、V、W 后，使用键输入数据项。

【例1-9】对某段距离等精度独立丈量了6次，距离丈量值分别为49.988、49.975、49.981、49.978、49.987、49.984，试计算其平均值x和一次丈量误差m。

进入单变量统计模式并清除了统计存储器后，按键操作如下：按键49.98849.97549.98149.97849.98749.984输入数据6个数据，按键调出统计计算结果，屏幕显示结果如下：Deviationx=49.98216666nσ=4.66964E-031-nσ=5.11533E-03再按键，屏幕显示结果如下：Sum∑2x=14989.30203∑x=299.893n=6其中1-nσ即为子样中误差。

也可以通过按键，在屏幕显示的图1-16所示的菜单中选择显示其中的某一个统计计算结果。

如果在程序中，不便于将存储器变量出现的顺序按照输入变量命令{}表中的顺序排列，当存储器变量只需要在程序中输入一次时，可以直接使用变量名并用连接符号“:”连接。

如编写一个程序，计算任意两点的边长和坐标方位角，其中第一点的坐标11,yx定义为X,Y存储器变量，第二点的坐标22,yx定义为U,V存储器变量，要求存储器变量提示的顺序为X=?,Y=?,U=?,V=?。

程序如下：X”X1”: Y”Y1”: U”X2”: V”Y2”G=U-X : H=V-YPol(G ,H): IJ0J=J+360变量X后的”X1”为提示字符，也可以不要，但加上后更便于理解输入数据项的意义。

上述程序执行完成后，再按键，程序开始重新计算并顺序提示X1=?,Y1=?,X2=?,Y2=?。

如果该程序由记数转移语句控制循环运算，则第二次运算时，程序将不会提示输入第一行的存储器变量。

QL（坐标反算）Lbi 0:C“X0”:D“Y0”:{XY}:X“X2”Y“Y2”:(X-C)=O=>Goto 1:≠Lbi 1:W“Q”=0◢Goto 0Lbi 2:Prog“FWJ”Fix 4W“Q”=IntW+0.01Int(60FracW)+0.006Frac(60FracW) ◢NormT“L”= ((X-C)2+(Y-D)2)◢Goto 0说明：（已知两点坐标，反算方位角及两点间的距离）先按FILE键，光标选择QL，按EXE运行。

输入：X0? 测站点（或起算点）X轴坐标，按EXEY0? 测站点（或起算点）Y轴坐标，按EXEX2? 后视点（或方向点）X轴坐标，按EXEY2? 后视点（或方向点）Y轴坐标，按EXE显示： Q 方位角（如：125.0325即表示125。

03’25”）,按EXE L 两点间距离再按EXE进行循环运算，重复输入X2？、Y2?否则按AC键退出。

XY(坐标正算)Lbi 0:C“X0”:D“Y0”:{WM}:W“Q”M“L”:X=C+McosW◢Y=D+MsinW◢Goto 0说明：（已知一点坐标、方位角、距离，求另一点坐标）先按FILE键，光标选择XY，按EXE运行。

输入：X0? 测站点（或起算点）X轴坐标，按EXE Y0? 测站点（或起算点）Y轴坐标，按EXE Q? 已知方位角，按EXEL? 两点间距离，按EXE显示：X 所求点X轴坐标，按EXEY 所求点Y轴坐标，按EXE再按EXE进行循环运算，重复输入Q? 、L?否则按AC键退出。

ZX（直线坐标计算）Lbi 0:G“QD”：A“QDX”: B“QDY”:Q“Q”:{L,K}:Prog“ZZ”:Goto 0说明：（计算直线段任意里程桩号坐标）先按FILE键，光标选择XY，按EXE运行。

输入：QD? 直线段起点里程，按EXEQDX? 起点X轴坐标，按EXEQDY? 起点Y轴坐标，按EXEQ? 已知方位角，按EXEL? 所求点里程，按EXEK? 所求点距中线的宽度（左负右正），按EXE显示：X 所求点X轴坐标，按EXEY 所求点Y轴坐标，再按EXE进行循环运算，重复输入L? 、K?否则按AC键退出。

4800计算器使用方法1.基本功能：4800计算器具备基本的算术运算功能，例如加法、减法、乘法和除法。

具体使用方法如下：-加法：输入第一个数字，按下“+”键，然后输入第二个数字，最后按下“=”键得到结果。

-减法：输入第一个数字，按下“-”键，然后输入第二个数字，最后按下“=”键得到结果。

-乘法：输入第一个数字，按下“×”键，然后输入第二个数字，最后按下“=”键得到结果。

-除法：输入第一个数字，按下“÷”键，然后输入第二个数字，最后按下“=”键得到结果。

注意，如果除数为零，将会显示错误。

2.百分比计算：4800计算器可以用于计算百分比。

具体使用方法如下：-除法计算百分比：输入需要计算的数值，按下“÷”键，然后输入百分数，并按下“%”键，最后按下“=”键得到结果。

-乘法计算百分比：输入需要计算的数值，按下“×”键，然后输入百分比，并按下“%”键，最后按下“=”键得到结果。

3.平方和平方根计算：4800计算器可以进行平方和平方根的计算。

具体使用方法如下：-平方计算：输入需要计算的数值，按下“ײ”键，最后按下“=”键得到结果。

-平方根计算：输入需要计算的数值，按下“√”键，最后按下“=”键得到结果。

4.三角函数计算：4800计算器可以计算正弦、余弦和正切值。

具体使用方法如下：- 正弦计算：输入需要计算的角度值，按下“sin”键，最后按下“=”键得到结果。

- 余弦计算：输入需要计算的角度值，按下“cos”键，最后按下“=”键得到结果。

- 正切计算：输入需要计算的角度值，按下“tan”键，最后按下“=”键得到结果。

5.小数值计算：4800计算器可以进行小数计算。

具体使用方法如下：-输入小数：直接输入小数，可以进行基本的四则运算计算。

-显示小数：按下“=”键得到的结果将显示为小数形式。

6.括号运算：4800计算器可以进行括号运算。

具体使用方法如下：-输入括号：按下“(”键表示左括号，“)”键表示右括号。

CASIO4800系列计算器线路线路正反算程序经本人苦心钻研，奋战多日，终于编写出了速度快，精度高，功能全的线路坐标正反算程序，欢迎试用并提出宝贵意见。

部分引用请注明出处。

功能简介及特点：1、选用高斯-勒让德公式作计算内核，保证精度，模块化设计，便于扩充功能。

2、线元数据可自动从数据库调用，也可手工输入。

3、可管理多条线路,如里程不在线路或线元范围，将警告里程偏大、偏小。

4、边桩计算设计为导线式递推方式，可用于由一个中桩推出结构物所有角点坐标。

5、反算实现了智能化操作，只需输入线路号（或手工输线元资料）、坐标，不需近似里程，即可自动从起点向后开始试算出里程、位置，如对算出里程、位置表示怀疑，还可以让计算器从终点起再向前试算下一个可能的位置（匝道、回头曲线同一坐标可能会有一个以上结果）。

6、程序代码规范简洁，便于阅读、理解。

程序清单:ZFS///正反算主程序Norm:Lbl 1:U"1 ZS 2 FS"=1=>Prog "ZS":≠>U=2=>Prog"FS":≠>Goto 1ZS///正算子程序{T}:Lbl 1:{K}:T"1 B"=1=>Prog"ZZ":Prog"WY":Goto 1△Prog"ZZ":Prog"ZB":Goto 1FS///反算子程序Lbl 1:{VW}:V"X"W"Y":U=2:Lbl 2:Prog "ZZ":Pol(V-X,W-Y:J=J-O:I=Rec(I,J:K=K+I:AbsI<0.001=>"KJ":K:Pause1:J◢{Z}:Z"0 NEXT"=0=>U=0:Goto 2△Goto 1△Goto 2GS///高斯法中桩子程序S=K-L:G=(P-R)÷2PQR:A=.1739274226:B=.5-A:C=.0694318442:D=.3300094782:E=1-C:F=1-D: I=4:Lbl 1:B[I]=O+180π-1SB[I](P-1+SGB[I]:Dsz I:Goto 1:O=O+180π-1S(P-1+SG：X=X+S(AcosC+BcosD+AcosE+BcosF:Y=Y+S(AsinC+BsinD+AsinE+BsinFZZ///中桩计算子程序Prog"XL":Prog"GS"WY///外移点计算子程序Lbl 1:I=0:J=90:{IJ}:I"L"≠0=>Z=J"<":J=O+J:O=O+Z:X=X+Rec(I,J:Y=Y+J:Prog"ZB":Goto 1ZB///坐标显示子程序"XY":X:Pause 1:Y◢YC///里程异常处理子程序U=2=>K=LΔU=0=>K=MΔU=1:K<L=>"<<!"◢H=1ΔK>M=>">>!"◢H=1Δ---------------------------以上为程序运算部分,以下为数据库部分-------------------------------------- XL///线路数据库选择子程序Lbl 1:H=0:N"0 SD":N=0=>Prog"0"△N=1=>Prog"1"△N=2=>Prog"2"△...有几条线路仿上行格式输几行H=1=>{NLXYOPQRK}:Goto 10///手工输入子程序L"K0"XYO"A0"Q"LS"P"R0"R"RN":M=L+Q:Prog"YC"1///线路一数据库子程序L=线路起点里程:M=线路终点里程:Prog"YC":H=1=>Goto EΔX=起点X坐标:Y=起点Y坐标:O=起点方位角:Q=线元长:P=起点半径:R=终点半径:K<L+Q=>Goto EΔL=123:X=123:Y=123:O=123:Q=123:P=123:R=123:K≤L+Q=>Goto EΔ...按里程由小到大，每条线元输一行。

主程序F3LbI 1:A“X1”:B“Y1”:C“X2”:D“Y2”N=0:E=C-A:F=D-B ↙ Prog“F1”↙{P}:P≥1 Prog“F2”△↙LbI 6:{XY}:E=X-A:F=Y-B:Prog“F1”:N≠1 L=G ↙Z≥L M=Z-L-180: M=Z-L+180: △↙M >0 M=180-M ▲M=180+Abs M▲△ Goto 6 ↙子程序F1E=0 Goto4 △ I=tan-1Abs(F÷E):S=√ (E2+F2) ▲F≥0 Goto2△E<0 G=180+I▲G = 360-I▲△Goto 5↙LbI 2:E<0 G=180-I ▲G = I ▲△ Goto 5 ↙LbI 4:F>0 G = 90 ▲G =270 ▲△ Goto 5 ↙LbI 5:N=N+1:N=1 Z= G △↙子程序F2LbI 9:{SI}:P=G+180-I:X=A+Scosp▲Y=B+SsinP ▲{o}:o≤0 Goto 9 △ o≤1 A=X:B=Y:G=P+180:G>360 G = G-360:Goto 9 △↙说明:1、主程序F3，已知座标放线；2、P<1主程序进入座标放样计算，P≥1时主程序进入座标计算；3、F3中的S是站点至待放点的距离，M是后视点至待放点的左角。

4、F2中的O表示站点，O>1迁站重新输入（X1，Y1）（X2，Y2）计算座标。

输入转角I时；转角左转I取“+”，右转I取“—”。

5、F2中的S，是表示站点至待求座标点的距离，用测距仪测定。

主程序：PQXLbI O:A“K0”:B“X0”:C“Y0”:D“L0”:E“A0”:F“B0”:G“K1”:N :R:T:Z:L=K-A:S=K-A-D:I=G-K ↙{K} ↙N<1 Prog “P1”:Goto O △↙N=1 Prog “P2”:Goto O △↙Prog “P3”↙Goto O ↙子程序：P1Z≤1 X=B+[L-L5÷(40R2D2)]CosE+[L3cos(E+90)]÷(6RD)▲Y=C+[L-L5÷(40R2D2)]sinE+[ L3sin(E+90)] ÷(6RD) ▲Y=C+[L-L5÷(40R2D2)]sinE+[ L3sin(E-90)] ÷(6RD)▲子程序:P2Z≤1 X=B+[D- D3÷(40R2)]cosE+[(D2÷(6R))]cos(E+90)+[S-S3÷(6 R2 )+ S5 /(120R4 )]Cos[E+(90D) ÷(πR )]+[ S2÷(2R)-S4÷(24R3)+S6÷(720R5)]cos[E+(90D)÷(πR)+90] ▲ Y=C+[D- D3÷(40R2)]sinE+[(D2÷(6R))]sin(E+90)+[S-S3÷(6R2)+S5÷(120R4)]sin[E+(90D)÷(πR)]+[S2÷(2R)-S4÷(24R3)+S6÷(720R5)]sin[E+(90D)÷(πR)+90] ▲X=B+[D-D3÷(40R2)]cosE+[(D2÷(6R)]cos(E-90)+[S-S3÷(6R2) +S5÷(120R4)]cos[E-(90D)÷(πR)]+[S2÷(2R)-S4÷(24R3)+S6÷(720R5)]cos[E-(90D)÷(πR)-90] ▲Y=C+[D-D3÷(40R2)]sinE+[(D2÷(6R)]sin(E-90)+[S-S3÷(6R2) +S5÷(120R4)]sin[E-(90D)÷(πR)]+[S2÷(2R)-S4÷(24R3)+S6÷(720R5)]sin[E-(90D)÷(πR)-90] ▲子程序:P3Z≤1 X=B+TcosE+Tcos(E+F)+[I-I5÷(40R2D2)]cos(E+F+180) +[I3÷(6RD)]cos(E+F+180-90)▲Y=C+TsinE+Tsin(E+F)+[I-I5÷(40R2D2)]sin(E+F+180) +[I3÷(6RD)]sin(E+F+180-90)▲X=B+TcosE+Tcos(E-F)+[I-I5÷(40R2D2)]cos(E-F+180) +[I3÷(6RD)]cos(E-F+180+90)▲Y=C+TsinE+Tsin(E-F)+[I-I5÷(40R2D2)]sin(E-F+180)+[I3÷(6RD)]sin(E-F+180+90)▲说明:1.K0为ZH点桩号;(X0，Y0)为ZH点座标；L0为缓和曲线段长度，A0为直线方位角；B0为转角；K1为HZ点桩号；N为条件参数；R为半径；T为切线长；Z为条件参数；K为待求点桩号。

卡西欧4500/4800计算器程序任意里程桩号计算程序1.主程序(TYQXjs)"1.SZ => XY"："2.XY => SZ"：N：U"X0"：V"Y0"：O"S0"：G"F0"：H"LS"：P"R0"：R"RN"：Q：C =1÷P：D=(P-R)÷(2HPR)：E=180÷π：N=1=>Goto 1：≠>Goto 2Δ←┘Lbl 1：{SZ}：SZ：W=Abs(S-O)：Prog "SUB1"：X"XS"=X◢Y"YS"=Y◢F”FS”=F-90◢Goto 1←┘Lbl 2：{XY}：XY：I=X：J=Y：Prog "SUB2"：S"S"=O+W◢Z"Z"=Z◢Goto 22. 正算子程序(SUB1)A=0.1739274226：B=0.3260725774：K=0.0694318442：L=0.3300094782：F=1-L：M=1-K：X=U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Bcos(G+QEFW(C+FWD))+Acos(G+QE M W(C+M WD))):Y=V+W(Asin(G+QEKW(C+KWD))+Bsin(G+QELW(C+LWD))+Bsin(G+QEFW(C+FWD)) +Asin(G+QE M W(C+M WD))) :F=G+QEW(C+WD)+90:X=X+ZcosF：Y=Y+ZsinF3. 反算子程序(SUB2)T=G-90：W=Abs((Y-V)cosT-(X-U)sinT)：Z=0：Lbl 0：Prog "SUB1"：L=T+QEW(C+WD)：Z=(J-Y)cosL-(I-X)sinL：AbsZ<1E-6=>Goto1：≠>W=W+Z：Goto 0Δ←┘Lbl 1：Z=0：Prog "SUB1"：Z=(J-Y)÷sinF二、使用说明1、规定(1) 以道路中线的前进方向（即里程增大的方向）区分左右；当线元往左偏时，Q=-1；当线元往右偏时，Q=1；当线元为直线时，Q=0。

CASIO-fx4800P型计算器连续计算线路高程、坐标及放样程序【简述】为了适应现场快速、准确、灵活的放样要求，作者根据线路施工测量特点，运用计算器的编程功能，使整条线路的施工测量计算数据能连续快速的计算，只要把整条线路各个交点处的计算要素输入子程序中，你便拥有整条线路的“数据库”。

在忙碌的施工现场，你不必携带大量的施工图和资料来查找平面、纵断面的设计要素，更不必担心设计要素的输入错误，从而使得计算和放样轻松、方便、快捷。

【计算范围】坐标部分包括：各等级公路和高速路的直线段、圆曲线段、加对称缓和曲线的圆曲线段中、边桩坐标及放样计算。

高程部分包括：各等级公路和高速路的直线段、竖曲线段、缓和超高段中、边桩高程及放样计算。

一、坐标及放样程序【起算数据】：交点里程桩号、交点坐标、前直线方位角、交点转角、圆曲线半径、缓和曲线长（一）主程序：XYFY2Fix4M"Xc=":P"Yc=" ＇如须放样输入测站坐标值,否则输入0Lbl0{HS}:H"K0+0":S"B=(-B,0,B)":Prog"A" ＇变量输入和声明S=0=>E=0:≠>E=90 ＇求边桩坐标时的偏角值判定L=πRN÷180+V ＇含有缓曲线的曲线总长T=(V÷2-V^3÷(240R^2))+(R+(V^2÷(24R)-V^4÷(2688R^3)))tan(N÷2)  ＇切线长A=Q-T:B=A+V:D=A+L:C=D-V ＇A-ZH(ZY)点桩号,B-HY点桩号,C-YH点桩号,D-HZ(YZ)点桩号Rec(T,F+180) ＇求ZH(ZY)点的坐标增量Z[1]=W+I:Z[2]=K+J ＇ZH(ZY)点坐标值Rec(T,F+GN) ＇求HZ(YZ)点的坐标增量Z[3]=W+I:Z[4]=K+J ＇HZ(YZ)点的坐标值Lbl1U=S÷(Abs(S+10E-19)):S=AbsS ＇左右偏角每件判定H<A=>Goto2: ≠> ＇第一直线上坐标计算判定H<B=>Goto3: ≠> ＇第一缓和曲线上坐标计算判定H<C=>Goto4: ≠> ＇净圆曲线上坐标计算判定H<D=>Goto5: ≠> Goto6⊿⊿⊿⊿ ＇第二缓和曲线和第二直线上坐标计算判定Lbl2Rec(Q-H,F+180) ＇第一直线上中桩坐标增量计算X=W+I:Y=K+J ＇中桩坐标值计算Rec(S,F+180-(180-E)U) ＇第一直线上与中桩同一断面的边桩增量计算X=X+I:Y=Y+J ＇边桩坐标值计算S=SU ＇边长条件判定Goto8Lbl3 ＇进入第一缓曲线段计算Z=H-A ＇待求点至ZH点的距离O=90Z^2÷(πRV) ＇所求点缓曲线对应的圆心角X=Z-Z^5÷(40R^2V^2)+Z^9÷(3456R^4V^4) ＇缓曲线上ZH点至待求的支距X坐标Z=Z^3÷(6RV)-Z^7÷(336R^3V^3)+Z^11÷(42240R^5V^5) ＇缓曲线上ZH点至待求点的支距Y坐标Lbl7Rec(X,F)X=Z[1]+I:Y=Z[2]+JRec(Z,F+90G) ＇把中桩支距坐标转换成测量统一坐标X=X+I:Y=Y+JRec(S,F+O G+EU) ＇曲线边桩坐标增量计算X=X+I:Y=Y+J ＇坐标计算结果S=SU ＇边长条件Goto8Lbl4 ＇进入主圆计算部分Z=H-A-V÷2 ＇曲线上待求点到HY点的里程O=180Z÷(Rπ) ＇待求点方位角所对应的圆心角X=Rsin O+(V÷2-V^3÷(240R^2))Z=R(1-cos O)+(V^2÷(24R)-V^4÷(2688R^3)) ＇主圆部分待求点支距坐标XY Goto7Lbl5 ＇进入第二缓和曲线计算Z=D-H ＇曲线上待求点到HZ点的里程O=90Z^2÷(πRV) ＇待求点方位角所对应的圆心角X=Z-Z^5÷(40Z R^2V^2)+^9÷(3456R^4V^4)Z=Z^3÷(6RV)-Z^7÷(336R^3V^3)+Z^11÷(42240R^5V^5) ＇待求点支距坐标XY Rec(X,F+GN+180)X=Z[3]+I:Y=Z[4]+J ＇把中桩支距坐标转换成测量统一坐标Rec(Z,F+GN+180-90G)X=X+I:Y=Y+JRec(S,F+GN+180-O G-(180-E)U) ＇曲线边桩坐标增量计算X=X+I:Y=Y+J ＇坐标计算结果S=SUGoto8Lbl6 ＇进入第二直线段计算部分Rec(H-D+T,F+GN) ＇中桩坐标增量计算X=W+I:Y=K+J ＇中桩坐标计算结果Rec(S,F+GN+EU) ＇边桩坐标增量计算X=X+I:Y=Y+J ＇边桩坐标计算结果S=SUGoto8Lbl8X=X◢ ＇显示坐标计算结果Y=Y◢M≠0=>Goto9: ≠>Goto0 ⊿Lbl9 ＇进入放样部分计算Pol(X-M,Y-P) ＇增量计算J<0=>J=J+360: ≠>J=J ⊿J"A"=Int J+0.01Int(60Frac J)+0.006Frac(60Frac J) ◢ ＇方位角计算结果（此显示值为度分秒格式）I"L"=I◢ ＇极距计算结果Goto0∙(二)子程序:AH≤ZY2(ZH2)=>Q=JD1:W=X1:K=Y1:R=R1:F=F0:N=N1:V=Ls1:G=1(-1):=>H≤ZY3(ZH3)=>Q=JD2:W=X2:K=Y2:R=R2:F=F1:N=N2:V=Ls2:G=1(-1):=>H≤ZY4(ZH4)=>Q=JD3:W=X3:K=Y3:R=R3:F=F2:N=N3:V=Ls3:G=1(-1):=>H≤ZY5(ZH5)=>Q=JD4:W=X4:K=Y4:R=R4:F=F3:N=N4:V=Ls4:G=1(-1):=>……………………………H≤ZY n+1(ZH n+1)=>Q=JD n:W=X n:K=Y n:R=R n:F=F n-1:N=N n:V=Ls n:G=1(-1)注:H—待求点桩号ZY n+1(ZH n+1)—后曲线起点桩号 Q—本曲线交点桩号 W—本曲线交点X坐标K—本曲线交点Y坐标 R—本曲线内圆曲线半径 F—前直线方位角 N—本交点转角V—本曲线内缓和曲线长 G—线路转向符,左转角-1,右转角为+1二、高程及放样程序【起算数据】：变坡点桩号A、变坡点高程B、前后纵坡C D、竖曲半径R、横坡度F、最大超高横坡度G、ZH点桩号、YH点桩号、HZ点桩号、施工层厚度N、视线高W （一）主程序：GCFYW"SXG="：N ＇常量输入（视线高程、施工层厚度）Lbl 1｛LО｝:L"K0+0"：О"B=" :Prog"B" ＇变量输入及声明K=C-D ＇坡度差及竖曲线偏角K>0=>J=-1:≠>J=1⊿ ＇凹凸竖曲线判断条件T=Abs(RK)÷2 ＇竖曲线切线长,如需显示则在后面加上◢H=A-T ＇竖曲线起点ZY桩号,如需显示则在后面加上◢X=A+T ＇竖曲线终点YZ桩号,如需显示则在后面加上◢M=L-A ＇待求点至变坡点的距离L≤H=>P=B+MC-N-W: ≠> ＇前纵坡直线段中桩高程计算L≤A=>P=B+MC+J(T-AbsM)2÷(2R)-N-W: ≠>  ＇前纵坡竖曲线中桩高程计算L≤X=>P=B+MD+J(T-AbsM)2÷(2R)-N-W: ≠> ＇后纵坡竖曲线中桩高程计算L>X=>P=B+MD-N-W⊿⊿⊿⊿⊿ ＇后纵坡直线段中桩高程计算E=0=>Goto 2 ＇直线部分中、边桩计算判断条件≠>L≤E=> Goto 2 ＇直线部分中、边桩计算判断条件≠>L>V=> Goto 2 ＇直线部分中、边桩计算判断条件≠>L>E=> Goto 3 ＇前缓曲超高部分中、边桩计算判断条件≠> L>U=> Goto 4⊿⊿⊿⊿ ＇后缓曲超高部分中、边桩计算判断条件Lbl 2O=0=>Z“H”=AbsP◢＇显示直线部分中、边桩高程计算结果≠>Y“HB”=Abs(P-OF)◢不需放样显示高程,否则显示放样水准尺计数⊿Goto 1Lbl 3S=（L-E）（F+G）÷（V-U）-F  ＇前缓曲线超高横坡度计算S≤F=> Goto 5：≠>S≤G=> Goto 6 ＇超高起点(终点)至零界面、零界面至全超高及全超高≠> Goto 7 ⊿⊿ 部分的计算判断条件Lbl 4S=（V-L）（F+G）÷（V-U）-F  ＇后缓曲线超高横坡度计算S≤F=> Goto 5：≠>S≤G=> Goto 6 ＇超高起点(终点)至超高变坡零界面、零界面至全≠> Goto 7 ⊿⊿ 超高、全超高部分计算判断条件Lbl 5O=0=>Z“H1”=AbsP◢＇超高起点(终点)至超高变坡零界面中、边桩高程≠>Y“H-D1”=Abs(P-OF)◢计算结果显示Q“H-G1”=Abs(P+OS)◢⊿Goto 1Lbl 6O=0=>Z“H2”=AbsP◢＇超高变坡零界面至全超高中、边桩高程≠>Y“H-D2”=Abs(P-OS)◢计算结果显示Q“H-G2”=Abs(P+OS)◢⊿Goto 1Lbl 7O=0=>Z“H3”=AbsP◢＇全超高中、边桩高程计算结果显示≠>Y“H-D3”=Abs(P-OG)◢Q“H-G3”=Abs(P+OG)◢⊿Goto 1∙∙注：W“SXG”-视线高N-施工层厚度L"K0+0"-待求点桩号О"B="-中桩至边桩距离（二）子程序：BL≤ZY2=>A=JD1:B=H1:C=I0:D=I1: R=R1:F=I h:E=ZH1:U=YH1:V=HZ1:G=I max1 :≠>L≤ZY3=>A=JD2:B=H2:C=I1:D=I2: R=R2:F=I h:E=ZH2:U=YH2:V=HZ2:G=I max2 :≠>L≤ZY4=>A=JD3:B=H3:C=I2:D=I3: R=R3:F=I h:E=ZH3:U=YH3:V=HZ3:G=I max3 :≠>L≤ZY4=>A=JD3:B=H3:C=I2:D=I3: R=R3:F=I h:E=ZH3:U=YH3:V=HZ3:G=I max3 :≠> ……………………L≤ZY n+1=>A=JD n:B=H n:C=I n-1:D=I n: R=R n:F=I h:E=ZH n:U=YH n:V=HZ n:G=I maxn注:ZY N+1:-下一个竖曲线起点桩号（如：变坡点2的计算范围为前竖曲线终点YZ1至后竖曲线起点ZY3，则在程序中“L≤ZY3”就应输入ZY3的里程桩。

卡西欧4800\4850计算器计算程序及说明一：坐标反算：(ZBFS)1 程序步骤：C”X1”:D”Y1”:E”X2”:F”Y2”:Fixm:Pol(E-C,F-D:I”S1-2=”▲J≤Ｏ＝＞J=J+360△J”A1-2=”2 操作过程：ZBFS→EXE→输入X1值→EXE→输入Y1值→EXE→输入X2值→EXE→输入Y2值→EXE→EXE→EXE注：①：S1-2:计算得出的距离。

②：A1-2:计算得出的角度。

（按shift°′″转换为60进制的角度）③：此程序可循环计算。

3 案例：已知：D1坐标（7811.23，606.136），D2坐标（7805.915，431.910）求解： a D1-D2(A1-2)=268°15′09.56 ″S D1-D2(S1-2)=174.3071二：坐标正算：(ZBZS)1 程序步骤：C”X1”:D”Y1”:S”S1-2”:R”A1-2”:Fixm:X”X2”=C+Rec(S,R) ▲Y”Y2”=D+J2 操作过程：ZBZS→EXE→输入X1值→EXE→输入Y1值→EXE→输入S1-2距离值→EXE→输入A1-2角度（例268°15′09.56 ″）值→EXE→EXE注：①：X2计算得出坐标，Y2计算得出坐标。

②：此程序可循环计算。

3 案例：已知：D1坐标（7811.23，606.136），两点距离：S D1-D2(S1-2)=174.3071方位角：a D1-D2(A1-2)=268°15′09.56 ″ 求解：D2坐标（7805.915，431.910三：线路曲线计算程序:（XLQXJS）(万能公式)1 程序步骤：1.Lbl 0:{E G}：A“XA”：B“YA”：C“CA”：D“1/RA”：E“1/RB”：F“DKA”： G“DKA”2.Lbl 1:{H O R}:H“DKI”：O“DL”：R“DR”：H＞G=﹥Goto 3⊿3.P=(E-D)/Abs(G-F):Q=Abs(H-F):I=P×Q:T=D+I4.J=C+(I+2D)×Q×90/π ▲5.M=C+(I/4+2D)Q×45/(2π):N=C+(3I/4+2D)Q×135/(2π):6.K=C+(I/2+2D)Q×45/π7.X=A+Q(cosC+4(cosM+cosN)+2cosK+cosJ)/12 ▲8.Y=B+Q(sinC+4(sinM+sinN)+2sinK+sinJ)/12 ▲9.U“XL”=X+Ocos(J-90) ▲10.V“YL”=Y+Osin(J-90) ▲11.W“XR”=X+Rcos(J+90) ▲12.Z“YR”=Y+ Rsin(J+90) ▲13. A=X：B=Y：C=J：D=T：F=H：Goto 1Lbl 3: A=X：B=Y：D=E：F=G：C=J：Goto 0程序说明：A- 曲线元起点A的坐标；B- 曲线元起点B的坐标；C- 曲线元起点A的切线坐标方位角；F- 曲线元起点A的里程；G- 曲线元起点B的里程；H- 曲线上待求点i的里程；D- 曲线元起点A的曲率；E- 曲线元终点B的曲率；XL-左边线点位X坐标；YL-左边线点位Y坐标；XR-右边线点位X坐标；YR-右边线点位Y坐标；X- 中线点位纵坐标；Y- 中线点位横坐标；DL-左边线距中线平距；DR-右边线距中线平距；该程序需要输入的数据为：（1）.曲线元起点A的坐标及切线坐标方位角，计算器上用“XA”，“YA”，“CA”显示；（2）.曲线元起点A和B的曲率，计算器上用I÷RA，I÷RB 显示（曲线左偏时取“-”）；（3）.曲线元起点A和终点B的里程，计算器上用“DKA”，“DKB”显示；（4）.输入待求点里程和该点距左右的水平距离，计算器上用“DKI”，“DL”，“DR”显示；每算完一个待求点的中线及边线坐标，程序又让输入下一点的“DKI”，“DL”，“DR”当输入的“DKI”大于“DKB”时程序中显示“1÷RB”和“DKB”，此时输入下一个曲线元起点的曲率和里程，然后重复步骤（4），即可计算下一个曲线中线及边线点位坐标。

十一．BI DAO XIAN（闭导线）1．用途：该程序是“闭合导线平差”的计算程序。

2．程序数学模型：3．程序清单：Defm 40：X“X0”：Y“Y0”：F“A0”：N“UNKNOWN POINT”：N=N+1↙I=0：E=0：C=0：Lbl 0 ↙I=I+1：{L，D}：Z[2I-1]=L：Z[2I]=D：E=E+L：C=C+D：I<NGoto 0 Δ B“FW”=E-180（N-2）◢R：A“FR”=RN◢B=-B÷N：I=1：Z[2N+1]=F：Lbl 1 ↙I+I+1◢F=F+Z[2I-1]：F180F=F+180：F=F-180 Δ F360F+F-360 ΔZ[2N+2I-1]“A”=F+（I-1）B◢I<NGoto 1Δ I=0：G=0：H=0：Lbl 2 ↙I+I+1：Z[2I-1]=Z[2I]cosZ[2N+2I-1]：G=G+Z[2I-1]：Z[2N+2I]=Z[2I]sin Z[2N+2I-1]：H=H+Z[2N+2I]：I<N Goto 2 Δ G“FX”◢H“FY”◢I“F”=（G2+H2）◢K=I÷C◢U=-G÷C：V=-H÷C↙I=0：Lbl 3 ↙I+I+1◢Z[2I-1]=Z[2I-1]+U Z[2I]：Z[2N+2I]=Z[2N+2I]+V Z[2I]：X=X+ Z[2I-1]◢Y=Y+ Z[2N+2I]◢I<N-1Goto 3：“END”4．程序说明：X0，Y0，A0——已知的起始点的纵、横坐标及起始边的坐标方位角。

UNKNOWN POINT——待求未知点的个数。

L，D——观测的导线各左转角及平距。

FW，R，FR——导线角度闭合差、角度闭合差的允许误差的系数及允许误差值。

I，A——各条导线边序号及其坐标方位角。

FX，FY——坐标增量ΔX、ΔY的闭合差。

F，K——导线全长闭合差、导线全长相对闭合差。

一、运行变量名称说明：M为待求桩号K为左右偏距(左-右+)G为路线正斜交角H、I为待求点的X、Y坐标U为待求桩即时切线方位角二、要素程序输入中的变量说明：XY为起点坐标W为单曲线段起始方位角E、F为单曲线段起止桩号A、B为单曲线段起止半径(起或止为缓和曲线的输为缓和参数) Q=-1、1分别指单曲线段的左转、右转J=1、-1分别为缓和曲线指ZH->HY、YH->HZ方向P=1、2、3分别指单曲线段为直线、圆曲线、缓和曲线另外：主线中Z=1、2为断链1、2段(如K8+273.243=K8+100) 三、主程序中第三句根据需求线路随时更换子程序名。

主程程序"ZBJS":Lbl 0{M}:"SQD"Prog "AB"X"X"Y"Y"W"FWJ"E"QD"P:"1 2 3"P=1=>Goto 1:≠=>P=2=>Goto2:≠=>P=3=>Goto 3 Lbl 1 进入直线段计算M{K}{G}F"FWJ"W◢H=X+(M-E)*cosW+K*cos(W+G)◢I=Y+(M-E)*sinW+K*sin(W+G)◢Goto 0M<F=>Goto 1:≠=>X=H:Y=I:E=M:P=0:Goto 0 Lbl 2 进入圆曲线计算A"R"M{K}{G}FO=X+A*cos(W+90Q) 圆心坐标(O,P)P=Y+A*sin(W+90Q)V=Abs(M-E)/A*180/π*Q"a0"U=W+V◢H=O+A*cos(U-90Q)+K*cos(U+G)◢I=P+A*sin(U-90Q)+K*sin(U+G)◢Goto 0M<F=>Goto 2:≠=>X=H:Y=I:W=U:E=M:P=0:Goto 0Lbl 3 进入缓和曲线计算A"QD R"B"AZ"M{K}{G}FC=B^2"ZH=1 HZ=-1"JL=C/AV=(F-E)/Abs(F-E)Z=W+L^2/(2C)*180/π*Q*(-J)T=L+(Abs(M-E))JU=Z+T^2/(2C)*QJV*180/π◢O=(T-L)-(T^5-L^5)/(40C^2)+(T^9-L^9)/(3456C^4)-(T^13-L^13)/599040C^6+(T^17-L^17)/175472640 C^8P=(T^3-L^3)/(6C)-(T^7-L^7)/(336C^3)+(T^11-L^11)/(42240C^5)-(T^15-L^15)/9676800C^7+(T^19-L^19)/3530096640C^9D=VJS=QJH=X+OD*cosZ+PD*cos(Z+90S)+K*cos(U+G)◢I=Y+ODsinZ+PDsin(Z+90S)+K*sin(U+G)◢Goto 0M<F=>Goto 3:≠=>X=H:Y=I:W=U:E=M:P=0:Goto 0主线"ZX":M>5865=>X=3361488.152:Y=449202.642:W=101`49`58`:E=5865:P=1M>5865.526=>X=3361488.044:Y=449203.157:W=101`49`58`:E=5865.526:A=9^60:B=1096.59:Q=-1: J=1:P=3:F=6235.526M>6235.526=>X=3361419.068:Y=449566.617:W=98`34`16.9`:E=6235.526:A=3250:Q=-1:P=2M>7674.84=>X=3361521.529:Y=450990.516:W=73`11`49.3`:E=7674.84:F=8044.84:A=3250:B=1096. 59:J=-1:Q=-1:P=3M>8044.84=>X=3361641.834:Y=451340.355:W=69`56`7.9`:E=8044.84:P=1:Z=2=>X=3361720.194:Y =451554.895:W=69`56`7.9`:E=8100:P=1匝"AB":M≥0=>X=3361721.181:Y=450482.643:W=85`46`15`:E=0:A=800:Q=1:P=2M>716.396=>X=3361468.151:Y=451127.474:W=137`4`44`:E=716.396:F=776.396:Q=-1:A=9^45:B=6 0:P=3:J=1M>776.396=>X=451174.516:W=108`25`51.6`:Q=-1:A=60:E=776.396:P=2M>842.929=>X=3361446.56:Y=451235.989:W=44`53`50`:A=60:B=60:Q=-1:E=842.929:F=902.929:J =-1:P=3M>902.929=>X=3361499.992:Y=451261.793:W=16`14`58`:E=902.929:F=947.929:Q=1:A=9^45:B=9 0:J=1:P=3M>947.929=>X=3361542.602:Y=451276.164:W=23`24`41.1`:E=947.929:Q=1:A=180:P=2M>1047.145=>X=3361618.517:Y=451338.083:W=54`59`34.26`:E=1047.145:F=1141.034:Q=1:J=-1:A =180:B=130:P=3匝"C":M≥842.929=>X=3361446.56:Y=451235.989:W=44`53`50`:E=842.929:A=60:Q=-1:P=2M>932.843=>3361528.246:Y=451238.793:W=319`02`08.44`:E=932.843:F=1067.843:Q=-1:J=-1:A=6 0:B=90:P=3M>1067.843=>X=3361541.195:Y=451111.894:W=354`34`40`:E=1067.843:P=1匝"D":M≥0=>X=3361640.231:Y=450877.857:W=115`7`37`:A=791.747:B=55:E=0:F=46.596:P=3:J=1:Q=1 M>46.596=>X=3361614.603:Y=450916.347:W=139`3`39.2`:E=46.596:A=60:Q=1:P=2M>101.697=>X=3361563.143:Y=450929.781:W=191`40`42.5`:E=101.697:F=234.195:A=60:B=90:Q= 1:J=-1:P=3匝"E":M≥0=>X=3361652.781:Y=450889.678:W=115`30`28`:E=0:F=53.571:A=9^45:B=150:Q=-1:J=1:P=3 M>53.571=>X=3361630.748:Y=450938.498:W=111`51`13.6`:E=53.571:A=420:Q=-1:P=2M>303.928=>X=3361610.206:Y=451184.308:W=77`42`1.6`:E=303.928:F=385.416:A=420.:B=185:J=-1:Q=-1:P=3M>385.416=>X=3361632.665:Y=451262.605:W=72`8`31.93`:E=385.416:P=1匝"FH":M≥0=>X=3361721.183:Y=450482.658:W=265`46`15`:E=0:P=1M>687.778=>X=3361670.463:Y=449796.752:W=365`46`15`:E=687.778:F=747.778:A=9^50:B=60:J= 1:Q=-1:P=3M>747.778=>X=3361656.351:Y=449739.118:W=237`7`22.6`:E=747.778:Q=-1:A=60:P=2M>956.691=>X=3361569.331:Y=449819.209:W=37`37`32.61`:E=956.691:F=1038.357:A=60:B=70:J= -1:Q=-1:P=3M>1038.357=>X=3361647.7:Y=449835.267:W=358`37`59`:E=1038.357:P=1匝"G":M≥838.838=>X=3361576.113:Y=449719.64:W=150`10`2`:A=60:B=60:E=838.838:F=898.838:J=-1:Q =-1:P=3M>898.838=>X3361537.147:Y=449764.388:W=121`31`9.6`:E=898.838:F=949.463:A=9^50:B=90:J= 1:Q=1:P=3M>949.463=>X=3361508.476:Y=449806.043:W=130`35`1.34`:E=949.463:A=160:Q=1:P=2M>1033.468=>X=3361439.935:Y=449852.931:W=160`39`56.8`:E=1033.468:F=121.958:A=160:B=13 0:J=-1:Q=1:P=3匝"I":{Z}M≥0=>X=3361694.914:Y=450016.224:W=265`46`15`:E=0:F=66.176:A=9^45:B=75:J=1:Q=1:P=3 M>66.176=>X=3361698.579:Y=449950.594:W=288`4`27`:E=66.176:A=85:Q=1:P=2M>105.294:=>X=3361718.698:Y=449917.45:W=314`26`32.5`:E=105.294:F=157.408:A=85:B=75:J=-1:Q=1:P=3M>157.408=>X=3361762.343:Y=449889.539:W=335`44`20`:E=157.408:A=400:Q=1:P=2M>256.758=>X=3361857.034:Y=449860.326:W=349`58`11`:E=256.758:F=337.758:A=400:B=180:J=-1:Q=1:P=3匝"J":M≥0=>X=3361678.559:Y=450017.433:W=265`46`15`:E=0:F=66.176:A=9^50:B=75:J=1:Q=-1:P=3 M>66.176=>X=3361665.281:Y=449953.056:W=243`28`2.8`:E=66.176:A=80:Q=-1:P=2M>104.77=>X=3361640.922:Y=449923.549:W=217`27`9`:E=104.77:F=161.779:A=85:B=80:J=-1:Q=-1:P=3M>161.779=>X=3361588.865:Y=449901.365:W=193`34`20.8`"E=161.779:A=350:Q=-1:P=2M>215.557=>X=3361535.825:Y=449892.803:W=184`46`8`:E=215.557:F=279.843:A=350:B=150:J=-1:Q=-1:P=3M>279.843=>X=3361471.579:Y=449891.389:W=179`30`25`:E=279`843:P=1FX4800P常用测量程序集1、由一个已知点坐标和一个已知方位角计算支导线坐标（程序名：ZBJS）程序清单：X：Y：T：Lb1 0：Fixm：{AS}：T=T+A-180：T〈0 =〉T=T+360⊿T〉360 =〉T=T-360⊿T◢X=X+Scos T◢Y=Y+Ssin T◢Goto 0程序运行说明：运行“ZBJS”，每运行一步按EXE键一次，显示X？时输入已知点X坐标，显示Y？时输入已知点Y坐标，显示T？时输入已知点由后视到前视的已知坐标方位角，运行一次本程序只需输入一次已知数据。