140731高三文科数学解析几何教师版

高三数学总复习专题10 解析几何方法点拨1．圆锥曲线中的最值 （1）椭圆中的最值12,F F 为椭圆()222210+=>>x y a b a b的左、右焦点，P 为椭圆上的任意一点，B 为短轴的一个端点，O 为坐标原点，则有： ①[],∈OP b a ； ②[]1,∈-+PF a c a c ；③2212,⎡⎤⋅∈⎣⎦PF PF b a ；④1212∠≤∠F PF F BF ． （2）双曲线中的最值12,F F 为双曲线()222210,0-=>>x y a b a b的左、右焦点，P 为双曲线上的任一点，O 为坐标原点，则有：①≥OP a ；②1≥-PF c a ． （3）抛物线中的最值点P 为抛物线()220=>y px p 上的任一点，F 为焦点，则有： ①2≥pPF ；②(),A m n 为一定点，则+PA PF 有最小值． 2．定点、定值问题（1）由直线方程确定定点，若得到了直线方程的点斜式：()00-=-y y k x x ，则直线必过定点()00,x y ；若得到了直线方程的斜截式：=+y kx m ，则直线必过定点()0,m ． （2）解析几何中的定值问题是指某些几何量(线段的长度、图形的面积、角的度数、直线的斜率等)的大小或某些代数表达式的值等和题目中的参数无关，不依参数的变化而变化，而始终是一个确定的值． 3．圆锥曲线中范围、最值的求解策略（1）数形结合法：利用待求量的几何意义，确定出临界位置后数形结合求解． （2）构建不等式法：利用已知或隐含的不等关系，构建以待求量为元的不等式求解．（3）构建函数法：先引入变量构建以待求量为因变量的函数，再求其值域． 4．定点问题的l 过定点问题的解法：设动直线方程(斜率存在)为=+y kx t 由题设条件将t 用k 表示为=t mk ，得()=+y k x m ，故动直线过定点(),0-m ．（2）动曲线C 过定点问题的解法：引入参变量建立曲线C 的方程，再根据其对参变量恒成立，令其系数等于零，得出定点．（3）从特殊位置入手，找出定点，再证明该点符合题意． 5．求解定值问题的两大途径（1）首先由特例得出一个值(此值一般就是定值)然后证明定值：即将问题转化为证明待证式与参数(某些变量)无关．（2）先将式子用动点坐标或动线中的参数表示，再利用其满足的约束条件使其绝对值相等的正负项抵消或分子、分母约分得定值． 6．解决探索创新问题的策略存在性问题，先假设存在，推证满足条件的结论，若结论正确则存在，若结论不正确则不存在．（1）当条件和结论不唯一时，要分类讨论．（2）当给出结论而要推导出存在的条件时，先假设成立，再推出条件． （3）当条件和结论都不知，按常规方法解题很难时，要思维开放，采取另外的途径．经典试题汇编一、选择题．1．（陕西省渭南市临渭区2021届高三一模）若直线:3=-l y kx 与直线2360+-=x y 的交点位于第一象限，则直线l 的倾斜角的取值范围是（ ）A ．ππ,43⎡⎫⎪⎢⎣⎭B ．ππ,32⎡⎫⎪⎢⎣⎭C ．ππ,42⎛⎫⎪⎝⎭ D ．ππ,32⎛⎫⎪⎝⎭2．（安徽省淮北市2020-2021学年高三一模）过圆2216+=x y 上的动点作圆22:4+=C x y 的两条切线，两个切点之间的线段称为切点弦，则圆C 内不在任何切点弦上的点形成的区域的面积为（ ） A ．πB ．32πC ．2πD ．3π3．（山西省大同市天镇县实验中学2021-2022学年高三一模）圆222440+-+-=x y x y 与直线2140()---=∈R tx y t t 的位置关系为（ ） A ．相离B ．相切C ．相交D ．以上都有可能4．（吉林省长春市2022届高三一模）已知圆22:(2)(3)2-+-=C x y ，直线l 过点(3,4)A 且与圆C 相切，若直线l 与两坐标轴交点分别为,M N ，则MN =（ ）A ．B ．6C ．D ．85．（河南省联考2021-2022学年高三一模）若点()2,1--P 为圆229+=x y 的弦AB 的中点，则弦AB 所在直线的方程为（ ）A ．250++=x yB ．250+-=x yC ．250-+=x yD ．250--=x y6．（四川省南充市2021-2022学年高三一模）若A ，B 是O ：224+=x y 上两个动点，且2⋅=-OA OB ，A ，B 到直线l 40+-=y 的距离分别为1d ，2d ，则12+d d 的最大值是（ ） A ．3B ．4C ．5D ．67．（湖南省长沙市雅礼中学2021届高三一模）过双曲线2214-=y x 的左焦点1F 作一条直线l 交双曲线左支于P ，Q 两点，若4=PQ ，2F 是双曲线的右焦点，则2△PF Q 的周长是（ ） A ．6B ．8C ．10D ．128．（四川省成都市2020-2021学年高三一模）已知抛物线24=x y 的焦点为F ，过F的直线l 与抛物线相交于A ，B 两点，70,2⎛⎫⎪⎝-⎭P ．若⊥PB AB ，则=AF （ ）A ．32B ．2C ．52D ．39．（湖南省湘潭市2021-2022学年高三上学期一模）已知抛物2:2C y px =（0>p ）的焦点为F ，点T 在C 上，且52=FT ，若点M 的坐标为()0,1，且⊥MF MT ，则C 的方程为（ ） A ．22=y x 或28=y x B ．2=y x 或28=y x C ．22=y x 或24=y xD ．2=y x 或24=y x10．（河南省联考2021-2022学年高三一模）点F 为抛物线22=y px ()0>p 的焦点，l 为其准线，过F 的一条直线与抛物线交于A ，B 两点，与l 交于点C ．已知点B 在线段CF 上，若BF ，AF ，BC 按照某种排序可以组成一个等差数列，则AFBF的值为（ ） A ．32或3B ．2或4C ．32或4D ．2或311．（贵州省遵义市2021届高三一模）双曲线221927-=x y 上一点P 到右焦点2F 距离为6，1F 为左焦点，则12∠F PF 的角平分线与x 轴交点坐标为（ ）A ．()1,0-B ．()0,0C ．()1,0D ．()2,012．（吉林省长春市2022届高三一模）已知P 是抛物线24=y x 上的一动点，F 是抛物线的焦点，点(3,1)A ，则||||+PA PF 的最小值为（ ）A ．3B ．C ．4D ．13．（多选）（湖南省湘潭市2021-2022学年高三一模）已知双曲线2222:1-=x y C a b（0>a ，0>b ）的左，右焦点为1F ，2F ，右顶点为A ，则下列结论中，正确的有（ ）A ．若=a b ，则CB ．若以1F 为圆心，b 为半径作圆1F ，则圆1F 与C 的渐近线相切C ．若P 为C 上不与顶点重合的一点，则12△PF F 的内切圆圆心的横坐标=x aD ．若M 为直线2=a x c（=c 0的一点，则当M 的纵坐标为时，2MAF 外接圆的面积最小 14．（江西省赣州市2021届高三3月一模）已知M 、N 是双曲线()2222:10,0-=>>x y C a b a b上关于原点对称的两点，P 是C 上异于M 、N 的动点，设直线PM 、PN 的斜率分别为1k 、2k ．若直线12=y x 与曲线C 没有公共点，当双曲线C 的离心率取得最大值时，且123≤≤k ，则2k 的取值范围是（ ） A ．11,128⎡⎤⎢⎥⎣⎦B ．11,812⎡⎤--⎢⎥⎣⎦ C ．11,32⎡⎤⎢⎥⎣⎦D ．11,23⎡⎤--⎢⎥⎣⎦15．（四川省成都市2021-2022学年高三一模）已知双曲线()222210,0-=>>x y a b a b的一条渐近线方程为=y ，则该双曲线的离心率为（ ）A B C ．2D ．316．（四川省成都市2020-2021学年高三一模）已知平行于x 轴的一条直线与双曲线()222210,0-=>>x y a b a b 相交于P ，Q 两点，4=PQ a ，π3∠=PQO （O 为坐标原点），则该双曲线的离心率为（ ）A B C D17．（甘肃省嘉谷关市第一中学2020-2021学年高三一模）已知双曲线22221(0,0)-=>>y x a b a b与抛物线2=x 共焦点F ，过点F 作一条渐近线的垂线，垂足为M ，若三角形OMF 的面积为2，则双曲线的离心率为（ ）AB ．16C D ．4或4318．（四川省乐山市高中2022届一模）已知双曲线()222210,0-=>>x y a b a b，过原点的直线与双曲线交于A ，B 两点，以线段AB 为直径的圆恰好过双曲线的右焦点F ，若ABF 的面积为22a ，则双曲线的离心率为（ ）AB C D ．219．（四川省达州市2021-2022学年高三一模）双曲线()222210,0-=>>x y a b a b的左顶点为A ，右焦点(),0F c ，若直线=x c 与该双曲线交于B 、C 两点，ABC 为等腰直角三角形，则该双曲线离心率为（ ）A ．2BCD ．320．（陕西省汉中市2022届高三一模）已知F 是椭圆2222:1(0)+=>>x y C a b a b 的右焦点，点P 在椭圆C 上，线段PF 与圆22239⎛⎫-+= ⎪⎝⎭c b x y 相切于点Q ，且2=PQ QF ，则椭圆C 的离心率等于（ ）A B ．23C ．2D ．1221．（广西柳州市2022届高三一模）已知1F ，2F 分别为双曲线C ：22221-=x y a b()0,0>>a b 的左，右焦点，以12F F 为直径的圆与双曲线C 的右支在第一象限交于A 点，直线2AF 与双曲线C 的右支交于B 点，点2F 恰好为线段AB 的三等分点(靠近点A )，则双曲线C 的离心率等于（ ）A B C ．3D ．12+ 二、填空题．22．（贵州省遵义市2021届高三一模）直线1=-+y kx k 与圆224+=x y 交于,A B 两点，则AB 最小值为________．23．（湖南省长沙市雅礼中学2021届高三一模）若抛物线22=y px 上一点()02,P y 到其准线的距离为4，则抛物线的标准方程为___________．24．（四川省成都市第七中学2021-2022学年高三一模）已知12,F F 为双曲线22:1169-=x y C 的两个焦点，,P Q 为C 上关于坐标原点对称的两点，且12=PQ F F ，则四边形12PF QF 的面积为________．25．（四川省达州市2021-2022学年高三一模）设直线()y kx k =∈R 交椭圆221164+=x y 于A ，B 两点，将x 轴下方半平面沿着x 轴翻折与x 轴上方半平面成直二面角，则AB 的取值范围是___________．26．（四川省成都市2021-2022学年高三一模）已知斜率为13-且不经过坐标原点O的直线与椭圆22+197x y =相交于A ，B 两点，M 为线段AB 的中点，则直线OM 的斜率为________． 三、解答题．27．（四川省成都市第七中学2021-2022学年高三一模）已知两圆221:(2)54C x y -+=，222:(2)6C x y ++=，动圆M 在圆1C 内部且和圆1C 内切，和圆2C 外切．（1）求动圆圆心M 的轨迹C 的方程；（2）过点()3,0A 的直线与曲线C 交于,P Q 两点，P 关于x 轴的对称点为R ，求ARQ 面积的最大值．28．（四川省成都市2020-2021学年高三一模）已知椭圆()2222:10+=>>x y C a b a b的离心率为2，且直线1+=x ya b与圆222+=x y 相切． （1）求椭圆C 的方程；（2）设直线l 与椭圆C 相交于不同的两点A ﹐B ，M 为线段AB 的中点，O 为坐标原点，射线OM 与椭圆C 相交于点P ，且O 点在以AB 为直径的圆上．记AOM ，△BOP的面积分别为1S ，2S ，求12S S 的取值范围． 29．（陕西省汉中市2022届高三一模）已知椭圆2222:1(0)+=>>x y C a b a b 的离心率为12，左､右焦点分别为12,F F ，O 为坐标原点，点P 在椭圆C 上，且满足2122,3π=∠=PF F PF ．（1）求椭圆C 的方程；（2）已知过点(1,0)且不与坐标轴垂直的直线l 与椭圆C 交于M ，N 两点，在x 轴上是否存在定点Q ，使得∠=∠MQO NQO ，若存在，求出点Q 的坐标；若不存在，说明理由．30．（四川省南充市2021-2022学年高三一模）已知椭圆()2222:10+=>>x y C a b a b的离心率为2，椭圆C 的下顶点和上顶点分别为1B ，2B ，且122=B B ，过点()0,2P 且斜率为k 的直线l 与椭圆C 交于M ，N 两点．（1）求椭圆C 的标准方程； （2）当1=k 时，求OMN 的面积；（3）求证：直线1B M 与直线2B N 的交点T 的纵坐标为定值．31．（江西省赣州市2021届高三3月一模）设离心率为12的椭圆2222:1(0)+=>>x y E a b a b 的左，右焦点分别为1F ，2F ，点P 在E 上，且满足1260∠=︒F PF ，12△PF F（1）求a ，b 的值；（2）设直线:2(0)=+>l y kx k 与E 交于M ，N 两点，点A 在x轴上，且满足0⋅+⋅=AM MN AN MN ，求点A 横坐标的取值范围．32．（广西柳州市2022届高三一模）已知椭圆C ：22221+=x y a b()0>>a b 的左右焦点分别为1F ，2F ，过2F 且与x 轴垂直的直线与椭圆C 交于A ，B 两点，AOB 的面积为﹐点P 为椭圆C 的下顶点，2=PF ． （1）求椭圆C 的标准方程；（2）椭圆C 上有两点M ，N (异于椭圆顶点且MN 与x 轴不垂直)．当OMN 的面积最大时，直线OM 与ON 的斜率之积是否为定值，若是，求出该定值；若不是，请说明理由． 33．（湖南省湘潭市2021-2022学年高三一模）已知圆锥曲线E 上的点M 的坐标(),x y=．（1）说明E 是什么图形，并写出其标准方程；（2）若斜率为1的直线l 与E 交于y 轴右侧不同的两点A ，B ，点P 为()2,1． ①求直线l 在y 轴上的截距的取值范围； ②求证：∠APB 的平分线总垂直于x 轴．34．（四川省乐山市高中2022届一模）如图，从椭圆22221(0)+=>>x y a b a b上一点P 向x轴作垂线，垂足恰为左焦点1F ．又点A 是椭圆与x 轴正半轴的交点，点B 是椭圆与y轴正半轴的交点，且=OP AB k ，13=F A ． （1）求椭圆的方程；（2）直线l 交椭圆于M ､Q 两点，判断是否存在直线l ，使点2F 恰为MQB △的重心？若存在，求出直线l 的方程；若不存在，请说明理由．35．（安徽省淮北市2020-2021学年高三一模）已知椭圆2222:1(0)+=>>x y C a b a b的离心率为12，左顶点为A ，右焦点F ，3=AF ．过F 且斜率存在的直线交椭圆于P ，N 两点，P 关于原点的对称点为M ． （1）求椭圆C 的方程；（2）设直线AM ，AN 的斜率分别为1k ，2k ，是否存在常数λ，使得12λ=k k 恒成立？若存在，请求出λ的值；若不存在，请说明理由．36．（湖南省长沙市雅礼中学2021届高三一模）已知椭圆()222210:x y a b a bC +=>>，连接椭圆上任意两点的线段叫作椭圆的弦，过椭圆中心的弦叫做椭圆的直径．若椭圆的两直径的斜率之积为22-b a，则称这两直径为椭圆的共轭直径．特别地，若一条直径所在的斜率为0，另一条直径的斜率不存在时，也称这两直径为共轭直径．现已知椭圆22:143x y E +=．（1）已知点31,2⎛⎫ ⎪⎝⎭A ，31,2⎛⎫-- ⎪⎝⎭B 为椭圆E 上两定点，求AB 的共轭直径的端点坐标；（2）过点()作直线l 与椭圆E 交于1A ､1B 两点，直线1A O 与椭圆E 的另一个交点为2A ，直线1B O 与椭圆E 的另一个交点为2B ．当11A OB 的面积最大时，直径12A A 与直径12B B 是否共轭，请说明理由；（3）设CD 和MN 为椭圆E 的一对共轭直径，且线段CM 的中点为T ．已知点P 满足：λ=OP OT ，若点P 在椭圆E 的外部，求λ的取值范围．参考答案一、选择题． 1CACCADDDADDC 13．【答案】ABD【解析】对于A 中，因为=a b ，所以222=a c ，故C的离心率==ce a所以A 正确； 对于B 中，因为()1,0-F c 到渐近线0-=bx ay的距离为==d b ，所以B 正确；对于C 中，设内切圆与12△PF F 的边1221,,F F F P F P 分别切于点1,,A B C ， 设切点1A (,0)x ，当点P 在双曲线的右支上时，可得121212-=+--=-PF PF PC CF PB BF CF BF1112=-A F A F ()()22=+--==c x c x x a ，解得=x a ，当点P 在双曲线的左支上时，可得=-x a ，所以12△PF F 的内切圆圆心的横坐标=±x a ，所以C 不正确； 对于D 中，由正弦定理，可知2MAF 外接圆的半径为222sin =∠AF R AMF ，所以当2sin ∠AMF 最大时，R 最小，因为2<a a c，所以2∠AMF 为锐角，故2sin ∠AMF 最大，只需2tan ∠AMF 最大，由对称性，不妨设2,⎛⎫ ⎪⎝⎭a M t c （0>t ），设直线2=a x c 与x 轴的交点为N ，在直角2△NMF 中，可得222tan ==∠-a c NF NM NMF ct ， 在直角△NMA 中，可得2tan =-=∠a a NA A NM NM c t，又由2222tan tan tan tan()1tan tan NMF NMAAMF NMF NMA NMF NMA∠-∠∠=∠-∠=∠⋅+∠222222()1c c a ab c a a a a c ct t a a c t a c c t tc t -==≤+-----⨯-+， 当且仅当()22-=ab c a t c t ，即=t 2tan ∠AMF 取最大值， 由双曲线的对称性可知，当=t 2tan ∠AMF 也取得最大值，所以D 正确，故选ABD ． 14．【答案】A【解析】因为直线12=y x 与双曲线()2222:10,0-=>>x y C a b a b 没有公共点，所以双曲线C 的渐近线的斜率12=≤bk a ，而双曲线C的离心率====c e a 当双曲线C 的离心率取最大值时，b a 取得最大值12，即12=b a ，即2=a b ，则双曲线C 的方程为222214-=x y b b，设()11,M x y 、()11,--N x y 、()00,P x y ，则2211222200221414⎧-=⎪⎪⎨⎪-=⎪⎩x y b b x y b b ， 两式相减得()()()()10101010224+-+-=x x x x y y y y b b ，即1010101014-+⋅=-+y y y y x x x x ， 即1214⋅=k k ， 又123≤≤k ，211,128⎡⎤∈⎢⎥⎣⎦k ，故选A ． 15．【答案】B【解析】双曲线22221-=x y a b 的渐近线方程为=±by x a，因为渐近线方程为=y ，所以=ba故可得====e B ． 16．【答案】D【解析】如图，由题可知，△POQ 是等边三角形，4=PQ a ，()2,∴P a ，将点P 代入双曲线可得22224121-=a a a b ，可得224=b a，∴离心率===c e a D ．17．【答案】C【解析】抛物线2=x 的交点坐标为(F ，又双曲线22221(0,0)-=>>y x a b a b与抛物线2=x 共焦点，∴双曲线的半焦距=c ，三角形OMF 的面积为2，且=OM a ，=MF b ，∴122=⋅ab ，即4=ab ， 有22217+==a b c ，∴1=a 或4=a ，∴双曲线的离心率为=e ，故选C ．18．【答案】B【解析】设双曲线的左焦点为'F ，连接'AF ，'BF ， 因为以AB 为直径的圆恰好经过双曲线的右焦点(),0F c ， 所以⊥AF BF ，圆心为()0,0O ，半径为c ， 根据双曲线的对称性可得四边形'AFBF 是矩形，设=AF m ，=BF n ，则222224122⎧⎪-=⎪+=⎨⎪⎪=⎩n m a n m c mn a ，由()2222-=+-n m m n mn ，可得222484-=c a a ，所以223=c a ，所以2223==c e a，所以=e ，故选B ．19．【答案】A【解析】联立22222221=⎧⎪⎪-=⎨⎪=+⎪⎩x cxy a b c a b，可得2=±b y a ，则22=b BC a ，易知点B 、C 关于x 轴对称，且F 为线段BC 的中点，则=AB AC ，又因为ABC 为等腰直角三角形，所以2=BC AF ，即()222=+b c a a， 即()222+==-a c a b c a ，所以=-a c a ，可得2=c a ， 因此，该双曲线的离心率为2==ce a，故选A ． 20．【答案】A【解析】圆22239⎛⎫-+= ⎪⎝⎭c b x y 的圆心为,03⎛⎫ ⎪⎝⎭c A ，半径为3=b r ． 设左焦点为1F ，连接1PF ，由于124,33==AF c AF c ， 所以12==AF PQAF QF，所以1//AQ PF ，所以12,2==-PF b PF a b ， 由于⊥AQ PF ，所以1⊥PF PF ， 所以()()()22222224+-==-b a b c a b ，2320,3-==b b a a ，===c e a ，故选A ．21．【答案】C【解析】设2=AF x ，则22=BF x ，由双曲线的定义可得1222=+=+AF AF a a x ，12222=+=+BF BF a a x ， 因为点A 在以12F F 为直径的圆上，所以190∠=F AB ，所以22211+=AF AB BF ，即()()()2222322++=+a x x a x ，解得23=x a ， 在12△AF F 中，1823=+=AF a x a ，223=AF a ，122=F F c ， 由2221212+=AF AF F F 可得()22282233⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭a a c ，即22179=a c ，所以双曲线离心率为3===e ，故选C ．二、填空题． 22．【答案】【解析】直线1=-+y kx k 过定点过()1,1M ， 因为点()1,1M在圆的内部，且OM == 由圆中弦的性质知当直线与OM 垂直时，弦长最短， 此时结合垂径定理可得AB ==故答案为 23．【答案】28=y x【解析】抛物线的准线方程为2=-p x ，点()02,P y 到其准线的距离为22+p ， 由题意可得242+=p，解得4=p ， 故抛物线的标准方程为28=y x ，故答案为28=y x ． 24．【答案】18【解析】由双曲线的对称性以及12=PQ F F 可知，四边形12PF QF 为矩形，所以1222212284100⎧-==⎪⎨+==⎪⎩PF PF a PF PF c ，解得1218=PF PF ， 所以四边形12PF QF 的面积为1218=PFPF ， 故答案为18．25．【答案】(⎤⎦【解析】设1122(,),(,)A x y B x y ，联立方程组221164=⎧⎪⎨+=⎪⎩y kx x y ，可得22(14)160+-=k x ， 可得1212216,014=-+=+x x x x k ，所以221221614==+x x k ， 将椭圆x 轴下方半平面沿着x 轴翻折与x 轴上方半平面成直二面角， 分别作,⊥⊥BC x AD x 于点,C D ，如图所示， 则2222=++AB BC CD AD ，又由222222222211,====BC y k x AD y k x ，2222212*********64()2()414=-=+-=+-=+CD x x x x x x x x x x k， 所以222222221226414=++=+++AB BC CD AD k x k x k 2222232648(417)78(1)141414+⋅++===⋅++++k k k k k ， 因为∈R k ，所以20≥k ，所以2411+≥k ，所以270741<≤+k ，所以2788(1)6414<⋅+≤+k ，即2864<≤AB，所以8<≤AB ，所以AB的取值范围是(⎤⎦，故答案为(⎤⎦．26．【答案】73【解析】设直线AB 的方程为13=-+y x b ，联立2213197⎧=-+⎪⎪⎨⎪+=⎪⎩y x b x y ，得221()3197-++=x b x ，即22869630-+-=x bx b ，由223632(963)0b b ∆=-->，得-<<b 设11(,)A x y ，22(,)B x y ，00(,)M x y ，则120328+==x x b x ，0011373388=-+=-⨯+=b by x b b ， 即37(,)88b bM ，则直线OM 的斜率为0073==y k x ，故答案为73．三、解答题．27．【答案】（1）2212420+=x y ；（2．【解析】（1）依题意，圆1C 的圆心()12,0C，半径1=r 圆2C 的圆心()22,0-C，半径2=r设圆M 的半径为r ，则有11=-MC r r ，22=+MC r r ，因此，1212124+=+=>=MC MC r r C C ，于是得点M 的轨迹是以12,C C为焦点，长轴长2=a 此时，焦距24=c ，短半轴长b 有22220=-=b a c ，所以动圆圆心M 的轨迹C 的方程为2212420+=x y ．（2）显然直线PQ 不垂直于坐标轴，设直线PQ 的方程为3(0)=+≠x my m ，1122(,),(,)P x y Q x y ，由22356120=+⎧⎨+=⎩x my x y ，消去x 得22(56)30750++-=m x my ， 则1226350+=-+m y y m ，1227556=-+y y m ， 点P 关于x 轴的对称点11(,)-R x y ，1211|2|||2=⋅⋅-PQRSy x x ，111232=⋅⋅-APRS y x ，如图，显然1x 与2x 在3的两侧，即21-x x 与13-x 同号， 于是得()()()1211121133=-=---=⋅---AQRPQRAPRSSSy x x x y x x x121212275|||75|||3|||||||6565|||==⋅-==⋅==++≤m y x y my my y m m m ， 当且仅当65||||=m m ，即=m 时取“=”，因此，当=m 时，max ()=AQR S，所以ARQ 面积的最大值4． 28．【答案】（1）22163+=x y；（2）⎣⎦．【解析】（1）∵椭圆的离心率为2，∴2=c a （c 为半焦距）， ∵直线1+=xy ab与圆222+=x y=，又∵222+=c b a ，∴26=a ，23=b ，∴椭圆C 的方程为22163+=x y ．（2）∵M 为线段AB 的中点，∴12==AOM BOP OMS S S S OP△△． （ⅰ）当直线l 的斜率不存在时，由⊥OA OB 及椭圆的对称性，不妨设OA 所在直线的方程为=y x ，得22=Ax ．则22=Mx ，26=P x，∴123==OM S S OP ； （ⅱ）当直线l 的斜率存在时，设直线():0=+≠l y kx m m ，()11,A x y ，()22,B x y ，由22163=+⎧⎪⎨+=⎪⎩y kx mx y ，消去y ，得()222214260++-=＋k x kmx m ， ∴()()()2222221682138630k m k m k m ∆=-+-=-+>，即22630-+>k m ．∴122421+=-+kmx x k ，21222621-=+m x x k ．∵点O 在以AB 为直径的圆上，∴0⋅=OA OB ，即12120+=x x y y ， ∴()()221212121210+=++++=x x y y k x x km x x m ，∴()22222264102121-⎛⎫++-+= ⎪++⎝⎭m km k km m k k ． 化简，得2222=＋m k ，经检验满足0∆>成立， ∴线段AB 的中点222,2121⎛⎫-⎪++⎝⎭km m M k k ， 当0=k 时，22=m，此时123==S S ； 当0≠k 时，射线OM 所在的直线方程为12=-y x k， 由2212163⎧=-⎪⎪⎨⎪+=⎪⎩y x k x y ，消去y ，得2221221=+P k x k ，22321=+P y k ， ∴==M P OM y OP y ∴12==S S12,33⎛∈ ⎝⎭S S ， 综上，12S S的取值范围为⎣⎦．29．【答案】（1）22143+=x y ；（2）存在，()4,0．【解析】（1）在12△PF F 中，1122,2=-=cPF a a ，所以，由余弦定理()224(22)4222=-+--c a a，解得2,==a b ，所以，椭圆方程为22143+=x y ．（2）假设存在点(),0Q m 满足条件，设直线l 的方程为()10=+≠x ty t ，设()()1122,,,M x y N x y ，联立()22221,34690143=+⎧⎪++-=⎨+=⎪⎩x ty t y ty x y ， 121212221269,,3434--+==+=+++--MQ NQy y t y y y y k K t t x m x m， 又因为∠=∠MQO NQO ，所以0+=MQ NQ K K ，即1212=--y y x m m x ， 即()()1211-=-y m x y m x ，将11221,1=+=+x ty x ty 代入化简得()()121212-+=m y y ty y ， 即()2261183434---=++t m tt t ，计算得4=m ，所以存在()4,0点使得∠=∠MQO NQO ．30．【答案】（1）2212+=x y ；（2）面积不存在；（3）证明见解析．【解析】（1）因为122=B B ，所以22=b ，即1=b ，因为离心率为2，所以2=c a ，设=c m，则=a ，0>m ， 又222=-c a b ，即2222=-m m b ，解得1=m 或1-（舍去），所以=a 1=b ，1=c ，所以椭圆的标准方程为2212+=x y ．（2）由22122⎧+=⎪⎨⎪=+⎩x y y x ，得()222220++-=x x ，23860++=x x ，284360∆=-⨯⨯<，所以直线与椭圆无交点，故OMN 的面积不存在．（3）由题意知，直线l 的方程为2=+y kx ，设()11,M x y ，()22,N x y ，则22212=+⎧⎪⎨+=⎪⎩y kx x y ，整理得()2221860+++=k x kx ，则()()22122122846120821621Δk k k x x k x x k ⎧=-⨯+>⎪⎪⎪+=-⎨+⎪⎪=⎪+⎩，因为直线和椭圆有两个交点，所以()()22824210k k ∆=-+>，则232>k ，设(),T m n ，因为1B ，T ，M 在同一条直线上，则111111313+++===+y kx n k m x x x ， 因为2B ，T ，N 在同一条直线上，则222221111-+-===+y kx n k m x x x ， 由于()21212283311213440621⎛⎫⋅- ⎪++-+⎝⎭+⋅=+=+=+k x x n n k k k m m x x k ，所以12=n ， 则交点T 恒在一条直线12=y 上，故交点T 的纵坐标为定值12．31．【答案】（1）2=a，=b （2）6⎡⎫-⎪⎢⎪⎣⎭． 【解析】（1）设椭圆短轴的端点为B ，则21sin 2∠=OBF ，所以26π∠=OBF ，123π∠=F BF ，所以点P 即为点B，所以12122=⋅⋅==△PF F S c b bc ，又12=c a ，222=-a b c ，所以2=a，=b（2）设(,0)A m ，()11,M x y ，()22,N x y ，MN 的中点()00,H x y ，由2223412=+⎧⎨+=⎩y kx x y ，得()22431640+++=k x kx ， 所以()()222(16)164348410k k k ∆=-+=->， 又0>k ，所以12>k ，所以1221643+=-+kx x k ， 所以12028243+==-+x x k x k ，0026243=+=+y kx k ，即2286,4343⎛⎫- ⎪++⎝⎭k H k k ， 因为()20⋅+⋅=+⋅=⋅=AM MN AN MN AM AN MN AH MN ， 所以⊥AH MN ，所以226143843+=---+k k k mk ，得2223434=-=-++k m k k k ， 因为12>k，所以34+≥k k，当且仅当=k =”号，所以⎡⎫∈⎪⎢⎪⎣⎭m ， 故点A的横坐标的取值范围是6⎡⎫-⎪⎢⎪⎣⎭． 32．【答案】（1）22184+=x y ；（2）12-，理由见解析．【解析】（1）由题意可得：在2OPF Rt 中，22222+=OP OF PF ，即)222+=b c ，所以=b c ，椭圆C ：22221+=x y a b 中，令=x c 可得2422221⎛⎫=-= ⎪⎝⎭c b y b a a，所以2=±b y a ，可得22=b AB a，所以22122=⋅⋅==AOBb bc Sc a a所以2=b c ，因为=b c ，222=+a b c，所以34====b b ， 可得24=b ，所以2==c b ，2228=+=a b c ，所以椭圆C 的标准方程为22184+=x y ．（2）设直线MN 的方程为=+y kx t ，()11,M x y ，()22,N x y ，由22184=+⎧⎪⎨+=⎪⎩y kx tx y ，可得()222214280+++-=k x ktx t ， ()()222216421280k t k t ∆=-+->，即2284<+t k ，122412-+=+ktx x k，21222812-=+t x x k ， 所以()()()2212121212=++=+++y y kx t kx t k x x kt x x t()()22222222222228124812121212-+-=-+=++++k t k t k t t k k k k k，12=-=MN x==， 点()0,0O 到直线=+y kx t的距离=d所以OMN的面积为1122⋅==MN d222284212+-+≤=+t k t k， 当且仅当22284=-+t k t 即2224-=t k 时等号成立，2222222122222128128241122828282-+--+⋅==⨯===-+---OM ONy y t k k t k t t k k x x k t t t ， 所以当OMN 的面积最大时，直线OM 与ON 的斜率之积是12-．33．【答案】（1）E是以()，)为焦点，长轴长为22163+=x y ；（2）①(3,-；②证明见解析． 【解析】（1）圆锥曲线E是以()，)为焦点，长轴长为的椭圆，其标准方程为22163+=x y ．（2）①设直线l ：=+y x m ，()11,A x y ，()22,B x y ，由22163⎧+=⎪⎨⎪=+⎩x y y x m ，消去y ，得2234260++-=x mx m ， 由题意，有()()22122124432604032603m m mx x m x x ∆⎧=-⨯->⎪⎪⎪+=->⎨⎪⎪-=>⎪⎩，解得3-<<m ， 所以直线l 在y轴上的截距的取值范围为(3,-．②因为点P 在椭圆上，若直线l 过点P ，即点A （或点B ）与P 重合，则l 与E 的另一个交点为25,33⎛⎫--⎪⎝⎭，不合题意，所以点A （或点B ）与P 不重合； 若AP 或BP 的斜率不存在，则直线l 过点()2,1-，此时，l 与E 只有一个交点， 所以AP 与BP 的斜率都存在，设直线AP 的斜率为1k ，直线BP 的斜率为2k ， 因为A ，B 在轴的右侧，结合图象，可知，要证∠APB 的平分线总垂直于x 轴，只要证120=+k k ， 因为11112-=-y k x ，22212-=-y k x ，也即证()()()()122112120--+--=y x y x ，而()()()()()()()()1221122112121212--+--=+--++--y x y x x m x x m x()()()2121241242344344033-⎛⎫=+-+-+=+---+= ⎪⎝⎭m m x x m x x m m m 成立， 故∠APB 的平分线总垂直于x 轴．34．【答案】（1）22143+=x y ；（2）存在，:80--=l y ．【解析】（1）由题可知，(,0)A a ，(0,)B b ，2,⎛⎫- ⎪⎝⎭b P c a ，因为=OP AB k，则200--=---b b a c a，解得=b ，故有2223+=⎧⎪=⎨⎪+=⎩a cb bc a ，解得2=a，=b椭圆方程为22143+=x y ．（2）法一：假设存在，易知直线l 的斜率存在， 设直线l 的方程为=+y kx m ，()11,M x y ，()22,Q x y ，联立22143=+⎧⎪⎨+=⎪⎩y kx mx y ，得()2223484120+++-=k x kmx m ， 则122212283441234⎧+=-⎪⎪+⎨-⎪=⎪+⎩km x x k m x x k ， 因为2F 为MQB △的重心，则121201303++⎧=⎪⎪⎨++⎪=⎪⎩x x y y，解得12123+=⎧⎪⎨+=⎪⎩x x y y则122128334⎧+=-=⎪+⎨⎪+++=⎩km x x k kx m kx m，化简得228334634⎧=-⎪⎪+⎨⎪=⎪+⎩km k m k，解得⎧=⎪⎪⎨⎪=⎪⎩k m ，所以直线:80--=l y ．法二：设()11,M x y ，()22,Q x y ，因为2F 为MQB △的重心，则120130++⎧=⎪⎪=x x，解得12123+=⎧⎪⎨+=⎪⎩x x y y设MQ 的中点R，则3,2⎛ ⎝⎭R ， 因为M ，Q 在椭圆22143+=x y 上，则22112222143143⎧+=⎪⎪⎨⎪+=⎪⎩x y x y ，两式相减得34⋅=-MQ OR k k，即=MQ k所以直线:80--=l y ．35．【答案】（1）22143+=x y ，（2）3λ=．【解析】（1）因为离心率为12，所以12==c e a ， 又3=AF ，所以3+=a c ，解得2=a ，1=c ， 又222=-c a b ，所以23=b ，所以椭圆方程为22143+=x y ．（2）由（1）知()1,0F ，()2,0-A ，设直线PN 的方程为1=+x my ，()11,P x y ，()22,N x y ， 因为M 与P 关于原点对称，所以()11,--M x y ， 所以1112=-y x k ，2222=+yk x ， 若存在λ，使得12λ=k k 恒成立，所以121222λ=-+y yx x ， 所以()()122122λ+=-y x y x ，两边同乘1y 得()()21221122λ+=-y x y y x ，又因为()11,P x y 在椭圆上，所以2211143+=x y ，所以()()2112113223144-+⎛⎫=-= ⎪⎝⎭x x x y ，所以()()()()112211322224λ-++=-x x x y y x ，当12≠x 时，则()()12213224λ-++=x x y y ， 所以()21212136124λ--+-=x x x x y y ①； 当12=x 时，M 与A 重合，联立方程221143=+⎧⎪⎨+=⎪⎩x my x y ，消元得()2234690++-=m y my ，所以212212934634-⎧=⎪⎪+⎨-⎪+=⎪+⎩y y m m y y m ，所以()212128234+=++=+x x m y y m ，()222121212412134-=+++=+m x x m y y m y y m ，代入①得22221236489124343434λ-+--+-=+++m m m m ， 整理得10836λ-=-，解得3λ=． 36．【答案】（1）2-⎭和2⎛ ⎝⎭；（2）直径12A A 与直径12B B 共轭，理由见解析；（3）λ>λ< 【解析】（1）由题设知32=AB k ，设所求直线方程为=y kx ，则34⋅=-AB k k ，则12=-k ， 故共轭直径所在直线方程为12=-y x ．联立椭圆与12=-y x ，即2212143⎧=-⎪⎪⎨⎪+=⎪⎩y x x y 可得23=x，=x故端点坐标为⎭和⎛ ⎝⎭．（2）由题设知，l 不与x 轴重合，故设l：=x my ()111,A x y ､()122,B x y ，联立方程()22223430143⎧=⎪⇒+--=⎨+=⎪⎩x my m y x y ，则12234+=+y y m ，122334-=+y y m ，2122121234-=+m x x m ，122223434=-=⋅=++S y mm 63=≤=，当且仅当2313+=m ，即223=m 时取等号， 此时121221222123312124-⋅===-=--A A B By y b k k x x m a，故直径12A A 与直径12B B 共轭． （3）设点()11,C x y ，()22,M x y ，当CD 不与坐标轴重合时，设CD l ：=y kx ，则MN l ：34=-y x k， 联立2222211221212,3434143=⎧⎪⇒==⎨+++=⎪⎩y kx k x y x y k k ， 同理可得22221634=+k x k ，222934=+y k． 由椭圆的对称性，不妨设C 在第一象限，则M 必在第二象限或第四象限，则1=x1=y若M在第二象限，则2=x2=y ，从而 ⎪⎝⎭T ，则⎫⎪⎪⎪ ⎪⎝⎭P ．又P在椭圆外，则223412⎫⎪⎪+>⎪ ⎪ ⎪⎝⎭⎝⎭， 化简可得22λ>，即λ>λ<若M 在第四象限，同理可得22λ>，即λ>λ<当CD 与x 轴垂直或重合时，由椭圆的对称性，不妨取()2,0C，(M ，则λ⎛⎫⎪ ⎪⎝⎭P ． 又P 在椭圆外，则2223341224λλλ+⋅>⇒>，即λ>λ<综上：λ>λ<。

高三文科数学（解析儿何）练习「已知椭圆C ：存$］心〉0）的离心仆孕原点到过点心。

），B （OT ）的直线的距离是琴.（I ）求椭圆C 的方程;（II ）若直线y = b + l 伙工0）交椭圆C 于不同的两点E, F, ME, F 都在以B 为圆心的圆上，求R 的值.解（I ）因为汁孚—22 ,2故所求椭圆C 的方程为二+上=1 ........................................................................ 6分16 4 （II ）由题意y = kx +1,<兀2 2 消去y ,整理得—+—= 1116 4 (1 + 4疋)兀 2+8&_12二0 ......................................................................... 7 分可知△>(). .................................. 8分EF 的中点是M (x w , y M ),所以心 + ky M + 2k = 0.-AL k即——+ -------- +220.1 + 4疋 1 + 4疋又因为kHO,1 逅所•以 k 2=-.^ 以 £=± 8 42 2 2.已知椭圆C ：l + £ = l （d>b>0）的四个顶点恰好是边长为2, —内角为60。

的菱形的四个顶点. dT b （T ）求椭圆C 的方程;所以a = 2h. ................................................................ 2分因为原点到直线AB ab \Ja 2+Z?2 4A /5解得a = 4, b = 2. ................................................................ 5分10分所以恋迸“ ................................................................ 11分.......................................... 13分(II)若直线y = kx 交椭圆C 于人B 两点，且在肓线/：x + y-3 = 0上存在点P,使得\PAB 为等边三角形，求£的 值.•内角为6(y 的菱形的四个顶点,所以a = ^b = l,椭圆C 的方程为—+/ = 1 ........................ 4分(I I)设 A (尢 I J),则 3(-兀］，一 ％ ),当直线AB 的斜率为0时，AB 的垂直平分线就是V 轴, y 轴与直线/ ：兀+ y - 3 = 0的交点为P(0,3), 又因为\AB\=^,\PO 1=3,所以ZPAO = 6(T,所以MAB 是等边三角形，所以直线AB 的方程为y = 0 .................... 6分当直线AB 的斜率存在且不为0时，设AB 的方程为V = kxy = kx 3宀33/ + 1设AB 的垂直平分线为y = --x f 它与直线l ：x + y-3 = 0的交点记为P(x 0,j 0) k♦y = -x + 3所以 1 ，解得V y =——JC 则心临分 因为APAB 为等边三角形，所以应有\PO l=V3IA(9l代入得釦治"需，解得® (舍)，7 ................................................................... 13分14分2 2 _____________________________________________________________________________________________________________ _ ______3.已知椭圆C:罕+ £ = l@>b>0)的右焦点F (1,0),长轴的左、右端点分别为人显2，且两・亦=—1. cr b° (I )求椭圆C 的方程;(II )过焦点F 斜率为R 伙H0)的直线Z 交椭圆C 于4, 〃两点，弦AB 的垂总平分线与X 轴相交于点Q.试问椭圆解: ⑴因为椭圆C:= l(a>b>0)的四个顶点恰好是一边长为2,所以=1 化简得(3P + 1)X 2=3 3k = ----- ° k-\ -3 儿=— 则肿=吋爲 所以C 上是否存在点E 使得四边形ADBE 为菱形？若存在，试求点E 到 轴的距离；若不存在，请说明理由. 解：(I )依题设£(一。

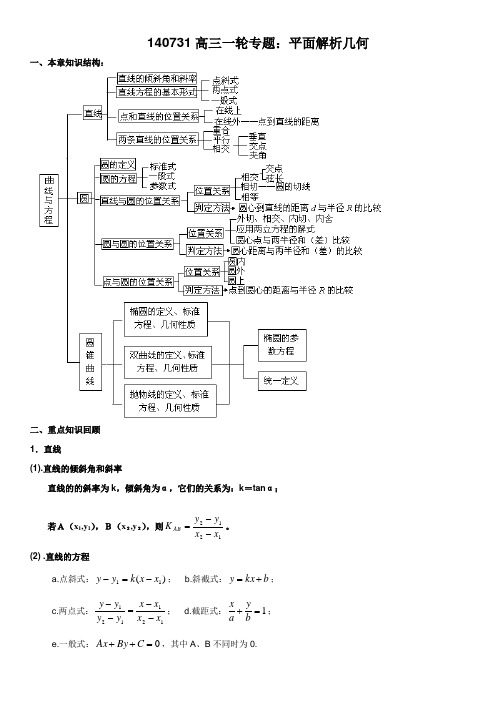
140731高三一轮专题：平面解析几何一、本章知识结构：二、重点知识回顾 1．直线(1).直线的倾斜角和斜率直线的的斜率为k ，倾斜角为α，它们的关系为：k ＝tan α；若Ａ（x 1,y 1），Ｂ（x ２,y ２），则1212x x y y K AB --=。

(2) .直线的方程a.点斜式：)(11x x k y y -=-；b.斜截式：b kx y +=；c.两点式：121121x x x x y y y y --=--； d.截距式：1=+bya x ；e.一般式：0=++C By Ax ，其中A 、B 不同时为0.(3).两直线的位置关系两条直线1l ，2l 有三种位置关系：平行（没有公共点）；相交（有且只有一个公共点）；重合（有无数个公共点）.在这三种位置关系中，我们重点研究平行与相交。

若直线1l 、2l 的斜率分别为1k 、2k ，则1l ∥2l ⇔1k ＝2k ，1l ⊥2l ⇔1k ·2k ＝－１。

（4）点、直线之间的距离点A （x 0，y 0）到直线0=++C By Ax 的距离为：d=220||BA C By Ax +++。

两点之间的距离：|AB|=212212)()y y x x -+-（ 2. 圆（1）圆方程的三种形式标准式：222)()(r b y a x =-+-，其中点（a ，b ）为圆心，r>0，r 为半径，圆的标准方程中有三个待定系数，使用该方程的最大优点是可以方便地看出圆的圆心坐标与半径的大小． 一般式：022=++++F Ey Dx y x ，其中⎪⎭⎫ ⎝⎛--22E D ，为圆心F E D 42122-+为半径，，圆的一般方程中也有三个待定系数，即D 、E 、F ．若已知条件中没有直接给出圆心的坐标（如题目为：已知一个圆经过三个点，求圆的方程），则往往使用圆的一般方程求圆方程．参数式：以原点为圆心、r 为半径的圆的参数方程是⎩⎨⎧==θθsin ,cos r y r x （其中θ为参数）．以（a ，b ）为圆心、r 为半径的圆的参数方程为⎩⎨⎧+=+=θθsin ,cos r b y r a x （θ为参数），θ的几何意义是：以垂直于y轴的直线与圆的右交点A 与圆心C 的连线为始边、以C 与动点P 的连线为终边的旋转角，如图所示．三种形式的方程可以相互转化，其流程图为：（2）．二元二次方程是圆方程的充要条件“A=C ≠0且B=0”是一个一般的二元二次方程022=+++++F Ey Dx Cy Bxy Ax 表示圆的必要条件． 二元二次方程022=+++++F Ey Dx Cy Bxy Ax 表示圆的充要条件为“A=C ≠0、B=0且0422>-+AF E D ”，它可根据圆的一般方程推导而得． （3）．参数方程与普通方程我们现在所学的曲线方程有两大类，其一是普通方程，它直接给出了曲线上点的横、纵坐标之间的关系；其二是参数方程，它是通过参数建立了曲线上的点的横、纵坐标之间的（间接）关系，参数方程中的参数，可以明显的物理、几何意义，也可以无明显意义．要搞清楚参数方程与含有参数的方程的区别，前者是利用参数将横、纵坐标间接地连结起来， 3.圆锥曲线(1).椭圆的标准方程及其性质椭圆2222x b y a +＝１的参数方程为：⎩⎨⎧==ϕϕsin cos b y a x （ϕ为参数）。

高三文科数学第十单元：《平面解析几何》课型：复习课课时数： 21 讲学时间： 2021年 12月4日班级：学号：姓名：【本章知识体系】直线的倾斜角直线的斜率两条直线平行与垂直的判定点斜式斜截式直线与方程直线的方程两点式截距式平一般式面两条直线的交点坐标交点坐标与距离公式两点间的距离直点到直线的距离两条平行线间的距离角圆的标准方程圆的一般方程坐圆的方程直线与圆的位置关系圆与圆的位置关系标直线与圆的方程的应用系椭圆定义标准方程几何性质应用圆锥曲线双曲线定义标准方程几何性质应用抛物线定义标准方程几何性质应用【本章备考建议】1、本单元知识特点（1）直线与方程、圆与方程是解析几何的基础，圆锥曲线是解析几何的核心，也是高考重点考查的内容之一。

（2）概念、公式较多，用坐标法研究平面几何的思想在解题中显得内容多、难度大、综合性较强。

（3）注重常规题型及常规方式在解决问题中的感化。

2、在复习过程中应分外注意：（1）与直线有关的各种题型解题方式的熟练应用。

（2）与圆锥曲线有关的定义、方程、图像、几何性质及应用。

（3）重视直线与直线位置关系的灵活应用，在解决直线与圆锥曲线有关问题中，注意与“距离”、“中点”、“弦长”相关的问题的解法。

（4）注意数形结合思想、函数与方程思想、转化与化归思想、分类整合思想在解题中的渗透。

第十单元（一）：直线与方程（3课时）一、【学习方针】：1、理解直线的倾斜角和斜率的概念，掌握过两点的直线斜率的计算公式。

2、能在平面直角坐标系中，结合具体图形，掌握确定直线位置的几何要素。

3、掌握直线方程的几种形式，了解斜截式与一次函数的关系。

二、【回归教材】：1、阅读必修2第三章《直线与方程》10182P P -,熟悉教材中的基本概念，基本题型以及基本方式。

2、应试策略：通过近十年的高考试题统计分析可以得出：在高考中主要考查基本概念和求在分歧条件下的直线方程，此类考题大都属于中，低档题，以选择题和填空题形式泛起。

专题05 解析几何一、单选题1. 【河北省衡水第一中学2021届全国高三第二次联合考试（1）】设抛物线22(0)y px p =>的焦点为F ，倾斜角为02πθθ⎛⎫<< ⎪⎝⎭的直线l 经过抛物线的焦点F ，且与抛物线相交于M ，N 两点.若22F N M N F F →→→⋅=-，则sin 2θ=（ ）AB ．13CD2. 【河北省衡水中学2021届高三上学期七调】已知直线210x y --=的倾斜角为α，则21tan 2tan2αα-=（ ）A ．14-B ．1-C ．14D ．13. 【河北省衡水中学2021届高三上学期七调】已知c 是双曲线2222:1x y C a b-=(0a >，0b >)的半焦距，离心率为e ，则1be c +的最大值是（ ）ABCD ．24. 【河北省衡水中学2021届高三上学期七调】已知点F ，A 分别为椭圆2222:1x y C a b +=(0a >，0b >)的左焦点左顶点，过原点O 的直线l 交C 于P ，Q 两点，直线QF 交AP 于点B ，且2QA QP QB +=，若||PF 的最小值为4，则椭圆C 的标准方程为（ ）A ．22198x yB ．2212516x y +=C ．2213632x y +=D ．2214936x y +=5. 【河北省衡水中学2021届全国高三第一次联合考试（全国卷）】已知圆22:4O x y +=与x 轴交于,M N 两点，点P在直线:0l x y +-=上，过圆O 上的任意两点,S T 分别向l 作垂线，垂足为,S T ''，以下说法不正确的是（ ）A ．||||PM PN +的最小值为B ．PM PN ⋅为定值 C ．SPT ∠的最大值为3πD ．当ST 为直径时，四边形SS T T ''面积的最大值为166. 【河北省衡水中学2021届全国高三下学期第二次联合考试（II 卷）】已知双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12,F F ，若过点2F 作渐近线的垂线，垂足为P ，且12F PF △的面积为2b ，则该双曲线的离心率为（ ）A ．1B ．1CD 7. 【河北省衡水中学2021届全国高三下学期第二次联合考试（II 卷）】已知圆22:1C x y +=，直线:2l x =，P 为直线l 上的动点，过点P 作圆C 的切线，切点分别为A ，B ，则直线AB 过定点（ ）A ．1,02⎛⎫ ⎪⎝⎭B ．(0,2)C ．(2,1)D ．1,12⎛⎫ ⎪⎝⎭二、填空题1. 【河北省衡水第一中学2021届全国高三第二次联合考试（1）】对于双曲线22221(0,0)x y a b a b-=>>来说，我们定义圆222x y a +=为它的“伴随圆”.过双曲线22241(0)9x y a a -=>的左焦点1F 作它的伴随圆的一条切线，设切点为T ，且这条切线与双曲线的右支相交于点P .若M 为1PF 的中点，M 在T 右侧，且||||MO MT -为定值12，则该双曲线的离心率为_______.2. 【河北省衡水中学2021届全国高三第一次联合考试（全国卷）】小明同学发现家中墙壁上灯光的边界类似双曲线的一支， O 为双曲线的一支的顶点.小明经过测量得知，该双曲线的渐近线相互垂直，且AB 与OC 垂直，80cm,20cm AB OC ==，若该双曲线的焦点位于直线OC 上，则在点O 以下的焦点距点O ______cm .三、解答题1. 【河北省衡水第一中学2021届全国高三第二次联合考试（1）】已知圆22:(32M x y +=，点Q 是圆M 上的一个动点，点(N .若线段QN 的垂直平分线交线段QM 于点T . （1）求动点T 的轨迹曲线C 的方程；（2）设O 是坐标原点，点(2,1)P ，点R （异于原点）是曲线C 内部且位于y 轴上的一个动点，点S 与点R 关于原点对称，直线,PR PS 分别与曲线C 交于A ，B （异于点P ）两点.判断直线AB 是否过定点？若过，求出定点坐标；若不过，说明理由.2. 【河北省衡水中学2021届高三上学期七调】设抛物线E ：()220y px p =>焦点为F ，准线为l ，A 为E 上一点，已知以F 为圆心，FA 为半径的圆F 交l 于B 、D 点．（Ⅰ）若60BFD ∠=︒，BFD △p 的值及圆F 的方程； （Ⅰ）若点A 在第一象限，且A 、B 、F 三点在同一直线1l 上，直线1l 与抛物线E 的另一个交点记为C ，且CF FA λ=，求实数λ的值．3. 【河北省衡水中学2021届全国高三第一次联合考试（全国卷）】已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ，点P 在C 上，但不在x 轴上，当点P 在C 上运动时，12PF F △的周长为定值6，且当112PF F F ⊥时，132PF =. （1）求C 的方程.（2）若斜率为(0)k k ≠的直线l 交C 于点M ，N ，C 的左顶点为A ，且1,,AM AN k k k -成等差数列，证明：直线l过定点.4. 【河北省衡水中学2021届全国高三下学期第二次联合考试（II卷）】已知椭圆2222:1(0)x yE a ba b+=>>的左、右顶点分别为A，B，M是椭圆E上一点，M关于x轴的对称点为N，且14MA NBk k⋅=．（1）求椭圆E的离心率；（2）若椭圆E的一个焦点与抛物线2y=的焦点重合，斜率为1的直线l与E相交于P，Q两点，在y 轴上存在点R，使得以线段PQ为直径的圆经过点R，且()0RQ RP PQ+⋅=，求直线l的方程．。

第3讲几何概型一、知识梳理1．几何概型 (1)几何概型的定义如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例，则称这样的概率模型为几何概率模型，简称几何概型．(2)几何概型的两个基本特点2．几何概型的概率公式P (A )＝构成事件A 的区域长度（面积或体积）试验的全部结果所构成的区域长度（面积或体积）.二、习题改编1．(必修3P142A 组T3改编)一个路口的红绿灯，红灯的时间为30 s ，黄灯的时间为5 s ，绿灯的时间为40 s ，当某人到达路口时看见的是红灯的概率为 ．答案：252．(必修3P142A 组T2改编)如图是某商场通过转动如图所示的质地均匀的6等分的圆盘进行抽奖活动，当指针指向阴影区域时为中奖，则顾客中奖的概率是 ．答案：13一、思考辨析判断正误(正确的打“√”，错误的打“×”)(1)几何概型中，每一个基本事件就是从某个特定的几何区域内随机地取一点，该区域中的每一点被取到的机会相等．( )(2)在几何概型定义中的区域可以是线段、平面图形、立体图形．( ) (3)随机模拟方法是以事件发生的频率估计概率．( ) (4)与面积有关的几何概型的概率与几何图形的形状有关．( ) 答案：(1)√ (2)√ (3)√ (4)× 二、易错纠偏常见误区(1)易混淆几何概型与古典概型；(2)几何概型的测度选择不正确．1．如图，在一边长为2的正方形ABCD 内有一曲线L 围成的不规则图形．往正方形内随机撒一把豆子(共m 颗)．落在曲线L 围成的区域内的豆子有n 颗(n <m )，则L 围成的区域面积(阴影部分)为( )A.2n mB.4n mC.n 2mD.n 4m详细分析：选B.S 阴影S 正方形＝落在L 围成的区域内的豆子数n落在正方形中的豆子数m ，所以S 阴影＝n m ×22＝4nm.2．记函数f (x )＝6＋x －x 2的定义域为D .在区间[－4，5]上随机取一个数x ，则x ∈D 的概率是 ．详细分析：由6＋x －x 2≥0，解得－2≤x ≤3，则D ＝[－2，3]，则所求概率为3－（－2）5－（－4）＝59. 答案：59与长度有关的几何概型(典例迁移)(2020·福建五校第二次联考)在区间[0，2]上随机取一个数x ，使sin π2x ≥32的概率为( )A.13 B.12 C.23D.34当x ∈[0，2]时，0≤π2x ≤π，所以sin π2x ≥32⇔π3≤π2x ≤2π3⇔23≤x ≤43.故由几何概型的知识可知所求概率P ＝43－232＝13.故选A.【答案】 A【迁移探究】 (变条件)若将本例中的不等式变为sin x ≤32，如何求概率？ 解：结合正弦曲线，在[0，π]上使sin x ≤32的x ∈⎣⎡⎦⎤0，π3∪⎣⎡⎦⎤2π3，π， 故所求概率为P ＝⎝⎛⎭⎫π3－0＋⎝⎛⎭⎫π－2π3π－0＝23.与长度有关的几何概型(1)如果试验的结果构成的区域的几何度量可用长度表示，则其概率的计算公式为 P (A )＝构成事件A 的区域长度试验的全部结果所构成的区域长度.(2)与时间、不等式等有关的概率问题可转化为几何概型，利用几何概型概率公式进行求解．1．(2020·湖北武汉模拟)某路公交车在6：30，7：00，7：30，准时发车，小明同学在6：50至7：30之间到达该车站乘车，且到达该车站的时刻是随机的，则他等车时间不超过10分钟的概率为 ．详细分析：小明同学在6：50至7：30之间到达该车站乘车，总时长为40分钟，公交车在6：30，7：00，7：30准时发车，他等车时间不超过10分钟，则必须在6：50至7：00或7：20至7：30之间到达，时长为20分钟，则他等车时间不超过10分钟的概率P ＝2040＝12. 答案：122．(2020·江西赣州十四县联考)在(0，8)上随机取一个数m ，则事件“直线x ＋y －1＝0与圆(x －3)2＋(y －4)2＝m 2没有公共点”发生的概率为 ．详细分析：因为m ∈(0，8)，直线x ＋y －1＝0与圆(x －3)2＋(y －4)2＝m 2没有公共点，所以⎩⎨⎧0<m <8，|3＋4－1|2>m，解得0<m <32，所以所求概率P ＝328.答案：328与面积有关的几何概型(多维探究)角度一与平面图形面积有关的几何概型(1)(2020·昆明市诊断测试)如图，先画一个正方形ABCD，再将这个正方形各边的中点相连得到第2个正方形，依此类推，得到第4个正方形EFGH(图中阴影部分)，在正方形ABCD内随机取一点，则此点取自正方形EFGH 内的概率是()A.14B.16C.18D.116(2)(2020·江西七校第一次联考)图中的图案是我国古代建筑中的一种装饰图案，形若铜钱，寓意富贵吉祥，在圆内随机取一点，则该点取自阴影区域内(阴影部分由四条四分之一圆弧围成)的概率是( )A.12B.13C.4π－1 D.2－4π(1)设第1个正方形ABCD 的边长为2，则第2个正方形的边长为2，第3个正方形的边长为1，第4个正方形EFGH 的边长为22，所以所求概率P ＝S 正方形EFGH S 正方形ABCD ＝⎝⎛⎭⎫22222＝18.故选C.(2)设圆的半径为1，则该点取自阴影区域内的概率P ＝S 阴影S 圆＝π×12－8⎝⎛⎭⎫14×π×12－12×1×1π×12＝4π－1，故选C. 【答案】 (1)C (2)C角度二 与线性规划知识交汇命题的几何概型(2020·广州综合测试)在平面区域{(x ，y )|0≤x ≤1，1≤y ≤2}内随机投入一点P ，则点P 的坐标(x ，y )满足y ≤2x 的概率为( )A.14 B.12 C.23D.34依题意作出图象如图，则P (y ≤2x )＝S 阴影S 正方形＝12×12×112＝14.【答案】 A与面积有关的几何概型的求法求解与面积有关的几何概型时，关键是弄清某事件对应的面积，必要时可根据题意构造两个变量，把变量看成点的坐标，找到试验全部结果构成的平面图形，以便求解．1．(2020·郑州市第一次质量预测)已知矩形ABCD 中，BC ＝2AB ＝4，现向矩形ABCD 内随机投掷质点M ，则满足MB →·MC →≥0的概率是( )A.π4 B.4－π4C.π2D.π－24详细分析：选B.由MB →·MC →≥0，知∠BMC 为锐角或直角，则点M 所在的区域如图中阴影部分所示，则所求概率P ＝1－12×π×224×2＝1－π4＝4－π4，故选B.2．某日，甲、乙两人随机选择早上6：00至7：00的某个时刻到达七星公园进行锻炼，则甲比乙提前到达超过20分钟的概率为 ( )A.79B.29C.23D.．13详细分析：选B.在平面直角坐标系中，设x ，y 分别表示乙、甲两人的到达时刻，当x －y >20时满足题意，由几何概型计算公式可得，甲比乙提前到达超过20分钟的概率为12×40×4060×60＝29.故选B.与体积有关的几何概型(师生共研)一个多面体的直观图和三视图如图所示，点M是AB的中点，一只蝴蝶在几何体ADF-BCE内自由飞翔，则它飞入几何体F-AMCD 内的概率为()A.34B.23C.13D.．12因为V F ­AMCD ＝13×S 四边形AMCD ×DF ＝14a 3，V ADF ­BCE ＝12a 3，所以它飞入几何体F -AMCD内的概率为14a 312a 3＝12.【答案】 D与体积有关的几何概型的求法对于与体积有关的几何概型问题，关键是计算问题的总体积(总空间)以及事件的体积(事件空间)，对于某些较复杂的问题也可利用其对立事件求解．在棱长为2的正方体ABCD -A 1B 1C 1D 1中，点O 为底面ABCD 的中心，在正方体ABCD -A 1B 1C 1D 1内随机取一点P ，则点P 到点O 的距离大于1的概率为( )A.π12 B ．1－π12C.π6D ．1－π6详细分析：选B.点P 到点O 的距离大于1的点位于以O 为球心，以1为半径的半球外． 记“点P 到点O 的距离大于1”为事件M ， 则P (M )＝23－12×4π3×1323＝1－π12.[基础题组练]1．已知集合A ＝{}a |y ＝10＋3a －a 2，若在集合A 内任取一个数a ，使得1∈{x |2x 2＋ax －a 2＞0}的概率为( )A.17B.37C.12D.34详细分析：选B.由10＋3a －a 2≥0，解得－2≤a ≤5，即A ＝[－2，5]．因为1∈{x |2x 2＋ax －a 2＞0}，故2＋a －a 2＞0，解得－1＜a ＜2.由几何概型的知识可得，所求的概率P ＝2－（－1）5－（－2）＝37.故选B.2.(2020·湖南长沙四县联考)如图，在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器，圆锥的底面圆周与鱼缸的底面正方形相切，圆锥的顶点在鱼缸的缸底上，现在向鱼缸内随机地投入一粒鱼食，则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是( )A ．1－π4B.π12C.π4D.1－π12详细分析：选A.鱼缸底面正方形的面积为22＝4，圆锥底面圆的面积为π，所以“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是1－π4，故选A.3.(2020·安庆二模)中国人民银行发行了2018中国戊戌(狗)年金银纪念币一套，如图所示是一枚3克圆形金质纪念币，直径为18 mm ，小米同学为了测算图中装饰狗的面积，他用1枚针向纪念币上投掷500次，其中针尖恰有150次落在装饰狗的身体上，据此可估计装饰狗的面积大约是( )A.486π5 mm 2B.243π10 mm 2C.243π5mm 2D.243π20mm 2 详细分析：选B.设装饰狗的面积为S mm 2.由题意得S π×⎝⎛⎭⎫1822＝150500，所以S ＝243π10 mm 2. 4．(2020·湖南省五市十校联考)一只蚂蚁在三边长分别为6，8，10的三角形内自由爬行，某时刻该蚂蚁距离三角形的任意一个顶点的距离不超过1的概率为( )A.π24 B.π48 C.112D.18详细分析：选B.由题意，可得三角形为直角三角形，其面积为12×6×8＝24，三角形内距离三角形的任意一个顶点的距离不大于1的区域如图中阴影部分所示，它的面积为半径为1的半圆面积，即S ＝12π×12＝π2，所以所求概率P ＝π224＝π48，故选B.5．在区间[0，6]上随机取一个数x ，则log 2x 的值介于1到2之间的概率为 ． 详细分析：由题知1<log 2x <2，解得2<x <4，故log 2x 的值介于1到2之间的概率为4－26－0＝13. 答案：136.如图，正四棱锥S -ABCD 的顶点都在球面上，球心O 在平面ABCD 上，在球O 内任取一点，则这点取自正四棱锥内的概率为 ．详细分析：设球的半径为R ，则所求的概率为P ＝V 锥V 球＝13×12×2R ×2R ×R 43πR 3＝12π.答案：12π7．(2020·西安市八校联考)从集合{(x ，y )|x 2＋y 2≤4，x ∈R ，y ∈R }中任选一个元素(x ，y )，则满足x ＋y ≥2的概率为 ．详细分析：如图，先画出圆x 2＋y 2＝4，再画出不等式组⎩⎪⎨⎪⎧x 2＋y 2≤4，x ＋y ≥2对应的可行域，即图中阴影部分， 则所求概率P ＝S 阴影S 圆＝14×4π－12×2×24π＝π－24π.答案：π－24π8．(2020·洛阳尖子生第二次联考)某港口有一个泊位，现统计了某月100艘轮船在该泊位的停靠时间(单位：小时)，如果停靠时间不足半小时按半小时计时，超过半小时不足1小时按1小时计时，依此类推，统计结果如表：设该月这100艘轮船在该泊位的平均停靠时间为a 小时． (1)求a 的值；(2)假定某天只有甲、乙两艘轮船需要在该泊位停靠a 小时，且在一昼夜的时间段中随机到达，求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率．解：(1)a ＝1100×(2.5×12＋3×12＋3.5×17＋4×20＋4.5×15＋5×13＋5.5×8＋6×3)＝4.(2)设甲船到达的时间为x ，乙船到达的时间为y ，则⎩⎪⎨⎪⎧0<x ≤240<y ≤24. 若这两艘轮船中至少有一艘在停靠该泊位时必须等待，则|y －x |<4，符合题意的区域如图中阴影部分(不包括x ，y 轴)所示．记“这两艘轮船中至少有一艘在停靠该泊位时必须等待”为事件A ， 则P (A )＝24×24－2×12×20×2024×24＝1136.即两艘轮船中至少有一艘在停靠该泊位时必须等待的概率为1136.[综合题组练]1.(2020·湖南省湘东六校联考)如图，一靶子是由三个全等的三角形和中间的一个小等边三角形拼成的大等边三角形，其中3DF ＝2BF ，若向靶子随机投镖，则镖落在小等边三角形内的概率是( )A.27B.449C.313D.31313详细分析：选B.因为3DF ＝2BF ，所以不妨设DF ＝2，BF ＝3，则DC ＝3，∠BDC ＝120°，由余弦定理可得BC ＝25＋9－2×5×3×⎝⎛⎭⎫－12＝7，所以镖落在小等边三角形内的概率是12×DF 2×sin 60°12×BC 2×sin 60°＝449，故选B.2．(2020·甘肃张掖第一次联考)如图，B 是AC 上一点，分别以AB ，BC (AB <BC )，AC 为直径作半圆，从B 作BD ⊥AC ，与半圆相交于D ，AC ＝6，BD ＝22，在整个图形中随机取一点，则此点取自图中阴影部分的概率是( )A.29B.13C.49D.23详细分析：选C.连接AD ，CD ，可知△ACD 是直角三角形，又BD ⊥AC ， 所以BD 2＝AB ·BC ，设AB ＝x (0<x <3)，则有8＝x (6－x )，得x ＝2，所以AB ＝2，BC ＝4，由此可得图中阴影部分的面积等于π×322－⎝⎛⎭⎫π×122＋π×222＝2π， 故概率P ＝2π12×9π＝49.故选C.3．(2020·广东六校第一次联考)在区间[－π，π]上随机取两个实数a ，b ，记向量m ＝(a ，4b )，n ＝(4a ，b )，则m ·n ≥4π2的概率为 ．详细分析：在区间[－π，π]上随机取两个实数a ，b ，则点(a ，b )在如图所示的正方形内部及其边界上．因为m ·n ＝4a 2＋4b 2≥4π2，所以a 2＋b 2≥π2，满足条件的点(a ，b )在以原点为圆心，π为半径的圆外部(含边界)，且在正方形内(含边界)，如图中阴影部分所示，所以m ·n ≥4π2的概率P ＝4π2－π34π2＝1－π4.答案：1－π44．在平面区域⎩⎪⎨⎪⎧x ＋y －4≤0，x >0，y >0内随机取一点(a ，b )，则函数f (x )＝ax 2－4bx ＋1在区间[1，＋∞)上是增函数的概率为 ．详细分析：不等式组表示的平面区域为如图所示的△AOB 的内部及边界AB (不包括边界OA ，OB )，则S △AOB ＝12×4×4＝8.函数f (x )＝ax 2－4bx ＋1在区间[1，＋∞)上是增函数，则应满足a >0，且x ＝4b2a ≤1，满足⎩⎪⎨⎪⎧a >0，a ≥2b ，可得对应的平面区域如图中阴影部分(包括边界OC ，BC ，不包括边界OB )，由⎩⎪⎨⎪⎧a ＝2b ，a ＋b －4＝0，解得a ＝83，b ＝43，所以S △COB ＝12×4×43＝83，根据几何概型的概率计算公式，可知所求的概率为838＝13.答案：13。

7．4 几何问题的代数解法[学习目标]1．理解坐标法的意义，并会用坐标法研究问题． 2．进一步掌握用解析法处理平面几何问题． [预习导引]1．解决几何问题的根本方法——解析法解析法是解决解析几何、立体几何等问题的重要方法，它是把几何问题转化成代数问题，通过建立适当的坐标系加以分析研究解决问题的方法． 2．用坐标方法解决平面几何问题的“三步曲〞为：(1)建立适当的平面直角坐标系，用坐标和方程表示问题中的几何元素，将平面几何问题转化为代数问题；(2)通过代数运算，解决代数问题；(3)把代数运算结果“翻译〞成几何结论并作答．要点一 用解析法证明几何问题例1 △ABD 和△BCE 是边AB ，BC 在直线AC 上且位于直线AC 同侧的两个等边三角形，用坐标法证明：|AE |＝|CD |.证明 如图，以B 点为坐标原点，取AC 所在直线为x 轴，建立直角坐标系．设△ABD 和△BCE 的边长分别为a ，c ，那么A (－a ，0)，E (c 2，32c )，C (c ，0)，D (－a 2，32a )，于是|AE |＝[c 2－〔－a 〕]2＋〔32c －0〕2＝a 2＋ac ＋c 24＋34c 2＝a 2＋ac ＋c 2.|CD |＝[〔－a 2〕－c ]2＋〔32a －0〕2＝a 24＋ac ＋c 2＋34a 2＝a 2＋ac ＋c 2. 所以|AE |＝|CD |.规律方法 坐标法的根本步骤第一步：建立适当的坐标系用坐标表示有关量． 第二步：进展有关代数运算．第三步：把代数运算结果“翻译〞成几何关系．跟踪演练1 在△ABC 中，D 是BC 边上任意一点(D 与B ，C 不重合)，且|AB |2＝|AD |2＋|BD |·|DC |，求证：△ABC 为等腰三角形．证明 如图，作AO ⊥BC ，垂足为O ，以BC 所在直线为x 轴，以OA 所在直线为y 轴，建立直角坐标系．设A (0，a )，B (b ，0)，C (c ，0)，D (d ，0)．因为|AB |2＝|AD |2＋|BD |·|DC |，所以由两点间的距离公式，得b 2＋a 2＝d 2＋a 2＋(d －b )(c －d )，即－(d －b )(b ＋d )＝(d －b )(c －d )， 又d －b ≠0，故－b －d ＝c －d ，即－b ＝c . 所以△ABC 为等腰三角形． 要点二 代数问题的几何解法例2 求函数y ＝x 2＋x ＋1－x 2－x ＋1的值域． 解 显然函数的定义域为R ，y ＝〔x ＋12〕2＋34－〔x －12〕2＋34＝〔x ＋12〕2＋〔0－32〕2－〔x －12〕2＋〔0－32〕2.设P (x ，0)，A (12，32)，B (－12，32)为平面上三点，那么|PA |＝〔x －12〕2＋34＝x 2－x ＋1，|PB |＝〔x ＋12〕2＋34＝x 2＋x ＋1.y ＝|PB |－|PA |.∵||PB |－|PA ||<|AB |，且|AB |＝1，∴|y |<1，即－1<y <1，故函数的值域为(－1，1)．规律方法 将被开方式配方，可化为两点间的距离公式的形式，结合几何意义求值域． 跟踪演练2 求函数y ＝x 2＋1＋x 2－4x ＋8的最小值． 解 ∵函数的解析式可化为y ＝x 2＋1＋x 2－4x ＋8＝〔x －0〕2＋〔0－1〕2＋〔x －2〕2＋〔0－2〕2.令A (0，1)，B (2，2)，P (x ，0)，那么问题转化为在x 轴上求一点P (x ，0)，使得|PA |＋|PB |取最小值．∵A 关于x 轴的对称点为A ′(0，－1)， ∴(|PA |＋|PB |)min ＝|A ′B |＝〔2－0〕2＋〔2＋1〕2＝4＋9＝13， 即函数y ＝x 2＋1＋x 2－4x ＋8的最小值为13. 要点三 坐标法的实际应用例3 一艘轮船沿直线返回港口的途中，接到气象台的台风预报，台风中心位于轮船正西70 km 处，受影响的范围是半径为30 km 的圆形区域，港口位于台风中心正北40 km 处，如果这艘船不改变航线，那么它是否会受到台风的影响？解 以台风中心为坐标原点，以东西方向为x 轴建立直角坐标系(如下图)，其中取10 km 为单位长度．那么受台风影响的圆形区域所对应的圆的方程为x 2＋y 2＝9， 港口所对应的点的坐标为(0，4)，轮船的初始位置所对应的点的坐标为(7，0)， 那么轮船航线所在直线l 的方程为x 7＋y4＝1，即4x ＋7y －28＝0. 圆心(0，0)到直线4x ＋7y －28＝0的距离d ＝|－28|42＋72＝2865，而半径r ＝3，∵d >r ，∴直线与圆相离，所以轮船不会受到台风的影响．规律方法 先以台风中心为原点建立适当的坐标系，把有关的几何元素用坐标和方程表示，然后把此实际问题转化为数学问题来解决．跟踪演练3 有弱、强两个喇叭在A ，O 两处，假设它们的强度之比为1∶4，且相距60 m ，问在什么位置听到两个喇叭传来的声音强度是相等的？(假设声音强度与距离的平方成反比)解 以直线OA 为x 轴，O 为坐标原点建立如下图的直角坐标系．那么O (0，0)，A (60，0)．设在P (x ，y )处听到O ，A 两处的喇叭声音强度相等． 由题设知|OP |2|PA |2＝14，即x 2＋y 2〔x －60〕2＋y 2＝14，整理，得(x ＋20)2＋y 2＝402.故P 点的轨迹是以(－20，0)为圆心，40为半径的圆，也就是在此圆周上听到的声音强度相等.1．过点A (－1，4)作圆(x －2)2＋(y －3)2＝1的切线，那么A 到切点的距离为( ) A. 5 B ．3 C.10 D ．5答案 B解析 设圆心C (2，3)，那么|AC |＝10，∴点A 到切点的距离即切线长l ＝10－1＝3.2．圆x 2＋y 2＝1上的点到直线3x ＋4y －25＝0的距离的最小值是( ) A ．6 B ．4 C ．5 D ．1答案 B解析 圆心到直线3x ＋4y －25＝0的距离为255x ＋4y －25＝0的距离的最小值为5－1＝4.3．圆x 2＋y 2＋2x －4y ＋4＝0关于直线y ＝2x ＋b 成轴对称，那么b ＝________. 答案 4解析 圆的圆心为(－1，2)，且点(－1，2)在直线y ＝2x ＋b 上，那么2＝－2＋b ，∴b ＝4. 4．假设点P (x ，y )在圆C ：(x －2)2＋y 2＝3上，那么y x的最大值是________． 答案3解析 半径长|PC |＝3，|OC |＝2，y x ＝y －0x －0是圆上的点与原点连线的斜率．当OP 与圆上方相切时，此时斜率最大，那么∠POC ＝60°， tan ∠POC ＝ 3.5．点P 在圆O ：x 2＋y 2＝1上运动，点Q 在圆C ：(x －3)2＋y 2＝1上运动，那么|PQ |的最小值为________． 答案 1解析 如下列图．设连心线OC 与圆O 交于点P ′，与圆C 交于点Q ′，当点P 在P ′处，点Q 在Q ′处时|PQ |最小，最小值为|P ′Q ′|＝|OC |－r 1－r 2＝1.1．利用数形结合思想求某些二元代数式的最值是直线和圆的方程的一个重要应用，它是利用代数式的几何意义转化为斜率、截距、距离等来求解．2．利用坐标法解决平面几何问题，将几何中“形〞的问题转化为代数中“数〞的问题．适当建系时，通常取定直线为坐标轴，定点或线段的中点为原点，使其具有对称性，这样便于设坐标．很多实际问题也可采用这种方法转化．一、根底达标1．△ABC 的三个顶点是A (5，5)，B (1，4)和C (4，1)，那么△ABC 的形状是( ) A ．直角三角形 B ．等腰三角形 C ．等边三角形 D ．等腰直角三角形答案 B解析 ∵|AB |＝〔5－1〕2＋〔5－4〕2＝17， |BC |＝〔1－4〕2＋〔4－1〕2＝32， |AC |＝〔5－4〕2＋〔5－1〕2＝17， ∴|AB |＝|AC |，∴△ABC 为等腰三角形． 2．方程y ＝－25－x 2表示的曲线是( ) A ．一条射线 B ．一个圆 C ．两条射线 D ．半个圆答案 D解析 由y ＝－25－x 2得x 2＋y 2＝25. ∵y ＝－25－x 2≤0, ∴曲线表示半个圆．3．点M ，N 在x 2＋y 2＋kx ＋2y －4＝0上，且点M ，N 关于直线x －y ＋1＝0对称，那么该圆的半径为( ) A ．2 2 B. 2 C ．1 D ．3答案 D解析 由M ，N 两点关于直线x －y ＋1＝0对称，可知直线x －y ＋1＝0过圆心 (－k2，－1)，∴k ＝4，∴圆的方程即为(x ＋2)2＋(y ＋1)2＝9，∴r ＝3. 4．点P 是直线2x ＋y ＋10＝0上的动点，直线PA ，PB 分别与圆x 2＋y 2＝4相切于A ，B 两点，那么四边形PAOB (O 为坐标原点)的面积的最小值为( ) A ．24 B ．16 C ．8 D ．4答案 C解析 ∵四边形PAOB 的面积S ＝2×12|PA |×|OA |＝2|OP |2－|OA |2＝2|OP |2－4，∴当直线OP 垂直直线2x ＋y ＋10＝0时，|OP |min ＝1022＋12＝2 5.此时，四边形PAOB 的面积的最小值为2〔25〕2－4＝8.5．直线x －2y －3＝0与圆(x －2)2＋(y ＋3)2＝9相交于E ，F 两点，圆心为C ，那么△CEF 的面积为________． 答案 2 5解析 圆心(2，－3)到直线x －2y －3＝0的距离为d ＝|2＋2×3－3|5＝5，∴|EF |＝2×9－d 2＝29－5＝4， ∴S △CEF ＝12×4×5＝2 5.6．x ＋y ＋1＝0，那么〔x ＋2〕2＋〔y ＋3〕2的最小值是________． 答案 2 2 解析〔x ＋2〕2＋〔y ＋3〕2表示点P (x ，y )和点(－2，－3)的距离，那么〔x ＋2〕2＋〔y ＋3〕2的最小值为点(－2，－3)到直线x ＋y ＋1＝0的距离d ＝|－2－3＋1|2＝42＝2 2. 7．有一种大型商品，A ，B 两地都有出售，且价格一样，某地居民从两地之一购得商品后，运回的费用是：每单位距离A 地的运费是B 地运费的3倍，A ，B 两地距离10 km ，顾客选A 或B 地购置这件商品的标准是：包括运费和价格的总费用较低，求A ，B 两地的售货区域的分界限的曲线形状，并指出曲线上、曲线内、曲线外的居民如何选择购货地点．解 如图，以A ，B 所确定的直线为x 轴，线段AB 中点O 为坐标原点，建立直角坐标系，那么A (－5，0)，B (5，0)，设某地P 的坐标为(x ，y )，假设居民选择A 地购置商品廉价，并设A 地的运费3a 元/千米，B 地的运费为a 元/千米，那么价格＋x A 地运费≤价格＋x B 地运费，∴3a 〔x ＋5〕2＋y 2≤a 〔x －5〕2＋y 2. ∵a >0，∴3〔x ＋5〕2＋y 2≤〔x －5〕2＋y 2. 化简为(x ＋254)2＋y 2≤(154)2.∴以点C ⎝ ⎛⎭⎪⎫－254，0为圆心，154为半径的圆是这两条购货区域的分界限．圆C 内的居民，从A 地购货廉价， 圆C 外的居民，从B 地购货廉价，圆C 上的居民，从A ，B 两地购货的总费用相等，因此可随便从A ，B 两地之一购货． 二、能力提升8．台风中心从A 地以每小时20 km 的速度向东北方向移动，离台风中心不超过30 km 地区为危险区，城市B 在A 地正东40 km 处，那么城市B 处于危险区内的时间是( ) A ．0.5 h B ．1 h C ．1.5 h D ．2 h答案 B解析 如下图，以A 地为原点，AB 所在直线为x 轴，建立平面直角坐标系，那么B (40，0)，以B 为圆心，30为半径的圆的方程为(x －40)2＋y 2＝302，台风中心移动到圆B 内时，B 城市将处于危险区，台风移动所在直线方程为y ＝x ，它与圆B 的相交弦为MN ，那么可求得|MN |＝2302－⎝ ⎛⎭⎪⎫4022＝20 (km)，|MN |20＝1 (h)，所以B 城市位于危险区内的时间为1 h.9．一束光线从点A (－1，1)出发经x 轴反射到圆(x －2)2＋(y －3)2＝1上的最短距离为________． 答案 4解析 A 关于x 轴的对称点为A ′(－1，－1)，A ′与圆心的距离为32＋42＝5，故所求最短距离为5－1＝4.10．两圆相交于两点(1，3)和(m ，－1)，两圆圆心都在直线x －y ＋c ＝0上，那么m ＋c 的值为________． 答案 3解析 由平面几何性质知：两相交圆圆心的连线与两圆的公共弦垂直，且经过弦的中点，那么3＋11－m＝－1，得m ＝5，∴弦中点坐标为(3，1)，∴3－1＋c ＝0，得c ＝－2，∴m ＋c ＝3. 11．x ，y 满足x 2＋y 2－2x ＋4y ＝0，求x －2y 的最大值．解 设x －2y ＝b ，那么点(x ，y )既在直线x －2y ＝b 上，又在圆x 2＋y 2－2x ＋4y ＝0上， 即直线x －2y ＝b 和圆(x －1)2＋(y ＋2)2＝5有公共点，故圆心(1，－2)到x －2y －b ＝0的距离小于或等于半径5，所以|1－2×〔－2〕－b |5≤5，即|b －5|≤5，所以0≤b ≤10，即x －2y 的最大值是10. 三、探究与创新12．假设圆x 2＋y 2－4x －4y －10＝0上至少有三个不同点到直线l ：ax ＋by ＝0(b ≠0)的距离为22，求直线l 斜率的取值范围．解 ∵圆x 2＋y 2－4x －4y －10＝0可整理为(x －2)2＋(y －2)2＝(32)2， ∴圆心坐标为C (2，2)，半径为r ＝3 2.要使圆上至少有三个不同的点到直线l ：ax ＋by ＝0的距离为22，那么圆心到直线的距离d 满足d ＝|2a ＋2b |a 2＋b 2≤2，∴(a b )2＋4(ab )＋1≤0，∴－2－3≤ab≤－2＋ 3. ∵k ＝－a b，∴2－3≤k ≤2＋3，∴直线ax ＋by ＝0的斜率范围是[2－3，2＋3]． 13．点P (x ，y )在圆x 2＋y 2－6x －6y ＋14＝0上． (1)求y x的最大值和最小值；(2)求x 2＋y 2＋2x ＋3的最大值与最小值； (3)求x ＋y 的最大值与最小值．解 圆x 2＋y 2－6x －6y ＋14＝0变形为(x －3)2＋(y －3)2＝4，故圆心为C (3，3)，半径r ＝2.如下图．(1)y x表示圆上的点P 与原点连线的斜率，显然PO 与圆相切时，斜率最大或最小．设切线方程为y ＝kx ，即kx －y ＝0，由圆心C (3，3)到切线的距离等于半径2，可得|3k －3|k 2＋1＝2，解得k ＝9±2145，所以，y x 的最大值为9＋2145，最小值为9－2145.(2)x 2＋y 2＋2x ＋3＝(x ＋1)2＋y 2＋2，它表示圆上的点P 到E (－1，0)的距离的平方再加2，所以，当点P 与点E 的距离最大或最小时，所求式子就取最大值或最小值，显然点P 与点E 的距离的最大值为|CE |＋2，点P 与点E 距离的最小值为|CE |－2，又|CE |＝〔3＋1〕2＋32＝5，所以x 2＋y 2＋2x ＋3的最大值为(5＋2)2＋2＝51，最小值为(5－2)2＋2＝11.(3)设x ＋y ＝b ，那么b 表示动直线y ＝－x ＋b 的纵截距，显然当动直线y ＝－x ＋b 与圆(x －3)2＋(y －3)2＝4相切时，b 取最大值或最小值．此时圆心C (3，3)到切线x ＋y ＝b 的距离等于圆的半径2，那么|3＋3－b |12＋12＝2， 即|b －6|＝22， 解得b ＝6±22，所以，x ＋y 的最大值为6＋22，最小值为6－2 2.。

第7章解析几何初步章末复习1．点的坐标(1)两点间距离公式：两点P 1(x 1，y 1)，Q (x 2，y 2)间的距离|PQ |＝〔x 2－x 1〕2＋〔y 2－y 1〕2. (2)定比分点坐标公式：分两点A (x 1，y 1)，B (x 2，y 2)所构成的有向线段AB →为定比λ的分点的坐标为(x 1＋λx 21＋λ，y 1＋λy 21＋λ)． (3)三角形重心坐标公式：以(x 1，y 1)，(x 2，y 2)，(x 3，y 3)为顶点的三角形的重心坐标为(x 1＋x 2＋x 33，y 1＋y 2＋y 33)．(4)三角形面积的公式：以向量(x 1，y 1)，(x 2，y 2)为两边的三角形的面积S ＝12|x 1y 2－x 2y 1|.2．直线与方程 (1)直线法向量的应用①直线垂直于向量(A ，B )(法向量)⇔直线方程Ax ＋By ＋C ＝0(C 待定) ②两条直线平行或重合⇔它们的法向量平行 两条直线相交⇔它们的法向量不平行 ③两直线垂直⇔它们的法向量垂直(内积为0) (2)直线方程的几种形式(3)斜率公式和点到直线的距离公式 ①k ＝y 2－y 1x 2－x 1(x 1≠x 2)②d ＝|Ax 1＋By 1＋C |A 2＋B 23．圆与方程(1)标准方程：以(a ，b )为圆心，r 为半径的圆的方程： (x －a )2＋(y －b )2＝r 2(2)一般方程：x 2＋y 2＋Dx ＋Ey ＋F ＝0(D 2＋E 2－4F >0)．其中圆心坐标(－D 2，－E2)，r ＝D 2＋E 2－4F2(3)直线与圆的位置关系由圆心到直线的距离d 与圆的半径r 的大小关系决定： 相离⇔d >r ； 相交⇔d <r ； 相切⇔d ＝r .(4)圆与圆的位置关系由两圆的半径R ，r 及圆心距d 决定，有如下关系：(不妨设R ≥r ) 外离⇔d >R ＋r ； 外切⇔d ＝R ＋r ； 相交⇔R －r <d <R ＋r ； 内切⇔d ＝R －r >0； 内含⇔d <R －r ； 同心⇔d ＝0. 4．空间两点间的距离空间两点P (x 1，y 1，z 1)，Q (x 2，y 2，z 2)间的距离： |PQ |＝〔x 2－x 1〕2＋〔y 2－y 1〕2＋〔z 2－z 1〕2.题型一 直线的方程(1)求直线方程的主要方法是待定系数法．要掌握直线方程五种形式的适用条件及相互转化，能根据条件灵活选用方程，当不能确定某种方程条件是否具备时要另行讨论条件不满足的情况．(2)运用直线系方程的主要作用在于能使计算简单．例1 过点P (－1，0)，Q (0，2)分别作两条互相平行的直线，使它们在x 轴上截距之差的绝对值为1，求这两条直线的方程．解 (1)当两条直线的斜率不存在时，两条直线的方程分别为x ＝－1，x ＝0，它们在x 轴上截距之差的绝对值为1，满足题意；(2)当直线的斜率存在时，显然斜率不为0，设其斜率为k ，那么两条直线的方程分别为y ＝k (x ＋1)，y ＝kx ＋2.令y ＝0，分别得x ＝－1，x ＝－2k.由题意⎪⎪⎪⎪⎪⎪－1＋2k ＝1，即k ＝1.那么直线的方程为y ＝x ＋1，y ＝x ＋2， 即x －y ＋1＝0，x －y ＋2＝0，综上可知，所求的直线方程为x ＝－1，x ＝0，或x －y ＋1＝0，x －y ＋2＝0. 跟踪演练1 将直线的方程x －2y ＋6＝0：(1)化成斜截式，并指出它的斜率与在y 轴上的截距； (2)化成截距式，并指出它在x 轴、y 轴上的截距．解 (1)将原方程移项得2y ＝x ＋6，两边同除以2，得斜截式y ＝12x ＋3，因此它的斜率k ＝12，在y 轴上的截距为3.(2)将原方程移项得x －2y ＝－6，两边同除以－6，得截距式x －6＋y3＝1.由方程可知，直线在x 轴、y 轴上的截距分别为－6，3. 题型二 直线的位置关系两条直线的位置关系有相交(特例垂直)、平行、重合三种，主要考察两条直线的平行和垂直．通常借助直线的斜截式方程来判断两条直线的位置关系．解题时要注意分析斜率是否存在，用一般式方程来判断，可以防止讨论斜率不存在的情况．例2 两条直线l 1：ax －by ＋4＝0，l 2：(a －1)x ＋y ＋b ＝0，求分别满足以下条件的a ，b 的值．(1)直线l 1过点(－3，－1)，并且直线l 1与直线l 2垂直； (2)直线l 1与直线l 2平行，并且坐标原点到l 1，l 2的距离相等． 解 (1)∵l 1⊥l 2，∴a (a －1)＋(－b )·1＝0， 即a 2－a －b ＝0.① 又点(－3，－1)在l 1上， ∴－3a ＋b ＋4＝0.② 由①②解得a ＝2，b ＝2. (2)∵l 1∥l 2且l 2的斜率为1－a ，∴l 1的斜率也存在，a b ＝1－a ，即b ＝a1－a .故l 1和l 2的方程可分别表示为l 1∶(a －1)x ＋y ＋4〔a －1〕a＝0，l 2：(a －1)x ＋y ＋a1－a＝0. ∵原点到l 1与l 2的距离相等，∴4⎪⎪⎪⎪⎪⎪a －1a ＝⎪⎪⎪⎪⎪⎪a 1－a ，解得a ＝2或a ＝23.因此⎩⎪⎨⎪⎧a ＝2，b ＝－2，或⎩⎪⎨⎪⎧a ＝23，b ＝2.跟踪演练2 直线l 1：x ＋my ＋6＝0，l 2：(m －2)x ＋3y ＋2m ＝0，求m 的值，使得： (1)l 1与l 2相交；(2)l 1⊥l 2；(3)l 1∥l 2；(4)l 1，l 2重合． 解 (1)由1×3≠m (m －2)， 即m 2－2m －3≠0， 解得m ≠－1且m ≠3.故当m ≠－1且m ≠3时，l 1与l 2相交． (2)当1·(m －2)＋m ·3＝0， 即m ＝12时，l 1⊥l 2.(3)当1×3＝m (m －2)且1×2m ≠6×(m －2)或(m ×2m ≠3×6)，即m ＝－1时，l 1∥l 2.(4)当1×3＝m (m －2)且1×2m ＝6×(m －2)， 即m ＝3时，l 1与l 2重合．题型三 直线与圆、圆与圆的位置关系1．直线与圆的位置关系是高考考察的重点，切线问题更是重中之重．判断直线与圆的位置关系以几何法为主，解题时应充分利用圆的几何性质以简化解题过程．2．解决圆与圆的位置关系的关键是抓住它的几何特征，利用两圆圆心距与两圆半径的和、差的绝对值的大小来确定两圆的位置关系，以及充分利用它的几何图形的形象直观性来分析问题．例3 如下图，在平面直角坐标系xOy 中，圆C 1：(x ＋3)2＋(y －1)2＝4和圆C 2：(x －4)2＋(y －5)2＝ 4.(1)假设直线l 过点A (4，0)，且被圆C 1截得的弦长为23，求直线l 的方程；(2)设P 为平面上的点，满足：存在过点P 的无穷多对互相垂直的直线l 1和l 2，它们分别与圆C 1和圆C 2相交，且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等，试求所有满足条件的点P 的坐标．解 (1)由于直线x ＝4与圆C 1不相交，所以直线l 的斜率存在．设直线l 的方程为y ＝k (x －4)，圆C 1的圆心到直线l 的距离为d ，因为直线l 被圆C 1截得的弦长为23，所以d ＝22－〔3〕2d ＝|1－k 〔－3－4〕|1＋k 2，从而k (24kk ＝0或k ＝－724，所以直线l 的方程为y ＝0或7x ＋24y －28＝0.(2)设点P (a ，b )满足条件，不妨设直线l 1的方程为y －b ＝k (x －a )，k ≠0，那么直线l 2的方程为y －b ＝－1k(x －a )．因为圆C 1和圆C 2的半径相等，且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等，所以圆C 1的圆心到直线l 1的距离和圆C 2的圆心到直线l 2的距离相等，即|1－k 〔－3－a 〕－b |1＋k2＝⎪⎪⎪⎪⎪⎪5＋1k 〔4－a 〕－b 1＋1k 2，整理得|1＋3k ＋ak －b |＝|5k ＋4－a －bk |，从而1＋3k ＋ak －b ＝5k ＋4－a －bk 或1＋3k ＋ak －b ＝ －5k －4＋a ＋bk ，即(a ＋b －2)k ＝b －a ＋3或(a －b ＋8)k ＝a ＋b －5. 因为k 的取值范围有无穷多个，所以⎩⎪⎨⎪⎧a ＋b －2＝0，b －a ＋3＝0或⎩⎪⎨⎪⎧a －b ＋8＝0，a ＋b －5＝0，解得⎩⎪⎨⎪⎧a ＝52，b ＝－12或⎩⎪⎨⎪⎧a ＝－32，b ＝132.这样点P 只可能是点P 1⎝ ⎛⎭⎪⎫52，－12或点P 2⎝ ⎛⎭⎪⎫－32，132.经检验点P 1和P 2满足题目条件．跟踪演练3 直线l 过点P (1，1)并与直线l 1：x －y ＋3＝0和l 2：2x ＋y －6＝0分别交于点A ，B ，假设线段AB 被点P 平分，求：(1)直线l 的方程；(2)以原点O 为圆心且被l 截得的弦长为855的圆的方程．解 (1)依题意可设A (m ，n )，B (2－m ，2－n )，那么⎩⎪⎨⎪⎧m －n ＋3＝0，2〔2－m 〕＋〔2－n 〕－6＝0，即⎩⎪⎨⎪⎧m －n ＝－3，2m ＋n ＝0， 解得A (－1，2)．又l 过点P (1，1)，易得直线AB 的方程为x ＋2y －3＝0， 即直线l 的方程为x ＋2y －3＝0.(2)设圆的半径长为r ，那么r 2＝d 2＋⎝ ⎛⎭⎪⎫4552，其中d 为弦心距，d ＝35，可得r 2＝5，故所求圆的方程为x 2＋y 2＝5. 题型四 与圆有关的最值问题在解决有关直线与圆的最值和范围问题时，最常用的方法是函数法，把要求的最值或范围表示为某个变量的关系式，用函数或方程的知识，尤其是配方的方法求出最值或范围；除此之外，数形结合的思想方法也是一种重要方法，直接根据图形和题设条件，应用图形的直观位置关系得出要求的范围．例4 圆C ：(x ＋2)2＋y 2＝1，P (x ，y )为圆C 上任一点． (1)求y －2x －1的最大值与最小值； (2)求x －2y 的最大值与最小值． 解(1)显然y －2x －1可以看作是点 P (x ，y )与点Q (1，2)连线的斜率．令y －2x －1＝k ，如下图，那么其最大、最小值分别是过点Q (1，2)的圆C 的两条切线的斜率． 对上式整理得kx －y －k ＋2＝0， ∴|－2k ＋2－k |1＋k 2＝1， ∴k ＝3±34.故y －2x －1的最大值是3＋34，最小值是3－34. (2)令u ＝x －2y ，那么u 可视为一组平行线，当直线和圆C 有公共点时，u 的范围即可确定，且最值在直线与圆相切时取得．当直线与圆相切时，有|－2－u |5＝1，解得u ＝－2±5，故x －2y 的最大值是－2＋5，最小值是－2－ 5.跟踪演练4 当曲线y ＝1＋4－x 2与直线y ＝k (x －2)＋4有两个相异交点时，实数k 的取值范围是( ) A.⎝ ⎛⎭⎪⎫0，512 B.⎝ ⎛⎦⎥⎤13，34 C.⎝⎛⎦⎥⎤512，34D.⎝ ⎛⎭⎪⎫512，＋∞ 答案 C解析 曲线y ＝1＋4－x 2是以(0，1)为圆心，2为半径的半圆(如图)，直线y ＝k (x －2)＋4是过定点(2，4)的直线．设切线PC 的斜率为k 0，那么切线PC 的方程为y ＝k 0(x －2)＋4，圆心(0，1)到直线PC 的距离等于半径2，即|1＋2k 0－4|1＋k 20＝2，k 0＝512. 直线PA 的斜率为k 1＝34.所以，实数k 的范围是512<k ≤34.题型五 分类讨论思想分类讨论思想是中学数学的根本思想之一，是历年高考的重点，其实质就是整体问题化为局部问题来解决，化成局部问题后，从而增加了题设的条件．在用二元二次方程表示圆时要分类讨论，在求直线的斜率问题时、用斜率表示直线方程时都要分类讨论．例5 直线l 经过点P (－4，－3)，且被圆(x ＋1)2＋(y ＋2)2＝25截得的弦长为8，求直线l 的方程．解 圆(x ＋1)2＋(y ＋2)2＝25的圆心为(－1，－2)，半径r ＝5.①当直线l 的斜率不存在时，那么l 的方程为x ＝－4，易求得直线与圆的两交点分别为(－4，2)，(－4，6)，显然弦长为8，故直线x ＝－4符合题意． ②当直线l 的斜率存在时，设其方程为y ＋3＝k (x ＋4)， 即kx －y ＋4k －3＝0.由题意可知⎝ ⎛⎭⎪⎫|－k ＋2＋4k －3|1＋k 22＋⎝ ⎛⎭⎪⎫822＝52， 解得k ＝－43，即所求直线方程为4x ＋3y ＋25＝0.综上所述，满足题设的l 方程为x ＝－4或4x ＋3y ＋25＝0.跟踪演练5 过点A (4，－3)作圆C ：(x －3)2＋(y －1)2＝1的切线，求此切线方程． 解 ∵(4－3)2＋(－3－1)2＝17>1， ∴点A 在圆外．①假设所求直线的斜率存在，设切线斜率为k ，那么切线方程为y ＋3＝k (x －4)． 因为圆心C (3，1)到切线的距离等于半径1，所以|3k －1－3－4k |k 2＋1＝1，解得k ＝－158..下载后可自行编辑修改，页脚下载后可删除。

2021年辽宁省沈阳市第一四七高级中学高三数学文上学期期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 《九章算术》中，将底面是直角三角形的直三棱柱称之为“堑堵”，已知某“堑堵”的三视图如图所示，则该“堑堵”的外接球的表面积为（）A．B．C．D．参考答案：B2. 抛物线的焦点为，准线与轴相交于点，过且倾斜角等于60°的直线与抛物线在轴上方的部分相交于点，，垂足为，则四边形的面积等于A． B． C． D．参考答案：C3. 若向量满足∥且，则（）A．4B．3C．2D．0参考答案：D略4. 正项等比数列{a n}中，存在两项a m、a n使得=4a1，且a6=a5+2a4，则的最小值是（）A．B．2 C．D．参考答案：A【考点】基本不等式在最值问题中的应用；等比数列的性质．【分析】由a6=a5+2a4，求出公比q，由=4a1，确定m，n的关系，然后利用基本不等式即可求出则的最小值．【解答】解：在等比数列中，∵a6=a5+2a4，∴，即q2﹣q﹣2=0，解得q=2或q=﹣1（舍去），∵=4a1，∴，即2m+n﹣2=16=24，∴m+n﹣2=4，即m+n=6，∴，∴=（）=，当且仅当，即n=2m时取等号．故选：A．【点评】本题主要考查等比数列的运算性质以及基本不等式的应用，涉及的知识点较多，要求熟练掌握基本不等式成立的条件．5. 已知数列，若利用如图所示的程序框图计算该数列的第10项，则判断框内的条件是（）A．B．C．D．参考答案：B通过分析，本程序框图为“当型“循环结构.判断框内为满足循环的条件第1次循环，s=1+1=2 n=1+1=2；第2次循环，s=2+2=4 n=2+1=3；当执行第10项时，，的值为执行之后加1的值，所以，判断条件应为进入之前的值。

故答案为：或,选B.6. 设抛物线y2=8x的焦点为F，准线为l，P为抛物线上一点，PA⊥l，A为垂足．若直线AF的斜率为，则|PF|=（）A．B．6 C．8 D．16参考答案：C【考点】抛物线的简单性质．【分析】先根据抛物线方程求出焦点坐标和准线方程，根据直线AF的斜率得到AF方程，与准线方程联立，解出A点坐标，因为PA垂直准线l，所以P点与A点纵坐标相同，再代入抛物线方程求P 点横坐标，利用抛物线的定义就可求出|PF|长．【解答】解：∵抛物线方程为y2=8x，∴焦点F（2，0），准线l方程为x=﹣2，∵直线AF的斜率为，直线AF的方程为y=（x﹣2），由，可得A点坐标为（﹣2，4），∵PA⊥l，A为垂足，∴P点纵坐标为4，代入抛物线方程，得P点坐标为（6，4），∴|PF|=|PA|=6﹣（﹣2）=8，故选C．7. 已知复数,则复数在复平面内对应的点在 ( )A．第一象限 B.第二象限 C. 第三象限 D.第四象限参考答案：D略8. △ABC的角A，B，C的对边分别为a，b，c，若cosA=，c﹣a=2，b=3，则a=（）A．2 B．C．3 D．参考答案：A【考点】余弦定理．【分析】由已知条件和余弦定理可得a的方程，解方程可得．【解答】解：由题意可得c=a+2，b=3，cosA=，∴由余弦定理可得cosA=?，代入数据可得=，解方程可得a=2故选：A9. 函数的部分图象如图所示，若将图象上所有点的横坐标缩短为原来的倍（纵坐标不变），再向右平移个单位长度，得到的图象，则的解析式为（）A．B．C ．D ．参考答案：A 由题意，，则，又，而，所以，即，所以，即，故选B ．10. 设全集，则为A ．B ．C ．D ．参考答案：B二、 填空题:本大题共7小题,每小题4分,共28分11. 已知实数满足则的最大值是_____ .参考答案：5【考点】线性规划 【试题解析】作可行域：因为目标函数为：所以z 的几何意义为：目标函数线纵截距的相反数。