小学奥数数图形(1)

第17周计数图形（一）一、知识要点我们已经认识了线段、角、三角形、长方形等基本图形，当这些图形重重叠叠地交错在一起时就构成了复杂的几何图形。

要想准确地计数这类图形中所包含的某一种基本图形的个数，就需要仔细地观察，灵活地运用有关的知识和思考方法，掌握数图形的规律，才能获得正确的结果。

要准确、迅速地计数图形必须注意以下几点：1.弄清被数图形的特征和变化规律。

2.要按一定的顺序数，做到不重复，不遗漏。

二、精讲精练【例题1】数出下面图中有多少条线段。

【思路导航】要正确解答这类问题，需要我们按照一定的顺序来数，做到不重复，不遗漏。

从图中可以看出：从A点出发的不同线段有3条：AB、AC、AD；从B点出发的不同线段有2条：BC、BD；从C点出发的不同线段有1条：CD。

因此，图中共有3＋2＋1＝6条线段。

练习1：数出下列图中有多少条线段。

解法一：4＋3＋2＋1＝10（条）解法二：5×（5－1）÷2＝10（条）解法一：（4＋3＋2＋1）＋（3＋2＋1）＝16（条）解法二：5×（5－1）÷2＋4×（4－1）÷2＝16（条）（2＋1）×2＋4＝10（条）【例题2】数一数下图中有多少个锐角。

【思路导航】数角的方法和数线段的方法类似，图中的五条射线相当于线段上的五个点，因此，要求图中有多少个锐角，可根据公式1＋2＋3＋…＋（总射线数－1），求得：1＋2＋3＋4＝10（个）。

练习2：下列各图中各有多少个锐角？解法一：3＋2＋1＝6（个）解法二：4×（4－1）÷2＝6（个）解法一：5＋4＋3＋2＋1＝15（个）解法二：6×（6－1）÷2＝15（个）解法一：7＋6＋5＋4＋3＋2＋1＝28（个）解法二：8×（8－1）÷2＝28（个）【例题3】数一数下图中共有多少个三角形。

【思路导航】图中AD边上的每一条线段与顶点O构成一个三角形，也就是说，AD边上有几条线段，就构成了几个三角形，因为AD上有4个点，共有1＋2＋3＝6条线段，所以图中有6个三角形。

第1讲 巧数图形一、知识要点小朋友，你想学会数图形的方法吗？要想不重复也不遗漏地数出线段、角、三角形……那就必须要有次序、有条理地数，从中发现规律，以便得到正确的结果。

要正确数出图形的个数，关键是要从基本图形入手。

首先要弄清图形中包含的基本图形是什么，有多少个，其次再数出由基本图形组成的新的图形，最后求出它们的和。

二、精讲精练【例题1】数一数，下图中有几条线段？ 练习1：（1）数出下图中有多少条线段？ （2）数出下图中有几个长方形？【例题2】数出图中有几个角？EABCDDABCODC BA练习2：数出图中有几个角？（1） （2）【例题3】数出下图中共有多少个三角形？练习3：数出图中共有多少个三角形？（1）（2）OCBA ED OC BA PDCBAFE AKG I H G A【例题4】数出下图中有多少个长方形？ 练习4：（1）数出下图中有多少个长方形？（2）数出下图中有多少个正方形？【例题5】有5个同学，每两个人握手一次，一共要握手多少次？ 练习5：（1）银海学校三年级有9个班，每两个班要比赛拔河一次，这样一共要拔河几次？DCBA DCBA（2）有1，2，3，4，5，6，7，8等8个数字，能组成多少个不同的两位数？三、课后作业1、数一数下图中各有多少条线段？（2）（3）2、数一数下图中有多少个锐角。

3、下列各图中各有多少个锐角？4、数一数下面图中各有多少个三角形。

5、数一数下面各图中分别有多少个长方形。

6、数一数，下面各图中分别有几个长方形？7、数一数下列各图中分别有多少个正方形？（每个小方格为边长是1的小正方形）。

数数图形
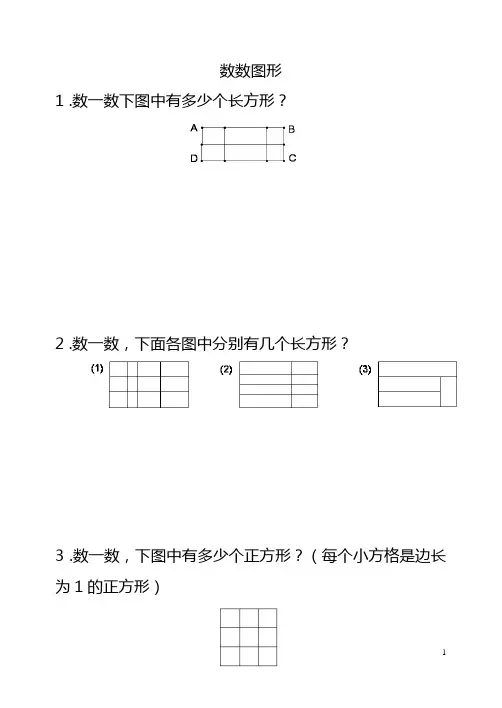
1 .数一数下图中有多少个长方形？
2 .数一数，下面各图中分别有几个长方形？
3 .数一数，下图中有多少个正方形？（每个小方格是边长为1的正方形）
4 .数一数下列各图中分别有多少个正方形？（每个小方格为边长是1的小正方形）
5 .数一数下图中有多少个正方形？（其中每个小方格都是边长为1个长度单位的正方形）
6.数一数下列各图中分别有多少个正方形。

7 .下图中有多少个长方形，其中有多少个是正方形？
8 .从广州到北京的某次快车中途要停靠8个大站，铁路局
要为这次快车准备多少种不同车的车票？这些车票中有多少种不同的票价？
9 .从上海到武汉的航运线上，有9个停靠码头，航运公司要为这段航运线准备多少种不同的船票？
10 .从上海至青岛的某次直快列车，中途要停靠6个大站，这次列车有几种不同票价？
11 .从成都到南京的快车，中途要停靠9个站，有几种不
同的票价？
12 .求下列图中线段长度的总和。

（单位：厘米）
13 .一条线段上有21个点（包括两个端点），相邻两点的距离都是4厘米，所有线段长度的总和是多少？
14 .求下图中所有线段的总和。

（单位：米）
15 .求下图中所有线段的总和。

（单位：厘米）。

第1讲 数数图形个数一、知识要点同学们，你想学会数图形的方法吗要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数，从中发现规律，以便得到正确的结果。

要正确数出图形的个数，关键是要从基本图形入手。

首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新的图形，并求出它们的和。

二、精讲精练【例题1】数出下图中有多少条线段【思路导航】方法一：我们可以采用以线段左端点分类数的方法。

以A 点为左端点的线段有：AB 、AC 、AD 3条；以B 点为左端点的线段有：BC 、BD 2条；以C 点为左端点的线段有：CD 1条。

所以，图中共有线段3+2+1=6（条）。

方法二：把图中线段 AB 、BC 、CD 看做基本线段来数，那么，由1条基本线段构成的线段有：AB 、BC 、CD 3条；由2条基本线段构成的线段有:AC 、BD 2条；由3条基本线段构成的线段有：AD 1条。

所以，图中一共有3+2+1=6（条）线段。

练习1：（1）数出下图中有多少条线段 （2）数出下图中有几个长方形【例题2】数出图中有几个角【思路导航】数角的个数可以采用与数线段相同的方法来数。

方法一：以OA 为一边的角有：∠AOB 、∠AOC 、∠AOD 3个；以OB 为一边的角还有： ∠BOC 、∠BOD 2个；以OC 为一边的角还有：∠COD 1个。

所以，图中共有角3+2+1=6（个）。

方法二：把图中∠AOB 、∠BOC 、∠COD 看做基本角来数，那么，由1个基本角构成的角有：∠AOB 、∠BOC 、∠COD 3个；由2个基本角构成的角有: ∠AOC 、∠BOD 2个；由3个基本角构成的角有：∠AOD 1个。

所以，图中一共有3+2+1=6（个）角。

练习2：数出图中有几个角（1）（2）DABCEA B C D ODC B A DOC B A OCB A【例题3】数出右图中共有多少个三角形【思路导航】方法一：我们可以采用按边分类数的方法。

数图形知识框架同学们，在数图形时，一定要仔细观察，要有条理按顺序地数，做到不要重复，也不要遗漏。

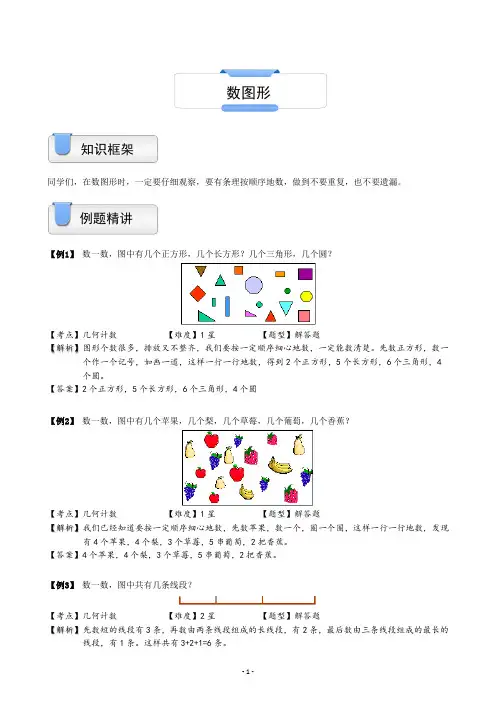
例题精讲【例1】数一数，图中有几个正方形，几个长方形？几个三角形，几个圆？【考点】几何计数【难度】1星【题型】解答题【解析】图形个数很多，排放又不整齐，我们要按一定顺序细心地数，一定能数清楚。

先数正方形，数一个作一个记号，如画一道，这样一行一行地数，得到2个正方形，5个长方形，6个三角形，4个圆。

【答案】2个正方形，5个长方形，6个三角形，4个圆【例2】数一数，图中有几个苹果，几个梨，几个草莓，几个葡萄，几个香蕉？【考点】几何计数【难度】1星【题型】解答题【解析】我们已经知道要按一定顺序细心地数，先数苹果，数一个，圈一个圈，这样一行一行地数，发现有4个苹果，4个梨，3个草莓，5串葡萄，2把香蕉。

【答案】4个苹果，4个梨，3个草莓，5串葡萄，2把香蕉。

【例3】数一数，图中共有几条线段？【考点】几何计数【难度】2星【题型】解答题【解析】先数短的线段有3条，再数由两条线段组成的长线段，有2条，最后数由三条线段组成的最长的线段，有1条。

这样共有3+2+1=6条。

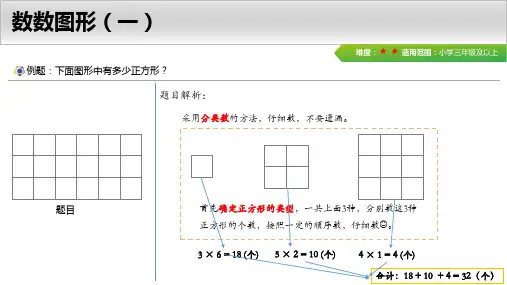
【例4】数一数，图中共有几个小正方形？【考点】几何计数【难度】2星【题型】解答题【解析】第一幅图有4个，第二幅图有3×3=9个，第三幅图有4×4=16个，第四幅图有5×5=25个，这样共有4+9+16+25=54个。

【答案】54个【例5】数一数，图中共有几个长方形？【考点】几何计数【难度】2星【题型】解答题【解析】先数单个的长方形有三个，再数由两个长方形组成的大长方形，有1个，最后数由三个长方形组成的最大的长方形有1个，这样共有3+1+1=5个。

【答案】5个【例6】数一数图中共有几个三角形？【考点】几何计数【难度】3星【题型】解答题【解析】数之前，先将每个图形编号，编好后，先数单个三角形1、4、3号，共3个。

再数两个图形合成的三角形，1+2号，2+3号，3+4号，4+1号，按顺序两个两个合并，共4个三角形。