大学物理-82电通量高斯定理

大学物理电场的高斯定律与电通量电场是物理学中一个重要的概念，它描述了电荷在空间中产生的力的作用。

为了更好地理解电场的性质与行为，科学家们提出了一系列电场定律。

其中，高斯定律是电场学中的基本原理之一。

本文将详细介绍大学物理中的电场的高斯定律以及与之相关的电通量。

一、电场的概念回顾在深入探讨高斯定律之前，我们先来回顾一下电场的概念。

电场是由电荷产生的一种物理场。

当一个电荷在空间中存在时，其周围就形成了一个电场。

电场可以用向量表示，它的方向和大小分别表示了该点上所受到的电场力的方向和大小。

二、高斯定律的提出高斯定律是由德国科学家高斯在19世纪初提出的。

该定律是描述电场与电荷分布之间关系的基本原理。

高斯定律的数学表达为：∮E·dA = Q/ε0其中，∮E·dA表示电场E通过闭合曲面的电通量，Q表示该闭合曲面内的电荷总量，ε0为真空中的介电常数。

三、电通量的概念在理解高斯定律之前，我们需要先了解电通量的概念。

电通量是表示电场通过某一给定曲面的电量的概念。

电通量可以用数学公式∮E·dA来表示，其中E为该点的电场强度矢量，dA表示曲面元素的面积，∮表示对整个闭合曲面进行积分。

四、高斯定律的意义与应用高斯定律的意义在于揭示了电荷分布如何影响电场的性质和分布。

通过高斯定律，我们可以计算电场通过一个闭合曲面的电通量，并利用电通量的性质推导相关的物理量。

高斯定律的应用非常广泛，例如在电场分析、电荷分布计算以及电场强度的测量等方面都有着重要的作用。

通过高斯定律，我们可以简化一些复杂的电场计算问题，节省时间和工作量。

五、高斯定律的适用条件高斯定律的适用条件主要有两个：1. 电场要具有空间的轴对称性或平面对称性。

这意味着，电场应当在某个坐标系下保持不变，使得我们可以简化电场的计算。

2. 电场的电荷分布应当在所选择的闭合曲面内或外具有一定的对称性。

这样，我们才能利用高斯定律进行计算。

六、高斯定律的推导过程我们通过推导可以更好地理解和应用高斯定律。

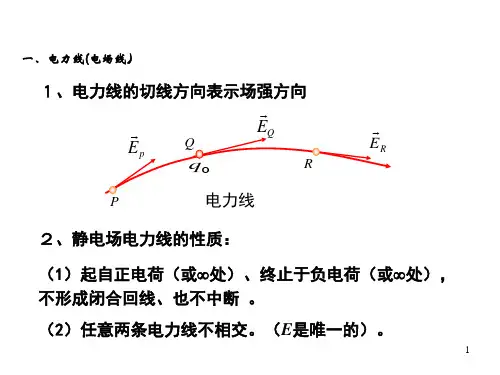
电通量、高斯定理1、均匀电场的场强E与半径为R 的半球面的轴线平行，则通过半球面的电场强度通量φ = πR 2E ，若在半球面的球心处再放置点电荷q ，q不改变E分布，则通过半球面的电场强度通量 φ =πR 2E ±q/2ε0。

2、真空中的高斯定理的数学表达式为∑⎰=⋅0/εq s d E i s ，其物理意义是静电场是有源场。

3、一点电荷q 位于一位立方体中心，立方体边长为a ，则通过立方体每个表面的E的通量是q/6ε0；若把这电荷移到立方体的一个顶角上，这时通过电荷所在顶角的三个面E的通量是 0 ，通过立方体另外三个面的E的通量是 q/8ε0。

4、两个无限大均匀带正电的平行平面，电荷面密度分别为σ1和σ2，且σ1＞σ2，则两平面间电场强度的大小是( C )(A)(B) (C)(D) 5、应用高斯定理求场强E时，要求E的分布具有对称性，对于没有对称性的电场分布，例如电偶极子产生的电场，高斯定理就不再成立，你认为这种说法：( B )(A)正确 (B)错误 (C)无法判断6、下述带电体系的场强分布可能用高斯定理来计算的是( D )(A)均匀带电圆板 (B)有限长均匀带电棒 (C)电偶极子 (D)带电介质球(电荷体密度是离球心距离r 的函数) 7、如果在静电场中所作的封闭曲面内没有净电荷，则( C )(A)封闭面上的电通量一定为零，场强也一定为零；()0212/εσσ+()021/εσσ+()0212/εσσ-()021/εσσ-(B)封闭面上的电通量不一定为零，场强则一定为零；(C)封闭面上的电通量一定为零；场强不一定为零；(D)封闭面上的电通量不一定为零；场强不一定为零。

8、无限长均匀带电圆柱体，电荷体密度为ρ，半径为R，求柱体内外的场强分布解：作一半径为r，高为h的同轴圆柱面为高斯面根据对称性分析，圆柱面侧面上任一点的场强大小相等，方向沿矢径方向⎰⎰⎰⎰⋅+⋅+⋅=⋅侧面下底上底s dEs dEs dEs dEs=⎰⋅侧面s dE=E⎰侧面ds=2rhEπ（1）r < R时, ∑=ρπhrqi2,2/2ερππhrrhE=,2ερrE=（2）r > R时, ∑=ρπhRqi2,2/2ερππhRrhE=,rRE22ερ=∴=E)(,2)(,22RrrRRrr><ερερ。

大学物理高斯定理简介大学物理中，高斯定理（也称为电通量定理）是电学领域中的一个重要定理，它描述了电场通过一个封闭曲面的总电通量与该曲面内的电荷量之间的关系。

高斯定理的数学表达式是一个面积分，通过对电场和曲面的特性进行积分计算，我们可以计算得到相应的电通量。

定理表述高斯定理可以用数学公式表述如下：其中， - 表示对封闭曲面 S 的面积分； - 表示电场的向量；- 表示面元矢量； - 是真空中的介电常数（气体中也可近似使用该值）； - 表示电荷密度在封闭曲面内的体积分。

解读根据高斯定理，电通量与环绕其的电荷量成正比。

如果电场线密集，表示电通量会相应增大，而如果电场线稀疏，表示电通量相应减少。

因此，高斯定理为我们提供了一种计算电场分布和电荷分布之间关系的方法。

高斯定理的背后思想是通过找到一个适当的曲面，使得计算曲面上的电场更加容易，从而求得电场的总电通量。

这个曲面可以是球面、柱面、立方体等等，具体选择曲面要与问题的几何特征和对称性相匹配。

应用举例例子1：均匀带电球考虑一个均匀带电球体，电荷密度为，半径为。

我们想通过高斯定理计算球内外的电场。

在这种情况下，由于球具有球对称性，我们选择一个以球心为中心的球面作为高斯曲面。

根据球对称性，球的电场在球面上处处相等，并且与球面的法线垂直。

因此，和在点积后等于，其中是球面上的电场强度。

曲面的面积元等于球的表面积元。

因此，高斯定理可简化为：等式的右边是整个球的表面积，用！表示。

由于电场是球对称的，且垂直于球面，所以电场与面积元相乘的结果在整个球面上是相等的。

由于曲面上的电场都是相等的，整个球面的面积元乘以电场强度后等于电场强度乘以整个球面的面积，所以可以简化为：解得：其中，为球内的总电荷量。

例子2：无限长均匀带电线考虑一个无限长均匀带电线，线密度为。

我们想通过高斯定理计算线外的电场。

在这种情况下，由于线具有柱对称性，我们选择一个以线为轴的柱面作为高斯曲面。

我们将柱面的两个底面分别设为 A 和 B，其中 A 的面积为，B 的面积为。